A non-autonomous multi-strain SIS epidemic model

Abstract

In this paper we consider a non-autonomous multi-strain SIS epidemic model with periodic coefficients. Reproduction numbers and invasion reproduction numbers are derived which agree well with their counterparts usually derived from autonomous epidemic models. With conditions on these reproduction numbers typical results are obtained, such as the local and global stability of the disease-free equilibrium. Existence and uniqueness of a single-strain periodic solution is established. Based on conditions on the invasion reproduction numbers, local stability of the single-strain periodic solution is shown. In a two-strain version of the model, conditions for uniform strong persistence are derived, and coexistence of the two strains is established. Coexistence, however, does not occur if the transmission rates of the different strains are linearly dependent.

Keywords:

• periodicity
• non-autonomous differential equations
• SIS epidemic model
• seasonality
• reproduction numbers
• invasion reproduction numbers
• competitive exclusion
• coexistence
• multi-strain interactions

AMS Subject Classification :

• 92D30
• 92D40

1. Introduction

The incidence of many infectious diseases fluctuates over time and often exhibits periodic behaviour. One of the well-known examples are data on weekly measles notification in England and Wales for the period 1948–1968 (see [5, Figure 6.3]). The number of measles cases per week oscillates with a period between two peaks of 2 years. Other childhood diseases such as mumps, chicken-pox, rubella, and pertussis have also been found to exhibit seasonal behaviour. The periodicity of 1 year in many childhood diseases is attributed to the periodic contact rate the children have during academic school years. Although not restricted to children, influenza also exhibits distinct seasonality, with a season in the US spanning the time between October and May. During the first 2-3 years after the first case, the number of human cases of avian influenza also seemed to follow seasonal pattern 33.

Numerous articles have been devoted to explaining the periodicity in the disease incidence rates (see 18 for a review). Various scenarios how periodicity may arise in epidemic models have been set forward. Those include

1.	the possibility that the presence of certain classes can destabilize the equilibrium of models with constant coefficients and lead to sustain oscillations,
2.	the possibility that the incidence is not bilinear but has more complex form,
3.	the possibility that the transmission rates are periodic,
4.	the presence of delay(s) in the model,
5.	the presence of host age-structure,
6.	the interaction of two strains, one of which mutates into the other 20.

The possibility that the contact rate is periodic has lead to the consideration of epidemic models with time-dependent coefficients. An epidemic SIS model with periodic contact rate was first considered by Hethcote 17. Epidemic SIR and SEIR models with periodic contact rate were considered by Dietz 15. The non-autonomous SIR and SEIR models were further investigated both analytically and numerically by Smith 36 and Schwartz (see 35 for a review). More recently Zhang and Teng 43 established persistence and extinction in the disease for a non-autonomous SEIR model with vital dynamics.

One of the key difficulties in working with non-autonomous models is defining the reproduction number ℛ₀. Many of the articles in the literature do not define a reproductive number but work with threshold conditions that fit best the analysis. Ma and Ma 26 consider the problem of defining adequate reproduction numbers for various non-autonomous SIR and SEIR models. The authors argue that the reproduction number should be defined as the reproduction number of a constant coefficient system obtained from the non-autonomous system by averaging the time-dependent coefficients. In all cases they are able to establish local stability of the disease-free equilibrium with the usual condition on the reproduction number . However, Ma and Ma show through simulation that the SEIR model can have a solution where the number of infected individuals goes to zero despite that the reproduction number is larger than one (see [26, Figure 1]). Thus, the condition does not necessarily lead to persistence.

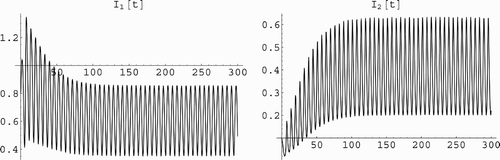
Figure 1. This figure gives an example of coexistence of the two strains in the population. The left figure illustrates that the number infected individuals with strain one I ₁(t) persists and tends to an oscillatory solution. The right figure illustrates that the number infected individuals with strain two I ₂(t) persists and tends to an oscillatory solution. The parameter values for both figures are: β₁(t)=1.1(1+0.9 sin(t)), β₂ (t)=1.5 (1+0.1 cos(t)), γ₁=0.1, γ₂=0.5, μ=0.5. The reproduction numbers of the two strains are ℛ₁=1.83333, ℛ₂=1.5.

The causative agents of many diseases are represented by multiple genetically distinct variants. Early autonomous multi-strain models suggested that competitive exclusion is the only possible outcome of the competition of many strains. Bremermann and Thieme 7 show that even if all reproduction numbers are larger than one, only the strain with the largest reproduction number persists while the remaining strains are eliminated. These results raised a question regarding the mechanisms that are responsible for the genetic diversity of pathogens in nature. Mechanisms such as super-infection 29 32, coinfection 30, mutation 20, vertical transmission 22, and host age heterogeneity 28 were proposed as possible mechanisms that support diversity of pathogens. There is a significant literature devoted to the problem of competition of strains in autonomous multi-strain epidemic models which is reviewed in 21 27 42.

Diseases that exhibit seasonality may also be represented by pathogens that experience mutation and exist as multiple strains. The most notable example of this scenario is influenza. Several intrinsic mechanisms such as quarantine 34 or host age structure 8, leading to periodicity in autonomous epidemic models, have been suggested as possible mechanisms for the influenza seasonality. Other possible mechanisms such as crowding during cooler months (increased contact rate), weakening of the host immune system (increased susceptibility), and ability of the viral particles to persist in cooler temperatures 25 could be modelled with periodic transmission rates. This would require the development and analysis of multi-strain non-autonomous models. Multi-strain non-autonomous epidemic models do not seem to have been discussed so far.

In this paper we consider a multi-strain SIS model with periodic coefficients. Since we assume the total population size constant and equal to one, we eliminate the variable for the susceptible individuals. The resulting system is a variant of the classical Lotka–Volterra n-species competition system. In contrast to multi-strain non-autonomous epidemic models, Lotka–Volterra competition systems have been studied extensively not only in the constant coefficient case but also in the case of time dependent (periodic) coefficients. The pioneering work on non-autonomous Lotka–Volterra competition systems is due to Jim Cushing, whose contribution to science in general, and to mathematical biology in particular, we are celebrating today on occasion of his 65th birthday. In the late 1970s and early 1980s, Cushing authored a number of articles devoted to the non-autonomous versions of many classical ecological models: Lotka–Volterra predator–prey models 10 13, Lotka–Volterra 2-species competition models 11 14, n-species predator-prey/competition models 9, and the more-general Kolmogorov systems with periodic coefficients 12. In 11 Cushing showed that competing species may coexist in a competitive systems with periodic coefficients even if they will competitively exclude each other in a system with constant coefficients equal to the time averages of the periodic coefficients. Cushing's early results were extended in 31. Cushing's work motivated a number of articles on competitive non-autonomous Lotka–Volterra systems (e.g. 1 3 6 16 19 23 37). Even today the questions on global persistence and extinction of the species in such systems is still being investigated 2 4 24.

This paper is structured as follows. Section 2 introduces the model, its re-formulations, the reproduction numbers and results on extinction of the disease. Section 3 establishes the existence of a single-strain periodic solution corresponding to each strain. Section 4 derives conditions for the local stability of the single-strain periodic solutions. Section 5 considers a two-strain version of the model and establishes the existence and convergence to a periodic coexistence solution. Section 6 discusses the special case when the transmission rate is a product of a periodic contact rate and a constant probability of transmission, and establishes competitive exclusion in that case. Section 7 summarizes the results and draws conclusions.

2. A non-autonomous SIS model

In this section we introduce a non-autonomous SIS epidemic model with multiple strains. We study a model with recruitment and deaths. We assume all newly recruited individuals are susceptible. The recruitment and mortality rate are assumed equal and denoted by μ(t). The function μ(t) is assumed non-negative and periodic. In nature the recruitment rate needs to be periodic if it models seasonality in births. Many species breed in strictly defined breeding seasons and the birth/recruitment rates may be periodic. The transmission rate of strain i is denoted by β _i (t) for i=1, …, n. All transmission rates are also assumed non-negative and periodic. The transmission rate may be periodic because of migratory patterns of host species. In human epidemic models the contact rate can vary with the time in the year as is the case with students academic years. Finally, we denote by γ _i (t) the recovery rate from strain i. All recovery rates are also assumed non-negative and periodic. All periodic functions have period ω. The SIS model with multiple strains takes the form:

The number of susceptibles in the population is denoted by S(t). The number of individuals infected by strain j is denoted by I _j (t). The total population is given by

The differential equation satisfied by the total population size is obtained by adding all equations in the system (1):

Integrating the equation for the total population size, we get

where N ₀ is the value of the total population size at time zero. Since

we have . In the remainder of this article we will assume that the total population size is constant and rescaled to one. Thus, we will assume that system (1) is subject to the initial conditions S(0)=S ₀, for j=1, …, n that satisfy

This assumption implies that N(t)=1 for all t. We use this equation to eliminate the number of susceptible individuals S(t). We have

Using this expression the system (1) can be rewritten in the form

The slightly more general case where the initial conditions do not add to one will lead to a system similar to system (2) in which the number 1 is replaced with the given function N(t). Such a system can be handled similarly to system (2) but will not be discussed in this article. We consider the system (2) on the set:

It is easy to see that the set Ω is positively invariant. Our aim is to define basic reproduction numbers of the strains such that if the parameter-functions μ(t), β _j (t), γ _j (t) are assumed constant, the reproduction numbers of the strains for the system with constant coefficients are recovered. To define the basic reproduction numbers of the strains, we first introduce the average of a periodic function over its period. If f(t) is a periodic function of period ω, then the average of f is given by

It is not hard to see (a proof is given in 41, Section 3.1.2) that

We define the reproduction numbers of the strains as

This definition is basically the same definition as in 26 and a special case of the definition preceding Theorem 3.1 in 40. The disease-free equilibrium of the system (1) is given by . To establish the local stability or instability of the disease-free equilibrium we linearize around the disease-free equilibrium. Let S(t)=s(t)+1, , for j=1, …, n, where s(t) and i _j (t) are the perturbations. Clearly i _j (t) are non-negative, but s(t) does not necessarily have a definite sign. The linearized system for the perturbations becomes:

Solving the equation for i _j (t) we get

If then for j=1, …, n. If, however, for some j, then . We have established the following result.

Proposition 2.1

The disease-free equilibrium of the system (1) is locally asymptotically stable if for all j=1, …, n. If there exists then the disease-free equilibrium ℰ₀ is unstable.

In fact a stronger result is possible. The following proposition gives a sufficient condition for the eradication of strain j. We will see in the next section that if that condition fails to hold, then the corresponding strain can survive in the absence of competition.

Proposition 2.2

If for some j, then

To see this result, notice that since S(t)≤1 we have

Solving this inequality we have

Thus, I _j (t)→0 as t→∞.

Proposition 2.2 implies that if for all j=1, …, n, then the disease-free equilibrium ℰ₀ is globally asymptotically stable.

3. Existence of single-strain periodic solution

In this section we show that if for some j and for all k=1, …, n and k≠j, then strain j may survive, while the rest will be eliminated. Without loss of generality we may assume , and the remaining basic reproduction numbers are smaller than one. As a first step we assume I _k (0)=0 for k=2, …, n. This implies that I _k (t)=0 for all t. We will show that if , then the equation

has a unique positive periodic solution ξ(t). In the above equation we have omitted the subscript one. Equation (4) is known as the periodic Bernoulli equation and has received much attention in the literature. As a result the fact that it has a unique periodic solution is well-known. For alternative approach to it see 41.

We are considering Equation (4) on the domain

To see the existence of a periodic solution, we define the operator 𝒫 which maps the interval [0, 1] into itself:

The operator 𝒫 is the Poincaré map whose action is defined as follows. If I(0)=I ₀, then

where, I(t, I ₀) is the solution of the Equation (4) which starts at I ₀. The Poincaré map is continuously differentiable, one-to-one. It satisfies: , and . The number I _p ∈(0, 1) is an initial value of a periodic solution if and only if

that is, if I _p is a fixed point of the Poincaré map. Therefore, in order to show existence of a positive, periodic solution of Equation (4), we have to show that the Poincaré map has a fixed point. Denote by

Then the derivative of the Poincaré map is given as follows:

One can obtain the derivative of the Poincaré map by differentiating the Equation (4) by the initial condition I ₀:

Differentiating the initial condition of I(0)=I ₀ by I ₀ we obtain the following initial condition for v: v(0)=1. The differential equation for v can be solved. That gives the following expression for the derivative of the Poincaré map:

Clearly . This implies that Poincaré map is increasing. Thus, if I ₁ and I ₂ are two initial conditions satisfying I ₁<I ₂ then . Furthermore,

This implies that because . Hence, for I ₀ small enough we have

Therefore,

for I ₀ small enough. Since then changes sign in the interval (0,1). Therefore, there exists I _p , such that

This establishes the existence of a positive periodic solution of Equation (4).

To show uniqueness, assume there exist two fixed points I _p1 and I _p2 which are distinct. Without loss of generality we may assume I _p1<I _p2. We have

where I _m satisfies . These last inequalities imply

First, we note that if I(t, I _p ) is a periodic solution that satisfies Equation (4), then

Hence,

Thus, we obtain a contradiction with Equation (5). The contradiction is a result of the assumption that we have two distinct positive periodic solutions.

Summarizing the results in this section we have the following theorem.

Theorem 3.1

For each i for which there exist a unique, positive periodic function ξ _i (t) such that is a solution to the system (2). Furthermore, if is a solution of the system (2) starting from I _i (0)>0, we have

To complete the proof of the Theorem 3.1 we have to establish the convergence to the periodic solution. We again assume that , and we consider the solutions of Equation (4). Let I(t) be an arbitrary solution, starting from the initial condition I ₀. We recall that I _p is the initial condition for the periodic solution. We assume that I ₀≠I _p . We have two choices or . Assume . The other case can be addressed in a similar way. Since the Poicarè map is increasing, we have . Consequently, the sequence is decreasing, and since it is bounded, it must have a limit:

The number I _∞ is necessarily a fixed point of the Poincarè map . Thus, I _∞=0 or . Assume that I _∞=0. Then for some N the number is small enough so that from the properties of the Poincarè map we have which contradicts the fact that the sequence is decreasing. Therefore, . Consequently, the limit (7) holds. This completes the proof of the Theorem 3.1.

4. Local stability of the single-strain periodic solutions

The single-strain periodic solutions play the role of the dominance equilibria in models with constant coefficients. Just as in the constant coefficient case, the stability properties of these single-strain periodic solutions determine the outcome of the competition of the strains. Determining the global stability of the single-strain periodic solutions is only possible in some cases but it is difficult in the general case. We, however, can consider the local stability. To determine the local stability of each single-strain periodic solution, one linearizes the system (2) around the single-strain periodic solution. Without loss of generality we may consider the single-strain solution corresponding to the periodic solution for strain one . The other cases are symmetrical. Let and , where x _j (t) with j=1, …, n are the perturbations. Then the linearized system takes the form:

The linear system (8) can be written in vector form as , where A(t) is the time-dependent matrix of the coefficients. The linearized systems gives the dynamics of the solutions near a periodic solution. To investigate the stability of the zeroth solution of the linearized system, one has to use Floquet theory. To use these theory, one needs a fundamental matrix. To find a fundamental matrix, we have to find a system of linearly independent solution of the system, that is we have to solve the system. Clearly, setting x _k (t)=0 for k=2, …, n, and then solving the first equation, will give us one solution. The first equation becomes:

one solution of which is , where a ₁₁(t) denotes the coefficient of x ₁ in the right-hand side. Hence, is the first column of the fundamental matrix. To obtain the remaining solutions, we set x _j (t)=0 for j=2, …, n and j≠k, where k≠1. Then we solve the kth equation:

where a _kk (t) is the coefficient in front of x _k in the right-hand side of the kth equation in the system (8). This value of x _k (t) is substituted in the first equation, and the first equation is then solved. The solution of the first equation in this case is a complex expression, which will be denoted by x _1k (t). The following fundamental matrix is obtained:

The Floquet multipliers are the eigenvalues of the matrix . It is straightforward to see that they are

From here one can read off the Floquet exponents. The first Floquet exponent is different from the remaining exponents, and is given by the expression

We recall that ξ₁(t) is the periodic solution of the first equation. Therefore, this periodic solution satisfies the Equation (4). We integrate Equation (4) from zero to ω. Since we have

we also have that

Hence, the Floquet exponents are:

Clearly, the Floquet exponent . Thus, the stability of the zero solution of the linearized system, and therefore the linear stability of the single-strain oscillatory solution of the system (2), depends on the remaining Floquet exponents. If for all j=2, …, n, then the single-strain oscillatory solution is locally asymptotically stable. If there exists for some 2≤k≤n, then the single-strain oscillatory solution is unstable.

From the Floquet exponents we can define the invasion reproduction numbers of strain j at the equilibrium of strain one:

The invasion reproduction numbers and the Floquet exponents are related: if and only if . The results of this section can be summarized in the following theorem.

Theorem 4.1

The single-strain periodic solution is locally asymptotically stable if

If for some j≠i, then the single-strain periodic solution is unstable.

In the remainder of this section we establish global stability of the single-strain periodic solution under given conditions. These conditions are sufficient but not necessary. We again derive the result for the single-strain periodic solution of strain one. Analogous results hold for the other single-strain periodic solutions.

Theorem 4.2

If and for j=2, …, n, then the single-strain periodic solution is globally stable.

To see this result we use Proposition 2.2. Let ε>0 be small so that . Since Proposition 2.2 implies that I _j (t)→0 for j=2, …, n as t→∞. Then there exists T such that

By shifting the dynamical system (2) we may assume that

Thus, the solution of the first equation in system (2) satisfies the following inequalities:

Together with the above inequalities, consider the following equations:

The solution of the first equation of system (2) I ₁(t) satisfies

where X ₁(t) and are the solutions of the above two equations with the same initial conditions. The smaller the ε, the closer is the solution to X ₁(t). We saw in Section 3 that the first equation in Equation (13) has a unique periodic solution ξ₁(t). Similar deliberations as in Section 3 can show that the same is true for the second equation in Equation (13), particularly because . Denote by the unique periodic solution of the second equation of Equation (13). It can similarly be shown that that periodic solution is globally stable. Taking the limit as t→∞ in inequalities (14) by Theorem 3.1 we get

Since the above inequalities are valid for any ε no matter how small, we obtain that as t→∞. This completes the proof.

5. Coexistence

In this section we show that coexistence in an oscillatory regime is possible. Although we believe that the result below can be extended to n strains, we consider a two-strain version of the model (2).

The system (15) is competitive ([38, p. 33]). If we denote by the right-hand side of equation i, for i=1, 2, then

Let 𝒫 be the Poincarè map for the system (15). Therefore, if , then . The following Theorem can be found in [39, p. 170].

Theorem 5.1

Let the sequence be bounded. Then the sequence is converging, that is there exists I _p such that

Moreover, I _p is a fixed point of the Poincarè map .

This theorem says that if is an arbitrary solution of system (15) starting from an arbitrary initial condition , then there exists a periodic solution of the system (15), denoted by such that the solution converges to that periodic solution. The theorem does not say whether and . Thus, in theory the limit periodic solution could be one of the single-strain periodic solutions or whose existence was established in the previous sections.

In what follows we show that under certain conditions the solution of the system (15) is persistent. We say that strain i is weakly uniformly persistent, if there exists δ>0, independent of the initial conditions, such that

We say that strain i is uniformly strongly persistent if there exists a number δ>0, independent of the initial conditions, such that

Clearly, if a strain is uniformly strongly persistent, it is also uniformly weakly persistent. The opposite statement is not true. We establish the uniform strong persistence for both strains in the following theorem.

Theorem 5.2

Assume and that the invasion reproduction number of strain i is larger than one, . Then, strain i is uniformly strongly persistent.

To see this result assume without loss of generality and . The first condition guarantees that strain one in the absence of strain two has a non-trivial periodic solution. The second condition says that strain two can invade the periodic solution of strain one. A consequence of the second condition is that . We will establish uniform strong persistence of strain two. The other case is established in the same way. First we establish the uniform weak persistence. Assume the contrary, that is assume that for every ε we have . Then for a fixed ε>0 there exists T such that for all t>T, we have .

From the first equation in system (15) we obtain the following inequality:

Let X(t) be the solution of the equation corresponding to the above inequality and starting from the same initial condition as I ₁ in the system (15). Thus, X(t) solves:

Then we have for all t. Since , we know that Equation (17) has a unique periodic solution ξ₁(t), and every solution to Equation (17) approaches that periodic solution. Thus, as t→∞. We note that ξ₁(t) is also the periodic function in the single-strain periodic solution . Furthermore, there exists T ₁ such that for all t>T ₁ we have

Shifting the dynamical system we may assume that and for all t>0. Using these inequalities in the second equation of system (15) we have

Solving this inequality we have

Assuming ε is small enough so that

we get that as t→∞. That is a contradiction with our assumption that I ₂(t) is not uniformly weakly persistent. To show uniform strong persistence we use Theorem 2.3 in 40. The existence of a compact attractive set follows from the fact that solutions are bounded I _j (t)≤1 for all t>0. The first condition in the theorem follows from the fact that for all s>0 such that I ₂(s)>0. Property (PS) in 40 can be established as in the case of the SIRS model in 40. Then Theorem 2.3 in 40 implies the uniform strong persistence.

The above result leads to the following corollary

Corollary 5.3

Assume and and that both invasion reproduction numbers are larger than one, that is and . Then, every solution converges to a coexistence periodic solution where and .

To see this corollary, we notice that under the above conditions Theorem 5.2 implies that both I ₁(t) and I ₂(t) are uniformly strongly persistent, that is there exists δ>0 such that

for all initial conditions with both components being non-zero. Theorem 5.1 implies, however, that those solutions converge to a periodic solution . Since,

we have that the two components of the periodic solution η₁(t) and η₂(t) are both non-zero. Therefore, the convergence is to a coexistence periodic solution.

We illustrate the periodic coexistence in Figure 1. The results in Theorem 5.2 and Corollary 5.3 presumably can be obtained from 31 but the rescaling there makes the mathematical conditions imposed difficult to interpret biologically.

6. Is periodicity in the contact rate sufficient for coexistence?

We motivated the consideration of multi-strain epidemic models with periodic coefficients by the observed periodicity in childhood diseases and influenza. In the case of the childhood diseases it has been suggested that periodicity stems from the school-year system which makes the contact rate among children periodic. Is periodic contact rate sufficient to sustain pathogen diversity? We address this question in this section. We recall that in the constant coefficient case the transmission rate of strain i is a product of the contact rate of the population c (assuming that all classes have the same contact rate) and the probability of transmission of strain i – p _i :

We consider the model (1) under the assumption that the strain-specific periodic transmission rate β _i (t) is represented as follows:

where the contact rate c(t) is a non-negative periodic function of period ω and the probability of transmission of strain i remains constant. The reproduction number of strain i is then given by

Surprisingly, coexistence does not occur, and competitive exclusion is the only outcome of the multi-strain competition in periodic environments, even if the remaining parameters μ(t) and γ _i (t) are still assumed periodic (see 43). As before, the strain with the largest reproductive number eliminates the rest. This result is established in the following theorem, where we have assumed without loss of generality that strain one has the largest reproduction number.

Theorem 6.1

Assume for i=1, …, n. Assume, in addition, that for j=2, …, n. Then,

and

To see the claim in this theorem, for a fixed j>1 consider the quantity

Differentiating η with respect to time we get

Simplifying the expression on the right-hand side we obtain

Dividing by η(t), integrating from zero to t, and dividing by t to get the averages, we are lead to:

Taking the limit as t→∞, the right-hand side above converges to the positive number

Since and η(0)>0, then clearly as t→∞. Since I ₁(t) is bounded, the fact that as t→∞ implies that

Then, similarly to Equation (4) one can show that strain one persists, and in fact the solutions of the system (2) converge to .

7. Summary of results

In this paper we introduce an n-strain SIS model with periodic coefficients. The birth and death rates are assumed to be the same so that the total population is constant and equal to one. That is, the number of individuals in each class is in fact the proportion of individuals in the various classes. For this model we succeed in defining reproduction numbers for each strain ℛ _i which agree with the corresponding reproduction numbers of the autonomous system obtained from system (1) by assuming all coefficients constant and equal to the averages of time dependent coefficients. We establish the following results:

1.	There is a unique disease-free equilibrium which is locally and globally stable if all reproduction numbers are smaller than one. The disease-free equilibrium is unstable if one of the reproduction number is greater than one. These observations agree with similar observations made for multi-strain autonomous models.
2.	Moreover, we establish that if for any strain i, then the number of individuals infected with this strain will go to zero, independently of the behaviour of the other infective classes.
3.	We establish that to each strain there corresponds a unique single-strain periodic solution, if its reproduction number is greater than one. This periodic solution is globally stable in the hyper-plane where all other strains are extinct.
4.	The single-strain periodic solution is locally stable if the invasion numbers of all other strains at the equilibrium of the resident strain are less than one. The single-strain periodic solution is unstable if there is an invasion number grater than one.
5.	For the model with two strains we establish the existence of at least one periodic coexistence solution. As a part of this result, we derive conditions on the reproduction numbers and invasion reproduction numbers that guarantee uniform strong persistence of a strain.
6.	Finally, for the n-strain model we establish that if the transmission rate is periodic because the contact rate is periodic, but the probability of transmission given a contact is constant, , then coexistence does not occur, and competitive exclusion is the only outcome. In agreement with the autonomous system the strain with the largest reproduction number eliminates the rest.

The techniques used to establish competitive exclusion for the multi-strain SIR model in 7 could be used to establish that competitive exclusion is the only outcome in the autonomous version of model (1) with constant coefficients equal to the averages of the periodic coefficients. In contrast, our results show that the non-autonomous model (1) allows for coexistence. This result, however, is not entirely surprising. Coexistence between two competing bacteria as a result of periodicity in the dilution rate has been obtained in 39. What causes the coexistence in our case? Our results show that coexistence occurs as a result of distinct, periodic transmission rates for the strains β _i (t) which are not linearly dependent. As Figure 1 shows in this case periodicity in the death and recovery rates is not necessary. If the transmission rates are periodic only because of the contact rate, that is, they have the form:

competitive exclusion is the only outcome. This observation has an interesting implication for influenza. The periodicity in influenza prevalence has fascinated researchers for quite some time. Influenza seasonality is still not very well understood. Multiple hypotheses have been set forth 25. Our results here suggest that from the hypotheses set forth in 25, the mechanism(s) that have the potential to lead to influenza's seasonality, given influenza's genetic diversity, are those that could lead to periodic probability of transmission/susceptibility.

Acknowledgements

This article was inspired by some modelling of avian influenza that my student Joseph Lucchetti did. The author thanks Horst R. Thieme for his valuable comments. The author also thanks the referees for their constructive remarks. The author acknowledges partial support from the NSF under grant DMS-0817789.