Association between competition and obligate mutualism in a chemostat

Abstract

In this paper, we consider a simple chemostat model involving two obligate mutualistic species feeding on a limiting substrate. Systems of differential equations are proposed as models of this association. A detailed qualitative analysis is carried out. We show the existence of a domain of coexistence, which is a set of initial conditions in which both species survive. We demonstrate, under certain supplementary assumptions, the uniqueness of the stable equilibrium point which corresponds to the coexistence of the two species.

Keywords:

• chemostat
• competition
• mutualism
• asymptotic behaviour
• coexistence
• Dulac criterion
• Thieme’s result

1. Introduction

The study of the cooperation of living organisms has become of great interest over the last few decades because it is a common feature in nature 2 3. Zientz et al. 27 emphasized that facultative or obligate intracellular bacteria can be found throughout the tree of life from protists to plants and animals, and that such biological relationships could have culminated with the stable integration of one cell into another as suggested in the endosymbiont theory 14 16. In many cases, using lab experiments, it has been shown that mutualistic relationships were obligatory 4 5 10 17 18 24 and thus prevent competitive exclusion. Then, such interactions could be seen as a major factor of biodiversity. The study of this kind of biological interaction is not only relevant from a fundamental point of view but also from an engineering one. Indeed, in many practical situations, rendering the presence of a microorganism stable within a complex ecosystem presents important advantages. In particular, such obligatory relationships appear to be a possible way of maintaining a given species into a natural ecosystem while most attempts to maintain it by only playing with environmental conditions failed. Following this idea, a new class of synthetic cooperative system has recently been proposed. They are called CoSMO for cooperation that is synthetic and mutually obligatory 19. In this paper, the yeast Saccharomyces cerevisiae was genetically modified to obtain two nonmating strains with different metabolic capabilities so that they behave essentially as two different species. More specifically they were made obligatory mutualists, the first one producing a protein necessary for the growth of the second one (while this synthesis was blocked within the metabolism of this second one) and conversely. Together, these two strains form a cooperative system that mimics two-species obligate mutualistic systems while being in competition on a single resource for their growth. The present paper aims at modelling such a complex system in a chemostat and at studying its theoretical properties.

The chemostat is an important laboratory apparatus used for the continuous culture of micro-organisms. In ecology, it is often considered as a model of a simple lake system or of a wastewater treatment process. It is an excellent experimental venue in which one can study the effect of simple microbial interactions, including competition. Different mathematical models have been developed and analysed extensively by many different investigators (see, for example, the recent monograph by Smith and Waltman 21 and the references therein). Mathematical models of the chemostat are among the few predictive models in microbial ecology. The classical model of competition for a nonreproducing substrate in a well-stirred chemostat operated under constant input concentration and dilution predicts competitive exclusion. That is, it predicts that at most one competitor population avoids extinction 6 21 25 26. However, the coexistence of competing populations is ubiquitous in nature. So, in order to explain this, it seems necessary to relax at least one of the assumptions in the above model. One natural approach is to introduce periodic coefficients to represent, for example, daily or seasonal variations in the environment. For this purpose, there has been some research on models of the chemostat involving either periodic nutrient input or periodic dilution rates 9 20 21. An other natural approach is to make the hypothesis of a ratio-dependent growth rate 8 13 12 11 15 in the sense of 1. As explained above, our approach in this paper is to consider obligate mutualism in the specific context of thecompetition of two species for a ressource.

Freedman et al. 7 have proposed a particular model of two mutualistic predators. They assumed that the resource is governed by a logistic law and proved the existence of a locally stable equilibrium with both predators present. But the global behaviour is not described since it can be complex.

Our objective in this article is to reconsider the analysis of Freedman et al. 7 in the simpler case of a CoSMO system in the chemostat where, as it is well known, the presence of an attractive invariant set allows us to return the qualitative study to dimension 2. We prove the existence of two positive invariant domains such that one of them predicts the extinction and the other ensures the coexistence of the two species. We demonstrate, under certain supplementary assumptions, the uniqueness of a stable equilibrium point which corresponds to the coexistence of the two species. Finally, we illustrate the above results by numerical simulations.

2. Mathematical model and results

In this section we present our model and our results as Theorems 1–3 and their corollaries.

Let s, x ₁ and x ₂ denote, respectively, the concentration of substrate and the two microorganisms present in the chemostat at time t. We ignore all species-specific death rates and only consider the dilution rate. Our model is described by the following ordinary system of differential equations:

where s _{i n} denotes the input concentration of nutrient and D is the dilution rate.

The functional response of each species satisfies:

• H1:f ₁ and f ₂ are two functions.

• H2:.

• H3: and .

• H4: and .

• H5:.

Hypothesis H2 expresses that no growth can take place without substrate; hypothesis H3 meansthat the growth increases with substrate. Hypothesis H4 expresses the mutualism between species and the hypothesis H5 characterizes the obligate case where no nutrient uptake by one species occurs unless the other species is present.

We do not claim that Equation (1) plus H1–H5 is a realistic model for the CoSMO system of bacteria. Actually it should be better to introduce in the model two supplementary state variables p ₁ and p ₂ representing the concentrations of the proteins produced, respectively, by species 1 and species 2, which are necessary for the growth of species 2 and species 1, respectively. But in this case the model would be in and thus much more difficult to study. The model (1) is just a first step and its interest relies on the fact that it is completely tractable from the mathematical point of view.

Let us recall two fundamental well-known properties of the model of the chemostat 21.

Proposition 1

• (1) For every initial condition in , the solution of system (1) has positive components and is bounded and thus is defined for every positive t.

• (2) The set is a positive invariant attractor of all solutions of system (1).

For the convenience of the reader, we provide a proof.

• (1) The invariance of is guaranteed by the fact that if s=0 then and if x _i =0 then for i=1, 2. Next we have to prove that the solution is bounded. If one adds the three equations of system (1), then one obtains, for z=s+x ₁+x ₂, a single equation:

  then
  Since each term of the sum is positive, the solution is bounded.

• (2) Point 2 is a direct consequence of the previous relation.

2.1. Restriction on the plane

We are interested in the asymptotic behaviour of the solutions of system (1). It is tempting to think that because the solutions of system (1) are exponentially convergent towards the set Ω, it is enough to restrict the study of the asymptotic behaviour of system (1) to Ω. In fact, this is false, in general, as shown by examples in 22 23. However, fortunately, in our case, thanks to Thieme’s results 22, the asymptotic behaviour of the solutions of the restriction of Equation (1) on Ω will be informative for the complete system. This justifies our study of the following reduced system.

Using the fact that s=s _{i n} −x ₁−x ₂, the projection, on the plane (x ₁, x ₂), of the restriction of system (1) on Ω is given by

Let

and

We remind that the nul-clines ( and ) of system (2) are the sets:

• H6: Assume that the nul-clines are in ‘general position’, which means that Γ₁ and Γ₂ have a finite number of intersection points where Γ₁ and Γ₂ are transverse.

System (2) admits as an equilibrium point. Hypothesis H5 implies that there is no equilibrium point of the form nor where and . However, this system can have positive equilibrium points.

Theorem 1

• (1) There cannot be periodic orbits nor polycycles inside Ω.

• (2)  is a locally asymptotically stable equilibrium point and if for at least one of the two species, then is the only equilibrium point.

• (3) If and , there can exist positive equilibrium points of the form where and . In this case, there exist two domains R ⁰ and R* such that for every initial conditions in R ⁰ , the two species go to extinction and for every initial conditions in R*, the two species persist.

Proof of Theorem 1.

(1) Let us make the change of variables X ₁=L n(x ₁) and X ₂=L n(x ₂), then system (2) becomes

Let

The divergence of G is given by

and the Dulac criterion 23 allows us to conclude.

• (2) As f ₁(s _{i n} , 0)=f ₂(s _{i n} , 0)=0, then, there exists a neighbourhood V ₁ of (0, 0) such as (f ₁(s _{i n} −(x ₁+x ₂), x ₂)−D)_{|V 1} <0 which implies that and a neighbourhood V ₂ of (0, 0) such that (f ₂(s _{i n} −(x ₁+x ₂), x ₁)−D)_{|V 2} <0, which implies that , then (x ₁, x ₂) converges to (0, 0)

  We can also deduce the local stability of by computing the Jacobian matrix at (0, 0).

  If for at least one of the two species, then there are no intersection points between the sets Γ₁ and Γ₂, then is the only equilibrium point.

• (3) Using the fact that functions and are decreasing, we deduce immediatly that the sets Γ₁ and Γ₂ are the graphs of two functions x ₁=γ₁(x ₂) and x ₂=γ₂(x ₁). If and , then the graphs Γ₁ and Γ₂ (the D-level line of function f ₁ and f ₂) are non-empty. By (H6), these sets can intersect only at a finite number of equilibrium points of the form , where and , called positive equilibrium points.

  Since is locally asymptotically stable, there exists an attraction domain R ⁰ to (0, 0).

  Assume that the sets Γ₁ and Γ₂ intersect at some points. Then R*=Ω∖R ⁰ is non-empty and is a persistence domain. Indeed, for every initial conditions in R ⁰, all species vanish and for every initial conditions in R*, (x ₁, x ₂) converges to a stable equilibrium point where and .

    ▪

Remark 1

There exist two limit values σ₁>0 and σ₂>0 such that if x _i (0)≤σ _i and 0≤x _j (0)≤s _{i n} for i, j=1, 2, i≠j, then the two species vanish. This means that the rectangles [0, σ₁]×[0, s _{i n} ] and [0, s _{i n} ]×[0, σ₂] are contained in R ⁰.

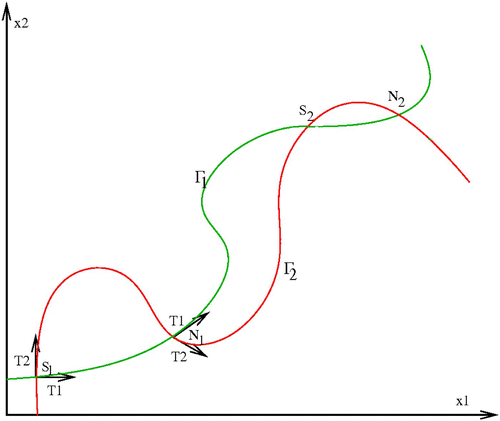
Assume that the sets Γ₁ and Γ₂ intersect at some points. Let us call S ₁, N ₁, S ₂, N ₂, …, S _n and N _n the intersection points along Γ₂ where we increase x ₁ from 0 (see Figure 1). The tangent vector to Γ₁ (respectively, Γ₂) at an intersection point is given by .

Figure 1. Location of graph Γ₁ with regard to the graph Γ₂.

The nature of the positive equilibrium points is given in the following lemma.

Lemma 1

• (1) If , the equilibrium is locally asymptotically stable and if the equilibrium is a saddle point.

• (2) The equilibrium points S _i , i=1, n, are saddle points and the equilibrium points N _i , i=1, n, are locally asymptotically stable.

Proof

The Jacobian matrix of system (2) at is given by

with characteristic equation for the eigenvalues:

The derivatives of γ₁ and γ₂ are given by

hence

We verify immediately that . Then:

• (1) If , then and the equilibrium is locally asymptotically stable and if , then and the equilibrium is a saddle point.

• (2) For the equilibrium points N _i , i=1, n , then , and they are locally asymptotically stable and for the equilibrium points , then and the points S _i , i=1, n, are saddle points.

   ▪

Remark 2

The nature of the positive equilibrium points depends on the location of the graph Γ₁ with regard to the graph Γ₂ at the intersection point. Assume that the orientation of Γ₁ is by increasing x ₂; then if Γ₁ is going inwards in the region of the x ₁ x ₂-plane bounded by the graph Γ₂ and the x ₁-axis, then this point is a saddle point and if Γ₁ is going outwards, then this point is locally asymptotically stable. In particular, the first intersection is a saddle point.

Example 1

In order to show that the number of positive equilibria could be greater than 2, we have constructed two functions that satisfy the necessary conditions of Theorem 1 for the existence of positive equilibrium points:

where the constants α _i , β _i and ω _i are strictly positive, such that α _i ω _i <β _i , i=1, 2. We present here the cases of four and six positive equilibrium points (see Figures 2 and 3).

Figure 2. β₁=2.2, β₂=2, α₁=α₂=0.35, ω₁=ω₂=5.

Figure 3. β₁=2, β₂=2.2, α₁=0.195, α₂=0.18, ω₁=ω₂=10.

Corollary 1

If is the only equilibrium point, then it is globally asymptotically stable and R ⁰=Ω.

Proof

We assume that is the only equilibrium point. Since the omega limit set of any trajectory is contained in the two-dimensional compact and positively invariant set Ω, and lies on the boundary of Ω, must be globally asymptotically stable by the Poincaré–Bendixson theorem.   ▪

2.2. Uniqueness of the stable equilibrium point

Next, we present some constraints on the response functional for which we have at most one stable positive equilibrium point.

Theorem 2

If Γ ₁ and Γ ₂ are concave, then system (2) has at most two positive equilibrium points. There exists a value D ₀ such that

• (1) If D<D ₀, system (2) has exactly two equilibrium points in the interior of Ω; one of them is locally asymptotically stable and the second is a saddle point.

• (2) If D>D ₀ , then there are no equilibrium points in the interior of Ω.

Proof of Theorem 2.

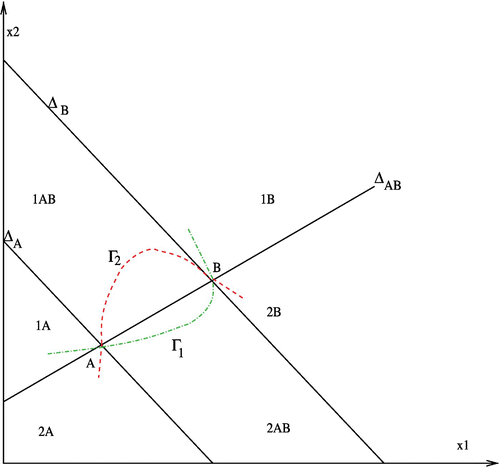
Assume that Γ₁ and Γ₂ intersect. Let A and B be two consecutive intersection points. Let Δ _{A B} be the straight line joining A and B, let Δ _A be the parallel to the second bissectrice passing through A and Δ _B the one passing through B. These three lines define six regions 1A, 1A B, 1B and 2A, 2A B, 2B in the plane (see Figure 4). Since the function (x ₁, x ₂) ↦ f ₁(s _{i n} −(x ₁+x ₂), x ₂) is monotone along any line x ₁+x ₂=k, it turns out that the lines Δ _A and Δ _B must not intersect Γ₁ except in A and B. Γ₁ is a graph of a concave function of x ₂, and the position of Γ₁ between A and B must belong to 2A B. This proves that Γ₁ must belong to 1A and 1B. For the same reasons, Γ₂ must belong to 1A B, 2A and 2B and by the way is reduced to A andB.

Figure 4. Γ₁ and Γ₂ are concave.

Using Lemma 1, A is a saddle point and B is a stable equilibrium point.

Γ₁ and Γ₂ are the D-level line of functions (x ₁, x ₂) ↦ f ₁(s _{i n} −(x ₁+x ₂), x ₂) and (x ₁, x ₂) ↦ f ₂(s _{i n} −(x ₁+x ₂), x ₁); hence there exists a value D ₀ such that if D<D ₀, system (2) has two equilibrium points inside Ω and if D>D ₀, there are no intersection points.   ▪

We present in the next corollary two particular cases for which the conditions of Theorem 2 are satisfied and by the way the uniqueness of the stable equilibrium point inside Ω.

Corollary 2

Let f ₁ and f ₂ be two functions. If one of the next conditions is satisfied,

• (1) f ₁ and f ₂ are concave functions,

• (2) f ₁ (s, x ₂ )=g ₁ (s) h ₁ (x ₂ ) and f ₂ (s, x ₁ )=g ₂ (s) h ₂ (x ₁ ) where g ₁ , g ₂ , h ₁ and h ₂ are four concave functions,

then system (2) has at most two equilibrium points inside Ω of which only one is locally asymptotically stable.

Proof

• (1) If the functions f ₁ and f ₂ are concave then their Hessians H ₁ and H ₂ are negative semidefinite matrix. In particular,

  where v ₁=(γ′₁(x ₂)+1, −1)^T and v ₂=(γ′₂(x ₁)+1, −1)^T.

  Hence the graphs Γ₁ and Γ₂ are concave and the result is deduced from Theorem 2.

• (2) If f ₁(s, x ₂)=g ₁(s)h ₁(x ₂) and f ₂(s, x ₁)=g ₂(s)h ₂(x ₁) where g ₁, g ₂, h ₁ and h ₂ are concave functions, then

  and
  then graphs Γ₁ and Γ₂ are concave and the result is deduced from Theorem 2.

   ▪

Remark 3

If f ₁(s, x ₂)=a ₁ x ₂ g(s) and f ₂(s, x ₁)=a ₂ x ₁ g(s), we can verify immediatly that:

then the qualitative study can be reduced to one dimensional.

2.3. Reconstruction of the asymptotic behaviour of system (1)

It turns out that the phase portrait of system reduced to Ω (2) contains only locally stable equilibria, saddle points and no trajectory joining two saddle points. Thus we can apply Thieme’s results 22 and conclude that the asymptotic behaviour of the solution of the complete system (1) is similar to the asymptotic behaviour described for the reduced system (2).

Let E ⁰=(0, 0, 0) and be the equilibrium points of system (1) such that its projection in the plane (x ₁, x ₂) are the equilibrium points and of system (2).

Theorem 3

• (1) E ⁰ is locally asymptotically stable.

• (2)  and E* have the same type of stability.

• (3) The ω-limit set of a solution of Equation (1) is reduced to one of the equilibria of Equation (1).

• (4) If the persistence domain is non-empty for the reduced system (2), then the persistence domain of the full system (1) is non-empty. Any trajectory of initial condition in this domain converges to an interior equilibrium point in Ω.

Proof of Theorem 3.

Let us recall that z=s+x ₁+x ₂. We verify immediately that system (1) is equivalent to the system below:

• (1) The Jacobian matrix at E ⁰ is −D I ₃, then E ⁰ is locally asymptotically stable.

• (2) The Jacobian matrix at E* is given by

  Thus −D is an eigenvalue and the two other eigenvalues are the same as those of associated to system (2), then the positive equilibrium points E* and have the same nature.

• (3) Let (s, x ₁, x ₂) some bounded solution of system (1) then its ω-limit, called ω, set is not empty. We have seen that s=s _{i n} −x ₁−x ₂+Ke^{−D t} and (x ₁, x ₂) is solution of

  For every value of s(0), we have a non-autonomous system (4) in which the right-hand side converges to the right-hand side of system (2). The set ω is contained in Ω, which contains only a finite number of equilibrium points. On the other hand, we saw that the reduced system (2) does not admit periodic orbits nor cyclic chains. From [22, Theorem 1.6], we deduce that the ω-limit set consists of an equilibrium of Equation (2).

• (4) Using Thieme’s results 22, we conclude that if systems (1) and (2) have the same asymptotic behaviour, then the persistence domain of the full system (1) is non-empty.   ▪

3. Numerical simulations

We performed numerical simulations on the two systems. The first uses classical Monod functions to express growth rates, and the second is somewhat artificial and uses the two functions we used in example 1 to show that the number of interior equilibria could be greater than 2.

In both cases, we compare two different values of the dilution rate D showing the bifurcation phenomenon (see Figures 5 and 6).

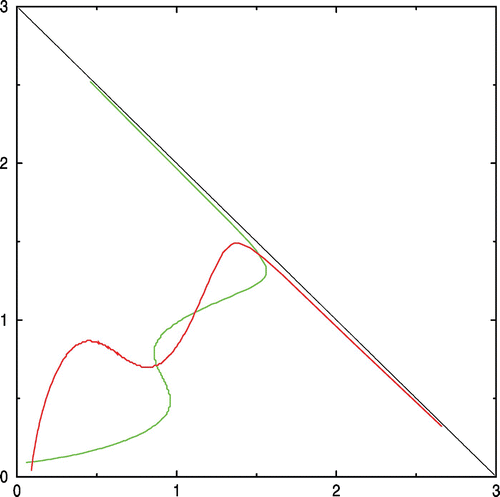
Figure 5. Left: the green trajectories are filling the domain R* of coexistence and converging to the equilibrium N. The red trajectories converge to (0, 0) and fill the domain R ⁰. The boundary of R ⁰ and R* consists in the two stable trajectories of the saddle point S. Right: the domain R ⁰ is the whole domain Ω. Available in colour online.

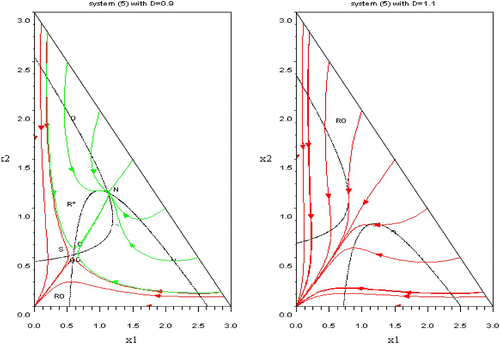
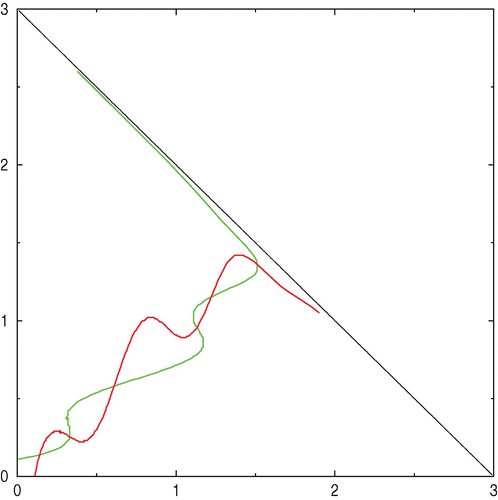
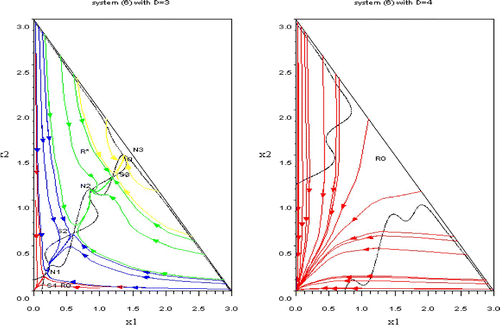
Figure 6. Left: the red trajectories fills the domain R ⁰. The blue, green and yellow trajectories are filling the coexistence domain R*. Blue trajectories converges to N ₁, green ones to N ₂ and yellow ones to N ₃; the reached equilibrium depends on initial conditions. Right: the domain R ⁰ is the whole domain Ω. Available in colour online.

3.1. Numerical test 1

3.2. Numerical test 2

4. Conclusion

We have considered the mathematical model (1) of competition for one resource with obligate mutualism. We proved, under general and natural assumptions of monotony on f ₁ and f ₂, the existence of a domain of extinction and a domain of persistance. Under these general assumptions the persistance equilibrium is not necessary unique as we showed with a somewhat artificial example (6). If we restrict to functions f ₁ and f ₂, which are the products of Monod functions as it is often the case in more specific biological models, the equilibrium is unique.

Acknowledgements

The authors wish to thank Professors T. Sari of INRA-INRIA team MERE and J. L. Gouzé of INRIA team COMORE for useful discussions. This work was done within a coporation program between the INRA-INRIA team MERE and the LAMSIN (www.lamsin.rnu.tn) supported by the program SARIMA (www.sarima.org). The LAMSIN’s researchers work is supported by the Tunisian Secretary of State and Technology (SERST) within the LAB-STI-02 program.