Dynamics of an age-structured population with Allee effects and harvesting

Abstract

We propose a discrete-time, age-structured population model to study the impact of Allee effects and harvesting. It is assumed that survival probabilities from one age class to the next are constants and fertility rate is a function of weighted total population size. Global extinction is certain if the maximal growth rate of the population is less than one. The model can have multiple attractors and the asymptotic dynamics of the population depend on its initial distribution if the maximal growth rate is larger than one. An Allee threshold depending on the components of the unstable interior equilibrium is derived when only the last age class can reproduce. The population becomes extinct if its initial population distribution is below the threshold. Harvesting on any particular age class can decrease the magnitude of the possible stable interior equilibrium and increase the magnitude of the unstable interior equilibrium simultaneously.

Keywords:

• Allee effects
• age-structure
• population threshold
• harvesting

AMS Subject Classification :

• 92D25
• 39A11

1. Introduction

Allee effects 1, the decrease in population growth rates at small populations or densities, include an inability to find mates, reduced foraging efficiency in social animals, lessened defences against predators, reduced reproductive success in cooperative breeders, and reduced fertilization success in broadcast spawners 4. As a consequence, Allee effects play a crucial role in resource management and conservation. Moreover, Allee effects have also been observed in the context of biological control, both to the introduction of the control agent and also to the extirpation of the pest requiring control 10. Recently, there has also been a surge of interest and a need to investigate Allee effects for epidemic models 9 11 20. See 5 7 8 12 13 14 15 16 17 23 24 and references cited therein for population models of Allee effects.

In this work, we propose a general age-structured population model with Allee effects and harvesting to study the impact of these mechanisms on the population level. In 13 15, the author studied Allee effects for a two-age classes population model and models of host-parasitoid interaction in which the host population is classified into two age classes and only the adult host can reproduce. Moreover, the fertility rates in 13 15 depend only on the adult population size and also satisfy some monotonic assumptions which include for example the modified Beverton–Holt functions. Using this monotonic assumption, a global analysis for the single population model is obtained. In the present study, this monotonic assumption is relaxed and it is also assumed that individuals in each age class can reproduce with fertility rate depends on a weighted total population size. Moreover, the population is constantly being harvested with harvesting rates depending on age classes.

Our results are expressed in terms of a threshold, the maximal growth rate of the population. The population will become extinct, independent of initial population distributions, if this growth rate is less than one. When the maximal growth is larger than one, the system may have two stable equilibria and the fate of the population then depends on its initial distribution. An Allee threshold in terms of the unstable interior equilibrium is deduced when only the last age class can reproduce. The population will become extinct if its initial distribution is below the threshold. Bifurcation analysis is also performed when there is only two age classes. While harvesting on any particular age class can drive the maximal growth rate of the population to below one on one hand, it can also decrease the magnitude of the possible stable interior equilibrium and increase the magnitude of the unstable interior equilibrium on the other hand. The overall effect of harvesting is negative. There is no lessened intraspecific competition observed in the model due to harvesting.

In the following section, a general n-age classes model is formulated and analysed. Section 3 derives an Allee threshold of the model when only the last age class can reproduce. Specific examples and simulations are presented in Section 4. The final section provides a summary and discussion.

2. An age-structured model with Allee effects and harvesting

In this section, we derive a general discrete-time, age-structured population model with Allee effects and harvesting. The survival probabilities are independent of time and population density, whereas the fertility function depends on weighted total population size. We present conditions for global extinction and for the existence of non-extinct equilibrium. We also study the stability of the equilibria and equilibrium size relative to model parameters.

2.1. The model, threshold, and equilibrium

Consider a population with n age classes, n≥2. Let x _i (t) denote the population size of age class i at time t, t=0, 1, …. The survival probability from age class i to age class i+1 is denoted by s _i , 0<s _i <1, . The fertility rate f is assumed to be a function of weighted total population size due to intra-specific competition, where p _i ≥0 for 1≤i≤n. Since each age class in general will have different fertility rate, the fertility function f is scaled for each age class by F _i , F _i ≥0 for 1≤i≤n. In particular, if F _i =0, then the ith age class does not reproduce. We assume that the last age class is reproductive since we can simply ignore the last few age classes which do not contribute to reproduction. Therefore, we assume that F _n >0 and p _n >0. Let h _j denote the age-specific harvesting rate, 0≤h _j <1, 1≤j≤n. The model takes the following form:

where parameters 0<s _i <1 for , and p _i ≥0, F _i ≥0, 0≤h _i <1 for i=1, …, n with p _n >0 and F _n >0.

Let

and

It is assumed that Allee effects act on the fertility rate f and we make the following assumptions:

(H1) , f(0)≥0, β f(0)<1 and f(x)>0 for x>0. There exists m>0 such that for 0≤x<m and for x>m, and .

The fertility function f increases first due to positive effect of increasing population size, reaches a maximum at population level m, and then declines due to intra-specific competition among individuals. A modified Beverton-Holt function for the fertility rate is analysed in 13 and a more general fertility function that satisfying for x>0 is studied in 15. Both of these models consist of only two age classes, juvenile, and adult. The assumptions of fertility function f in the present study do not have these restrictions.

It is clear that solutions of Equation (1) remain nonnegative and Equation (1) always has a trivial steady state where the population is extinct. If a component of a nontrivial steady state is positive, then all of the components of the steady state are positive. Therefore, we consider the existence of an interior steady state . Let

Then an interior steady state must satisfy the following equality:

It follows that Equation (5) has no positive solution if β f(m)<1, has a unique positive solution X*=m if β f(m)=1, and has two positive solutions X _i *, i=1, 2 with if .

Note if is a solution of Equation (5), then a direct computation shows that the components x¯ _i , i=1, …, n, of the interior steady state are given by

The Jacobian matrix of system (1) evaluated at has the following form:

Therefore E ₀ is always locally asymptotically stable since zero is an eigenvalue of J(E ₀) with algebraic multiplicity n. In the following, we show that E ₀ is globally asymptotically stable for Equation (1) if β f(m)<1, where β f(m) can be interpreted as the maximal growth rate of the population.

Theorem 2.1

If β f(m)<1, then is globally asymptotically stable for system (1).

Proof

Let be a solution of Equation (1), where T denotes matrix transpose. Since for all x≥0, we see that for t≥0, where A _m is given by

Note that A _m is nonnegative and irreducible since F _n >0. Hence A has a dominant (none of the other eigenvalues with modulus exceed it), simple, positive eigenvalue 6. We consider the following matrix difference equation

with Y(0)=X(0). Then for t≥0. The characteristic equation of A _m can be written as

We apply the Descartes's rule of signs 21 to the characteristic equation. Let P(λ) denote the left-hand side of Equation (10). Since for and S _n H _n F _n >0, there is only one change of signs of coefficients of P(λ) with and . Therefore, Equation (10) has only one positive real root. Since , the positive real root is less than one and thus the dominant positive eigenvalue of A _m is less than one. Consequently, for all nonnegative solutions Y(t), and as a result, . Therefore, E ₀ is globally asymptotically stable since it is locally asymptotically stable and globally attracting.   ▪

When β f(m)=1, the maximal growth rate of the population is one. System (1) then has a unique interior steady state with . Since , the Jacobin matrix of Equation (1) evaluated at E*, J(E*), is A _m given in Equation (8). Using the argument as in the proof of Theorem 2.1, we can verify that the dominant eigenvalue of J(E*) is now 1. Therefore, E* is nonhyperbolic, and its local stability cannot be determined using the linear theory.

Theorem 2.2

If β f(m)=1, then Equation (1) has two steady states and where E ₀ is locally asymptotically stable and E* is nonhyperbolic.

Suppose now β f(m)>1. Then Equation (5) has two positive solutions X _i * with , and Equation (1) has two interior steady states

with

At E ₁*, the Jacobian matrix J(E ₁*) is given by

where

Let

Since , a _i >0 for 1≤i≤n. Therefore J(E ₁*) is also nonnegative and irreducible. The characteristic polynomial of J(E ₁*) can be shown to have the following form:

Note and . Since there is only one change of signs in the coefficients of , has only one positive root. Now,

Therefore, the positive solution of exceeds one and the dominant positive eigenvalue of J(E ₁*) is greater than one. We conclude that the steady state E ₁* is unstable.

On the other hand, the Jacobian matrix of system (1) evaluated at E ₂*, J(E ₂*), is given by

where

Let

Since , b _i may not be nonnegative and hence the matrix J(E ₂*) may no longer be nonnegative. We consider the following conditions on the fertility rates f and F _i , and p _i :

and

If Equations (12) and (13) hold, then and it can be shown that E ₂* is locally asymptotically stable. Indeed, by Equation (12) and for 1≤i≤n. Hence J(E ₂*) is also nonnegative and irreducible. The characteristic polynomial of J(E ₂*) has the following form:

Similar to the previous discussion on E ₁*, we see that and . Since coefficients of Q ₂ have only one change of signs, has only one positive real root. Moreover, since ,

Therefore, the dominant positive eigenvalue of J(E ₂*) is less than one and E ₂* is locally asymptotically stable.

In the following, we derive a sufficient condition for which E ₂* is locally asymptotically stable when either Equation (12) or (13) is not satisfied. Towards this end, using the characteristic equation given by Equation (14) and applying Rouche's theorem 3, we let and . On the unit circle,

We assume that

Then and thus Q ₂=g ₁+g ₂ has n zeros inside of the unit circle. We conclude that the spectral radius of J(E ₂*) is less than one and E ₂* is locally asymptotically stable. We summarize these results into the following theorem.

Theorem 2.3

Let β f(m)>1. Then system (1) has three steady states E ₀ and E _i *, i=1, 2, where E ₀ is locally asymptotically stable and E ₁* unstable. If either Equations (12) and (13) are satisfied or Equation (15) holds, then E ₂* is locally asymptotically stable.

Note that if F _i =F>0 and p _i =1 for 1≤i≤n, i.e., if Equation (13) holds, then Equation (15) becomes

which is automatically satisfied if Equation (12) is valid. However, conditions imposed in Equation (15) are sufficient conditions for local stability of E ₂* which work for all types of fertility functions that satisfy (H1), and violation of inequality (15) does not imply that E ₂* is unstable.

2.2. Equilibrium size and parameters

In this subsection, we study the effects of parameters relative to the magnitude of the equilibrium. Since , β is a decreasing function of h _i and an increasing function of both F _i and s _i for all i. From Equation (5) we have

and

Since the only dependence of x _1j * on F _i is through X ₁*, we immediately obtain

Using x ₁₁* given in Equation (6), we see that

Since , we have

On the other hand,

Therefore, whether x ₁₂* is a decreasing or an increasing function of h ₂ depends on the individual fertility function f. Inductively, we see that

Similarly, we have

and implies that the sign of cannot be determined without knowing f explicitly. Inductively, it can be shown that

We can perform a parallel analysis for x _2i *. The results are summarized below.

The rest of the signs such as and cannot be determined explicitly using the recursive formula (6). Moreover, since β is independent of p _i , X _j * is independent of p _i for 1≤i≤n and j=1, 2. Therefore we obtain

From the above discussion, we see that the weighted total population size X ₂* in the equilibrium E ₂* increases with increasing survival probability s _i and fertility rate F _i but X ₂* decreases with increasing harvesting rate h _i . Therefore, harvesting can reduce weighted total population size in the equilibrium E ₂*, which may be locally asymptotically stable.

3. Allee thresholds

It is well known that populations are more likely to go extinct if the populations are subject to Allee effects 4. In this section, we will derive Allee thresholds for model (1) when β f(m)>1, i.e. the maximal growth rate of the population is greater than one. Since the extinction steady state is locally asymptotically stable, there exists a basin of attraction for E ₀. We only consider the case when F _i =0 for . System (1) then becomes

where all the parameters have the same biological meanings as in Section 2 and f satisfies (H1). Notice in this case that .

Since Equation (24) is a special case of system (1), we see that global extinction occurs if β f(m)<1. When β f(m)=1, then an increase of harvesting rate h _i will drive the maximal growth rate to below one so that global extinction will happen. Moreover, since many life history parameters cannot be estimated precisely, the case of β f(m)=1 is hardly attained in the real world situation. We are more interested in the case when β f(m)>1, where system (24) has two interior steady states , i=1, 2. Denoting the two positive solutions of Equation (5) by X _i * as in the previous section, then

and also

Suppose that initial conditions of Equation (24) satisfy

We show that Equation (25) provides a threshold below which population goes to extinction.

Theorem 3.1

If solutions of Equation (24) with initial conditions satisfy Equation (25), then the solutions converge to .

Proof

Let be a solution of Equation (24) with initial condition satisfying Equation (25). We first claim that

Note Equation (25) implies . Since f is strictly increasing on (0, m) by (H1) and X ₁*<m, it follows that

and

Therefore, Equation (26) holds for t=1. Suppose inequality (26) is true for t=k for some k>1. Then similar to the argument just used, it can be shown that Equation (26) holds for t=k+1. Consequently, Equation (26) are valid for t≥1. We rewrite Equation (24) as , where X(t) is the column vector and A(t) is given by

Note that for t≥0,

A simple calculation yields

where

Since is a diagonal matrix, the nth iteration of Equation (24) can be written as

Using Equation (26), we see that

Therefore,

As a result, the following limits exist:

with

We prove that for and i=1, …, n. Observe that

If , then by the last equation we have which contradicts Equation (32). This shows that . Similarly, for ,

If , then one would have which is impossible by Equation (32). Therefore, for . For i=2 and

We also arrive at for . By applying the same analysis, we can conclude that for j=0, 1 and for i=3, …, n and . Consequently, the solution converges to E ₀ and this completes the proof.   ▪

Theorem 3.1 deduces the following forward invariant rectangular region

for system (24). Solutions of Equation (24) converge to (0, …, 0) if the solutions lie inside of Γ initially. Therefore, x _1j * provides a threshold for population extinction. On the other hand, the basin of attraction of may be larger than Γ.

Recall from Equation (18) we arrived at for all j. Therefore, an increase of fertility F _n can make the region Γ smaller and reduce the possibility for population extinction. On the other hand, from Equation (19) we see that an increase of h _j will increase x ₁₁* for any j=1, …, n. As a consequence, an elevated harvesting on any age classes will enlarge Γ in the x ₁-direction. Since Equation (20) also holds, the overall effect of harvesting on the Allee threshold is complicated and is not easy to determine if the number of age classes of the population is large. However, the total weighted population level X ₁* will always increase when harvesting is implemented on any age classes.

4. Examples and bifurcations

In this section, we use specific examples for the fertility functions to discuss possible bifurcations. We consider two age-classes. The model then takes the following form:

where 0≤h _i <1 for i=1, 2, 0<s ₁<1, p ₁≥0, p ₂>0, F ₁≥0 and F ₂>0. We assume β f(m)>1 so that Equation (34) has two interior steady states and with , 1≤i≤2. It is known that E ₁* is unstable and the Jacobian matrix, , of Equation (24) evaluated at E ₂* is given by Equation (11) with n=2. Applying Jury conditions 2, we see that E ₂* is locally asymptotically stable if . It can be verified that always holds since . As a consequence, system (34) cannot undergo a +1 bifurcation when E ₂* loses its stability. Moreover, if and only if

and is equivalent to

At those parameter values for which inequality (35) becomes equality, one of the eigenvalues of J ₂* is −1 and hence a period-doubling bifurcation may occur. On the other hand, a discrete Hopf (or Neimark-Sacker) bifurcation 18 19 22 may occur at those parameter values for which Equation (36) becomes equality since in this case the eigenvalues of J ₂* do not cross the unit circle through the real axis.

We now use the weights of total population size in the fertility function as a bifurcation parameter. Specifically, we let

Note that X ₂* is independent of p ₁ and p ₂ and hence X ₂* is independent of θ. We have

and Equation (35) becomes

If , then Equation (35) clearly holds for all θ≥0. Assume

and define θ _P to be

Then is equivalent to provided Equation (39) holds. If Equation (39) is violated then is trivially true for all θ≥0. Notice inequality (39) is reversed if and . Therefore E ₂* does not loss its stability via a period-doubling bifurcation if these two inequalities hold.

On the other hand, condition (36) is equivalent to

We assume that

and define θ _H to be

Then is equivalent to provided Equation (41) is valid. Otherwise, trivially holds for all θ>0 if Equation (41) is violated. Note that if , then the inequality (41) is reversed and holds. Therefore, if a modified Beverton–Holt function is used as the fertility rate, then Equation (34) cannot undergo a discrete Hopf bifurcation when E ₂* loses its stability. We summarize these results into the following proposition.

Proposition 4.1

System (34) does not undergo a +1 bifurcation when E ₂* loses its stability. If then E ₂* as an interior steady state of Equation (34) does not loss its stability via a discrete Hopf bifurcation. In addition, if then E ₂* is locally asymptotically stable for Equation (34).

If inequalities (39) and (41) are satisfied, then a simple calculation yields

If , then and vice versa. If , then E ₂* is always unstable for θ≥0. If , then E ₂* is locally asymptotically stable for .

Proposition 4.2

Let inequalities (39) and (41) hold. Then E ₂* is always unstable for θ≥0 if and E ₂* is locally asymptotically stable for if .

In the following, we use specific fertility functions to investigate the system (34). All the simulations below are performed using MatLab. Since Beverton–Holt type functions appear frequently in the fishery literature, we first consider a Beverton–Holt type function with Allee effects. Specifically, we let

where a>0 and λ>0. Clearly and the maximum value of f occurs at x=a with

We assume that this last inequality holds. Then the two positive solutions of β f(X)=1 are

with . Since for x>0, system (34) neither undergoes a discrete Hopf (or Neimark–Sacker 18 19 22) bifurcation in which a closed invariant curve appears nor a +1 bifurcation when E ₂* loses its stability by Propositions 4.1 and 4.2. The only possible bifurcation is a period-doubling (or −1) bifurcation. At the bifurcation point , one of the eigenvalues of J ₂* is −1 and a 2-cycle solution may appear for system (34).

We let λ=a=1 in our numerical simulations with the following parameter values:

Then , , , and . We let θ=0 initially and then increase θ by 0.01 for each step until θ=2 so that p ₁ is twice of p ₂. When θ=0, , and . We discard the first 5000 iterations and plot the next 1000 iterations for each θ value until θ=2 and we repeat this procedure for 100 times. The resulting bifurcation diagram for x ₁ population size is provided in Figure 1(a), where we can see that the population may go extinct for some randomly chosen positive initial conditions for each fixed θ.

Figure 1. This figure provides simulation results for system (34) with f given by Equation (44). (a) and (b) are bifurcation diagrams with h ₁=0.1 and h ₁=0.5, respectively. The rest of the plots are basins of attraction of (0, 0) for different parameter values. In particular, F ₁=10 and p ₁=0 in (c), F ₁=0 and p ₁=0 in (d), F ₁=10 and p ₁=1.5p ₂ in (e), and F ₁=0 and p ₁=1.5p ₂ in (f).

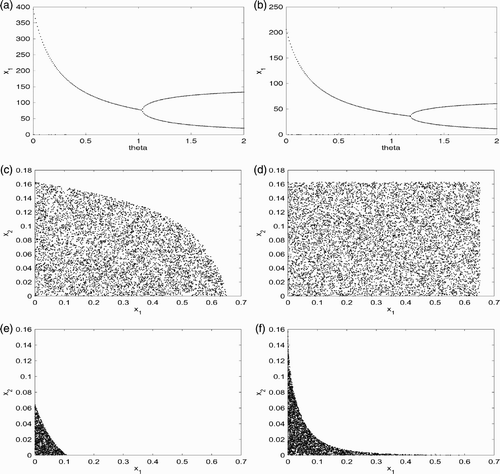
A period-doubling bifurcation occurs and the system has a period-two solution when θ is just beyond 1 which agrees with the earlier calculation of . We did not obtain more complicated dynamical behaviour by varying parameter values and increasing θ further. See Figure 1(b) for the same parameter values with h ₁=0.1 been increased to h ₁=0.5. In this case . Recall from Equation (22) that an increase of h ₁ will decrease x _2j * for j=1, 2, and our simulations in Figure 1(a) and (b) confirm this analytical result. Comparing Figure 1(a) and (b), we also see that an increase of h ₁ with every other parameter value being fixed can increase the θ value for which the period-doubling bifurcation occurs. From this point of view, increasing harvesting rate of the young can help to stabilize the population. Similar results are obtained if we increase the number of age classes from 2 to 3.

It was shown in Theorem 3.1 in terms of the present content that if the initial population distribution lies inside the rectangular region , then the population goes extinct. In Theorem 3.1, it was assumed that only the last age class can reproduce. In this two-age classes model with F ₁=0, we have , , , and and when θ=0. We plot those initial conditions for which the solutions converge to (0, 0). In Figure 1(c) we used the same parameter values as in Figure 1(a) with p ₁=0. Figure 1(d) provides the region with the addition that F ₁=0. Note that in this situation of , the basin of attraction of (0, 0) has been studied in 13 16 which is given precisely by Γ. From these two plots, we see that the reproduction of smaller age class can have a smaller region of basin of attraction for the extinction steady state (0, 0). This observation was derived in Equation (18) along with Theorem 3.1.

We repeat the same simulations with p ₁=1.5p ₂ where the model has an asymptotically stable 2-cycle. Figure 1(e) and (f) plot basin of attraction for (0, 0) when F ₁=10 and F ₁=0, respectively. When F ₁=0, we see that and and the region lies inside the numerically simulated basin of attraction of (0, 0). Since the region in Figure 1(e) is smaller than the region in Figure 1(f), we arrive at the same conclusion that reproduction of the young can help the population to avoid extinction. This conclusion was analytically deduced in Equation (18) and our numerical simulations confirm this earlier analytical finding.

We next consider a Ricker type function with Allee effects for the fertility rate. The Ricker functions have also been used frequently in the fishery modelling. Let

where 0<c<K and r>0. The maximum value of f occurs at m=(K+c)/2. A simple calculation yields β f(0)<1 if and only if and β f(m)>1 is equivalent to . We assume that the following conditions hold for model (34) with f given in Equation (45):

It follows that f satisfies (H1) with β f(m)>1 and , and β f(X)=1 has two positive solutions

and

where .

Recall from Equation (43) that if and only if . When f is given by Equation (45), this latter inequality is equivalent to Let . Then if and only if h(X ₂*)<0. Note that h is a concave down parabola with positive vertical intercept and h(K)≤0 is equivalent to r(K−c)≥4. Moreover, it can be verified that X ₂*>K if β>1. Hence, we have when β>1 and r(K−c)≥4.

Let

Then , , , , , , and . Moreover,

Proposition 4.2 implies that is locally asymptotically stable when . At , we randomly choose initial conditions that are close to E ₂*. Specifically, we use for i=1, 2, where rand is the random number generator in MatLab. Simulations demonstrate that these solutions do converge to E ₂*. Figure 2(a) provides the x ₁ component of such a particular solution. We then increase θ to and randomly choose an initial condition that is very close to E ₂*. Figure 2(b) provides the time evolution of the x ₁-component of the solution for t≤300 while Figure 2(c) provides the time evolution for . The magnitude of the solution although increases first, it can be seen that the solution does settle to a 2-cycle. Similar plots are obtained for initial conditions that are close to E ₂*. We conclude that a period-doubling bifurcation occurs at , which confirms our analytical result derived earlier. When we increase θ to 0.006006, the solution although oscillates initially, it eventually crashes and the population goes extinct. A particular solution is plotted in Figure 2(d). Similar plots are obtained as we increase θ to 0.00601, see Figure 2(e). However, comparing Figure 2(d) and (e), we see that the population will go extinct faster as we increase θ. We obtain similar results as we increase θ further. The system does not exhibit more complicated dynamical behaviour when we increase θ to beyond θ _P from the left. A bifurcation diagram for θ in [0.0058, 0.0078] is presented in Figure 2(f), where we increase θ by 0.00001 in each step. We see that populations go extinct for all large θ.

Figure 2. This figure provides simulation results for system (34) with f given by Equation (45) and parameters are being chosen so that θ _H =0.00561<θ _P =0.00600. (a) is the time evolution of the x ₁ component of a solution when θ=0.0059. (b) and (c) are the time evolutions of the x ₁ component of a solution when θ=0.00600001, while θ=0.006006 in (d) and θ=0.00601 in (e). Plot (f) is the bifurcation diagram for θ in [0.0057, 0.0078].

We now decrease θ to 0.00562 and simulate solutions with randomly generated initial conditions that are very close to E ₂*. As stated in Proposition 4.2, since E ₂* is locally asymptotically stable, such solutions converge to E ₂. Simulations confirm this result and a particular solution is plotted in Figure 3(a). When we decrease θ further to 0.0056009, we obtain an invariant closed curve solution in the x ₁ x ₂- plane by truncating the first 30,000 iterations and recording the next 1000 iterations. An invariant closed curve is plotted in Figure 3(b). Therefore, a discrete Hopf bifurcation does occur at . We plot bifurcation diagrams for the model using θ as the bifurcation parameter. The θ value is set to be 0.0059 initially and decreases by 0.00001 for each step until for the diagram provided in Figure 3(c). We see that the model is chaotic when θ decreases to below θ _H from above. Figure 3(d) presents another bifurcation diagram with θ ranging from 0.0001 to 0.0059. The population goes extinct for all small θ values as can be seen from Figure 3(d) and also for large θ values as demonstrated in Figure 2(f).

Figure 3. This figure provides simulation results for system (34) with f given by Equation (45). The parameter values are the same as those in Figure 2 except θ. (a) plots a solution when θ=0.00562. In (b), there is an invariant closed curve solution when θ=0.0056009. (c) and (d) are bifurcation diagrams of Equation (34) with θ∈[0.0049, 0.0059] and θ∈[0.0001, 0.0059], respectively.

5. Discussion

The interest of studying Allee effects on population and epidemic models has been increased in recent years due to fragmentation of habitats, invasion of new species, and biological control of pest, etc 4. In this study, we propose an age-structured model of a single population with Allee effects and harvesting to investigate the impact of these mechanisms on the population level. The dynamics of the population depend on the lumped parameter, β f(m), which can be interpreted as the maximum growth rate of the population. It is the maximum average number of offspring that an individual can reproduce during its life span. The population will definitely go extinct if the maximal growth rate is less than one (cf. Theorem 2.1). The population may survive if the maximal growth rate is larger than one. In this situation, the model has two interior steady states E ₁* and E ₂*, where E ₁* is always unstable. The other interior steady state may be locally asymptotically stable under some conditions (cf. Equations (12) and (13), or Equation (15)). Therefore, the model may exhibit multiple attractors and the fate of the population depends on its initial distribution.

Since the extinction steady state E ₀ is always locally asymptotically stable, the basin of attraction provides a threshold for the population below which the population becomes extinct. If we assume that only the last age class can reproduce with fertility rate depends on the weighted total population size, then the region Γ can be systematically deduced (cf. Theorem 3.1) and is given by Equation (33). The population will become extinct if its initial population distribution lies inside of Γ which depends on the components of E ₁*. Since β is a decreasing function of the harvesting rate h _i , an increase of h _i will increase X ₁* and decrease X ₂*. As a consequence, the weighted threshold in E ₁* is larger, and the system has a smaller weighted population size in the equilibrium E ₂*. Therefore, the population may stabilize in a smaller equilibrium when E ₂* is locally asymptotically stable and harvesting is in effect.

On the other hand, the weighted population size in the equilibrium X ₂* increases with increasing fertility rate F _i and survival probability s _i by Equation (17). Also Equation (18) implies that an increase of F _i can reduce x _1j * for all i and j. As a result, increasing fertility rate F _i has an overall positive effect on the population. However, the impact of h _j on x _1i * is complicated and cannot be determined explicitly as demonstrated at the end of Section 2. Furthermore, an increase of harvesting rate h _i may decrease the maximal growth rate β f(m) to below one so that global extinction can occur.

We also investigate a general two-age classes model, system (34), and with two specific fertility functions, Equations (44) and (45). Using θ as our bifurcation parameter, where , we conclude that the only possible bifurcation is either a period-doubling or a discrete Hopf bifurcation when the interior steady state E ₂* loses its stability for general system (34) (cf. Proposition 4.1). Moreover, E ₂* is unstable for all θ≥0 if and E ₂* is locally asymptotically stable for if (cf. Proposition 4.2). However, a discrete Hopf bifurcation cannot occur if a modified Beverton–Holt function such as Equation (44) is used as the fertility function (cf. Proposition 4.1). We numerically simulate this particular model. We also simulate system (34) with f given by Equation (45). From this numerical study, we see that an early reproduction (that is, F ₁>0) can help the population to avoid extinction for both fertility functions. When a modified Ricker type function (45) is used as the fertility function with two age classes, we simulate the model with parameter values such that , and thus E ₂* is locally asymptotically stable when . A period-doubling bifurcation occurs when and we do not obtain more complicated dynamical behaviour as we increase θ. Moreover,the system does exhibit an invariant closed curve solution when θ just passes θ _H from above. The system is chaotic for some θ values as we decrease θ further.

The impact of harvesting can be drastic for populations that are also subject to Allee effects. Population extinction is certain if harvesting decreases the maximal growth rate of the population to below one even if the population distribution seems large from observation. In addition to the possibility of global extinction, harvesting plays a role on the magnitude of X ₁*. Increasing h _i will increase X ₁* so that the weighted size in Γ is larger. However, this deleterious effect of harvesting can be balanced out if the population can reproduce at a younger age. Since life history parameters are not easy to estimate, harvesting without regulations may impose risk for population extinction especially when there is a mechanism of Allee effects operating in the population. Any resource management plan should take Allee effects into consideration before it is implemented.