Stability and permanence in gender- and stage-structured models for the boreal toad

Abstract

The boreal toad Bufo boreas boreas, once common in the western USA, is listed as an endangered species in Colorado and New Mexico, and protected in Wyoming. Populations have dramatically declined due to the presence of the fungal pathogen Batrachochytrium dendrobatidis (Bd). A gender- and stage-structured model for the boreal toad is formulated which depends on its life cycle and breeding strategies. In addition, an epizootic model for the spread of Bd is formulated. Analysis of these models provides two thresholds. The first threshold, the basic reproduction number for the population, ℛ₀, determines whether the population persists and the second threshold, the basic reproduction number for the fungal disease, ℛ_F, determines whether the disease persists. If ℛ₀>1 and ℛ_F<1, then the population becomes disease-free. However, if both thresholds are greater than one, the population levels are severely reduced by the fungal pathogen.

Keywords:

• boreal toad
• chytridiomycosis
• difference equations
• permanence

AMS Subject Classification :

• 39A11
• 92D25

1. Introduction

A recently identified fungal pathogen known as Batrachochytrium dendrobatidis (Bd) has been associated with amphibian declines worldwide. This fungal pathogen causes a disease known as chytridiomycosis in susceptible amphibians which results in very high mortality 8 12 22 29 35 36. The decline of the boreal toad (Bufo boreas boreas) in the western USA has been attributed to multiple factors, including the presence of this fungal pathogen 8 9 33. The boreal toad is currently listed as an endangered species by Colorado and New Mexico, and is a protected species in Wyoming (http://wildlife.state.co.us/Research/Aquatic/BorealToad/). Environmental factors such as low water availability and freezing temperatures may have also impacted this decline 8. The boreal toad is found at elevations ranging from sea level to 12,000 feet. The higher elevations in the mountains of Colorado (7000–12,000 feet) and cooler temperatures are favourable conditions for the growth of Bd 6 8 11 14 21.

Our goal in this investigation is to develop models that accurately incorporate the developmental stages and reproductive behaviour of the boreal toad. The models will be useful to further study populations in areas where they are threatened or endangered. A variety of mathematical models have been developed to study the impact of the environment or disease on small or declining populations of amphibians 3 7 15 16 24 25 30 31. We will summarize these models and discuss how they relate to our modelling efforts.

A Leslie matrix model was developed for the boreal toad to study the sensitivity of model parameters and to understand the contribution of specific life stages to persistence of wild populations in near-equilibrium conditions 24. This model did not include Bd infection nor the within-year life cycle stages. In 15 16, stage-structured models were formulated with two or three developmental stages in a generic amphibian life cycle, larvae (tadpoles), juveniles (non-reproductive), and adults (LJA or JA model). Free-living fungi were included as another variable F. Density-dependent survival was assumed from egg to larval stage. To distinguish whether the stage was infected with Bd, each stage was identified as susceptible, infectious, or recovered, denoted as S, I, or R. Complete vertical transmission was assumed because infected adults contaminate ponds, where eggs and larvae mature and become infected. For the models in 15 16, conditions were derived on model parameters for complete population extinction. In 3, a simplified model with susceptible and infectious adult amphibians was analysed. A threshold was derived for the adult-fungi model so that below the threshold the population becomes disease-free. A simple metapopulation model was formulated with different movement patterns for susceptible and infectious adult stages.

A more complete analysis of 15 was performed by Salceanu and Smith 30 31. In 30, for the three-stage LJA–SIR model, criteria for persistence of the population were established as well as global stability results for host extinction and for the disease-free equilibrium. Salceanu and Smith 31 extended their analysis to the two-stage JA–SI model by considering <100% vertical transmission.

In 7, a hybrid model was applied to the mountain yellow-legged frogs (Rana mucosa), a system of difference equations for larvae and adult stages and a system of differential equations for disease transmission and reproduction of infected individuals during summer months. Environmental stochasticity was included through Monte Carlo simulations of randomly chosen combinations of parameters. The model was shown to be consistent with data. In 25, a system of partial differential equation models with delay was applied to tadpole development for the European common toad Bufo bufo, a toad infected by Bd. Long-term survival of Bd in encysted form was assumed 13. In numerical simulations, it was shown that a free-living saprobic stage of Bd is able either to cause extinction of the toad population or to establish an enzootic level of infection but with the host population severely reduced in numbers. None of the preceding models include gender-structure and none apply to B. b. boreas, except for the model of McDonald and Tse 24.

Discrete-time population models for seasonally breeding populations with some of the same features as the models in this investigation were studied by Ackleh and Jang 1 and Ackleh et al. 2. Stability and persistence were studied in these latter investigations.

In the following sections, a set of basic model assumptions is described that is unique to the life cycle of the boreal toad. Then, an annual model is formulated, a system of difference equations for the female population. Based on the model assumptions, a threshold ℛ₀ is derived, the basic reproduction number for the population. A globally stable positive equilibrium exists if and population extinction occurs if . Under a weaker set of assumptions, it is shown that the population is permanent, if . The population model is extended to an epizootic model with Bd infection. A second threshold, the basic reproduction number for the fungal disease, , is derived to show that if and , then the disease-free equilibrium is stable. The effects of environmental change, modelled as a change in the timing of the onset of reproduction or in the breeding frequency, are considered in Section 4. Some numerical results, presented in Section 5, illustrate the possible effects on the boreal toad population due to Bd infection in breeding and non-breeding sites. The conclusion summarizes the results and suggests further research.

2. Population model

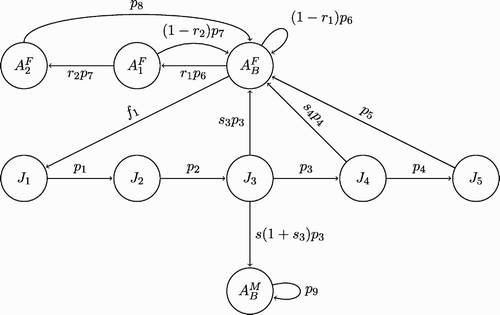
Our mathematical model is based on the life history characteristics of boreal toads taken from the literature 8 9 27 32 34. The year is divided into five periods which describe breeding, tadpole development, metamorphosis, dispersal, and hibernation. In addition, the developmental stages of the toad are divided into egg E; tadpole T; juvenile, J (non-reproductive); and adult A stages. The five periods that occur each year are described in Table 1. We include the approximate timing during the year that corresponds to boreal toad populations in the Southern Rocky Mountains. However, these times vary with latitude, elevation, and weather conditions.

Table 1. Life cycle stages of the boreal toad during a 1 year period.

Period	Approximate time	Description
1. Dispersal	Early September–Mid-September	Breeding males and females and first-year juveniles disperse from breeding ponds
2. Hibernation	Mid-September–Mid-May	Juveniles and adults are in winter hibernacula
3. Breeding	Mid-May–Mid-June	Breeding males and females gather at ponds; eggs are laid
4. Tadpole	Mid-June–Late June	Eggs hatch to tadpoles
5. Metamorphosis	Early July–Late August	Metamorphosis of tadpoles and stages updated

Breeding begins after snow and ice melts 8. Males arrive at the breeding pond first, awaiting the arrival of females. After breeding, a female toad may lay, on average, 6600 in one to five clutches 8 or up to 12,500 eggs in two strings in shallow water 34 or even as high as 16,000 in a single clutch 32, depending on the situation of the habitat. Given a sufficient number of males, the total number of eggs depends on the number of breeding females. If males are scarce, then the number of eggs will also depend on both breeding males and females. Females are generally not reproductively mature until 4, 5, or even 6 years of age and they do not necessarily breed every year 8 27. After breeding, eggs develop into tadpoles, which generally takes about two weeks. The number of tadpoles that develop from eggs depends upon the temperature, a parameter we neglect in our preliminary stage-structured model. Metamorphosis is the transition from tadpoles to toadlets or first-year juveniles. A density-dependent relationship is assumed at metamorphosis, where the number of first-year juveniles that develop from tadpoles depends on the density of tadpoles. This assumption is based on the supposition that predation and competition among tadpoles for food and space limits the number of first-year juveniles. At this time, all stages are updated; that is, tadpoles become first-year juveniles, first-year juveniles become second-year juveniles, and so on. After mating, females leave the breeding site and disperse into the surrounding areas (surviving primarily by feeding on insects) and males stay at the breeding site longer than females 27. Dispersal and metamorphosis occur simultaneously. For modelling purposes, we assume that dispersal takes place after metamorphosis. After dispersal, toads hibernate and activities cease; this is the last period of the life cycle.

2.1. Model assumptions

We make some assumptions based on the previous discussion to formulate a population model. Additional assumptions are made in Section 3.1 to formulate an epizootic model, when Bd infection is included in the model. Our population model is based on the following characteristics concerning breeding age, breeding frequency, and life history of the boreal toad.

• (H1) Males generally do not breed until age four, and females generally begin breeding at either 4, 5, or 6 years of age 8,26.

• (H2) After females become reproductive, they may breed every year, every 2 years, or every 3 years depending on their body sizes and environmental conditions [27 . For modelling purposes, we assume the proportion of females that breed every year is (1−r ₁), the proportion that breed every second year is r ₁(1−r ₂), and the remaining proportion of females that breed every third year is r ₁ r ₂.

• (H3) The gender is determined at the age of four.

• (H4) The developmental stages include an egg stage E; a tadpole stage T; three juvenile stages, where gender is not yet determined, J ₁, J ₂, J ₃; two female juvenile stages J ₄, J ₅; three female adult stages, one breeding and two non-breeding stages, , and ; and one breeding male adult stage, .

For notational convenience, we refer to the five juvenile stages of the toad as stages i=1, …, 5, the breeding females as stage 6, the first stage of non-breeding females () as stage 7, those who delay breeding at least 1 year, the second stage of non-breeding females () as stage 8, those who delay breeding 2 years, and finally, the breeding males as stage 9.

We make five more model assumptions about births, density-dependent survival, and sex ratio.

• (H5) The birth function, , is a function of breeding females, where we have assumed that there is a sufficient number of males. Unless noted otherwise, we shall assume the birth function B is a linear function of , , where c is the clutch size [10 .

• (H6) At metamorphosis, the proportion of first-year juveniles that develop from tadpoles is ρ(T), a strictly decreasing differentiable function of T, the density of tadpoles, and ρ(T)T is a non-decreasing function of T for such that

• (H7) The sex ratio is constant for a given population. The ratio s, s>0, is the proportion of males to females.

• (H8) The survival probability of eggs to the tadpole stage is a constant d, 0<d<1.

• (H9) The survival probability of toads in stage i to stage i+1 during period 5 is a constant satisfying 0<p _i5<1, i=1, …, 5 and survival probability of stage i during period j is a constant satisfying , i=1, …, 9,\; j=1, …, 4.

Assumption (H6) is relaxed in Section 2.4. A family of functions satisfying assumption (H6) is

where c ₀, c ₁>0, and . In particular, ρ(T)T has the form of a Beverton–Holt type function 5 when α=1.

2.2. Difference equations

A system of difference equations is formulated for the population dynamics of boreal toads during the five periods based on assumptions (H1)–(H9). The five periods are important for modelling of Bd infection, which depend on the time spent in the water. The model can be simplified to an annual model with time beginning in period 1 (Table 1). First, we consider this annual population model, and then we consider the epizootic model. Population counts are made prior to period 1, before dispersal. Since, at this stage, there are neither eggs nor tadpoles, those stages are not included in the annual model and only the juvenile stages and adult stages are included. The time spent (fraction of a year) for each of the five periods, beginning with the dispersal period, is denoted as t _j , j=1, …, 5; the interval t ₀ to t ₅ denotes 1 year.

For period l, l=1, …, 4, the model has the form

where

The parameters and d are probabilities of survival and c is clutch size, defined in (H9), (H8), and (H5), respectively.

For period 5, the model has the form

where ρ is the density-dependent survival of the tadpoles, assumption (H6), r _i , i=1, 2, determine breeding frequency, assumption (H2), and the other parameters are survival probabilities and transitions between various stages which can be more easily interpreted using the annual life cycle graph shown in Figure 1.

Figure 1. Annual life cycle graph of the boreal toad.

The derivation of the annual model consists of repeated back substitution of the variables at the intermediate times into the preceding system of equations. The annual model is

where the functions f ₁, f ₂, constants r ₁, r ₂, and the parameters p _i , i=0, 1, …, 8, a product of survival probabilities during the various developmental periods, are defined as

s ₃, s ₄, s ₅>0, and . The parameters s _i , i=3, 4, 5, are for notational convenience; s ₅=1. Juveniles in stages 1–3 include both males and females, assumption (H3). The probability that a stage 3 juvenile survives to the next year and becomes a non-reproductive juvenile female is p ₃, a reproductive adult female is s ₃ p ₃, or a reproductive male is s(1+s ₃)p ₃. The probability that a stage 4 juvenile female survives and remains juvenile is p ₄ or becomes reproductive is s ₄ p ₄. By the sixth year, females that survive become reproductive adults.

Note that the first eight equations in system (3) do not depend on the breeding males, . This is due to the fact we have assumed . Thus, to study system (3), it is not necessary to include the breeding males. If J ₃(t) is known, the solution to the breeding males is a solution to a linear, constant coefficient non-homogeneous difference equation. Hence, we reduce the system of difference equations (3) to a system of eight equations, written in matrix form as follows:

where

(tr denotes transpose of the vector) and

with initial conditions non-negative and not identically zero, and . For this model, we show that either the population approaches extinction or a positive equilibrium. First, we calculate the equilibria, then verify their stability under certain restrictions.

2.3. Equilibria and stability

Let

denote an equilibrium of system (5). Then, we have

System (6) gives rise to the equation

where

Hence, the equilibria are given by or the solution to . It follows from Equation (6) that if and only if . The equation has a unique positive solution if and only if ρ(0)>1/P. This follows directly from assumption (H6) and the limit in Equation (1). If , then it follows from Equation (6) that each of the components of F¯ are strictly positive; there exists a unique positive equilibrium. Hence, we denote the following expression as the basic reproduction number of the population model (5):

For the sake of simplicity, we write

so that . In biological terms, ℛ₀ represents the expected number of offspring that one typical female boreal toad produces during its lifetime when density dependence is ignored. The term c is the number of offspring per reproductive female (clutch size). The numerator P _N/c is the probability that a female boreal toad survives until stage and is the probability a female survives during the reproductive period, where

Next, we verify the global stability of the extinction equilibrium when and of the positive equilibrium when .

Theorem 2.1

Assume model (5) satisfies assumptions (H1)–(H9). If , then the extinction equilibrium of system (5) is globally asymptotically stable and if , then the extinction equilibrium is unstable and the positive equilibrium of system (5) is globally asymptotically stable.

Proof

The existence of the equilibria has already been verified. To prove the global asymptotic stability of the extinction equilibrium, observe that the Jacobian matrix J ₀ of system (5), evaluated at the zero equilibrium, is given by

Since ρ is a decreasing function, we also observe that . It follows from Equation (5) that

By induction, it follows that . The characteristic polynomial h(λ) of J ₀ is given by

Frobenius Theorem 17 and Descartes’ Rule of Signs 23 guarantee the existence of a unique positive strictly dominant eigenvalue of h(λ). If , then we see that

in which case the positive eigenvalue is less than unity. In this case, so that , the zero vector. Thus, the zero equilibrium is locally stable and globally attractive, which imply that it is globally asymptotically stable.

Now suppose that so the positive equilibrium exists. Then, the Jacobian matrix evaluated at the zero equilibrium, J ₀, has a unique positive strictly dominant eigenvalue greater than unity since h (1)<0; the zero equilibrium is unstable. In order to prove the global asymptotic stability of the positive equilibrium, we first prove the local stability. The Jacobian matrix of system (5), evaluated at the positive equilibrium F¯, is given by

where and ′ denotes differentiation with respect to . Since ρ is decreasing (assumption (H6)), then so that for . Also, is non-decreasing (assumption (H6)), so that for . The characteristic polynomial of J ₊ is given by

Frobenius Theorem 17 and Descartes’ Rule of Signs 23 again guarantee the existence of a unique positive strictly dominant eigenvalue of J ₊, and this eigenvalue is less than unity if h ₊ (1)>0. This condition is satisfied when the positive equilibrium exists since

Hence, the positive equilibrium is locally asymptotically stable.

In order to prove the global stability, we write system (5) in an equivalent form, as a scalar nonlinear difference equation in and use the fact that is a globally (locally) stable equilibrium of this difference equation if and only if the vector F¯ is a globally (locally) stable equilibrium of Equation (5). We apply a result of Grove and Ladas [18, Theorem 1.10, p. 15] to prove the global asymptotic stability of the positive equilibrium. This theorem is stated as Theorem A1 in the appendix for reference purposes.

System (3) can be expressed as a scalar nonlinear, fifth order, difference equation in ,

Letting and be the right-hand side of Equation (9), , where I=(0, ∞) and f is non-decreasing in each variable. In addition, , where , is a positive equilibrium of the difference Equation (9) such that

for all since ρ (hence f ₁) is a decreasing function by assumption (H6). Hence, it follows by Theorem A1 in the appendix that is globally attractive. Since we have already proved the local stability of the positive equilibrium in system (5) for , we conclude that the positive equilibrium is globally asymptotically stable and the theorem follows.   ▪

2.4. Permanence

It is worthwhile to look at the permanence of the corresponding system which determines whether the population persists independent of the stability of the equilibrium. Permanence ensures that the population neither vanishes nor blows up. We prove a theorem about permanence of system (5) imposing some weaker assumptions on the density-dependent function ρ. Assumption (H6) is replaced with the following assumption:

• (H6)′ The functions and are non-negative, continuous and bounded above for .

The weaker assumption (H6)′ allows for more general density-dependent functions for ρ. For example, if

then is known as a Ricker curve 10.

We apply a theorem of Kon et al. [20, Theorem 3, p. 519] to show permanence which is given in the appendix as Theorem A2 for reference purposes. The theorem requires that system (5) be dissipative. First, we state formal definitions of dissipative and permanence.

Let

where is an n-vector and A is an n×n matrix. System (10) is said to be dissipative if there exists a compact set such that for all , there exists a time t(X(0)) satisfying X(t)∈U for all t≥t(X(0)). Let be the total population density. Then, Equation (10) is said to be permanent if there exists positive constants, m and M, such that

for all satisfying N(0)>0.

In order to prove that a system is dissipative, it suffices to prove that each stage is uniformly bounded over time. That is, there exists [Mtilde] such that for every X(0) there exists a time t(X(0)), where , i=1, …, n, for all . Then the set serves as the required compact set.

Theorem 2.2

Assume the population model (5) satisfies assumptions (H1)–(H5), (H6)′, (H7)–(H9). Then system (5) is permanent if .

Proof

To apply Theorem A2 in the appendix to model (5) requires that the vector C(F(t))F(t) be continuous, the system be dissipative, matrix C(0) be irreducible, and be forward invariant. The continuity of C(F(t))F(t), the forward invariance of , and the irreducibility of C(0) are obvious. The only non-trivial part is to show that the system is dissipative. Suppose that for . Let ε>0 be given. It follows from systems (3) and (9) that, for all t,

Choose a number p such that

and set

Then, we show first, using generalized mathematical induction, that for all t≥0, . The result is clearly true for t=0, 1, and 2. Suppose for . Then, for t≥3, Equations (12) and (13) imply that

where the second inequality follows since p ⁱ <p for i=2, 3, and hence the result follows by induction. Now, we may choose t ₀>0 such that p ^t M<1 for t>t ₀. Hence, for all t>t ₀ and the uniform boundedness of follows and, consequently, that of and follow from Equation (3).

Thus, each stage is uniformly bounded independent of the initial conditions so that system (5) is dissipative. The condition guarantees the existence of an eigenvalue whose magnitude is greater than one (see proof of Theorem 2.1). Hence from Theorem A2 in the appendix, it follows that the system is permanent.   ▪

This definition of permanence allows some stages to be zero during certain years. For example, there may be no juveniles in a particular stage in one year but in subsequent years, this stage must have some individuals for the population to be permanent. This is a weaker form of permanence which is sometimes called p-permanence 19. A stronger form is c-permanence in which every stage is positive. For c-permanence, the expression in Equation (11) is replaced by

for positive constants m and M and for all i. As a corollary, we can apply Theorem 4.3 [19, p. 621] to show that our system is c-permanent. The theorem requires that matrix A(0) in Equation (10) be primitive 19. But A(0)=J ₀, given by the expression in Equation (8), is a primitive matrix.

Corollary 2.3

Assume the population model (5) satisfies assumptions (H1)–(H5), (H6)′, (H7)–(H9). Then system (5) is c-permanent if .

The proof follows directly from Theorem A3 19, given in the appendix.

3. Epizootic model

In this section, we include infection in the boreal toad population by the fungus Batrachochytrium dendrobatidis, more commonly referred to as chytrid fungus or simply Bd. The disease in amphibians is known as chytridiomycosis. The infective stage of Bd is the zoospore. Bd zoospores grow in the epidermis of adult amphibians or in the keratinized mouth parts of tadpoles, where they develop asexually within a sporangium 19. Mature zoospores emerge from discharge tubules of the sporangium. The skin of infected amphibians generally sloughs or peels off. We model the susceptible (healthy) and infected juvenile and adult amphibians based on the population model developed and analysed in the previous sections. We assume that amphibians do not recover. This new model is known as the epizootic model.

Throughout this section, both males and females are considered with the birth function . We use the decomposition of the year into the five periods shown in Table 1. This division of the year is required for the epizootic model because the disease is spread by different methods during these periods. Boreal toads are susceptible to chytridiomycosis, resulting in a high mortality rate; infected toads die in about 2 weeks (experimentally infected toadlets died an average of two weeks after exposure 9). We use, in the superscripts, the letter ‘S’ to denote susceptible toads and the letter ‘I’ to denote infected and infectious toads. Thus, our population vector is

where F _B and F _N denote the amount of free-living Bd (zoospores, measured in a suitable unit) in breeding ponds and non-breeding sites (e.g. overwintering sites), respectively.

3.1. Model assumptions

We assume that infection via fungal zoospores depends on the density of free-living chytrid F _B or F _N or on the density of infected amphibians (which produce zoospores that are released into breeding ponds or non-breeding sites). We use a Poisson distribution to model infection,

where k is the number of encounters between a susceptible amphibian and either an infected amphibian or Bd in breeding or non-breeding sites, F _B or F _N, that result in infection of a susceptible amphibian. The parameter λ is the average number of encounters per susceptible individual during the time interval [t, t+1] 3 15 16. It takes just one successful encounter to become infectious. Hence, the probabilities that a susceptible amphibian becomes infectious or does not become infectious are 1−p(0) and p(0), respectively. Under the assumption of mass action, the parameter λ for the spread from free-living chytrid, for example, at breeding ponds, to susceptible breeding amphibians satisfies , k=MS, FS. This assumption leads to density-dependent transmission 3 15 16, where the probability that a breeding amphibian is not infected at the breeding ponds is

and the probability that it is infected is

Alternately, frequency-dependent transmission has the form

where K is the amphibian population density. Density-dependent transmission during all stages leads to a simple annual model which is analysed in Section 3.3. In the numerical examples, we also compare frequency-dependent transmission in periods 3 and 4 to density-dependent transmission, when males and females are at the breeding ponds.

Some additional assumptions relate the life cycle of the boreal toad and the mode of infection by Bd for each of the five periods as described in Table 1.

• (H10) In the dispersal period 1, the disease does not spread between amphibians and there are no new infections.

• (H11) During hibernation, period 2, infection of all the stages may occur via contacts with fungal zoospores F _N that may be present in non-breeding sites.

• (H12) In period 3, breeding males and females may become infected through contacts with fungal zoospores F _B in contaminated breeding ponds.

• (H13) During tadpole development, if breeding males remain at the breeding ponds, then adult males may become infected through contact with fungal zoospores F _B in contaminated breeding ponds.

• (H14) During metamorphosis, first-stage juveniles may become infected through contacts with fungal zoospores F _B or from infected males (fungal zoospores from infected males) in contaminated breeding ponds.

• (H15) Juvenile and adult toads infected during period j do not survive to the next period j+1.

3.2. Difference equations

Define the following three vectors, representing various infectious stages,

and

In the model, the infectious states I _B occur during metamorphosis, period 5, the infectious states during tadpole development, period 4, and infectious states I _N during and after hibernation, when Bd infection increases in non-breeding sites. The subscripts B and N refer to breeding or non-breeding sites. The dot notation is the scalar product, e.g. denotes the scalar product of a non-negative vector with the vector I _B. Similarly, and are defined, where

The dot product or the resulting sum of terms represents the contribution to free-living fungi in breeding sites (F _B), and , or in non-breeding sites (F _N), , from infected amphibians. The parameter values in the vectors β_N, γ_B, and δ_B are assumed nonnegative and if, for example, males or females are infected at the breeding ponds, then the release of zoospores from infected amphibians could make a significant contribution to F _B; and for i=1, 2.

The last term in each of the scalar products denotes the survival of fungi, , and , rather than reproduction. We assume that free-living fungi does not reproduce (requires keratin from amphibians), hence , and represent only survival (not reproduction) of free-living fungi, which means these parameters are less than one. More specifically,

• (H16) .

The five periods that contribute to the annual epizootic model are described. All parameters are non-negative, unless noted otherwise.

In the dispersal period 1, there are no new infections, only survival of susceptible individuals. All amphibians that became infected during the previous period die (assumption (H15)). Thus, there are only susceptible amphibians,

The parameters represent survival probabilities for the different stages (during this period and other periods as well).

During period 2, hibernation, all stages can be infected if the site for hibernation is contaminated with chytrid F _N, assumption (H11). Frequency-dependent transmission is not assumed during hibernation because toads generally hibernate in groups; hence, density-dependent transmission may be more realistic. The parameters α _i , i=1, …, 7, come from the Poisson distribution (14), where . The expression accounts for the proportion of amphibians that does not become infected from the free-living fungi in non-breeding ponds, and is the proportion that does become infected. The model for period 2 is

During period 3, only the breeding males and females can become infected if the breeding site is Bd-infected, F _B, assumption (H12). Non-breeding sites may increase their Bd infection if amphibians were infected during hibernation, . The expressions , i=6, 9 account for the proportion of breeding amphibians that does not become infected from the free-living fungi in the breeding ponds, and is the proportion that does become infected. The model for period 3 is

During period 3, it is not known whether frequency-dependent transmission or density-dependent transmission occurs. In the simulations, we check the numerical results for both types. For comparison purposes, at the positive disease-free equilibria (DFE), we assume the transmission parameters are equal. Thus, for frequency-dependent transmission, we replace the parameters β _i by , where and denote the equilibrium stages of the population model (5). In addition, the are replaced by

After breeding, in period 4, tadpoles are produced but at this stage, we do not include infection of tadpoles. Tadpoles are only infected in their mouth parts. Free-living Bd may increase if breeding males and females are infected, . In addition, breeding males that remain at the pond can become infected during this stage (assumption (H13), where the probability of no infection is and the probability of infection is . The model for period 4 is

In frequency-dependent transmission, parameter γ₉ is replaced by , where denotes the equilibrium stage of the population model (5). The expression is replaced by

During period 5, metamorphosis from the tadpole stage to first-stage juvenile may result in infection of first-stage juveniles from Bd-infected ponds (F _B), assumption (H14). The probability of infection is , and the probability of no infection is . Production of free-living fungi in breeding sites is . The model for period 5 is

The non-negative parameters p _Bi , i=1, 2, 3 and p _Ni , i=1, 2, 4, 5 are the survival probabilities of the fungi populations in breeding and non-breeding ponds, respectively during the ith period.

Combining the models for each of the five periods, an annual model, , can be expressed as follows:

where

, and j=B, N.

System (15) can be written in matrix form:

where

is the vector of 11 stages in system (15), and is given by

Matrix C ₁(X(t)) is a 9×9 matrix, 0 is the 9×2 zero matrix, C ₂(X(t)) is a 2×9 matrix, and C ₃ is a 2×2 constant diagonal matrix whose entries are strictly between zero and one. Matrices C ₁ and C ₂ can be written explicitly, but they are not given here because they are not needed in the analysis. In the next section, explicit forms for the Jacobian matrix of this system and an upper bound on matrix are given. In the particular case that free-living Bd is not present in breeding and non-breeding sites, , then ; the epizootic model (15) reduces to the population model (5). We assume F _B(0)>0 and F _N(0)>0, unless noted otherwise.

In the epizootic model (15), we assumed density-dependent transmission. However, as noted previously, during the breeding stages, periods 3 and 4, frequency-dependent transmission may also be a reasonable assumption. Frequency-dependent transmission implies that transmission depends on the population proportion rather than the population density as in density-dependent transmission. In the breeding stages, periods 3 and 4, it is not clear whether the transmission should be frequency-dependent or density-dependent. Thus, we compare the dynamics of density-dependent and frequency-dependent transmission in the numerical examples in Section 5. The following analysis applies to the epizootic model with density-dependent transmission.

3.3. Equilibria and stability

To find the DFE for the epizootic model with density-dependent transmission, we set the infectious stages to zero. Then we are left with the population model (5). There are two DFE (the extinction equilibrium and the positive equilibrium) defined by Equation (6). To test the stability of these DFE, we calculate the Jacobian matrix of (16) and evaluate at each of the DFE. The Jacobian matrix has the following form:

When i=0, the Jacobian matrix is evaluated at the extinction equilibrium and when i=1, it is evaluated at the positive DFE.

In the case of the extinction equilibrium, matrix

and in the case of the positive DFE, matrix

where the entry * denotes the vector and 0 is an 8×1 column vector. Matrix M _i2 has the following form:

where

The equilibrium values of are either equal to zero (extinction DFE, i=0) or equal to their values at the positive DFE, i=1. Define

The disease persists only if the fungus survives either in breeding sites (m ₁>1) or in non-breeding sites (m ₂>1). Disease persistence depends only on the fungus because infected toads do not survive to the next period. Thus, can be considered the basic reproduction number of the disease. We show if and , then the positive DFE is locally asymptotically stable.

Matrix U does not affect stability because M is a block triangular matrix. Matrices J ₀ and J ₊ are the matrices studied in system (3). We can apply the results from Theorem 2.1 to the matrices M ₀₁ and M ₁₁: if , the spectral radius of M ₀₁ is less than one, and if , the spectral radius of matrix M ₀₁ is greater than one but the spectral radius of M ₁₁ is less than one. The local stability of the positive DFE depends on the eigenvalues of the matrix M ₁₂.

Theorem 3.1

Assume model (15) with density-dependent transmission satisfies assumptions (H1)–(H16). Then, there exists two DFE of system (15), an extinction DFE and a positive DFE. If , then the extinction equilibrium is globally asymptotically stable. If , then the extinction equilibrium is unstable and furthermore, if , where m ₁ and m ₂ are defined as above and evaluated at the positive equilibrium, then the positive DFE is locally asymptotically stable.

Proof

The existence of the two DFE can be easily verified by substituting zero for infected stages together with F _B and F _N in system (15) and then solving the resulting system. Therefore, we prove only the stability results in detail. Suppose . Using the fact that for θ>0, we derive the following inequality from system (15):

where

and The eigenvalues of C ₃ are between 0 and 1. Assumption (H16), together with the previous results in Section 2.2 about matrix M ₀₁, implies that the magnitude of the eigenvalues of M ₀₁ and hence, those of are less than one. Thus,

and the globally asymptotic stability of the extinction equilibrium follows. Next, suppose that . Then, the strictly dominant eigenvalue of M ₀₁ is greater than one, so the extinction equilibrium is unstable.

The Jacobian matrix of system (15), evaluated at the positive DFE, is

It can be observed that the eigenvalues of M are those of M ₁₁ and M ₁₂. We proved in Theorem 2.1 that the magnitude of the strictly dominant eigenvalue of J ₊ was less than one when . Since the eigenvalues of M ₁₁ are those of J ₊ and p ₉, in order to prove the local stability of the positive DFE, it suffices to show that the magnitude of the strictly dominant eigenvalue of M ₁₂ is less than one. This is, of course, the case when and the theorem follows.   ▪

4. Effects of environmental change on reproduction

The models discussed thus far are based on the life history characteristics of the boreal toads B. b. boreas in the western USA. The life cycle in various regions depends on many factors including latitude, temperature, and water availability. For example, the female boreal toad found in Southern Rocky Mountains in Colorado is generally not reproductive until the age of six 8 and does not breed every year. However, in the Oregon Cascade Range, females are reproductive as early as 4 years of age but the breeding frequency varies, from 1 to 4 years 27. Environmental changes that result in increased temperatures, earlier springs and shorter winters, may affect the reproductive pattern of boreal toads. We investigate the effect of changes in reproductive patterns on the threshold value ℛ₀. Increases or decreases in ℛ₀ ultimately result in either a greater or smaller chance of survival for the boreal toad, respectively.

Suppose environmental change affects the onset of breeding in females and the breeding frequency. That is, suppose the parameters r _i , i=1, 2 and s _i , i=3, 4 are affected by changes in temperature or other factors. For example, if r ₁=0, then females breed every year and if r ₁=1 and r ₂=0, then females breed every 2 years. In addition, if s ₃=0, then females do not become reproductive until age five. The parameters for Bd growth also vary with temperature. For example, Bd does not grow under laboratory settings at temperatures above 30 °C 28. Here, we only consider environmental changes as they might affect the population through the model (5) and not the impact on Bd. We investigate the impact of the parameters r _i , i=1, 2 and s _i , i=3, 4 on ℛ₀. All other survival and reproduction parameters are the same as in the previous sections: the probability that a stage i toad survives to the next stage during period k=1 (or in the same stage during periods k=2, …, 5) is p _ik for i=1, …, 9.

Example 4.1

Suppose and r ₁=0 in the population model (5). A female becomes reproductive at age four and breeds every year. In this case, the new threshold is

Toad survival is increased; it is always the case that .

Example 4.2

Suppose s ₃=0=s ₄ and r ₁=0 in the population model (5). A female becomes reproductive at age six and breeds every year. The threshold value for this model is

It is obvious that . However, whether this change in breeding onset is detrimental to survival depends on whether females that do not breed every year but breed earlier have a larger value of ℛ₀, .

Example 4.3

Suppose s ₃=0=s ₄, r ₁=1 and r ₂=0 in model (5). A female becomes reproductive at age six and breeds every 2 years. The threshold value for this model is

.

Example 4.4

As a final example, suppose s ₃=0=s ₄, r ₁=1, and r ₂=1. A female becomes reproductive at age six and breeds every three years. In this case,

It is always the case that and .

In the next section, some numerical values are assigned to the parameters to illustrate some possible quantitative changes in breeding onset and frequency.

5. Numerical examples

Several numerical examples are given to illustrate some of the models’ dynamics. Only a few of the large number of parameters are available in the literature. The scarcity of data prompted us to use hypothetical but reasonable values for many of the parameters. First, we consider the population model described in Section 2. Samollow 32 estimated clutch size as 16,000. Carey et al. 8 estimated average clutch sizes of 6600 with one to five clutches per female for populations in the Southern Rocky Mountains. Stebbins 34 gave estimates of up to 12,500 eggs in two strings in shallow water. We use c=8000 for total number of eggs per reproductive female. The survival probabilities ) are taken from McDonald and Tse 24 and adjusted to our model. Juvenile toad survival is p _i =0.422, and adult reproductive toad survival is p _i =0.8. These probabilities are based on an equilibrium distribution for females with half of the females breeding every year beginning in year 6. In our model, we also need to account for males and for early breeding of females. Since censuses are taken directly after breeding in McDonald and Tse 24, our value of p ₁ does not have the same meaning. Thus, we let p _i =0.422 for i=1, 2 and the female survival probabilities for years 3 and 4 which correspond to and . In addition, p _i =0.8 for i=5, …, 9 (Table 2). In our model, the egg and tadpole survival is set to dp ₀=0.02, but an additional mortality is assumed due to the density-dependent factor ρ. The sex ratio at the breeding pond can vary depending on many factors. Olson 27, whose data is based on Bufo boreas in the Oregon Cascade range, observed that the sex ratio (male:female) at the breeding ponds generally fluctuated between 2 and 3 for a period of 8 years. This was probably due to the fact that the non-breeding adult females who breed every 2 or 3 years are not present at breeding ponds. We assume that the sex ratio for all amphibians is s=1. In addition, we assume a Beverton–Holt type function for density-dependent survival, ρ with α=1 in Equation (2), equal to

where parameter values c ₁=1 and c ₂=0.0003. Stability is not affected by the value c ₂, but the equilibrium values depend on c ₂ (Theorem 2.1). The smaller the value for c ₂, the larger the value of the breeding female population. Values for r ₁ and r ₂ are based on the frequencies of site attendance of female toads at breeding sites in the Oregon Cascade range observed by Olson 27 in which 15% breed every year, 55% breed every other year, and 30% breed every two or more years. Therefore, we choose r ₁ and r ₂ such that 1−r ₁=0.15 and , which imply that r ₁=0.85 and r ₂=0.35. Values s ₁ and s ₂ are hypothetical and chosen for illustration purposes. Values of s ₃=0.25 and s ₄=0.5 imply the ratio of reproductive females to nonreproductive females in the fourth year is 1:4 and the ratio of new reproductive females to nonreproductive females in the fifth year is 1:2. Table 2 summarizes the parameter values for the population model (5).

Table 2. Parameter values for the population model (5).

Parameter	Value
s	1
s 3	0.25
s 4	0.5
r 1	0.85
r 2	0.35
c	8000
dp 0	0.02
	0.422
	0.8

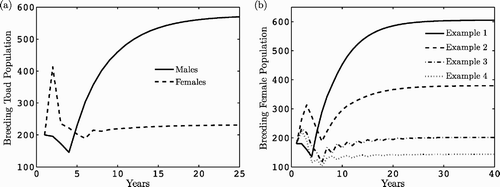
Figure 2 (a) shows the dynamics over time of the breeding females and males ( and ) in the population model (5) for the parameter values given in Table 2. Note that the breeding pond sex ratio is approximately 2.5 (), which is consistent with the sex ratio observed by Olson 27 at three sites in the Oregon Cascade range. Figure 2(b) are graphs of the breeding females () for the parameter values in Table 2 and based on the assumptions for Examples 4.1–4.4. It is clear that survival is greatest for the parameters in Example 4.1 and lowest for Example 4.4.

Figure 2. Dynamics over time of (a) breeding female and male populations for the general model (5) where ℛ₀=12.13 and (b) breeding females for the parameter values in Examples 4.1–4.4 where ℛ₁=30.06, ℛ₂=19.24, ℛ₃=10.69, and ℛ₄=7.88.

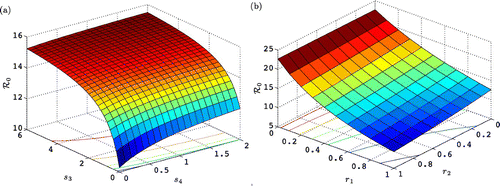
The threshold value ℛ₀ as a function of breeding onset s _i , i=3, 4 and breeding frequency, r _i , i=1, 2 is graphed in Figure 3. The threshold ℛ₀ increases rapidly with s ₃ but levels off at a maximum value as , that is, when but is constant, so that breeding onset for females is at age four. Also ℛ₀ is smallest when r ₁=1=r ₂, when female breeding frequency is every third year.

Figure 3. Threshold value ℛ₀ as a function of (a) breeding onset, parameters s ₃ and s ₄, and (b) breeding frequency r ₁ and r ₂. All other parameter values are given in Table 2.

Parameter values used in the simulations for the epizootic model (15) are given in Table 3, in addition to those in Table 2. The parameters p _ji satisfy , j=1, …, 9, so that they agree with the values in the population model, see Equation (4). These parameter values are hypothetical and chosen for illustration purposes.

Table 3. Parameter values for the epizootic model (15).

Parameter	Value
	0.2
	0.1
	0.2
βN
γB
δB	(1, 0.2)^tr

Figure 4(a) shows the dynamics of the breeding males and females in the population model (5) and in the epizootic model (15) with density-dependent transmission. In this case, . In Figure 4(b), breeding males and females are graphed in the epizootic model with frequency-dependent transmission. The equilibrium vectors

corresponding to Equation (17) in the epizootic model are estimated numerically from the simulations in the two cases (a) and (b),

and

respectively. For comparison purposes, the parameter values for frequency-dependent and density-dependent transmission were chosen so that at the DFE the parameters are equal. In example (a), Bd survives in the non-breeding sites, , and in example (b), Bd survives in breeding sites, (non-zero values for F _B and F _N represent the presence of Bd). In the population model with no disease,

the equilibrium value for breeding males is and for breeding females is (Figure 2(a)). In general, if disease reduces the population size below the DFE, then frequency-dependent transmission will reduce the population size more than density-dependent transmission, as illustrated in Figure 4 and in the preceding equilibrium values. Of course, the amount of reduction depends on the choice of parameter values.

Figure 4. Dynamics over time of breeding female and male populations for the population model (5) and the epizootic model. In (a), density-dependent transmission is assumed and in (b), frequency-dependent transmission. The parameter values are given in Tables 2 and 3.

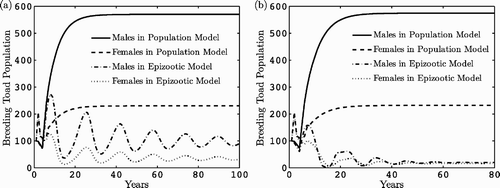
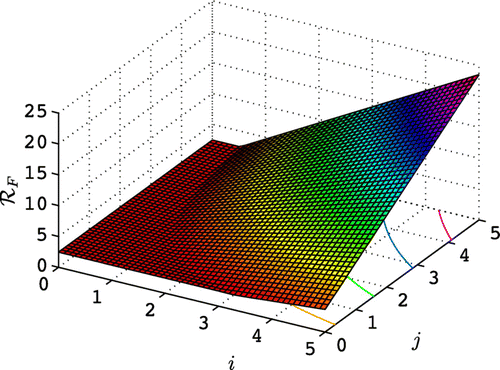
The graphs give an indication of the possible impact of disease on the population. The larger the value of β_N, the greater potential for survival of Bd in non-breeding sites leading to a reduction in the toad population. On the other hand, the larger the values of δ_B and γ_B, the greater potential for survival of Bd in breeding sites, which also leads to reduction in the toad population. The impact of the two parameter vectors δ_B and γ_B on the basic reproduction number in the epizootic model (Theorem 3.1) can be seen in Figure 5 for the parameter values in Tables 2 and 3. The term m ₁ depends on Bd in breeding sites and m ₂ depends on Bd in non-breeding sites. The parameters γ_B and δ_B affect Bd in breeding sites, the term m ₁. For small values of γ_B and δ_B, , infection is maintained in non-breeding sites. For larger values of γ_B and δ_B, then increases and infection is primarily dependent on Bd in breeding sites.

Figure 5. Threshold value ℛ_F as a function of parameters i and j, where γ_B=i (0.2, 1, 0.2)^tr and δ_B=j(1, 0.2)^tr for 0≤i, j≤5.

6. Conclusion

New population and epizootic models were formulated for the boreal toad based on life history and breeding strategies. For the autonomous population and epizootic models, two threshold parameters, ℛ₀ and , were defined for population survival or for disease survival. If , then population extinction occurs. If and , then the population survives without Bd infection. But if and , then Bd infection can become established and cause severe reduction in toad populations. These two thresholds identify important relationships among parameters that affect boreal toad survival. The parameter ℛ₀ was used to compare the effects of female breeding onset and breeding frequency on toad survival (Examples 4.1–4.4). In addition, increasing the value of parameters related to growth of Bd at breeding sites was shown to significantly increase the value of (Figure 5). In the epizootic model formulation, frequency-dependent versus density-dependent transmission of Bd at breeding sites needs to be carefully considered. Frequency-dependent transmission of Bd was shown to have a more drastic reduction on toad populations than density-dependent transmission (Figure 4).

Numerical simulations can be used to investigate more thoroughly the effects of environmental changes and Bd infection on various life stages of the boreal toad in these new population and epizootic models. In addition, the basic modelling framework can be extended to investigate the effects of temporally varying parameters, environmental and demographic variability, and spatial effects on toad survival.

Acknowledgements

Financial support was provided by the National Science Foundation DMS-0718302. We thank Keith Emmert, for the help with the initial formulation of this model. In addition, we thank two anonymous referees for their helpful suggestions.

Appendix. Theorems

The following theorem is used to verify the global stability results in Theorem 2.1 for the population model (5).

Theorem A.1

[18 Theorem 1.10, p. 15] Let [xtilde]∈I be an equilibrium of the difference equation

where and I is an open interval in ℝ. Suppose f satisfies the following two conditions:

1. f is non-decreasing in each of its arguments, and

2. f satisfies for all .

Then, [xtilde] is a global attractor of all solutions of Equation (A1).

The following theorem is used to verify permanence in Theorem 2.2 for the population model (5).

Theorem A.2

[20, Theorem 3, p. 519] Suppose the dynamical system (10) is continuous and dissipative. Assume the matrix is irreducible and is forward invariant (i.e. for all . Then, system (10) is permanent if has an eigenvalue whose magnitude is greater than unity.

The following theorem is used to verify c-permanence in Corollary 2.3 for the population model (5).

Theorem A.3

[19, Theorem 4.3, p. 621] Suppose dynamical system (10) is continuous, dissipative, for X(t)≥0 and for X(t)>0. Also suppose that A(X(t)) is irreducible for all , holds for all X(t)∈ bd and system (10) is p-permanent. Then system (10) is c-permanent if and only if A(0) is primitive.