Competitive outcomes changed by evolution

Abstract

When evolution plays a role, population dynamic models alone are not sufficient for determining the outcome of multi-species interactions. As an expansion of Maynard Smith's concept of an evolutionarily stable strategy, evolutionary game theory (EGT) combines population and evolutionary dynamics so that natural selection becomes a dynamic game with phenotypic traits as strategies. Using EGT, we show how evolution can change the outcome of the interaction between two competing species. We are particularly interested in situations where the interaction changes from one of competitive exclusion to one of coexistence and where the interaction changes from the exclusion of one species to the exclusion of the other. There are two crucial factors that determine whether or not such events can occur: the rate of evolution (which is proportional to the amount of variability in phenotypic traits within a species) and what we term the boxer effect, a phenomenon that concerns how the intensity of interspecies competition relates to species’ trait differences. We apply the theory to data from two historical competition experiments involving species of flour beetle from the genus Tribolium. In both applications, we show how EGT can explain certain seemingly ‘anomalous’ experimental results.

Keywords:

• competition
• competitive coexistence
• competitive exclusion
• evolutionary game theory
• evolutionarily stable strategy

1. Introduction

We investigate, using evolutionary game theory (EGT), ways in which evolution can change the outcome of a competitive interaction between two species. In addition to being interested in these possibilities as a general phenomenon in the theory of competitive interactions, we are motivated by two sets of data collected from the experiments using two species of flour beetles (Tribolium castaneum and Tribolium confusum). The first data set, which comes from experiments of Park 13, provides evidence for a change from competitive exclusion to coexistence. The data from another experiment carried out by Dawson 8 exhibited a reversal in competitive outcome, i.e. a change from the exclusion of one species to the exclusion of the other. We will examine these data sets and show how EGT can provide explanations of these observations.

We consider a two-species competition model derived from EGT (Section 3). In this study, we introduce the notion of a boxer effect by which is meant that maximal competitive intensity does not occur between species possessing identical (or nearly identical) phenotypic traits (i.e. utilizing identical strategies). The boxer effect assumes that maximal interspecific competition occurs when species traits differ by a non-zero amount. This name derives from an analogy with a boxing match: each boxer's punch has its greatest impact on the opponent when the two boxers are at an optimal distance apart. In Section 4, we will see that in the absence of this effect, while our EGT model will allow evolution from competitive exclusion to coexistence (under suitable conditions), it will not do so in a way that results in an evolutionarily stable strategy (ESS) nor in a way that can result in an evolutionary path applicable to Park's competition experiments. In Section 5, we will see, on the other hand, that the presence of a boxer effect can lead to evolutionary transitions that do result in changes in competitive outcomes and in an ESS. In Section 6, we use our theory and models to offer explanations for both Park's and Dawson's experimental results.

2. EGT models

Exclusion to coexistence evolution by natural selection is like a mathematical game in the sense that it has players, strategies, strategy sets, and pay-offs. The players are individual organisms, strategies are phenotypic traits with heritable components, the strategy set is the collection of all evolutionarily feasible strategies for a particular organism, and the pay-off to an individual is determined by its individual fitness. The fitness of an individual directly influences changes in the strategy's frequency within the population as that strategy is passed from generation to generation. The evolutionary game has to do with the survival of a given strategy within a population of individuals using potentially many different strategies.

One can investigate many evolutionary processes using EGT. Here, we use the theory to investigate how evolution can change the outcome of a competitive interaction between species. Such an evolutionary scenario is particularly relevant to situations in which species are suddenly allowed to mix, such as with the appearance of invasive species into a natural habitat or, in an experimental setting, with the introduction of species into a controlled or laboratory habitat.

We follow the modelling methodology for EGT presented in 21. The methodology derives equations that describe the population dynamics of n interacting species x _i together with the dynamics of (mean) phenotypic traits u _i (or strategies) which serve to characterize all individuals of a particular species. Species differ only with respect to the traits u _i , which are assumed to have a heritable component.

Let denote the vector of population densities and denote the vector of all strategies used by the species, which are distinct and drawn from the same set 𝒰 of evolutionarily feasible traits. Population dynamic models in terms of differential or difference equations often have one of the forms

where Equation (1) is a differential equation (in which [xdot] _i denotes differentiation with respect to time) and Equation (2) is a difference equation (in which denotes, following 11, the value of x _i after iteration by one time unit). We refer to as the fitness function for species x _i . As indicated, fitness is, in general, a function of the densities of all species and the strategies used by all species (i.e. a species fitness depends not only on its own trait, but also those of the other species). Fitness-generating functions (G-functions) play an important role in EGT 21. A function is a fitness-generating function (G-function) for the population dynamics if (and only if)

In terms of the G-function, the population dynamic equations become

EGT postulates that strategies will evolve according to the equations

where is the variance in traits (strategies) present in species x _i about the mean trait u _i 21. The population dynamics and the trait dynamics (4a) and (5a) (or (4b) and (5b)) together constitute a dynamical system for the 2n-vector

This dynamic describes an evolutionary process known as Darwinian dynamics 21. These equations allow us to investigate the role evolution plays in determining, for example, the dynamic outcomes of competitive interactions.

Darwinian dynamics will often possess a (locally asymptotically) stable equilibrium . Suppose this equilibrium remains stable when additional species (with their associated traits) are added to the community. This means that the coalition of traits u _i associated with those species present in the equilibrium (i.e. for which ) is able to resist invasion by other species with their other traits. By this we mean, mathematically, that the 2n-dimensional equilibrium, when embedded in the higher 2m-dimensional space of the larger community (m>n), remains (locally asymptotically) stable. In this case, we say that this coalition of traits is an ESS.

The ESS maximum principle provides a necessary condition for a coalition of traits in an equilibrium to be an ESS 21. According to this principle, if a coalition of strategies is an ESS, then the G-function evaluated at equilibrium conditions, i.e. , takes on an isolated global maximum with respect to v at each trait in the coalition. Furthermore, this maximum value must equal 0 for the differential equation model and must equal 1 for the difference equation model.

3. EGT competition models

The classic Lotka–Volterra model for the competition between two species has fitness functions

We are interested in competition between similar species and will therefore assume that the intrinsic growth rate r=r _i is common to all species. The resulting Lotka–Volterra EGT competition model is obtained from the general Darwinian dynamic equations (4a) and (5a) by use of the G-function 1 19 22

Here, we let

where and hence K(u _i ) is the equilibrium level of species i in the absence of species j, and measures the competitive effects that individuals of species j≠i using strategy u _j have on the fitness of individuals of species i using strategy u _i .

The discrete time Leslie–Gower competition model 13

has fitness functions 5

The asymptotic dynamics of this model have the same familiar phase plane portraits possessed by the Lotka–Volterra differential model 3 19 20. The Leslie–Gower EGT competition model is obtained from the general Darwinian dynamic equations (4b) and (5b) by using the G-function

where

and r, K(v), and (with ) have the same interpretations as in the Lotka–Volterra model.

Because Leslie et al. 13 utilized the Leslie–Gower competition model in the design and analysis of Park's experiments, we focus in this paper on the Leslie–Gower EGT model. Our results remain valid, however, for the Lotka–Volterra EGT competition model 17. The Darwinian dynamics for the Leslie–Gower EGT model are given by the (discrete time, difference) equations

The location of the point

in the competitive outcome plane determines which of the four possible phase portraits occur for the Leslie–Gower model (6). Figure 1 shows that each of the four quadrants in this plane is associated with one of the four possible phase portraits. We call a point , with x _i >0, a competitive coexistence point if it produces a point in the (interior of) SW quadrant1 of the competitive coexistence plane. If produces a point in (the interior of) any of the other three quadrants, it is a competitive exclusion point.

Figure 1. We refer to the [c ₁₂−c ₂₂, c ₂₁−c ₁₁]-plane as the competitive-outcome plane. Each of the four possible phase portraits associated with the Leslie–Gower model (6) corresponds to one of the quadrants in this plane, which we denote by the compass directions.

The competitive outcome implied by a phase portrait in Figure 1 would (asymptotically) result if the traits u ₁, u ₂ were to remain fixed in time. However, the Darwinian dynamics for the Leslie–Gower model (9) result in traits u ₁, u ₂ that evolve in time. Given initial conditions, the model produces an orbit of points that in turn produces a path of points

in the competitive-outcome plane in Figure 1. If an orbit of the Leslie–Gower EGT model approaches an equilibrium , then this evolutionary path in the competitive-outcome plane will asymptotically approach an end point

If this end point lies in the SW quadrant, then the equilibrium is a coexistence equilibrium and represents a coalition of two species 21. If this end point lies in one of the other three quadrants, then the equilibrium is an exclusion equilibrium and represents a coalition of one species.

In this paper, we are interested in determining conditions under which the Leslie–Gower EGT model predicts an evolutionary change in the outcome of a competitive interaction. What we mean by this is the existence of an evolutionary path in the competitive exclusion plane that has an (asymptotic) end point which lies in a quadrant different from that of its starting point.

An example is an evolutionary path associated with an orbit that begins at a competitive exclusion point and ends at (i.e. asymptotically converges to) a coexistence equilibrium. In this case, we say that the orbit indicates an evolution to competitive coexistence. Such an orbit would be associated with an evolutionary path that ends in the SW quadrant, but that initiates in one of the other three quadrants. In our application to Park's experiment, for example, it will turn out that we will be interested in evolutionary paths from the NE to the SW quadrant.

Another example is an orbit whose evolutionary path starts in the SE quadrant and ends in the NW quadrant (or vice versa). Such a path indicates an evolutionary reversal in the competitive outcome in that what initially would have resulted in the elimination of one species, if evolution did not occur, results in the elimination of the other species when evolution does occur.

The Leslie–Gower EGT model will be fully specified once we have modelled the way in which the competition coefficients c(v, u _j ), or more specifically and K(v) in Equation (8), depend on species traits. Let U denote an interval (which can be infinite) of feasible trait values on which the function K(·) is defined. With regard to the competition coefficients, our basic assumption in this paper is that competition between the two species is a function of the difference between the two species traits. Thus, where the function must be defined on the interval . Specifically, we assume the following.

The requirement in H(b) that α (0)=1 is necessary so that K(u _i ) is the equilibrium level of species x _i in the absence species x _j .

Under assumption H, the competition coefficients in the Leslie–Gower EGT competition model (9) are

and a pair of traits u ₁, u ₂ yield the point

in the competitive-outcome plane. We rewrite this formula as

and note that either the ratio or its reciprocal must be greater than or equal to 1. Since a point lies in the NE quadrant of the competitive-outcome plane if and only if both coordinates are positive, we obtain the following result.

Theorem 1

Assume the coefficients (10) in the Leslie–Gower EGT model (9) are defined by K and α that satisfy H. If then no traits u ₁, u ₂ produce a point that lies in the NE quadrant in the competitive-outcome plane ( Figure 1).

If then the maximum interspecific competition is experienced by both species when their trait difference w=u ₂−u ₁=0, that is to say, when the species are identical. This is commensurate with, for example, the assumption that as two species become more similar the competitive intensity between them increases 6. On the other hand, if , then there exists a trait difference w*≠0\ at which .

Theorem 1 shows that a boxer effect is necessary for evolutionary paths, generated by the Leslie–Gower EGT model (9) and (10), to intersect the NE (competitive exclusion) quadrant in Figure 1. In particular, any application of this model to Park's competition experiments, which it turns out requires an evolutionary path from the NE to the SW quadrant (Section 6), must include a boxer effect. As we will see in Section 5, the existence of a boxer effect can allow for evolutionary paths from the exclusion NE quadrant to the coexistence SW quadrant.

The Gaussian distribution

is widely used for the carrying capacity K in the context of EGT Lotka–Volterra models 18 21 22. This distribution assumes the maximum inherent equilibrium level K _m for each individual single species, using strategy v, in the absence of other species is attained at trait v=0, and that K(v) is normally distributed around v=0 with variance . We use this distribution for K throughout this paper.

4. A canonical model with no-boxer effect

A frequently utilized competition coefficient is 18 21

which, since its maximum value is 1, does not exhibit a boxer effect. This distribution implies that competitive intensity is normally distributed around a maximum value of 1, with a variance , as a function of trait difference w=u _i −u _j . Note that the maximum competitive intensity occurs when the two species have identical traits, i.e. w=u _i −u _j =0.

In this section, we consider the Leslie–Gower EGT model (9) with Equation (11) and the canonical no-boxer effect competition coefficient (12). The fundamental question in which we are interested is whether or not the model can produce evolutionary paths in the competitive-outcome plane (Figure 1) that initiate in one quadrant and end (asymptotically equilibrate) in a different quadrant, that is to say, for which evolution changes the competitive outcome. In this regard, note that Theorem 1 is applicable to this model and as a result no evolutionary path generated by orbits of the model can intersect the NE (competitive exclusion) quadrant. A basic question to address is the existence of equilibria of the Darwinian equations (9) and the location of the corresponding points in the competitive-outcome plane. We focus on two possibilities: the existence of coexistence equilibria and the existence of exclusion equilibria.

4.1. Coexistence equilibria

Can an evolutionary path begin in an exclusion quadrant and (asymptotically) end in the competitive coexistence SW quadrant? In this section, we will show that this is possible. Such a path cannot originate, however, in the NE exclusion quadrant in the absence of a boxer effect (Theorem 1).

Necessary for an evolutionary path to (asymptotically) approach an end point in the SW quadrant is the existence of at least one coexistence equilibrium. The following theorem (whose proof appears in the appendix) describes the conditions under which coexistence equilibria exist for the Leslie–Gower EGT model (9) with no-boxer effect.

Theorem 2

Consider the Leslie–Gower EGT model (9) with coefficients (10) defined by Equation (11) and the canonical no-boxer effect competition coefficient (12).

a.	If then there exists no coexistence equilibrium
b.	If then there exist exactly two coexistence equilibria. These equilibria are given by the formulas

Moreover, for both of these equilibria we have

where G is given by Equation (7).

The inequality means there is less variance in the inherent carrying capacity K(v) as a function of the (mean) trait than there is in the interspecific competition coefficient α (w) as a function of trait differences. The carrying capacity K(v) is a surrogate for the intensity of intraspecific competition. Therefore, in this sense, we can view part (a) of Theorem 2 as asserting that if there is less variability in the intensity of intraspecific competition than there is in the intensity of interspecific competition, then the species cannot coexist in equilibrium.

Part (b) asserts, on the other hand, that coexistence equilibria exist when the variability in interspecific competitive intensity is less than that of intraspecific competition (i.e. than the variability in the inherent equilibrium level). We conclude that for (equilibrium) coexistence to occur it is necessary, in the case of the Leslie–Gower EGT model, that there be a sufficient amount of variability in the inherent carrying capacity (intraspecific competition) as a function of the (mean) trait (when compared with the variability in interspecific competition). The equilibria in (b) can be found in 18, although no uniqueness assertion is made there).

Theorem 2 does not address the stability of the coexistence equilibria, which is important with regard to the dynamic evolution to the coexistence equilibrium. We conjecture that under the conditions of Theorem 2(in part (b)) the coexistence equilibria are (locally asymptotically) stable. Computer simulations support this conjecture (Figure 2).

Figure 2. No-boxer effect: evolution to coexistence and a non-ESS. A simulation is shown of the Leslie–Gower EGT model (9) with no-boxer effect coefficients defined by Equations (11) and (12) and parameter values r=0.25, K _m =100, , , . The initial condition [u, x] = [3.8, 4.3, 25, 25] leads to the coexistence equilibrium [u, x] ≈ [−1.8211, 1.8211, 73.564, 73.564], producing an evolutionary path from the NW to the SW quadrants as shown in graph (i). Graph (ii) shows that the equilibrium traits are located at minima of the G-function. In graph (iii), we see that despite the fact that species x ₁ has a rapid rise in density and would ultimately out compete species x ₂, the speed of evolution (set by and ) is sufficient for species x ₂ to recover and ultimately coexist with (and reach the same equilibrium population number as) species x ₁.

The inequality (13) has an important consequence with regard to the notion of ESS. Since Equation (13) implies that is not a maximum at the trait (strategy) associated with either coexistence equilibrium, it follows from the ESS maximum principle 21 that the traits associated with these coexistence equilibria are not ESS. This means that both coexistence equilibria are destabilized by the addition of other competing (invasive) species, or in other words, the two coexisting species are vulnerable to invasion by other competing species. This fact, while relevant to natural populations where invasion by additional species might be possible, is not relevant to controlled laboratory experiments such as those of Park and Dawson.

Figure 2(i)–(iii) shows an example of an orbit of the Leslie–Gower model (9) with canonical no-boxer coefficient (12) that converges to a coexistence equilibrium and produces an evolutionary path from competitive exclusion to coexistence. Specifically, this example shows an evolutionary path that begins in the NW quadrant of the competitive-outcome plane (where, if traits did not evolve, species x ₂ would go extinct) and ends (asymptotically equilibrates) at a coexistence point in the SW quadrant (where the two species coexist in equilibrium). Figure 2(ii) shows that the equilibrium traits are located at minima of the G-function, which illustrates the fact that at the coexistence equilibrium the two species do not form an ESS coalition of two.

4.2. Exclusion equilibria

As a consequence of Theorem 1, in the absence of a boxer effect there cannot exist a competitive exclusion equilibrium of the Leslie–Gower EGT model whose corresponding point lies in the NE quadrant of the competitive-outcome plane. Under certain circumstances, however, it is possible that there exists exclusion equilibria for which lies in the other quadrants of the plane. This is shown in the following theorem, whose proof appears in the appendix.

Theorem 3

Consider the Leslie–Gower EGT model (9) with coefficients (10) defined by Equation (11) and the canonical no-boxer effect competition coefficient (12). Assume .

a.	If both species evolve , then there exist no competitive exclusion equilibria with x 2=0.
b.	If , then there exist infinitely many competitive exclusion equilibria with x 2=0, namely where u 2 is arbitrary. These equilibria give points in the competitive-outcome plane satisfying These equilibria are non-hyperbolic. If they are unstable.
c.	If then there exist infinitely many competitive exclusion equilibria with x 2=0, namely where u 2 is arbitrary. These equilibria give points in the competitive-outcome plane satisfying These equilibria are non-hyperbolic. If , they are unstable.

The theorem is stated for exclusion equilibria in which species x ₂ is absent. This is no loss in generality since the labelling of the two species is arbitrary. Thus, there is a symmetric theorem for exclusion equilibria with x ₁ absent.

Remark 4

Suppose . That is to say, suppose variability in the intraspecific competition intensity is greater than that in the interspecific competition intensity. Then there exist (exactly two) coexistence equilibria (Theorem 2). Theorem 3(a) implies that if both species evolve, neither can evolve to extinction, at least in the sense that their orbit approaches an exclusion equilibrium. These facts suggest that in this case the species will evolve to coexistence. The stability of the coexistence equilibria, however, remains an open question.

If only one species evolves, Theorem 3(b) implies that exclusion equilibrium with is unstable and consequently that the non-evolving species will not be driven to extinction. This again points to the stability of the coexistence equilibria (but this remains an open question). On the other hand, Theorem 3(c) does not rule out the stability of the exclusion equilibrium, with the resulting extinction of the non-evolving species, with . The proof in the appendix shows that all the eigenvalues of the linearization at the exclusion equilibria in Theorem 3(c) satisfy (if is small, i.e. evolution is not to fast), but that one eigenvalue equals 1. Consequently, the stability of the equilibrium cannot be deduced from a linearization analysis. Whether these exclusion equilibria are stable or not remains an open question.

Remark 5

Suppose . That is to say, suppose variability in the interspecific competition intensity is greater than that in the intraspecific competition intensity. In this case, there exist no coexistence equilibria (Theorem 2). Theorem 3(a) implies that if both species evolve, there do not exist any exclusion equilibria either. The asymptotic dynamics in this remain an open question. Computer simulations suggest in this case that evolutionary paths tend to a point on the axes in the competition-outcome plane, which indicates that the population dynamic phase portrait evolves to a non-generic phase portrait (overlapping isoclines).

If only one species evolves, Theorem 3(b) and (c) implies the existence of competitive exclusion equilibria. This suggests, along with the absence of coexistence equilibria, that in this case evolution will eliminate one species. Because of the non-hyperbolicity of these equilibria, however, a linearization analysis does not establish their stability and this possibility remains an open question. The cases of instability available in Theorem 3(b) and (c) provide some instances of non-extinction.

Figure 3 shows an example that demonstrates how the Leslie–Gower EGT model (12) with the canonical no-boxer competition coefficient (12) can produce an evolutionary path that implies a competitive reversal. The graphs in Figure 3 show an evolutionary path that begins in the SE quadrant of the competitive-outcome plane (where, if traits did not evolve, species x ₁ would go extinct) and ends at a point in the NW quadrant (where species x ₂ goes extinct). Theorems 2 and 3, together with the parameter values used in this simulation: with and , imply that there exist exclusion equilibria, associated with the NW quadrant, in which species x ₂ is absent and that there are no coexistence equilibria. The simulation (and others not shown) suggests the stability of the exclusion equilibrium (Remark 5). Moreover, Figure 3(ii) shows that species x ₁ evolves to a maximum point on the adaptive landscape and as a result the maximum principle for an ESS is satisfied. This example is motivated by Dawson's experiment 8 in which a reversal in the expected competitive outcome was observed in a culture in which one of the species underwent a genetic change during the course of the experiment (Section 6.2.)

Figure 3. No-boxer effect: evolutionary reversal in competitive outcome and an ESS. A simulation is shown of the Leslie–Gower EGT model (9) with coefficients defined by Equations (11) and (12) and with parameter values r=0.25, K _m =100, , , , . The initial condition [u, x] = [4, 3.8, 25, 25] produces a point in the SE quadrant of the competitive exclusion plane and results in an orbit that approaches an exclusion equilibrium [u, x] ≈ [0, 3.8, 100, 0], thus producing an evolutionary path from the SE to the NW quadrant, as shown in graph (i). Graph (ii) shows that the first species has evolved to a maximum point on the adaptive landscape. The second species, unable to evolve, dies out with time. In graph (iii), we see that species x ₁ has a rapid rise in density and x ₂ rapidly dies out.

4.3. Summary remarks

In this section, we considered the Leslie–Gower EGT competition model under the assumption that no-boxer effect is present (specifically, the coefficients (10) are given by Equation (11) and the canonical competition coefficient (12)). Table 1 summarizes some (asymptotic) transitions between quadrants in the competitive-outcome plane that can or cannot take place by evolutionary paths in this model (as ascertained from the analytic results in this section, supplemented by computer simulations).

Table 1. For the Leslie–Gower EGT model (9) with (no-boxer effect) coefficients (10) defined by Equations (11) and (12), this table shows some (asymptotic) quadrant transitions of evolutionary paths, which terminate in a equilibrium point of the Darwinian dynamics that can and cannot occur in the competitive-outcome plane (Figure 1).

	Possible evolutionary paths without boxer effect
	NW to SW	SE to SW	NE to SW	SE to NW (or vice versa)
	No	No	No	No
	Yes, but not an ESS (U is unbounded)	Yes but not an ESS (U is unbounded)	No	Yes, but only if one species evolves or

When , simulations suggest that all evolutionary paths tend to the origin in the competitive-outcome plane, which implies that the two species traits evolve to the same value. This might be considered a case of convergent evolution, except that the end result cannot be interpreted as two different species (because they are indistinguishable in terms of adaptive parameters). In order for two species to coexist it is necessary that , but even then a coexistence equilibrium is not an ESS and the coexisting species are subject to invasion by additional species.

5. Boxer effect

Of particular interest to us is the case of saddle phase portraits that occur in the NE quadrant of Figure 1. This is the competitive exclusion phase portrait that is of relevance to the coexistence treatment in Park's experiments with Tribolium. Specifically, it is of interest to know whether it is possible for the Leslie–Gower EGT model (9) to produce evolutionary paths in the competitive-outcome plane that begin in the NE quadrant and end in the SW quadrant.

By Theorem 1, the answer is ‘no’ in the absence of a boxer effect. In this section, we show that when a boxer effect is present such evolutionary paths – and in particular paths from the NE to the SW quadrants – are indeed possible. We do this by using the competition coefficient

A boxer effect is present, i.e. the maximum of α does not occur at w=0, if and only if (see Lemma 7 in the appendix). This distribution is symmetric around w=0 (Figure 4). (Asymmetric distributions possessing a boxer effect have been used in Darwinian dynamic models based on Lotka–Volterra models 21 22.) Figure 5 shows two examples obtained from this model that produce evolutionary paths initiating in a competitive exclusion quadrant and ending in the competitive coexistence SW quadrant. Note that we retrieve the canonical no-boxer distribution (12) by setting β=0.

Figure 4. (a) For β<σ _a the competition coefficient α (w) given by Equation (14) has a maximum at w=0 and hence does not exhibit a boxer effect. (b) When β>σ _a the maxima of the competition coefficient α (w) are greater than 1, illustrating a boxer effect.

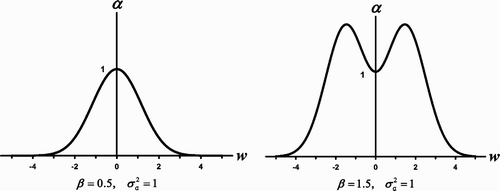
Figure 5. Boxer effect. (a) Global exclusion to coexistence and an ESS. Graphs (i)–(iii) show the results of a simulation of the Leslie–Gower EGT model (9) with K(v) given by Equation (11) and a symmetric boxer effect defined by Equation (14) with parameter values given by r=0.25, K _m =100, , , , β=2. The initial condition [u, x] = [1, 4, 25, 25] produces a point in the NW quadrant of the competitive exclusion plane and results in an orbit that approaches a coexistence equilibrium [u, x] ≈ [−1.1537, 3.7803, 90.578, 47.437], thus producing an evolutionary path from the NW to the SW quadrant, as shown in graph (i). In this case, the equilibrium solution obtained under Darwinian dynamics results in an ESS coalition of two, as is evident by the equilibrium points that lie on the two peaks of the adaptive landscape shown in graph (ii). Graph (iii) illustrates that the movement from the NW quadrant is rapid; the trajectory reaches the SW quadrant in just over 25 time units while several hundred time units are required before the point essentially equilibrates. (b) Conditional (saddle) exclusion to coexistence and an ESS. Graphs (iv)–(vi) arise from Leslie–Gower EGT model (9) with (symmetric boxer effect) coefficients (10) defined by Equations (11) and (14) with parameter values r=0.25, K _m =100, , , , and β=2. The initial condition [u, x] = [1, 4, 25, 25] produces a point in the NE quadrant of the competitive exclusion plane and results in an orbit that approaches a coexistence equilibrium [u, x] ≈ [−1.6148, 3.1883, 85.398, 59.266], thus producing an evolutionary path from the NE to the SW quadrant, as shown in graph (iv). Graph (v) shows that the equilibrium traits are located at maxima of the G-function, which illustrates the fact that at the coexistence equilibrium the two species form an ESS coalition of two. The time series plots of the species densities and their traits appear in graph (iv).

Figure 2(i)–(iii) shows an evolutionary path that begins in the NW quadrant (of competitive exclusion) that ends at an coexistence equilibrium point to the SW quadrant. In this regard, this evolutionary path is similar to that shown in the left column of graphs in Figure 2 in the absence of a boxer effect. However, an important difference is that in the no-boxer case (Figure 2), the final traits are not an ESS (since they are located at minima of the G function), whereas with a boxer effect present (Figure 5(i)–(iii)), the final traits are located at maxima of the G function and consequently the ESS maximum principle is satisfied.

Figure 5(iv)–(vi) show an example with an evolutionary path that is impossible without a boxer effect, namely an evolutionary path travels from the NE quadrant (the saddle case of competitive exclusion) to the competitive coexistence SW quadrant. This scenario is relevant to Park's experimental data, which we explore in Section 6. In addition to showing that such an evolutionary path is possible, this example shows that the traits associated with the resulting coexistence equilibrium can be an ESS.

The two examples in Figure 5 demonstrate two important consequences that can result from the presence of a boxer effect. A boxer effect can produce evolutionary paths not otherwise possible (in this case, initiating in the NE quadrant and ending in the SW quadrant). Secondly, a boxer effect can produce a coexistence equilibrium whose traits constitute an ESS when, in the absence of a boxer effect, the path would result in traits that are not ESS.

6. Applications to experimental competitive systems

In this section, we apply the Leslie–Gower EGT competition model (9) to two historical experiments that utilized species from the genus Tribolium (the flour beetle). In the context of flour beetle evolution, the strategy used in our model is a phenotypic trait that is determined by many genes that affect the competitive ability of the species, such as cannibalism/predation, mobility, and egg production. All of these factors affect the fitness of an individual as well as the fitness of others. We do not attempt to describe the specific genetic mechanisms and interactions, but rather consider these factors in terms of a single one-dimensional strategy that has been normalized to vary between zero and one.

We assume K(v) and are given by Equations (11) and (14) and choose parameters so that the model time series closely matches the data for the two cases discussed below (see tables in Figures 6 and 7).

Figure 6. Graphs (i) and (ii) illustrate an evolution from competitive exclusion to coexistence by both Park's data and a simulation of the experiment by the Leslie–Gower EGT model (9) with K(v) given by Equation (11) and a symmetric boxer effect defined by Equation (14). The parameters used in the simulation appear in the table under the heading ‘coexistence’ and run for the 32 time steps corresponding to the data (collected every 2 weeks). Note that a boxer effect is present (β>σ_α). The data were obtained from 13. Graph (i) compares the time series obtained from both the data and the simulation. Without evolution, T. castaneum (x ₂) would die out. With evolution, however, it recovers from near extinction as the system leaves the NE and NW exclusion quadrants and enters the coexistence SW quadrant (graph (ii)). Graphs (iii)–(iv) illustrate the fact that evolutionary path does not leave the NE quadrant unless the evolution of T. castaneum is fast enough ( is too small), with the result that T. castaneum goes extinct (the value of x ₂ in the simulations is less than 1 at week t=68).

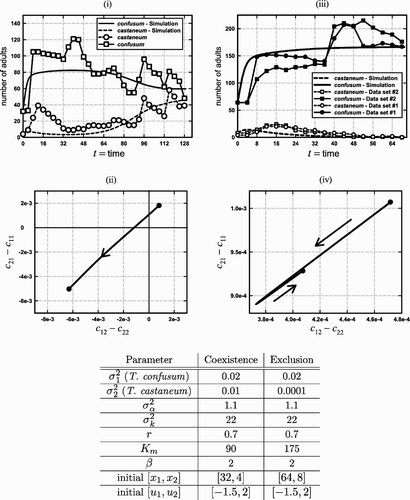
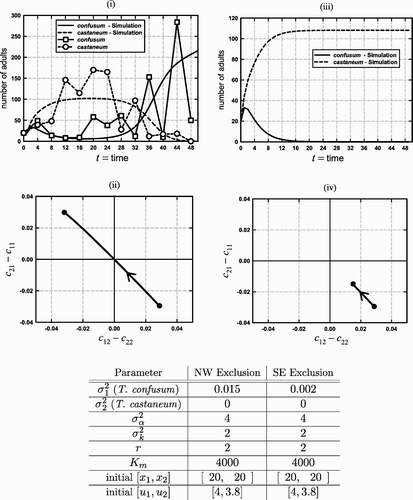
Figure 7. Graphs (i) and (ii) illustrate evolution from the SE exclusion quadrant to the NW exclusion quadrant by both Dawson's data and a simulation of the experiment by the Leslie–Gower EGT model (9) with K(v) given by Equation (11) and the canonical no-boxer competition coefficient (12). The parameters used in the simulation appear in the table under the heading ‘NW exclusion’ and run for the 50 time steps corresponding to the data (collected every 4 weeks). The data were obtained from 8. Graph (i) compares the time series obtained from both the data and the simulation. Without evolution, T. confusum (x ₁) would have died out. With evolution, however, it recovers from near extinction as the system leaves the SE exclusion quadrant to the NW exclusion quadrant, resulting instead in the extinction of T. castaneum (graph (ii)). Although no data are available for Dawson's replicates of ‘slow’ evolution (no observed genetic change), we show a model simulation of slow evolution in graphs (iii) and (iv), which illustrate the expected result that T. confusum dies out. The evolutionary path in the competitive-outcome plane appears in graph (iv).

6.1. Park's competition experiment

The flour beetle Tribolium was first used in ecological research by Chapman 2 to study the growth of single species. Intrigued by the beetle as a laboratory animal model, Park 14 further described the beetle and began a long-term study of competition using T. castaneum Herbst and T. confusum Duval 15. The two species data that we examine were obtained from the experiment reported by Leslie et al. 13. Twenty-four cultures with different initial adult numbers of T. castaneum strain cIV-a and T. confusum strain bI were cultured in shell vials with 8 gm of standard medium and adults were counted (and the medium changed) at 30-day intervals. With parameters estimated from earlier studies, the Leslie–Gower competition model (6) predicted an unstable coexistence equilibrium, with a saddle phase portrait characteristic of the NE quadrant in the competitive-outcome plane in Figure 1 16. The predicted (initial condition-dependent) competitive exclusion was indeed observed in all but one of the experimental cultures. In the anomalous culture neither species went extinct. The population data from this culture appear in Figure 6(i). These populations were initiated with four adults of T. castaneum cIV-a and 32 adults of T. confusum bI. Although T. castaneum was expected to be eliminated, competitive exclusion was not observed; both species grew successfully throughout the experiment of 960 days (32 generations). Park and co-workers were unable to explain this unexpected observation 13.

One hypothesis put forth to explain the failure of competitive exclusion in Park's anomalous culture appears in 9 where the authors make use of an observation reported in 13 concerning certain behavioural changes that occurred in the culture during the course of the experiment: ‘It was quickly apparent from an analysis of the adult numbers at the time of the second census on day 60, that a change had occurred in the strain bI and that it now had, relatively speaking, a much greater “effect”, presumably by way of cannibalistic powers, on cIV than it possessed originally’. Edmunds et al. 9 speculate that this change is reflected in parameter changes in a competitive model (namely the competitive LPA model specifically designed for the dynamics of flour beetles) which in turn result in movement across a bifurcation diagram that predicts a change from competitive exclusion to coexistence 4. They do not, however, model or attempt to describe the dynamics of these trait changes in an evolutionary context.

We offer another hypothesis for Park's coexistence case. This hypothesis is also based on Park's observed behavioural changes in the competitive intensities between the two species, but unlike Edmunds et al. we utilize an EGT model to describe the evolutionary dynamics of the interaction. Our explanation is based on the Leslie–Gower EGT model (9) and (10) and two important assumptions: that a boxer effect is present and evolution occurs sufficiently fast. The need for the first assumptions follows from Theorem 1 and the fact that Park's experiment initiated with the (saddle) exclusion phase portrait of the NE quadrant in the competitive-outcome plane. The second assumption is necessary so as to avoid competitive exclusion before evolution can move the evolutionary path to the coexistence SW quadrant. We have no analytic results that prove, under these assumptions, that the model can produce evolutionary paths from the NE to the SW quadrant. That such paths exist (and do so with population time series that reasonably well fit the experimental data) is clearly seen, however, by means of computer simulations (Figure 6).

The Leslie–Gower EGT model simulation of the population numbers shown in Figure 6(i) agrees qualitatively (and reasonably well quantitatively) with the experimentally observed time series. The parameter values used are given in Figure 6 and indicate that a boxer effect is present (). The corresponding evolutionary path (Figure 6(ii)) begins in the (saddle) exclusion NE quadrant and ends in the coexistence SW quadrant. This simulation, illustrating an evolutionary path from exclusion to coexistence, demonstrates that with sufficient trait variability the species can evolve fast enough for both to survive (the phenotypic variance of T. confusum is and that of T. castaneum is ). Put another way, values of the competitive coefficients that correspond to exclusion in the absence of evolution (which Park predicted for the bI/cIV-a competitive system) can evolve to coefficient values that correspond to a stable ESS coexistence state (which Park observed in the bI/cIV-a system).

Figure 6(iii) shows data for two cultures with similar but different initial numbers of adults, [x ₁, x ₂]=[64 bI, 8 cIV-a] and [64 bI, 4 cIV-a]. In contrast to the time series data in Figure 6(i), in these cases T. castaneum strain cIV-a went extinct. The EGT evolutionary path reveals (Figure 6(iv)) that there is not enough trait variability for the system to evolve to coexistence, i.e. the speed of evolution is too slow ( and ).

6.2. Dawson's competition experiment

Dawson 7, in experiments with T. castaneum and T. confusum, emphasized the role of the genetic founder effect in the interpretation of beetle competition experiments initiated with small numbers of adults 12. The time series data we consider here, given in 8, come from experiments in which Dawson initiated 10 cultures with 20 adults of each species and observed that in nine of the replicate cultures T. confusum was eliminated. (Details of the experiment can be found in Dawson 7.) However, in one replicate the outcome was reversed and T. castaneum was eliminated, even though adult numbers of T. castaneum initially increased and those of T. confusum decreased (Figure 7(i)). Dawson 8 wrote:

During the course of a ‘competition’ experiment involving the flour beetles Tribolium castaneum and T. confusum, an eye colour mutant appeared in T. castaneum. The frequency of the mutant gene increased and at the same time this species was eliminated from the culture, even though it was the winner in nine other replicates. It is suggested that the reproductive load placed on T. castaneum as a result of the reshuffling of the gene pool accompanying selection for the new allele may have been great enough to provide T. confusum with an advantage in competition.

In relating Dawson's experimental results to the Leslie–Gower EGT model, we note that Theorem 3 gives conditions under which there exist competitive exclusion equilibria (in the absence of a boxer effect) when only one species evolves. Figure 7(i)–(ii) shows an evolutionary path generated from the (no-boxer effect) model (9)–(12), with , that involves a reversal of the competitive outcome, as occurred in one replicate in Dawson's experiment in which T. castaneum went extinct and the genetic change was observed. For the parameter values chosen (Figure 7), the time series of population numbers agrees qualitatively (and reasonably well quantitatively) with the experimental data. In this simulation, the speed of evolution (i.e. the phenotypic variance ) is sufficiently large so as to allow the migration of the evolutionary path from the SE to the NW quadrants in the competitive exclusion plane.

For slower speeds of evolution, however (and, of course, for no evolution at all), the path fails to leave the SE quadrants and there is no competitive reversal in outcome, as in fact occurred in Dawson's other nine replicate cultures (in which no genetic change was observed and T. confusum went extinct). See Figure 7(iii)–(iv) in which the simulation is repeated except that the speed of evolution is decreased (). These examples illustrate the important role that the speed of evolution plays in causing evolutionary changes in competitive outcomes.

7. Concluding remarks

In this paper, we investigated the evolution of competitive interactions between two species. In particular, using evolutionary game theoretic models, we studied changes in the predicted outcome of a competitive interaction that result from the dynamic evolution of species-specific (mean) phenotypic traits. By this we mean that the competitive outcome predicted for initial trait values (were they to remain fixed in time) is different from the outcome predicted after traits change through time by Darwinian evolution.

We utilized an EGT version of the Leslie–Gower two-species competition model, which has the four competitive-outcome phase portraits of classic Lotka–Volterra theory as summarized in the competitive-outcome plane in Figure 1. Our study concerned the paths in this plane, generated by trajectories of the EGT Leslie–Gower model (9) and (10) as the model's competition coefficients evolve in time, that change quadrants, and hence predict an evolutionary change in the competitive outcome. Motivated by two experimental studies that resulted in unexpected outcomes when two species of Tribolium competed 8 13, we were particularly interested in conditions under which evolutionary paths initiate in the NE quadrant and terminate in the SW quadrant or initiate in one of the SE or NW quadrants and terminate in the other.

Models of Darwinian dynamics, as provided by EGT, are well suited for studies of evolutionary and adaptive changes in phenotypic traits that occur on a time scale commensurate with that of the population dynamics (as in the experiments of Park and Dawson). We showed in this paper how EGT models based on classic Lotka–Volterra-type competition models can result in changes in the predicted outcome of the competitive interaction (i.e. the outcome predicted when phenotypic traits are not allowed to evolve). In particular, we showed that such models can, under appropriate conditions, predict an evolution from a state of competitive exclusion to one of competitive coexistence (as in Park's experiment) and can, under other conditions, predict a reversal in the predicted winner in the competitive interaction (as in Dawson's experiment). In addition, we showed that EGT models (in our case, the EGT Leslie–Gower competition model) can also fit experimental data reasonably well.

Darwinian dynamics requires the specification of sub-models for how vital population parameters depend on the species’ mean phenotypic traits. Our study makes it clear that predictions made by EGT models are critically dependent on, and can be very sensitive to, the detailed characteristics of these sub-models and hence to the specific biological mechanisms assumed to be in play.

For example, we showed, by using canonical distributions for the Leslie–Gower model coefficients, that not only is the speed of evolution crucially important in determining evolutionary changes in competitive outcomes, but also the detailed nature of the competitive interaction as the traits of the species becoming increasingly similar. We distinguished two cases: when maximum competitive intensity does or does not occur at identical traits. These two different characteristics make different predictions concerning what is evolutionarily possible for the outcome of the competitive interaction. Indeed, we showed, for example, that the latter case (which we term a boxer effect) is necessary for the EGT Leslie–Gower model to be able to predict evolutionary paths between certain competitive outcomes (i.e. pairs of quadrants in the competitive-outcome plane).

In this paper, we based our study of competitive interactions on the framework of classical Lotka–Volterra dynamics. In general, EGT is a methodology for adapting any ecological model to the evolutionary context. The theory thereby provides a means for investigating the consequences of changes in population parameters as they depend on phenotypic traits that evolve by natural selection (and whose dynamic changes are in turn affected by the population dynamics). For more investigations using this approach to study competitive interactions among more than two species and involving more trophic levels see 17 21.

Acknowledgements

R. Rael and J.M. Cushing were supported in part by NSF grant DMS 0917435.

Additional information

Notes on contributors

R. C. Rael

Current address: Department of Ecology and Evolutionary Biology, University of Michigan, 2041 Kraus Natural Science Building, 830 N. University, Ann Arbor, MI 48109-1048, USA

T. L. Vincent

Thomas L. Vincent died on 26 October 2009.

Notes

When we say a point lies in one of the four quadrants in Figure 1, we always mean that it lies in the interior of the quadrant.

Appendix

A.1. Proof of Theorem 2

By definition a coexistence equilibrium is an equilibrium with x _i >0 for which the associated point lies either in the NE or the SW quadrant (Figure 1). (For convenience, we drop the asterisks denoting an equilibrium from now on.) For model coefficients (10) with competition coefficient α given by Equation (12), we have and by Theorem 1 no coexistence equilibrium can produce a point lying in the NE quadrant. Thus, for these coefficients it is necessary for a coexistence equilibrium that the trait dynamics u _i satisfy

With K and α given by Equations (11) and (12), we have the formula

for the Leslie–Gower model coefficients (10). The inequalities (A1) imply

and since

it follows that u ₂≠u ₁ is necessary for a coexistence equilibrium.

The equilibrium equations for [u ₁, u ₂, x ₁, x ₂] are

The last two equations (A2c) and (A2d) is a linear homogeneous system of algebraic equations satisfied by x _i >0, and therefore the determinant of its coefficient matrix must vanish:

This equation, together with the necessary condition u ₁≠u ₂, implies u _i ≠0. Moreover, if , this equation reduces to the contradiction

If we rewrite the last two equilibrium equations (A2c) and (A2d) as

we obtain (using (A2a) and (A2b))

from which it follows that u ₁ and u ₂ must have opposite signs (in order that x _i >0).

In summary, necessary conditions for a coexistence equilibrium [u ₁, u ₂, x ₁, x ₂] are

Proof of (a)

A substitution of Equation (A4) into the first two equilibrium equations (A2a) and (A2b) yields, after some algebraic manipulations

Referring to Equation (A1), we see that if u ₂>u ₁, then the first equation implies , while if u ₂<u ₁, then the second equation also implies . Thus, there cannot exist a coexistence equilibrium if .   ▪

Proof of (b)

From the proof in part (a), we have that necessary conditions for a coexistence equilibrium [u ₁, u ₂, x ₁, x ₂] are . Since we can label the species arbitrarily, without any loss in generality we need only to consider the existence of coexistence equilibria for which

i.e. solutions [u ₁, u ₂, x ₁, x ₂] of the equilibrium equations (A2) for which these inequalities hold and for which x _i >0. We can uncouple these four nonlinear equations in the following way.

As we point out in the proof of part (a), the determinant condition (A3) makes the two equilibrium equations (A2c) and (A2d) for x ₁ and x ₂ dependent. We can then replace the last equation (A2d) by the determinant condition (A3) and obtain a system of four equations equivalent to the equilibrium equations (A2). However, the first two equilibrium equations (A2a)–(A2b) can uniquely be solved for x _i as given in Equation (A4), with the result that the four equilibrium equations are equivalent to the following four equations:

Here, we have used Equations (11) and (12) to rewrite the formulas for x ₁ and x ₂. If we substitute the formulas for x _i into the third equation, then we reduce the four equilibrium equations to the two latter equations for u ₁ and u ₂. Our goal then becomes to show that the resulting system has a unique solution satisfying u ₁<0<u ₂ (and that x _i >0 for that unique solution). It is convenient to consider these two equations in terms of the new variables defined by u=u ₂>0, . After some algebraic manipulations, the two equations for u ₁, u ₂ become the equations

for u, ρ. The formula for the exponential provided by the second equation, when used in the first equation, results (after algebraic manipulations) in the equivalent equations

for positive ρ and u. These equations can be uncoupled by solving the second for u ² and placing the answer into the first equation. The result is

In summary, the equilibrium equations (A2) subject to the constraint u ₁<0<u ₂ are equivalent to solving the single equation (A6) for ρ>0, after which u ₁=−ρ u, u ₂=u>0 where u ² is given by Equation (A7) and x ₁, x ₂ are given by (A5).

Equation (A6) has a unique positive solution ρ, namely ρ=1. That ρ=1 is a root is obvious. That it is unique follows from the fact that the left side of Equation (A6) is an increasing function of ρ>0 and the right side of Equation (A7) is an decreasing function of ρ>0.

Placing ρ=1 in Equation (A7) and calculating x ₁, x ₂ from Equation (A5), we obtain the formulas in Theorem 2.

Finally, the explicit formulas for u ₁=−u ₂ and a (tedious but straightforward) calculation of the second derivative of

evaluated at v=±u yields

  ▪

A.2. Proof of Theorem 3

For competition coefficients (10), the equilibrium equations are

where

Lemma 6

Assume α (0)=1, , and a(w)≤1 (no-boxer effect). Assume both species evolve, i.e. . A competitive exclusion equilibrium with x ₂ absent, i.e. of the form with x ₁>0, exists if and only if u _i solve the two equations

in which case x ₁=K(u ₁). Such a competitive exclusion equilibrium is unstable if any one of the following inequalities holds:

If all these inequalities are reversed, then the competitive exclusion equilibrium is stable for small.

An analogous (and symmetric) lemma holds for competitive exclusion equilibria with x ₁=0.

Proof

Because , the equilibrium equations when x ₂=0 reduce to the three equations

the first of which implies x ₁=K(u ₁) provided the u _i solve the latter two equations.

A computation of the Jacobian evaluated at an exclusion equilibrium , although 4×4, has calculable eigenvalues:

The lemma follows from an investigation of when these eigenvalues satisfy .   ▪

Proof of Theorem 3(a)

For the coefficients (10) with Equations (11) and (12), the equilibrium equation (A8a) implies u ₁=0 and Equation (A8b) reduces to

Since we have that u ₂=0. It follows that the only equilibrium with x ₂=0 is

However, the point does not lie in (the interior of) a competitive exclusion quadrant NW, NE, or SE. Therefore, it is not an exclusion equilibrium of the Leslie–Gower EGT model.

A similar argument that holds for equilibria with x ₁=0 (using the analogue of Lemma 6 mentioned above) leads to the same conclusion.   ▪

Proof of Theorem 3(b)

When , , the equilibrium equations (A2) reduce, for x ₂=0 and x ₁>0, to the two equations

for x ₁ and u ₁ (and hence u ₂ is arbitrary). For the coefficients (10) with Equations (11) and (12), the second equation implies u ₁=0 and the first gives x ₁=K _m . Moreover, for these coefficients and equilibria, a calculation shows that the point equals

whose first component is negative and the sign of whose second component is the same as the sign of .

The Jacobian of the Darwinian equations (9) (with coefficients (10), (11), and ( 12)) when evaluated at the equilibrium is

where the entries denoted by asterisks are irrelevant. The eigenvalues of this matrix are

Because λ₄=1 these equilibria are non-hyperbolic. They are unstable if λ₂>1, which occurs if (and only if) .   ▪

Proof of Theorem 3(c)

When , , the equilibrium equations (A2) reduce, for x ₂=0 and x ₁>0, to the two equations

for u ₁, u ₂ and x ₁>0. For the coefficients (10) with Equations (11) and (12) the second equation gives

and hence

where u ₂ is arbitrary. Moreover, for these coefficients and equilibria, a calculation shows that the point equals

The location of this point in the competitive outcome plane depends on the signs of and and, specifically, leads to the alternatives given in the theorem.

The Jacobian of the Darwinian equations (9) (with coefficients (10), (11), and (12)) when evaluated at the equilibrium is

where the entries denoted by asterisks are irrelevant. The eigenvalues of this matrix are

Because λ₃=1 these equilibria are non-hyperbolic. They are unstable if λ₂>1, i.e.

which occurs if (and only if) .   ▪

A.3. Boxer effect

Lemma 7

If in the competition coefficient α (w) given by Equation (14), then . If then α (0)=1 is a global maximum of α (w).

Proof

(a) Suppose . Since , it follows that α (0)=1 is a local minimum and hence α (w) has values greater than 1.

(b) Suppose . The function α (w) is positive and asymptotic to 0 as . That α (0)=1 is the global maximum of α (w) follows from the fact that w=0 is the only critical point of α (w) if . To see this, we note that critical points are solutions of or equivalently

Since α (w) is symmetric about ω=0, we need only show that this equation has no positive roots. We rewrite this as

and note that a positive root w of Equation (A9) could only lie between 0<w<β. Then note that f(0)=1, f(β)=0 and

Since it follows that f(w) is strictly decreasing on 0<w<β and hence f(w)≠1 on this interval. It follows that Equation (A9) has no positive roots.   ▪