Spatial segregation in stage-structured populations with an application to Tribolium

Abstract

Spatial segregation among life-cycle stages has been observed in many stage-structured species, including species of the flour beetle Tribolium. We investigate density-dependent dispersal of life-cycle stages as a possible mechanism responsible for this separation. We explore this hypothesis using stage-structured, integrodifference equation (IDE) models that incorporate density-dependent dispersal kernels. We first investigate mechanisms that can lead to spatial patterns in juvenile–adult IDE models. We show, via numerical simulation, that density-dependent dispersal can lead to the spatial segregation of life-cycle stages in the sense that each stage peaks in a different spatial location. We then construct a three-stage spatial model to describe the population dynamics of Tribolium castaneum and Tribolium confusum and assess density-dependent dispersal mechanisms that are able to explain spatial patterns that have been experimentally observed in these species.

Keywords:

• density-dependent dispersal
• spatial patterns
• segregation of life-cycle stages
• integrodifference equations
• population dynamics

AMS Subject Classification :

• 92D25
• 45G15
• 39B42
• 39A11
• 39A60

1. Introduction

The spatial separation of similar species is a commonly observed phenomenon, allowing coexistence in situations where competitive exclusion might otherwise drive one of the species to extinction 7 10 22. These differences in spatial distributions may be due to niche partitioning as a result of differing food or shelter preferences as well as differing predation risks.

Spatial segregation has also been observed to occur between different stages of development in cannibalistic species 11–15,20 23. This non-uniform spatial structure may be promoted by interactions among age classes or life-cycle stages, as spatial heterogeneities can provide vulnerable stages an opportunity to escape from the cannibalistic stages and minimize predation risk. The utilization of available refuges in the presence of cannibals has been demonstrated experimentally in Saduria entomon 13, Thermosphaeroma thermophilum 23 and Gammarus pulex 15. Leonardsson 14 gives evidence that small isopods avoid larger conspecifics, and that the severity of this avoidance behaviour increases with the density of the larger isopods.

Cannibalism may play an important role in spatial structure as well as in density regulation. Many cannibalistic species exhibit age- or stage-dependent habitat selection, potentially evolutionary adaptations to reduce predation mortality. A study of the cave-dwelling mysids Hemimysis speluncola 20 found juveniles near the cave entrance while adults inhabited the innermost parts of the cave. Juveniles of the amphipod species Pallasea quadrispinosa 11 tend to occupy shallow waters while adults are mainly found in deeper, cooler waters. Juveniles of several species of gammaridean amphipods 12 undergo a change in phototactic response upon reaching an age when they become less susceptible to cannibalism.

Ghent 9 experimentally documented differences in the spatial distribution of life-cycle stages in the cannibalistic flour beetles Tribolium castaneum and Tribolium confusum. He studied the depth distribution of these beetles in cylindrical vials and discovered that the adult- and larval-stage densities peaked at different depths. Ghent's experiment is described further in Section 3.2.

The above examples show interactions between age classes or life-cycle stages can promote differences in their spatial distributions. We suggest density-dependent interstage interactions alone can be the sufficient cause for the formation of these spatial patterns, and that the spatial segregation of life-cycle stages may be the result of density-dependent dispersal rather than stage-specific resource niches.

In this paper, we introduce a two-dimensional stage-structured density-dependent integrodifference equation (IDE) model of the form developed in 21 and investigate mechanisms that can lead to spatial patterns. We show, via numerical simulation, that under certain conditions, density-dependent dispersal can lead to the segregation of life-cycle stages in the sense that juveniles and adult numbers peak in different spatial locations. We then develop a spatial extension of the well-studied larva–pupa–adult (LPA) model for Tribolium 2 dynamics and study its spatial attractors. Specifically, we look for conditions promoting the spatial separation of larvae and adults. We compare the results to Ghent's experimental findings.

2. A juvenile–adult model

2.1 Model construction

In this section, we study a juvenile–adult IDE model with density-dependent dispersal kernels on a closed domain. General stage structured models of this type were developed and analysed in 21. In these models, a discrete time matrix model is used to describe the non-spatial population dynamics and a (possibly density-dependent) dispersal kernel is used to dictate the rules for movement in space, although not all individuals are required to disperse. Here we explore if and when density-dependent dispersal can lead to spatial patterns in a two-stage model, specifically to patterns in which juveniles and adults are spatially segregated.

To describe the non-spatial dynamics of our populations of interest, we consider a juvenile–adult difference equation model:

We introduce the (density-independent) dispersal kernels K _J (x, y) and K _A (x, y), to describe the redistribution by time t+1 of juveniles and adults, respectively, from a source location y at time t. These kernels impose hostile boundary conditions on the domain Ω=[0, L] if and , implying that there is zero probability of moving to either boundary. Furthermore, the integral over x, the possible settling locations, of the kernels must be less than or equal to one. An integral equal to one ensures that individuals are not gained or lost during the dispersal process, only redistributed in space. Finally, we note that we will take the dispersal kernels to be equal for juveniles and adults. This implies both stages have the same spatial preferences, or the same probability of settling anywhere in the spatial domain.

The dispersal of an individual may be affected by other individuals as well as by innate spatial preferences. We now incorporate density-dependent dispersal by assuming that each stage tries to avoid the other. That is, the presence of adults at a given spatial location decreases the probability of a juvenile moving there, and visa versa. Specifically, we modify the density-independent dispersal kernels as follows:

The fraction of juveniles (respectively, adults) dispersing to any location decreases as the density of adults (respectively, juveniles) at that location increases. The coefficients D _J and D _A can be thought of as dispersal sensitivities. For a set number of adults (respectively, juveniles) at a location, increasing D _J (respectively, D _A ) decreases the probability of a juvenile (respectively, adult) moving there.

We note that although the general density-dependent IDE theory developed in 21 allows for density to affect an individual's decision to disperse as well as distance dispersed, here we assume that all individuals disperse every time step. We also note that with kernels (2) a chance of mortality accompanies dispersal, since the integral over space is always less than or equal to one. Biologically, this means individuals can be lost, but not gained, during dispersal.

Our juvenile–adult IDE model, with population dynamics given by Equation (1) and the density-dependent dispersal kernels (2), is

2.2 Model results

In this section, we look at some model simulations for specific population dynamics and dispersal kernels. We consider the following juvenile–adult difference equation model:

In model (4), b represents the maximal birth rate, μ _J is the juvenile death rate and μ _A is the adult death rate per unit time. There exists a unique positive equilibrium that is locally asymptotically stable for parameter values satisfying . We use a rational function, or Beverton–Holt, nonlinearity for density regulation rather than an exponential, or Ricker, nonlinearity in order to keep population dynamics tame and avoid confounding the effects of density-dependent dispersal with any complex dynamics exhibited by the non-spatial model.

We take the density-independent dispersal kernels to be

on the spatial domain . Note that for this choice of kernels, dispersal probabilities do not depend on the source location or distance dispersed, but only on properties of the destination location. With kernels (5), the middle of the habitat is most desirable and the boundaries are hostile.

We incorporate density dependence into kernels (5) in the same way as kernels (2):

Our IDE model becomes

If we set D _A =D _J =0, both dispersal kernels reduce to the density-independent kernels (5) and all sets of parameter values for b, μ _J and μ _A result in a temporal equilibrium with no spatial segregation. The spatial distributions of both stages are multiples of the function determining the dispersal kernel, in this case sin(x), with no individuals at the boundaries and maxima at the midpoint of the domain. A simulation illustrating the case where D _J =D _A =0, b=25, and appears in Figure 1(a).

Figure 1. Representative attractors of juvenile–adult IDE model (7). b=25 μ _L =μ _A =0.2 for all simulations. (a) Temporal equilibrium: D _J =D _A =0. (b) Temporal equilibrium, spatial segregation of juveniles and adults: D _J =0.5, D _A =0. (c) Two-cycle, temporal segregation of juveniles and adults: D _J =0, D _A =0.5. (d) Four-cycle, temporal segregation of juveniles and adults: D _J =D _A =0.5.

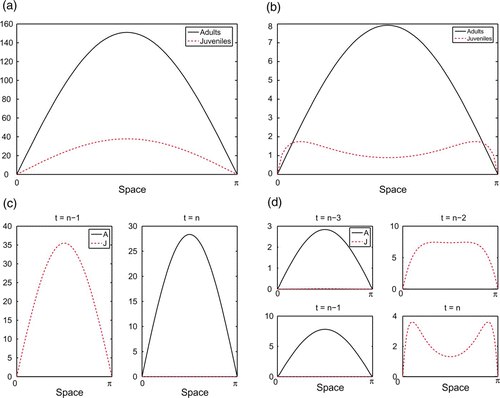
If we increase D _J from 0 to 0.5 so juveniles ‘avoid’ adults (keeping all other parameters the same), we still have a temporal equilibrium. However, we now see spatial segregation of juveniles and adults in the sense that the stages peak in different spatial locations (Figure 1(b)). Adult numbers are still greatest in the centre of the domain, but juveniles now accumulate towards the sides of the domain, exhibiting a bi-modal distribution with two peaks and a dip between them in the centre of the domain.

If we return D _J to 0 and instead increase D _A to 0.5 so adults ‘avoid’ juveniles (all other parameters remain the same), we see temporal segregation rather than spatial segregation. We no longer have an equilibrium in time, but instead a temporal two-cycle. At any given time, one stage dominates at all spatial locations. The other stage is present, but only in very small numbers. The dominant stage alternates temporally between juveniles and adults, each peaking in the centre of the domain. An illustration of this appears in Figure 1(c).

Next we look at the case where D _J =D _A =0.5, keeping all population dynamics parameters the same. The result is a temporal four-cycle, again showing what we call temporal segregation. Juveniles, when dominant, exhibit a bi-modal distribution. This is shown in Figure 1(d).

Figure 2 shows the properties of the model attractor for various regions in the D _J , D _A parameter plane for increasing values of b. For , no spatial segregation is possible for any values of D _J or D _A . This is consistent with the mathematical results obtained in 21, namely that near the primary bifurcation point , non-extinction equilibrium distributions J _t (x) and A _t (x) resemble the eigenvector, which here has components that are multiples of sin(x).

Figure 2. Shown is a section of the D _J −D _A parameter plane, 0≤D _J ≤1 and 0≤D _A ≤1, for increasing values of b. (a) For b=2.5, all combinations of D _J and D _A in the range shown result in equilibrium dynamics for model (7). Spatial segregation is possible for large enough D _J and small enough D _A . (b) For b=10 we can see two-cycles and temporal segregation in addition to the model (7) attractors seen for b=2.5. (c) For b=25, we can see four-cycles and four-cycles with temporal segregation in addition to the model (7) attractors seen for b=10.

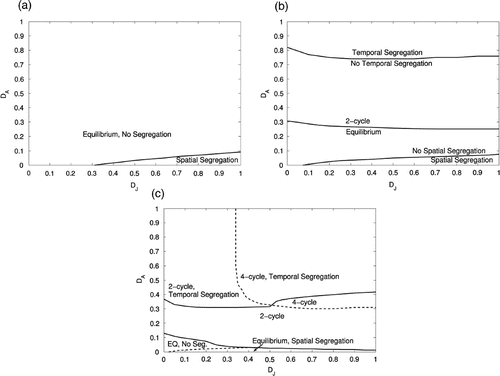
As b is increased, we see through simulation that more patterns become possible. For b=2.5, there is only a small region of parameter space where we see spatial segregation of adults and juveniles (Figure 2(a)). D _J must be sufficiently large, and D _A must be sufficiently small. All attractors are temporal equilibria.

Increasing b to 10, we can achieve temporal two-cycles as well as equilibria. If D _A is large enough, we see temporal segregation in the sense defined earlier (Figure 2(b)). If b is increased to 25, we add temporal four-cycles to the list of potential attractors (Figure 2(c)).

2.3 Conclusions

We have shown in this section (through simulation) that low-dimensional stage-structured IDE models can result in both spatial and temporal segregation of life-cycle stages. Specifically, our study of this model suggests the following conclusions. Increasing D _J (the sensitivity of juveniles to adult densities) tends to increase the degree of spatial segregation, while increasing D _A (the sensitivity of adults to juvenile densities) tends to increase the degree of temporal segregation between the two life-cycle stages. Increasing the birth rate leads to larger D _J −D _A parameter regions where juvenile–adult spatial segregation occurs, and an increase in the number of possible types of model behaviour.

3. Application to Tribolium

In this section, we apply the modelling methodology in Section 2, and the illustrated mechanisms that can cause the spatial segregation of life-cycle stages, to an experimental system in which such spatial patterns were observed to occur, namely Ghent's experiments for species of Tribolium 9. To do this, we base the spatial model on a matrix population model that is appropriate for the organisms involved, and we utilize dispersal kernels appropriate for the experimental setup. The population model is a three life-cycle stage model called the LPA model, which has been shown to be an accurate model of experimental cultures of Tribolium 1–6.

3.1 Density-dependent dispersal

There is substantial evidence that density plays a role in the dispersal of the mobile stages of both T. castaneum and T. confusum 17 24. Naylor 18 documented an interstage density-dependent avoidance response in T. confusum. When presented with a choice between unoccupied flour and flour occupied by medium-sized larvae, adult females tended to choose the unoccupied flour. Furthermore, the number of adults found in vials of flour decreased with increasing larval density. The tendency of T. confusum to move to locations of unoccupied flour over occupied flour was also observed by Naylor 16.

Further evidence of the avoidance of larvae by adults comes from an experiment conducted by Prus 19 to look at emigration ability and surface numbers of adult beetles of different strains and sexes. All cultures were composed of a single sex of adults, except for one replicate where several males accidentally were mixed in with a culture of females. This resulted in the appearance of larvae, and a notable increase in the surface numbers and emigration ability of this replicate 19. Later investigations confirmed the effect of the presence of larvae in increasing adult surface numbers. In adult-only cultures, the intensity of emigration was found to depend on the relation of the current density of beetles to the maximum possible density 25.

3.2 Depth distribution of life-cycle stages

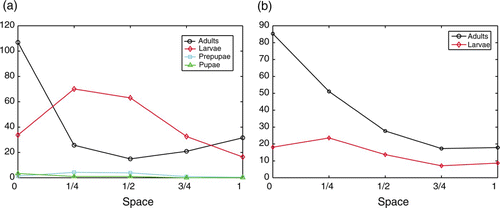
In 1966, Ghent 9 studied the depth distribution of the life-cycle stages of the cannibalistic species and in vials of flour. For each species, he placed 200 adults on the surface of a cylindrical fractionable-shell vial filled with flour. The vial was divided into five rings, each being 10 mm in high. Eight grams of flour filled this vial to 41–42 mm. So each of the bottom four rings were filled and the last contained the surface layer made up of the uppermost 1–2 mm of flour. Ghent placed this vial in an incubator for 26 days and counted the number of individuals in each stage in each of the four quarters of flour and on the surface. For the two species of flour beetles studied, 26 days is enough time to produce eggs, larvae and pupae, but not new adults. Ghent found adults of both species to be most abundant near the surface of the flour, while larval densities peaked slightly below the surface in the upper quarter of flour. Figure 3 shows the observed depth distributions for various life stages of T. castaneum and T. confusum.

Figure 3. Data from Ghent 9. 0 represents the surface of the vial and 1 represents the bottom. (a) Depth distribution of larvae, pre-pupae, pupae and adults in T. castaneum. (b) Depth distribution of larvae and adults in T. confusum.

3.3 LPA model

One of the most heavily analysed and well-validated models in mathematical ecology is the LPA model, a three-dimensional system of nonlinear difference equations designed to describe the population dynamics of T. castaneum and T. confusum 2:

L _t represents the number of larvae at time t, P _t gives the number of individuals in the ‘P stage’ (which includes non-feeding larvae, pupae and callow adults) at time t and A _t gives the number of sexually mature adults at time t. Animals transit to the next class in two weeks, so this is used as the time step for the model. Upon reaching the adult class, animals remain there until death. Larval recruitment in the absence of egg cannibalism occurs at an inherent rate b. Eggs must survive cannibalism by larvae and adults in order to become larvae, and the exponential represents the survival rate per unit time. and are cannibalism coefficients of eggs by larvae and eggs by adults, respectively. Larvae die at a rate μ _L , 0<μ _L <1, and so a fraction (1−μ _L ) survive to become pupae. The natural death rate of pupae is negligible, so there is no μ _P term included in the model. Pupae must escape cannibalism by adults (c _pa) to become adults. Adults die at a rate μ _A , 0<μ _A <1, and so at each census, the fraction of surviving adults is (1−μ _A ).

3.4 Spatial LPA model

The LPA model is one of the most successful models in mathematical biology in the sense that it has been parameterized and well-validated with laboratory data, and laboratory experiments have verified its predicted dynamics, attractors and bifurcations (including a route to chaos) 5 6. Many modifications of the LPA model have also been successful over the last decade in investigations of numerous phenomena, such as competition between flour beetle species 8 and population dynamics in a periodically fluctuating habitat 1.

Here, we construct a spatial extension of the LPA model in order to determine if the spatial patterns in T. castaneum and T. confusum described in Section 3.2 can be explained by density-dependent interstage interactions. The spatial patterns observed by Ghent 9 in a cylindrical vial of flour can be looked at as one-dimensional in space, where the spatial dimension is depth. Due to gravity, there is a gradient of increasing flour density from the surface to bottom of the bottle 9. Individuals can live on the surface but cannot pass above it. We model this environment as a one-dimensional domain with mixed boundary conditions, where the bottom of the bottle is a hostile boundary and the surface is a no-flux boundary. In order to construct the spatial LPA model, we need to make assumptions regarding the dispersal behaviour of the two mobile life-stages – larvae and adults (pupae are immobile and have zero probability of dispersing). We assume that adults prefer areas with lower larval densities than their current location, and larvae prefer areas with lower adult densities than their current location. Thus, the fraction of larvae that move from one location to another depends on the difference in adult densities, after population dynamics occur, between the two locations. Adult dispersal depends similarly on density of larvae. We assume both larvae and adults view the environment in the same way, preferring flour near the surface over the more dense flour near the bottom and so take our spatial domain Ω to be the finite interval [0, π/2] representing depth in a cylindrical vial, with 0 corresponding to the surface and π/2 corresponding to the bottom of the vial. The kernels for larval and adult spatial redistribution are given by the following, respectively:

where C ₁ and C ₂ are the following normalization constants:

The term cos ^m (x) in the dispersal kernel incorporates density-independent spatial preference. As the parameter m increases, the undesirable region at the bottom of the bottle grows in size. After simplification, the spatial LPA model becomes

where

Our initial conditions are triples of continuous functions on [0, π/2] that satisfy and . It is a feature of the kernels that the right side of model (11) returns a triple of continuously differentiable functions that satisfies and for all subsequent time. We consider initial conditions with the form for model simulations, where C _L , C _P and C _A are real positive constants.

3.5 Spatial LPA model results

Figure 4 shows simulations of model (11) for various parameter values in the dispersal kernel (9). Parameters for population dynamics were chosen so as to fall in the maximum likelihood 95% confidence intervals calculated from control cultures of the Desharnais experiment for LPA parameters 3. The LPA model equilibrates for this set of parameter values.

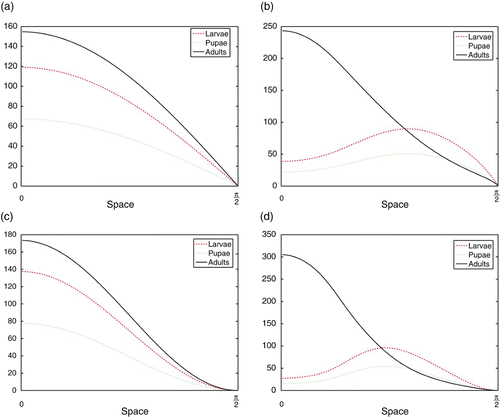
Figure 4. Simulations of the spatial LPA model (11) for various parameter values in the dispersal kernels (9). All attractors shown are temporal equilibria. LPA parameter values given by b=10, c _el=0.01, c _ea=0.0175, μ _L =0.435, c _pa=0.016, μ _A =0.075. (a) m=1, D _LA =D _AL =0. (b) m=1, D _LA =D _AL =0.01. (c) m=2, D _LA =D _AL =0. (d) m=2, D _LA =D _AL =0.01.

When D _LA =D _AL =0 in the kernel, there is no spatial segregation between stages in simulations of model (11) for any set of LPA parameter values. Spatial distributions of all stages reflect that of the kernel, cos ^m (x), reaching a maximum at the no-flux boundary 0 and reaching their minimum (of zero) at the hostile boundary π/2. This can be seen in Figure 4(a), where m=1, and Figure 4(c), where m=2.

If the adults and larvae have equal dispersal sensitivities of , the larvae are ‘pushed’ towards the bottom of the vial along with the pupae, while adult density peaks on the surface. This is shown in Figure 4(b) for m=1 and Figure 4(d) for m=2. Both of these results are qualitatively similar to Ghent's observations shown in Figure 3. As the parameter m is increased, the bottom of the habitat becomes increasingly undesirable to both stages. The adults reach their maximum density at the surface for all values of m, but the peak of the larval distribution moves towards the surface as m increases.

In general, spatial segregation of larvae and adults is observed for a range of D _LA >0, even if D _AL =0. The effect is more severe when combined with values of D _AL >0, but this is not necessary. However, the reverse is not true. It is necessary that larvae move in response to adult densities; if D _LA =0 and only adults disperse in response to larval densities, we do not see the segregation. Adults will not be pushed to the bottom of the habitat for any values of D _LA and D _AL . Furthermore, if D _LA and/or D _AL become too large, we begin to see temporal patterns as well.

We did not observe multiple attractors of the spatial LPA model for the range of parameter values considered. Initial conditions of the form where C _L , C _P , C _A and m are real positive constants lead to the attractors in Figure 4. The boundary conditions can also be satisfied by piecewise continuous step functions of the form where C _L , C _P , C _A are real positive constants and is equal to 1 on and 0 on . This set of initial conditions also leads to the attractors in Figure 4.

4. Discussion

Making use of IDE models with density-dependent kernels, we have shown that density-dependent dispersal can lead to the segregation of life-cycle stages in stage-structured populations (such as flour beetles). These results are not intuitively obvious. In the case of a juvenile–adult species, even if juveniles and adults avoid each other, juveniles will eventually become adults and adults will give rise to new juveniles, seemingly leading to spatial mixing between stages.

We referenced spatial habitat segregation as a potential adaptation to avoid cannibalism or predation. In Tribolium, larvae are not being directly cannibalized by the adults but density-dependent dispersal, and the avoidance of adults, may still be a beneficial adaptation. T. castaneum and T. confusum pupae are cannibalized by adults, so if larvae pupate in a location inhabited by a large number of adults, they may not survive the pupal stage.

Based on our studies, we also hypothesize about mechanisms that promote adult dispersal. Eggs of both species are cannibalized by larvae, and the adults may want to lay their eggs in flour where they have the greatest chance of hatching, and where there is the greatest food supply once their young become larvae. This is our rationale for adults avoiding larvae in the dispersal kernels for the spatial LPA model.

The toy models analysed in Section 2 show that density-dependent dispersal can result in both spatial segregation of life-cycle stages as well as temporal segregation (if mortality is associated with dispersal). We stress that complex population dynamics are not necessary for the formation of these spatial patterns and that our models do not result in spatial segregation in the absence of density-dependent dispersal (as long as all mobile stages ‘view’ the environment the same way).

As an application that offers some validation of our modelling methodology, we aimed to explain the uneven depth distribution of larval and adult flour beetles of the species T. castaneum and T. confusum observed by Ghent 9. Due to gravity, flour is more dense at the bottom of a vial of flour than at the top, and most likely less desirable an environment to beetles than the less dense flour near the surface. We modelled this biological system assuming no-flux boundary conditions at the surface and hostile boundary conditions at the bottom of the bottle, as well as the density-dependent dispersal of adults and larva (assuming adults avoid larvae and visa versa). Even though larvae and adults have the same spatial preferences, the adults end up with higher densities in the preferred flour. Larvae and pupae appear to be ‘pushed’ towards the bottom of the bottle. These model-predicted results agree qualitatively with what Ghent observed (Figure 3).

We do not expect highly accurate quantitative agreements between model results and Ghent's data for multiple reasons. First, parameter values for flour beetle populations can vary from strain to strain, and parameter values for the strain used by Ghent are not available. Second, the vials used by Ghent held 8 g of flour, while the typical bottles used in experiments and parametrization of the LPA model held 20 g of flour 3 4. Also, Ghent's data were collected after 26 days in the vial, not long enough for new adults to emerge. Our results are asymptotic model attractors.

As discussed in Section 3.1, there is literature to support the density-dependent dispersal of flour beetles, but the exact mechanisms and rates of dispersal are unknown. Our results do show that density-dependent interactions and the resulting dispersal kernels are possible explanations for the observed spatial distributions. A main message of this case study is that density-dependent dispersal can produce a spatial pattern very similar to that experimentally observed by Ghent and is likely to have been a factor in its development.

Acknowledgements

This work was done as part of S.L. Robertson's PhD thesis, Spatial patterns in stage-structured populations with density-dependent dispersal, Interdisciplinary Program in Applied Mathematics, University of Arizona, 2009.

Additional information

Notes on contributors

Suzanne L. Robertson

Present address: Mathematical Biosciences Institute, The Ohio State University, Columbus, OH 43210, USA.