A model for Chagas disease with controlled spraying

Abstract

Chagas disease is a vector-borne parasitic disease that infects mammals, including humans, through much of Latin America. This work presents a mathematical model for the dynamics of domestic transmission in the form of four coupled nonlinear differential equations. The four equations model the number of domiciliary vectors, the number of infected domiciliary vectors, the number of infected humans, and the number of infected domestic animals. The main interest of this work lies in its study of the effects of insecticide spraying and of the recovery of vector populations with cessation of spraying. A novel aspect in the model is that yearly spraying, which is currently used to prevent transmission, is taken into account. The model's predictions for a representative village are discussed. In particular, the model predicts that if pesticide use is discontinued, the vector population and the disease can return to their pre-spraying levels in approximately 5–8 years.

Keywords:

• Chagas disease
• nonlinear ODE system
• Trypanosoma cruzi
• numerical simulations
• vector control
• insecticide spraying
• epidemic dynamics
• dynamical systems

AMS Subject Classification :

• 34A12
• 92B05
• 34A34

1. Introduction

Chagas disease, caused by infection with the parasitic protozoan Trypanosoma cruzi, is responsible for significant morbidity and mortality throughout much of Latin America. The disease is responsible for disability and early death in approximately a third of those infected 3. Recent estimates of Chagas disease burden indicate that 8–10 million people are currently infected 41 52. This is a dramatic decrease from the 1980s, when over 20 million people were thought to be infected, and is primarily due to vector control measures.

Current control measures responsible for decreasing Chagas include improving the quality of housing and health care, and treatment of homes with residual insecticides. Health initiatives include blood screening to prevent transmission by transfusion, and treatment for acute Chagas disease and congenital transmission 29 50. Two chemotherapeutic agents, nifurtimox and benznidazole, currently recommended for Chagas, appear to be useful for early treatment of the disease. However, because of toxicity and questionable efficacy of the current drug treatments during the chronic stages of the disease and the lack of an effective vaccine control, the transmission of Chagas disease remains largely based on vector control by insecticides and on blood-bank screening 19 47 49 53.

The most widespread and important vector of T. cruzi is Triatoma infestans, a species of blood-sucking insects (reduviids), which has evolved into a primarily domestic vector, preferring to live in and around homes. In the 1990s, the Southern Cone Initiative was implemented, aimed at the interruption of transmission of Chagas disease in South American countries. The primary focus of the programme has been to use residual pyrethroid insecticides to kill domestic insects and screening the blood supply 49 50 53. This programme has led to a dramatic decrease in transmission in several countries in South America, with some regions now reporting the eradication of T. infestans and transmission virtually at zero 11 35.

T. infestans live either in domestic or peridomestic habitats, which allow for control with spraying and vigilant follow-up. In Bolivia, where true T. infestans wild foci are documented, reinfestation from surrounding sylvatic areas has complicated control efforts 46. The use of insecticides for vector control has drawbacks, including cost, the need to reapply, the possibility that the insects develop resistance, and potential effects on species other than the intended target. Resistance to insecticides by reduviids has not been a major problem historically 60. However, some strains of Rhodnius prolixus from Venezuela and T. infestans from Brazil have been found to be resistant to pyrethroid insecticides 59. Recently, populations of T. infestans in northern Argentina were found to have high levels of resistance to pyrethroids 42. Multiple studies have shown that, despite spraying, triatomines sometimes survive insecticide treatment 14 15 16 17 20 42 44 57 59.

Insecticide resistance is particularly worrisome in light of studies which demonstrate that reduviid vectors can resurge after spraying 44. It is found in field studies that increased numbers of reduviids over pre-spray population levels were encountered 3–6 months after spraying stopped in peridomestic areas. Further, while domestic triatomines had not returned to pre-spray populations within 12 months, a significantly higher infection rate was seen in those triatomines that were present 44. Reinfestation of houses by adult vectors has been shown to occur within four months after insecticide treatment 15. Based on these studies, it may be argued that spraying is not the ultimate answer to the control of Chagas disease.

Due to the complex nature of T. cruzi transmission, including multiple sylvatic hosts and vectors, Chagas infection will likely remain endemic in the indigenous mammalian populations throughout the Americas despite continued spraying. The goal of the Southern Cone Initiative is not eradication of the insect vectors, but rather to prevent infestation of homes by them, thereby preventing vector-borne transmission to humans and their domestic animals.

History has shown that while vector control can have a considerable impact on disease burden, long-term maintenance of such programmes can be problematic. The initial positive results obtained by the Global Malaria Eradication Program that began in 1955 took place mostly in temperate or subtropical areas where transmission was less intense 18 34. The general consensus at the time was that complete eradication was in sight, leading to a decline in the support for malaria research. However, the transmission cycle in the tropics was never broken. It took more than three decades to modify the strategies for malaria containment in these regions, and eradication programmes were abandoned in areas lacking financial resources. Many countries which had enjoyed little or no malaria saw a resurgence of malaria as well as of other vector-borne diseases 39 58.

While spraying for Chagas vectors has led to a 70% decrease in new infections in the last decade, improved housing, better drugs, and the development of an effective vaccine are needed 36. Neither insect control nor current drug treatment is optimal for this disease because of the entrenched sylvatic cycle, the long lifespan of infected human hosts, triatomine insecticide resistance, and the ease with which protozoans develop drug resistance 4 13 38 59.

In this work, we develop a mathematical model, in the form of four nonlinear differential equations, for the dynamics of Chagas disease transmission. The equations predict, for the given data, the dynamics of the total numbers of vectors, infected vectors, infected humans, and infected domestic animals (dogs). Our main interest is to study the effects of insecticide spraying and its cessation. The model allows us to predict the effects of various spraying scenarios on the populations, including outcomes when spraying is stopped. Unlike Cohen and Gürtler 10, where a mathematical model for a small population (one household) was described, here we describe the dynamics of large populations. The model can be used to test the effects of various hypotheses on the disease process. More specifically, we believe that it may be used for optimizing spraying schedules. We note that a simpler model was used very recently in 2 24 to study issues of the control of the non-domiciliated Chagas disease vectors in the Yucatan Peninsula, Mexico.

The model is presented in detail in Section 2, with particular stress on its underlying assumptions. One important, simplifying assumption is that the various developmental stages of the insects are not modelled. These may be added in future work if necessary. The model was numerically discretized by using the Adams–Bashforth method with the Molton Corrector scheme. The numerical scheme was implemented and the results of some of the computer simulations are presented in Section 3. First, simulation results of a typical case are shown. Second, cases with discontinuous spraying are presented. Using the model, multiple simulations were run in representative communities with data found in the literature. The simulations were found to be in agreement with what is seen in reinfested regions where spraying has been halted 15 20.

The steady states of the mathematical model presented in this work were recently studied and numerically simulated. It was found that with averaged coefficients of our baseline case in Section 3, the model has two unstable disease-free equilibria (one without vectors and one in which they are infection-free) and a stable and attracting endemic equilibrium.

As a contribution to the research on Chagas disease, access to the computer programme is freely available via an internet interface 54. It provides the interested researcher with a tool to examine the disease dynamics in specific cases under various model assumptions. The authors would like to point out that this mathematical model has not been validated, and therefore the model simulations may not have any predictive value.

2. The model

This section presents a mathematical model for Chagas disease dynamics. The life cycle of the vectors, the parasites, and details of the relevant biological processes can be found primarily in Cohen and Gürtler's 10 work, as well as several other relevant studies 5 6 9 10 43 44 45. The model represents the overall dynamics of the populations of vectors, infected vectors, infected humans, and infected domestic animals – represented in the model as ‘dogs’. There is also a population of animals that can act as a source of blood meals, but which cannot serve as a host for T. cruzi – represented in the model as ‘chickens’. (Only mammals can serve as hosts for T. cruzi.) The goal of this model is to replicate the known dynamics of the disease when spraying with insecticides is used to control the vector population and to study the effects of interrupted spraying 5 15 20 21 23. The model can be used to predict the population dynamics under various scenarios and parameter sets.

We consider a population in a rural village in Argentina and describe the dynamics using differential equations, which means that we deal with a relatively large population. Our numerical simulations indicate that the model can be successfully applied to a rural village with 400 humans. We do not consider the population's spatial spread, only the total numbers. The dynamics which take into account a spatial distribution lead to partial differential equations, which entail a much higher level of complexity and will be investigated in the future, if necessary.

The basic components and the variables in our model of Chagas disease are illustrated in Figure 1.

Figure 1. Schematic of the major variables in the model. It depicts the interactions among the vectors (V), the infected vectors (V _i ), and the various blood sources. While chickens (C) are a preferred blood source (4.8×over humans (N)), they cannot harbour the parasite. Dogs (D) are preferred over humans (2.45×) and play a significant role in transmission. Housing plays a role in providing reservoirs for vectors to survive insecticide treatment. Wildlife [wtilde] also can contribute to perpetuate disease transmission, but was not considered in the simulations.

It is assumed that there exists a wildlife population which is infected with the disease agent and that can neither be eradicated nor controlled, thus acting as a background source of infection. Most importantly, the model assumes that a subpopulation of triatomines (the vectors) survives the spraying each year, matures, and reproduces, thereby increasing the total insect population. Field work and studies show that there are always some survivors of spraying; this ‘survivor subset’ is assumed to have recently fed and to have then retreated deep into cracks in homes where they are not exposed to the insecticide 20 22. While there is a role for reinfestation by sylvatic triatomines, those sources are not considered explicitly in this model.

The infected vectors can transmit the disease when they take a blood meal from mammalian hosts. At each feeding, there is an estimated probability that the human or dog will become infected. When a susceptible vector bites an infected mammalian host, there is a probability that it can become infected. These probabilities are the transmission rate coefficients and are provided in Table 1. Vector preferences of different blood sources were taken into account and were measured in units of ‘human factors’ (Table 1) 10.

Table 1. The model parameters, baseline simulation values, and the sources.

Parameter	Definition	Baseline Simulation Value	Source
V	Total number of vectors (vectors/village)	V(0)=33, 995	This study^a
N	Total number of humans (humans/village)	400	This study^a
D	Total number of domestic dogs (dogs/village)	100	This study^a
C	Total number of chickens (chickens/village)	100	This study^a
H	Total number of houses (houses/village)	100	This study^a
V i	Infected domestic triatomines (vectors/village)	V i (0)=10, 946	This study^a
N i	Number of infected humans (humans/village)	N i (0)=90	This study^a
D i	Number of infected dogs (dogs/village)	D i (0)=52	This study^a
V min	Minimum number of vectors (vectors/village)	2000	Starting value
d hτ	Egg hatching rate (1/day)		Figure 12
d m	Death rate of vectors (1/day)	Seasonal piecewise linear	Estimation from 5, Figure 2(a)
τ	The delay factor (days)	20	Estimation from 5
r(t)	The spraying rate (1/day)	Equation (9) and Figure 3	This study 44
b(t)	Biting rate (1/day)	Seasonal piecewise linear	Estimation from 5 6, Figure 2(b)
	Human to vector infection probability (per bite)	0.03	10
	Dog to vector infection probability (per bite)	0.49	10
	Vector to human infection probability (per bite)	0.00008	Estimate from 10
	Vector to dog infection probability (per bite)	0.001	Estimate from 10 43
d f	Human factor of one dog	2.45	30
c f	Human factor of one chicken	4.8	30
	Mortality rate of infected humans (1/day)		Estimate from 9 45
	Mortality rate of infected dogs (1/day)		Estimate 8 years
a ^−1	Value of V at which growth rate the largest (vectors)	50,000	500·H
d 1	First day of fall (day of year)	0	20 March
d 2	First day of winter (day of year)	91.25	21 June
d 3	First day of spring (day of year)	182.5	22 September
d 4	First day of summer (day of year)	273.75	21 December
^a See Section 3.1.

Let the number of humans in the village be N, the number of domestic animals that can be infective D, and the number of those that cannot be infective C. For the sake of simplicity, we assume that these are known constants. In general, however, they can be time-dependent functions and can easily be incorporated into the model.

We denote by V=V(t) the number of carrier insects living in the houses at time t, the number of infective insects by V _i =V _i (t), the number of infective humans by N _i =N _i (t), and the number of infective dogs by D _i =D _i (t). The number of susceptibles (non-infected) in each population is , and D−D _i (t), respectively.

We model the rate of change of each population, noting that the natural time unit is a day. The rate of change in the number of the carrier insects depends on the natural mortality rate of the domestic triatomines, d _m , on the successful hatching of eggs after τ days (gestation time) with rate coefficient , and on the mortality rate due to spraying r=r(t). Thus,

Since the natural mortality rate d _m depends on the season, and spraying is typically performed only once a year, it is natural to assume that d _m =d _m (t) and the death rate per capita due to spraying r=r(t) are periodic functions with a period of 1 year.

The first term on the right-hand side is similar in form to Nicholson's blowflies model where the growth rate at time t (days) depends on the population size at time t−τ (days) 25 32 40. However, in the Nicholson model, d _hτ is a constant, since blowflies have only two stages of development: pupae and adult. In contrast, triatomines have six distinct stages of life: five instar stages and an adult stage. The egg hatching rate at time t depends on the fraction of adult females at time t−τ, as well as other factors including seasonal temperatures and blood supply. In particular, the growth term attains a maximum when the number of vectors in the village houses at time t−τ reaches the value of 1/a. The growth rate is described in more detail in Section 3. It should be noted that recently the authors also simulated the vector equation using the same d _hτ coefficient with a delayed logistic term that governs the vector equation, and it was found that the results were almost identical. In this work, the model equation for the vectors was chosen for simplicity, since the appropriate data were available (and extracted) for the coefficients. Otherwise, the vector equation might be split into six coupled equations for the different stages of development of the triatomines, which will be studied by the authors elsewhere.

The model assumes that a subpopulation of insects V _min is able to survive spraying because they rest deep within the cracks while satiated from a recent blood meal and do not re-emerge until the effects of the insecticide wane. This survivorship is modelled in Equation (1) by the term , where (f)₊ denotes the positive part of a function f (i.e. (f)₊=f if 0<f and (f)₊=0 if f≤0). This assumption is based on studies where a subpopulation of vectors was shown to survive insecticide treatment 20 22. This refuge of vectors appears to occur regardless of the population densities prior to insecticide application; the studies were carried out in experimental chicken houses where migration and reinfestation were not considered. The net effect is that the presence of a survivor reservoir assures a minimum number V _min of vectors. However, in Section 3, we let V _min decrease incrementally during the years of spraying, to take into account the cumulative effect of spraying. The term d _m (t)V(t) represents the natural death rate of vectors.

Finally, [wtilde] describes the supply of vectors available from the wildlife. Biologically, [wtilde] models the effects of sylvatic Chagas disease on the domestic cycle 1 15 17. This term is not used in models where no reservoir host exists, such as in those for human malarias which lack other host species.

We next describe the dynamics of the infected insects, humans, and dogs.

The growth rate of the infected insects V _i depends on the numbers of susceptible vectors, infected humans, infected domestic animals, and chickens. It also depends on the natural death rate of vectors, on the rate of spraying, and on the rate of infection from infected wildlife sources.

We denote by b=b(t) the seasonally varying number of bites per insect per day, and so b(V−V _i ) represents the total number of bites or blood meals by susceptible insects per day. A detailed description of b is provided below. Vector preference was taken into account with a higher preference for domestic dogs or chickens rather than humans 28. We use d _f and c _f to denote the preference weight factors for domestic dogs and chickens, respectively, in terms of the human factor h _f=1. Next, the total blood supply is weighted by preference in terms of human factors 28. It can be written as follows:

This number is used to normalize the probability for a susceptible insect to become infected. We denote by and the probabilities of a vector becoming infected in one bite from an infected human or an infected dog, respectively, in the absence of preference (or if either dogs or humans are not present). We assume that the infection rate is of the ‘standard incidence’ type, i.e. it is proportional to and , respectively 33 56. Thus, the infection rates per day per capita from infected humans is and from infected dogs is .

These observations show that the rate of infection of vectors from infected humans and infected dogs is

We now describe the biting rate function b. We let

be a normalization factor and set , where B(t) is a seasonal feeding function, described in Section 3. Finally, we let

To describe the death rate caused by spraying, we assume that the infected vectors’ population in the deep cracks are not affected by spraying. Also, it has the same proportion of infectives as the total population, i.e. . Thus, the rate is

The natural death rate of the infective insects is d _m V _i .

Collecting the terms above yields the rate equation for the infective vectors,

The term does not have a counterpart in malaria models. Here, the term describes the fact that the disease has a wild foci, occurring outside the population studied in the model. Future studies will include this term, and here it is taken to be zero.

Next, the mortality rates of infected humans and infected dogs are and , respectively. These are likely to be higher than those of the susceptible populations. The rates of infection by infective vectors are assumed to be of the ‘standard incidence’ form, too. Therefore, the rate of change of the number of infected humans N _i (t) is

The first term represents the rate of increase of infected humans caused by b V _i bites per day by infected insects. The number of the susceptible humans is N−N _i , and the infected vector to human transmission probability in one bite is . Similarly, the rate of change of the number of infected dogs D _i (t) is

Here, is the infected vector to dog transmission probability in one bite, and D−D _i is the susceptible dog population.

To complete the model, we prescribe the initial numbers of the respective populations when the process starts (conveniently chosen as t=0), , together with

Here, due to the delay τ in Equation (4), the function V ₀(t) must be prescribed on the time interval .

Collecting the equations and conditions above yields the following mathematical model for Chagas disease.

Find the functions such that

Here, .

Equation (4) for the total vector population is not coupled to the other equations, and so it can be solved independently. Then, the coupled system of Equations (5)–(7) for , and D _i (t), for 0<t≤T, has to be solved simultaneously.

The coefficient functions , and b _i are assumed to be periodic with a period of one year. Their exact form must be determined in each application of the model, based on specific information for the setting under study. In the simulations presented in the next section, each one was assumed to be continuous, and their exact forms can be found there.

The existence and uniqueness of the solutions to the model is established in the appendix. It is based on the observations that on each bounded time interval [0, T], Equation (4) leads to a positive bounded solution V if the function [wtilde] is positive and bounded. This guarantees that Equations (5)–(7) lead to bounded solutions on [0, T], since , and D _i (t) are bounded by V, N, and D. If V _i (t) exceeds V then the term V−V _i becomes negative, leading to the decrease in V _i (t), and similar observations hold for the other two terms. Further mathematical analysis of the model, especially the study of the steady states and their stability, is addressed elsewhere.

3. Simulation results

We describe the numerical algorithm used to simulate the disease dynamics and the various input functions and coefficients. Then, we describe the results of some of the numerical simulations. We depict and explain the baseline case, and three cases of the model that show the effects of spraying in different circumstances, as well as the effects of changing the blood supply.

We used the fourth-order Adams–Bashforth predictor corrector method to compute the numerical approximations to the model (Equations (4)–(7)). The values of the various system parameters which were used in the numerical simulations are provided in Table 1. The simulations were run using gfortran on a 3.0 GHz Intel Core 2 Duo CPU with Cent OS 5. A typical simulation of 100 years with 100 time steps per day ( time steps) took approximately 300 s. It was found that very long runs over a few hundred years (tens of millions of time steps) produced reproducible results, which indicate that the solution algorithm was stable.

The model is continuous; so when the total number of triatomines is less than two, it is set to be zero. This prevents the code from numerically reproducing vectors when there is not even one pair of vectors available.

The dimensions of the variables and the various coefficients are as follows. The populations have the dimensions of individuals per unit area, which, in our simulations, is chosen as one village. The rate coefficients have the dimensions of inverse time. A detailed description can be found in Table 1. By the ‘baseline case’, we mean the dynamics of a village with 100 houses and a blood supply in each household of four humans, one dog, and one chicken.

We first describe the model seasonal coefficient functions.

The functions and d _m =d _m (t) in Equation (4) represent the hatching rate of the surviving healthy eggs and the mortality rate of the triatomines, respectively. The growth term is of the form used in models for blowflies. The delay τ represents the gestation period from the time the eggs are laid until they hatch. We extracted the following seasonal data from Castanera et al. 5: the ratio of adults to the entire population of triatomines is 0.03 (so we assume that the ratio of adult females is half that number), the ratio of eggs that survive is 0.83, and the number of (eggs/bite)/(fed female) is 20 5 22. We obtained a part of the growth factor by multiplying the product of these numbers by the biting rate evaluated τ days prior to the current time t (due to the gestation period), thus

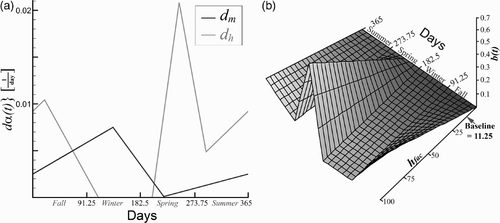
The growth term d _hτ and the mortality rate coefficient d _m are assumed to be the piecewise linear functions depicted in Figure 2(a). In this graph, and in those that follow, each year begins with the first day of fall. The seasonal biting rate b(t) [bites/day/vector] is also assumed to be a piecewise linear function, illustrated in Figure 2(b) for the baseline case the parameters of which are listed in Table 1 5 6. The function attains its highest value at the beginning of the spring and its lowest value in the winter. We also assume that vectors bite at a rate that is proportional to the available blood supply 5 6. Therefore, we take the biting rate to be that found in Figure 2(b) times , with . This is consistent with the definition in Section 2.

Figure 2. Parameters for total vectors. (a) Growth d _hτ(t) and mortality d _m (t) rates are piecewise linear functions. The growth rate is directly proportional to the biting rate since egg production requires a blood meal. (b) The biting rate b(t) varies with the seasons and with the blood supply (human factors) 5 6. The biting rate is linear relative to the blood supply and piecewise linear when the blood supply is fixed. The biting rate varies due to seasonal temperate changes in temperate regions.

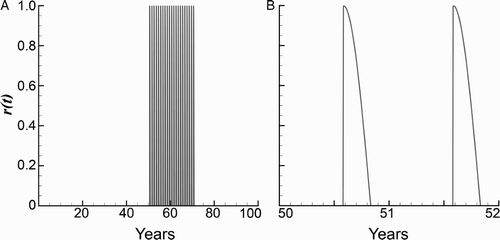
We assume that the insecticide spraying rate r=r(t) is applied (as explained in Section 2) only to the vectors that are not living in the cracks, V−V _min. Moreover, in the simulations, to take into account the cumulative effect of spraying on the vectors in the cracks, V _min was assumed to be time-dependent, and it was decreased by one insect per house in each consecutive year of spraying, until it reached the value zero.

The following rate coefficient function r was used in the simulations:

The values of the coefficients in the simulations were chosen to be

with t ₁=212.5 days and t ₂=303.75 days for a full season of spraying starting in the spring. Here, r _max is the highest intensity of spraying. The function and a 2-year detail are depicted in Figure 3.

Figure 3. The spraying function r(t). (a) All spraying simulations begin at year 50 and continue yearly for 21 or 30 years. (b) Close-up of spraying from years 50–60. Spraying occurs once a year (in spring) and the insecticide's effectiveness decays exponentially over a period of three months. The model assumes that the average home has cracks/reservoirs that allow initially 20 vectors to survive, the surviving number deceasing each spray cycle.

We turn to the results of the numerical simulations. Initial simulations were run without insecticide spraying, but since they can be inferred from the runs with spraying before the spraying starts, we do not depict them.

To gain insight into the model's predictions, we studied the effects of insecticide spraying for 5, 13, 21, and 30 consecutive years for each one of the cases below. For one of the cases, we also ran it with 50 years of consecutive spraying to study long-term eradication.

The parameters used in the model are summarized in Table 1, and the values in the baseline case are provided in Table 1, together with the references from where they were obtained, inferred, or estimated. In each run, we report the number of triatomines in the upper-left corner, the number of infected triatomines in the upper-right corner, the number of infected humans in the lower-left corner, and the number of infected dogs in the lower-right corner, as functions of time.

3.1. Baseline case

The baseline case simulates a representative village in South America with 100 houses. Each household contains four humans, one dog, and one chicken. Chagas affects the mortality of both humans and dogs. We estimated that 30% of humans will have a decreased life expectancy 45. Figure 4 illustrates the yearly periodicity of the total vector population with and without spraying. Due to the seasonal dependency of the model coefficients, the numbers of vectors and infected vectors oscillate.

Figure 4. Baseline simulation of total number of vectors (V(t)) in the village (four humans, one dog, one chicken per home in a village of 100 homes) over 100 years. (a) A stable model vector population. (b) Seasonality of the vectors, years 50–52. The vector population reaches its maximum in fall and the minimum in late winter. The vector population fluctuations are due to growth and mortality (shown in Figure 2(b)). (c) Baseline simulation of total number of vectors (V(t)) in the village with spraying during years 50–71. (d) Seasonality of the vectors, years 50–52 during the initiation of spraying in year 50 during spring.

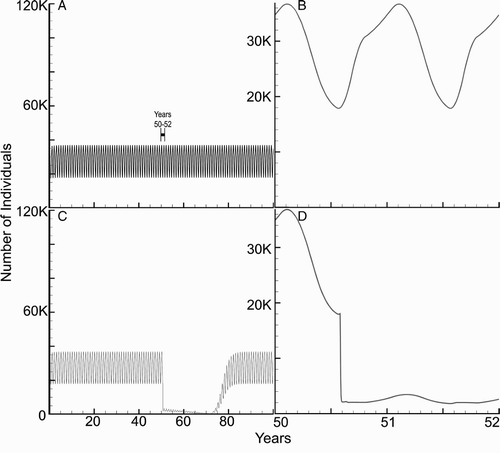
The results for 21 and 30 years of consecutive spraying, beginning at year 50, are shown in Figure 5(a) for the baseline case. Note that the total number of vectors oscillates about the average value of approximately 30,000, while the number of infected vectors, infected humans, and infected dogs oscillates about 8000, 80, and 48, respectively. The size of the populations return to their original states in approximately 5–10 years after spraying ceases. However, in the case of 30 years of consecutive spraying, the baseline simulation predicts that the infected vectors die out, as is seen in Figure 5(a), because of the incremental lowering of V _min.

Figure 5. Spraying simulation of vectors (V), infected vectors (V _i ), infected humans (N _i ), and infected dogs (D _i ) are graphed over 100 years. (a) The baseline population (village) underwent 21 or 30 years of successive spraying. After cessation of insecticide use after 21 years, the number of triatomids in the village returns to the pre-spray population in 5–10 years. Due to the extended life span of humans, the infection is still present in the population and re-establishes over time. The infections’ return in each species varies due to the lifespan/turnover rate. After 30 years, the domestic triatomids have been eradicated from the village. (b) Spraying simulation of increased blood supply to two dogs and five chickens per household. The population (village) underwent 21 or 30 years of successive spraying. After cessation of insecticide at both 21 and 30 years, the number of triatomids in the village return to the pre-spray population. (c) Effects of number of dogs per household. Increased number of dogs per household to 3 or 300 per village. (d) Effects of number of chickens per household. Increased number of chickens per household to 3 or 300 per village.

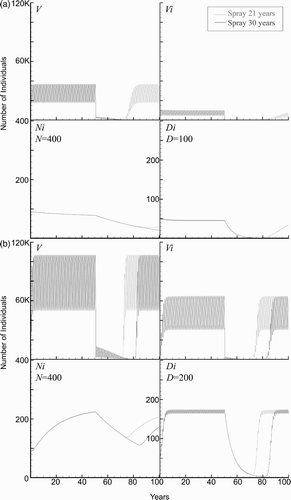
3.2. Blood supply effects on disease transmission

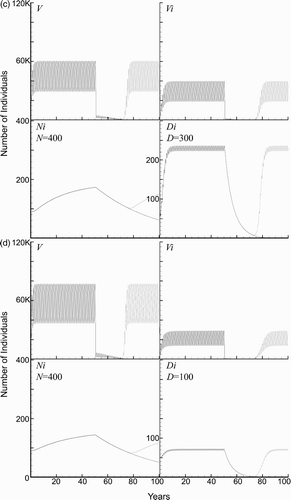
An important part of the disease dynamics is determined by the available blood supply. To study the effects of a change in the blood supply, we tested the scenario where all the baseline parameters were used, except for an increase to two dogs and five chickens per household, so that the total blood supply was increased from a baseline value of 10.7 human factors to 32.9 human factors. The model predicts that the number of triatomines and infected humans more than doubles, while the number of infected dogs more than triples. The simulations with 21 and 30 years of consecutive spraying are shown in Figure 5(b). Furthermore, even at 30 years of consecutive spraying, the vectors returned to previous levels once spraying was suspended. The simulations revealed that the model is sensitive to changes in the blood supply available to the vectors. However, the model predicts that 50 years of consecutive spraying does, in fact, eradicate the domestic vector population (the results not shown).

The effects of the blood supply were further studied to examine the separate effects of either dogs or chickens within the household. Figure 5(c) simulates the effects of increasing the number of dogs to three per household. Due to the ease of transmission to dogs and the higher number of triatomids supported by the increased blood supply, approximately 50% of humans become infected prior to spraying.

A related aspect of the blood supply that we studied was the dependence of the disease dynamics only on the number of chickens. The model in Cohen and Gürtler predicted a very slight decrease in the human disease as the number of chickens increased 10. We studied this scenario by increasing the number of chickens in a household to three while using the baseline values for all other parameters. We found that the number of vectors increased substantially and this caused more infections since humans and dogs received more daily bites (Figure 5(d)).

4. Discussion

The transmission dynamics of Chagas disease are complex and depend on both geographic location and socioeconomic conditions. The model presented here allows for the qualitative, and partly quantitative, prediction of disease growth, and the model's simulation results agree with observed information, when available. It is intended to simulate medium to large communities, since it is a continuous model. The authors would like to point out again, as stated in the introduction, that the model has not been validated and therefore may not have any predictive value. The purpose of the model is to gain insight into Chagas disease dynamics.

The goal of this model is to replicate the known dynamics of the disease when insecticide spraying is used to control the vector population and to study the effects of interrupted spraying. The model can be used to predict population dynamics under various scenarios and parameter sets.

The mathematical model presented in this work consists of a system of ordinary differential equations. It is useful for studying Chagas disease dynamics in households in villages, due to the large numbers in each of the populations that it tracks over time. The model seems to quantitatively and qualitatively replicate the known disease dynamics, even when controlling the vector population by spraying with insecticides. It can also be used to study the effects of interrupted spraying and spraying at different times during the year.

This mathematical approach to studying Chagas disease dynamics lends itself quite easily to other studies. In particular, the model can be simulated with changes in the spraying rate function, including the intensity of the spraying effect, possibly dependent upon the type of insecticide administered, as well as the duration and time period for spraying. Also, the model can be simulated with changes in any of the following parameters: the (seasonal) biting rate, the (seasonal) hatching rate, the (seasonal) vector mortality rate, the mortality rate of infected vectors, the mortality rate of infected humans, and the mortality rate of infected domestic animals. The human factors for dogs and chickens can be changed as can the probabilities of infection from infected vectors to dogs, infected vectors to humans, from infected dogs to vectors, and infected humans to vectors.

Another point worth mentioning is that the model could easily take into account seasonality in the household blood supply, so that we could simulate other scenarios such as the following: chickens remain in the houses in the fall and winter, but not in the spring and summer. In addition, another trivial change would be to assume that the minimum number of vectors in a household does not change with consecutive spraying years.

As mentioned above, a web interface has been created and the model was designed, in part, in a way that allows the use of multiple parameters as inputs for online study of conditions at specific locations 54.

The simulations presented here do not take into account the reintroduction, due to sylvatic vectors, of the disease, which could increase the rate of reinfestation of homes with non-domestic triatomids 1. The introduction of non-domestic triatomids dynamics will increase the complexity of the model. We have focused on domestic and peridomestic vectors that have been shown to survive at low numbers after spraying 20. The model simulations show that in some circumstances, the human disease resurfaces even after 30 years of spraying and re-establishes its original level within 5–10 years. We have simulated residual insecticides that diminish in effect over three months. The baseline conditions are in general agreement with what was seen in northern Argentina; this is the region with most detailed data currently available on insect dynamics 21 27.

The model and simulations presented also do not take into account insecticide resistance. This is due to the limited amount of data available to treat this aspect of Chagas disease dynamics reasonably.

Also, many other factors can be taken into account. For example, assuming that the village modelled is connected to another village, we ran the baseline case with the assumption that an additional 20 vectors, five of which are infected, enter the village each month from the neighbouring village 51. The simulations revealed that even after 30 consecutive years of spraying, ceasing to spray caused the disease to return within 5–10 years.

The model shows that spraying with insecticides is an effective way to control the disease in humans. However, when spraying is discontinued, the number of infected vectors in homes returns to its previous levels in a matter of 5–10 years and with it, the disease. Of significance, the model also highlights the importance that dogs play in the spread of domestic infections. In Figure 5(a), the baseline simulation shows that just under 25% of the human population was infected, whereas in Figure 5(c) with a change from one dog to three dogs per household, the infected human population approaches a two-fold increase. The increase in human disease is due to dogs’ high infection rate and may be influenced by several factors. Dogs can be infected by nipping reduviids while they feed, licking the bite site contaminated with reduviid faeces, ingestion of infected wild animals, and transplacentally 43. This effect is amplified by the hostfeeding preference for dogs of domestic triatomids 26 30 31. It is most likely that the nipping and licking behaviour accounts for dogs having such high infection rates, as well as the fact that many dogs will readily eat insects when available. Canine behaviour explains their role in domestic T. cruzi infections and why dogs should be excluded from homes if triatomids are present 10.

While the cost of spraying was estimated in 1999 to be at US$30 yearly per home versus US$700 for improved housing, the long-term protection provided by reducing available sites for infestation could have greater public health significance 48. Multiple studies have demonstrated that the prevalence of domestic triatomid infestation and disease rates are associated with home quality 7 8 27 37. The fact that several communities have already begun to report insecticide resistance, requiring them to switch insecticides, could further raise the cost of insecticide treatment over time 20. Spraying programmes have made substantial headway in controlling Chagas disease in Latin America 12 35. These programmes must be maintained, but focus should also be placed on alternative means of control of this disease, including improved housing, chemotherapy, and immunoprophylaxis.

Acknowledgements

We thank Prof. Darrell Schmidt for the references to the Nicholson blowflies mathematical model, Ms April Clark for multiple literature searches and help in determining initial parameters in earlier versions of the model, Mr Qi Lu and Prof. Harvey Qu for their contributions to earlier versions of the model and estimates of the parameters, Mr McBride for his editorial help, and Prof. Serge Kruk and Mr Michael DuChene for setting up the web interface. We also thank the reviewers for their helpful suggestions.

Appendix. Existence and uniqueness

For the sake of completeness, we establish the unique solvability of the model. To that end, we first introduce a new notation and rewrite it. Let the new dependent variables be

let and set

The model (4)–(8) can be written, using the prime to denote the time derivative, as the following.

Find the quadruple of functions such that

together with the initial conditions

We make the following assumptions on the problem data.

(H ₁) The coefficient functions , defined on [0, ∞), possibly periodic, are non-negative, bounded, and continuous.

(H ₂) are non-negative constants, while are positive constants. Moreover, D _i0≤D, N _i0≤N, and .

(H ₃) The functions and are identically zero.

(H ₄) The function V ₀(t), defined on , is non-negative, bounded, and continuous. The function a ₁ is defined on , non-negative, bounded, and continuous.

We have the following existence and uniqueness result.

Theorem A1

Assume that assumptions H ₁–H ₄ hold. Then, system (A1)–(A7) has a unique global solution on [0, ∞).

The proof is presented in the following four steps.

First, we note that Equation (A1) (together with Equation (A7)) is not coupled to the other equations, so it can be solved independently. It is a delay differential equation of a type that has been studied in the literature (see, e.g. 32 and the references therein). It is straightforward to show the following [32, pp. 4, 51].

Proposition A1

Assume that H ₁–H ₄ hold. Then, problem (A1) and (A7) has a unique bounded solution v on [0, ∞).

We note that one can find in Györy and Ladas 32 conditions for oscillatory behaviour of v.

We turn now to the system (A2)– (A6). We have the following.

Lemma A1

Assume that H ₁–H ₄ hold. Then, there exists 0<T such that problem (A2)–(A6) has a unique bounded solution (x, y, z) on [0, T].

Proof

The right-hand sides of Equations (A3)–(A5) are locally Lipschitz continuous; hence the conclusion follows from standard results on systems of ODEs.   ▪

To show that the solution is global, i.e. exists for all 0<T, we show that the solution is bounded. It follows from Proposition A1 that there exists 0<M such that v(t)≤M on [0, ∞). Then, we have the following.

Proposition A2

The rectangle is forward invariant for the system (A3)–(A5).

Proof

We need only to show that the vector field points inward on the boundary of the domain Ω. Consider the face . It follows from Equation (A3) that v−M≤0 when x=M and, since , we conclude that x′<0 on this face. Next, we observe that if y≥N then Equation (A4) shows that y′<0, and so the claim is true on the face . Similarly, it follows from Equation (A5) that if z=D then z′<0 on the face . Considering now the other three faces x=0, y=0, and z=0, we find that the derivatives are positive, and hence the vector field points inward.   ▪

Proof of Theorem A1

It follows from the above that the system has a local solution that is bounded in Ω if the initial conditions belong to Ω. The theorem now is a consequence of standard results for systems of ODEs 55.   ▪

We assumed that there is no contribution from wildlife. If we wish to include the influence of wildlife on the model dynamics, all we need to do it to replace assumption H ₃ with

([Htilde] ₃) the functions [wtilde] and , defined on [0, ∞), are non-negative, continuous, and

on [0, ∞) with some 0<M _*.

All the results above hold in this case, only the proofs are more technical. The rectangle Ω needs to be enlarged to .