Notes from the heterogeneous: a few observations on the implications and necessity of affinity

Abstract

The problem of who is mixing with whom is of great theoretical importance in the context of heterosexual mixing. In this article, we publish for the first time, data from a study carried out in 1989 that had the goal of estimating who is mixing with whom, in heterosexually active college populations in the presence of co-factors like drinking. The gathering of these data and the challenges involved in modelling the interaction between and among heterosexually active populations of individuals are highlighted in this manuscript. The modelling is based on the assumptions that at least two processes are involved: individual affinities or preferences determine ‘what we want’ while mixing patterns describe ‘what we get’. We revisit past results on the role of affinity/preference on observed mixing patterns in one- and two-sex mixing populations. Some new results for homosexually active populations are presented. The study of mixing is but the means to an end and consequently, we also look at the role of affinity on epidemics as filtered by observed mixing patterns. It would not be surprising to observe that highly distinct preference or mixing structures may actually lead to quite similar epidemic patterns.

Keywords:

• like-with-like mixing
• affinity
• paired events
• SIS epidemic
• networks
• two-sex models
• HIV
• drinking
• STDs
• marriage functions
• contact matrices

AMS Subject classification :

• 91D30
• 92D30

1. Introduction

The question of who interacts with whom and the reasons behind recorded or observed preferential patterns of interactions among or between individuals is of interest in population dynamics, demography, epidemiology, and social dynamics. Formulating suitable frameworks that incorporate preferential interactions between or within groups or subpopulations and scaling them up to the level of the population or community is important in the study of processes where heterogeneity may be relevant to the time evolution of a population or to the selective pressures that shape its structure 9 10 12 14 15 24 25 27 30 31 37 39 72. Identifying precise mechanisms responsible for observed mixing patterns is riddled with difficulties because a multitude of behavioural patterns can lead to ‘identical’ population mixing patterns. There is an inherent lack of uniqueness in the identification of the individual-level mechanisms that shape community patterns; that is, similar mixing population-level patterns may result from distinct individually driven contact structures. Not surprisingly, the study of the role of individuals’ preferences or affinities on population dynamics has been studied under rather simplified settings or avoided all together. The modus operandi (classical mathematical demographic models) has been to focus on the study of role of vital rates (birth and death processes) on population dynamics while ignoring the contact structures or mating systems responsible for the reproduction process. This effort has been carried out quite effectively in the context of single-sex (female) models 18 56 57 61.

While mating structures have been extensively studied in population genetics 23, they have not received the same level of attention at the population level partly because the resulting system of equations are not easy to analyse. Nevertheless, the desire to develop a framework that naturally incorporates diverse mating processes has always been of interest to biologists and demographers alike. Here is some history on the mixing problem.

The study of population-level mating structures often called marriage functions in demography was pioneered over three decades ago 27 50 51 62 65 66. A large number of solid extensions 16 17 18 38 72 have been carried out, but unfortunately, they have not been implemented by other behavioural epidemiologists, sociologists, or relevant policy-makers. The HIV/AIDS epidemic attracted the attention of an increasing number of theoreticians to the study of mating systems, including the role of preference on two-sex dynamics. Hence, the study of questions such as who mixes with whom and their consequences accelerated with the emergence of the HIV/AIDS pandemic 10 24 25 30 31 33 34 40 41 42 43 44 45 47 48 52 53 54 69 70 71 73. Furthermore, emphasis has been put on the study of the dynamics of social networks and their applications to the study of the transmission dynamics of infectious or sexually transmitted diseases 4 5 7 21 28 29 32 49 55 64 68. This is an area of extensive active research.

Our own efforts have involved the development of theoretical models as well as empirical studies aimed at identifying and quantifying mixing patterns. A survey instrument 37 22 was developed with the goal of confronting the complications associated with the estimation of contact structures (who is mixing with whom) in populations living in ‘controlled’ environments. Our focus has been on residential college student populations. The college survey focused on identifying who mixes with whom in the context of sexual or ‘dating’ activities. The role of co-factors like alcohol, which plays a critical role in college-drinking dynamics 63, was explored as well. Our approach is flexible and quantifiable and can be applied to the study of a multitude of processes that include disease dynamics, the transmission dynamics of cultural traits, general demographic processes, and even frequency-dependent predation 39 59 8 9 5 7 4 10 14 15. Serious efforts to connect these models to data are found in 38 37 68 6. Recent theoretical results and applications include those in 26 20 72.

This paper provides an incomplete overview of the problem of mixing, focusing on questions involving the structure described in 8 9 5. Section 2 revisits a two-sex mixing framework expansion developed in 11 12 5 8 37. Our theoretical efforts in the two-sex case 8 9 4 5 6 68 38 37 drove us not only to the development of a survey instrument but to its implementation 37 22. Two-sex, P−Q, mixing matrices directly computed from survey college mixing data are presented, for the first time, to illustrate the challenges involved in connecting data with mixing. Our two-sex formulation is a natural expansion of the single-sex version that first appeared in 8 9 4 5. Its presentation serves as a prelude for the introduction of new results (via simulations) on one-sex mixing, the object of Sections 3 and 4. Section 3 highlights the theoretical results associated with the discrete version of the single-sex mixing group framework developed in 8 9 4 5 37 14 38 12. In addition to the prior results, we analytically and computationally explore the effects of stochastic fluctuations within the affinity component of the mixing matrix on the role of preference, e.g. the patterns of who mixes with whom in the one-sex framework. Section 4 explores the impact of mixing in homosexually active populations on disease dynamics. A two-group susceptible–infectious–susceptible (SIS) model is used to explore how the level of variation inherent in the simplest form of heterogenous mixing (proportionate mixing) filters over an epidemic process. Section 5 discusses mixing in the context of past, current, and future applications.

2. Two-sex mathematical formulation

Marriage functions have been studied extensively in demography 50 51 27 62 65 66. However, the lack of useful results (theoretical results that can be connected to data) managed to reduce interest in the study of the dynamics of ‘mating’ at the population level for some time. The start of the HIV/AIDS pandemic in developed nations regenerated theoretical and practical interest in the study of marriage functions, given the importance naturally placed in the study of the dynamics of heterosexually transmitted diseases. Questions like who mixes with whom and subsequent studies on the consequences of social dynamics became increasingly important again as HIV/AIDS grew 24 25 30 31 33 73 10 34. The study of heterosexually transmitted diseases have also contributed to the growing interest in the study of epidemics on social networks. Recent advances in the network theory have in fact increased the expectation that the theory may finally provide useful insights on the dynamics (outcomes) of ‘two-body’ problems in biology 49 28 55 21 29 32 64.

The two-sex framework presented was first introduced in 11 as a natural extension of the modelling work carried out by Sir Ronald Ross on the dynamics of vector-transmitted diseases 67. Ross’ solutions, found in a primitive fashion in Ross's 67 article, are used to describe more general forms of mixing. The extensions and results on two-sex mixing have been taken from the detailed descriptions provided in 12 38 37.

In order to present the two-sex framework, the following additional notation and definitions are required: p _ij (t) is the probability that a male in group i mixed with a female in group j at time t given that he mixed with somebody; q _ji (t) is the probability that a female in group j mixed with a male in group i at time t given that she mixed with somebody; is the number of males in group i at time t, is the number of females in group j at time t; the average (not necessarily constant) number of female partners per group-i male per time unit, which is per capita pair formation rate for group-i males, is the average (not necessarily constant) number of male partners per group-j female per time unit, which is per capita pair formation rate for group-j females.

Definition

The matrices Q=(q _ji (t)) are called a mixing/pair formation matrix if and only if they satisfy the following properties at all times:

• (A1) .

• (A2)  for all i, and for all j.

• (A3)  for all i, j.

• (A4) If for some i and/or some j, we have for some t, then we define .

It is important to point out that in general, it would be impossible to maintain the above constraints (first put forward in terms of constant contact rates by Ross) under the assumption that the per capita rates of activity for males and females are constant. In fact, in general, the and must be functions of both the availability of male and females. This point is evident from the single-group two-sex formulations found in 50 51 27 62 65 66 and in the relatively recent extension of 39.

The only separable solutions to (A1)–(A4) are known as the Ross’ solutions. They are denoted by (p¯ _j (t), q¯ _i (t)), where

Moreover, all solutions to (A1)–(A4) can be represented as multiplicative perturbations to Ross’ solutions. Explicitly,

where denotes the degree of preference that males in group i have for females in group j and denotes the degree of preference that females in group j have for males in group i. In addition, the following relationships must be satisfied:

and

where , and , is defined, for notation's sake, as one minus the weighted average preference of group-i males, or of group-j females. We observe that if (constant) and (constant) for all i and j, then the general solution reduces to the Ross solution which corresponds to random heterosexual mixing.

Also as a consequence of this relationship among the φ values, we have the so-called it takes two to tango theorem 37.

Theorem 2.1

(T ³) The non-negative affinities of two genders, and , obey the following explicit relationship at all times, letting and

where for all i but not all may be 1, and Γ is an arbitrary constant with frequency-dependent range

Conversely,

where for all j but not all can be 1, and Δ is an arbitrary constant with the frequency-dependent range

This was also generalized to include age structure in 37 and role of preference explored in this last context in 13.

2.1. Estimating p _ij and q _ij from survey data

The spread of sexually transmitted diseases may depend on a few small groups of individuals (core groups) 35. Estimation of the sizes and behaviours of the core groups is thus very relevant for a correct prediction of the epidemics, especially for HIV/AIDS. For this purpose, a survey was conducted in 1989 in Cornell University to investigate social and sexual patterns among undergraduate students 22. Two versions of a questionnaire with identical appearance were prepared: the indirect and the direct versions. The common questions in both versions included frequencies of attending lectures and social activities, availability and consumption of alcohol at different social activities, number and gender of pair-off partners at different social activities, study year and demographics of the partners, as well as personal information of the respondent, such as study year, gender, living in campus or not, marital status, age, family gross annual income, religion, and ethnicity. The indirect version included further questions about frequency of intimate behaviour and the association between pair-off and consumption of alcohol/drugs. The direct version included questions regarding explicit sexual intercourse, including frequency, use of condoms, and the association of these behaviours with the consumption of alcohol/drugs. Two thousand names were randomly drawn from the registrars list of all undergraduates and invited by a letter to participate in the survey. The participants received either questionnaire version by random choice with equal chance and answered the questions in an anonymous way. The indirect questionnaire was filled out by 493 students, while the direct questionnaire by 502 students. Students received a small reward for participating or had a chance to participate in a lottery that offered a larger reward.

Based on data of sexually active respondents, the sizes of active population and the mixing patterns were estimated 38. In heterosexually dating active respondents, the proportion of alcohol drinker among females is highest among freshmen (33%) and lowest among seniors (10%), while among males the proportion of alcohol drinker is similarly high in the first three study years (28–32%) and reduced by about half for seniors (14%). Even the size of the non-targeted population, graduate/staff/faculty and non-Cornell, was estimated using the mark–recapture method, as shown in 68. Specifically, a modified mark–recapture approach was used to estimate total size of these active populations from a single survey and then a sort of minimized least squares approach was used to estimate the and the contact rates.

The data were placed into two larger categories, mixing with or without alcohol along with stratifications by year, as shown in Figures 1 and 2. In heterosexually dating active female respondents, the mean, standard deviation, and median of the number of partners are, respectively, 1.86, 1.35, and 2 for non-alcohol drinkers and 1.68, 1.04, and 1 for drinkers; the difference between the two alcohol groups is statistically significant (Wilcoxon two-sample test p=0.0019). In male respondents, the corresponding mean, standard deviation, and median are 3.28, 2.42, and 3 for non-alcohol drinkers and 3.19, 4.50, and 2 for drinkers; the difference between the two alcohol groups is statistically non-significant (Wilcoxon two-sample test p=0.086). Results of these two tests suggest that the effect of alcohol on number of partners is different between female and male respondents. Without alcohol, we arrive at mixing matrices

and

and with alcohol at

and

These data are visualized in Figures 3 and 4. In either situation, the alcohol consumption of who is mixing with is irrelevant as we are capturing how a group's alcohol consumption affects how members in that group make contacts. The matrices have rows corresponding to freshmen, sophomores, juniors, and seniors, and columns corresponding to the same with graduate/staff/faculty and non-Cornell appended as the last two. These two groups do not have their own rows since data are not available as to how they are making contacts just who is making contacts with them. In either situation, alcohol or no, there is observable homophily in the first four groups (freshman, sophomores, juniors, and seniors), and heavily varied behaviour with respect to the other two groups (graduate/staff/faculty and non-Cornell) with a quantifiable bias towards non-Cornell over graduate/faculty/staff.

Figure 1. Distribution of number of pair-off partners in female respondents with heterosexual dating activity. (a) Stratified by status of alcohol consumption; (b) stratified by study year of respondent.

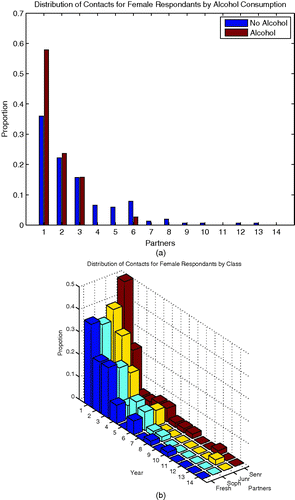
Figure 2. Distribution of number of pair-off partners in male respondents with heterosexual dating activity. (a) Stratified by status of alcohol consumption; (b) stratified by study year of respondent.

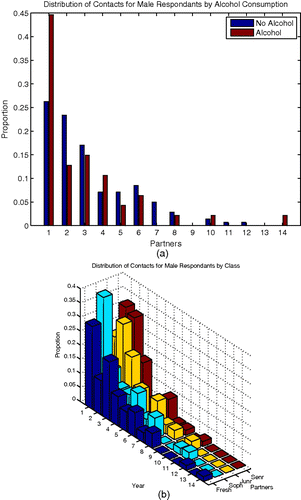
Figure 3. Pair-off mixing matrix of female respondents with heterosexual dating activity. (a) In respondents without alcohol consumption; (b) in respondents with alcohol consumption.

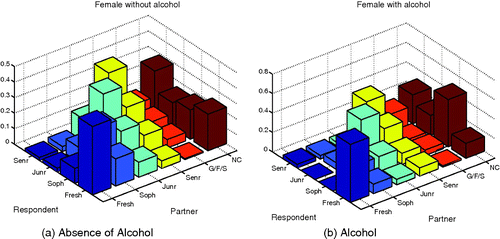
Figure 4. Pair-off mixing matrix of male respondents with heterosexual dating activity. (a) In respondents without alcohol consumption; (b) in respondents with alcohol consumption.

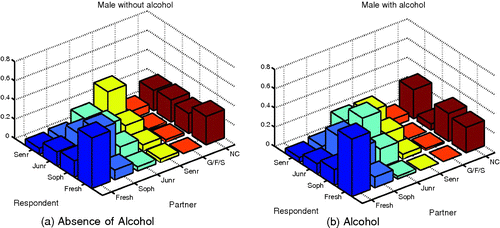
The presence of alcohol dramatically increases the likelihood of sophomores mixing with non-Cornell individuals for females and freshmen with freshmen interactions for both groups. Males experience a large increase in their mixing with juniors in the presence of alcohol with most at the junior mixing with junior level. It should be noted, however, that the total increase in reinforcement due to alcohol is about 17% larger in females than in males. Also for each strata we have data on, except for sophomores, increases in the like-with-like mixing patterns are observed in the presence of alcohol.

In Figures 5 and 6, it is shown that for both genders sophomores experienced the most aversion from other groups when alcohol is present. Females experience a higher tendency to mix with juniors in the absence of alcohol second only to their tendency to mix with sophomores. There are also large differences in the interactions of freshmen with non-Cornell and sophomores with freshman when alcohol is present with such interactions more likely to take place in the absence of alcohol.

Figure 5. Shown here is the difference of the female and male mixing matrices without alcohol from that with alcohol. Reinforced behaviours are those with positive difference and may be interpreted as mixings more likely when drinking.

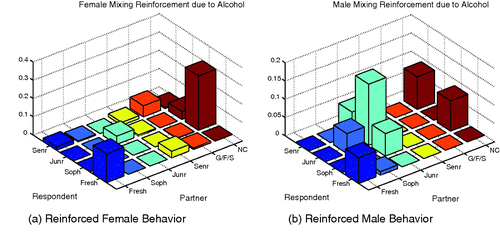
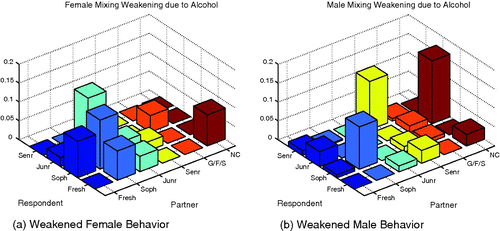
Figure 6. Shown here is the difference of the female and male mixing matrices without alcohol from that with alcohol. Weakened behaviours are those with negative difference and may be interpreted as mixings more likely to occur when sober.

The role of heterogeneity on disease dynamics depends strongly on preferences and mixing. Studying STD (Sexually Transmitted Disease) dynamics in the context of highly heterogenous populations that include heterosexually, homosexually, and bisexually active populations as well as sex workers males and females is a rather complex problem but progress can be made 49.

3. Single sex mixing distributions

Work done in 8 9 5 sets forth the axiomatic approach used to formulate the process of mixing among heterogenous groups. We describe this setting in the context of a fixed number of interacting subpopulations, each constituted or defined by behaviourally equivalent individuals in a single-sex setting. The mixing is described in terms of a conditional probability matrix P with entries P _ij , each denoting the fraction of contacts that individuals from group or subpopulation i have with individuals in group or subpopulation j given that a member from group i has made a contact. It is assumed that the subpopulations involved are large (each with size N _i ; i=1, 2, …, L), and that the per capita average contact rates (C _i , i=1, 2, …, L) are constant and large enough so that all groups are connected. The mixing matrix (P _ij ; i, j in ) is assumed to satisfy three properties or mixing axioms:

The first two make P a stochastic matrix while the third asserts that the average total contact rates between pairs of groups must be balanced. Or in other words, shared contacts per unit of time between two groups must be maintained. In 8 9 5 6 it was shown that the only separable solution to the mixing axioms is proportionate mixing, . In fact, it was shown that all matrices P _ij satisfying the above mixing axioms can be generated as multiplicative perturbations of proportionate mixing via the ‘preference’ symmetric matrix Φ (for alternative, recent result, see 26):

Theorem 3.1

[5 6 8 9] The unique separable solution to the mixing axioms is given by where , and is an L×L symmetric matrix, that is ∀ i, j .

Efforts to interpret the matrix as group affinities have been carried out but several questions remain. Do the relation between the φ-entries of the Φ-matrix provide a useful relative measure of the ‘desire’ of individuals of group i to mix with those in group j? The work in 4 7 8 14 37 strongly supports this perspective, but there are no conclusive analytical results. Here, we continue to explore the relationship between the φ-entries of the Φ-matrix and the P-matrix through simulations. We explore this question in the context of single sex for simplicity and understanding (similar work in the two-sex case is quite complicated). We refer to Φ as the affinity matrix and P as the mixing matrix in the remainder of this manuscript. Further, our baseline perspective starts from the observation that when with α a constant, the matrix P _ij reduces to proportionate mixing, that is, for all . In other words, in the absence of pronounced differences in the preferences, or affinities, proportionate mixing drives population-level mixing under this framework.

3.1. Analytical results

We explore the role that variation in the Φ-matrix has on the matrix P starting from the case proportionate mixing case, that is, when with α a constant ( for all ). Specifically, it is first assumed that each for appropriately chosen Φ _ij values (positive and less than one). It is further assumed that the entries of the Φ-matrix are independent, identically distributed random variables with support on . Next, a prior distribution for the elements of the affinity matrix Φ is selected. Samples from the Φ distribution are used to explore its role on the distribution of the P-matrix.

In summary, it is assumed that {Φ _ij } is a collection of i.i.d. random variables on for i≤j each with density function . The assumed symmetry of Φ-matrix means that for all j>i. We use Φ _ij to stress the fact that we are dealing with a random variable and φ _ij to refer to particular values of the random variable. Φ denotes the random matrix itself.

Now, we are ready to consider the conditional mixing matrix P whose entries, P _ij , are defined in Theorem 3.1. The goal would be to calculate the distribution function of P _ij but how to do it is not obvious in general. Here we look at the case L=2 for simplicity and proceed to condition on the assumption that values of the diagonal elements of the Φ-matrix are known. Hence, we have that

where if i≠j

and if i=j

Since each element of Φ is independent, save Φ₁₂ from Φ₂₁, we may compute the marginal distribution of P _ij by integrating over the marginals of Φ₁₁ and Φ₂₂. Proceeding in this way, we have that

which implies

An immediate result from this calculation is that P ₁₁ and P ₂₂ are i.i.d. when . In fact, letting gives

The use of uniform distributions on Φ _ij leads to computationally explicit formulae, that is, reduces the area of integration to resulting in

where .

3.2. Numerical results

In this section, we carry out a few computational experiments based on the above results and formulae. Letting P _ij , V, and R _i be defined as before with denoting a symmetric random matrix whose entries are continuous random variables supported on a given subset of (0, 1). We proceed to analyse several cases. For simplicity, we only include the situation where there are two subpopulations, L=2 when C _i =C and N _i =N all constants, in fact removing generality from the distribution of P _ij . However, this is not critical, since the focus here is not in the study of general P-matrices but rather on isolating the role/effect of the distribution of Φ _ij on the matrix P. Hence, we consider the case where φ _ij are i.i.d. uniform on . Thus, this family of random variables has mean 0.5 and variance δ²/3. We also consider the case where the distribution for the φ _ij ’s is given by a beta distribution with the parameters chosen so that these beta distributions have the same mean and variance as the pre-selected family of uniform distributions. The expressions for the beta parameters are thus

It is unclear at this point how a particular matrix Φ built from a family of distributions (i.i.d. uniform on ) would impact the matrix P. In particular, how ‘close’ would this perturbation be from proportionate mixing? That is, from the matrix P that results when all φ-entries are equal to the mean, here to 0.5. We explore ‘closeness’ numerically by considering situations where the uniform is defined on , and (0, 1) and treat these as very tight, tight, and very loose Φ ‘perturbations’ with the average leading to the same proportionate mixing distribution.

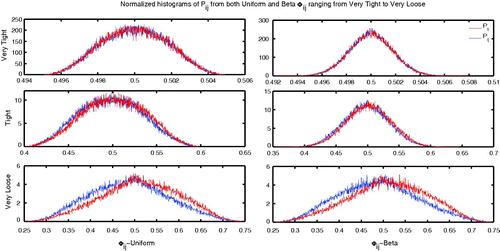
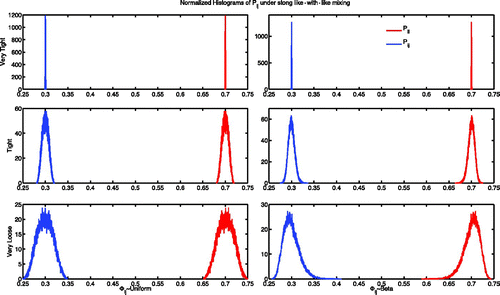
For the very tight distributions the mean of P _ij is 0.5, with slight deviations like 0.4999, regardless of the distribution on Φ _ij and the variance is on the order of 10⁻⁶, again with deviations at the 10⁻⁸ spot. This represents a slight loss of variance in the transformation from Φ _ij to P _ij . Important to note is that too, from the perspective of machine precision, 10⁻¹⁵, the distributions are also not dependent on i or j. For tight parameters, the mean of P _ij for i≠j was approximately 0.498 and that of P _ii was 0.502 with little difference regardless of the family used uniform and beta for the Φ-matrix. Variance for all terms was about 0.0012 with differences between φ distributions in the order of 10⁻⁵. This marks yet again a loss of significant value in the variance between Φ _ij and P _ij . For the very loose parameter regime, we see a mean of 0.5118 for diagonal elements and 0.48818 for off-diagonal elements when uniform distributions were used for the Φ-entries and 0.5116 and 0.4884 when beta distributions were in place. The variance was essentially constant when beta or uniform distributions were used regardless of i and j. In fact, they were 0.0076 and 0.00758 for uniform and beta, respectively. In other words, when the differences in affinity or preference as modelled by the Φ-matrix are small, the P-matrix essentially corresponds to proportionate mixing, but otherwise there seemed to be a drift towards like-with-like mixing as the support grew, as seen in Figure 7.

Figure 7. Histograms of the P _ij values top to bottom with the very tight, tight, and very loose parameter choices. We can observe a definite difference in shape between the uniform and beta shapes but the first and second moments are roughly equivalent.

Certainly, from the observation that the relationship between limited variability in affinities and proportionate mixing is strong, we cannot distil the exact role of these preferences on the mixing patterns. Hence, in our preliminary efforts to gain further understanding, we explore, as a source of comparison, the role the following like-with-like affinity matrix on P. We repeat the above procedure with Φ _ii having means 0.9 and Φ _ij means 0.1, taking care not to exceed (0, 1) on either end (albeit this is probably not that relevant). Here very tight shall be , tight and very loose . This represents a population group's desire to mix within their own group rather than with another.

In the case of like-with-like mixing (Figure 8), we can see that the process from seems to represent, in the case of uniform φ distributions, a smoothing of the P distribution. Regardless of the uniform distribution the means of each hump, P _ii and P _ij , all seem to shift closer to 0.5, from their values at 0.9 and 0.1, respectively. Also the fact that seems to be preserved with P. The shape of the P _ij distribution seems to preserve affinity differences.

Figure 8. Histograms of the P _ij under like-with-like affinity assumptions values top to bottom with the very tight, tight, and very loose parameter choices. We can observe a definite difference in shape between the uniform and beta shapes, but the first and second moments are roughly equivalent.

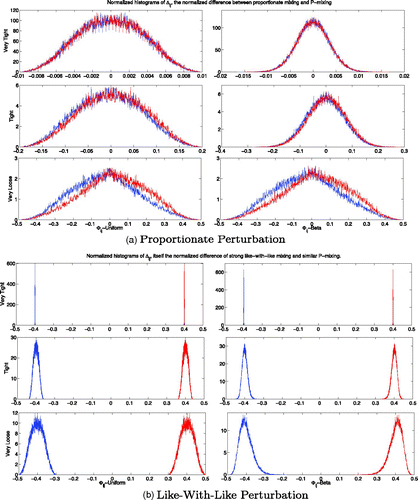
Given an affinity matrix Φ and thus a resulting mixing matrix P, we define the random matrix

that is, in some sense Δ _ij is a measure of how a particular group's affinity is affecting the deviation from proportionate mixing. If Φ _ij were much different than what would give proportionate mixing in the resulting P then the difference of would be large to reflect this. With this interpretation, if Δ _ij >0 would means that there is a positive affinity, or adherence, beyond proportionate mixing between group i and group j. Similarly Δ _ij <0 would mean that there is a ‘negligence’ (disaffinity) of interactions with group j by group i. Here, for the very loose parameters, we see that the average while . Thus, when stochasticity is added to proportionate mixing in the way described above, there is a resulting stronger desire to mix with unlike individuals rather than with like, or in other words, there is a strong correlation between preferences and outcomes. This qualitative behaviour was maintained regardless of whether we use a uniform or beta distribution on the affinities and the level of tightness. The distribution of Δ _ij , assuming P¯ _i =1/L, will simply be shifted and scaled as in Figure 9.

Figure 9. Pictured here are the distributions of Δ _ij . It is easily seen in (a) that the P formed via Φ being a deviation from a constant matrix have a nearness to proportionate mixing and that the variance on Φ weakens this nearness. The like-with-like mixing matrices, as seen in (b), have more or less a constant ‘distance’ from proportionate mixing.

4. Application in epidemiology

The structure (including its contact structure) of a population plays a central role in the transmission dynamics of diseases, cultural traits, genetic traits, etc. 1 2 3 8 9 10 37 38 58. Extensive applications of the role of mixing in the context of HIV/AIDS have been carried out in the past. Some significant efforts include those found in 10 24 25 30 31 33 34 40 41 42 43 44 45 47 48 52 53 54 69 70 71 73.

Here, we focus on the role of mixing in the simplest possible two-group SIS population. That is, affinity-based mixing is incorporated in a setting that can be easily used to carry out test-bed experiments that explore the role of preference and mixing on higher level processes, here an epidemic. We carry out numerical solutions of this model, a system of ODEs (Ordinary Differential Equation), over a large number of Φ realizations, and thus P realizations, in order to assess informally the impact of Φ-variability on the dynamics of S _i (t) and I _i (t) via the mixing matrix P.

4.1. System equations

Consider a two-group SIS system, with just enough recruitment in the susceptible class so as to maintain constant population size. In the absence of disease-induced mortality, we arrive at the following two-group, single-sex SIS epidemic model:

Here the parameter λ _i models differential susceptibility; μ _i , i=1, 2 denote the per capita death and recruitment rates; and denote the per capita recovery rates. The matrix P with entries P _ij is the general solution of the mixing conditions and is a symmetric matrix with .

If we let C _i =C and N _i =N for i=1, 2 we arrive the simplified model that will be used in our simulations, namely

where

Note that if each then

4.2. Epidemic calculations

It is assumed that disease contraction is difficult for subpopulation 1, recovery is a short process, and that the entry and removal into this subpopulation is moderate. Thus we assign , and . We pair this subpopulation with a second subpopulation for which disease contraction is easier, recovery takes longer, and the entry and removal of new individuals are faster. Thus, we let , and . 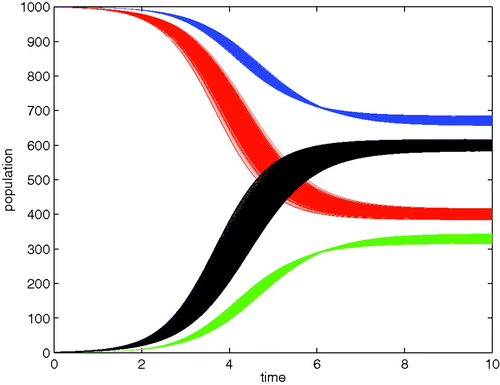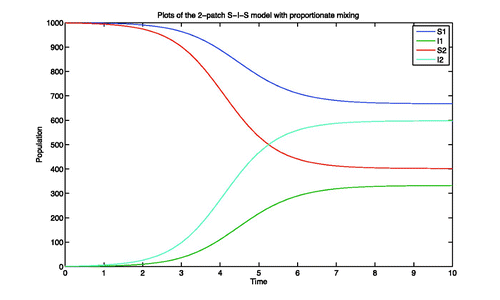Finally, we set which defines our baseline formulation which results in the proportionate mixing curves displayed in Figure 10.

Figure 10. Plot of S ₁, I ₁, S ₂, and I ₂ with each patch having a total population of 1000 and each infectious class initialized with a single individual.

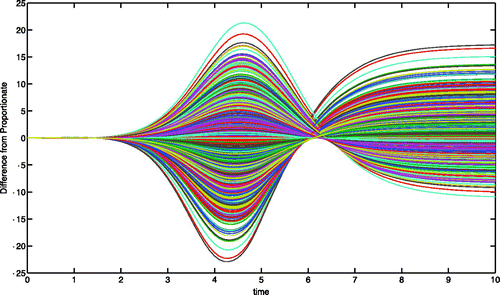
The perturbations of proportionate mixing via δ are explored. Hence, we let each φ _ij be an i.i.d. uniform random variable on for i≤j and for i>j let . Each solution is an instantiation of what effect the difference from proportionate mixing could have. Figure 11 collects the results of 1000 such repetitions of this idea under the tight parameter regime of (0.3,0.7). From this figure, we can see non-constant, and non-monotonic, variance along the time series for each system state variable.

Figure 11. 1000 instantiations with α=0.5 and δ=0.2. It is clear from the trajectories that the variance is non-constant. In fact, it seems to be a function of both time and the derivative of the state variable.

4.3. Some results

We now explored how the variation in Φ impacts the model outcome and hence, arbitrarily, we subtract the trajectory of the S ₁ state variable under proportionate mixing from each trajectory of S ₁ under the effects of an instantiation of P, and thus Φ. All such trajectories in Figure 12 have the property that if by mid-epidemic they have values above those of proportionate mixing, then they will have lower endemic levels and vice versa. Of interest would be to classify this behaviour via Φ or P.

Figure 12. 1000 instantiations with α=0.5 and δ=0.2 represented via the difference from the mean of S ₁.

We proceed to collect all of the Φ’s that correspond to an endemic equilibrium below the mean (the ones that are above average at first) and call that Φ ^b and similarly define Φ ^a to be the collection of the matrices Φ such that endemic levels are above average. Now consider the determinant of a matrix . From our simulations, this determinant is always less than zero (i.e. ). This may imply that the mixing between unlike groups is greater than same-group mixing. For a great deal of the results, we have that for (i.e. . That is, same-group mixing seems more likely than unlike-group mixing. It turns out that if the endemic susceptible population under some non-proportionate mixing, call it , is less than the one corresponding to proportionate mixing, S _∞, there are a few cases, about 8% out of 10,000 in our preliminary simulations, where the determinant of the affinity matrix is negative but as shown in Figure 13.

Figure 13. This plot collects the eigenvalues of 10,000 Φ-affinity matrices coloured blue if the limiting size of S ₁ under affinity-based mixing, [Stilde]₁, was greater than that of S ₁ under proportionate mixing and green otherwise. The red highlight those Φ matrices that have [Stilde]₁>S ₁ but det (Φ)<0. These matrices had a negative minimal eigenvalue, a characteristic dominated by those Φ such that [Stilde]₁<S ₁.

If we instead consider the mixing matrices that result from each of these groups of affinity matrices, that is, P ^a and P ^b , it turns out that and for every realization. This was verified over 200,000 realizations of the process without a single exception. This would seem to imply that systems under like-with-like dynamics, i.e. P _ii ≫P _ij , are probably more likely to experience a lower infected population and hence, proportionate mixing (the narrow version used here may indeed correspond to the worst case scenario 26 19). Thus we put forward the following hypothesis in the form of a proposition.

Proposition 4.1

Given a system of equations as defined in Equation (24) with the mixing matrix P=(P _ij ), let [Stilde] _i be the limiting susceptible population in group i under this mixing and S _i be that under proportionate mixing. We have that

In other words, if the limiting susceptible population under the mixing described via P is greater than that of proportionate mixing, then P has positive determinant, and if the limiting susceptible population under the mixing described via P is less than that of proportionate mixing, then P has negative determinant.

5. Discussion

This work revisits classical and relatively recent work on the problem of who mixes with whom, a problem of importance to those involved in the modelling and the study of the dynamics of interacting populations. We have conducted further numerical explorations on the role of affinity (what individuals want) in order to gain additional understanding of its role on mixing patterns (what individuals get). It is our hope that further theoretical and empirical research will be carried out on the questions raised in this manuscript (see 26, for recent contributions).

The focus here has been primarily on exploring the role of affinity or preference (what we want, Φ-matrix) via simulations on resulting mixing patterns (P-matrix). We have also proceeded to investigate numerically and in a rather simple setting, the role of affinity/mixing processes on disease dynamics. Several issues are highlighted including a hypothesis (presented in the form of a proposition) on the role of affinity at the epidemic level that we are exploring numerically in the context of an arbitrary number of interacting subpopulations. We are also interested in finding out what the eigenvalues of P tell us about processes utilizing P 26. The study of the role of selection on mixing patterns and consequently, on the evolution of affinities is also a question of interest that we may be able to pursue in this setting. However, in order to carry this out, the mixing must connect interacting subpopulations with differential vital rates due, for example, to disease-induced deaths.

We have also revisited some of our earlier work on two-sex mixing. In this manuscript, we have included mixing data that includes alcohol as a co-factor and have shown its effect on affinity-based mixing. It is known that alcohol is a key driver of the dynamics of sexually transmitted diseases, but not much modelling work has been done in this direction 63. Expanding the work outlined here in the context of a two-sex model involving two subpopulations, as in the one-sex SIS model, presents quite interesting challenges that we hope to pursue.

Acknowledgements

This project have been partially supported by grants from the National Science Foundation (NSF – Grant DMS – 0502349), the National Security Agency (NSA – Grant H98230 – 06-1-0097), the Alfred T. Sloan Foundation, and the Office of the Provost of Arizona State University. A special thank you to the editors and reviewers who have helped us craft a much better paper.