Backward bifurcations in simple vaccination/treatment models

Abstract

We describe and analyse by elementary means some simple models for disease transmission with vaccination and treatment. In particular, we give conditions for the existence of multiple endemic equilibria and backward bifurcations. The results are applicable to epidemic models in which demographic effects are ignored, but there is temporary immunity following recovery from infection.

Keywords:

• backward bifurcation
• vaccination
• treatment
• temporary immunity

1. Introduction

The central concept in the analysis of compartmental models for the transmission of communicable diseases is the basic reproductive number ℛ₀, representing the mean number of secondary infections caused by a single infective introduced into a susceptible population. As ℛ₀ increases through 1, there is an exchange of stability between the disease-free equilibrium, which is asymptotically stable for and unstable for , and the endemic equilibrium which exists if . 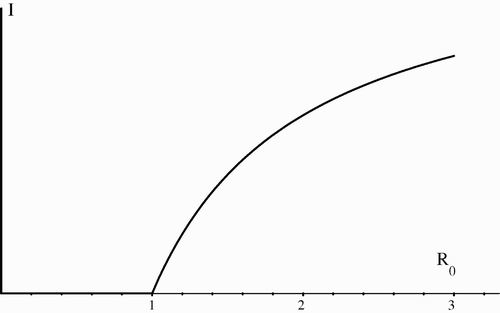The usual transition is a forward, or transcritical, bifurcation at , with an asymptotically stable endemic equilibrium and an equilibrium infective population size depending continuously on

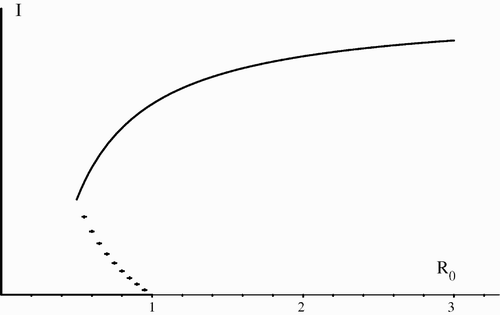
The behaviour at a bifurcation may be described graphically by the bifurcation curve, which is the graph of the equilibrium infective population size I as a function of the basic reproductive number ℛ₀. It has been noted 2 3 4 6 that in epidemic models with multiple groups and asymmetry between groups or multiple interaction mechanisms, it is possible to have a very different bifurcation behaviour at . There may be multiple positive endemic equilibria for values of and a backward bifurcation at . The qualitative behaviour of a system with a backward bifurcation differs from that of a system with a forward bifurcation and the nature of these changes has been described in 1. Since these behaviour differences are important in planning how to control a disease, it is important to determine whether a system can have a backward bifurcation.

In 1, we have analysed a simple SIS disease transmission model which includes vaccination of susceptibles and have obtained by elementary methods conditions for the existence of a backward bifurcation. We were able to give a complete qualitative analysis of the resulting two-dimensional model which had previously been examined in 6 using the centre manifold theorem and examination of normal forms 5. Here, we consider models that include temporary immunity after recovery and treatment of infectives. The same approach yields conditions for the existence of a backward bifurcation, but the qualitative analysis of these higher-dimensional models remains incomplete. Our treatment is very elementary, depending largely on the analysis of the number of positive solutions of a quadratic equation. We are able to analyse the bifurcation behaviour by elementary methods, without making use of the bifurcation theory.

2. A vaccination model

We begin by adding vaccination to a simple SIRS model with a constant birth rate Λ in the susceptible class, a proportional natural death rate μ in each class and no disease deaths,

To model (1), we add the assumption that in the unit time a fraction ϕ of the susceptible class is vaccinated. The vaccination may reduce but not completely eliminate susceptibility to infection. We model this by including a factor σ, , in the infection rate of vaccinated members with σ=0 meaning that the vaccine is perfectly effective and σ=1 meaning that the vaccine has no effect. We assume also that the vaccination loses effect at a proportional rate θ. We describe the new model by including a vaccinated class V,

with N=S+V+I+R. The SVIR model is the special case ψ=0 and the SVIS model is the special case . We remark that if the vaccine is completely ineffective, σ=1, then Equation (2) is equivalent to the SIRS model (1).

In model (2), it is easy to see by adding the equations in Equation (2) that as t→∞. If R=N−S−V−I is substituted into the first equation in Equation (2), then the first three equations uncouple from the fourth and are asymptotically autonomous with the limiting system

Equilibria of model (3) are solutions of

If I=0 then the first equation of Equation (4) is satisfied, and solution of the remaining equilibrium conditions leads to

This is the disease-free equilibrium.

Since we have a population which is not completely susceptible, we speak of a control reproduction number rather than a basic reproduction number. We will use to denote the control reproductive number of model (3), and the control reproduction number is

If σ=1, meaning that the vaccine has no effect, model (3) is equivalent to the SIRS model (1) and if there is a unique endemic equilibrium which is globally asymptotically stable. If endemic equilibria are solutions of the system of Equations (4).

We use the first two equations of Equation (4) to express S and V in terms of I,

Then substitution into the third equation of Equation (4) gives a quadratic equation

for I, with

The coefficients A, B, C are functions of β, and we will indicate this dependence explicitly when necessary. When , and there is exactly one positive root of Equation (6), corresponding to an endemic equilibrium.

The condition C=0, or , corresponds to a critical value β _c of β, given by

Then, there are two equilibria given by the roots I=0, I=−B/A of the quadratic equation (6). The first is the disease-free equilibrium and the second is an endemic equilibrium if .

All endemic equilibria lie on the bifurcation curve (6). In drawing the bifurcation curve (the graph of I as a function of ), we think of β as a variable with the other parameters being constant. Since is a constant multiple of β, we may think of β as the independent variable in the bifurcation curve.

Implicit differentiation of the equilibrium condition (6) with respect to β gives

We see from Equation (7) that . At the equilibrium I=0 with ,

Thus, the slope of the bifurcation curve at this equilibrium has the same sign as B(β _c ). This shows that if , there is a backward bifurcation as well as a positive endemic equilibrium at . If B(β _c )>0, there is a forward equilibrium at . In either case, there is a single endemic equilibrium for .

These two possibilities are illustrated by Figures 1 and 2.

Figure 1. Backward bifurcation.

Figure 2. Forward bifurcation.

If C>0 and either B≥0 or B ²<4AC, there are no positive solutions of Equation (6) and thus there are no endemic equilibria. Equation (6) has two positive solutions, corresponding to two endemic equilibria, if and only if C>0, or , and B<0, B ²>4AC, or . If B=−2√AC there is one positive solution I=−B/2A of Equation (6).

If , so that there is a backward bifurcation at , there are two endemic equilibria for an interval of values of β from β _c corresponding to to a value β₀ defined by B=−2√AC. Since both B and AC are linear functions of β, the equation B ²=4AC is quadratic and has two roots. One of these roots, namely the root corresponding to B=−2√AC, satisfies B<0 and determines the value of β₀. While it is possible to give an analytic expression for β₀, in practice it would be more efficient to compute its value numerically.

The condition , necessary and sufficient for the existence of a positive endemic equilibrium and a backward bifurcation at , is

Algebraic simplification reduces this condition to

If ψ=0, the case of an SIR model, the condition (9) reduces to

Since the expansion of the left side of this inequality contains a term this condition cannot be satisfied. Thus there cannot be a backward bifurcation for the SVIR model.

The SVIS model is the special case . To analyse this case, we divide both sides of the inequality (9) by μ+ψ and let , so that

Then, the condition (9) takes the form

equivalent to the condition obtained in 1.

The necessary and sufficient condition (9) for a backward bifurcation can be written as a cubic inequality,

with

For a backward bifurcation, it is necessary that R<0. Normally, the disease time scale is much faster than the demographic time scale, and we have μ small compared with the other rates. There is a backward bifurcation for sufficiently small μ if and only if R<0.

Similarly, examination of the condition (10) shows that a necessary condition for the SVIS model to have a backward bifurcation is

and this condition is sufficient for a backward bifurcation for sufficiently small μ. In particular, the case μ=0 corresponds to an epidemic model with temporary immunity after recovery from infection.

3. A vaccination/treatment model

To the vaccination model (2), we add treatment of infectives at rate γ. It is assumed that treatment eliminates infectivity and changes the recovery rate to η. This leads to the model

with N=S+V+I+T+R.

In model (12), just as for model (2), it is easy to see that as t→∞. If R=N−S−V−I−T is substituted into the first equation in Equation (2), then the first four equations uncouple from the fifth and are asymptotically autonomous with the limiting system

for which

The disease-free equilibrium of Equation (13) is the same as the disease-free equilibrium of Equation (2). Endemic equilibria of model (13) are solutions of

We use the first three equations of Equation (14) to express S, V, T in terms of I, obtaining

Then substitution into the last equation of Equation (14) gives the quadratic equation (6) with

We note that, just as for the vaccination model (3), C>0 if and C<0 if , and there are two equilibria at if and only if .

The condition C=0 corresponds to

and this defines the critical value β _c . The treatment now follows that of the vaccination model (3) exactly. The condition , necessary and sufficient for a backward bifurcation, is

Algebraic simplification reduces this condition to

Much as for the model (3) without treatment, the necessary and sufficient condition (17) for a backward bifurcation can be written as a polynomial inequality of the form g(μ)<0, where g is now a fourth-degree polynomial whose coefficients except for the constant term are positive. For a backward bifurcation, it is necessary that the constant term be negative and there is a backward bifurcation for sufficiently small μ if and only if the constant term is negative. Thus, for the model (13), a necessary condition for a backward bifurcation is

and for sufficiently small μ this condition is also sufficient.

We may summarize our main result as follows.

Theorem 3.1

For both the vaccination model (3) and the vaccination/treatment model (3), there is a necessary and sufficient condition for the existence of an endemic equilibrium and a backward bifurcation at . Also, there is a necessary condition not involving the natural death rate μ that is also sufficient if μ is small.

Strains of communicable diseases such as influenza often mutate rapidly enough that immunity following vaccination or recovery from infection by a specific strain is only temporary. A short-term epidemic of such a disease may be modelled by Equation (3) or (13) with μ=0, and our results indicate the possibility of a backward bifurcation in such models. The condition (18) is satisfied, for example, if θ=0 (no loss of vaccine efficacy), if η=α (treatment does not change the infective period) and

If the loss of immunity is slow, the parameter ψ is small, and thus there could be a backward bifurcation only for small vaccination rates ϕ unless σ is very close to zero, but there cannot be a backward bifurcation if σ=0. Whether the possibility of a backward bifurcation is of importance in a specific situation would depend critically on the value of ψ.

4. The bifurcation curve

In Section 2, we have examined the slope of the bifurcation curve (6) at the equilibrium I=0 when . In general, the slope of the bifurcation curve is given implicitly by

We see from Equation (15) that , and thus has the same sign as 2AI+B if

In order to show this, we write

with Q positive and independent of β. Then

and

For equilibria with , and it follows that for has the same sign as 2AI+B. This implies that the bifurcation curve has positive slope at equilibrium values with 2AI+B>0 and negative slope at equilibrium values with 2AI+B<0. If there is not a backward bifurcation at , then the unique endemic equilibrium for satisfies

and the bifurcation curve has positive slope at all points where I>0. If there is a backward bifurcation at then there is an interval on which there are two endemic equilibria given by

The bifurcation curve has a negative slope at the smaller of these and a positive slope at the larger of these.

We conjecture that has the same sign as 2AI+B for all β, not just for values corresponding to , but we have not been able to establish this except in the special case studied in 1. In this special case, the condition 2AI+B>0 is also significant in the local stability analysis of endemic equilibria. Because the model in this case is two-dimensional, it is not difficult to show that an endemic equilibrium is (locally) asymptotically stable if and only if it corresponds to a point on the bifurcation curve at which the curve is increasing. It is also possible to show that there are no periodic orbits and thus to obtain a complete picture of the global behaviour. We conjecture that these facts extend to the model (13).

5. Conclusions

We have examined simple vaccination models and have shown by elementary algebraic means how to analyse the existence of multiple endemic equilibria when the basic reproduction number is less than 1. In the simplest case, with permanent immunity following recovery and no treatment an equilibrium corresponding to a point on the bifurcation curve with negative slope is unstable, and an equilibrium corresponding to a point on the bifurcation curve with the positive slope is asymptotically stable; we conjecture that this is true also for more complicated vaccination models. Our model appears not to admit the possibility of oscillations about an unstable endemic equilibrium.

The models we have examined could also be treated by using the centre manifold theory and normal forms. However, the required preliminary transformations would be at least as complicated technically as our approach. For models with more compartments, the analysis by elementary means becomes hopelessly complicated and a centre manifold approach would be necessary. It would be of considerable interest to determine if the properties we have found in simple examples carry over to more complicated models such as models involving the age of infection.

Although the introduction of a vaccination policy may lead to backward bifurcations, we emphasize that it always decreases infective population size. The danger of a vaccination policy is that an unforeseen backward bifurcation may require a larger than expected vaccination fraction to control a disease. If a vaccine can be developed which is completely effective, this possibility does not arise, and a programme which decreases the contact rate can also control a disease without leading to backward bifurcations. Nevertheless, a vaccination programme, even one which is not fully effective, may be a useful approach in controlling infections.

Acknowledgements

The exposition of backward bifurcations and multiple endemic equilibria has been improved substantially by the suggestion of an anonymous reviewer. This research was supported by NSERC Research Grant OGPIN #203901-99.