Modelling of transgenic mosquitoes and impact on malaria transmission

Abstract

Transgenic mosquitoes that are resistant to malaria infection become one of the effective weapons to control malaria transmission. To investigate the impact of releasing transgenic mosquitoes on the malaria transmission, we first formulate mathematical models for interactive wild and transgenic mosquitoes based on systems of differential equations. We consider both dominant and recessive transgenes and include density-dependent vital rates in the mosquitoes population and provide fundamental analysis for the dynamics of the interactive mosquitoes. Using a simple compartmental SEIR (susceptible-exposed-infective-recovered) malaria transmission model as our baseline model, we then introduce transgenic mosquitoes into the baseline model. We study the dynamics of the simple baseline model and the models with the transgenic mosquitoes. Based on the reproductive numbers and endemic equilibria for these models, we investigate the impact of releasing transgenic mosquitoes on malaria transmission.

Keywords:

• population models
• transgenic mosquitoes
• stability
• malaria transmission
• impact of transgenic mosquitoes releasing

AMS Subject Classification :

• 34C60
• 34D99
• 92D25
• 92D30
• 92D40

1. Introduction

Mosquito-borne diseases, including malaria, transmitted between humans by mosquitoes, are big concerns in public health. Malaria is the fifth cause of death from infectious diseases worldwide (after respiratory infections, HIV/AIDS, diarrheal diseases, and tuberculosis), and the second leading cause of death from infectious diseases in Africa, after HIV/AIDS. It is a public health problem today in more than 109 countries and territories inhabited by some 3.3 billion people. Approximately half of the world's population is at risk of malaria, particularly those living in lower-income countries. There were 247 million cases of malaria in 2006, causing nearly 1 million deaths, mostly among African children, and 190–311 million clinical episodes, and 708,000–1,003,000 deaths in 2008. Malaria has been eliminated in the USA since the early 1950s. However, 63 outbreaks of locally transmitted mosquito-borne malaria have occurred between 1957 and 2009, and 1500 cases of malaria, on average, are reported every year in the USA 7 28.

The transmission of malaria is not directly from a human to a human, but through mosquitoes. It is due to infection by one of four Plasmodium species. The life cycle of the malaria parasites is complicated. The infection in human begins when sporozoites are injected into the blood of a human host by a female mosquito of the genus Anopheles. The sporozoites migrate to the liver where they enter liver cells and develop schizonts, which give rise, via asexual reproduction, to the form of the merozoites that invade the blood cells. In the blood, some merozoites differentiate into sexual erythrocytic stages (gametocytes), and the gametocytes are ingested by a mosquito when it ingests human blood. Within the mosquito, the gametocytes develop into microgametes and macrogametes (the male and female gametes) that fuse to form a zygote. This becomes a motile ookinete form which bores through the gut wall of the vector and forms an oocyst, from which large numbers of sporozoites are released. These sporozoites then invade the salivary glands of the mosquito, from which they are injected into human host when the vector feeds. Such does the life cycle of the Plasmodium species cause the transmission of malaria between humans and mosquitoes 1 3 27.

No vaccines are available for malaria and other mosquito-borne diseases. An effective way to prevent them is to control mosquitoes, which has been one of the major intensive efforts in many years. Massive spraying of insecticides or eliminating breeding sites has greatly limited malaria in some areas, but the number of malaria cases still continues to climb.

The development of genetically altered or transgenic mosquitoes, which are resistant to the malaria infection, may provide a new and effective weapon against malaria 26 29. The new techniques use a peptide, termed SM1, that binds to the mosquitoes’ gut and salivary glands, to inject into or feed mosquitoes 4 6 9. The peptide blocks the receptor and stops the parasite from getting a hold on the epithelium of mosquitoes so that it inhibits parasite invasion. A transgenic mosquito that produces this peptide in the gut or salivary glands then becomes inhospitable to the parasite 11 13 20.

While these developments are promising and exciting, many questions have to be answered before the techniques can be implemented and transgenic mosquitoes can be deployed in the field 10. Such questions include the determination of gene or genotype distributions of mosquitoes in the future generations after transgenic mosquitoes are released, in particular, as density-dependent fitnesses are taken into account 25.

To gain insight into such a complex process, we have formulated simple mathematical models for interactive wild and transgenic mosquitoes based on systems of difference or differential equations 15 17. We assumed, in those studies, that the transgenes are dominant such that mosquitoes with either one or two copies of the transgenes are malaria resistant. We divided mosquitoes into two groups: the malaria-resistant and non-resistant individuals. We included the heterozygous mosquitoes with only one copy of the transgenes and the homozygously mosquitoes with two copies of the transgenes in the malaria-resistant group. We then assumed that the offspring produced by matings between malaria-resistant mosquitoes are all malaria resistant in 15 17.

Mosquitoes are diploid. Each individual carries two copies of genes. Homozygously wild mosquitoes have two copies of the wild genes, denoted by WW, and homozygous transgenic mosquitoes have two copies of the transgenes, denoted by AA. After their matings, three different types of mosquitoes are produced. In addition to those with either WW or AA, there are heterozygous mosquitoes with a copy of the wild genes and a copy of the transgenes, denoted by WA. Moreover, the matings between heterozygous mosquitoes with gene WA can produce offspring with two copies of the wild genes or two copies of the transgenes. The heterozygous mosquitoes can be either malaria resistant or malaria non-resistant depending on whether the transgene is dominant or recessive, which significantly distinguish model structures. To investigate the impact of releasing transgenic mosquitoes, these possibilities need to be more specifically considered, and we formulated discrete-time models to include these considerations and explored the dynamics of the interactive mosquito populations in 19.

Our aim, in this paper, is more on the impact of transgenic mosquitoes on malaria transmission. We first formulate continuous-time models in Section 2 with similar considerations as in 19. We include the heterozygous mosquitoes into either the malaria-resistant or non-resistant group and consider the offspring produced by matings between the malaria-resistant mosquitoes to be either malaria resistant or non-resistant, depending on the dominance of the transgenes. We then focus our investigation on the case where the mating rates are constant in Section 3. With the fundamental mathematical analysis for the interactive mosquito models, where we determine the existence and stability of all possible equilibria and provide numerical examples to illustrate these dynamics, in order to study the impact of releasing transgenic mosquitoes on malaria transmission, we formulate a simple compartmental SEIR malaria transmission model as our baseline model in Section 4. We divide the human population into groups of susceptible, latent (incubating), infective, and recovered individuals, respectively, but the mosquito population only consists of susceptible, latent (incubating), and infective individuals. We then introduce the transgenic mosquitoes into the baseline malaria model where the susceptible mosquitoes consist of the malaria-resistant and non-resistant mosquitoes in Section 5. We derive formulas of the reproductive numbers for the models without and with transgenic mosquitoes and prove that there exists an endemic equilibrium for each model as the reproductive number exceeds one. We investigate the impact of transgenic mosquitoes on malaria transmission through the analysis of the reproductive numbers and endemic equilibria. We finally give brief discussions in Section 6.

2. General model formulation

We let w(t), h(t), and g(t) be the numbers of homozygously wild, heterozygous, and homozygously transgenic mosquitoes at time t, respectively. The dynamics of the interactive mosquitoes are described by the following system:

where is the number of offspring in group j produced by a mosquito in group i, per unit of time, D _i is the per capita death rate of mosquitoes in group i, i, j=w, h, g, and P=w+h+g 16.

Following the line of the mosquito population models in 15 17 19, we assume harmonic means for matings in the birth functions 5 14, and let C(P) be the numbers of matings per mosquito, per unit of time. Then, the number of matings that are with homozygously wild, heterozygous, or homozygously transgenic mosquitoes is C(P) w/P, C(P) h/P, or C(P) g/P, respectively.

Let c _1j , j=1, 2, 3, be the numbers of homozygously wild offspring produced per mating, c _2j , j=1, …, 7, the numbers of heterozygous offspring produced per mating, and c _3j , j=1, …, 4, the numbers of homozygously transgenic offspring produced per mating, respectively. Then the general formulas of the birth functions are

We further assume that the death functions are simple linear functions such that $d_i(x,y) = \mu_i + \xi_i P$, where the constants μ _i >0, ξ _i ≥0, i=1, 2, are density-independent and density-dependent death rates, respectively. Similarly, as in 15 17 19, due to the fact that the SM1 transgene does not impose a fitness load to the mosquitoes 13 21, we assume that all mosquitoes have the same death rate and hence the same survival probability such that and . Based on these assumptions, the equations for the model system (1) become

We focus on the impact of the transgenes on malaria transmission. If the transgenes are dominant – that is, the mosquitoes with either one or two copies of the transgenes are malaria resistant, we denote the population size of the malaria non-resistant – that is, the wild mosquitoes – by x. We then combine the heterozygous and the homozygously transgenic mosquitoes as one group and denote the population size of this group of malaria-resistant mosquitoes by y, as shown in Figure 1.

Figure 1. In the case of dominant transgenes, we include all mosquitoes with two copies of the wild genes into group x and include all mosquitoes with one or two copies of the transgenes into group y.

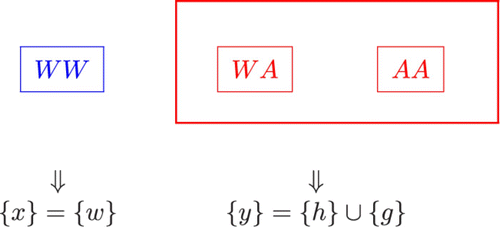
The dynamics of the model system for the dominant transgenes are then governed by

where N=x+y, for x≥0, y≥0, and (x, y)≠(0, 0), where a _i and b _j have similar meanings as c _ij in Equation (3).

If the transgenes are recessive – that is, the mosquitoes with only one copy of the transgenes are malaria non-resistant, we include the heterozygous mosquitoes into the homozygously wild mosquitoes as one group and denote its population size by x. We then denote the population size of the homozygously transgenic mosquitoes with two copies of the transgenes by y, as shown in Figure 2.

Figure 2. In the case of recessive transgenes, we include all wild mosquitoes and mosquitoes with only one copy of the transgenes into group x and include all mosquitoes with two copies of the transgenes into group y.

The dynamics of the interactive mosquitoes for the recessive transgenes are described by the system

for x(0)≥0, y(0)≥0, and , for all t≥0.

3. Constant mating rate

The mating rate C(N _n ), in general, is density dependent. However, contacts for anophelines are usually associated with swarming in relative open areas in Africa 8, and with a sufficiently large population size, mosquitoes can easily find their mates. Then we assume the matings are saturated so that the mating rate is constant, denoted by C(N):=c. By merging c into the other coefficients and using the same a _i and b _j for the parameters, the model equations with the dominant transgenes become

for x≥0, y≥0, and (x, y)≠(0, 0), for all t≥0, and those for the recessive transgenes become

for x≥0, y≥0, and (x, y)≠(0, 0), for all t≥0.

We assume, for system (D),

and, for system (R),

such that the origin is a repeller to all solutions of either system (D) or system (R).

3.1 Boundary equilibria

For system (D), an equilibrium satisfies the equations

It follows from Equation (F1) that if x=0, then y=0. Hence, there exists no boundary equilibrium with x=0 and y>0.

Setting y=0 in Equation (F1), and then solving the resulting equation for a positive solution x, we obtain a unique boundary equilibrium of system (D),

Similarly, we obtain a unique boundary equilibrium of system (R),

The boundary equilibrium E ₁, or E ₂, exists if and only if a ₁>μ, or β₃>μ.

Simple linearizing analysis shows that E ₁ is locally stable if a ₁>b ₁, and unstable if a ₁<b ₁, and that E ₂ is locally stable if , and unstable if .

Note that, in the case of dominant transgenes, a ₁ is the birth rate of the wild offspring with no transgenes, per wild mosquito, through all homogeneous matings, that is, the matings within wild mosquitoes, and b ₁ is the birth rate of the transgenic offspring with one or two copies of the transgenes through all heterogeneous matings. Then the transgenic mosquitoes with one or two copies of the transgenes can survive if a ₁<b ₁ which implies that the birth rate of the offspring with one or two copies of the transgenes through heterogeneous matings exceeds the birth rate of the wild offspring with no transgenes, per wild mosquito.

We also note that the mosquitoes with the transgenes can be possibly wiped out because the homozygously transgenic and heterozygous mosquitoes are bunched up as a group in the case of the dominant transgenes and can become extinct all together, whereas the wild mosquitoes with no transgenes cannot be wiped out because the existence of the heterozygous mosquitoes which produce wild offspring.

The biological interpretation for the recessive transgenes can be similarly obtained.

3.2 Positive equilibria

Systems (D) and (R) may have positive equilibria whose two components are both positive. We give details only for establishing the existence conditions for the positive equilibria of system (D) as follows.

From equations (F1) and (F2), it follows that

or

Solving for y in Equation (10) in terms of x yields

where

Define . The existence of positive A ₁, by simple algebra, can be summarized in Table 1.

Table 1. Summary table of the results for positive A ₁ in Equation (11).

a 1<b 1	a 1≥b 1
	a 2≥b 2	a 2<b 2
		C 1<a 1−b 1	C 1=a 1−b 1
∃! A 1	≠xists A 1	≠xists A 1	∃! A 1	∃

Suppose a positive A ₁ exists. Substituting it into Equation (F2) and solving for x, we obtain a positive solution

if and only if

since we have assumed b ₂>μ. We summarize the existence of positive equilibria as follows.

Theorem 3.1

System (D) has no positive equilibrium if

or

It has a unique positive fixed point if a ₁<b ₁, or a ₂<b ₂ and

in addition to Equation (13). System (D) has two positive equilibria, x ^{±}, if, in addition to Equation (13), a ₁>b ₁, a ₂<b ₂ and

where x ^{±} correspond to respectively.

Similarly, we define , and

The existence of positive A ₂ is summarized in Table 2.

Table 2. Summary table of the results for positive A ₂ in Equation (16)

∃! A 2			∃! A 2	∃

If a positive A ₂ exists, solving for y, we obtain a positive solution

if and only if

since we have assumed . In summary, we have the following results.

Theorem 3.2

System (R) has no positive fixed point if

or

It has a unique positive fixed point if or and

in addition to Equation (18). System (R) has two positive equilibria, y ^{±}, if, in addition to Equation (18), and

where y ^{±} correspond to respectively.

We next investigate stability of the positive equilibria of system (D) by linearization.

Let the Jacobian matrix at a positive equilibrium be J ₁ for system (D). Then

where x and y are evaluated at the positive equilibrium. By simple linear algebra, the determinant of J ₁ equals

and the trace of J ₁ equals

Suppose system (D) has two positive equilibria with , where . Then it follows from

that

For , we have

Then the determinant of J ₁ is negative, which implies that the positive equilibrium with is a saddle point. For , we have

and it follows from Equation (22) that the trace of J ₁ is negative. Hence, the positive equilibrium with is locally asymptotically stable. It can also be easily shown that this equilibrium is a stable node.

If a ₁<b ₁ and condition (13) is satisfied such that there exists a unique positive equilibrium, we can show that this equilibrium is a stable node from Equations (21) and (22). The proof is similar to that above and is skipped.

For the case of C ₁=a ₁−b ₁, which is biologically rare and less interesting, we can show, as in 17, that the unique positive equilibrium is a saddle node.

In a similar manner, we can obtain conditions for the stability of the endemic equilibrium for system (R). In summary, we have the following results.

Theorem 3.3

If a ₁<b ₁ and condition (13) is satisfied for system (D), or if and condition (18) is satisfied for system (R), such that there exists a unique positive equilibrium, the unique positive equilibrium is a locally stable node.

If system (D) or (R) has two endemic equilibria, or respectively, where x ^{±} and y ^{±} are given in Equations (12) and (17) corresponding to and respectively, then and are both saddle points, and and are both stable nodes.

In the case of C ₁=a ₁−b ₁ for system (D) or for system (R), there exists a unique positive equilibrium, respectively, and this equilibrium is a saddle node.

We provide simple numerical examples to demonstrate our results of Theorem 3.3 as follows.

Example 3.1 We use the following set of parameters

It follows from a ₁>b ₁ and a ₁>μ that there exists a boundary equilibrium (2.6, 0) which is a stable node. Since b ₂<a ₂, there exists no positive A ₁ and hence no positive equilibrium. The phase portrait is shown on the left part in Figure 3.

Figure 3. For the left figure, the parameters are given in Example 3.1, where there exist a stable boundary equilibrium and no positive equilibrium. Solutions approach the boundary equilibrium. For the middle figure, the parameters are given in Example 3.2, where the boundary equilibrium is a saddle point and there exists a unique positive equilibrium which is a sable node. Solutions approach the unique positive equilibrium. For the right figure, the parameters are given in Example 3.3, where there exist a stable boundary equilibrium and two positive equilibria, one of which is a saddle point and one of which is a stable node. Solutions approach either the boundary equilibrium or the stable positive equilibrium depending on their initial conditions.

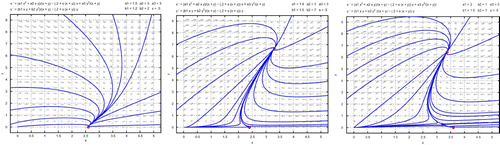
Example 3.2 In this example, we set parameters as

Then it follows from a ₁<b ₁ that the boundary equilibrium (2.4, 0) is a saddle point. There exists a unique positive equilibrium (3.2996, 6.6538) which is a sable node. The phase portrait is shown in the middle in Figure 3.

Example 3.3 We use, in this example, the same parameters as in Example 3.2 except a ₁=2. It follows from a ₁>b ₁ and a ₁>μ that there exists a boundary equilibrium (3.6, 0) which is a stable node. It follows from that there also exist two positive and hence two positive equilibria . Positive equilibrium associated with is a saddle point and positive equilibrium associated with is a stable node. The separatrix consisting of the stable manifolds of divides the first quadrant into two regions such that solutions approach either boundary equilibrium E ₁ or positive equilibrium depending on their initial conditions. The phase portrait is shown on the right part in Figure 3.

4. Baseline model for malaria transmission

Before incorporating the interactive wild and transgenic mosquitoes to study their impact on malaria transmission, we formulate a simple SEIR malaria model as a baseline model in this section.

We divide the human population into groups of susceptible, latent or incubating, infective, and recovered individuals. Here the latent or incubating period is defined as the time from initial infection to the appearance of gametocytes in the blood 1. Using index h for the humans, we let S _h be the number of susceptible humans, E _h the number of latent or incubating humans, who are infected but not infectious yet, I _h the number of infective humans, who are infected and also infectious, and R _h the number of the humans who are recovered from infection but partly lose immunity 18 22 23 24. The model equations for humans are given by

where is the input flow of the susceptible humans, μ_h and δ_h are the natural and disease-induced death rates for humans, respectively, θ_h is the rate of immunity loss, γ_h is the developing rate of incubating humans to become infectious, such that is the incubation period, η_h is the recovery rate for infectious humans, and is the infection rate or the incidence of infection from an infective mosquito to a susceptible human. Notice that if there is no infection, the human population has an asymptotically stable steady state such that .

For the mosquito population, we divide it into groups of susceptible, latent, and infective individuals. Since the mosquito lifespan is usually shorter than their infective period, we assume that there is no group of recovered mosquitoes. We denote the numbers of susceptible, latent, and infective mosquitoes, by S _v, E _v, and I _v, respectively. We further assume, in the absence of infection, that the mosquito population follows the logistic dynamics. Then model equations for the mosquitoes are given by

where b _v and μ_v are the per capita birth and death rates of mosquitoes, respectively, which are assumed to satisfy , γ_v is the rate of incubating mosquitoes becoming infectious, and is the infection rate for mosquitoes.

Let be the total human population size, the total mosquito population size, r the number of bites on humans by a single mosquito per unit of time, and β_h the transmission probability per bite to a mosquito from an infective human. The infection rate for mosquitoes is given by

Similarly, the infection rate for humans is given by

where β_v is the transmission probability from an infective mosquito to a susceptible human per infected bite, and the number of bites that a human is received per unit of time is by the balance constrain.

4.1 The reproductive number

We derive a formula for the reproductive number by investigating the local stability of the infection-free equilibrium. The Jacobian matrix at the infection-free equilibrium , with and , has the form of

where

and we write , , , . Then the infection-free equilibrium is locally asymptotically stable if the eigenvalues of J ₂₂ all have negative real part.

Noticing that all off-diagonal elements of −J ₂₂ are non-positive, and the first three leading principal minors of −J ₂₂ are , , and , respectively, which are all positive. Then it follows from the M-matrix theory 2 12 that all eigenvalues of J ₂₂ have negative real part; that is, the infection-free equilibrium is locally asymptotically stable, if the determinant

is positive.

Define the reproductive number of infection for system Equations (24) and (25) as

Then if R ₀<1, the infection-free equilibrium is locally asymptotically stable. If R ₀>1, the determinant of J ₂₂ is negative, which implies that there exists at least one positive eigenvalue of J ₂₂, and hence the infection-free equilibrium is unstable.

4.2 Endemic equilibrium

We explore the existence of an endemic equilibrium as follows. Similarly as in 18, the components for the humans at an endemic equilibrium can be solved, in terms of , as

where . We further write , and have

Solving for the mosquito components at an endemic equilibrium yields

Then, at an endemic equilibrium, we have

where , .

Write for convenience. It follows from Equation (32) that

where . Define function

Then there exists an endemic equilibrium if and only if there exists a positive solution to equation . Since , and , if R ₀>1, there exists an endemic equilibrium.

5. The models with transgenic mosquitoes

We now introduce the transgenic mosquitoes into the baseline model. We assume that the mosquito population is sufficiently large such that the mating rate for mosquitoes is constant as studied in Section 3. Then the part of the model equations for humans is the same as in system (24), and the part of the model equations for mosquitoes, in the case where the transgenes are dominant, is given by the system

where we use S _a for the number of the malaria-resistant mosquitoes.

In the case where the transgenes are recessive, the part of the model equations for mosquitoes is given by the system

We only give detailed analysis for the case of dominant transgenes in the next sections. The analysis for the recessive transgenic mosquitoes is similar and will be only briefly stated.

5.1 The reproductive number

Now the Jacobian matrix of system (24) and (35) at the infection-free equilibrium has the form of

where

J ₃₃ is the Jacobian matrix of system (D) at either a boundary or a positive equilibrium, and S _v is evaluated at the equilibrium.

There are infection-free equilibria for system (24) and (35) associated with the equilibria of system (D), but we are only concerned with the stable boundary or positive equilibrium of system (D). Then the eigenvalues of matrix J ₃₃ both have negative real part, and hence the local stability of the infection-free equilibrium is determined by matrix J ₃₂.

We denote the reproductive number for system (24) and (35) with a boundary or a positive equilibrium of the interactive mosquito model (D) by or , respectively.

At the infection-free equilibrium with boundary equilibrium E ₁, where and S _a =0 and we assume a ₁>b ₁, the reproductive number is the same as R ₀ given in Equation (28) for system (24) and (25). The releasing of transgenic mosquitoes has no impact on malaria transmission. If a ₁<b ₁ and condition (13) is satisfied, there exists a unique stable positive equilibrium, where we write the component of the wild mosquitoes as , given in Equation (12) corresponding to the unique positive . If there exist two positive equilibria where is stable for system (D), the component of the wild mosquitoes at is also given by Equation (12), corresponding to the positive . Then, in either case, the reproductive number of infection for system (24) and (35) has the same formula as in Equation (28), but is replaced by

5.2 Endemic equilibrium

An endemic equilibrium is usually bifurcated from an infection-free equilibrium as the reproductive number exceeds one. We consider the existence of an endemic equilibrium in the following three cases.

Case 1

There exists no positive equilibrium for system (D) and hence the boundary equilibrium E ₁ is the only stable equilibrium. The reproductive number is the same as that for system (24) and (25). Then as is shown in Section 4.2, there exists an endemic equilibrium if .

Case 2

If there exists a unique A ₁ and hence a unique positive equilibrium for system (D), the boundary equilibrium E ₁ is unstable and the positive equilibrium E _D is stable. We show that if there exists an endemic equilibrium as follows.

We have the same expressions for the components of the humans as in Equations (29) and (30) in terms of . We then solve the components for the mosquitoes and have

where

and

Hence we have the same expression, at such an endemic equilibrium, for as in Equation (32), that is,

but

We again write . Substituting into Equation (40), we obtain

with given in Equation (38).

As in Section 4.2, we define

Notice that is positive for , as long as is positive, and that which implies that is bounded for λ≥0. Then lim_λ→∞ g(λ) = ∞. Hence it follows from which leads to that there exists an endemic equilibrium for system (24) and (35) if .

We provide a numerical example to illustrate the results for Case 2 in Example 5.1.

Example 5.1 With the parameters for the interactive mosquitoes given in Example 3.2, there exist a saddle boundary equilibrium and a unique stable nodal positive equilibrium for the mosquitoes. We use the following parameters for the malaria transmission:

The reproductive number of infection for system (24) and (35) at the infection-free equilibrium with is , which is greater than 1. Hence there exists a stable endemic equilibrium . The solutions of the system (24) and (35) approach this endemic equilibrium as t→∞.

Case 3

If there exist a boundary equilibrium E ₁, and two positive equilibria, for system (D), as is shown in Section 3.2, E ₁ and are both locally stable nodes. We define the reproductive numbers and for system (24) and (35) at the infection-free equilibria with E ₁ and , respectively. Then as shown in Cases 1 and 2, if an endemic equilibrium bifurcates from E ₁, and if an endemic equilibrium bifurcates from . The results for Case 3 are illustrated in Example 5.2.

Example 5.2 We use the same parameters for the interactive mosquitoes as in Example 3.3 and the following parameters for the malaria transmission:

The reproductive number associated with the infection-free equilibrium with the stable boundary equilibrium E ₁=(3.6, 0) for the mosquito model (D) is , and the reproductive number associated with the endemic equilibrium with the positive equilibrium is . Both reproductive numbers are greater than one. Solutions for the malaria model (24) and (35) approach either of the two stable endemic equilibria and , depending on their initial conditions, where E _b is bifurcated from the infection-free equilibrium with E ₁, and E _e is bifurcated from the one with .

5.3 Impact of the transgenic mosquitoes

The impact of transgenic mosquitoes on malaria transmission is different for the three cases shown in Section 5.2, and also depends on whether the transgenes are dominant or recessive.

If there exists no positive A ₁ for the dominant transgenes, nor A ₂ for the recessive transgenes, and hence no positive equilibrium, the boundary equilibrium E ₁ or E ₂ is the only stable equilibrium for the interactive mosquitoes. In the case of dominant transgenes, the transgenic mosquitoes can be eventually wiped out and the reproductive number is the same as that for the baseline malaria model without transgenes. Hence the releasing of transgenic mosquitoes has no impact at all. On the other hand, if the transgenes are recessive, all mosquitoes will eventually become malaria resistant and the reproductive number is reduced to zero. Hence the malaria transmission is ultimately stopped. This is an ideal situation, but may not be feasible in practice.

In the case where there exists a unique positive equilibrium for the interactive mosquitoes, it is the only stable equilibrium. Then the reproductive number is calculated at the infection-free equilibrium with the mosquito components at this positive equilibrium. Notice that this unique positive equilibrium for the mosquitoes exists and is stable only if a ₁<b ₁ for the dominant transgenes and for the recessive transgenes. This implies that although the malaria non-resistant mosquitoes produce more malaria-resistant mosquitoes through heterogeneous matings, they keep producing non-resistant mosquitoes with the same rates. As a result, more mosquitoes exist and hence more malaria non-resistant mosquitoes are reproduced as well. This may drive the reproductive number above the threshold while the infection is below the threshold when no transgenic mosquitoes are released. We need to be extremely cautious when this happens. A numerical example demonstrating such a possibility is given in Example 5.3.

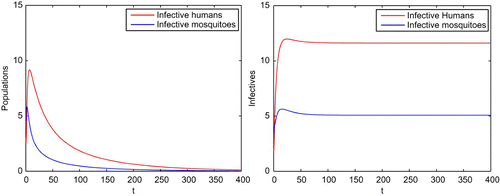
Example 5.3 We use the same parameters given in Example 5.1. Before the transgenic mosquitoes are introduced, the mosquito population at the steady state is S _v=2.4 such that the reproductive number for the malaria model (24) and (25) is R ₀=0.9427 and hence the infection dies out eventually, as is shown on the left in Figure 4. However, after the transgenic mosquitoes are introduced, both malaria-resistant and non-resistant mosquitoes are stimulated and the steady state for the two kinds of mosquitoes becomes and the reproductive number is increased to . The malaria transmission then spreads, as is shown on the right part in Figure 4.

Figure 4. With the same parameters given in Example 5.1, the reproductive number is R ₀=0.9427 and hence the infection dies out when there are no transgenic mosquitoes released as in the left figure. With the transgenic mosquitoes released, the numbers of malaria-resistant and non-resistant mosquitoes are both increased. The reproductive number becomes which results in the spread of the infection as shown in the right figure.

Nevertheless, if both malaria-resistant and non-resistant mosquitoes have higher homozygous birth rates than the heterozygous birth rates such that a ₁>b ₁ and b ₂>a ₂, there exist two positive and hence two positive equilibria , provided condition (13) is satisfied, in the case of dominant transgenes. One of the two positive equilibria and the boundary equilibrium for the interactive mosquitoes are locally stable nodes. Solutions approach to one of the two stable nodes, depending on their initial conditions. Moreover, the component S _v at seems always less than at E ₁, although we have not been able to prove it. Then the reproductive numbers at the infection-free equilibria associated with E ₁ and , respectively, have . If and are both less than one, the infection dies out eventually. If , as is shown in Section 5.2, there exists an endemic equilibrium bifurcated from the infection-free equilibrium associated with E ₁. Although the infection with the initial mosquito population size close to E ₁ spreads, the infection with the initial mosquito population size close to can be eliminated eventually. Furthermore, if both and are greater than one, there are two endemic equilibria bifurcated from E ₁ and , respectively, such that the infection spreads with any mosquito population initial sizes. Nevertheless, the infection components at the endemic equilibrium bifurcated from are not necessarily smaller than the infection components at the endemic equilibrium bifurcated from E ₁ even though as shown in Example 5.2. Then it becomes critical and important in selecting the initial sizes of the transgenic mosquitoes to be released.

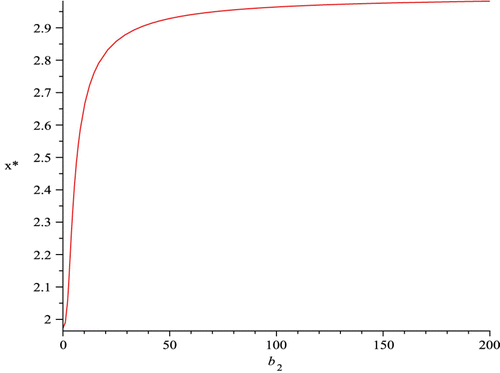
We also notice that S _v at the stable positive equilibrium for the interactive mosquitoes and hence in the formula for is given by S _v* in Equation (37) which include most of the biological parameters for the mosquitoes and the malaria transmission. Through sensitivity analysis of the parameters included in , we are able to gain further insight into how to make the releasing of transgenic mosquitoes more effective. For example, we fix the parameters

but use b ₂ as a variable. The component of the malaria-non-resistant mosquitoes in the malaria model with transgenic mosquitoes, as a function of b ₂, is plotted in Figure 5. With such parameters, S _v is an increasing function of b ₂ and approaches a constant value of 2.964, which is less than .

Figure 5. The component of the malaria non-resistant mosquitoes S _v=x* at the infection-free equilibrium of the malaria model with transgenic mosquitoes, given in Equation (37), is plotted as a function of b ₂ which shows that x* is an increasing function of b ₂, and approaches 2.964 as b ₂ increases.

6. Concluding remarks

To better understand the impact of releasing transgenic mosquitoes on malaria transmission, we formulated continuous-time models based on differential equations in this paper. As in 19, we first included all homozygously wild, heterozygous, and homozygously transgenic mosquitoes to formulate a three-dimensional system (3) with a more general setting. Our goal is to focus on the study of the impact on malaria transmission, and we also consider the cases where the transgenes are either dominant or recessive such that heterozygous mosquitoes with one copy of the transgenes are either resistant or non-resistant to malaria transmission. We then divided the total mosquito population into two groups to simplify the model structure and to make our analysis more mathematically tractable. One of the two groups consists of only homozygously wild mosquitoes and the other group consists of heterozygous and homozygously transgenic mosquitoes if the transgenes are dominant, and one of the two groups consists of homozygously wild and heterozygous mosquitoes and the other group consists of only homozygously transgenic mosquitoes if the transgenes are recessive. Model system (3) is reduced to the two-dimensional system (4) or (5), depending on the transgenes being dominant or recessive. We assumed constant mating rates, and then provided the analysis of the existence of the boundary and positive equilibria and their stability in Section 3. We showed that the boundary equilibrium with positive non-resistant mosquitoes, which implies that the transgenic mosquitoes do not survive, exists only for the model with dominant transgenes, and the boundary equilibrium with positive resistant mosquitoes, which implies that the wild mosquitoes are wiped out, exists only for the model with recessive transgenes. We also showed that it is possible in both the models for no positive equilibrium, a unique positive equilibrium, or two positive equilibria to exist where the components for the non-resistant and resistant mosquitoes are both positive, which implies that they coexist. We further obtained stability conditions for all of the equilibria in Section 3.

We then formulated a simple compartmental SEIR model for malaria transmission in Section 4. This is our baseline model to be used for incorporating transgenic mosquitoes into the malaria transmission. We derived a formula for the reproductive number and showed the existence of an endemic equilibrium, as the reproductive number is greater than one for the baseline model.

To study the impact of transgenic mosquitoes on malaria transmission, we combined the models for the interactive mosquitoes in Section 3 and the baseline malaria model in Section 4 and arrived at the models including transgenic mosquitoes in Section 5. We showed that the reproductive number for the model with transgenic mosquitoes has the same formula as the model without transgenic mosquitoes but in the baseline model is replaced by the value of S _v in a stable equilibrium for the interactive mosquitoes. We also showed that if the reproductive number is greater than one, an endemic equilibrium is bifurcated from the infection-free equilibrium where the reproductive number is computed. The reproductive number gives the threshold conditions that determine whether infections spread in a population. The impact of releasing transgenic mosquitoes hence can be explored through the analysis of the reproductive number. We provided brief investigations for the malaria model with transgenic mosquitoes in Section 5.3.

The reproductive number computed at the infection-free equilibrium with a stable boundary equilibrium for the mosquitoes model with dominant transgenes is the same as that for the baseline model. Then the transgenic mosquitoes have no impact on malaria transmission. On the other hand, the reproductive number at the infection-free equilibrium with a stable boundary equilibrium for the mosquitoes model with recessive transgenes becomes zero and thus the malaria transmission can be eradiated, as the transgenic mosquitoes completely replace the wild mosquitoes. While these cases are in the extreme and may be only ideal but not realistic in practice, it warns us that releasing dominant transgenes does not necessarily lead to better outcomes with releasing recessive transgenes.

A more realistic and desired situation, however, as is discussed in Section 5.3, seems to be that the two kinds of mosquitoes co-exist (approaching the stable positive equilibrium), but the size of the non-resistant mosquitoes is significantly reduced at the infection-free equilibrium with the stable positive equilibrium for the interactive mosquitoes, and then the reproductive number of the malaria transmission is brought to below one. Even if the reproductive number is still above one, the ultimate infective components for both humans and mosquitoes are reduced compared with those with no transgenic mosquitoes, as illustrated in Section 5.3. This may as well be a better strategy ecologically and economically.

While we provided investigations of the impact of releasing transgenic mosquitoes on malaria transmission, such investigations are only preliminary. The interactions between the wild and transgenic mosquitoes and hence the effects on malaria transmission can be complex. Moreover, we simplified our model formulations by grouping the mosquitoes with one or two copies of the transgenes or one or two copies of the wild genes together. Such simplification made the models more mathematically tractable, but since the existence of the heterozygous mosquitoes makes the extinction of either homozygous mosquitoes impossible, the analysis of the boundary equilibria for the interactive mosquito models and then the analysis of the equilibria of the malaria models associated with those boundary equilibria may not completely reveal the real biological situation. Therefore, it may be necessary to study the original three-dimensional system (3) and associated malaria transmission models which may raise more challenging and interesting mathematics questions as well.

Acknowledgements

This research was supported partially by the U.S. National Science Foundation grant DMS-0931213. The author thanks an anonymous referee for valuable comments and suggestions.