Socially induced ovulation synchrony and its effect on seabird population dynamics

Abstract

Spontaneous oscillator synchrony is a form of self-organization in which populations of interacting oscillators ultimately cycle together. This phenomenon occurs in a wide range of physical and biological systems. In rats and humans, oestrous/menstrual cycles synchronize through social stimulation with pheromones acting as synchronizing signals. In previous work, we showed that glaucous-winged gulls (Larus glaucescens) can lay eggs synchronously on an every-other-day schedule, and that synchrony increases with colony density. We posed a discrete-time mathematical model for reproduction during the breeding season based on the hypothesis that pre-ovulatory luteinizing hormone surges synchronize by means of visual, auditory and/or olfactory cues. Here, we extend the seasonal model in order to investigate the effect of ovulation synchrony on population dynamics across reproductive seasons. We show that socially stimulated ovulation synchrony can enhance total population size and allow the population to persist at lower birth rates than would otherwise be possible.

Keywords:

• bifurcation
• cannibalism
• discrete-time model
• gull colony
• ovulation synchrony

AMS 2000 Mathematics Subject Classification :

• 92B25
• 39A28

1. Introduction

‘Spontaneous oscillator synchrony’ is a phenomenon of self-organization in which a population of interacting oscillators ultimately cycles together. Spontaneous oscillator synchrony occurs in a wide range of physical and biological systems, including cardiac pacemaker cells, Malaysian fireflies, pendulum clocks, lasers and chemical reactions 21 27. In Norway rats and humans, ovulation cycles can synchronize through social stimulation with pheromones acting as synchronizing signals 16 17 18 19.

Females of a wide range of taxa experience similar kinds of hormonal fluctuations that drive ovulation cycles. Mammals and birds experience a surge of luteinizing hormone (LH) before each ovulation in a periodic fashion 31. In women, LH surges approximately every 28 days; in domestic fowl, LH surges every 24 h during the laying season 14. For animals that breed or congregate in dense social groups, there is at least the possibility that ovulation synchrony may occur. This has been tested, however, only in Norway rats and humans; currently, we are testing for ovulation synchrony in glaucous-winged gulls (Larus glaucescens).

Glaucous-winged gulls lay eggs at approximately 2-day intervals 30; this suggests a 48-h ovulation cycle. We would expect that ovulation synchrony in these birds might be manifest by synchronous every-other-day egg-laying. In previous work 12, we collected egg-laying data for three summers in a glaucous-winged gull colony on Protection Island, Washington, and showed that eggs were laid synchronously on an every-other-day schedule. We also showed that synchrony increased with colony density. The study suggested the possibility of socially stimulated synchrony of 48-h ovulation cycles. To probe this hypothesis, we posed a discrete-time mathematical model for population-level ovulation dynamics within the breeding season based on the hypothesis that 48-h LH surges synchronize by means of olfactory, visual and/or auditory cues. Model predictions were consistent with the data.

If socially stimulated ovulation synchrony is found to occur across a wide range of taxa, the question of selective advantage becomes paramount. There are at least three possibilities. First, synchrony could be an epiphenomenon with no selective advantage but could be associated with some other advantageous trait. Second, synchrony might have been advantageous in a common ancestor and may or may not retain selective advantage. Third, synchrony could arise convergently in a number of taxa in which similar mechanisms confer similar selective advantage. For example, in many taxa, including many that experience periodic LH surges such as rats, gulls and primates, adult animals cannibalize the young of conspecifics in densely populated environments 13 22. If ovulation synchrony, induced by social stimulation in crowded living conditions, were to confer a selective advantage in the presence of cannibalism, then synchrony might arise convergently in a number of such taxa.

The goal of this paper is to investigate the effect of avian ovulation synchrony on population dynamics in the presence of egg cannibalism. We show how socially stimulated ovulation synchrony can enhance total population size and allow the population to persist at lower birth rates than would otherwise be possible. Section 2 presents an overview of the life history and breeding phenology of glaucous-winged gulls. Section 3 reviews the method by which we measured the level of synchrony in time series data in 12, as well as the within-breeding season model proposed in that study. Section 4 extends the within-breeding season model to track population dynamics across breeding seasons. Section 5 presents a linear stability analysis at the origin and proves the existence of a transcritical bifurcation of nontrivial cycles. Section 6 contains analyses of two limiting models: one with no social stimulation and one with infinitely strong social stimulation. These special cases provide a framework for simulation studies that categorize the dynamic possibilities.

2. Life history and breeding phenology of glaucous-winged gulls

Glaucous-winged gulls breed in large colonies along the west coast of North America from Alaska to Oregon. At Protection Island, Washington where our field work is based, gulls return in February from winter feeding grounds, set up territories in early spring, build nests from early to mid-May, and lay eggs in late May/early June. From one to three (rarely four) eggs are laid at approximately two-day intervals per female per season 30. Territories begin to break down in late summer, and by mid-October most gulls have left the island (7, unpublished data).

Birds such as glaucous-winged gulls that breed in temperate regions experience yearly cycles controlled by the endocrine system in interaction with the external environment. As days lengthen in the spring, direct photic stimulation of the female hypothalamus results in release of neurohormones which are carried to the anterior pituitary gland. In response, the pituitary begins to synthesize and secrete LH and follicle-stimulating hormone (FSH) which promote dramatic growth of the ovaries. FSH, in concert with LH, is primarily responsible for maturation of the ova contained within the ovarian follicles at the surface of the ovary 5. Proximate factors such as cool weather can delay this process 25 29.

Maturation of the ovum involves yolk deposition and growth and development of the germ cell itself. Yolk deposition in glaucous-winged gulls takes about 12 days 24. During this time yolk materials pass from the follicle cells into the ovum via intercellular bridges. At the end of the 12-day period, an LH surge causes the ovum to break through the follicle (ovulation). Once in the body cavity, it is engulfed by the infundibulum, or upper end of the oviduct, where fertilization takes place. The fertilized egg is propelled by peristalsis through the oviduct to the vagina. Along the way, the albumin, egg membranes and shell are added, in sequence, over the yolk. In gulls, this process apparently takes approximately 48 h. The next LH surge occurs, followed directly by oviposition (the laying of the egg) and the ovulation of the next follicle in the hierarchy. This process is repeated until the clutch is complete 5.

Following clutch completion, the ovaries begin to shrink due to photorefractoriness, the state in which photic stimulation loses effectiveness. At this time the female enters a period of reproductive senescence, similar to menopause, until the next spring, when once again it enters a phase analogous to adolescence accompanied by sexual maturity.

Incubation may begin after the first egg is laid, but most commonly is delayed until the laying of the second or third egg. Male and female parents take turns incubating. Following an average incubation period of 27.5 days, the semiprecocial chicks hatch. During the first day or so post-hatching, chicks usually remain within the nest cup. Afterwards, young chicks hide nearby in vegetation, under logs, or within crevices. Chicks are fed by both parents until fledging, approximately six weeks following hatching. Glaucous-winged gulls reach sexual maturity at four years of age, at which point they choose a mate for life and often return to their natal colony to breed. Glaucous-winged gulls rarely survive more than 15 years 7 30 but have been known to live up to 32 years in the wild 1.

Eggs and chicks are vulnerable to conspecific cannibals. Any gull will eat an unprotected egg, but a few adults in the colony specialize in cannibalizing the eggs of neighbours 8 20 28. Territories of cannibalistic gulls are littered with large numbers of eggshell fragments. Cannibals, typically males, prey on nests when the incubation activities in neighbouring territories are disturbed by eagles or other predators. Parent gulls temporarily flee their territories during these disturbances, leaving eggs exposed and unprotected. Chicks that run into neighbouring territories during disturbances are sometimes cannibalized as well. On Protection Island, egg cannibalism was significantly higher during an El Niño year when food was scarce than during other years 9.

A variety of predators take gull eggs, chicks and adults 10. On the Protection island colony, however, nearly all predation is due to bald eagles, cannibalism and the predation of eggs by crows. During the gull incubation period, it is common to find all eggs in entire sections of the colony destroyed after eagles have hopped from nest to nest devouring the contents. Chicks are taken by eagles that swoop down from perch sites and snatch them from the colony surface. Adult gulls are taken while on territory, or, less often, while in flight. Eagle predation and flyovers cause large numbers of gulls to flee their nests, providing opportunity for gull cannibals and crows to snatch unprotected eggs.

The chance that a glaucous-winged gull egg on Protection Island will be fertile, avoid predation, and hatch ranges from 29% to 88%, depending on nest habitat, degree of predation, parent age and year (unpublished data). Fledging success is difficult to determine, but estimates range from 51% to 55%, depending on time of clutch onset 30. Survivorship post-fledging ranges from 40% to 87% per year of life, with first year mortality being the highest 7.

3. Egg-laying and ovulation synchrony

We collected egg-laying data for three summers in a glaucous-winged gull colony on Protection Island, Washington 12. We showed that egg-laying occurred synchronously on an every-other-day schedule, and that the level of synchrony increased with colony density. We also posed a mathematical model based on the hypothesis that ovulation cycles synchronize as a result of social stimulation. In order to validate the model, we estimated its parameters on one of 15 data sets and successfully predicted the remaining 14 data sets without re-parameterizing. Model predictions were consistent with the data. In this section, we give a brief review of (1) the method used to measure egg-laying synchrony in noisy time series of egg-laying data, (2) the argument used to show that the observed levels of synchrony were significantly different from those that arise by chance, (3) the mathematical model introduced in 12, and (4) the connection between social stimulation and ovulation synchrony in that model. Details are found in 12.

3.1. Measuring egg-laying synchrony in time series

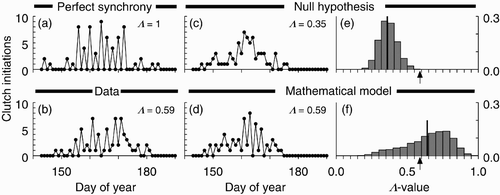
If a group of gulls were perfectly synchronized, the number of eggs laid per day, and the number of clutches initiated per day, would look like the simulation in Figure 1a. Such a time series would have two distinguishing characteristics. First, it would have a 2-cycle-like oscillation with every-other-day ‘highs’ of (probably) irregular height. Second, the ‘lows’ of the oscillation would equal zero. Because the egg-laying interval of these birds is slightly greater than two days 30, and because there might be days on which no eggs were laid, the time series could have ‘skips’ of two or more zeros in a row (Figure 1a). Observed time series, of course, are noisy. Figure 1b shows one of the 15 observed time series analysed in 12. To measure the level of egg-laying synchrony in noisy time series, we defined a measure Λ of synchrony for time series of the form , where E _i is the number of eggs laid on day i, days 1 and m refer to the first and last days on which eggs were laid, and E ₀ and E _m+1 are defined to be zero:

The numerator measures the total variation of the time series; the denominator gives the total variation for any perfectly synchronous time series with the same total number of eggs. The value Λ=1 indicates perfect synchrony (Figure 1a) and Λ<1 indicates a departure from perfect synchrony (Figure 1b).

Figure 1. Clutch initiation data, simulations, and distributions of Λ-values. (a) Simulation of perfect synchrony. (b) Data from 2006. (c) Monte Carlo simulation of null hypothesis. (d) Simulation of stochastic version of egg-laying model in 12. (e) Distribution of Λ -values generated from Monte Carlo simulations of null hypothesis. Vertical bar indicates distribution mean; arrow indicates observed Λ -value. The null hypothesis is rejected (p=0.0006). (f) Distribution of Λ-values generated from stochastic version of egg-laying model. Vertical bar indicates distribution mean; arrow indicates observed Λ -value. The egg-laying model is not rejected.

3.2. Testing the null hypothesis

In order to test whether the observed time series showed a level of synchrony significantly different from that which is expected to occur by chance, we tested the predictions of three null Monte Carlo models.

The first null model was based on the hypothesis that clutch initiations were random-normally distributed in time. For each observed time series of clutch initiations, we computed the total number of clutches initiated (W), the number of days spanning the clutch initiation period (X), and the sample mean clutch initiation date and standard deviation (Y and Z). In each Monte Carlo simulation, we randomly selected W real numbers from a truncated normal distribution lying within the time interval [0, X], and then we binned the W numbers by 1-day intervals to produce a simulated clutch initiation time series.

The second null model was based on the hypothesis that clutch initiations were random-uniformly distributed in time. The simulations were computed as above except the truncated normal distribution was replaced by a uniform distribution on the time interval [0, X].

The third null model was based on the hypothesis that ovipositions (egg-laying events) were random-normally distributed in time. In each Monte Carlo simulation, we random-normally distributed the observed clutches by random-normally distributing clutch initiation dates, as above. Within each clutch, we randomly selected laying intervals from a normal distribution with mean and variance equal to those of the observed intervals. Finally, we binned all simulated ovipositions into one-day intervals in order to produce a simulated oviposition time series.

For each null model, we used the program Matlab to compare for the observed time series to the distribution of Λ -values estimated from 10⁶ simulated time series. p-values were computed as the proportion of simulations satisfying . Each of the resulting p-values was computed five times to check convergence of the result.

For a particular time series, rejection of the null models indicates a level of synchrony unlikely to be attained by chance. Details of the Monte Carlo hypotheses, analyses, and results appear in 12.

Figure 1c shows a single Monte Carlo simulation of the first null model, along with its corresponding Λ-value. Figure 1e shows the null distribution of 10⁶ such simulated Λ -values, along with the observed Λ -value (arrow) for the observed time series shown in Figure 1b. For the observed time series in Figure 1b, p=0.0006, and so the null hypothesis was rejected.

3.3. Within-season model

We posed the following reproduction model in 12:

where , , and

with a time step of one day. Figure 2a shows a conceptual diagram of the model. Here w _t is the number of adult gulls that have not yet begun ovulation cycling by day t in the spring, x _t is the number of adults that ovulate on day t and y _t is the number of adults that are cycling but did not ovulate on day t. The fraction f∈(0, 1) is the probability that a non-cycling individual is ready to begin ovulation cycling, and is the probability that a cycling individual or one ready to cycle will ‘skip’ a day in order to synchronize, where c≥0 is the strength of social stimulation. The fraction 1−q, for q∈(0, 1), is the probability that a bird in the second phase of the cycle (the y class) will stop cycling and incubate.

Figure 2. Conceptual diagrams for models. (a) Within-season dynamics model (2). Here w _t is the number of adult gulls that have not yet begun ovulation cycling by day t in the spring, x _t is the number of adults that ovulate on day t and y _t is the number of adults that are cycling but did not ovulate on day t. (b) Across-season dynamics model (3). Here w _t , x _t and y _t are as above, and z _t is the number of eggs, chicks and adults that are incubating and chick-rearing. See text for complete description.

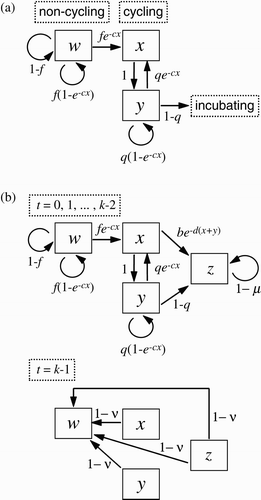
Remark 1 Note that the number of ovulations x on day t is the number of eggs laid on day t+2; in this model egg-laying is synchronized if and only if ovulation cycles are synchronized. Ovulation (and hence egg-laying) synchrony therefore is measured in the x component of the time series of model (2) using Equation (1). Perfect ovulation synchrony occurs when the x component shows 2-cycle-like oscillations with ‘lows’ equal to zero, as in Figure 1a.

We presented a stochastic version of model (2) in 12. Figure 1d shows a stochastic simulation with its Λ -value. Figure 1f shows the estimated distribution of Λ-values arising from the stochastic model, along with the observed value of Λ (arrow) from the observed time series in Figure 1b.

The model in 12 was nonautonomous; both f and c were expressed with time-dependent submodels in order to model the relationship between temperature-related delays in the onset of ovulation and the fixed endpoints of the reproductive season as set by photoperiod. In this study, however, we disregard the possibility of temperature-related delays in ovulation, and we take f and c to be constant.

Ovulation synchrony is measured in the x component of transient time series of model (2). The asymptotic dynamics are uninteresting, as the following argument shows.

Both the open positive cone and its closure are forward invariant under the map defined by . For any orbit in we have the inequalities

and hence

for all t≥0. It follows that all orbits in are forward bounded. These inequalities also show that the function is a Lyapunov function on , since they imply that V decreases along orbits: . The largest invariant set contained in

is the origin . It follows from LaSalle's invariance principle [Theorem 6.3]15 that approaches the origin, that is to say, the origin is a global attractor relative to . The origin is also locally asymptotically stable because the eigenvalues 1−f and ±√q of the Jacobian at the origin are all less than 1 in absolute value. Thus, we have the following theorem:

Theorem 2

For the matrix model (2) the origin is a globally asymptotically stable equilibrium relative to .

3.4. Connection between social stimulation and ovulation synchrony

In this study our goal is to extend model (2) across breeding seasons and to categorize the effect of socially stimulated ovulation synchrony on population-level dynamics. We wish to do this by studying the population dynamics as a function of the social stimulation parameter c. First, however, we must mention the connection between the level of ovulation synchrony Λ in transient time series of model (2) and the level of social stimulation c. 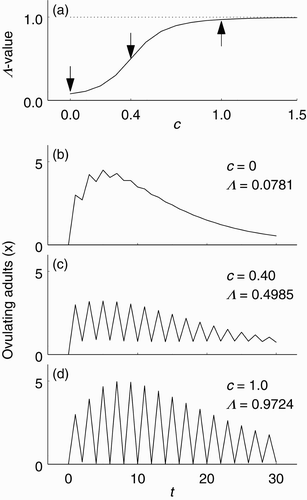Model (2) was designed to express the hypothesis that increasing social stimulation c increases ovulation synchrony. The nonlinear mechanism by which this is accomplished is that birds in the w and y classes can ‘skip’ returning to the x class until the x class is large. The relationship between % Λ and c is illustrated in Figure 3a, which shows a graph of Λ as a function of c for deterministic time series of model (2). The three arrows indicate pairs of (c, Λ) for which time series (for x) are shown in Figure 3b–d. In Figure 3b, social stimulation is zero and the synchrony level is low. In Figure 3c, social stimulation is moderately high and the synchrony level is near 0.5. In Figure 3c, social stimulation is very high and the time series is almost perfectly synchronous.

Figure 3. The relationship between social stimulation and ovulation synchrony in model (2), as illustrated with parameters f=0.1, q=0.6, μ=0.05, d=0.01, ν=0.2 and initial condition (30, 0, 0)^⊤. (a) Λ -value (level of ovulation synchrony) as a function of c (level of social stimulation). For each value of c, the Λ -value was computed for the deterministic time series of length 31. The arrows indicate the (c, Λ) pairs corresponding to the time series shown in (b)–(d). (b) Time series for x when c=0. (c) Time series for x when c=0.40. (d) Time series for x when c=1.0.

In the next section we extend model (2) to include births and deaths across breeding seasons. We then study the effect of socially stimulated ovulation synchrony on population dynamics by studying the effect of the parameter c.

4. Across-season population model

Extending model (2) across breeding seasons requires tracking births and deaths from year to year. Figure 2b shows a conceptual diagram of the extended model, in which we make a number of simplifying assumptions in order to reduce dimensionality.

First, in this model we assume that the total number of ‘births’ (eggs laid) on day t+1 is the number of ovulations x on day t reduced by a factor b∈(0, 1] to account for unfertilized/addled eggs and also reduced by a factor with d≥0 to account for the cannibalism of eggs by neighbouring nesting gulls. (Note, however, that in the biological system the number of eggs laid on day t+1 is the number of ovulations on day t−1, and that an egg is subject to cannibalism every day before hatching, instead of just the day it is laid). Thus, b is the ‘birth rate per ovulation’ in the absence of cannibalism. The parameter b plays an important role in the analysis that follows. In particular, we will use b as a bifurcation parameter in proving the existence of periodic solutions of the across-season model.

Second, in this model we place eggs and chicks, along with adults that are incubating and chick-rearing, into a single class (z) with a common death rate (per day) of μ∈(0, 1) due to predation by eagles. We assume no other source of mortality during the breeding season other than egg cannibalism. In particular, the model does not include the cannibalism of chicks by neighbouring adults.

Third, we track the dynamics of the breeding season using a time step of one day as in model (2), and at the end of the breeding season we assess (in one time step) an over-winter mortality ν∈(0, 1) on all birds and return the survivors to the w class to begin the next breeding season. In this model, therefore, juveniles are assumed to mature in one year. This is a major simplification, given that in the biological system juveniles require four years to mature.

Mathematically, we pose the model in the following way.

Let be the number of days in the breeding season. The periodically forced population-level model is

where . The time step is one day, and the k% -periodic projection matrix is defined by

and extended periodically for t≥k, with

We take t=0 to be the beginning of the initial breeding season; hence the times mark the beginnings of subsequent breeding seasons. Note that the application of matrix Q at t=k−1 returns the over-winter survivors in all classes back to class w to begin the next breeding season.

The initial condition has the form

since all birds are in the pre-ovulatory class at t=0. This, together with the form of matrix Q, implies that the (k−1)^th composite map

has orbits of the form

We also can write the composite map (5) as

where

The composite map is therefore equivalent to an autonomous scalar map of the form

where the time unit is equal to k time units in the original model.

Remark 3 In this study, we will focus on the asymptotic dynamics of the composite model (5). Note, however, that ovulation synchrony is still measured in the x component of within-season transient time series of model (3) using Equation (1), just as it was for the within-season model (2). Also, as in model (2), we increase ovulation synchrony by increasing the social stimulation parameter c. For example, Figure 4(b,g) show the x time series for two trajectories of model (3). 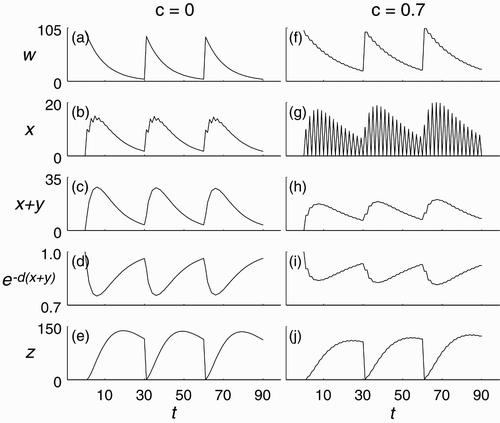There is essentially no ovulation synchrony in time series with c=0 (Figure 4b), whereas the time series shown for c=0.7 exhibits strong ovulation synchrony (Figure 4g).

Figure 4. Simulation of model (3) with initial condition (100, 0, 0, 0)^⊤ and parameters b=0.9, k=31, f=0.1, q=0.6, μ=0.05, d=0.01, ν=0.2. (a)–(e) Without synchrony (c=0). (f)–(j) With synchrony (c=0.7).

Our first goal will be to study the asymptotic dynamics of the across-season population model (3). Using bifurcation theoretic methods, we will study the existence and stability of (annual) periodic solutions of this nonautonomous, periodically forced matrix model. We will then obtain results on how these attractors (or more specifically, how bifurcating branches of periodic solutions) depend on the social stimulation coefficient c. According to Remark 3, this will permit us to determine the relationship between socially stimulated ovulation synchrony and characteristics of the population dynamics (e.g., total population size).

5. Existence and stability of periodic solutions of model (3)

In this section, our goal is to prove the existence of nontrivial k -periodic solutions of model (3). We do this by proving the existence of nontrivial equilibria of the scalar map (6), and hence the composite map (5), using a bifurcation theoretic approach. Specifically, we use b as a bifurcation parameter and show that the trivial equilibrium destabilizes as b increases through a critical value b _k . This destabilization results in the bifurcation of a continuum of nontrivial equilibria. The bifurcating branch consists of two sub-branches, one of positive equilibria, and one of negative equilibria that have no biological relevance. The bifurcation is called supercritical (or forward, or to the right) if the positive equilibria near the origin correspond to b>b _k ; it is called subcritical (or backward, or to the left) if they correspond to b<b _k . The branches of nontrivial equilibria of the scalar map (6), and hence the composite map (5), correspond to branches of nontrivial k-periodic solutions of the k-periodically forced map (3), and the stabilities of the corresponding branches are the same.

Thus, in this section our goal is to prove the following theorem.

Theorem 4

Consider the model (3) with d>0.

• (a)  There exists a unique critical value b _k >0 for which the origin is locally asymptotically stable for 0<b<b _k and unstable for b>b _k .

• (b) As a function of b there exists a branch of positive k -cycles that bifurcates from the origin at b=b _k . If where g is given in Equation (6), the bifurcation is supercritical and the bifurcating k -cycles are (at least for b near b _k ) locally asymptotically stable. If the bifurcation is subcritical and the bifurcating k -cycles are (at least for b near b _k ) unstable.

We begin by posing a slightly different model and proving several technical lemmas that will be useful in this section as well as in Section 6.

5.1. Some lemmas

Let {s _t } be a real-valued k-periodic sequence satisfying s ₀>0 and for all t≥0. Consider the k-periodic map

with initial condition (4), where

and

Because of the structure of matrix Q, the Jacobian

of the (k−1)th composite of Equation (7) evaluated at the origin has zero entries in all but the first row. The eigenvalues of J are therefore 0 (multiplicity three) and the upper left-hand entry of J, which we denote by λ (k). Note that λ (k) is the product of 1−ν and the sum of the entries of the first column of . The first column of is generated by applying the map

k−2 times starting with initial conditions

Thus, the dominant eigenvalue of the Jacobian J is

Remark 5 The linearization of model (5) at the origin is

where

Note that if s _t =1 in model (7), Equation (8) becomes J=QP ^k−1. In that case, λ (k) is the dominant eigenvalue of the linearization of the composite model (5) at the origin, and λ (k) is also the eigenvalue of the linearization of scalar map (6) at the origin.

Lemma 6

For all t≥0, p ₁(t), p ₂(t) and p ₃(t) are nonnegative and independent of b. For all t≥1, p ₄(t) is linear in b with a nonnegative intercept at b=0 and slope m(t)>0.

Proof

It is obvious that p _i (t)≥0 for all t. Since Equations (9a)–(9c) are uncoupled from (9d), it is clear that p ₁(t), p ₂(t), and p ₃(t) are independent of b. We prove the rest of the lemma by induction on t. Let t=1. Then

is linear in b with slope m (1)=fs ₀>0 and intercept equal to 0. For purposes of induction, let t≥2 and assume that p ₄(t−1) is linear in b with slope m(t−1)>0 and nonnegative intercept at b=0. Now,

Since p ₂(t−1) and p ₃(t−1) are nonnegative and independent of b, it is clear that p ₄(t) is linear in b with a nonnegative intercept and slope

  ▪

Lemma 7

For all the eigenvalue λ (k) has the form

where α (k) and β (k) are independent of b and satisfy

Proof

Equation (10) and Lemma 6 imply that λ (k) is linear in b with slope

We proceed by induction on k to show that the intercepts β (k) are less than 1. Let k=4. Given Equations (9a)–(9d) and (10), it is straightforward to calculate

which has intercept . Let k≥5 and assume, for purposes of induction, that%

where α (k−1) and β (k−1) are independent of b. Now, by Equations (9a)–(9d) and (10),

By Lemma (6), p ₂(k−3) is nonnegative and independent of b, and p ₄(k−3) is linear in b with positive slope m(k−3) and nonnegative intercept. Thus, % λ (k) has the form

where

are independent of b. Moreover, by the induction hypothesis, and the induction is complete.   ▪

Lemma 8

Let d>0 in model (7). Given initial condition (4) we can, for each t=2, …, k−1, write

where and ζ _t are scalar sequences that are independent of w ₀ and satisfy

and where the sequence of functions satisfies

Proof

Given initial condition (4), it is straightforward to calculate%

Here the constants , , , and ζ₂=0 satisfy (11) and satisfies Equation (12). Suppose, for purposes of induction, that

where the scalar sequences are independent of w ₀ and satisfy Equation (11) and where satisfies (12). Then

By the induction hypotheses, the quantities

are independent of w ₀ and satisfy Equation (11). Also,

satisfies

  ▪

5.2. Proof of Theorem 4

We are now ready to prove Theorem 4. The proof appeals to the bifurcation theory for nonlinear scalar maps. In particular, the proof verifies a list of sufficient conditions that are stated in existence and stability theorems for primary bifurcations in scalar maps. The reader can obtain these conditions for scalar maps from more general versions, which can be found, for example, in 2 3 11.

Proof

[Proof of Theorem 4] (a) Let s _t =1 . By Remark 5, λ (k) is the eigenvalue of the linearization of scalar map (6) at the origin. By Lemma 7, we know that λ (k) is a linear, increasing function of b that is less than 1 for b=0. Clearly there exists a unique b _k >0 such that

and

Thus, the origin is stable for 0<b<b _k and unstable if b>b _k . (b) Given Equations (13)–(14), the bifurcation theory of nonlinear scalar maps implies the bifurcation of a branch of positive equilibria at b=b _k for the scalar map (6). Since

it follows that the bifurcation is supercritical if and subcritical if . Moreover, the bifurcating positive equilibria are (locally asymptotically) stable if the bifurcation is supercritical, and they are unstable if the bifurcation is subcritical. These results, when pulled back to the composite map (5) and the k-periodic map (3), establish Theorem (4).   ▪

It is not easy to determine the direction of bifurcation (and stability of the bifurcating branch) since in general we do not have a formula for g(w). We will see in the next section that the bifurcation can be either supercritical or subcritical. We will also see that in the subcritical bifurcation case, the branch of bifurcating k-cycles bends back to the right—and even back again to the left and back again to the right—producing multiple attracting states and hystereses (Figure 5b).

Figure 5. Possible bifurcation structures. (a) k=31, f=0.1, q=0.6, μ=0.05, d=0.01, ν=0.2. (b) k=25, f=0.1, q=0.22, μ=0.05, d=0.05, ν=0.1. (c) k=7, f=0.1, q=0.6, μ=0.15, d=0.1, ν=0.2. (d) Same as for (c).

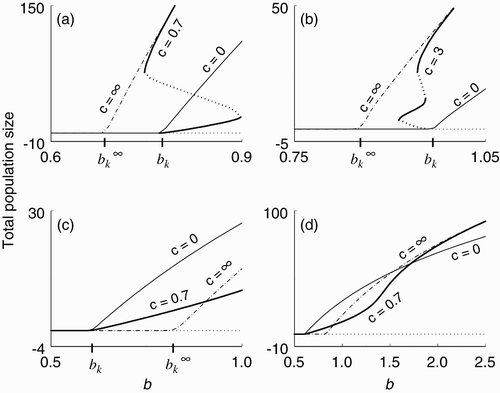
6. The effect of socially stimulated synchrony

We begin this section by considering two limiting cases that superscribe the geometry of all possible bifurcating branches: the case in which there is no social stimulation and essentially no ovulation synchrony (c=0), and the case in which there is strong social stimulation and perfect ovulation synchrony ().

6.1. First limiting case: c=0

For the case of no social stimulation, we will show that the bifurcation described in Theorem 4 is supercritical. Note that when c=0 we have

in model (3).

Theorem 9

If c=0, then the bifurcation described in Theorem 4 is supercritical and the bifurcating branch is stable.

Proof

By Theorem 4, it is sufficient to show that when c=0. We determine the function g by a direct calculation of the map g(w ₀)w ₀ in Equation (6). Let denote the L ¹ norm. An application of Lemma 8 with d>0 and implies

Thus, . Since satisfies it follows that

  ▪

6.2. Second limiting case: c→∞

It turns out, as we will see in Section 6.3, that the limiting case as in the population model (3) serves as a second reference point for the geometry of the bifurcating branches of periodic solutions as they depend on c.

Define

and

Formally, as , the nonlinear expression e^−cx becomes a step function that equals 0 for x>0 and equals 1 for x=0. Thus, because x ₀=0 in the initial condition (4), for this limiting case of model (3) we have

Therefore , and hence

which implies that x ₂=0. It is easy to see that x ₃>0, x ₄=0, and so on. The limiting case of matrix equation (3) with initial condition (4) as is therefore

where

An application of Lemmas 7–8 with

yields the following result.

Theorem 10

Consider the model (18) with d>0. There exists a unique critical value for which the origin is locally asymptotically stable for and unstable for . There exists a branch of positive k -cycles that bifurcates supercritically from the origin as a function of b, and the bifurcating k -cycles are (at least for b near locally asymptotically stable.

As we illustrate in the next section, the relative positions of b _k (as defined in Theorem 4) and (as defined in Theorem 10) provide the framework for understanding the effect of social stimulation c, and hence of ovulation synchrony, on the behaviour of model (3).

6.3. Direction of bifurcation for 0<c<∞

By Equation (15), the direction of bifurcation at the origin is determined by the sign of g′(0) at the bifurcation point. The goal of this section is to develop a computational method for calculating the direction of bifurcation in model (3) for general values of c>0 and to illustrate the various bifurcation configurations that can arise.

We begin by scaling the state variables of model (3) by a factor 1/w ₀. Setting , we see that the scaled model is

with initial condition

where%

The orbits of the original model (3) are w ₀ times the orbits of the scaled model, that is,

Thus, from Equation (16) we calculate%

and hence

The sign of g′(0) is therefore the same as the sign of

In what follows, we simplify the notation by dropping the ‘hats’ from the scaled state variables, replacing w ₀ with r≗ w ₀, and denoting by . For each , we have

Differentiation with respect to r followed by evaluation at r=0 yields

where the w _t , x _t and y _t on the right-hand sides of Equations (23)–(26) are computed by iterating Equations (19)–(22) with r=0.

We can therefore calculate Γ _k by iterating a nonlinear map that acts on with block triangular matrix

k−1 times starting from the initial condition (1, 0, 0, 0, 0, 0, 0, 0)^⊤. Then

The bifurcation is supercritical if Γ _k <0 and subcritical if Γ _k >0, where Γ _k is computed using the parameter values at the bifurcation point.

This method is easily implemented on the computer, for example in MatLab. The bifurcations shown in Figure 5, which illustrate the various types of bifurcation structures possible in this model, were located in parameter space by computing Γ _k for a range of periods and parameter values using MatLab.

Our numerical explorations suggest that the primary bifurcations in this system have three basic configurations.

In the first type, illustrated by the example in Figure 5a, the primary bifurcation for the system with c=∞ is to the left of the primary bifurcation for the system with c=0; that is, . The bifurcating branch corresponding to c>0 (in this example, c=0.7) is supercritical and below the branch corresponding to c=0. The branch corresponding to c=0.7 eventually undergoes two saddle-node bifurcations: first to the left and then back to the right, creating a hysteresis, and then asymptotically approaches the branch corresponding to c=∞. The second saddle-node bifurcation in the hysteresis occurs at a value of b<b _k .

The second type of configuration is illustrated by the example in Figure 5b. Here as in Figure 5a, but in this case the bifurcation corresponding to c>0 (in this example, c=3) is subcritical. The branch bends back to the right, back again to the left, and finally back to the right, creating multiple attracting states at which the population can survive for b<b _k .

The third type of configuration is illustrated by the example in Figure 5c. Here the primary bifurcations are reversed, , and the bifurcation corresponding to c>0 is supercritical and the branch lies below the branch corresponding to c=0. Figure 5d shows the configuration in this example at larger values of b.

We summarize our findings in this section as follows.

• (1) In the first two types of bifurcation configurations (Figure 5a,b), the subcritical bifurcation and hystereses show that socially stimulated ovulation synchrony can enhance total population size by allowing the population to

  • (a) persist at birth rates less than the critical birth rate (b<b _k ) for which it could not persist if c=0, and

  • (b) exist at a higher total population size for birth rates exceeding the critical birth rate (b>b _k ) than it would if c=0.

• (2) In the first and third types (Figure 5a,c), socially stimulated ovulation synchrony can be deleterious by depressing total population size for birth rates exceeding the critical birth rate (b>b _k ).

7. Discussion

Our results indicate that socially stimulated ovulation synchrony in the presence of egg cannibalism can enhance total population size in two ways.

First, for birth rates exceeding the critical birth rate, socially stimulated ovulation synchrony can increase the total population size over what it would be without synchrony. Second, for birth rates less than the critical birth rate, socially stimulated ovulation synchrony can allow the population to persist even though it would go extinct in the absence of synchrony. In this second case, the population persists if the population size exceeds an Allee Effect threshold, and goes to extinction otherwise. The relationship between population size and fitness is complex 23 26, and our model makes no direct predictions about fitness. It does suggest, however, that reproductive synchrony could lead to increased fitness, an outcome often associated with increased population size.

It is not straightforward to explain, intuitively or from a biological point of view, the mechanisms by which population size is enhanced by socially stimulated ovulation synchrony in this model – partly because this does not occur for every set of parameters. A partial mathematical explanation is that, on average over time, the presence of socially stimulated ovulation synchrony can depress recruitment from the w class (Figure 4a,f) into the x class (Figure 4b,g). This is related to Jensen's Inequality and the fact that the nonlinearity e^−cx is concave up. This reduces x+y (Figure 4c,h), which in turn increases egg survivorship from cannibalism (Figure 4d,i). Also, the slower progression of birds through the series of classes decreases the average amount of time an adult spends in class z (Figure 4e,j), which decreases its exposure to the mortality rate μ by eagles.

Biologically speaking, the model suggests that total population size can be enhanced by socially stimulated ovulation synchrony through the following mechanisms. On average over time, ovulation synchrony can slightly delay the onset of ovulation in enough birds to (1) decrease the risk that a given egg is cannibalized by neighbours, and (2) decrease the average amount of time an adult spends incubating and chick-rearing (which decreases its risk of predation by eagles).

Several caveats and comments deserve mention.

First, the two mechanisms (stated above) for enhancing total population size rest on two model assumptions: (1) only birds experiencing ovulation cycles (classes x and y) cannibalize eggs, and (2) adults not yet incubating or chick-rearing (w, x, y classes) do not suffer eagle predation. The first of these assumptions is plausible: adult birds that have not yet laid eggs (w class) leave their territories unattended much of the day while loafing and foraging off the colony; hence they are not as likely to cannibalize conspecifics on the colony. Similarly, an adult that is incubating or tending chicks (z class) is less likely to leave its territory to predate neighbouring nests. The second assumption is also plausible: adult birds that are incubating or rearing chicks (z class) probably exhibit greater aggression and territory tenacity and are more likely to be taken by eagles, whereas adult birds with less reproductive investment in their territories (w, x, y classes) may be more likely to flee and escape. Note, however, that birds that delay ovulation and spend less time chick rearing at the end of the season may have to abandon their unfledged chicks when the adults leave the colony in the fall, hence reducing their fitness; this type of chick mortality is not accounted for in our model.

Second, the ovulation synchrony hypothesis remains to be verified by observations and experiments. At the present we are certain only that egg-laying events can be synchronized. We currently are doing experiments to test whether this corresponds to ovulation synchrony. We also are doing experiments to test whether the means of oscillator ‘communication’ is olfactory, auditory, and/or visual.

Third, the model in this study contains several major simplifications (listed in Section 4) that will be addressed in a future paper. In particular, the current model assumes that juveniles mature after one year, whereas glaucous-winged gulls mature after four years. A more realistic model will require three juvenile classes in addition to the class for incubating/chick-rearing adults. At the end of the breeding season (time t=k−1) individuals in the first two juvenile classes will advance to the next juvenile class rather than advancing to the w class.

Fourth, the type of reproductive synchrony addressed in this paper is different from the reproductive synchrony posited by Fraser Darling 4. Darling hypothesized that social stimulation in colonial birds results in a tightened annual reproductive pulse. He suggested that birds in larger colonies experience more social stimulation that accelerates the breeding cycles and leads to earlier and more synchronous breeding than in smaller colonies. Increased breeding synchrony would be advantageous to colonial birds, he argued, in that predators quickly become satiated and consume fewer young than if reproduction were spread out over a longer period of time. Thus, selection should favour increased breeding synchrony. This postulated phenomenon became known as the ‘Fraser Darling effect’.

Gochfeld 6 discussed Darling's hypothesis and noted that evidence has been presented by some investigators to support at least some aspects of Darling's conjecture, while other investigators have doubted the value of the concept. Gochfeld concluded that ‘in certain cases synchrony is occurring and requires study and explanation’, and that ‘social factors contribute strongly to synchrony’ when it occurs. For example, he noted that studies with ring-billed gulls (L. delawarensis) and common terns (Sterna hirundo) provide evidence that breeding displays such as wing-flashing during copulation can be contagious and provide a medium through which social stimulation could play a synchronizing role.

The difference between the Fraser Darling effect and the every-other-day synchrony described by our model is, of course, the time scale. Our within-season model as given in 12, however, pointed to an interesting prediction. If clutch initiation is delayed, say by cooler than average spring weather, the breeding window is compressed and ovulation synchrony is disrupted 12. Thus, the Fraser Darling effect should be most apparent during years with delayed breeding; by contrast, ovulation synchrony should be most apparent during other years. Our limited field data comport with this prediction. In 2008, an La Niña year, clutch initiation was delayed and the breeding window was compressed, and egg-laying synchrony was not observed. By contrast, in 2006, a ‘normal year’, and 2007, an El Niño year, the breeding window was not compressed and egg-laying synchrony was observed in both years 12.

In this study, we hint at the possible selective advantage of socially stimulated ovulation synchrony by asking whether it enhances population size, that is, by asking whether ovulation synchrony enhances the fitness of an individual in a population of identical individuals. The next step is to assume a trait variation within the population on which selection can act. This leads to Darwinian Dynamics models, in which the population model is coupled to a dynamic model for an evolving trait. We will consider such a model in a future paper.

Acknowledgements

We thank Kevin Ryan, U. S. Fish and Wildlife Service, for the permission to work on the gull colony at Protection Island National Wildlife Refuge. Rosario Beach Marine Laboratory provided logistical support. This work was supported by the National Science Foundation grant DMS-0613899 and by an Andrews University Faculty grant.