Persistence and global stability in a selection–mutation size-structured model

Abstract

We analyse a selection–mutation size-structured model with n ecotypes competing for common resources. Uniform persistence and robust uniform persistence are established, when the selection–mutation matrix Γ is irreducible, i.e. individuals of one ecotype may contribute directly or indirectly to individuals of other ecotypes. Similar results are also presented for a particular reducible form of Γ. In the case of pure selection in which the offspring of one ecotype belong to the same ecotype, i.e. Γ=I, the identity matrix, we prove that the boundary equilibrium that describes competitive exclusion, with the fittest being the winner ecotype, is globally asymptotically stable. We show that small perturbations of the pure selection matrix lead to the existence of globally asymptotically stable interior equilibria. For the case when the selection–mutation matrix is reducible, we present and discuss the outcome of a series of numerical simulations.

Keywords:

• continuous size-structured model
• selection–mutation
• uniform persistence
• robust persistence
• global asymptotic stability

AMS Subject Classification :

• 92D25
• 34D23
• 34D10

1. Introduction

There is a large and growing body of literature on continuous structured population models which assume that individuals are distinguished from one another by characteristics such as size, age or spatial position(e.g. 3 7 11 13 14 16 17 18 20 22 33). Continuous structured models have been successfully used to study many biological problems. For example, such models have been used to understand the dynamical behaviour of red coral (Corallium rubrum, L.) growth 20 and tumour growth 33. The authors in 7 derived a model that describes the dynamics of an amphibian population. In 17, age-size structured models have been developed to describe a cell population. A population model that incorporates age, size and spatial structure has been studied in 33.

Selection–mutation models have been extensively studied in the literature (e.g. 2 9 19). These are models that describe the dynamics of a population with respect to some discrete or continuous evolutionary trait. The pure selection process describes the faithful reproduction, i.e. individuals of one ecotype (having the same trait) reproduce individuals of the same ecotype, while mutation describes unfaithful reproduction.

Recently, several researchers have devoted attention to integrating selection–mutation models with continuous size-structured models. The resulting models are partial differential equation systems which assume that differences between individuals are not only due to differences in size and/or age, but also are due to individuals belonging to different ecotypes. The reproduction process in these models is assumed to be open (mutation occurs) or closed (pure selection). In 1 4 5 6, nonlinear selection–mutation size-structured models that describe the dynamics of a population with n competing ecotypes are studied. In 4, a finite difference scheme to approximate the solution is developed and the convergence of the approximation to the unique bounded variation solution of the model is proved. In 5, the authors show, using a contraction mapping argument, that a unique solution of the model exists for all positive time. Conditions on the individual rates which guarantee competitive exclusion in the pure selection case are provided. In the case of an irreducible selection–mutation matrix where individuals of one subpopulation contribute offspring, either directly or indirectly, to all the other subpopulations, the authors proved that all ecotypes coexist.

Ackleh and Deng 1 formulate a quasi-linear PDE model for a population consisting of n ecotypes competing for common resources, but they reduce it to a 2n-dimensional ODE. Working with the ODE, the authors consider first the pure selection case, i.e. Γ=I. They prove that competitive exclusion among the ecotypes occurs and provide conditions which determine the fittest ecotype (the one that wins the competition). Second, they consider the case when the selection–mutation matrix is irreducible and prove coexistence of all ecotypes under a very restrictive condition on the model parameters.

Here, using theoretical tools from the persistence theory, we extend the results in Ackleh and Deng 1. The main novelties of our work are: (1) when the selection–mutation matrix Γ is irreducible and the extinction equilibrium is unstable in the linear approximation, we obtain coexistence of all ecotypes in the form of uniform persistence. As a consequence, we get the existence of interior equilibria; (2) we obtain a similar persistence result for a special form of a reducible matrix Γ; (3) we prove that the persistence is uniform with respect to small changes in the parameters (i.e. the persistence is robust); (4) we show that irreducible perturbations of the pure selection matrix lead to existence of globally asymptotically stable interior equilibria.

Our paper is organized as follows. In Section 2, we give a brief presentation of the model in Ackleh and Deng 1. Our main results are in Section 2. In particular, in Section 3, we give conditions for the coexistence of all ecotypes in the form of uniform persistence when Γ is irreducible; in the case Γ is reducible of a particular form, we provide conditions under which some ecotypes coexist. In Section 3.2, the uniform persistence is extended to robust uniform persistence. In Section 3.3, we show that, in the pure selection case, the boundary equilibrium which describes the survival of the fittest is globally asymptotically stable. This leads to globally asymptotically stable interior equilibria, by perturbing the pure selection matrix. In Section 4, we perform numerical simulations for a model with reducible selection–mutation matrices. Finally, we discuss our conclusions and future work in Section 5. Additional mathematical tools, such as definitions, notation and results that we use throughout the paper can be found in the Appendix.

2. The model

Here, we present the model considered in 1, for the dynamics of n ecotypes competing for common resources. We reproduce this model below, but slightly change the notation (the total population size at time t, which is denoted by P(t) in 1, is now N(t)) in order to avoid confusion with other notation that we use in this paper.

where the function u _i (x, t), i=1, 2, …, n, represents the density of individuals of the ith ecotype (i.e. carrying the ith trait) having size x at time t. The total population at time t is . The functions g _i , m _i and β _i denote the growth rate, the mortality rate and the reproduction rate of an individual in the ith subpopulation, respectively. We denote the selection–mutation matrix by Γ, where the constant parameters represent the probability that an individual of the jth ecotype will reproduce an individual of the ith ecotype. Clearly, , for all j=1, …, n.

As in 1 11 22, we assume the following submodels for the growth and reproduction rates for each subpopulation

where and are positive constants, k _i ∈(0, 1) is the fraction of ingested food channelled to growth and maintenance and 1−k _i is the fraction channelled to reproduction. Also, the mortality rates m _i are assumed to be independent of size x.

For this choice of growth, reproduction and mortality rates, integrating the first equation of (1) (with respect to x∈[0, 1]), we obtain the differential equation for and then multiplying the first equation of (1) by x, and integrating it (again, with respect to x), we obtain the differential equation for . Thus, we have the following system of coupled ordinary differential equations

So P _i is the total number of individuals of ecotype i, Q _i is the total biomass of the population belonging to ecotype i and is the total number of individuals in the population. For a complete presentation of this model, we refer the reader to 1.

3. Main results

All the analysis in this section is with respect to Equation (2). Notation and other results used in the proofs are contained in Section 3. In order to be consistent with the biological interpretations of P _i s and Q _i s, we consider our state space to be (i.e. ). Notice that whenever , hence X is positively invariant. We make the following assumption.

• (H1) f _i is a continuously differentiable non-increasing function, f _i (0)>0, and m _i is a continuously differentiable increasing function, i=1, …, n. We also assume that equation

  has a (unique) positive root for some i, and for each j≠i either it has a positive root, or for all y≥0.

3.1. Coexistence of ecotypes

By setting , the model (2) can be written in the form

where

For simplicity, we denote A(0) by A. Also, recall that .

Lemma 3.1

If Γ is irreducible then so is A.

Proof

Suppose that A is reducible. Then there exists a partition J∪K of such that for all j∈J and k∈K, a _jk =0. Note that for 1≤i≤n, so n+i and i are either both in J or both in K. Suppose, without loss of generality, that and , where m<n. So a _jk =0 for all and . But this contradicts the assumption that Γ is irreducible. Hence, A is irreducible.   ▪

The next result establishes dissipativity for our model.

Lemma 3.2

Assume that (H1) holds. Then there exists R>0 such that is positively invariant and attracts all solutions of Equation (2). Hence Equation (2) is dissipative.

Proof

Since Q _i ≤P _i , we find by changing the order of summation that

Let R=max _i R _i , where R _i is the root of (if such a root exists). From (H1) we have R>0. Then clearly N(t) cannot stay greater than 2R for all t≥t ₀, for some t ₀≥0, because then there would be a ξ>0 such that for all t≥t ₀, thus N(t)→0, as t→∞, and we would have a contradiction. On the other hand, since N′(t)≤0, whenever N(t)=R, we have that is positively invariant. Hence Equation (2) is dissipative.   ▪

As dissipativity plays an important role in our subsequent results, we will just assume that (H1) holds hereafter.

Theorem 3.3

If Γ is irreducible and s(A)>0, then there exists such that, for all non-zero solutions of Equation (2), there holds

Proof

Let and . Suppose there exists . Then for such an x, let x(t) be the solution with x(0)=x. Considering the form (5) of Equation (2) and using that A(x(t)) is quasi-positive and irreducible, for all t≥0, from [Theorem 1.1]29 we have that x(t)≫0, for all t>0. Hence X ₀={0}. Next, we want to apply Theorem A.2 to conclude Equation (7). Lemma 3.2 shows that Equation (2) is dissipative, which implies that it has a global attractor of points (the result that can be found in [Chapter 1]27). Conditions in 2(a) and 2(b) in Theorem A.2 are clearly satisfied by taking S=X ₀={0}, while conditions in 2(c) and 2(d) follow if we show that {0} is a uniformly weak repeller (see Appendix). For this, we make use of Lemma A.4, where we take M={0} and regard {0} as a periodic orbit of period T=1. P(t, 0), the fundamental matrix of solutions for u′(t)=A u(t) (see Appendix), is e ^{t A} . Hence , which is a primitive matrix, because A is irreducible (in fact, e ^A has all entries positive, as mentioned in the proof of Theorem A.12.(i) of 29). The spectral radius of e ^A is e ^s(A), hence it is greater than one, according to our hypothesis that s(A)>0. Then, from Lemma A.4, we obtain that {0} is a uniformly weak repeller, which concludes our proof.   ▪

Corollary 3.4

There is an equilibrium point with all coordinates positive.

Proof

Let B be the set guaranteed by Lemma 3.2. Then B is convex (i.e. B contains the entire line segment connecting any two points in B) and positively invariant. From Theorem 3.3, there exists an such that Equation (7) holds. Thus, if we take we have that [Btilde] is compact and convex and, without loss of generality, we can assume it to be positively invariant. Then, from [Theorem 4.8]32, [Btilde] contains an equilibrium.   ▪

In our persistence result presented in Theorem 3.3 above, we took advantage of the fact that the set where the persistence function evaluated along an orbit is always zero consisted only of the trivial state {0}. This simplification allowed us to formulate an explicit sufficient condition for uniform persistence of all ecotypes, namely for the extinction equilibrium to be unstable in the linear approximation. A similar situation occurs when the fertility matrix Γ is reducible, but of a particular form, case that we present below. Consider matrix Γ of the form

where Γ₁ is an l×l matrix, 0<l<n, and O represents the zero matrix. C is a non-negative matrix that does not have columns consisting entirely of zeros. Biologically this means that offspring of any ecotype i, are produced by at least one ecotype j, . On the other hand, individuals of any ecotype 1, …, l cannot produce offspring of ecotypes l+1, …, n. Intuitively, one would expect this to lead to persistence of ecotypes 1, …, l, a fact that will be proved below.

Let

Theorem 3.5

If Γ₁ is irreducible and s(A ₁(0))>0, then there exists such that, for all non-zero solutions of Equation (2), there holds

Proof

Let , and x=(x ¹, x ²). Let . Let be a solution to Equation (2). First we show that

Thus, consider the equation

Note that, because A ₁(x(t)) is quasi-positive for all t≥0, is positively invariant for Equation (12). Also we have that

Next we show that if u(t) is a solution to Equation (12), u(0)=x ¹(0), then , for all t≥0. For this, we ‘mimic’ the proof of Theorem B1 in 28. Thus, let u _m (t) be the solution to

where and . Write . Let u _mi (t) denote the ith component of u _m (t). Then, using Equation (13), we have

From the above, we have that there exists a θ>0 such that for all . Now if does not hold for all t>0, then such that , and . Thus, using again Equation (13), we have

which obviously represents a contradiction. Hence , for all t≥0. Then, using that as m→∞, uniformly in , for any [ttilde]>0, we obtain that , for all t≥0. Now again, because A ₁(x(t)) is quasi-positive and irreducible for all t≥0, applying Theorem 1.1 from 29, we have that u(0)>0 implies u(t)≫0 for all t>0. Hence

It should be clear that X ₀ is a positively invariant set (see Appendix for definition). Now suppose that X ₀ contains a point x ₀ with Q _j >0, for some . Then, from our assumption on matrix C, we have that there exists such that γ _ij >0. This implies, considering the solution x(t) to Equation (2), x(0)=x ₀, that P _i ′(0)>0. But this contradicts Equation (17), since X ₀ is positively invariant. Hence

It follows then that X ₀ contains no points with P _j >0, , because if such a point [xtilde] ₀ existed, then considering the solution starting at [xtilde] ₀, we would have . Using again that X ₀ is positively invariant, we would have a contradiction to Equation (18). Hence Equation (11) holds. As before, we want to apply Theorem A.2 to conclude Equation (10). Conditions in 2(a) and 2(b) in that theorem are clearly satisfied by taking S=X ₀={0}. We claim that there is a neighbourhood V of 0 in X that does not contain any positively invariant set other than {0}. Once we prove this claim, conditions 2(c) and 2(d) in Theorem A.2 will follow directly and our proof will be complete. Thus, denote by P(t, x) the fundamental matrix of solutions for Equation (12), P(0, x)=I, where x=x(0). Let η be a non-negative unit vector in . P(t, 0)η represents the solution to that satisfies u(0)=η. Since A ₁(0) is irreducible and s(A ₁(0))>0, we have that becomes unbounded as t→∞ (see [Theorem A.45.]31). In particular, for any such η, there exists τ>0 such that (*). Now suppose that the claim we made above does not hold. Then, using (*) and that is positively invariant for Equation (12), one can obtain, by following the same idea of proof as for [Lemma 3.4]24, that there exist a sequence in ℝ₊ and a constant c>1 such that

for some . But P(t, x)x ¹ is the solution u(t) to Equation (12), u(0)=x ¹. This implies , for all t≥0, where we used that and that both u(t) and x ¹(t) are non-negative, for all t≥0. Hence, we get a contradiction to Equation (19), because Equation (2) is dissipative (so all solutions are bounded). Thus, the claim holds and with this our proof is complete.   ▪

Our next goal is to study the case of small mutations of the pure selection model which has been addressed by many researchers to help understand some aspects of adaptive dynamics 8 9 10 12 15 21 23. The authors in 8 9 show that the non-trivial equilibria of selection–mutation models tend to concentrate at the evolutionary stable strategy (ESS) when the mutation rate or the size of the mutation is small. Furthermore, the study of small mutations has proved to be relevant in the treatment of diseases, such as HIV and influenza, where mutations have a profound impact on therapy 21 23.

To achieve our goal and investigate the dynamics of the model with small mutation, we take advantage of the perturbation result developed in 28. In order to apply this perturbation result, we will first need to establish (in Section 3.2) robust persistence, and then prove (in Section 3.3) that the steady state of the pure selection model (unperturbed system) is globally asymptotically stable.

3.2. Robust uniform persistence

In this section, we address the question of robust uniform persistence, that is, persistence that is uniform with respect to small changes in the parameters involved in the model.

Let be a compact set, for some positive integer k. We regard Λ as the parameter space and assume that the right-hand side of Equation (2) is continuous in . Let be the semiflow generated by Equation (2) and A _λ be A=A(0), both corresponding to the parameter . Hence the map is continuous. We often write for .

For simplicity, we present here only the robust persistence result for an irreducible fertility matrix corresponding to parameter λ₀, but a similar result for the case when is of the form (8) can be obtained in a completely analogous fashion.

Theorem 3.6

Let and assume that the corresponding matrix is irreducible and . Then

whenever , and .

Proof

From Lemma 3.2, it follows that for every there is a such that

Also, R(λ) depends continuously on λ, as it can be easily noticed in the proof of the same lemma. This shows that

where is the omega limit set of x with respect to . Next we claim that {0} is a robust uniformly weak repeller, that is,

• (C)  and Λ₀ a bounded neighbourhood of λ₀ such that, for all and , .

It suffices to show that (C) holds for x in some bounded neighbourhood of 0. Let (i.e. U is the set of unit vectors in ). Again, by regarding {0} as a periodic orbit of period one and using that is primitive and has a spectral radius equal to (as shown in the proof of Theorem 3.3), from Corollary 3.12 and Lemma 3.4 in [24 (applied with M={0} ) it follows that

where (see Appendix) is the fundamental matrix of solutions for . Because is continuous, for each η∈U, there are τ_η>0, c _η>1 and bounded neighbourhoods V _η, and U _η of zero, λ₀ and η, respectively, such that , for all x in V _η, λ in and η˜ in U _η (where τ_η comes from Equation (22)). Since U is compact, there exist finitely many , such that . Let , and for all i, and (note that c>1). Thus, we have

Now if we negate the claim (C), we obtain

Take η=x/|x|. Then, using Equation (23) it follows, by the same arguments as in the proof of Lemma 3.4 in 24, that there exists a sequence such that , for all n. But . Hence as n→∞, which contradicts Equation (24). Thus, the claim (C) holds. Finally, our hypotheses imply, as shown in the proof of Theorem 3.3, that conditions (1) and (2) in Theorem A.2 hold. Combining this with Equation (21) and claim (C) and applying [Theorem 5]30, we obtain that Equation (20) holds.   ▪

3.3. Globally asymptotically stable interior equilibria

In this section, we consider to be a fixed parameter, for which the corresponding is the identity matrix. For convenience, we re-order the equations in (2) such that the equations for P ₁′ and Q ₁′ are the first two equations, the equations for P ₂′ and Q ₂′ the next two, and so on. When Γ=I, the system of differential equations (2) becomes

for i=1, …, n. We set

In Ackleh and Deng [Lemma 2]1, it is shown that as t→∞. Based on this, we see that Equation (25) can have a boundary equilibrium of the form if and only if . We assume that such non-trivial E _i exists for some i. Without loss of generality, we take i=1 and make the following assumption:

• (H2) .

Thus, the population corresponding to i=1 turns out to be the ‘fittest’ ecotype (i.e. the ecotype that wins the competition), as shown in [Theorem 5, Theorem 6]1, but under slightly stronger assumptions than (H2). However, with minor modifications in the argument used in 1, one can show, under hypothesis (H2), that E ₁ is an equilibrium that attracts all solutions of Equation (2) starting with P ₁(0)>0. Moreover, the next lemma shows that E ₁ is globally asymptotically stable in –result that will be used later to prove that small perturbations of the fertility matrix lead to globally asymptotically stable interior equilibria.

Lemma 3.7

If (H2) holds, then is globally asymptotically stable in .

Proof

As mentioned above, the proof for E ₁ attracting all solutions in is analogous to the proofs in [Theorems 5 and 6]1 and we will omit it here. Next we show that E ₁ is asymptotically stable. Evaluating the Jacobian of Equation (25) at E ₁, we find that E ₁ is asymptotically stable in the linear approximation if and only if matrices

and

have all eigenvalues with negative real parts. By assumption (H1), trace(A ₁)<0. Using that and assumption (H2), from direct calculation, we obtain

where we used that α _i s satisfy

Hence eigenvalues of A ₁ are negative. Clearly, trace of A _i is negative for all i≥2.

By (H2), we have , for all i≥2. Then from Equation (29), we have

where again we used Equation (28). Thus each A _i has negative eigenvalues. This concludes our proof.   ▪

The next result, used in the proof of Theorem 3.9 below, shows that each neighbourhood of E ₁ attracts all initial conditions, uniformly in λ ‘close’ to λ₀.

Lemma 3.8

For each a neighbourhood of E ₁ there exists Λ₀ a neighbourhood of λ₀ such that

Proof

We argue by contradiction: suppose that there is a neighbourhood of E ₁ such that, for every neighbourhood of λ₀, there exists and with the property that for each T>0, for some t≥T. Consequently, there exist sequences and with as such that

where ω _m (x) is the omega limit set of x with respect to the semiflow and is the complement of . Using Equation (21) again, we have that is bounded in the complete metric space of all compact subsets of with the Hausdorff distance, thus it has a convergent subsequence . Let L be a non-empty compact subset in such that as . Since is continuous in (x, λ) and is compact, as m→∞, uniformly on , for each τ>0. From [Lemma 2]30, we obtain that L is invariant for . Also Equation (32) implies that

Now since E ₁ is asymptotically stable (with respect to ), we can find a positively invariant (again, with respect to ) neighbourhood of E ₁. It follows then that Equation (25) has a global attractor of compact sets (see the result in [Chapter 1]27) contained in , which contains all compact invariant sets (with respect to ). But this contradicts Equation (33), and with this the proof is complete.   ▪

Theorem 3.9

There exists an ϵ-neighbourhood of λ₀ in Λ such that for every λ in there is an equilibrium point E _λ corresponding to that is globally asymptotically stable in . In particular, λ can be chosen so that E _λ has all components positive.

Proof

Let . Let be a bounded neighbourhood of E ₁ and let Λ₀ be a neighbourhood of λ₀ granted by Lemma 3.8. We restrict our parameter space to Λ₀ (that is, take ). Then, applying [Corollary 2.3]28 in connection to Lemmas 3.7 and 3.8, we obtain that here exists an ϵ-neighbourhood of λ₀ in Λ such that for every λ in there is an equilibrium point E _λ corresponding to , such that , for all x in X ₁. We can assume that ϵ is sufficiently small such that, by using that has all eigenvalues with negative real parts (see Lemma 3.7), to have E _λ be asymptotically stable, hence it is globally asymptotically stable in X ₁. Now each eigenvalue of the Jacobian of Equation (2) evaluated at zero corresponding to λ₀ (i.e. each eigenvalue of ) is also an eigenvalue of

The determinants of these matrices are

But . Consequently, using Equation (28), we have

Thus . Since eigenvalues of A _λ depend continuously on λ, we can choose λ in sufficiently close to λ₀, but with the corresponding matrix being irreducible, so that to have . Then, using Theorem 3.3, we have that E _λ has all components positive.   ▪

4. Numerical simulations

In the previous section, the dynamical behaviour of the system when Γ is irreducible is well studied, but the behaviour of the model in the case Γ is reducible is not completely clear yet. So, in this section, we present numerical simulations of system (2) when Γ is reducible. In 2, the authors considered a selection–mutation model (without any size-structure) with constant birth rate and linear death rate functions. They proved that if Γ is completely reducible, competitive exclusion occurs while in the case Γ is reducible but not completely reducible, competitive exclusion and coexistence are possible outcomes.

Our main objective in this section is to numerically investigate the dynamical behaviour of model (2) when Γ is reducible and with birth rates not all being constants and death rates not all being linear (cf. 2). To this end, we consider a population with four different ecotypes (phenotypes). We denote by P _i the number of individuals carrying phenotype i, i=1, 2, 3, 4, at time t. We choose the following values of parameters in model (2): and . As for the birth and death functions, we let and . The above parameters are merely chosen to illustrate the dynamical outcome of the model when Γ is reducible.

We focus on the following two cases of reducible Γ (cf. 2): (1) completely reducible (2) reducible but not completely reducible. We fix all the above chosen parameters and vary c in model (2) to investigate the influence of c on the dynamics of P ₁, P ₂, P ₃ and P ₄. Note that, as c increases, the mortality of individuals carrying phenotype 3 increases and thus the fitness of these individuals decreases.

We begin with the first case. Assume that Group A consists of individuals of ecotypes 1 and 2 (i.e. carrying phenotypes 1 and 2) and that the offspring of these two ecotypes belong to Group A. Similarly assume that Group B consists of individuals of ecotype 3 and 4 and that offspring of Group B belong to Group B. We describe such a scenario using the following completely reducible selection–mutation matrix:

From Figure 1, we see that P ₁ and P ₂ go extinct when the value of c is small while P ₃ and P ₄ survive and converge to a positive equilibrium. As the value of c increases and crosses a critical value denoted by , P ₁ and P ₂ survive and converge to a positive equilibrium, while P ₃ and P ₄ go extinct. To have a better view of this, in Figure 2, we zoom on the value c*. In particular, we provide plots for values of c near 0.299. Figure 2 shows that the dynamical outcome of the model is sensitive to c around the value c*. When c<c*, P ₁ and P ₂ go extinct while P ₃ and P ₄ converge to a positive equilibrium; when c>c*, P ₁ and P ₂ converge to a positive equilibrium but P ₃ and P ₄ become extinct; thus 0.299 seems to be a bifurcation value. From Figures 1 and 2, we conjecture that when Γ is completely reducible, the most probable outcome is that of competitive exclusion between groups of ecotypes defined by the blocks of the completely reducible matrix Γ. In the example above, Γ has two blocks which define two groups A=(P ₁, P ₂) and B=(P ₃, P ₄). From the above results, it is clear that Group A survives if c>c* and Group B survives if c<c*. This outcome represents competitive exclusion, where the four ecotypes cannot coexist and the ‘fittest’ group survive (wins the competition). The biological interpretation is as follows: when c is small the mortality of phenotype 3 is small, hence the fitness of these individuals is high and in turn the fitness of Group B is high exceeding that of Group A and driving it to extinction. However, when c increases this reduces the fitness of Group B until if falls below that of Group A. Hence, after the critical point c*, Group A is more fit and wins the competition with Group B.

Figure 1. The dynamical behaviour of P ₁, P ₂, P ₃ and P ₄ with respect to time and parameter c, when Γ is completely reducible.

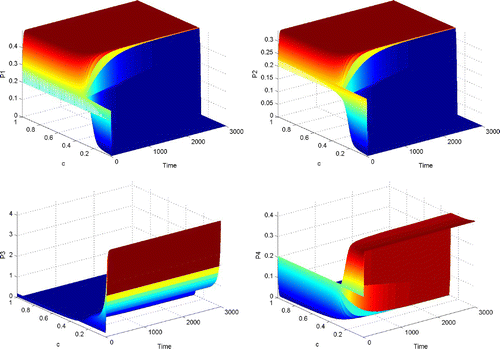
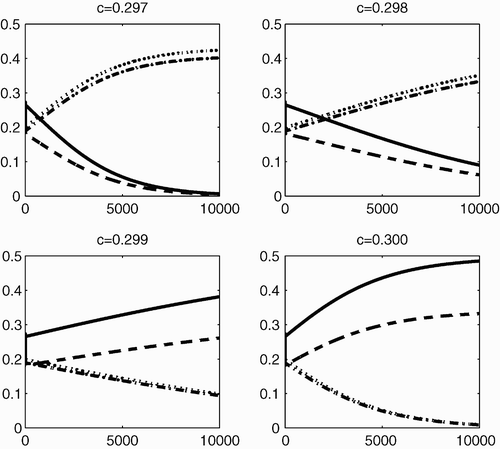
Figure 2. The dynamical behaviour of P ₁ (solid line), P ₂ (dashed line), P ₃ (dotted line) and P ₄ (dashed-dotted line) with respect to time, for different values of c (0.297, 0.298, 0.299 and 0.300), when Γ is completely reducible.

Next we will investigate the dynamical behaviour of model (2) when Γ is reducible but not completely reducible. Still consider the above example of a population with individuals belonging to one of four different ecotypes (carrying one of four phenotypes). Suppose again that ecotypes 1 and 2 are in Group A and ecotypes 3 and 4 are in Group B. As before, offspring of individuals in Group A belong to Group A. On the other hand, assume that individuals of Group B have a probability of producing offspring in Groups A and B. We describe such a scenario using the following reducible selection–mutation matrix:

The values of the parameters and functions are chosen as in the above example. Note that this Γ is of the form (8). Thus, Theorem 3.5 applies and we know that for this case ecotypes 1 and 2 will always persist. However, Theorem 3.5 does not tell us what happens to ecotypes 3 and 4.

From Figure 3 and Figure 4, we can see that when Γ is reducible but not completely reducible, competitive exclusion and coexistence are possible outcomes of the dynamical behaviour of system (2). When the value of c is small (less than 0.3), coexistence among P ₁, P ₂, P ₃ and P ₄ occurs. As the value of c increases above 0.3, the populations of P ₃ and P ₄ go extinct while P ₁ and P ₂ survive. Thus competitive exclusion occurs.

Figure 3. The dynamical behaviour of P ₁, P ₂, P ₃ and P ₄ with respect to time and parameter c, when Γ is reducible but not completely reducible.

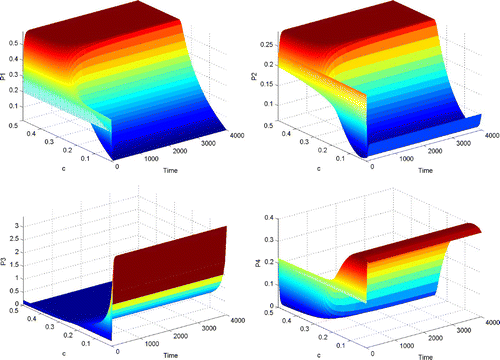
Figure 4. The dynamical behaviour of P ₁ (solid line), P ₂ (dashed line), P ₃ (dotted line) and P ₄ (dashed-dotted line) with respect to time, for different values of c (0.10, 0.15, 0.20, 0.25, 0.30 and 0.35), when Γ is reducible but not completely reducible.

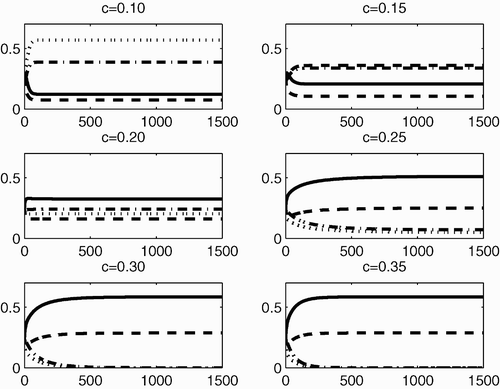
To interpret this biologically, again note that the smaller the value of c the more fit ecotype 3 is, leading to a higher fitness in Group B. Thus, Group B survives and since individuals of Group B produce individuals of Group A, this leads to Group A surviving and hence coexistence occurs. On the other hand, when c becomes large, the fitness of Group A exceeds that of Group B. Thus, Group A survives and Group B goes extinct (since individuals of the more fit Group A do not produce individuals of Group B).

5. Conclusions and future work

In this paper, we analysed a selection–mutation size-structured model where the population consists of n ecotypes. We showed that, in the case of an irreducible selection–mutation matrix Γ (i.e. when individuals of one subpopulation contribute directly or indirectly to individuals of another subpopulation), the origin is a uniformly weak repeller (see Definition A.3) and all ecotypes coexist in the form of robust uniform persistence. In the case of the pure selection matrix Γ=I (the offspring of one ecotype belong to the same ecotype) the authors in 1 proved that competitive exclusion occurs: the fittest subpopulation survives and all other subpopulations die out. We extended this result and showed, under less restrictive assumptions, that the boundary globally attracting equilibrium corresponding to the fittest ecotype is globally asymptotically stable. Moreover, for Γ irreducible, but ‘close’ to the identity matrix, the model (2) has a globally asymptotically stable interior equilibrium.

Our numerical simulations suggest that, in the case when Γ is completely reducible, competitive exclusion is the most probable outcome, while in the case when Γ is reducible, but not completely reducible, either competitive exclusion, or coexistence are possible outcomes. Our future efforts will focus on theoretically studying the dynamical behaviour in the reducible case. In particular, we are interested in finding conditions that determine which ecotypes persist and which go extinct.

Furthermore, our numerical results suggest that even in the case of reducible or completely reducible matrix Γ, the total population persists (i.e. at least one ecotype survives). Therefore, we conjecture that Theorem 3.3 can be established by dropping the assumption on irreducibility. In fact, we discussed this case, but only for a particular form of Γ, as given in Equation (8). As we already mentioned, more general cases can be treated by using similar ideas, but then explicit conditions for uniform persistence are improbable to obtain, as one needs information about the dynamics on the boundary corresponding to the extinction states, and this dynamics could be quite complicated.

In our model (2), k _i ∈(0, 1) is a fraction of ingested food that is channelled to growth and maintenance and (1−k _i ) is the fraction channelled to reproduction. Throughout our discussion, we assumed that each , is constant. But many populations reproduce seasonally and thus in many cases, k _i are better represented by periodic functions of t. In our future work, we plan to study this periodic version of system (2).

Acknowledgements

The authors would like to the thank an anonymous referee for his valuable comments and in particular for suggesting Theorem 3.5. The research of A.S. Ackleh and Baoling Ma is supported in part by the National Science Foundation under grant # DMS-0718465.

Appendix

Let be the non-negative cone in ℝ ^m . By abusing notation, we define the norm of to be , where |x _i | represents the absolute value of x _i . Let d be the distance induced by this norm, i.e. . S¯ denotes the closure of .

We call a matrix A non-negative (strictly positive), and write, A≥0 (A≫0), if each entry of A is a non-negative (positive) number. We call A positive, and write A>0, if A≥0, but A is not the zero matrix. Assume analogous definitions (and notation) for vectors.

Denote by s(A) and r(A) the stability modulus and the spectral radius of a matrix A, respectively. I denotes the identity matrix (whose dimension will be clear from the context).

Consider a differential equation

for which we assume existence and uniqueness of solutions. Let be the dynamical system (or semiflow) generated by Equation (A1).

Let be continuous and not identically zero. Let and , for some set , where ω(x) represents the omega limit set of x. A set S is said to be positively invariant (with respect to φ) if x∈S implies , .

Definition A.1

The system (A1) is called uniformly (strongly) ρ-persistent if there is an such that , whenever .

Usually ρ is referred to as the ‘persistence function’. Also, one may omit the word ‘strongly’ and just say ‘uniformly persistent’.

The next theorem, which is a particular case of Theorem 3 in 30, is well known in persistence theory and is one of the main tools used for our persistence results. Detailed explanation of the terminology used in this theorem (e.g. invariant set, isolated set, etc.) can be found, for example, in 27 30 34.

Theorem A.2

Assume that the following hold:

• (1) φ has a global attractor (of points).

• (2) There exists a finite sequence of disjoint, compact and invariant sets in X ₀ having the properties:

  • (a) ;

  • (b) S is acyclic;

  • (c) S _i is isolated in ;

  • (d) .

Then Equation (A1) is uniformly (strongly) ρ-persistent.

W ^S (S _i ) above denotes the stable manifold of the set S _i , that is, , where .

However, verifying conditions (c) and (d) in the above theorem can be quite a task, even when the sets S _i are ‘simple’, such as equilibria or periodic orbits. If S _i s are uniformly weak repellers (see definition below) then these conditions are satisfied, with the additional requirement (for c)) that S _i be asymptotically stable in X ₀. Characterization of such boundary attractors as uniformly weak repellers can be found in 24, or in 25 26 (for discrete time).

Definition A.3

A non-empty set is called a uniformly weak repeller if there exists such that .

A square non-negative matrix A is called: (1) reducible, if it can be set in the form

by interchanging its rows and columns (i.e. by reordering the standard basis vectors), where B and D are non-negative square matrices; (2) irreducible, if it is not reducible; (3) completely reducible, if it is the direct sum of square non-negative irreducible matrices, that is, A can be set in the form

by interchanging its rows and columns, where are square non-negative irreducible matrices; (4) primitive, if there exists a positive integer k such that all entries of A ^k are positive.

Assume that x(t) satisfying Equation (A1) can be written as , where and A(x) is a continuous matrix function such that A(x ¹, 0) is quasipositive (it has all off-diagonal entries non-negative). In this setup, x ¹(t) could be an empty vector, in which case x ²(t)=x(t). Assume that the set , as well as its complement, is positively invariant for Equation (A1). Let M be a compact and positively invariant set contained in . Let P(t, x) denote the fundamental matrix of solutions for

where u(t) has the same dimension as x ²(t).

Given a periodic orbit 𝒫 of Equation (A1), of period T>0, r(P(T, x)) has the same value for all (see [Lemma 3.10]24). Denote this common value by . Next result, reproduced here (in a simplified form) from 24 ([Corollary 3.12]24), is especially useful in the particular case when the boundary attractor consists of periodic orbits.

Lemma A.4

Assume that Ω(M) is a union of periodic orbits and the following hold:

• (1)  a periodic orbit of period T, is primitive;

• (2)  for each periodic orbit .

Then M is a uniformly weak repeller.