Global behavior of solutions of a periodically forced Sigmoid Beverton–Holt model

Abstract

Our aim in this paper is to investigate the boundedness, the extreme stability, and the periodicity of positive solutions of the periodically forced Sigmoid Beverton–Holt model:

where {a _n } is a positive periodic sequence with period p and δ>0. In the special case when δ=1, the above equation reduces to the well-known periodic Pielou logistic equation which is known to be equivalent to the periodically forced Beverton–Holt model.

Keywords:

• Sigmoid Beverton–Holt model
• periodically forced
• extreme stability
• periodicity
• attractivity

AMS Subject Classification :

• 39A23
• 39A30

1. Introduction and preliminaries

In this paper, we investigate the boundedness, the extreme stability, and the periodicity of solutions of the periodically forced Sigmoid Beverton–Holt model

with initial condition

and where {a _n } is a positive p-periodic sequence such that

In the special case when δ=1, Equation (1) reduces to the well-known periodically forced Pielou logistic equation

({a _n } is a positive p-periodic sequence) which is also equivalent to the periodically forced Beverton–Holt equation

({K _n } and {r _n } are positive p-periodic sequences, r _n >1). The dynamics and properties of both equations have been studied in great detail in recent literature (see, for example 3 4 5 6 9 10 11 12 13 16 17 18 19 20 21 22 23 24 25 26 30 36 39)

The autonomous case of Equation (1)

where a, δ>0, has been introduced by Thompson 41 as a “depensatory generalization of the Beverton–Holt stock-recruitment relationship used to develop a set of constraints designed to safeguard against overfishing”. This model has been used in the study of fish population dynamics, particularly when overfishing is present 15 33 34 35 40. A very important feature of the Sigmoid Beverton–Holt model is that, in the case δ>1, it exhibits the so-called “Allee effect.”

The “Allee effect” is originally attributed to W.C. Allee 1 8 38, who broadly defined it as a “…\ positive relationship between any component of individual fitness and either numbers or density of conspecifics”. Practically speaking, the Allee effect causes, at low population densities, per capita birth rate decline. Under such a scenario, at low population densities, the population may slide into extinction. There are various scenarios in which the Allee effect appears in nature (see 7 8 and references cited therein) and can be attributed, for example, to difficulties in finding mates when the population size is small, a higher mortality rate in juveniles when there are not enough adults to protect them from predation, or uncontrollable harvesting, as in overfishing. On the other hand, the Allee effect can be beneficial in some situations such as in controlling a population of fruit flies which are considered to be one of the worst insect pests in agriculture 7. The techniques used to control them is the release of sterile males to create an Allee effect.

Several discrete mathematical models exhibiting the Allee effect are known and studied in the literature (2 15 33 34 35 40 and references cited therein). They all have the following features in common: (i) the existence of three equilibrium points: 0, T – Allee threshold, and K – carrying capacity of the environment (0<T<K); (ii) equilibria 0 and K are stable, while T is unstable; (iii) if the population size drops below T, then the population slides into extinction, so it approaches 0.

Periodically forced population models exhibiting the Allee effect are relatively new in the literature 14 32 42. In 32 several periodically forced discrete models exhibiting the Allee effect are studied, while a class of general unimodal maps with such properties has been investigated in 14. The effects of harvesting in some periodically forced population models with the Allee effect are studied in 42.

The following proposition summarizes the known results about the dynamics of the autonomous Sigmoid Beverton–Holt model (3). For easy reference in the sequel, we define

Proposition 1

Consider Equation (3) with a, δ>0 and initial condition x ₀>0. Then the following statements are true:

	(i) If then Equation (3) has two non-negative equilibria: an unstable equilibrium 0 and a stable positive equilibrium K.
	(ii) If δ=1, then for a∈(0, 1] the only equilibrium of Equation (3) is 0 and it is stable, while for Equation (3) has two non-negative equilibria: an unstable equilibrium 0 and a stable positive equilibrium K=a−1, which attracts all positive solutions.
	(iii) Let and a crit be defined by (4). Then the following cases are possible: (a) If then the only equilibrium of Equation (3) is 0 and it is stable; (b) If then Equation (3) has two non-negative equilibria: the positive equilibrium with the basin of attraction [K, ∞), and the stable equilibrium 0 with the basin of attraction [0, K). (c) If then Equation (3) has three non-negative equilibria: 0, K, and T such that . The 0 equilibrium is stable with the basin of attraction [0, T); T is unstable (repellor), while K is stable with the basin of attraction (T, ∞).

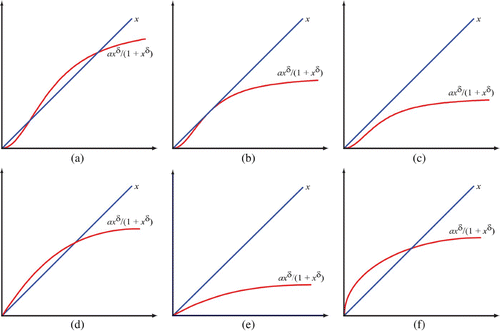
The following graphs (Figure 1) of the function illustrate the above statements.

Figure 1. Graphs of the function ax ^δ/(1+x ^δ). (a) Case δ>1, a>a _crit; (b) Case δ>1, a=a _crit; (c) Case δ>1, a<a _crit; (d) Case δ=1, a>1; (e) Case δ=1, a≤1; (f) Case δ>1.

The study of stability properties and attractivity in non-autonomous systems is far more complex than autonomous systems because non-autonomous systems, in most cases, do not posses an equilibrium. One way to overcome this difficulty is to study the so-called “extreme stability,” the property of the system in which all of the solutions converge to each other. It is a powerful tool in the study of the long-term behavior of solutions that do not necessarily converge to a “nice” structure like an equilibrium or a periodic solution. In particular, in the case of periodic systems, extreme stability appears to provide a means for obtaining an attractivity result not otherwise readily obtained; namely, the extreme stability and existence of a periodic solution imply the uniqueness and the attractivity of that periodic solution. Extreme stability was originally introduced (for continuous systems) by LaSalle and Lefschetz 31. Other approaches include the so-called “convergent systems” – systems in which the solutions all tend to a particular bounded and asymptotically stable solution called a “limiting” solution (see, for example 37 and references cited therein) and “path stability” (see, for example 27 28) which is equivalent to the notion of extreme stability.

A difference equation is said to be extremely stable if for any pair of (positive) solutions {x _n } and {x̄ _n }

Clearly, if {x _n } and {x̄ _n } are bounded from below and above by positive constants ( n=0, 1, …) condition (5) is equivalent to

The following theorems will be useful in the sequel.

Theorem A

(Brouwer fixed point theorem 43) The continuous operator has at least one fixed point when M is a compact, convex, non-empty set in a finite dimensional normed space over .

In this paper, we will consider only the cases when δ≠1. Section 2 is devoted to the case δ>1, while in Section 3, we focus on the case δ<1. In the case δ=1, Equation (1) becomes a well-known periodically forced Beverton–Holt model. The dynamics and properties of solutions of this equation when δ=1 are studied in detail in the literature so we will not consider this case in the sequel. However, for the sake of completeness we are summarizing here the properties of this equation when δ=1 6 9 12 13 18 19 22.

Theorem B

Let {a _n } be a positive periodic sequence with period p. Consider the equation

Then the following statements are true:

	(i) If then all solutions of Equation (6) converge to 0.
	(ii) All solutions of Equation (6) are bounded from above by a positive constant.
	(iii) If then all solutions of Equation (6) are bounded and persisting; that is, they are bounded from above and below by positive constants.
	(iv) If condition (7) is satisfied, then Equation (6) is extremely stable.
	(v) If condition (7) is satisfied, then Equation (6) has a unique positive p-periodic solution and {x̄ n } is a global attractor of all positive solutions.

2. Case δ∈(1, ∞)

In this section we study the global behavior of solutions of Equation (1) in the case when δ>1. First, we introduce the following two technical lemmas:

Lemma 2

Let

where a, δ>0. Then the following statements are true:

	(i) Assume either δ∈(0, 1) or δ=1 and a>1. Let K be the unique positive fixed point of the function f. Then K is an increasing function of a.
	(ii) Assume and a>a crit. Let T and be the only two positive fixed points of the function f. Then T is a decreasing function of a and K is an increasing function of a.

Proof

(i) Clearly K is the only positive solution of the equation

After differentiating the equation with respect to a we obtain

and

and the proof is complete. (ii) In this case both T and K ( are the only positive solutions of the equation . Since then similarly, as in case (i), we obtain

and the proof is complete.   ▪

Lemma 3

Assume that {a _n } is a positive periodic sequence with period p, let . Let the sequence of functions {f _n } be defined by

Then the following statements are true:

	(i) If , then for all x>0
	(ii) If , then the function f n has the unique positive fixed point K n . In addition,
	(iii) If then the function f n has two positive fixed points T n and . In addition and

Proof

The proof, except for (10), follows directly from Proposition 1 and is omitted. From Lemma 2(ii) it follows that K _n is an increasing function of a _n and T _n is a decreasing function of a _n . Let . Then for i=1, …, p we have which implies K _i ≥K _m and T _i ≤T _m . Therefore,

which completes the proof of the lemma.   ▪

In the case when

we have

so for every n=0, 1, … functions f _n have two positive fixed points T _n and K _n , respectively, such that . Each of the sequences {T _n } and {K _n } is p-periodic. The sequence {K _n } represents the\ sequence of carrying capacities, while the sequence {T _n } we will call the sequence of Allee thresholds.

The following lemma establishes the attractivity character of the 0 equilibrium in the case when Equation (1) has no carrying capacities and Allee thresholds.

Lemma 4

Let {a _n } be a positive periodic sequence with period p and . If

then for all positive solutions {x _n } of Equation (1)

Proof

Let {x _n } be a positive solution of Equation (1). From (11) it follows that

% \noindent and by using Lemma 3(i) we obtain

So, {x _n } is decreasing and bounded from below by 0 and it converges to a non-negative limit

Assume, for the sake of contradiction, L>0. Then, by letting in Equation (1) we obtain that the sequence {a _n } also converges, which is impossible since {a _n } is p-periodic. Therefore, L=0 and the proof is complete.   ▪

The next theorem establishes the existence of invariant intervals for the given equation.

Theorem 5

Assume that {a _n } is a positive periodic sequence with period p, and

Then the following statements are true:

	(i) All positive solutions of Equation (1) are bounded from above by a positive constant.
	(ii) Equation (1) has an invariant interval [A, B] where and {K n } and {T n } are p -periodic sequences of carrying capacities and Allee thresholds of Equation (1), respectively.
	(iii) Equation (1) has an invariant interval [0, C] where and {T n } is the p -periodic sequence of Allee thresholds of Equation (1).
	(iv) If x 0>B, then for some positive integer k.

Proof

(i) Let {x _n } be a positive solution of Equation (1). Then for n=0, 1, …

Therefore,

so the sequence {x _n } is bounded from above. (ii) Consider the sequence of functions {f _n } defined by Equation (9). Since f _n is increasing and A<B we have

Also, since

from Lemma 3(iii) we obtain

Also,

and we get

so [A, B] is an invariant interval for Equation (1); that is,

(iii) Since f _n (0)=0 and

from Lemma 3(iii) we obtain

so

and [0, C] is an invariant interval for Equation (1). (iv) It follows directly from Lemma 3(iii). The proof is complete.   ▪

The following technical lemma will be useful in the sequel.

Lemma 6

Let {a _n } be a positive periodic sequence with period p, and let {K _n } be the sequence of carrying capacities and let {T _n } be the sequence of Allee thresholds of Equation (1). If

then the following statements are true:

	(i) If and then the function g n is increasing on (0, x c ) and decreasing on .
	(ii)  .
	(iii) Let {x n } be a solution of Equation (1). If for some non-negative integer k, then there exists an integer l>k such that for all i≥l.
	(iv) Let α∈(0, 1). Then the function is increasing with respect to x on and decreasing on .
	(v) There exists α∈(0, 1) such that In addition for such α,
	(vi) Let {x n } be a solution of Equation (1) such that for n=0, 1, …. Then there exist α∈(0, 1) and a positive integer l such that for all i≥l.

Proof

(i) The proof follows directly from

(ii) Since using inequality (14) we obtain

From Lemma 3(iii) it follows that

which implies

Since f _n (B)<B, then B>K _n for all n and the remaining inequality follows. (iii) Let for some non-negative integer k. The following two cases are possible. Case 1. x _c ≤A. Then x _k ≥x _c and we have, since the function f is increasing,

and by induction we conclude x _i >x _c for all i>k, which completes the proof. Case 2. A<x _c <B. If for some k, x _k ≥x _c then, as in case 1, we obtain x _i >x _c for all i>k. So assume for the sake of contradiction for all i≥k. Since for all i we have

and by induction we obtain that {x _n } eventually increases. Since it is bounded it converges

This implies that {a _n } also converges and that is a contradiction. (iv) Again, as in part (i) the proof follows directly from

(v) Let and consider the function for . Since then ϕ increases for and we have . Since , and then there exists such that . Taking we obtain from which (15) follows. Since

from Lemma 3(iii) it follows that

which implies (16) and completes the proof of part (v). (vi) The proof is similar to the proof of part (iii) where x _c is replaced with . Using α∈(0, 1), the existence of which is established in part (v), and the fact that, for such α, the conclusion follows and the proof is complete.   ▪

The next theorem establishes the asymptotic behavior of solutions trapped in each of the invariant intervals.

Theorem 7

Assume that {a _n } is a positive periodic sequence with period p, and let condition (12) hold. Let {x _n } and {y _n } be two positive solutions of Equation (1). Then the following statements are true:

	(i) If for some non-negative integer k, where then
	(ii) If for some non-negative integer k, where then

Proof

(i) Since we have x _k <T _k and from Lemma 3(iii) it follows that

Since [0, C] is an invariant interval, by induction, we obtain x _n+1<x _n , for n≥k, so {x _n } converges to a non-negative limit:

Then each of the subsequences also converges to x:

By letting in

we obtain

This is true only for x=0 since, according to Lemma 3(iii) we have f _p (x)<x, for 0<x<C<T _p . (ii) Let {x _n } and {y _n } be two positive solutions of Equation (1) such that

% \noindent where

Then, from Theorem 5(ii) it follows that

According to Lemma 6(iii), without loss of generality, we may assume

where . Assume that for some integer k≥0

The case when x _k /y _k <1 is similar and the proof will be omitted. Then, since the function is increasing, we have

Also, since the function for δ>1, is decreasing on the interval we obtain

By induction, it follows that the sequence {x _n /y _n } is bounded from below by 1 and non-increasing so it converges. Let

Assume, for the sake of contradiction, L>1. Let such that . Then there exists a positive integer such that

From Lemma 6(vi) it follows that there exist α∈(0, 1) and a positive integer l such that for all i≥l. Furthermore, from Lemma 6(iv) it follows that the function is decreasing on , so we obtain, for

% \noindent and

Since is arbitrary, it follows

which is a contradiction. Therefore,

and the proof of the theorem is complete.   ▪

The existence of an attracting p-periodic solution is established in the following theorem.

Theorem 8

Assume that {a _n } is a positive periodic sequence with period p and let and let condition (14) hold. Let [A, B] be an invariant interval of Equation (1) where

and where {K _n } and {T _n } are p -periodic sequences of carrying capacities of Allee thresholds of Equation (1), respectively. Then, in the interval [A, B], there exists a unique p -periodic solution {x̄ _n } of Equation (1) \ for n=0, 1, …)\ which attracts all positive solutions of Equation (1) with initial conditions in [A, ∞).

Proof

Proving the existence of a p-periodic solution of Equation (1) is equivalent to showing that the following nonlinear system

has a positive solution . Define the function by

where the sequence of functions {f _n } is defined by Equation (9). To establish the existence of a positive solution of system (17) it suffices to show that the function F has a positive fixed point. Since [A, B] is an invariant interval of Equation (1), we have so

% \noindent where and . Then

or

Clearly, [A, B] ^p is a compact, non-empty and convex set in ℝ ^p , so by applying Theorem A we obtain that the function F has a fixed point . Defining the sequence {x̄ _n } as

we obtain that {x̄ _n } is a p-periodic solution of Equation (1). Furthermore, from Theorem 7(ii) we obtain

for all positive solutions {x _n } of Equation (1) with initial conditions in [A, B]. Therefore, {x̄ _n } attracts all such positive solutions. If then from Theorem 5(iv) it follows that for some positive integer k, x _k ≤B and such solution will be also attracted by {x̄ _n }. So {x̄ _n } attracts all positive solutions with initial conditions in [A, ∞). Furthermore, {x̄ _n } is a unique positive p-periodic solution of Equation (1) in the interval [A, B]. Otherwise, the existence of another p-periodic solution will contradict the attractivity of {x̄ _n }. The proof is complete.   ▪

Our next step is to focus on the study of the character of solutions when initial conditions are near the Allee thresholds . We will examine preimages of the map f _n , defined by (9) in the case when . Namely, from Equation (1) we get

Since the sequence {a _n } is p-periodic it can be easily extended for negative values of n as

So, starting with and using (18) we can evaluate inverse images and we can continue this process as long as terms remain in the interval .

Consider the difference equation

where the p-periodic sequence {b _n } is defined as

The following technical lemma establishes the relationship between the periodic solutions of Equations (1) and (19).

Lemma 9

Assume that {a _n } is a positive periodic sequence with period p, and let condition (14) hold. Assume that is a positive p -periodic solution of Equation (19) with (20). Then Equation (1) has a positive p -periodic solution defined by

Proof

Since is a positive p-periodic solution of Equation (19) we have

which is equivalent to

Finally, using (21) we obtain

so , defined by (21) is a positive p-periodic solution of Equation (1).   ▪

Next we define the p-periodic sequence of functions {p _n } as

where {b _n } is given by (20). The following technical lemma summarizes the properties of functions p _n and will be useful in the sequel.

Lemma 10

Assume that {a _n } is a positive periodic sequence with period p, and conditions (14) and (20) hold. Let the sequence of functions {f _n } and {p _n } be given by (9) and (22), respectively, and let the positive p -periodic sequences {S _n } and {L _n } be defined by

Then the following statements are true:

	(i) Functions f i and p p−1−i are inverse to each other and
	(ii) Functions p n , for n=0, 1, … are increasing on (0, ∞).
	(iii)
	(iv)
	(v) Functions n=0, 1, … are decreasing on the interval
	(vi) For every the functions n=0, 1, … are decreasing on the interval .

Proof

(i) For from (20) we obtain

and

We will only prove for n=0, 1, …. The proof of \ is similar and it is omitted. Since for we obtain

Using the periodicity of {p _n } and {S _n } we obtain for n=0, 1, …. (ii) It follows directly from the fact that f _i and p _p−1−i are inverse to each other and f _i is increasing. (iii) Let where . From Lemma 3(iii) it follows that . Since p _i is increasing and inverse to f _p−1−i we have . Similarly, the other inequalities follow. (iv) It is trivial, so the proof is omitted. (v) Since

it follows that q _n (x) decreases for . Therefore, all functions q _n (x), n=0, 1, … decrease on . (vi) Similarly as in part (v) we obtain

so the functions are decreasing on .   ▪

Next we establish the existence of an invariant interval for Equation (19) and study the asymptotic behavior of solutions which are trapped in it.

Theorem 11

Assume that {a _n } is a positive periodic sequence with period p and let and let conditions (14) and (20) hold. Then the following statements are true:

	(i) Equation (19) has an invariant interval [D, E]where and where {K n } and {T n } are p -periodic sequences of carrying capacities and of Allee thresholds of Equation (1), respectively.
	(ii) If for some non-negative integer k, where {u n } and {v n } are two solutions of Equation (19), then

Proof

(i) Since

from Lemma 10(ii)–(iii) it follows that

so the interval [D, E] is invariant. (ii) Let {u _n } and {v _n } be two positive solutions of Equation (19) such that

Then, from part (i) it follows that

Assume that for some integer k≥0

The case when u _k /v _k <1 is similar and the proof will be omitted. Then, since the function p _n (x) is increasing, we have

Also, since the function is decreasing on the interval and we obtain

By induction, it follows that the sequence {u _n /v _n } is bounded from below by 1 and non-increasing so it converges. Let

Let such that . Then there exists a positive integer such that

Let satisfy the condition

Since

is equivalent to

we obtain that such an α exists. Then the function is decreasing on . Then, for we obtain

and

Since is arbitrary, it follows

which is a contradiction. Therefore,

and the proof of the theorem is complete.   ▪

Next, we will prove the existence of a p-periodic solution of Equation (19) and therefore of Equation (1).

Theorem 12

Assume that {a _n } is a positive periodic sequence with period p and let and conditions (14) and (20) hold.

	(i) Let [D, E] be an invariant interval of Equation (19) where Then Equation (19) has a unique p -periodic solution \ for n=0, 1, …\ which attracts all positive solutions of Equation (19) with initial conditions in [D, E].
	(ii) In the interval [D, E] there exists a unique p -periodic solution of Equation (1), which is defined by

Proof

(i) Proving the existence of a p-periodic solution of Equation (19) is equivalent to showing that the following nonlinear system:

has a positive solution . Define the function by

where the sequence of functions {p _n } is defined by (22). To establish the existence of a positive solution of the above system it suffices to show that the function G has a positive fixed point. Since [D, E] is an invariant interval for the functions p _n , n=0, 1, …, we obtain

Then

or

Clearly, [D, E] ^p is a compact, non-empty, and convex set in ℝ ^p , so by applying Theorem A we obtain that the function G has a fixed point . Defining the sequence as

we obtain that is a p-periodic solution of Equation (19). From Theorem 11(ii) it follows that attracts all positive solutions of Equation (19) with initial conditions in [D, E]. Then, clearly, is a unique positive p-periodic solution of Equation (19) in the interval [D, E]. Otherwise, the existence of another p-periodic solution in the same interval contradicts Theorem 11(ii). (ii) It follows directly from part (i) and Lemma 9. The proof is complete.   ▪

3. Case δ∈(0, 1)

In this section we consider the remaining case when δ∈(0, 1). Most of the proofs are similar to the proofs from the previous section and so we will only provide outlines indicating some possible differences.

Lemma 13

Assume that {a _n } is a positive periodic sequence with period p and let δ∈(0, 1). Then Equation (1) has a unique positive p -periodic sequence of carrying capacities {K _n } where K _n is a unique positive fixed point of the function f _n defined by

that is, it is a unique positive solution of

Proof

The existence of carrying capacities {K _n } follows directly from Proposition 1(i) while its periodicity is the consequence of the periodicity of {a _n }.   ▪

Theorem 14

Assume that {a _n } is a positive periodic sequence with period p and let δ∈(0, 1). Then the following statements are true:

	(i) All positive solutions of Equation (1) are bounded from above and below by positive constants.
	(ii) Equation (1) has an invariant interval [A, B] where and where {K n } is the p -periodic sequence of carrying capacities of Equation (1). Also, all solutions {x n } of Equation (1) become trapped in an invariant interval [A, B].

Proof

(i) Let {x _n } be a positive solution of Equation (1). Then, by applying the same arguments as in the proof of Theorem 5(i) we obtain so the sequence {x _n } is bounded from above. Consider the sequence of functions {f _n } defined by (24). Clearly, the functions f _n (n=0, 1, …) are increasing and from Proposition 1 satisfy the following condition:

Let A be a positive number which satisfies and let m be the smallest non-negative integer such that x _m ≥A. Clearly, such an integer exists. Otherwise, for all n=0, 1, …

and

Therefore, the sequence {x _n } is increasing and bounded from above so it converges to a positive limit . By letting in Equation (1) we obtain that {a _n } converges and that is impossible since it is periodic with period p. Next we will show, by induction, that

So assume x _n ≥A. The following two cases are possible: Case 1: . Then

Case 2: . Then, since the function f _n is increasing we get

Therefore, x _n+1>A and by induction inequality (25) follows. Therefore,

so {x _n } is bounded from below and the proof of part (i) is complete. (ii) Consider the sequence of functions {f _n } defined by (24). Since f _n is increasing and A<B we have . Also, since we have

Thus [A, B] is an invariant interval for Equation (1), that is

Finally, from the proof of part (i) is follows that all solutions become eventually trapped in an invariant interval [A, B], which completes the proof.   ▪

Theorem 15

Let {a _n } be a positive periodic sequence with period p and let δ∈(0, 1). Then the following statements are true:

	(i) Equation (1) is extremely stable.
	(ii)  Equation (1) has the unique p-periodic positive solution {x̄ n } which is a global attractor of all positive solutions of the same equation.

Proof

(i) Let {x _n } and {y _n } be two positive solutions of Equation (1). Assume that for some integer k≥0

The case when x _k /y _k <1 is similar and the proof will be omitted. Then, since the function is increasing, we have

Also, since the function is decreasing for we obtain

By induction, it follows that the sequence {x _n /y _n } is bounded from below by 1 and non-increasing so it converges. Let

Assume, for the sake of contradiction L>1. Let such that . Then there exists a positive integer such that

Then

Since is arbitrary it follows that

which is a contradiction. Therefore

and Equation (1) is extremely stable. (ii) The proof is similar to the proof of Theorem 8 and it is omitted.   ▪

4. Concluding remarks

The dynamics in the case δ∈(0, 1) in many ways mimics the dynamics of the periodic Pielou difference equation, that is the case δ=1. Furthermore, some of our results obtained here also can be obtained from the recent results of Krause 29. The most interesting case is clearly the case δ>1. However, in such a case there are several open questions that need further investigation.

First, the condition

is sufficient for the existence of Allee thresholds {T _n } and carrying capacities {K _n } of Equation (1). On the other hand, in the case

there are no Allee thresholds and carrying capacities and all positive solutions of Equation (1) tend to 0. It is not clear what happens when neither of the above two conditions is satisfied; that is, when

or, equivalently, when there exists such that and .

Next, in the case when the existence of two attractors (0 and a p-periodic solution) and one repellor (another p-periodic solution) was established. The complete description of basins of attraction of attractors is an open question.

Both problems could be approached by focusing on the special cases p=2 and 3 before attempting to solve the general case.

Acknowledgements

Thanks are due to the anonymous referees for making valuable comments that were incorporated in the final version of the paper.