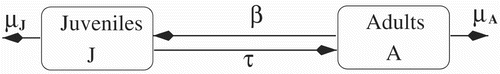A multi-structured epidemic problem with direct and indirect transmission in heterogeneous environments

Abstract

In this work, we analyse a deterministic epidemic mathematical model motivated by the propagation of a hantavirus (Puumala hantavirus) within a bank vole population (Clethrionomys glareolus). The host population is split into juvenile and adult individuals. A heterogeneous spatial chronological age and infection age structure is considered, and also indirect transmission via the environment. Maturation rates for juvenile individuals are adult density-dependent. For the reaction–diffusion systems with age structures derived, we give global existence, uniqueness and global boundedness results. A model with transmission to humans is also studied here.

Keywords:

• multi-structured
• epidemic problem
• heterogeneous environment

AMS Subject Classification :

• Primary: 35Q92
• 35K58
• 92D25
• 92D30

1. Introduction

We are mainly interested in the mathematical analysis of a deterministic mathematical model describing the propagation of a macroparasite within a single-structured host population. This study is supplemented by a related epidemiological model, wherein a macroparasite is transmitted from a reservoir host population to a second host population. This work is motivated by the specific Puumala hantavirus (PUU) – bank vole (Clethrionomys glareolus) system in Europe. In that particular system, the macroparasite is benign in the reservoir host population and can be transmitted to humans, an epidemiological dead end, with a mild lethal impact (see 22–24,31 32 for details).

First, in addition to the age-dependence that is commonly used in population dynamics 2,14–16,28, we want to take into account a stage structuration, due to the fact that the sexual maturation of juveniles depends on the density of adults: the higher the density of the adults, the slower the maturation 24. We have included that the hantavirus seems not to affect the demography of the bank vole population (but may be lethal for humans) and that there is no vertical transmission of the disease (offspring of infected individuals are healthy at birth). Two modes of horizontal propagation are considered: by direct contacts from infected to healthy individuals, and by contacts of healthy individuals with the environment that can be contaminated by infected individuals 24. In addition to time and chronological age, we consider a third structure variable which is the age of the disease in a given animal. This first model was constructed and studied in Wolf 30. Numerical simulations based on this model 31 lead to dynamics close to those which were observed on fields.

Moreover, bank voles also move in space, but the previous model does not take into account this fact. A spatial-dependent model was constructed and studied in Wolf et al. 32. This model highlighted the importance of the spatial structuration in infection evolution, at local and global scales. But the model studied there was simply structured for age and disease status (non-infected and infected juveniles or adults), which is not well adapted to the evolution of the disease 30.

The purpose of this work is to suggest and analyse a model combining the whole of these important phenomena into a single system. This will lead to a strongly structured system which is too complex for qualitative studies of the dynamic. Nevertheless, we prove that the solution of this system is unique and bounded and thus this model is a good one in order to understand the epidemic spreading and dynamic.

In Section 2, we construct a disease-free model for a closed population; we derive here a global existence, uniqueness result and then we give a global uniform bound on solutions.

Next in Section 3, we construct the epidemic model and supply global existence, uniqueness and boundedness results.

Then in Section 4, we look at a simplified model which includes transmission of the parasite to a second host population.

Lastly in Section 5, we give the proof of the results stated in the previous sections.

2. The JA disease-free model

In this section, we analyse a disease-free demographic model described in Section 1.

2.1. Modelling

The construction of the model is first based on a disease-free one for the host population. Because of intraspecific competition and different behaviours between juvenile and adult individuals (5 17 22 and references therein), the host population is split into juvenile (J) and adult (A) sub-populations. Let J(t, x, a) and A(t, x, a) be their respective densities at time t, position x∈Ω, , n≥1, and chronological age for juveniles and for adults, with a ₁>0 16 26 28. The host population reads . We assume maturation of juveniles depends on the total density of adults and cannot occur prior to age a ₁. Let be the maturation rate at time t of juveniles having age a and position x for a spatial density of adults given by ; we assume τ is non-increasing with respect to the last variable, 𝔸. Let , be the adult fertility rate depending on the spatial population density given by . Let and be the respective mortality rates for juveniles and adults.

The resulting compartmental model is depicted in Figure 1; see Wolf et al. 32.

Figure 1. The juvenile–adult host population system.

Populations disperse via Fickian law with diffusion rates d _J (t, a, x) and d _A (t, a, x). The resulting mathematical model is the following:

with

and

2.2. Assumptions

We introduce a set of conditions used through out this work.

Definition 2.1

Suppose:

•	,
•	is non-negative,
•	is non-negative,
•	, ∀ R>0 is non-negative,
•	, ∀ R>0 is non-negative.

Let

Definition 2.2

For all R>0,

•	There exists such that for ,
•	There exists K τ(R)>0 such that for ,
•	For Z=J, A, there exists K Z (R)>0 such that for ,

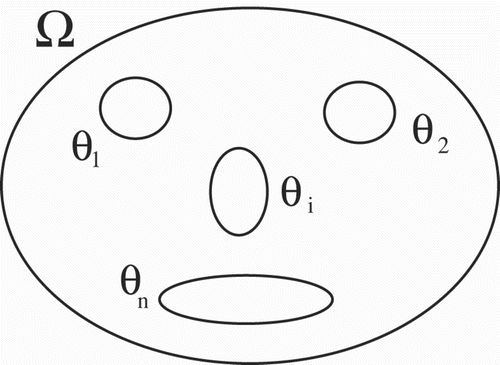
Let Ω be an open-bounded domain in ℝ ⁿ with a smooth boundary , such that locally Ω lies on one side of its boundary. Let η(x) be a unit normal vector to Ω along . In order to take into account spatial heterogeneities, we introduce open subsets θ _i with , having the same regularity properties as Ω (Figure 2).

Figure 2. The spatial domain.

Let:

and assume diffusion rates satisfy the following:

Definition 2.3

For Z=J, A, we suppose that

•	,
•	for , where .

Remark 2.4

Discontinuity in diffusion rates implies that we cannot expect the spatial regularity afforded by classical diffusion processes. Systems with such diffusion rates are, for example, studied in Fitzgibbon et al. 8–10,12.

2.3. Main results

We are now interested in the study of system (1) and (2). We first establish the existence of weak solutions, for which a definition is given below (see also 13 19 21).

Definition 2.5

For (J, A) is a weak solution of Equations (1) and (2) in if

solution in the weak form of Equations (1) and (2), this is as follow:

for all and all and satisfying initial conditions of Equations (1) and (2).

and a similar definition for :

Definition 2.6

For (J, A) is a weak solution of Equations (1) and (2) in if for all (J, A) is a weak solution of Equations (1) and (2) in .

We have the following Theorem:

Theorem 2.7

Suppose that assumption Hypothesis 2.1–2.3 are satisfied and that initial conditions (J ₀, A ₀) are continuous, non-negative and L ^∞ in Q _{J, a} and Q _{A, a} . Then for all T>0 problems (1) and (2) have a unique global weak solution (J, A) with non-negative components defined in .

Remark 2.8

We could also consider continuous μ _J and μ _A going to infinity when a is going to a _† when . It follows that densities go to 0 in a _†; see Naulin 21. An additional truncation step is then required in the following proofs.

The proof goes through several steps: first we solve two auxiliary problems, then we derive a fixed point method. The proof can be found in Section 5.1.

Under additional assumptions, we establish a global bound L ^∞ for solutions of system (1) and (2). More precisely, we prove that we can estimate quantities and independently on t.

The additional assumption are

Hypothesis 2.9

Diffusion rates d _J and d _A are not dependent on chronological age a. and, in order to consider death rates of logistic types:

Hypothesis 2.10

For Z=J, A, we have an under bound of the form: there exists such that

Thus one has:

Theorem 2.11

Suppose assumption Hypotheses 2.1–2.10 satisfied and with non-negative components. If (J, A) is a solution of system (1) and (2), then there exists a positive constant independent on t such that

The proof is based on many estimates derive by iterations each depending on the others and is given in Section 5.2.

3. Epidemic model

We are now interested in the analysis of an epidemic model.

3.1. Modelling

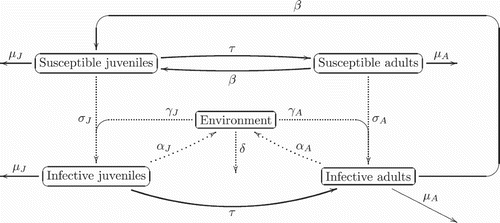
Concerning the epidemic model for a single-host population, we shall consider a basic SI model with susceptible (S) and infective (I) classes. Newly infected individuals highly excrete the virus and are very infectious, but chronically infected individuals excrete very few viruses and are less infectious 23. Thus, we will consider a continuous age structure with the age of infection b≤b _† where the age of infection is the duration of the disease. Then we have four classes of population

•	J s (t, a, x) represents susceptible (i.e. not yet infected) juveniles,
•	represents infected juveniles witch is infected since a time b
•	A s (t, a, x) represents susceptible adults,
•	and represents adults infected since a time b

We assume the microparasite is benign in the host population: this means there is no additional mortality due to the parasite, fertility and maturation rates, as well as diffusivities of infected individuals being identical to those of susceptibles. We use different incidence functions for direct transmission of the parasite from infected individuals, since different times b to susceptibles: a frequency-dependent rate for the former and a density-dependent one for the latter 4 6 7.

In our model, we also consider that indirect transmission of the parasite through the environment is possible. We shall also need an equation to handle the evolution of the proportion (G) of the contaminated environment. The resulting compartmental model is depicted in Figure 3 31.

Figure 3. Epidemic model with continuous age of infection structure.

For direct propagation, newly infected individuals are more infective than chronically infected ones. Then the type of incidence change with the age of the infection (mass action type incidence is dominant for small values of b and proportionate mixing type incidence is dominant for high values of b). The incidence functions are given below (Equation (7)).

Indirect transmission occurs by via the release of the virus from the faeces, vomit, urine and other bodily fluids. Hence, infective individuals will contaminate the environment at a rate (α _J or α _A depending on the infected class); while susceptible individuals are infected by the contaminated environment at a rate for juveniles and for adults. G(t, x) represents the proportion of the contaminated environment. We consider that the environment eliminates viruses with time at a rate . Let 𝕀 (t) be the density of infected individuals, and G(t)≥0 be the percentage of contaminated environment; for unstructured population, an equation for G(t) has the form: 3.

The resulting compartmental model is depicted in Figure 3.

The resulting mathematical model couples the partial differential equations to an ordinary differential equation.

Let , the system corresponding to the epidemic model is

with the ordinary differential equation

and considering the initial conditions:

and Neumann boundary conditions: for Z=J, A,

The matrix of diffusion rates D and vectors Φ(U) for demography, Ψ(U) for transmission rates in the host population (direct and indirect), and Υ representing the environment contamination by infected individuals are as follows:

and, for Z=J, A:

Finally, we set for

Remark 3.1

Integrating in b the equation for J _i and adding the result with the equation for J _s on one hand and those for A _i and A _s , on the other hand, one gets system (1) and (2).

3.2. Assumptions

We suppose that initial conditions in t=0 , , and are continuous, non-negative and L ^∞. In addition to assumptions Hypotheses 2.1–2.3, concerning demographic and diffusion rates, we make the following two assumptions concerning transmission rates.

Definition 3.2

•	for Z=J, A, let be non-negative with:
•	for Z=J, A and z=n, c, let be non-negative with:
•	and for Z=J, A, Z′=j, a, and z=pm, am let be non-negative with:

Definition 3.3

Let in and in with .

This last assumption is useful to prove Lemma 5.18 which is used to treat the proportionate mixing part in the following:

In order to simplify the notations, we set the following:

and

And for T>0:

3.3. Mains results

As in the previous section, we prove existence and uniqueness of a global weak solution for system (3)–(6). The notion of weak solution is defined in Definitions 2.5 and 2.6.

We have the Theorem:

Theorem 3.4

Suppose assumptions Hypotheses 2.1–2.3, 3.2 and 3.3 are satisfied, and that initial conditions are continuous, non-negative and L ^∞ in Q _{J, a} and Q _{A, a} . Then for all T>0 problem (3)–(6) has a unique global weak solution with non-negative components, with and defined in .

The proof is similar to those of Theorem 2.7. Details for the points that make it more complicated are given in Section 5.3.

As for the JA demographic model, assuming assumption Hypothesis 2.9 is satisfied, it follows:

Theorem 3.5

Suppose assumptions Hypotheses 2.1–2.10, 3.2 and 3.3 are satisfied. If is a solution of system (3)–(6) with non-negative and , then there exists a positive constant independent on t such that

Proof

We have seen that . Furthermore, it is easy to check that is invariant by a system (3)–(6). Thus, integrating on b the equation for J _i and adding the equation of J _s, but also those for A _i and A _s, one gets Equations (1) and (2). One can conclude using Theorem 2.11.   ▪

4. Model with transmission to humans

Let us now consider the situation where the parasite is indirectly transmitted through the environment from the previous host population, a reservoir, to a second host population spatially distributed in a neighbouring spatial domain (Ω _H ) with . Assuming different times scales between these two host populations, neither age structure nor demography are considered in the second one. We use a basic spatially structured SIR epidemic model for the second population with an additional mortality rate.

4.1. Modelling

We extend the previous model by taking into account transmission to humans. We consider that this transmission is only due to the contamination of humans by the infected environment. Humans do not contaminate the environment, and there is no transmission from human to human; see Sauvage 22. The model used here is inspired by the works of Sauvage 22 and Fitzgibbon et al. 12. We consider three classes of human population: H _s represents susceptible individuals, H _i represents the infected (but not infectious) individuals and H _r represents recovered individuals, whom we will consider as immune. Let γ_H be the contamination rate by the environment, λ be the rate at which infected individuals are recovered and ϵ be the survival rate of the disease (it can be lethal for humans). Considering the smallness of times for bank voles demography, transmission and incubation of the virus, we do not take demography into account for humans.

It is also useless to introduce an age structure for humans; only a space structure is considered in our model. Thus, the system is composed of Equations (3)–(6) with the additional equations for humans: for t>0 and x∈Ω,

We consider the following assumption:

Definition 4.1

•	Let λ>0 and ,
•	Let be non-negative,
•	and for x∈Ω, let .

Differences with the previous epidemic model comes only from the additional equations for humans. However, the human population is only influenced by the equation for contaminated environment and does not influence equations for the host population neither those for contaminated environment. Thus, results obtained in the previous section are still true and we can study the system (8)–(10) with the minimal assumption that for all T.

We have the following result: see Fitzgibbon et al. 12:

Theorem 4.2

Suppose initial conditions are non-negative and continuous on Ω. Then there exists a unique global classical solution of system (8)–(10) with non-negative components and uniformly bounded on . Furthermore one has the following:

Proof

Local existence comes from the Banach fixed point Theorem. Global existence is granted by a priori estimates and regularity results in Ladyzhenskaya et al. 18. For the system considered here, this a priori estimate comes from the maximum principle and the fact that applied to the three equations for H _s, H _i and H _r; it follows inequalities in Equation (8); see Fitzgibbon et al. 10–12.   ▪

Remark 4.3

Integrating the three Equations (8)–(10) in space and adding them, one gets

thus the global human population is logically non-increasing. This comes from the fact that there is no demographic supply in our model, but only mortality for infected individuals due to the virus.

5. Proofs

5.1. Proof of Theorem 2.7

First, we will study two auxiliary problems, which will be useful in the general case.

5.1.1. First auxiliary problem

We consider the following system:

and we suppose that

Definition 5.1

•	and u 0 is non-negative,
•	and μ is non-negative,
•	and b is non-negative,
•	, with ,
•	d satisfies the assumption Hypothesis 2.3.

Then we have the proposition:

Proposition 5.2

Suppose assumption Hypothesis 5.1 is satisfied. Then problem (11) has a unique solution u in non-negative and satisfying

weak solution of Equation (11), i.e. satisfying

for all and satisfying initial conditions of Equation (11).

Proof

A proof is based on the Galerkin method using a convenient regular basis of H ¹(Ω) and tools of Garroni and Langlais 13. We can also use the characteristics method and classical results for hyperbolic problems 25. We treat here the case , but the case can be treated in similar ways. We begin by considering 0<t<a. Let , , and we set t=c, a=a ₀+c and . Then w is solution of the following linear parabolic problem: for and x∈Ω,

The Classical theory for linear parabolic problems gives existence, uniqueness and non-negativeity of u under the characteristic t=a. When 0<a<t, we consider t ₀>0 and and we set a=c, t=t ₀+c and . Then w is solution of the following linear parabolic problem: for and x∈Ω:

The Classical theory for linear parabolic problems gives existence, uniqueness and non-negativeity of u over the characteristic t=a.   ▪

There exists for parabolic equations a comparison theorem, from which we can get from the previous proof the following corollary:

Corollary 5.3

If in Q _J , in Q _{J, a} , in Q _J and in Q _J then corresponding solutions of system (11) satisfies in Q _J .

We now establish a boundedness result for the solution of system (11):

Proposition 5.4

Suppose that assumption Hypothesis 5.1 is satisfied for all T>0. Then: If , for all T>0 there exists a constant M ₀(T)>0 depending on such that u solution of Equation (11) satisfies

If for all T>0 and all ā>0, there exists a constant depending on such that u solution of Equation (11) satisfies

Proof

We only deal with the case . Yet we know that u≥0 and using Corollary 5.3 it is sufficient to consider the case of . We use the characteristics method and the results in Alikakos 1 and Ladyszenskaya et al. 18. We first consider 0<t<a. We use the notations in the proof of Proposition 5.2 to get w(c, x) solution for and x∈Ω of

If f ≡ 0, integrating on one gets

A similar result than those in Alikakos 1 or the maximum principle gives the existence of M ₁(T)>0 depending on d, such that

If f≠0, one has to use a result of Ladyzhenskaya et al. 18 to get the existence of M ₁ depending this time also on such that . For 0<a<t, similar arguments give the existence of M ₂(T)>0 or M ₂ such that .   ▪

5.1.2. Second auxiliary problem

We are interested in solutions (J*, A*) of the following problem:

Proposition 5.5

For all T>0, for all 0<A<a _†, system (12) and (13) has a unique solution with non-negative components. Furthermore, if the following estimate is satisfied:

Proof

Existence and uniqueness in L ^∞ is a consequence of a similar result in a more complicated case; see Wolf 30. Furthermore, adding the two systems, one has

and integrating the first equation in age from 0 toward a _†, and using the Gronwall lemma, it follows estimate (14).   ▪

5.1.3. End of proof of Theorem 2.7

We only deal with the case , the case can be treated similarly by truncation.

Let (J*, A*) be the solution of Equations (12) and (13).

Let also 𝒦 be the closed convex set defined by

At least, let defined by where J, A is the solution of the linear problem:

Proposition 5.2 insures the existence of (J, A).

Comparing J to the solution of Equation (11) with μ=0, f=0 and and using Corollary 5.3, one has

Similarly comparing A to the solution of Equation (11) with μ=0, and and using Corollary 5.3, one gets

This way is well defined.

It remains to prove that Φ is a strict contraction to have the existence of fixed point, and then to show that this fixed point is a weak solution.

Thus we consider and . The following lemma holds:

Lemma 5.6

There exist two constants k ₁ and k ₂ depending on and , for Z*=J*, A* such that for t∈(0, T), one has

Proof

k _i , i≥3 will be constants with the same property as k ₁ and k ₂. We begin by estimating the equation corresponding to J ₁−J ₂, that we multiplied by J ₁−J ₂. one gets

and

By integrating on Ω, it follows that

thus as , and using assumption Hypotheses 2.1–2.3 and boundedness (17), one has

Integrating in a on (0, a _†), one gets

with

Moreover, Holder's inequality for a function f implies that

so using also Cauchy–Schwarz inequality, one has

Also

It follows, as for I ₁:

Finally, we have

this way

and one gets

Working similarly on the equation in A, one gets

with

and

Substituting inequalities (21), (22) and (23) in (20) and (25) and (26) in (24), one completes the proof of Lemma 5.6. We can deduce from Lemma 5.6 the following:

Lemma 5.7

The mapping Φ is a strict contraction on with τ* small enough, i.e. there exists such that

Proof

First, note that if y(t) is solution of the system:

with k ₁, k ₂≥0, then

so when is non-decreasing

Using Equation (19) to use this with

it follows Equation (27) with , smaller than 1 for t small enough.   ▪

As Φ is a strict contraction on a Banach space, there exists a unique fixed point such that . Furthermore, one has from Equation (17)

Otherwise, by dominated convergence, one checks that if (J _n , A _n ) tends towards (J, A) in 𝒦 then tends towards in . Thus, using dominated convergence, continuity of τ, β, μ _J and μ _A in the last variable and strong convergence in L ², it follows that is a weak solution of Equations (1) and (2) (see, e.g. Naulin 21 for details in a similar case). Then we can make again the same work to get the result on (0, T).   ▪

5.2. Proof of Theorem 2.11

First, in order to justify calculations below, we need the following Corollary of Proposition 5.2 for regularity of 𝕁 and 𝔸:

Corollary 5.8

Suppose assumption Hypotheses 2.1–2.3 and 2.9 are satisfied. The the unique non-negative weak solution u in of problem (11) satisfies

Proof

We return to the proof of Proposition 5.2, if the diffusion rate d does not depend on the variable (Assumption 2.9) one can guarantee regularity on . So as to get this, we work with the approximate solutions given by the Galerkin's method which have sufficient regularity: . Taking in the weak formulation, one has

where C depends on b, u ₀ and f, and one gets the result by assumption Hypothesis 2.3.   ▪

Integrating Equation (1) in a from 0 towards a _†, i.e. using u=1 as a test function, one has

thus one gets a first partial differential inequality for 𝕁:

Similarly, one has a second partial differential inequality for 𝔸:

Our goal is to prove the existence of a constant M ₀>0, independent on t such that

In order to do this, we adapt a work of Fitzgibbon et al. 10. First, we establish the following lemma:

Lemma 5.9

If are classical non-negative solutions of Equations (1)–(2) in then noting

Furthermore

Moreover, for non-negative l and l* there exists a constant C _{l, l*} depending on and such that if ,

Also if l is large enough, then C _{l, l*} can be taken independent on and l.

Proof

Integrating the inequality in 𝕁 on Ω, one has

But by the edge condition on so

Similarly, one gets for the inequality in 𝔸:

thus, adding the two inequalities, we get

Then is bounded for 0<t<∞ by the solution of problem:

so Equations (29) and (30) are proved. In order to prove Equation (31), remain that for and , one has (Young inequality):

Applying this to the right-hand side of the first inequality of Equation (32), it follows that

thus integrating in time on l, l+l*:

and Equation (30) achieved the proof.   ▪

Now we give the following result, for regularity:

Lemma 5.10

Suppose initial conditions (J ₀, A ₀) are non-negative and continuous on Ω¯, and assumptions Hypotheses 2.1–2.10 are satisfied. Then there exists such that for 0 ≤ l<T:

Proof

From Lemma 5.9, ons has that ℙ and so 𝕁 and 𝔸 are bounded in L ²(Q(0, T)). Multiplying inequality (28) by 𝕁 and integrating on Ω one gets

Similarly, one has

Then, adding the two previous estimates, it follows that

thus there exists such that for t<T:

then, integrating Equation (33) in time and using Lemma 5.9, one gets the existence of such that for 0≤l<T:

Moreover, multiplying the inequality in 𝕁 by 𝕁² and integrating on Ω, one has

thus for ϵ small enough the existence of and such that

Similar work for the equation in 𝔸 gives

and, adding the two estimates:

So one has existence of such that for t<T:

and integrating Equation (34) in time, one gets existence of such that for 0≤l<T:

Similarly, multiplying inequalities in 𝕁 and 𝔸 by 𝕁³ and 𝔸³, it follows estimates of and in L ⁴(Ω), but also of 𝕁 and 𝔸 in . Thus, with multiplication by 𝕁⁴ and 𝔸⁴, one gets existence of C ₇ and estimates of and in L ⁵(Ω), and also of 𝕁 and 𝔸 in .   ▪

As 𝕁 and 𝔸 are bounded in L ⁶(Q(0, T)), each component of

is bounded in L ³(Q(0, T)), thus one has existence of M(t)≥0 continuous on R ⁺ such that for t>T:

The following lemma completes the estimates given in Lemma 5.9:

Lemma 5.11

If are non-negative classical solutions of Equations (1)–(2) on then

Furthermore,

where C is independent on initial conditions.

Proof

For , one has using the Holder inequality:

In particular, for being non-negative one gets

and

Otherwise, from Equation (33), it follows that

thus, using Equation (37) with u=𝕁 and v=𝔸:

Then where y(t) is solution of a logistic equation:

and Equations (35) and (36) follows.   ▪

We now have the following result:

Proposition 5.12

For fixed l large enough and l*>0, there exists a constant C(6, l*) independent on initial conditions and such that for Z=J, A,

Proof

Integrating estimate (33) in time from l towards l+l*, one has

But using Lemma 5.11, for l large enough the second term of the right-hand side of Equation (38) is controlled, thus one gets existence of such that

Similarly to the proof of Lemma 5.9 and continuing estimates, Lemma 5.11 follows.   ▪

Finally, we can get the global estimates given in Theorem 2.11:

Proof

From Proposition 5.12, one has existence for l large enough (l≥l ₀) of C(6, l*) such that

% \noindent Let J̄ and Ā solutions in of

The maximum principle 25 gives for t≥0 and x∈Ω:

Using regularity results in Ladyzhenskaya et al. 18, it follows:

and for l≥l ₀ and l*>0:

But we want an estimate independent on J̄ and Ā at time l. Thus, we set l*=1, l≥l ₀−1 and an auxiliary mapping φ(t) non-negative, C ¹ on ℝ such that

Then we set the function . If l≥0, one has for t∈[l+1, l+2] and ρ(l, x)=0. Deriving ρ towards time, one gets

with

Thus, we have global estimates of in , and using regularity results in Ladyzhenskaya et al. 18 one has a global estimate in for ρ(t, x), and it follows a global estimate in for J̄(t, x). Then for all (l, l+1) with l≥l ₀ one has

with C independent on and l. So, as

one gets a global bound for J̄, so for 𝕁. Similar arguments give the same result for 𝔸.   ▪

Remark 5.13

A priori estimates allowing estimates in Lemma 5.9 and M(t) in the proof of Proposition 5.10 can be obtained directly from equations of system (1) and (2) by integrating also equations in age a. However, we do not have results concerning the theory of parabolic equations from, for example, Smoller 25 or Ladyzhenskaya et al. 18 to conclude global existence of solutions of the system.

5.3. Proof of Theorem 3.4

In order to prove Theorem 3.4, we will need these two results:

5.3.1. Environment equation

This result is proved by the variation of the constant

Lemma 5.14

The solution of equation

with is given by

We also need another auxiliary problem:

5.3.2. Third auxiliary problem

We consider the following system:

and we suppose that

Definition 5.15

•	and u 0 is non-negative,
•	and μ is non-negative,
•	and b is non-negative,
•	, with ,
•	d satisfies the assumption Hypothesis 2.3.

Then one gets

Proposition 5.16

Suppose Assumption 5.15 is satisfied. Then the problem (39) has a unique weak solution u in non-negative and satisfying

Proof

As in the Proposition 5.2 we prove this result by the characteristics method and classical results for hyperbolic problems. This time there are three different cases: 0<a<t, b, 0<b<t, a and 0<t<a, b. We begin by considering 0<a<t, b. Let u be a solution of Equation (39). For c>0, we set . w is a solution of the following system:

The two other cases lead to two similar parobolic problems by denoting, respectively: if 0<b<t, a and if 0<t<a, b. In each case, the parabolic equations theory implies the existence of a unique solution.   ▪

As for the first auxiliary problem, comparison theorem for parabolic equations implies the following corollary:

Corollary 5.17

If and in Q _J , in Q _{J, a} then the solutions of Equation (39) are non-negatives.

5.3.3. Proof of the Theorem 3.4

Proof

Let (J*, A*) be the solution of Equations (12) and (13). Let 𝒦 be the closed convex subset of defined by

  ▪

First note that we have the following lemma, useful in order to treat the incidence part corresponding to the proportionate mixing term:

Lemma 5.18

Let w _j (respectively w _a ) the non-negative solution of the linear problem (11) with d=d _J (respectively, d=d _A ), (respectively, f=0, β=0 and (respectively, . Then there exists a constant m(T)>0 such that

Proof

By the Assumption 3.2:

and in a similar way

Thus, inequalities and come from the comparison result, Corollary 5.3. m(T) results from integration along the characteristics of , as detailed in 20 using assumption Hypothesis 3.3, as it is done in Wolf 30 for the proportionate mixing part.   ▪

Let us also define the mapping by where (U, G) is solution of the linear problem:

with D and Υ as in Equation (7) and

with for Z=J, A:

On one side, integrating in b, the equation in J _i and adding with the one in J _s and on the other side those in A _i and A _s one has Equations (15) and (16). Thus, one gets and .

Equation for J _s is of the form (11) with and f=0, so that J _s is non-negative.

Equation for J _i is of the form (39) with and f=0, so that J _i is non-negative.

Equations for A _s and A _i can be treated in the same way. Furthermore, one then gets for all t, because all rates are non-negative. Using results for linear equations in the previous section and lemma 5.14, is well defined.

We now have to check that Φ is a strict contraction. We consider and .

Lemma 5.19

There exist constants k ₁ and k ₂ depending on and for Z=J, A such that for t∈(0, T), one has

Proof

Let k _i , i≥3 be constants with the same property as k ₁. The main differences with the proof of Lemma 5.6 are that there is also a term for the transmission of infection, the equation of infected individuals are more structured, and there is the equation for G. Let us focus on the equations for J _s, J _i and G. First multiply the equation corresponding to J _{s, 1}−J _{s, 2} by J _{s, 1}−J _{s, 2}, and integrating on Ω, it follows:

Then, integrating in a on (0, a _†), one gets

with I ₁, I ₂ and I ₃ as in the proof of Lemma 5.6 and

thus using the positivity result Lemma 5.18:

Moreover, one has

Now, focus on the equation for J _{i, 1}−J _{i, 2}. Multiply the equation for J _{i, 1}−J _{i, 2} by J _{i, 1}−J _{i, 2} and integrating on Ω, it follows:

Integrating in a on (0, a _†) and in b on (0, b _†) and using initial condition, one gets

where

•
•
•
•

I ₆ and I ₇ are estimated as in the proof of Lemma 5.6. I ₈ and I ₉ are estimated as I ₄ and I ₅ in the inequation for Same work on G ₁−G ₂ gives

so integrating in x and using Holder and Cauchy–Schwarz inequalities and assumption Hypothesis 3.2:

Similar work on equations for A _s and A _i gives Lemma 5.19.   ▪

Similarly to Lemma 5.7, there is

Lemma 5.20

The mapping Φ is a strict contraction on with τ* small enough, i.e. there exists such that

The end of the proof of Theorem 3.4 is similar to those of Theorem 2.7.

6. Conclusion

Our objective in this paper was to build and study a deterministic mathematical model describing the propagation of a virus within a structured host population.

In the existing literature on propagation of diseases, various features have been identified, which govern the propagation of a given virus 4–7,16 17 22 23 26 28 30 32. Motivated by these previous works, our model has been built so as to take into account three major features which are important in the specific case of the Puumala hantavirus – bank vole system in Europe.

	(1) Maturation of juveniles depending on the density of adult individuals. This leads to a stage structure with juvenile and mature individuals, and a chronological age structure on each stage;
	(2) transmission rates depend on the time elapsed since infection. Hence, in addition to the usual stage structure between susceptible and infected, we use a third chronological variable: the age of the disease;
	(3) a spatial structure is considered for the host population.

Our new model combines all the structures into a single strongly structured system. In this model, we also considered three other assumptions, based on the Puumala hantavirus – bank vole system: (1) the virus is benign in the host population, (2) virus propagation occurs through direct transmission from infective to susceptible individuals and through indirect contamination of susceptibles via the contaminated environment, and (3) the dispersion rates are discontinuous. Most of these features may be of some interest for most of the epidemiological systems.

We first analysed a demographic model for a closed population with chronological age and spatial structure and we derived here a mathematical analysis of this model. We get global existence, uniqueness and global boundedness results.

Then we studied an epidemic model with a continuous structure in age of infection and direct and indirect transmission. Global existence, uniqueness and global boundedness results was also performed in this case.

Finally, we looked at a model including the transmission of the virus to human populations with possible lethal consequences, and we also had global existence, uniqueness and global boundedness results.

The next step of this work will be to take into account some others biological assumptions, such as density dependencies for mortality rates or maturation rates (that should be decreasing towards adult density because of adults’ pressure on maturation in the Puumala hantavirus – bank vole system). In the same way, density-dependent diffusion rates may also be of some interest: diffusion is favoured by high-population densities because of territorial reasons.

Hence, we obtained a well-posed model taking into account many significant features. We believe this model can be very useful in diseases propagations studies. Unfortunately, this system seems to be too complex to allow qualitative studies mathematically; but numerical simulations may give lots of information of biological interest and may be compared with data collected in the field. A difficult point in simulating this system is its very strong structured character that leads to a 1+1+1+2 dimension problems, but parameters t, a and b are basically the time, thus numerical simulations can be related to 3D ones. Some parameters are quantifiable with field data, but others will be more difficult to estimate. However, qualitative studies are possible and sensitivity studies can help to determine importance of the parameters that are poorly known; we will focus on this.

Numerical simulations (27 29 and references therein) have studied the hantavirus system, without spatial structure, in the case when the parameters depend periodically with time. These works show that the demography and the propagation of diseases change dramatically when the coefficients differ from their average. This is especially true as far as propagation to a human population is concerned. In this direction, our model investigates the effect of the spatial variations of the coefficients (as opposed to temporal variations). The corresponding numerical study work is in progress.

Additional information

Notes on contributors

S. Madec

Current affiliation: Institut de Mathématiques de Bordeaux, UMR CNRS 5251, Université Victor Segalen, Bordeaux 2, France.

C. Wolf

Author Email: [email protected]