An evolutionary model of influenza A with drift and shift

Abstract

Influenza A virus evolves through two types of evolutionary mechanisms – drift and shift. These two evolutionary mechanisms allow the pathogen to infect us repeatedly, as well as occasionally create pandemics with large morbidity and mortality. Here we introduce a novel model that incorporates both evolutionary mechanisms. This necessitates the modelling of three types of strains – seasonal human strains, bird-to-human transmittable H5N1 strains and evolved pandemic H5N1 strain. We define reproduction and invasion reproduction numbers and use them to establish the presence of dominant and coexistence equilibria. We find that the amino acid substitution structure of human influenza can destabilize the human influenza equilibrium and sustained oscillations are possible. We find that for low levels of infection in domestic birds, these oscillations persist, inducing oscillations in the number of humans infected with the avian flu strain. The oscillations have a period of 365 days, similar to the one that can be observed in the cumulative number of human H5N1 cases reported by the World Health Organization (WHO). Furthermore, we establish some partial global results on the competition of the strains.

Keywords:

• avian influenza
• evolution
• drift
• shift
• bird-to-human avian strain
• pandemic strain
• human seasonal influenza
• reproduction numbers
• invasion reproduction numbers
• global stability
• persistence

1. Introduction

The world is recovering from the most recent flu pandemic, the so-called ‘swine flu’ H1N1 virus emerged in Mexico and swept across the planet. The relative mildness of the ‘swine flu’ pandemic, which generated disease-induced mortality comparable to the one of seasonal flu 37, should not prevent us from keeping the dangers of pandemic influenza in focus, as the three big pandemics in 1918, 1957 and 1968 combined took the lives of an estimated 40–50 million people. What makes this supposedly ‘mild’ pathogen, which we experience every year, capable of so much devastation? The answer lies in the unique evolutionary capabilities of the flu virus. The pathogen that causes human influenza evolves through two types of evolutionary mechanisms – drift and shift. Drift describes small and gradual changes in the surface proteins (antigens) of the virus through random mutational processes. Although each strain is believed to impart permanent immunity to the host 5, drift allows the pathogen to evade our immune response and infect repeatedly. Since the newly infectious strain is structurally similar to the previous one, our immune system is still quite effective against the new strain and thus capable of protecting us against serious health risk.

Shift evolution occurs when an influenza virus of subtype that normally does not infect humans, becomes adapted to the human population. Influenza viruses of different subtypes infects many other species – predominantly birds both domestic and wild, also pigs, horses, marine mammals, cats and others 6. Differences in the surface proteins prevent these viruses from jumping across the species barrier and causing infection in humans 19. However, highly pathogenic H5N1 viruses have succeeded in crossing the species barrier and have started infecting humans, creating conditions for shift evolution to occur. First human infections with the H5N1 subtype were reported in Hong Kong in 1997 39. As of March 2011, WHO has reported 526 cases with 311 deaths – mortality of 59% 40. Most infections this far are predominantly from bird-to-human transmission. The highly pathogenic H5N1 can become pandemic among humans if it acquires a highly efficient human-to-human transmission mechanism, while retaining high pathogenicity. This can happen if an H5N1 strain can exchange genetic components via reassortment with seasonal human-to-human transmittable influenza strain within a common host. The shift mechanism gives rise to a new evolved strain. A novel strain, obtained through shift evolution, is structurally different from its parent strains and represents adaptation of new influenza subtype to humans with potentially dangerous consequences.

In this article, we introduce a new model that incorporates both the drift and the shift mechanisms of influenza A evolution. Those two influenza A evolution processes were modelled separately. The drift evolution in seasonal influenza was first modelled as a partial differential equation in 29. The shift expected in avian influenza was recently modelled in a sequence of articles by Iwami et al. 13 14 15. We draw on these results to build the model that incorporates both drift and shift as evolution mechanisms of influenza. The main question that we address is how the presence of antigenic drift in human influenza impacts the dynamics and the competition in the system human influenza–avian influenza.

The threat of a pandemic caused by H5N1 has motivated a stream of research on avian influenza. Mathematical modelling is at the core of this development, providing valuable insights on epidemic scenarios and control strategies in case an influenza pandemic occurs. Many of these models, particularly those with elaborate realistic features, are necessarily simulational 7 8 22 27. The spread of pandemic influenza has also been explored with deterministic and stochastic metapopulation-type multi-city models 3 4 9. All these models on pandemic preparedness and containment are focused on the human population. Other models study the distribution of the avian influenza virus in wild birds and domestic poultry. Much of the transmission of avian influenza, particularly transmission among wild birds, is environmental. Environmental transmission potentially plays an important role in generating the oscillatory pattern, observed in data 2. Most animal-based models focus on domestic birds. Spatial farm-based model treating poultry-farms as units 20, SIR model for within flock transmission of H5N1 36, and a model with LPAI and HPAI 23 were considered. Early models basically ignored the complexities of the multi-species avian influenza transmission. However, recently models with at least two species have appeared 1 10 13 14 15. Time dependent optimal control strategies for the prevention of avian influenza pandemic were discussed in 17. Spatial spread of avian influenza was the focus of 16 18 21.

This article is organized as follows. In Section 2 we introduce a novel influenza A model with both drift and shift. As the model involves three strains, in Section 3 we investigate separately single strain equilibria and introduce each strain reproduction number. Section 4 is devoted to coexistence equilibria. Two scenarios are investigated: continuous mutation or instantaneous mutation into a pandemic strain. Section 5 presents the analysis of the local stability of equilibria. Section 6 derives conditions for global stability. We summarize our results in Section 7.

2. A deterministic evolutionary model of avian flu

In this section we introduce an evolutionary model of influenza A which includes for the first time, both the drift and shift evolutionary mechanisms of influenza A.

Shift in the evolution of influenza A occurs when strains which normally circulate in other species become adapted to humans. We model the transition domestic birds humans of influenza A H5N1 subtype. Highly pathogenic avian influenza (HPAI) strains from the subtype H5N1 are currently endemic in some domestic bird populations 23. They have evolved sufficiently to infect humans through bird human transmission. This defines the current pre-pandemic scenario which does not involve human-to-human transmission of H5N1. To model this scenario, we model the infection in the domestic bird population. Denote by B(t) the number of healthy domestic birds at time t, and by Y(t) the number of infected domestic birds. We model the epidemic among the domestic birds by an SI model that assumes no recovery, based on observed high mortality and culling. The model is given by

where is the birth rate of the domestic birds, μ_b the natural death rate, and ν_b the disease-induced death rate. The total avian population is given by

The total avian population satisfies a differential equation obtained from the sum of the two equations above:

Because of its enormous public health concern, we focus on the evolution of the pathogen in humans. The influenza shift evolution, via reassortment, has apparently given rise to the pathogens that caused the 1918, 1957 and 1968 pandemics 30 31. To model evolution through reassortment, we incorporate seasonal human influenza, which evolves through drift, and coinfection in a human host by the avian high pathogenic H5N1 strain and seasonal human flu strain. Although reports of such coinfection had not withstood scrutiny, the prospects of such a possibility cannot be overlooked.

To introduce the human epidemic model, let S(t) be the number of susceptible human individuals and I(t) the number of those infected with human influenza. We model the drift evolution of influenza by a(τ) the number of the amino acid substitutions from the strain circulating at time t, where τ is time-since-recovery. We assume the rate of change of a(τ) to be constant a′(τ)=k 29 32. With this notation, the quantity r(a, t) represents the density of individuals recovered from human influenza strain that differs by a(τ) amino acid substitutions from the strain at time t, that is

gives the number of recovered from human influenza individuals that were last infected by a virus that differed by more than a ₀ and less than a ₁ amino acid substitutions from the virus strain prevalent at time t. Furthermore I _b(t) is the number of infected humans with the bird-to-human strain. Individuals infected with human flu can get infected with the bird-to-human flu to become coinfected. The class J(t) denotes the number of co-infected individuals. Finally, Z(t) is the number of individuals infected with the evolved human-to-human transmittable H5N1 pandemic strain. A list of dependent variables and their descriptions is given in Table 1.

Table 1. List of dependent variables.

Notation	Meaning
B(t)	Number of susceptible birds at time t
Y(t)	Number of H5N1-infected birds
P(t)	Total population size of birds
S(t)	Number of susceptible individuals at time t
I(t)	Number of individuals infected with seasonal human influenza
r(a, t)	Density of recovered individuals who are a amino acid substitutions away from the strain at time t
R(t)	Number of recovered individuals from seasonal human influenza
I b(t)	Number of humans infected with the bird-to-human transmittable flu strain
J(t)	Number of individuals jointly infected with seasonal human flu and the bird-to-human transmittable flu
Z(t)	Number of individuals infected with the pandemic strain at time t
N(t)	Total human population size at time t

The human epidemic model is built on the foundation of Pease's influenza drift model 29. Pease constructed his model without demographics to show that due to the drift process influenza A can persist, even if there is no recruitment into the population. In contrast to Pease's model, we include a susceptible class and demography. This is necessary since the H5N1 ‘spill over’ infection has already been continuing for more than 10 years, so we are looking at long time-scales for the demographics to be ignored. Susceptible humans are recruited at birth rate Λ, and die at a natural death rate μ. Susceptible individuals become infected with seasonal human flu at a rate β, with avian flu from birds with rate β _Y , and with pandemic flu, when such occurs at rate β _Z . Recovered individuals from seasonal human flu become reinfected at a rate γ(a) and return to the human flu-infected class. Those infected with human influenza can also become infected with avian influenza at a rate β _J . Infected with seasonal flu individuals recover at a rate α. Recovered individuals are assumed to become infected with avian flu or pandemic flu at the same rates as susceptible: β _Y and β _Z , respectively. Individuals infected with avian influenza leave the class at a rate ν which includes recovery and death. Since nearly 60% die, and those who recover cannot be reinfected with avian influenza, those individuals leave the system. The exit rates from the jointly infected class and the class of those infected with pandemic flu is ν _J and ν _Z , respectively. Pandemic influenza emerges at a mutation/reassortment rate ρ. We will assume that it may occur on continuous bases ρ≠0 or instantaneously, in which case ρ=0 and the process is modelled by Dirac delta function. Parameters are listed in Table 2. The human part of the influenza epidemic model with drift and shift is given by

where is the total recovered human population from human influenza at time t. We note that, in general, immune status of recovered individuals may affect the spread of new strains. However, we assume that since the pandemic avian strain in our model is of a different subtype, no cross-immunity exists between the human and the pandemic strain. This is incorporated in the model by assuming that the transmission rate for susceptible and recovered individuals is the same. The total human population size is given by

Adding all equations in system (2), we see that the total human population size N(t) satisfies the differential equation

As we see the rate of change of the total population size is reduced by the number of individuals per unit of time who exit the system while in the I _b, J and Z class.

Table 2. List of parameters.

Notation	Meaning
	Birth/recruitment rate into the domestic bird population
μb	Per capita natural death rate for domestic birds
νb	Per capita disease-induced death of domestic birds
βb	Transmission coefficient of avian influenza in domestic birds
Λ	Birth/recruitment rate into the human population
μ	Per capita natural death rate
β	Transmission coefficient of human influenza A strains to susceptibles
γ(a)	Transmission coefficient of human influenza A to recovered individuals
β Z	Transmission coefficient of the pandemic flu strain for susceptible and recovered individuals
k	Rate of amino acid substitutions in the virus population
β Y	Transmission coefficient of bird-to-human transmittable avian flu strain
β J	Transmission coefficient of bird-to-human transmittable avian flu strain for those infected with human influenza A
α	Per capita recovery rate from the class I
ρ	Per capita mutation rate of the bird-to-human transmittable strain into human-to-human transmittable strain
ν	Per capita death/recovery rate of infected with bird-to-human flu strain
ν J	Per capita death/recovery rate of jointly infected individuals in class J
ν Z	Per capita death rate of infected with pandemic flu strain

In this model, we consider an invasion scenario. This scenario focuses on the early stages of the invasion of the avian strain as human-to-human transmittable strain. This scenario is characterized by lack of drift evolution of the pandemic strain — that is, upon recovery from the human-to-human transmittable strain, recovered individuals are protected from future infection with it. We model that by lumping the recovery and death into the per capita rate ν _Z .

In the next section, we investigate the single strain equilibria and introduce the reproduction numbers of the seasonal flu, avian flu and pandemic flu.

3. Single strain equilibria

Equilibria are time-independent solutions of the system. Since the avian dynamics is independent of the human dynamics, we first consider the equilibria in the avian system. Those satisfy the system

This system always has the avian population disease-free equilibrium, obtained by setting Y=0 and given by

Furthermore, there exists a unique endemic equilibrium if and only if the basic reproduction number of the disease in the avian population, given by

satisfies . The endemic equilibrium in the avian population

can be explicitly computed. Thus,

The equilibria of the human dynamics satisfy the following system:

The system always has the disease-free equilibrium for which I=0, I _b=0, J=0, and Z=0. These conditions, considering the equations above, also imply that r(a)=0. We note that the human population disease-free equilibrium exists only if the avian flu strain has not established itself in the bird population. Thus, we can have scenario in which in the long run both the avian and the human populations are disease-free, but we cannot have a scenario that the disease has established itself in the avian population but the human population is disease-free. Consequently, we have the following disease-free equilibrium of the full system (1) and (2):

If the bird population is disease-free, then the human influenza A may be at equilibrium in the human population, that is, if Y*=0 we may have I≠0, I _b=0, J=0, and Z=0. That equilibrium satisfies the system:

where the remaining equations are trivially satisfied. This is a system related to the systems for the equilibria obtained from Pease's system 29 which has been studied before. However, we consider it here again and we show that Equation (5) allows for backward bifurcation, specifically in the case when γ(a) is taken to be the Pease function, that is, .

To obtain the equilibria we integrate the differential expression in Equation (5) to get

where throughout the paper we adopt the following notation: if a given parameter is used with subscript or superscript k, it means that the original parameter has been divided by k, e.g.:

From the first expression in Equation (5) one can express S in terms of I:

Substituting S and r(a) from Equation (6) in the second expression of Equation (5), after cancelling I, we obtain the following equation for I:

where Γ _k (I) denotes the following function of I:

Denote by F(I) the left-hand side of Equation (8). The first summand of F(I) is a decreasing function of I. The second summand of F(I) is an increasing function of I. To see this, consider . Using integration by parts, we obtain the following equivalent expression for :

For further reference we will denote the integral in the right-hand side of this equality by φ(I). Clearly, φ(I) is a decreasing function of I. Thus the right-hand side in the identity above is a positive, increasing, concave down function of I which remains smaller than one. The same is, of course, also true for the left-hand side. To investigate the presence and number of equilibria, we introduce the reproduction number of the human influenza A:

To interpret ℛ₁, note that β gives the number of secondary infections one infected individual can produce per unit of time per individual. The fraction gives the number of time units that one infectious individual is infectious, and Λ/μ is the number of susceptible individuals in an entirely susceptible population. Thus, ℛ₁ gives the number of secondary infections one infected individual can produce in an entirely susceptible population during its lifetime as infectious. We note that ℛ₁ does not depend on γ(a). This is because in a disease-free population there are no recovered individuals, and consequently there are no new infections of recovered individuals. In investigating Pease's model, however, Inaba 12 defined a basic reproduction number of human influenza that depends on the recovery rate γ(a). In particular, he assumed that is the transmission rate for susceptible individuals, and replaced β with .

To see the existence of a dominance endemic equilibrium of the human influenza, assume that . Then

On the other hand, as I→∞ the first term in F(I) goes to zero. To see the limit of the second term, note that φ(I) goes to zero, and therefore, . Thus, we have that

This implies that the equation F(I)=1 has at least one positive solution. We cannot show that the solution is unique. If there are multiple solutions of the equation F(I)=1, to each solution there corresponds one dominance endemic equilibrium of human influenza. We note that if there are multiple solutions I*, and they are all simple, that is , then there must be an odd number of them. We summarize these observations in the following proposition.

Proposition 3.1

Let . Then, there is at least one dominance endemic equilibrium of the human influenza

If there are multiple endemic equilibria and they are all simple, then there must be an odd number of them.

We note that all our simulations in the case resulted in a unique endemic equilibrium of the human flu strain. We illustrate this scenario in Figure 1. When Equation (8) may or may not have solutions. It will have solutions if the bifurcation at the critical value of the reproduction number (obtained when I=0) is backward bifurcation. If we assume that Equation (8) defines β implicitly as function of I, and we differentiate in Equation (8) with respect to I, then the bifurcation at the critical value of the reproduction number will be backward if and only if β′(0)<0. Replacing with , differentiating implicitly with respect to I and setting I=0 we get the following expression for β′(0):

We note that φ′(0)<0, thus the expression on the right-hand side could be negative. With , the value of φ′(0) can be explicitly computed:

Replacing the value of φ′(0) and the value of which is computed from , we obtain the following necessary and sufficient conditions for backward bifurcation to occur:

We note that this condition is satisfied by the parameters in Figure 1. So if the transmission rate β is sufficiently low to give a reproduction number below one, backward bifurcation should occur. This is indeed the case. We illustrate it in Figure 1.

We summarize this result in the following proposition.

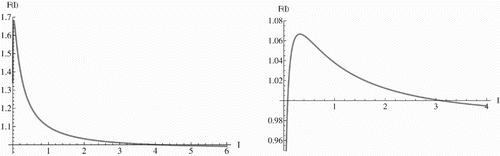
Figure 1. The left figure shows a graph of the function F(I) in the case ℛ₁>1. The graph clearly intersects the horizontal line y=1 at around I*≈ 3.5. The right figure shows a graph of the function F(I) in the case ℛ₁<1. The graph clearly intersects the horizontal line y=1 at two points I*₁ ≈ 0.1 and I ₂*≈ 3.0. The parameters for the two figures are taken as Λ=13.3 births per year, μ=0.0133 (years)⁻¹, α=52 (years)⁻¹, k=3.6 (years)⁻¹, γ(a)=γ a with γ=0.005 (amino acid substitution)⁻¹ (years)⁻¹ (person)⁻¹. The left figure has β=0.07 cases per person per year, while the right figure has β=0.02 cases per person per year. The reproduction numbers for the two figures are ℛ₁=1.34 for the left figure, and ℛ₁=0.38 for the right figure.

Proposition 3.2

Assume . Let . Then, there may be no dominance endemic equilibrium of the human influenza. If backward bifurcation occurs, that is if condition (12) is satisfied, then there are at least two endemic equilibria

for the values of the reproduction number in the interval and there are no endemic equilibria for .

Inaba 12 established for Pease's model 29, which does not involve demography, that it has a unique endemic equilibrium. That endemic equilibrium also cannot be explicitly computed. Even with demography and a susceptible class incorporated, Thieme and Yang 35 find that there is a unique endemic equilibrium in an influenza epidemic model with variable reinfection rate. Thus, our results of occurrence of backward bifurcation in the human influenza model somewhat contrast the results in these two studies. Part of the reason is the constitutive form of γ(a). Pease 29 fitted the percentage infected with a strain from a given year against the year when the immunizing strain was isolated for several studies, and found that this relationship is linear. Thus, he assumed that . However, the data he used were for a period of time spanning eight years. It is probably unlikely that this relationship will persist since the immunized individuals will be eventually completely naive with respect to the challenging strain. Thus, it is reasonable to assume that γ(a) is an increasing but bounded function:

Moreover, it can be expected that the maximal reinfection rate is smaller or equal to the transmission of human influenza for susceptible individuals: . Under this assumption Thieme and Yang establish uniqueness of the endemic equilibrium. Their approach can also be applied in our case to also result in uniqueness of the endemic equilibrium. We summarize this observation in the following Proposition.

Proposition 3.3

Assume that γ(a) is increasing and bounded so that . If then, there is a unique dominance endemic equilibrium of the human influenza

If then there are no endemic human flu equilibria.

The number of humans infected with the avian flu will be nonzero at equilibrium only if the avian flu is at nontrivial equilibrium in the bird population. In the absence of human flu, that is I=0, the nontrivial equilibrium of the avian flu strain in the human population will have I _b≠0 with J=0 and Z=0. We summarize the result on the avian flu strain in humans infection equilibrium in the following proposition.

Proposition 3.4

Assume . Then, there exists a unique dominance equilibrium of the avian flu virus in the human population:

where

The total population size at equilibrium in this case is given by

A couple of remarks are in order. First, the equilibrium of the bird-to-human transmittable avian flu strain is unique and can be explicitly computed. Second, it exists based solely on the assumption that guarantees persistence of the disease in the bird population; there is no additional reproduction number or threshold condition that gives its persistence in the human population. This is a result of the fact that if the avian flu strain has become established in the bird population, which happens if , then it is automatically established in the human population (a ‘spill over infection’). We conclude that, if the avian flu strain is endemic in the bird population, it will be endemic in the human population too.

We introduce the reproduction number of the human-to-human transmittable pandemic flu strain

There exists only one equilibrium of the pandemic avian strain which can be explicitly computed. We summarize that in the following proposition.

Proposition 3.5

If then there is a unique dominance endemic equilibrium of the human-to-human transmittable avian influenza

where

If then there are no endemic equilibria corresponding to the human-to-human transmittable pandemic flu strain.

4. Coexistence equilibria

The results in the previous section show that there could be three different strains that can exist in the human population independently: the human influenza, the bird-to-human avian influenza, and the pandemic avian influenza. In terms of coexistence, in the case of continuous mutation into the pandemic strain (ρ≠0), there are three possible scenarios: in absence of the human influenza, bird-to-human and pandemic avian influenza may coexist, in the absence of bird-to-human avian influenza, human and pandemic influenza may coexist, and all three strains may coexist. This case is investigated in the first subsection.

The current pre-pandemic scenario where the human influenza and bird-to-human strain coexist but there is no pandemic strain only occurs in model (3) if the appropriate reassortment into a pandemic strain has not occurred, that is, if ρ=0. If the reassortment that creates the pandemic strain is spontaneous, then the conditions for invasion of the pandemic strain with ρ=0 are different. The case ρ=0 is investigated in the second subsection.

4.1 Coexistence in the case of continuous mutation (ρ≠0)

This section investigates the coexistence equilibria in the case when all parameters, including ρ are non-zero. Conditions for existence of coexistence equilibria depend on the reproduction numbers and invasion reproduction numbers. The invasion reproduction number of strain i at the equilibrium of strain j gives the number of secondary infections one strain-i infected individual will produce in a population where strain j is at equilibrium during his lifespan as infected. Mathematically, the invasion reproduction number of strain i at the equilibrium of strain j is computed similarly to the basic reproduction number, that is as a criterion for stability of the equilibrium of strain j. Reproduction numbers and invasion reproduction numbers are listed in Table 3.

Table 3. List of reproduction and invasion reproduction numbers and their interpretation.

RN/IRN	Explanation
	Reproduction number of human influenza
	Reproduction number of avian influenza
	Reproduction number of pandemic influenza
	IRN of pandemic strain at equilibrium of avian strain
	IRN of human strain at the equilibrium of pandemic strain
	IRN of pandemic strain at the equilibrium of human strain
	IRN of human flu at eq. of bird and pandemic strains
	IRN of human flu at eq. of the avian flu strain (ρ=0)
	IRN of pandemic flu at eq. of bird and human flu (ρ=0)

The coexistence equilibria satisfy the system (4). One can solve for I _b* and J*:

Case 1

Coexistence of bird-to-human transmittable and pandemic strains. In this case I*=0, that is, there is no human strain. We define the invasion reproduction number of the pandemic strain when the bird-to-human strain is at equilibrium:

The following proposition gives the conditions for coexistence of the bird-to-human and the pandemic strain.

Proposition 4.1

If and the invasion reproduction number of the pandemic avian influenza strain then there exists a unique coexistence equilibrium of bird-to-human and pandemic influenza strains

where

The proof of Proposition 4.1 is straightforward and is omitted.

Case 2

Coexistence of the human and pandemic strains. In this case, Y*=0. This also implies that I _b*=0 and J*=0. From the last equation in Equation (4) we have

The non-zero values in the equilibrium also satisfy

Integrating the ordinary differential equation above, and adding all three equations the following equation is obtained:

from where Z can be expressed as a function of I:

which is defined and nonnegative for

We define the invasion reproduction number of human influenza at the equilibrium of the pandemic strain

In addition we define the invasion reproduction number of the pandemic strain at the equilibrium of the human strain

Assume γ(a) is increasing and . Recall that in this case Equation (8) has a unique solution, denoted by I ₁*, that participates in the invasion reproduction number above, and the equilibrium ℰ₁. We note that if and only if

The following gives coexistence of human and pandemic influenza:

Proposition 4.2

Assume γ(a) is increasing and . Assume and . Further, assume that the human strain can invade the equilibrium of the pandemic strain and that the pandemic strain can invade the equilibrium of the human strain, . Then there exists at least one coexistence equilibrium of the human and pandemic influenza strains

where I ₄* a solution of the equation F(I)=1 with

The remaining components are

The parameter .

Case 3

Coexistence of all three strains. With ρ≠0 if the human and the bird-to-human strains coexist, there always exists the pandemic strain too. This gives coexistence of all three strains. The analysis of the full coexistence equilibrium is similar to the analysis of the coexistence equilibrium of the human and bird-to-human strains. As in the case of coexistence of the human and pandemic strains, we integrate the differential equation in system (4) and add the equations for the susceptible individuals, individuals infected with the human strain and recovered individuals which gives:

From here we can express (S+R) in terms of I and Z:

Clearly, S+R is nonnegative if I satisfies

Substituting (S+R) in the equation for Z in system (4) we obtain the following equation in I and Z:

For I≠0, I satisfying Equation (18), and I fixed, the left hand side of the above equation is an increasing saturating function of Z which for Z=0 has a positive value. On the other hand, the right-hand side is a linear increasing function of Z, going through the origin. The two functions have a unique intersection in the first quadrant. That defines a function

for all values of I in the interval (18) except I=0. For I=0, Equation (19) has two solutions for Z:

where the second solution exists and is positive if and only if . Direct calculation shows that

Therefore, we define by continuity f(0)=Z*. This defines Z as a function of I on the entire interval (18): Z=f(I). This function is continuous for all values of I in Equation (18). From the equation for the recovered individuals, we solve for

where , , and . Replacing r(a) in the equation for the infectious individuals, we obtain the following equation in I:

We define the invasion reproduction number of the human flu at the equilibrium of the bird-to-human flu and pandemic flu:

The following proposition gives the existence of an equilibrium with all three strains nonzero:

Proposition 4.3

Assume and . Further assume that the pandemic strain can invade the bird-to-human strain, that is . Finally assume that the human strain can invade the equilibrium of the bird-to-human and the pandemic strains, that is . Then there exists an equilibrium of all three strains:

Proof

Denote by

We have . Furthermore, for we have

Therefore, there exists I ₅* in the interval (18), such that . Once I ₅* is determined, the remaining values of the equilibrium can be determined as follows:

This concludes the proof.   ▪

As in the case of human influenza equilibria, we cannot rule out the possibility of multiple coexistence equilibria. In the case ρ≠0, there is no condition for invasion of the pandemic strain. Because of the continuous mutation, the pandemic strain exists, and is non-zero, as long as both the bird-to-human strain and the human strain exist.

4.2 Coexistence in spontaneous mutation ρ=0 – pre-pandemic scenario and invasion of the pandemic strain

In this subsection, we investigate the current pre-pandemic scenario, and the invasion of the pandemic strain.

Case 1

Current pre-pandemic scenario: coexistence of bird-to-human and human strains. Occurs in model (4) only if ρ=0. Currently, two types of strains circulate in the human population – regular seasonal strains, and we include in this category the Swine flu strains, and a bird-to-human transmittable avian influenza strain. The bird-to-human cases occur through a ‘spill over infection’ from domestic birds. Because model (3) includes a continuous mutation from the coinfected state into the pandemic strain, when the human and the bird-to-human strains are present, that necessarily leads to the presence of the pandemic strain, if ρ≠0. Thus, the current pre-pandemic scenario is not part of the model (3) if all parameters are nonzero. However, the only reason that the pandemic avian influenza strain has not occurred is the absence of an appropriate mutation into such a strain. To have the current pre-pandemic situation, we should have ρ=0. In this subsection, we investigate the equilibria with ρ=0, and the distinctly different scenario when the pandemic strain has to invade the pre-pandemic strains to become established.

When ρ=0, possibility for an equilibrium exists with Z=0. Integrating the differential equation in system (4) and adding the three equations for the human flu we arrive at:

from where one can express S+R:

Solving for r(a) in the differential equation and S from the first expression in Equation (4), an equation F(I)=1 can be obtained. The details of the derivation are given in the more general case above. The equation F(I)=1 has an appropriate solution if and only if where is the invasion number of the human influenza at the equilibrium of the bird-to-human influenza. The value of the invasion reproduction number is given by

We summarize these findings in the following proposition:

Proposition 4.4

Assume ρ=0, and . Assume further that the invasion number of the human influenza at the bird-to-human influenza . Then there is a pre-pandemic equilibrium

where I ₆* is a solution of F(I)=1, and the remaining entries are given by

Case 2

Invasion of the pandemic strain. Occurs in model (4) only if ρ=0. In this case, we are looking for a solution with Z≠0. To express Z as a function of I, we add the susceptible, infected and recovered from human flu in system (4) which gives:

From here, we can express (S+R) in terms of I and Z:

Clearly, S+R is nonnegative if I satisfies

Substituting (S+R) in the equation for Z in system (4) we obtain the following equation in I and Z:

This equation has a unique solution given by

The quantity Z is nonnegative if I lies in the interval

Denote the right-hand side of this inequality by Ĩ:

We note that Ĩ>0 if and only if . If I is in the interval given in Equation (28), then both Z and S+R are nonnegative. Define the invasion reproduction number of the pandemic strain at the equilibrium of the human and bird-to-human strain:

As in Proposition 4.2 a function can be defined. If we assume that , we have that

The assumption implies that . We have , consequently, there is a value I ₇*, satisfying such that .

We can now formulate the theorem that gives coexistence of all three strains, after invasion of the pandemic strain of the pre-pandemic scenario.

Proposition 4.5

Assume ρ=0, and . Assume further that the invasion number of the human influenza at the bird-to-human influenza and that the invasion number of the pandemic influenza at the bird-to-human influenza . Furthermore, assume that the human strain can invade the equilibrium of the pandemic and bird-to-human strains: and that the pandemic strain can invade the equilibrium of the bird-to-human and human strains: . Then there exists an equilibrium in which all strains coexist:

where I ₇* is a solution of and the remaining entries are given by

Conditions for existence of equilibria are summarized in Table 4.

Table 4. List of equilibria and conditions for existence.

Equilibrium	Notation	Conditions for existence	Comments
Human flu	ℰ1
Bird flu
Pandemic flu	ℰ2
Bird + Pandemic	ℰ3	,
Human + Pandemic	ℰ4	, ,
		,
Bird + Human	ℰ6	, ,	ρ=0
All three	ℰ5	, ,
All three		,
All three	ℰ7	, ,
All three		, , ,	ρ=0

5. Local stability of equilibria

In this section we derive conditions for local stability of equilibria. Those conditions typically depend on the reproduction numbers and the invasion reproduction numbers. To introduce the linearized system we define the perturbations: , , , , , , , , where the quantities with superscript ‘*’ denote any of the equilibria. We also use and . Looking for exponential solutions with growth rate λ, we arrive at the following linear eigenvalue problem. The system for the bird population takes the form

Since the system for the bird population is independent from the system for the human population, it can be investigated separately. The following result is not hard to obtain:

Proposition 5.1

The equilibrium is locally asymptotically stable if and unstable otherwise. The endemic equilibrium is locally asymptotically stable whenever it exists, that is, if .

The linearized system for the human population takes the form:

The following result gives the local stability of the bird–human system disease-free equilibrium ℰ₀:

Proposition 5.2

The bird–human system disease-free equilibrium ℰ₀ is locally asymptotically stable if the following inequalities all hold:

If one of the above inequalities does not hold, the disease-free equilibrium is unstable.

In what follows we investigate the local stability of the single-strain equilibria.

5.1 Human influenza equilibrium

The human influenza equilibrium has the most complex stability pattern, as, because of the presence of the amino acid substitution structure a, the equilibrium can be destabilized and sustain oscillations are possible 34. Recently, the presence of oscillations in Pease's model has been established rigorously, and through simulations 24. We consider the stability of the human influenza equilibrium in the context of the presence of the remaining strains, and refer the reader to 24 for a more detailed discussion of the human influenza only case. In the human equilibrium case we have Y*=0, I _b*=0, J*=0 and Z*=0, but I*≠0 and r*(a)≠0. To guarantee the local stability of the equilibrium we assume throughout this subsection that . We consider system (32) with and Y*=0. The eigenvalues of the system are , , , and all λ’s that satisfy the human influenza system:

We note that if λ is taken different from all other eigenvalues, that implies y=0 and z=0. Hence, we have . Solving the first equation for x, the last equation for w and substituting in the second equation, we obtain the following characteristic equation

where the quantities with subscript k represent the original quantity divided by k. Integrating by parts the double integral, the characteristic equation reduces to:

We denote the left-hand side by f(λ) and the right-hand side by g(λ). We denote by Σ all solutions to the characteristic equation (35):

If the pandemic strain can invade a given equilibrium of the human strain, that is if for that I*, then that equilibrium is unstable.

Proposition 5.3

Assume the pandemic strain can invade a given equilibrium of the human strain, that is if and if does not belong to the spectrum Σ, then that equilibrium of the human strain is unstable. In addition, if the bird-to-human strain can persist, that is if and does not belong to Σ, then any equilibrium of the human influenza only is unstable.

In what follows we will assume that the pandemic strain cannot invade the given equilibrium of the human strain, that is for that I*, in addition to the assumption that . Then the stability of the human strain equilibrium is controlled by the solutions of the characteristic equation (35). In investigating the characteristic equation (35) a key role is played by the equation in I for the equilibrium. Equation (8) given by

which we rewrite in the form:

Denote by f _I (I) the left-hand side of the above equality (37), and by g _I (I) the right-hand side. Then, if , we have . Since, f _I →0 as I→∞, while g _I →μ>0 as I→∞ the two functions have at least one intersection. At that intersection the slopes of the two functions satisfy:

This inequality implies that for such an equilibrium I*, from the characteristic equation (35) we have f(0)>g(0). Alternatively, an equilibrium for which the opposite inequality is satisfied in Equation (38), we have f(0)<g(0). For an equilibrium for which Equation (38) does not hold, we have f(0)<g(0) and for real λ as , while , so the characteristic equation will have a positive real root. Such an equilibrium will be unstable.

Recall that for there are multiple simple equilibria, defined in Proposition 3.2 under the assumption that . For the lower equilibrium inequality (38) does not hold, while for the next equilibrium inequality (38) holds. Thus, the lower equilibrium is unstable.

We turn to investigating the stability of equilibria for which Equation (38) does hold. We investigate the case when is a constant and does not depend on a and refer to 24 for the general case. The characteristic equation of the corresponding ordinary differential equation model when γ is constant, can be obtained from Equation (35), which simplifies to:

where . In standard form this equation becomes

where the coefficients are given by

Proposition 5.4

Assume and . Then the endemic equilibrium for which Equation (38) holds is locally asymptotically stable.

Proof

Clearly, a ₂>0. Condition (38) implies that a ₀>0. This implies that

or since ,

or

To apply Routh-Hurwitz criterion, we need to show that a ₂ a ₁>a ₀, which easily follows from inequality (41).   ▪

The proposition below follows from the results in 24.

Proposition 5.5

Assume and γ(a) depends on a. Then the endemic equilibrium for which Equation (38) holds can become unstable in the sense that Equation (35) can have complex solution λ with positive real part. In this case sustained oscillations are possible.

5.2 Pandemic influenza strain only

When the pandemic influenza strain is the only strain present, then I*=0, Y*=0, r*(a)=0, and I _b=0, but Z*≠0. We assume again that , which implies that one of the eigenvalues . We will use the linearized human system (32) with I*=0, Y*=0, r*(a)=0, and I _b=0, but Z*≠0. From the sixth equation we obtain . The equation for i gives an eigenvalue

which is negative if and only if or when the human strain cannot invade the equilibrium of the pandemic strain. We express x from the first equation, with i=0, y=0, and substitute it in the last equation, where W=0. Noting that

we obtain the following characteristic equation of the pandemic strain

It is easy to see that this equation has two negative eigenvalues, or two complex conjugate eigenvalues with negative real parts. We summarize the results in the following theorem.

Theorem 5.6

Assume and that the human strain cannot invade the equilibrium of the pandemic strain, that is . Then the pandemic influenza equilibrium is locally asymptotically stable. If then the pandemic influenza equilibrium is unstable.

5.3 Bird-to-human strain only

In this section, we investigate the conditions for local stability of the bird-to-human equilibrium. In this case I*=0, r*(a)=0, J*=0, Z*=0, but Y*≠0 and . We assume that , a condition that guarantees that Y*≠0. We use system (32) with I*=0, r*(a)=0, J*=0, Z*=0, but Y*≠0 and .

From the equation for i, we have the first eigenvalue:

which is negative if , that is, if the human strain cannot invade the equilibrium of the bird-to-human strain, and it is positive if . The remaining eigenvalues are obtained with i=0. The eigenvalue corresponding to the equation for j is . From the equation for z we have the eigenvalue

which is positive, if the pandemic strain can invade the equilibrium of the avian strain, that is if . From the equation for x and u we have also the eigenvalues and . We summarize these results in the following theorem:

Theorem 5.7

Assume . If the human and the pandemic strains cannot invade the equilibrium of the bird-to-human strain, that is if

then the bird-to-human strain equilibrium is locally asymptotically stable. If the invasion reproduction number of the human strain, or the pandemic strain is larger than one, then the bird-to-human strain equilibrium is unstable. If both invasion reproduction numbers are greater than one, the bird-to-human influenza equilibrium is unstable, if .

5.4 Avian and pandemic strain coexistence equilibrium

In the absence of the human strain, we can expect that the avian and the pandemic strains coexistence equilibrium is stable. Indeed, in this case we have I*=0, r*(a)=0, J*=0, but Y*≠0, I _b≠0, and Z*≠0. We use system (32) with I*=0, r*(a)=0, J*=0, but Y*≠0, I _b≠0, and Z*≠0.

From the equation for i we have the eigenvalue , which is negative if and only if the human influenza strain cannot invade the equilibrium of the bird-to-human and pandemic strains: . If we look at eigenvalues that differ from λ₁, then i=0, which, in turn implies that w(a)=0. From the equation for j we have that either or j=0. From the equations for x and z we obtain the following quadratic characteristic equation

where and . Since , the equation above has either two negative real roots, or complex roots with negative real parts. We summarize the result from this subsection in the following theorem.

Theorem 5.8

Assume and . Assume further that the human influenza cannot invade the equilibrium of the bird-to-human and pandemic coexistence strains, that is, assume . Then the equilibrium of the bird-to-human and pandemic strains is locally asymptotically stable. If it is unstable.

5.5 Avian and human strains (ρ=0)

Investigations on the Pease's model for human strain evolution through drift have shown that the presence of amino acid evolution can destabilize the equilibrium, and sustained oscillations are possible 24. It is expected that in the presence of the bird-to-human strain, at least when the prevalence of infection in birds is relatively low, the oscillations would continue to exist. A more interesting outcome of the stability analysis here is that bird-to-human strain in a sufficiently high level of prevalence has the potential to stabilize the human strain equilibrium, particularly when coinfection is very low, as it is in reality. We consider the linearized system (32) for the coexistence equilibrium of the bird-to-human and human strains with J*=0 and Z*=0 (ρ=0). For the bird-to-human strain to exist, we need that , so that y=0. In the equation for z, we use

to obtain the first eigenvalue

If the pandemic strain can invade the coexistence equilibrium of the bird-to-human and human strains, that is, if then the equilibrium ℰ₆ is unstable. For the remainder of this section, we assume . Solving the equations for w(a), we have

where . Substituting in the equation for i, integrating by parts, we obtain the following characteristic equation:

The sign of the eigenvalues of the characteristic equation (45) depends on the type of equilibrium. In particular, we consider the following form of the equation for the number of cases of human influenza

Denote by f _I (I) the left-hand side of the above equality. We have f _I (I)→0 as I→∞. If , then . If all solutions to the equation above are simple, at the first solution (and all other odd-numbered ones) the slope of f _I (I) satisfies , which takes the form

Adding β S* and rearranging this inequality we have

Now we can establish the following theorem:

Theorem 5.9

Assume . If

and the coexistence equilibrium ℰ₆ is an equilibrium for which inequality (48) holds, then that equilibrium is locally asymptotically stable.

Proof

We denote the left-hand side of the characteristic equation (45) by F(λ) and the right-hand side by G(λ). For λ with , inequality (49) implies that

On the other hand

From inequality (48) we have

Therefore, for we have

Hence, the characteristic equation has no roots with non-negative real part. Let Σ′ be the set of all solutions to the characteristic equation (45):

Assume λ is not in Σ′. Then i=w(a)=x=0. Consequently, the remaining two eigenvalues are and . Thus, all eigenvalues of the eigenvalue problem (32) have negative real parts, and the equilibrium is locally asymptotically stable.   ▪

If inequality (48) fails for the equilibrium ℰ₆, then that equilibrium is unstable. We have the following result.

Proposition 5.10

If and or inequality (48) fails, then equilibrium ℰ₆ is unstable.

Proof

If , then there is a positive eigenvalue, and the equilibrium ℰ₆ is unstable. Assume now inequality (48) fails. Then F(0)<G(0). On the other hand for λ real, as , while . Thus, the equation has a real positive solution.   ▪

Example

In what follows, we will exhibit a specific example in which sustain oscillations occur. We make the following assumptions:

Assumption 5.1

Assume

•	The reinfection rate is a step function
•	Infection of susceptible and recovered individuals occurs at the same rate:
•	Coinfection in humans does not occur, that is β J =0.

In the case there is a unique equilibrium that can be explicitly computed. The density of the recovered individuals in that equilibrium is given by

From the equilibrium equation for the susceptibles we have that . Furthermore, we can express in terms of I*:

Substituting in the equilibrium equation for I we obtain the following equation for I:

Solving for I* we have

We now turn to the characteristic equation (45). With this form of γ(a) the double integral simplifies to

Substituting this expression in the characteristic equation, taking into account that and also , the characteristic equation (45) reduces to the following simplified form:

This is a transcendental equation. We can use the analytical methods in 38 to show that an equation of that form can exhibit Hopf bifurcation. Those methods can be used for equation (58) to establish this result. Here, we take an approach that will allow us to determine parameter values that give periodic solutions 24 28. Let . Separating the real and imaginary part in the equation above we obtain the following system

where A _k =A/k represents the number of time units after recovery when individuals become completely susceptible to the flu again. We proceed as follows. We first assume that the real part ξ=0.001. We assume values of μ and β _Y Y*. We solve for γ I* and as functions of w. Figure 2 gives a parametric plot of the two functions in the plane, treating w as a parameter. The quotient of the two functions gives α as a function of w. The parameter α as a function of w is also plotted in Figure 2. We select w, so that we compute a realistic value for α. We fix Λ and from the value of γ I* and formula (56) we compute γ. The resulting parameters are given in Table 5.

Figure 2. The left figure shows parametric plot in the (γ I*,αγ I*) plane. The right figure shows α as a function of w. The plots are made with w∈[π/32, π/16].

Table 5. List of parameter values for simulation. See 25 for discussion.

Parameter	Value
Λ	1000/365 (×10^5) people/day
α	1/5.068732 days^−1
γ	0.000115785 people^−1days^−1
β Y Y*	0.00000001189 days^−1
μ	1/(65*365) days^−1
A k	365 days
ν	1/20 day^−1

We construct a finite difference method along the characteristic lines. The characteristic lines of system (2) are the lines a=kt. Approximation of the partial derivative is done similarly as in the case k=1; however, the step in a is k times the step in t. The parameter k can be obtained from 32 and is estimated there as k=3.6 years⁻¹. It turns out that for realistic values of the parameters, as discussed in 25, the oscillations in the human influenza still remain. Although we have showed that for large enough prevalence of avian influenza in birds and humans, stabilization may occur, it seems that for the parameters and values we obtain from the WHO data in 25 stabilization does not occur. We present the results of simulations in Figure 3. We note that the oscillations have period of 365 days. The period of the oscillations appears to be equal to A _k .

Figure 3. The left figure shows oscillations in I(t). We note that the period of the oscillations is 365 days. The scale of the y-axis gives the number of infected people when multiplied by 10⁵. The right figure shows the resulting oscillations in I _b(t).

6. Global results on coexistence and competitive exclusion

The results in the previous section are local, that is, if an equilibrium is locally asymptotically stable, solutions only converge to it, if the initial conditions are sufficiently close to the equilibrium. In this section, we derive global results on persistence and extinction of the strains. As before, we strive to derive those results based on the reproduction and invasion reproduction numbers.

We begin with the global stability of the disease-free equilibrium.

Theorem 6.1

Assume and and . Then the disease-free equilibrium is globally asymptotically stable.

We note that the condition for the global stability of the disease-free equilibrium cannot be omitted. In other words, global stability cannot be established based only on the assumptions , , . As we saw earlier, if the condition is not satisfied, backward bifurcation and subthreshold equilibria may exist. In this case, the disease-free equilibrium is not globally asymptotically stable.

Proof

To see the global stability of the disease-free equilibrium, we first show that Y(t)→0 as t→∞. From system (1) we know that . Hence, given ε>0, for t>T. From the second expression in Equation (1), and after shifting the systems, we have:

Since , when ε is small enough, the coefficient on the right-hand side of the above inequality is negative. Therefore, Y(t)→0 as t→∞. Since and , the equation for I in Equation (2) becomes

Bounding S+R with the total human population size we obtain the following inequality for I:

As before, for ε small enough the coefficient in the right-hand side of the above inequality is negative. We conclude I(t)→0 as t→∞. As I→0 and Y→0, it can be shown that J(t)→0 as t→∞. Finally, since , applying the same methodology, we obtain that Z(t)→0 as t→∞. That concludes the proof.   ▪

Before we consider the global results for the whole system, we investigate the global stability of the bird system (1). This is established in the following Proposition.

Proposition 6.2

Assume . The system (1) has no periodic solutions, homoclinic loops, or oriented phase polygons inside the first quadrant. Consequently, the equilibrium E ^b is globally stable.

Proof

We recall that E ^b is locally stable. Dulac criterion implies the global stability. We introduce the notation:

The system satisfies Dulac's criterion with a Dulac multiplier 1/Y. We have

  ▪

The global stability of the equilibria of the domestic bird population, and the fact that the bird system is linked to the human system but it is not dependent on it, suggests that depending on the reproduction number we are essentially investigating two human systems (2) – one where Y=0, and another, where Y=Y*. The following Proposition states the global stability of the bird-to-human equilibrium under the very restrictive conditions that the reproduction numbers of the human and pandemic influenza are smaller than one. This proposition can be established with techniques similar to the ones used for the global stability of the disease-free equilibrium.

Proposition 6.3

Assume and and . Then the bird-to-human equilibrium is globally asymptotically stable.

Next we formulate and establish a much more serious global stability result, one that we establish with conditions similar to the conditions for the local stability of the bird-to-human equilibrium. Those state that the human and pandemic strains would not persist, if their invasion reproduction numbers are smaller than one. We note that in the Theorem below, we do not assume that the reproduction numbers of human and pandemic influenza are smaller than one.

Theorem 6.4

Assume . Assume that human influenza and pandemic influenza cannot invade the equilibrium of the bird-to-human influenza, that is, assume and . Assume further that and . Then the bird-to-human equilibrium is globally asymptotically stable.

Proof

To see the claim, we integrate the partial differential equation directly, and add the equations for S, I, and R. If , we obtain the following differential inequality for N _H:

Therefore,

where we have used that . Next, from the equation for I in Equation (2) we obtain the following differential inequality:

Using the bound for S+I+R we obtain that for arbitrary ε>0 we have:

Since , for ε small enough the coefficient of I on the right-hand side of this inequality is negative. Consequently, I(t)→0 as t→∞. Similar arguments imply that J(t)→0 and Z(t)→0 as t→∞. Finally, we have to show that and where S _b* and I _b* are components in the equilibrium . To see this, choose ε>0 and arbitrary. Since I, R, and Z go to zero, we may assume that

Thus,

where S _ε and X satisfy

Taking lim sup _t in the double inequality (63), we obtain

Since this inequality holds for every ε, we have

Similar reasoning leads to as t→∞.   ▪

Proposition 6.5

Assume . Assume that human influenza can invade the equilibrium of the bird-to-human influenza, that is assume while pandemic influenza cannot invade the equilibrium of the bird-to-human strain, that is and . Assume further that and ρ=0. Then the bird-to-human and human influenza persist, while the pandemic strain cannot persist.

Proof

We sketch the proof here. For a more detailed proof of persistence, we refer to 26. Similar reasoning as in Theorem 6.4 leads to Z(t)→0 as t→∞. We will say that human influenza persists, if it is uniformly strongly persistent, that is, if there is η>0, such that

To see that human influenza is uniformly strongly persistent given that its invasion reproduction number is larger than one, we have to show that 33:

(1) It is uniformly weakly persistent, that is, there is η>0 independent of the initial conditions such that

(2) The solutions of the system (2) have a compact global attractor, a maximal compact set that attracts the solutions. This is typically established by splitting the solution semigroup into two parts. The first one U(t) is obtained from system (2) with zero boundary conditions for the partial differential equation, and W(t) is obtained from system (2) with zero initial condition for the partial differential equation. It can be established that U(t)→0 as t→∞, while W(t) is compact for t large enough. Compactness in L 1 is usually established with the application of Fréchet–Kolmogorov Theorem [p. 275]41.

We here provide a proof of the uniform weak persistence which is the main step that is complicated due to the presence of multiple strains. This is the step that makes use of the fact that the invasion reproduction number of human influenza is larger than one. To show uniform weak persistence, we assume the contrary, namely, for every ε>0, there exist T>0 such that

By shifting the dynamical system we may assume

We also have

From the first expression in Equation (2) we obtain the following inequality

This inequality implies that

Hence, we have for t>0, after possibly shifting the dynamical system,

Substituting S in the equality for I, and disregarding the term that accounts for the contribution of the recovered individuals, we obtain the following inequality for I:

Taking the Laplace transform from both sides of this inequality, we obtain

where is the Laplace transform of I(t), and I ₀=I(0). The above inequality is, however, impossible for λ>0 and ε>0 but sufficiently small since , and the right-hand side of Equation (69) is positive, while the left-hand side is negative, for I ₀>0. The contradiction implies that there exists η>0 such that

  ▪

7. Discussion

Influenza A has the unique capability to evolve through both drift and shift and allow the virus to infect us repeatedly, as well as reassort with variants that normally infect other species to generate a novel strain capable of creating pandemics with high mortality. In this paper we introduce for the first time a model that incorporates both the drift and the shift mechanisms of evolution of influenza A. The model combines strains from the seasonal human flu that evolves through drift with strains of the H5N1 subtype which normally affect avian species but recently have started infecting humans as well. This is the pre-pandemic scenario which is currently in place. The H5N1 subtype can create a pandemic among humans if strains from that subtype become fully human-to-human transmittable. We incorporate this hypothetical pandemic scenario also in the model. Thus, the model involves three possible strains: human flu strain, avian strain that circulates in domestic birds and through ‘spill over’ infection in humans, and a hypothetical pandemic strain. We compute the reproduction numbers of all three strains. We find the following novel results related to the dynamics of this three-strain system.

	(1) Regarding human influenza, we find that there could be more than one dominance equilibrium corresponding to human influenza, some of which may be arising through backward bifurcation. Pease's drift influenza model has been studied in several articles 11 12 24 but multiple equilibria associated with influenza drift model are found here for the first time.
	(2) Coexistence of all three strains in the case ρ=0 will occur if a pandemic strain emerges through a spontaneous mutation, and invades the equilibrium of the human and bird-to-human strains. Thus, for a pandemic to occur, it is necessary that invasion number of the pandemic strain at the human and bird-to-human coexistence equilibrium to be larger than one. The value of this invasion number is inversely proportional to the level of infection in birds, and the seasonal flu levels in humans. This implies that control measures directed to eliminating or reducing those infections essentially increase the invasion capabilities of the pandemic strain and may facilitate a pandemic. This result is similar to the one obtained by Iwami 14, that the elimination of the avian influenza in birds can lead to more infections of humans by the pandemic strain and is a manifestation of the competition among the strains.
	(3) The disease-free equilibrium is locally stable if all three reproduction numbers are below one. The disease-free equilibrium is globally stable if all three reproduction numbers are below one and . Here we discuss for the first time the global stability of the disease-free equilibrium in the presence of subthreshold equilibria.
	(4) In a recent article, Magal and Ruan 24 find that the human influenza equilibrium can become destabilized by the drift evolution and oscillations are possible in the Pease's model. The same holds for the human strain equilibrium in our model. Furthermore, we show that the current pre-pandemic coexistence equilibrium, in which the human strain coexists with the bird-to-human strain, can also become destabilized and oscillations are possible. Our results also determine that sufficiently high levels of infection in birds (see, inequality (49)) can stabilize this equilibrium. However, as we show, for realistic parameters the oscillations still persist. Our oscillations are in the period of 365 days, well in line with the oscillations observed both in human seasonal flu and in the data of H5N1 infection in humans 40. The fact that the drift evolution in human influenza can produce oscillations in both human influenza and avian influenza in humans within a realistic period is a novel result which we obtain here for the first time.

We also obtain several novel global stability and persistence results in multi-strain systems. We note that these global stability results are established despite the presence of oscillations. In particular, we show the following.

(1) If the reproduction number of the bird-to-human strain is above one, but the other two reproduction numbers are below one, then the bird-to-human equilibrium is globally stable. We also establish a stronger result: if the invasion reproduction numbers of the human strain and the pandemic strain at the equilibrium of the bird-to-human strain are below one (with some additional conditions), then the bird-to-human strain equilibrium is globally stable.

(2) Finally we establish persistence of the human strain and bird-to-human strain and extinction of the pandemic strain if the invasion reproduction number of the pandemic strain at the bird-to-human equilibrium is below one, while the invasion reproduction number of the human strain is above one. As we show this persistence may be in an oscillatory way.

Acknowledgements

The author acknowledges support from the NSF under grant DMS-0817789. The manuscript has benefitted from discussions with Manojit Roy. The author thanks Horst Thieme for pointing her to reference 24. Furthermore, the author thanks two knowledgeable referees, who contributed enormously to the improvement of the manuscript.