Density-dependent quiescence in glioma invasion: instability in a simple reaction–diffusion model for the migration/proliferation dichotomy

Abstract

Gliomas are very aggressive brain tumours, in which tumour cells gain the ability to penetrate the surrounding normal tissue. The invasion mechanisms of this type of tumour remain to be elucidated. Our work is motivated by the migration/proliferation dichotomy (go-or-grow) hypothesis, i.e. the antagonistic migratory and proliferating cellular behaviours in a cell population, which may play a central role in these tumours. In this paper, we formulate a simple go-or-grow model to investigate the dynamics of a population of glioma cells for which the switch from a migratory to a proliferating phenotype (and vice versa) depends on the local cell density. The model consists of two reaction–diffusion equations describing cell migration, proliferation and a phenotypic switch. We use a combination of numerical and analytical techniques to characterize the development of spatio-temporal instabilities and travelling wave solutions generated by our model. We demonstrate that the density-dependent go-or-grow mechanism can produce complex dynamics similar to those associated with tumour heterogeneity and invasion.

Keywords:

• tumour invasion
• cell migration/proliferation
• go-or-grow
• diffusion-driven instability
• travelling wave solutions
• spatio-temporal heterogeneity

AMS Subject Classification :

• 35Q92
• 35K57
• 92C15

1. Introduction

Tumour invasion of normal tissue is a complex process, involving cell migration and proliferation. In this paper, we focus on the invasiveness of glioma, an aggressive form of brain tumour, where mutant cells invade the tissue in a diffuse manner. Gliomas are extremely difficult to treat since small numbers of tumour cells may travel to other areas of the brain where they go undetected. Experimental evidence suggests that cell motility and proliferation are inversely correlated in gliomas 9, with proliferating tumour cells moving slowly and rapidly migrating tumour cells proliferating slowly. This observation is commonly referred to as the migration/proliferation dichotomy (or the ‘go-or-grow’ hypothesis). Although it is likely that genetic mutations play a role in glioma invasiveness, Giese et al. 9 have shown that upregulation of genes relating to motility contributes to the invasive phenotype of malignant glioma. Giese and coworkers have also proposed that cells with lower proliferation rates are less susceptible to conventional cytotoxic treatments. Thus, a predominantly migratory phenotype (i.e. the expression of a specific motility trait of glioma cells) with a temporarily lowered proliferation rate may be able to invade the surrounding brain parenchyma even in the presence of treatment. Therefore, it is important to understand the role of a migration/proliferation phenotypic dichotomy in invasion dynamics. However, despite advances in our understanding of glioma invasion 12 (see also the recent reviews of cancer modelling 4 18), the mechanisms that regulate such phenotypic switches remain to be elucidated.

Two identical cells may spontaneously become phenotypically different due to stochastic variation in gene expression levels 22 or because they respond in a different manner to their local micro-environment 16. Because the molecular details of how cells communicate density changes and respond to those changes are often unclear, cell density itself can be examined as a source of signalling events 3 that may alter cell motility and cell growth (a process termed contact inhibition). Even though there is no extended study of the dependence of glioma cell motility on local cell density, Deisboeck et al. 7 have reported that density-dependent motility is likely to occur in glioma invasion. In particular, onset of invasion could be triggered when tumour cell density reaches a threshold.

Based on these remarks, and in order to understand better the invasiveness of malignant gliomas and what controls changes in cell phenotype, we present a mathematical model of the reaction–diffusion type and propose that phenotypic change is regulated by the cell density. The reaction–diffusion framework 21 is often used to model the growth and spread of a population. One of the best-known examples is Fisher’s equation, which has also been used to model glioma growth 27. A prominent feature of Fisher’s equation is the existence of a fixed-profile solution which travels at a constant speed 21, and corresponds to an invasive front. Other authors have studied the growth and invasion of gliomas by developing extended reaction–diffusion systems 29, accounting in particular for directed cell movement due to chemotaxis 15 or for anisotropy of the environment 14.

The concept of studying mixed populations of stationary and migratory species was first applied to ecological systems. For examples, Lewis and Schmitz 17 modelled the invasion of microbes by distinguishing mobile and stationary sub-populations. Hadeler and Lewis 10 extended Fisher’s equation to describe the situation in which one part of the population is sedentary and reproducing while the other part is migrating, and analysed the corresponding phenomenon of spread. Hillen 13 derived a similar reaction–diffusion system as the diffusive limit of a transport model for populations in which individuals move according to a velocity jump process and stop moving when they reach areas of shelter or food.

Several recent studies have investigated the influence of the migration/proliferation dichotomy on tumour invasion. Athale et al. 2 proposed an agent-based model to test the effect of a regulatory network related to the ‘go-or-grow’ mechanism on the emergence of invasive phenotypes and found that decisions at the single-cell level impact on the spatial dynamics of the entire tumour. A lattice-based game theoretical approach 19, involving motile and proliferating populations, has also been used to investigate the dynamics of tumour growth. Alternatively, Fedotov and Iomin 8 studied the ‘go-or-grow’ hypothesis by formulating a continuous random walk model. In a similar framework, Chauviere et al. 5 proposed a two-component model for motile and immotile cells (go-or-rest type) to explore sub- and super-diffusive dynamics in cell migration. They successfully used their model to reproduce experimental data from an invasion assay of glioma cells by assuming regulation of the phenotypic switch by the cell density. In another recent work, Chauviere et al. 6 described the phenotypic transition using two complementary density-dependent mechanisms to model fast and slow moving (diffusing) cells; they found that their system exhibits Turing instabilities under one mechanism and remains stable under the other. The instability eventually leads to phase separation of the slow and fast moving cells. Hatzikirou et al. 11 have investigated the role of the migration/proliferation dichotomy in the emergence of tumour invasion under hypoxic conditions by using a lattice-gas cellular automaton. Finally, in 28, the ‘go-or-grow’ hypothesis has been identified as a central mechanism for reproducing in vitro data relating to the invasion of glioma cells 26.

In this paper, we investigate the tumour dynamics when the phenotypic switch is regulated by the local cell density. Our paper is organized as follows. In Section 2, we introduce our go-or-grow model. In Section 3, we use a combination of numerical and analytical techniques to show how the Turing instability in our model is affected by cell proliferation. In Section 4, we present simulations of the go-or-grow dynamics. In Section 4.1 we identify distinct regions of parameter space which give rise to qualitatively different types of travelling wave solutions and in Section 4.2 we present the corresponding two-dimensional (2D) simulations. We conclude and discuss possible directions for future work in Section 5.

2. Model equations

2.1. Go-or-grow model

We decompose the tumour cells into two sub-populations: a migrating population with density ρ₁ and a proliferating population with density ρ₂. Then ρ=ρ₁+ρ₂ represents the total population density. We use a reaction–diffusion framework to model the population spread (assuming linear diffusion) and logistic growth to model cell proliferation. We focus on modelling phenotypic switches driven by environmental stimuli only and do not account for subcellular processes such as genetic mutations. Therefore, the phenotypic switch that we model refers to an exchange between the two sub-populations. We denote by Γ(ρ) the probability that an immotile cell becomes motile. In this way, we avoid having to specify a particular signalling pathway and are able instead to focus on the effect that local changes in the cell density have on cell phenotype.

The system of equations that we study is

where D is the diffusion coefficient of motile cells, μ is the rate at which cells change their phenotype, r is the proliferation rate, and ρ _m is the carrying capacity associated with the logistic growth term. Following 6, we consider two complementary mechanisms for the phenotypic transitions, these being modelled by the following normalized sigmoidal functions:

Under mechanism M₁ the cells become more motile (i.e. switch from immotile (Type 2) to motile (Type 1)) when the local total density ρ is low (in a sparse environment), and less motile when the density is large (in a crowded environment), which corresponds to contact inhibition of cell locomotion 1. Conversely, under mechanism M₂, cells become more motile when the local total density is high, which reflects the effect of population pressure 21. The parameter ρ* is a density threshold at which the probabilities of remaining stationary or moving are equal (Γ=1/2) and α (>0) describes the sharpness of the phenotypic switch. Initial and boundary conditions for Equations (1) are discussed below.

2.2. Non-dimensionalization

We define the following non-dimensional variables:

where x is the position vector, L and T are length and time scales, and ρ _c is a characteristic value of the cell density, which may be chosen to normalize the initial mass of the system, or by setting ρ _c =ρ _m , the carrying capacity. We consider the length scale L to be characteristic of the domain size (e.g. the radius of a cell culture dish in an in vitro experiment) and we specify the diffusive timescale T=L ²/D as the timescale of interest. Dropping the primes, we obtain the non-dimensional go-or-grow model:

wherein ρ′ _m =ρ _m /ρ _c and the dimensionless parameters M and R are defined by

3. Turing instability analysis

In the absence of proliferation, R=0 in the second of Equations (5) and the system simplifies to the go-or-rest model 5. In this section, we compare the spatio-temporal dynamics of the go-or-rest and go-or-grow systems in the context of the development of diffusion-driven instabilities in a one-dimensional (1D) Cartesian geometry.

3.1. Go-or-rest model

When R=0, Equations (5) reduce to give

We solve Equations (7) on the unit interval 0≤x≤1, imposing periodic boundary conditions at x=0 and x=1. We choose the characteristic density ρ _c to normalize the (time-independent) mass of the system, so that

When seeking a spatially uniform steady-state solution to Equations (7), the global mass conservation (8) becomes local (i.e. at each location of the domain). We use this property in the right-hand side of Equations (7) and find that there is a unique spatially uniform steady-state given by . It is possible to show that for both mechanisms, this solution is locally, linearly stable to time-dependent perturbations, which we write to satisfy the local mass conservation, since the growth rate λ of such perturbations is given by λ=−M (<0).

It is straightforward to show that, under certain conditions, the spatially uniform steady-state may be destabilized via diffusion-driven instability, leading to the emergence of spatial patterns. Following the classical stability analysis (see 21, for example), we find that a necessary condition for instability is

where Γ(1)∈(0, 1) regardless of the switching mechanism and Γ′=dΓ/dρ. Under mechanism M₂, Γ′(1)>0 and so the uniform steady-state is unconditionally linearly stable to spatio-temporal perturbations. In contrast, under mechanism M₁, which can be seen as autocatalytic, Γ′(1)<0 and instabilities can occur, leading to the formation of patterns for certain parameter ranges. In particular, condition (9) can be rewritten as

for α>1/2. Since f(α) has a maximum at α=α _m , f(α _m )≃1.278, then when ρ*>f(α _m ) the uniform steady-state is linearly stable to spatio-temporal perturbations for all values of α. By contrast, when ρ*<f(α _m ), there exist values of α for which is linearly unstable to spatio-temporal perturbations.

In order to study the development of instability, we use a mass-preserving finite-volume method to solve numerically Equations (7) with a symmetric splitting operator scheme of order 2. The parabolic part is solved using a Crank–Nicholson scheme.

In Figure 1(a), we illustrate the pattern that is generated from the instability that emerges under mechanism M₁ when (M, α, ρ*)=(5.0, 4.0, 0.9). We plot the spatial distribution of the static population at time t=5. At this time, we observe the formation of immotile aggregates. The spatio-temporal evolution of the motile and static cell densities is presented in Figures 1(b) and (c) in the (x, t)-plane. Initially, the perturbed uniform steady-state ( and for the parameters of the simulation) density of motile cells ρ₁ remains quasi-uniform, but then decreases rapidly to very small values, while the immotile cells start forming sharp-edged aggregates. The dynamics are due to exchanges between the populations and conservation of total mass within the domain. In between the aggregates, both populations are present, but the concentration of immotile cells is much lower than that of the motile ones.

Figure 1. Turing instability and pattern formation for the go-or-rest model. (a) Spatial distribution of the cell populations in the domain [0, 1] at times t=0 and t=5. The initial densities ρ₁(x, t=0) and ρ₂(x, t=0) are shown by dotted and dashed lines, respectively. The solid line corresponds to the spatial distribution of the static population at time t=5. The corresponding profile ρ₁(x, t=5) for the motile population is not presented since the values are much smaller in magnitude. (b) Spatio-temporal evolution of the motile cell density ρ₁. The horizontal axis is used for space and the vertical one for time. The three contour levels indicate (from bottom to top) the iso-values ρ₁=10⁻¹, 10⁻² and 10⁻³. (c) Spatio-temporal evolution of the static cell density ρ₂. The horizontal axis is used for space and the vertical one for time. The contour level corresponds to the value ρ₂=1 used as the initial value of the total density. Parameter values: (M, α, ρ*)=(5.0, 4.0, 0.9).

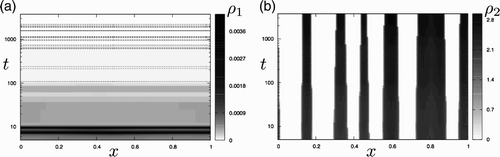
The system seems to relax rapidly to a quasi-steady configuration (Figures 1(b) and (c)). However, although only an infinitesimal portion of the population lies in the motile phase, it is sufficient to affect the global dynamics, which leads to a system characterized by extremely long timescales associated with metastability. This process is illustrated in Figure 2(a) and (b) where we present the spatio-temporal evolution of ρ₁ and ρ₂ over longer times. We observe that each immotile aggregate slowly shrinks over time and increases its density. This process is achieved through two steps. First, bursts of immotile cells are released at the aggregate edges into the motile population, which sharpens the aggregates and reduces their width. Second, these motile cells are then spatially redistributed (by diffusion) and halted by sharpened aggregates (due to mechanism M₁), giving rise to locally increased density. This autocatalytic process concentrates the cell density of each cluster in a quasi-static manner, until the density ρ₂ reaches non-physical values.

Figure 2. Long-time behaviour of the patterns generated from the Turing instability for the go-or-rest model. Spatio-temporal evolution of (a) motile and (b) static populations. The horizontal axis is used for space and the vertical one for time, with a logarithmic time scale that covers several orders of magnitude. Both curves correspond to the long-time evolution of the simulations presented in Figures 1(b) and (c). (a) The dashed lines represent the contour levels ρ₁=4×10⁻⁵ and indicate brief increases in the number of motile cells released at the edges of the static aggregates. The quasi-horizontal contour levels suggest an almost spatially uniform distribution (i.e. ρ₁(x, t)≃ρ₁(t)). (b) The solid lines represent the contour levels ρ₂=1 as in Figure 1(c) and show the slow shrinkage of the static aggregates.

3.2. Go-or-grow model

We next investigate how proliferation affects the dynamics of Equations (5) by assuming R>0. We fix the characteristic density ρ _c to be the saturation density ρ _m in the logistic growth term (i.e. ρ′ _m =1). By setting R=1, Equations (5) become

in the domain [0, 1], with periodic boundary conditions at x=0 and x=1.

By inspection, we note that Equations (11) admit two spatially uniform steady-state solutions: the trivial solution (0, 0) and a non-trivial solution that are identical to the one of the go-or-rest model. A linear stability analysis of the non-trivial steady-state reveals that, as for the go-or-rest model, it is stable to spatially homogeneous perturbations. Further, it is possible to show that a necessary condition for the development of Turing instability is

This condition is never satisfied under switching mechanism M₂ since Γ′(1)>0. However, under mechanism M₁, Γ′(1)<0 and there exist parameter values for which condition (12) is satisfied (see also Section 4.1), leading to the development of spatio-temporal instabilities.

As before, and for comparison with the results of Figure 1, we focus on mechanism M₁ and present in Figure 3 numerical results obtained for the same parameter set as for the go-or-rest example, i.e. (M, α, ρ*)=(5.0, 4.0, 0.9). The spatio-temporal evolution of ρ₁ and ρ₂ in the (x, t)-plane is presented in Figures 3(b) and (c). As for the go-or-rest model, immotile cells accumulate at early times forming distinct sharp-edged aggregates in which the immotile cells proliferate, while the motile population remains approximatively uniformly distributed and simply decreases in density over time. At later times, the system dynamics diverge from those of the go-or-rest model since proliferation of immotile cells occurs until the saturation threshold is reached. This also maintains the motile population at non-negligible density due to the phenotypic exchange between the populations. When the aggregate density rises above the saturation limit, the logistic growth term not only limits the aggregate density, but also accelerates its shrinkage. This situation is illustrated in Figure 3(a), where the spatial distribution of motile and immotile cells is presented at time t=5 for direct comparison with the go-or-rest pattern of Figure 1(a).

Figure 3. Development of Turing instabilities for the go-or-grow model. (a) Spatial distribution of the cell populations in the domain [0, 1] at time t=5. The solid line corresponds to the spatial distribution ρ₂(x, t=5) of the static population, whereas the dotted line represents the spatial distribution ρ₁(x, t=5) of the motile population. (b) Spatio-temporal evolution of the motile cell density ρ₁. The horizontal axis is used for space and the vertical one for time. The three lines correspond to the same iso-value ρ₁=0.15 and suggest an almost spatially uniform distribution. (c) Spatio-temporal evolution of the static cell density ρ₂. The horizontal axis is used for space and the vertical one for time. The contour level corresponds to the value ρ₂=1 used as the initial value of the total density. Parameter values (M, α, ρ*)=(5.0, 4.0, 0.9) are identical to those used in Figure 1.

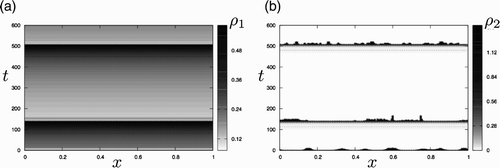
Figure 4 reveals that, at later times, the go-or-grow dynamics differ radically from those of the go-or-rest model. Since the logistic term causes net cell death in regions where the cell density exceeds the carrying capacity (here scaled to unity), a large part of the immotile population is actually removed from the system (i.e. the global mass decreases). When the density of the aggregates falls below the threshold ρ*, the phenotypic switch is reactivated and the motile population starts to increase almost uniformly, while the immotile population declines to low levels. Thereafter, both the motile and immotile cell distributions are quasi-uniformly distributed in space such that ρ=ρ₁+ρ₂<1 throughout the domain. Proliferation is subsequently reactivated, the resting density increases and a second wave of instability is triggered at t≃140. The dynamics repeat in time, as suggested by the presence of a third wave of instability that occurs at t≃500, so that eventually oscillatory dynamics are generated.

Figure 4. Oscillatory dynamics generated from the Turing instability for the go-or-grow model. Spatio-temporal evolution of (a) motile and (b) static populations. The horizontal axis is used for space and the vertical one for time. Both curves correspond to the long-time evolution of the simulations presented in Figures 3(b) and (c). (a) The dashed lines represent the contour level , the value of the initial uniform steady-state ( for the simulation). These contour levels suggest an almost spatially uniform distribution of motile cells that increases after the initial instability depicted in Figure 3(b) and (c) until a threshold (reached at t≃140), where motile cells become static (i.e. ρ₁ decreases by feeding the static population). This corresponds to the development of a new instability of the static population, which later stabilizes and feeds again the motile population, thus increasing again until similar dynamics are repeated at t≃500. (b) The dotted and dashed lines represent the contour levels ρ₂=0.01 and ρ₂=0.1, respectively. They suggest that low values of the static population correspond to almost uniform distributions (i.e. ρ₂(x, t)≃ρ₂(t)). When the immotile population increases enough due to an influx from the motile population (at times t≃140 and t≃500), an instability occurs and briefly leads to a non-uniform distribution of immotile aggregates. The latter disappear shortly by releasing cells into the motile population due to the lack of density until the process repeats.

While both the go-or-rest and the go-or-grow dynamics have the potential to generate patterns under mechanism M₁, the oscillatory nature of the go-or-grow dynamics differs radically from that of the go-or-rest. In the following section, we will show that the proliferation term in the go-or-grow model also allows for the formation of travelling wave solutions. We show that condition (12) gives rise to regions of (M, ρ*)-parameter space for which travelling wave solutions exhibit irregular dynamics behind the front. We discuss this and the oscillatory dynamics in more detail in the following section.

4. Travelling wave solutions

In this section, we construct numerical solutions of Equations (11) in order to establish whether the go-or-grow model admits travelling wave solutions. In so doing, we aim to investigate further the influence of an immotile/stationary cell population on the dynamics of the emerging travelling wave solutions.

4.1. Parameter space exploration

We look for 1D numerical travelling wave solutions of Equations (11). In the previous section, we identified two fixed points of Equations (11): the trivial steady-state (0, 0) and the non-trivial one . We speculate on the existence of a travelling wave solution connecting these critical points.

We numerically solve Equations (11) in a large spatial domain (−150≤x≤150) to avoid boundary effects associated with the no-flux boundary conditions we impose at x=±150. The initial condition for the moving population ρ₁ is chosen as an even distribution through a sharp sigmoidal function representing a core centred at x=0 and a maximal value given by the non-trivial steady-state Γ(1). The initial condition for ρ₂ is evaluated from ρ₁ so that the exchange term (i.e. the term multiplied by M in Equations (11)) is zero. We will discuss the choice of this particular initial condition and its consequences for the resulting patterns in the next section.

We study the formation of travelling waves for mechanisms M₁ and M₂. By means of numerical investigation, we find that under mechanism M₂ the solutions of Equation (11) always give rise to a simple travelling wave, that is a moving front with constant shape and speed. In contrast, mechanism M₁ leads to more complex behaviours such as those presented in Figure 5 and discussed below.

In the definition of mechanism M₁ (Equation (2)) we arbitrarily fixed α=4 (which allows for Turing instability) and explored numerically (M, ρ*)-parameter space. We found three types of solutions corresponding to the regions 1–3 in the top graph of Figure 5. We have selected three points P _i (i=1, 2, 3) in this parameter space by fixing M=1.6 and increasing ρ* to illustrate the types of solutions that arise in each region.

In region 1, one can observe the formation of a well-defined travelling wave with a time-independent profile and a spatially uniform core behind the moving front. Remark that, in this region, the non-trivial fixed point is stable with respect to Turing instability. The profile of the travelling wave, invading from left to right, is shown at time t≃377 in the bottom-left plot of Figure 5 and corresponds to the parameter values at P ₁, i.e. (M=1.6, ρ*=0.57). Of course the speed c of this travelling wave depends on the choice of parameter values (we will study this dependence in future work by performing a systematic travelling wave analysis and using the travelling wave coordinate ξ=x−c t as done, for example, in 17).

The upper curve that limits region 2 is the analytical instability condition (12). Thus, the non-trivial fixed point is also stable with respect to Turing instability in region 2. The lower curve defining region 2 has been obtained by numerical investigation (see top graph of Figure 5) and is characterized by a stationary non-uniform core behind the moving front. Indeed, even though the core is stable with respect to diffusive processes, the densities behind the front stabilize to spatially non-uniform distributions and not to the non-trivial fixed point . The corresponding density profiles at time t≃377 are shown in the bottom-central plot of Figure 5 at P ₂, i.e. (M=1.6, ρ*=0.6). We observe an oscillatory profile of the moving front, where peaks of immotile cells form and remain as fixed patterns after the front went past.

Figure 5. Types of travelling wave solutions for the go-or-grow model under mechanism M₁. (Top) Parameter regions of (M, ρ*)-plane corresponding to different behaviours of the solutions ρ₁ and ρ₂ (for a fixed value of the sharpness parameter (α=4)). Region 3 is defined as unstable to diffusion-driven processes (i.e. condition (12) is satisfied) and corresponds to simple travelling wave solutions. The dotted line that separates regions 1 and 2 is the result of numerical investigation. In region 2, solutions are characterized by an oscillatory profile of the moving front, where peaks of immotile cells form and remain as fixed patterns after the front went past. In region 3, the solutions degenerate behind the moving front into irregular spatio-temporal oscillations with no apparent order. (Bottom) Snapshots at time t≃377 of the density profiles of the motile (ρ₁ – red line) and static (ρ₂ – green line) populations corresponding to the points P _i in the top graph. The value of M is kept fixed while ρ* is increased from left to right, which corresponds to the vertical path between P ₁ and P ₃ in the top graph. (Left) Simple travelling wave solutions – P ₁=(1.6, 0.57) in region 1. Note the small peak of the static population at the edge of the front. (Centre) Oscillatory moving front – P ₂=(1.6, 0.6)) in region 2. The oscillatory nature of the peak results in the formation of stationary patterns of immotile cells behind the moving front. (Right) Irregular spatio-temporal oscillations behind the moving front – P ₃=(1.6, 0.75) in region 3.

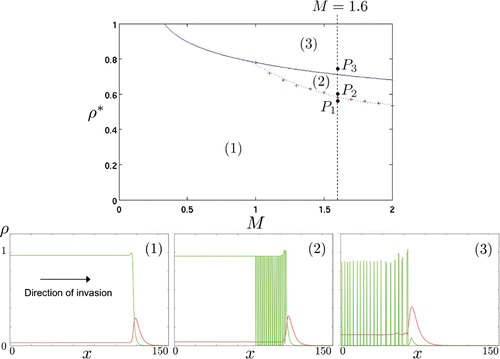
Region 3 in Figure 5 is defined by the analytical instability condition (12). During the transient period in which the travelling wave is established, the densities ρ₁ and ρ₂ tend to the non-trivial steady-state , respectively. Here, this steady-state is unstable with respect to diffusive processes (i.e. condition (12) is satisfied). Illustrative density profiles are exemplified at P ₃, i.e. for the values (M=1.6, ρ*=0.75) in the bottom-right plot of Figure 5. In the core, behind the moving front, the solutions degenerate into irregular spatio-temporal oscillations with no apparent order, similar to results obtained in 23.

4.2. 2D numerical results

In this section, we numerically investigate the go-or-grow model in a 2D Cartesian geometry.

We solve the 2D version of Equations (11) on a rectangular domain using a nonlinear, multilevel/multigrid method 30 combined with an adaptive, block-structured Cartesian mesh refinement. This algorithm allows us to restrict mesh refinement to where it is needed (e.g. front profile), thus minimizing computational costs. The equations are discretized in space, using the centred difference scheme and in time using a semi-implicit Crank–Nicholson-type approximation.

For comparison with the 1D simulations, we prescribe the initial distributions ρ₁(x, y, t=0) and ρ₂(x, y, t=0) to be such that the exchange terms in Equations (11) are null, and add a perturbation to the front in the y-direction. Here we consider δ=1 and l=0.4.

We solve Equations (11) over the domain (−150≤x, y≤150) using a regular grid of 128×128 points to cover the domain. Three levels of refinement are used so that the mesh has a resolution equivalent to a uniform grid of size 1024×1024. The mesh refinement criterion is |∇ρ _i |>ε for some tolerance ε. The timestep is Δt=10⁻². Note that the computational domain is taken large enough such that all the dynamics take place away from the boundary to avoid edge effects.

First, we explore the regimes presented in the 1D configuration in Figure 5, using parameters across the three regimes. We focus only on mechanism M₁ since the system is stable to spatio-temporal perturbations under mechanism M₂. Results are presented in Figure 6 by showing time-snapshots of the contour levels of the immotile population ρ₂ over a 2D domain for five different parameter sets.

Figure 6. Types of 2D travelling wave solutions for the go-or-grow model under mechanism M₁. We present plots of the immotile and proliferating cell population ρ₂, our choices of M and ρ* being guided by the parameter regimes depicted in Figure 5. Cases (a)–(c) are obtained by fixing M and increasing ρ*; they correspond to the points P _i shown on Figure 5. Cases (c)–(e) are obtained by fixing ρ* and decreasing M. For each set of parameter values, we plot the density over the 2D domain at times when the dynamics change. The density level is given by the colour bar to the right of each figure. Cases (a) and (e) are associated with region 1 (simple travelling wave), cases (b) and (d) with region 2 (non-uniform stationary core behind the oscillatory moving front), and case (c) with region 3 (irregular spatio-temporal oscillations behind the oscillatory moving front).

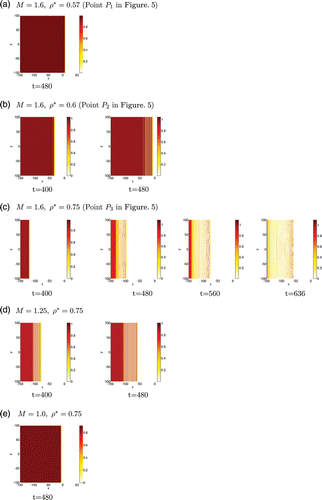
The first observation is that the 2D results in Figure 6 confirm the 1D results summarized in Figure 5. There exist three regions of the (M, ρ*)-parameter space associated with different behaviours: simple travelling wave with uniform core in region 1, stationary non-uniform core behind the oscillatory moving front in region 2, and irregular spatio-temporal oscillations behind the oscillatory moving front in region 3. Our results also show that the perturbation size δ decreases to zero before any dynamical development, suggesting that there is no front instability for these parameter sets (which we will analytically confirm in a future work).

In Figures 6(a)–(e), we present the transitions between the three regimes. In particular, Figures 6(a)–(c) show the regime for the three points P _i defined in the parameter space in Figure 5. When fixing M=1.6 and successively increasing ρ* from 0.57 (P ₁) to 0.6 (P ₂) and 0.75 (P ₃), one goes from regions 1 to 3: In Figure 6(a), we observe a stable travelling wave with a uniform core; in Figure 6(b), we observe that the front starts oscillating and leaves right behind it fixed patterns of immotile cells, which leads to heterogeneity in the core; finally, in Figure 6(c), the oscillations at the edge of the front propagate backward within the core, which leads to irregular spatio-temporal oscillatory dynamics extending over the entire domain behind the moving front.

As an additional confirmation, we now fix ρ*=0.75 and decrease M, thus drawing a horizontal segment in the (M, ρ*)-parameter space, starting from P ₃ where M=1.6 to further consider the values M=1.25 and M=1. We find again the expected regimes: a travelling wave with fixed patterns behind the moving front (after a transient period indicated by the uniform density in the central core) in Figure 6(d) corresponding to region 2; a stable travelling wave with a uniform core in Figure 6(e) corresponding to region 1.

Thus, we have shown here that the 2D results confirm the parameter regimes and the 1D simulations presented in Figure 5.

So far, we have used a particular initial condition satisfying a null exchange between the two populations. The reason for this particular initial condition lies in the observation that the patterns forming in the core during the establishment of the travelling wave depend on the initial condition. With such an initial condition, we have limited the occurrence of unusual patterns forming during the transient establishment of the travelling wave and we have clearly isolated the three regimes discussed previously. Here, we investigate the dynamics of the go-or-grow model, using another initial condition and find different patterns as a result. We consider the following two initial conditions:

and

that correspond to geometries that are initially rectangular and circular, respectively. The results presented in Figures 7 and 8 show the spatio-temporal evolution of the densities ρ₁ of motile cells (left column) and ρ₂ of immotile proliferating cells (right column).

Figure 7. 2D pattern emerging from the go-or-grow travelling wave in rectangular geometry. We present the spatio-temporal evolution of the motile population ρ₁ (left column) and proliferating population ρ₂ (right column) evolving over a 2D rectangular domain. The density level is given by the colour bar to the right of each figure. The initial condition is given by Equations (13) and shown in (a). Plots (b)–(f) show the dynamics of the initially perturbed front at several later times. For direct comparison with (f), plot (g) shows the solution at time t=180 obtained by using the unperturbed front (i.e. no transverse perturbation in Equation (13)) as the initial condition.

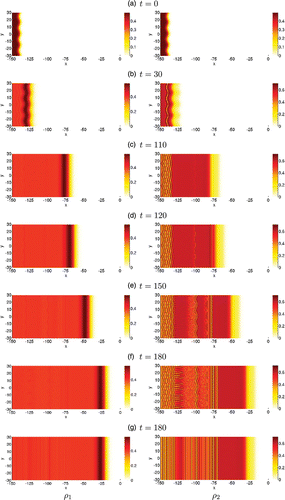
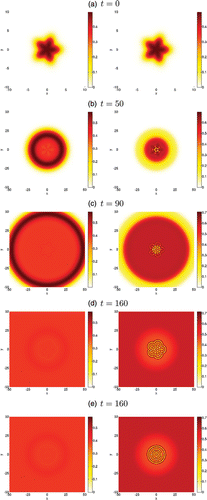
Figure 8. 2D pattern emerging from the go-or-grow travelling wave in circular geometry. We present the spatio-temporal evolution of the motile population ρ₁ (left column) and proliferating population ρ₂ (right column) evolving over a 2D domain. The density level is given by the colour bar to the right of each figure. The initial stellar condition is given by Equations (14) and shown in (a). Plots (b) to (d) show the dynamics of the initially perturbed front at several later times. For direct comparison with (d), plot (e) shows the solution at time t=160 obtained by using the unperturbed front (i.e. no transverse perturbation in Equation (14)) as the initial condition.

In the rectangular geometry, when starting with an initially perturbed front, the first instability that develops is located between the core and the travelling front. This instability is initiated in the immotile population and maintains the same shape as the initial perturbation as shown in Figure 7(b). At later times, another instability having the same shape as the initial perturbation forms between the wave front and the first instability, which has now generated patterns (Figure 7(c)) that propagate backward towards the left of the domain. Soon after, oscillations (vertical stripes) develop at the right of the second instability (Figure 7(d)). Note that we observe three instabilities of different shapes occurring at different times and locations. The differences in shape and density eventually result in a mixture of irregular and structured patterns as the oscillations and/or the instabilities coalesce as shown in Figure 7(f). When the front is not perturbed, we observe oscillations forming only within the core (Figures 7(g)). We remark that the heterogeneities that arise from the instabilities are composed mainly of immotile cells (right column of Figure 7), whereas motile cells typically localize at the edge of the invading front, with a portion of them remaining almost uniformly distributed in the core. There the density is, on average, too low to completely stop their movement (left column of Figure 7)).

Meanwhile, simulations of the model in the circular geometry give rise to different patterns. We present in Figure 8 the spatio-temporal evolution of the densities ρ₁ of motile cells (left column) and ρ₂ of immotile proliferating cells (right column). When the front is initially perturbed, we observe unusual patterns that branch within the core (Figures 8(b)–(d), right) and give rise to stationary geometric structures. In the case of an initially unperturbed front, we observe the formation of circular patterns as shown in Figure 8(e). Regardless of the initial condition, the formation of these various patterns suggests a spatially heterogeneous distribution of immotile cells that are mostly located within the core. As for the rectangular geometry, motile cells are preferentially located at the edge of the front, i.e. near the surface of the spheroid (Figures 8(b) and (c), left), with a portion remaining almost uniformly distributed in the core. The spatial localization of each cell type is thus consistent with experimental observations, the additional outcome of our model being that the regulation of the go-or-grow by the local cell density allows for the formation of spatial heterogeneities within the tumour’s core.

5. Discussion and conclusion

We have used a reaction–diffusion framework to study the invasion of glioma cells guided by experimental evidence which shows that glioma cells exhibit a proliferation/migration dichotomy, i.e. proliferating cells move slowly and migrating cells proliferate slowly 9. We have considered a cell population that contains two distinct (migratory and proliferating) phenotypes associated with tumour invasion. We have derived a system of partial differential equations to model this system and have proposed a density-dependent term to model phenotypic switches between the two sub-populations. In the absence of proliferation, motile cells can enter resting phases and become immotile, which characterizes a sub-case of our model that we denoted as go-or-rest. When proliferation is included, only immotile cells can proliferate, which characterizes our go-or-grow model.

We have performed a Turing instability analysis of both models and found that both instability criteria depend on the switching mechanism. We have shown that neither model exhibits Turing instabilities under switching mechanism M₂, whereas under the autocatalytic mechanism M₁, Turing instabilities can occur for certain parameter ranges. We have investigated the stability of the spatially uniform steady-state by solving numerically the go-or-rest model, using a slightly perturbed uniform steady-state as the initial condition and have found that immotile cells accumulate to form aggregates due to the crowding effect when M₁-regulated, which in turn limits cell motility. By adding proliferation to the immotile population (as a logistic term) and solving numerically the go-or-grow model, we have found that the same mechanism leads to irregular oscillatory dynamics. Interestingly, for both models, the logistic term is not sufficient to limit solutions to the saturating density that is exceeded when the non-trivial uniform steady-state within the core is unstable.

Another interesting aspect of our go-or-grow model is the travelling wave behaviour. We have shown that there are three regions of the (M, ρ*)-parameter space where travelling wave solutions exist with either a spatially uniform core behind the moving front, stationary patterns within the core resulting from the oscillations at the moving front, or irregular oscillatory dynamics that extend to the entire domain behind the moving front. These dynamical, heterogeneous spatio-temporal solutions demonstrate the ability of the density-dependent go-or-grow mechanism to produce complex dynamics associated with tumour heterogeneity during invasion. Other recent modelling approaches have shown that heterogeneity within the tumour’s core can be obtained by considering interactions with the micro-environment. Matzavinos et al. 20 proposed a model of solid tumour growth, prior to angiogenesis, where the effect of an immune system response gives rise to complex heterogeneous spatio-temporal dynamics. Stamper et al. 25 proposed a model of vascular tumour growth where a combination of cell proliferation and vessel occlusion produces waves developing into regular or irregular spatio-temporal oscillations. By contrast, here, we propose that such complex behaviours can also emerge without external coupling to an additional field, but simply by considering cell–cell interactions through density-dependent regulation.

Another intriguing aspect is that the front speed seems to increase along the stabilization of the core (Figure 5) which is related to the increase of the effective total proliferation rate, a phenomenon that we will study in more detail in a future work. Solving the go-or-grow model on a 2D domain has further shown that the spatio-temporal dynamics depend on the initial conditions. In particular, similar to results obtained by Sherratt et al. 24 in the context of predator–prey invasion, the influence of initial perturbations can be observed in long-time solutions, which, in our model, gives rise to different types of pattern within the tumour’s core. This observation suggests that the tumour’s spatial heterogeneity can be generated by mechanisms of invasion driven by phenotypic adaptation only. The question that arises is why glioma tumours would adapt to a particular strategy to invade the surrounding tissue. In our model, the selection of a particular mechanism of invasion (i.e. the three sub-cases of M₁ or M₂) is associated with a specific type of growth. Our model shows that glioma tumours can grow fast and homogeneously (case (1) in Figure 5) or slow and heterogeneously (case (3) in Figure 5), which may correlate with its progression and grade. Therefore, we suggest that tumour progression may be associated with phenotypic adaptation through the selection of particular mechanisms of invasion.

The migratory and proliferating dichotomy may also have implications on the tumour’s response to therapy. For example, if a glioma is treated with a standard chemotherapeutic drug (which targets mainly the immotile, proliferating cells), then motile cells may contribute to relapse after chemotherapy. This suggests that therapies which target the non-proliferative cells are needed and should be used in combination with standard chemotherapy. Additionally, the space liberated following the death of immotile cells (i.e. a decrease of the cell density) would stimulate phenotypic adaptation to the new micro-environmental conditions. In vivo, invading cells may later encounter different environmental conditions that would favour a return to a proliferating phenotype after a cycle of chemotherapy, eventually leading to tumour recurrence. There, mechanisms M₁ and M₂ would play different roles. If we assume that the switching mechanism M₁ applies, then invading cells would propagate into the tissue until reaching denser areas that would make them stop and proliferate to form islands distant from the initial primary tumour. Under mechanism M₂, motile cells would stop and, after a cycle of chemotherapy, start proliferating at the location of the initial tumour where the density has decreased. Therefore, additional cycles of chemotherapy may target these cells that re-enter the cell cycle, which would make a local therapy more effective by ‘keeping the invasion under control’. Thus, the investigation of the phenotypic adaptation as a new therapeutic target could help for a better control of the tumour re-growth.

The main goal of this paper was to investigate the dynamics of a population of tumour cells for which the switch from a migratory to a proliferating phenotype (and vice versa) depends locally on the cell density. An important observation of malignant tumour invasion is the formation of front protrusions (fingering phenomenon). In this study, we have focused our analysis on pattern formation associated with diffusion-driven instabilities and we have not observed front instability. In a follow-up paper, we will investigate the influence of the mechanism of phenotypic switch on the emergence of front instabilities associated with invasive fingering.

Acknowledgements

J.L., K.P. and X.L. acknowledge support from the National Science Foundation Division of Mathematical Sciences (DMS) and from the National Institutes of Health through grant P50GM76516 for a Centre of Excellence in Systems Biology at the University of California, Irvine. A.C., H.H. and V.C. acknowledge support from The Cullen Trust for Health Care and the National Institute for Health, Integrative Cancer Biology Program: 1U54CA149196, for the Center for Systematic Modeling of Cancer Development. V.C. also acknowledges the National Science Foundation, Division of Mathematical Sciences for grant DMS-0818104. H.B. acknowledges partial support by Award No. KUK-C1-013-04, made by King Abdullah University of Science and Technology (KAUST).

Additional information

Notes on contributors

Helen M. Byrne

Current affiliation: Oxford Centre for Collaborative Applied Mathematics, Mathematical Institute, 24–29 St Giles, Oxford, OX1 3LB, UK