Analytical and numerical approaches to coexistence of strains in a two-strain SIS model with diffusion

Abstract

This article introduces a two-strain spatially explicit SIS epidemic model with space-dependent transmission parameters. We define reproduction numbers of the two strains, and show that the disease-free equilibrium will be globally stable if both reproduction numbers are below one. We also introduce the invasion numbers of the two strains which determine the ability of each strain to invade the single-strain equilibrium of the other strain. The main question that we address is whether the presence of spatial structure would allow the two strains to coexist, as the corresponding spatially homogeneous model leads to competitive exclusion. We show analytically that if both invasion numbers are larger than one, then there is a coexistence equilibrium. We devise a finite element numerical method to numerically confirm the stability of the coexistence equilibrium and investigate various competition scenarios between the strains. Finally, we show that the numerical scheme preserves the positive cone and converges of first order in the time variable and second order in the space variables.

Keywords:

• diffusion
• multi-strain
• reproduction numbers
• finite element method
• competition and coexistence

AMS Subject Classification:

• 92D30

1. Introduction

Most communicable diseases exhibit variation in epidemiological characteristics throughout space. For instance, different countries have different incidences of a given infectious disease. Key epidemiological parameters, such as transmission and often recovery, are intrinsically spatially dependent. Disease transmission through direct contact is always local, and its intensity can be linked to the spatial location. This suggests that when the classical epidemic models are recast to include diffusion and incorporate spatial heterogeneity explicitly, the transmission coefficients should be functions of the spatial location where the contact occurs. It is surprising to see that most classical epidemiological spatially heterogeneous models have a reaction part where rates are constant with respect to location. Notable exceptions exist. The spatial effects have been widely studied through patch models (e.g. 19) or by adding diffusion to an ordinary differential equation (ODE) model 25. The authors in 19 studied how banning travel of symptomatic or infected individuals from high to low prevalence patch will effect the spread of the disease by considering a multi-patch model where transmission and recovery are patch-dependent.

In three papers Fitzgibbon et al. study a number of directly, environmentally and vector-transmitted diseases where the transmission rate is spatially heterogeneous 15 16 17. The authors derive analytical results on well-posedness of the systems as well as various limiting properties of the solutions. Epidemiologically relevant threshold conditions, however, are derived in the case of constant coefficients 15.

Studying the classical epidemiological models with spatially heterogeneous coefficients presents significant difficulties. The first article that derives a reproduction number for a simple SIS models with spatially heterogeneous transmission and recovery appears to be the one by Allen et al. 2. The reproduction number defined there is not explicit in the sense that if the parameters were known the value may still be not easy to compute. Furthermore, this reproduction number does not seem to follow the next generation approach 12 but possesses the usual threshold property. The authors also derive useful epidemiological characteristics such as dependence of the reproduction number on the diffusion coefficients.

In this paper we consider a two-strain extension of the model presented in 2. The two strain model does not incorporate any explicit trade-off mechanisms, such as co-infection or super-infection 23 that may lead to coexistence of the strains even in the model’s ODE counterpart. The main question that we address is whether space alone could allow for coexistence. We expect and obtain a positive answer to our question. The continuous scenario that we investigate is analogous to a discrete multi-patch model where the disease cannot persist on any of the individual patches, but can persist in the system. The ability of the diseases to persist in a system of sink habitats, that is patches with basic reproduction number smaller than one, has been observed before in various multi-patch epidemiological models (e.g. 11).

We approach the problem both analytically and numerically. Analytical studies of multi-strain epidemic models with diffusion are scarce. Kim et al. 22 discusses a spatial version of an avian influenza multi-strain model with nonlocal transmission in humans, but the strains there do not compete as each one is established in a different species. Competition has more thoroughly been addressed in ecology in the context of Lotka–Volterra competition models 7, p. 224]. In an ecological context, the effect of diffusion on coexistence in competing populations has been studied in multiple scenarios. For instance, Pacala and Roughgarden [25 consider a pair of coupled Lotka–Volterra competition equations with diffusion on one-dimensional spatial habitat. The only spatially heterogeneous parameter is the carrying capacity which is defined as a step function. Furthermore, the effects of spatial heterogeneity on the persistence of two competing species have been investigated in 8 where the authors studied the dynamics of the two interacting populations by considering a coupled reaction diffusion system having spatially dependent reaction terms. The impact of space on competing species in an ecological context has much in common with the question we study in this paper.

Here, addressing our main question, we show analytically that a coexistence equilibrium exists. This is the case if the invasion numbers of the two strains, defined analogously to the reproduction numbers, are larger than one. To show stability of the coexistence equilibrium we develop a fully discrete finite element method. Finite element methods are a natural approach to diffusion problems including in epidemiology 21. The main challenge is to develop a finite element method that preserves the positivity of the solution. We use the finite element method to demonstrate through simulations the convergence to a coexistence equilibrium as well as to investigate other outcomes of the competition of the strains based on the reproduction numbers and invasion numbers. Since the reproduction numbers and invasion numbers for our examples cannot be computed exactly, even when the parameters of the model are known, we develop a novel numerical method that estimates the relation of these numbers to one.

This paper is structured in the following way: In Section 2 we introduce the two-strain model and the reproduction numbers of the strains. In Section 3 we investigate the local stability of the disease-free equilibrium (DFE) and the semi-trivial equilibria. We also introduce the invasion numbers and their relation to the corresponding principal eigenvalue. In Section 4, we use the monotonicity of the equilibrial system to show the existence of coexistence equilibrium in the case when both invasion numbers are larger than one. In Section 5 we introduce our finite element method. Furthermore, we establish its order of convergence and we show that it preserves the positivity of the solutions. Section 6 is devoted to the numerical computation of the reproduction numbers and invasion numbers. Section 7 shows numerical evidence of the convergence of our finite element method. Furthermore, we investigate through simulations various outcomes of the competition of the strains governed by the reproduction and invasion numbers. Section 8 contains a summary of our results.

2. A two-strain SIS model with diffusion

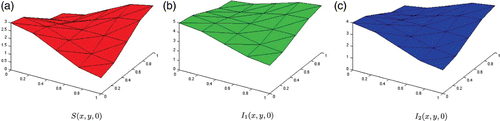
In this section we introduce a two-strain SIS epidemic model with diffusion. The total population size is divided into nonintersecting classes of susceptibles, infected with strain one and strain two. Let S(x, t) be the density of the susceptible individuals at position x at time t>0. Let I ₁(x, t) and I ₂(x, t) represent the densities of infected individuals with respect to strain one and two, respectively. We consider the following reaction diffusion system:

where Ω is a bounded domain in R ⁿ (with n≥1) with smooth boundary ∂Ω. The vector n is the unit outward normal to the boundary ∂Ω. We assume no flux boundary conditions. Thus, the population remains confined to Ω for all time. System (1) is equipped with positive initial conditions. We assume that there is initially a positive number of infected individuals, i.e.

This model is a two-strain extension of the model in 2. It is clear from the standard theory of semilinear parabolic systems that a unique classical solution (S, I ₁, I ₂) of (1) exists for all time 18. In this model, we assume the diffusion coefficients d _s ,  d ₁, and d ₂ for the susceptible and infected populations to be positive coefficients. Reaction terms, β₁(x)(S I ₁/(S+I ₁+I ₂)) and β₂(x)(S I ₂/(S+I ₁+I ₂)) , give the incidence of the disease, that is, the number of newly infected susceptible individuals per unit of time who have contracted the disease and have become infected at a given position x∈Ω. Here, β₁(x),  β₂(x) are the space-dependent rates of disease transmission by infectives with strain one and strain two, respectively, at position x∈Ω. Infected individuals with strain one and strain two recover and become susceptible with space-dependent rates of recovery γ₁(x) and γ₂(x) for position x∈Ω. We assume that β₁(x), β₂(x), γ₁(x), and γ₂(x) are positive Hölder continuous functions on . Assume also that

Let

be the total population size in Ω at time t. Note that ∂V /∂t=0, since

We conclude that the population size, V , is constant, and equal to the total population size at time zero. Therefore, we have,

Setting , , , and substituting into (1), we get similar equations. Dropping the bar on , we get the same system of equations (1) with the following conditions:

In the rest of this article we consider system (1) subject to the above constraint.

We denote by the basic reproduction number which gives the number of secondary infections that one infected individual will produce in an entirely susceptible population. The basic reproduction number determines whether there is an epidemic or not. The reproduction number of strain i is given by

We note that the reproduction number of strain i depends explicitly on space. However, its computation if the coefficients of the system are known, is not straightforward.

Then the basic reproduction number is defined as . We show in the next section that if , then both strains die out. It is expected that if , then at least one of the strains persists.

3. Local stability of the DFE and semi-trivial equilibrium

We are interested in the equilibrium solutions of (1), i.e. the time-independent solutions of the following system:

This system is augmented with no flux boundary conditions,

In (2) quantities , , denote the densities at equilibrium of susceptible and infected individuals at location x∈Ω. The equilibrium values also satisfy

A DFE is a solution of (2) in which both strains and vanish at every x∈Ω at equilibrium, i.e. . A strain-one equilibrium, I ₁-equilibrium, is a solution of (2) in which only strain two, vanishes at every x∈Ω at equilibrium. Similarly, a strain-two equilibrium, I ₂-equilibrium, is a solution of (2) in which only vanishes at every x∈Ω at equilibrium. An endemic equilibrium (EE) is a solution in which both strains coexist, i.e. and for some x∈Ω. To distinguish between these four types of equilibria, we use different notations for each. Throughout the paper, we denote DFE by , I ₁-equilibrium by , I ₂-equilibrium by , and EE by .

Theorem 3.1

There exists a unique DFE and it is given by

Proof

Since in DFE both , by (2) we have . With boundary condition , implies that is a constant in Ω. Clearly any constant is a solution, but note that since and and is a constant, , where |Ω| is the measure of the domain Ω.

Theorem 3.2

If then DFE is locally stable,  if then it is unstable.

Proof

To study the stability of the equilibrium, let

We linearize (2) around DFE and obtain the following system of perturbation equations:

with boundary conditions; ∂η/∂n=∂ξ₁/∂n=∂ξ₂/∂n=0 on ∂Ω. We search for solutions of system (4) in the form η(x, t)=e ^−λt φ(x), ξ₁(x, t)=e^−λt ψ₁(x), ξ₂(x, t)=e^−λt ψ₂(x). Substituting in system (4) we obtain the following eigenvalue problem:

with boundary conditions: ∂φ/∂n=∂ψ₁/∂n=∂ψ₂/∂n=0 on ∂Ω.

Since the total population size is constant, we have

Therefore,

It is easy to see that the vector (c, 0, 0) where c is a nonzero constant satisfies system (5)–(7) with the boundary conditions. However, this solution does not satisfy the constraint in (8), and hence, λ=0 is not an eigenvalue of the system (5)–(7) subject to the constraint (8). Observe that (6) and (7) are decoupled. If (λ₁, ψ₁) and (λ₂, ψ₂) are eigenpairs of (6) and (7) respectively, then λ _i ,  i=1, 2,  are real since, the operators on the left side of these equations are self-adjoint. Note that both (6) and (7) have infinite sequence of eigenvalues:

which are bounded from below. Let denote the first eigenvalues, and , denote the corresponding eigenfunctions of (6) and (7), respectively. Since the first eigenvalues, are simple, both and are positive in Ω 13 29. It is well known that is given by the following variational characterization:

Similarly, satisfies the following variational formulation:

Note that eigenpairs of the scalar equations (6) and (7) are also the solutions of the system (5)–(7), if we consider the solutions of the form (λ₁, φ, ψ₁, 0) or (λ₂, φ, 0, ψ₂). Clearly, and , whenever , and ; and , whenever , and ; and and , whenever , and . The perturbation system (4) is stable, iff , and , that is, iff .

Theorem 3.3

If then DFE is globally stable,  if then it is unstable.

The proof follows from the proof of Lemma 2.5 from 2.

Next, we consider the two semi-trivial equilibria. The I ₁-equilibrium satisfies the following system:

where . The I ₂-equilibrium satisfies the same system with the subscripts 1 and 2 interchanged, and with . This is exactly the same system for the EE discussed in 2. We conclude that there exists a unique equilibrium and a unique equilibrium. Since the existence results for I ₁ and I ₂ equilibria are direct consequences of results in [2, Section 3.2], they will not be derived here.

To investigate local stability of semi-trivial equilibria, let S(x, t)=S*(x, t)+φ(x, t), , and I ₂(x, t)=ψ₂(x, t) and then linearizing (1) around we obtain

Since (12) decouples, we consider the following eigenvalue problem:

Let λ* denote the principal eigenvalue of (13), which is given by the following variational formulation:

The system (9) is the exact system for EE of the single-strain model studied in 2. The eigenvalue problem associated with the linearization of the single-strain model at the EE is given as follows:

Theorem 3.4

Let λ*<0 and suppose that λ* is not an eigenvalue of (15)–( 16),  then the I ₁ equilibrium is unstable.

Proof

We use the principle of linearized stability theorem which states that the stability of the equilibrium is determined by the spectrum of the linearization at the equilibrium 24 27. So, we consider the following eigenvalue problem:

For λ*<0, we need to show that (λ*, φ, ψ₁, ψ*) is a solution of (17), where λ* is the principal eigenvalue and ψ* is the corresponding positive eigenfunction of the eigenvalue problem (13). For given (λ*, ψ*), we need to solve the following nonhomogenous problem:

Since λ* is not an eigenvalue of (15) and (16), the operator on the left-hand side is invertible.

Similar analysis is true for the I ₂-equilibrium . For the I ₂-equilibrium, we consider the following eigenvalue problem:

We denote the principal eigenvalue of (18) by , and its variational formulation is given as follows:

We denote by the positive eigenfunction corresponding to the principal eigenvalue of (18).

Theorem 3.5

Let and suppose that is not an eigenvalue of the following eigenvalue problem:

then the I ₂ -equilibrium is unstable.

Proof

Similar to the proof of Theorem 3.4.

We denote the invasion numbers of strain one and strain two by , and , respectively. The two invasion numbers are defined as follows:

Invasion number gives the ability of strain one to invade the I ₂-equilibrium measured as the number of secondary infections one strain one-infected individual can produce in a population where strain two is at equilibrium. Similarly, invasion number gives the ability of strain two to invade the I ₁-equilibrium .

Lemma 3.1

The following statements are true for the invasion numbers of strains one and two, respectively.

i.	is a positive and monotone decreasing function of d i >0;
ii.	when when , and when
iii.	when λ*<0,  when λ*=0,  and when λ*>0.

Proof

(i) The functions β₁,  β₂,  γ₁, and γ₂ are nonnegative on the domain Ω. Positivity of the invasion numbers , are satisfied by the existence of the positive single-strain equilibriums and . It is straightforward to show that the invasion numbers , are decreasing functions of d ₁ and d ₂, respectively.

(ii) Let φ(x) be the nonzero function in H ¹(Ω) for which the is achieved in (20). Thus,

We assume that φ is nonnegative, since if not, φ can be replaced with |φ|. Let v(x) be the nonzero function in H ¹(Ω) and consider the following function:

Since φ is the element for which the is achieved, we have f′(0)=0. Expanding the squares in (22), we obtain:

Taking derivative w.r.t. ε and setting ε=0 we obtain:

Thus;

The last equality is satisfied for any trial function v. Then by Green’s identity we obtain

By rewriting (23) and considering the eigenvalue problem (18) we obtain

Recall that the pair denotes the principal eigenvalue and corresponding positive eigenfunction of (18). Multiplying (24) by and multiplying (25) by φ, integrating both equations over the domain Ω, and then adding the resulting equations we obtain

Since , φ and are all positive on Ω, and have opposite signs.

(iii) Proving this statement is similar to the analysis in (ii).

4. Coexistence equilibrium

Coexistence equilibrium, , satisfies the system (2) with Neuman boundary conditions (3). Since and it follows that for some positive constant κ

We normalize by κ. Set,

Hence,

To guarantee that we define

Taking into account that the original system (2) reduces to:

Let

Lemma 4.1

We have

when .

Proof is immediate and it is omitted. Lemma 4.1 implies that the operator G=(g ₁, g ₂) is quasi-monotone nondecreasing.

From the work of Nevai et al. 2 we know that there are unique single-strain solutions and with and . We assume that Theorems 3.4 and 3.5 hold and therefore both of the semi-trivial equilibria are linearly unstable.

For vectors , we say that x≤ _K y if and only if x ₁≤y ₁ and x ₂≥y ₂. We say that is a super-solution for (26)–(28) if

We say that I=(I ₁, I ₂) is a sub-solution for (26)–(28) if ≤ _K is replaced by ≥ _K in (31).

We have the following result 26 27.

Lemma 4.2

Let I =(I ₁ ,  I ₂) be a sub-solution and be a super-solution for (26)–( 28). If in Ω,  then (26)–( 28) has a solution with .

Lemma 4.3

System (26)–(28) has a positive sub-solution I and super-solution .

Proof

We claim that for all sufficiently small ε>0, the following choices work:

Recall that, are principal eigenvectors of the linearization of (26)–(28) at and , respectively. In particular,

and

By our assumption that and are linearly unstable it follows that

Let us verify that is a super-solution for all sufficiently small ε>0. We need to show that

Clearly, the boundary condition holds. We also have that

where we used the fact that solves (26), and that g ₁ is nonincreasing in its second argument. Moreover,

for all sufficiently small ε>0. Here we used the fact that (εψ*) solves (34), that −λ*ψ*>0, and that . Thus, we have established that (36) holds, and hence that is indeed a super-solution of (26)–(28) for all sufficiently small ε>0.

Similar arguments show that is a sub-solution of (26)–(28) for all sufficiently small ε>0.

Lemma 4.4

Let (I*₁ , 0) and be linearly unstable single-strain solutions of (26)–(28). Then (26)–(28) has a positive solution . Moreover,  if we set

then,  .

Proof

Let . Then,

Thus, u satisfies the following equation:

where and are the given solution of (26)–(28) and are assumed to be given functions in the above equation. First, we notice that is a solution to the above equation for u. Second, denoting the left-hand side of the above equation by , we see that . Hence, zero is a sub-solution. Therefore,

This concludes the proof.

5. Numerical method

In this section we approximate the solution of the model problem (1). We derive the approximate solution of (1) in two steps. In the first step we approximate the solution by means of functions which for each fixed time belong to a finite dimensional space. These functions will be the solution of h-dependent finite system of ODEs in time and referred to as spatially discrete solutions. In the second step, we discretize this system in the time variable to obtain a fully discrete approximation of (1) by a finite difference method. For the notational convenience, we rewrite (1) in the vector form:

where u=(S(x, t), I ₁(x, t), I ₂(x, t)) ^T , is the time derivative, is the diffusion matrix, and F(u) is the right-hand side vector of the form:

We adopt the standard notation for the Hilbert Spaces 1 6 20;

In general, we denote by H ^m (Ω) the Hilbert space of all L ² functions with m derivatives (m≥0) in L ²(Ω). These Hilbert spaces are endowed with the norms

and

and semi-norm,

where D ^α denotes an arbitrary derivative of order |α|, with α=(α₁, α₂, …, α _d ), and The usual L ² inner product over the domain Ω is denoted by (⋅, ⋅).

A variational formulation of (39) is derived by first multiplying both sides of (39) by functions v in H ¹(Ω). We, then obtain the weak formulation of (39) by Green’s formula. We look for a function u(x, t)∈H ¹(Ω)×H ¹(Ω)×H ¹(Ω) (that is, for every t>0 the function is in H ¹(Ω)×H ¹(Ω)×H ¹(Ω)), such that

We have used the following notation:

and a(u, v) is a bilinear form given by,

We introduce the semi-norm which is equivalent to the H ¹ semi- norm:

We first pose the spatially semi-discrete problem based on the weak formulation (40). The Galerkin approximation of (40) is simply constructing the discrete variational problem in a finite dimensional subspace of H ¹(Ω). Let χ _h be a family of finite dimensional subspaces of H ¹(Ω), then the discrete weak formulation of (40) is:

Find u _h (x, t)∈χ _h ×χ _h ×χ _h (that is, for every t>0 the function is in χ _h ), such that

where u _0h is the approximation of u ₀ in χ _h ×χ _h ×χ _h . Note that in (41), u _h is a vector function of the form u _h =(u _s , u ₁, u ₂), where u _s (x, t), u ₁(x, t), u ₂(x, t) are semidiscrete approximations of S(x, t), I ₁(x, t),  and I ₂(x, t), respectively. Thus, (41) is: Find u _s , u ₁, u ₂∈χ _h s.t.

∀v _h ∈χ _h , t>0, and u _h (0)=u _0h .

We define χ _h first by partitioning the domain Ω into triangles. Let denote the partition of Ω into triangles τ, such that no vertex of any triangle lies on the interior of a side of another triangle. Let h denote the mesh size, which is the maximal length of sides of the triangles in triangulation . The parameter h is a measure of how refined the mesh is, the smaller the h,  the finer the mesh. We assume that is a quasi-uniform mesh in the sense that the triangles in are essentially the same size. We also assume that all the angles in the triangulation are acute, which means that all the angles are less than π/2. We denote the union of triangles in by Ω _h which is a convex polygonal domain. Clearly, Ω _h is an approximation of bounded domain Ω with smooth boundary, and the error in approximating the domain Ω−Ω _h does not change the rate of convergence 9. We thus assume Ω _h =Ω.

We define χ _h to be the space of continuous functions on Ω which are linear polynomials in each triangle of .

Let be the nodes of the triangulation , and let be the basis for χ _h , then u _s (x, t)∈χ _h is uniquely determined by:

Similar expansions are true for u ₁(x, t) and u ₂(x, t).

We now, discretize (42) with respect to the time variable to obtain fully discrete approximation of (1). Let T denote the maximum time, k denote the time step, and J be a fixed nonnegative integer, then

We approximate the time derivative in (42) by the backward Euler difference quotient. Thus, let represent the approximation of respectively, then we denote by D the following finite difference operator:

Now, (42) becomes: Find u _s , u ₁, u ₂∈χ _h s.t.

∀v _h ∈χ _h , and u _h (0)=u _0h , n=1, 2, …, J.

We linearize the system by using discretization , for the approximation of nonlinear terms S I ₁/(S+I ₁+I ₂), S I ₂/ (S+I ₁+I ₂), respectively. At each time step, we solve three linear systems of algebraic equations simultaneously.

We use the vertex quadrature rule to approximate the L ₂ inner product in χ _h . Let be the vertices of the triangle τ, then the vertex quadrature rule, q _τ, h (f), is defined as follows 30:

We then define the following discrete inner product in χ _h . Let u, v∈χ _h then,

Clearly [ϕ _i , ϕ _j ]=0 if i≠j since ϕ _i (x)ϕ _j (x) vanishes at all nodes of the triangulation if i≠j.

The system (44) can be rewritten as:

5.1. Error analysis

We assume that the family of finite dimensional sub-spaces, χ _h , of H ¹(Ω) possesses the following approximation property 30: Let u∈H ²(Ω) and v∈χ _h , then

Since the family of finite dimensional subspaces, χ _h , of H ¹(Ω) are based on shape regular triangulation of and χ _h consists of piecewise linear polynomials, we have the following inverse inequality 30:

Let be the so-called elliptic projection, π _h , onto χ _h , which we define as the orthogonal projection with respect to L ² inner product. For u∈H ¹(Ω),

In our error analysis, we adopt the following notation (where (u _s , u ₁, u ₂) is the solution of (44)):

Clearly, ; ; i=1, 2. Since χ _h possesses the approximation property (46), one can easily obtain the following:

We note here that since we have the desired bounds for ||ρ _s (t)|| and ||ρ _i (t)||, for i=1, 2, we concentrate on bounds for and ; i=1, 2.

Before considering the error estimates for the fully discrete approximation, we prove the following lemma.

Lemma 5.1

Let u=(S, I ₁ , I ₂) be the solution of (39),  and let u _h =(u _s , u ₁ , u ₂)>0 be the solution of (41),  then

i.
ii.
iii.

where and .

Proof

Here we demonstrate the proof of (ii), since the proofs of (i) and (iii) are similar. Adding and subtracting terms β₁(S u ₁/(u _s +u ₁+u ₂)) and β₁(S u ₁/(S+I ₁+I ₂)) we obtain

We now perform error analysis for the fully discrete scheme.

Theorem 5.1

Let u=(S, I ₁ , I ₂ ) and u _h =(u _s , u ₁ , u ₂ ) be the solution of ( 39 ) and ( 44 ),  respectively,  then

Proof

Setting , in which we use the fact that the elliptic projection commutes with the finite difference operator, we obtain

using the definition of elliptic projection, and (44) we obtain

Applying a similar procedure for , in (44) we obtain

where the residuals , are defined as follows:

Let us denote the nonlinear terms in the residuals by and . That is

In (47), taking v _h =θ _s , noting that is nonnegative, and using the Cauchy–Schwartz inequality we obtain

Substituting, we obtain,

Applying the same procedure to (48) we obtain

Thus,

Next, we estimate the residual terms. Estimation of the first terms in the residuals, are standard, and it is described in [30, Theorem 1.5].

where the constant C depends on the initial conditions, first and second time derivatives of (S, I ₁, I ₂). We focus on the analysis of the nonlinear terms in the residuals .

Using Lemma 4.1 for the remaining terms in we obtain

Since we arrive at the estimates

Using similar arguments for and , we obtain

Thus, applying discrete Gronwall’s inequality we finally obtain,

5.2. Positivity of solutions

In this section we study the positivity of the solution to the problem (45). We want to know whether any positive initial condition will lead to a positive solution of the system (45). Let denote the time-dependent coefficients of the approximate solution (u _s (x, t), u ₁(x, t), u ₂(x, t)) determined by the basis functions . Using, α ⁿ =α(t _n ), in matrix notation (45) becomes

where is a block diagonal matrix, whose blocks are the diagonal mass matrix with components m _{i j} =[ϕ _i , ϕ _j ]. The matrix is a block diagonal matrix where is the stiffness matrix with a _{i j} =(∇ϕ _i , ∇ϕ _j ). The matrix,

is a 3×3 block matrix where the block matrices are diagonal matrices with components; , , (γ₁) _i, j =[γ₁(x)ϕ _i , ϕ _j ], (γ₂) _i, j =[γ₂(x)ϕ _i , ϕ _j ].

The initial condition α⁰ is the components of given initial approximation of u _0h . Note that α⁰>0, since by (43) α _s, j (t ₀)=u _s (η _j , t ₀)>0.

The above system of equations may be written as

Introducing the notation, X=M+k A−k F(α ⁿ⁻¹), (49) can be rewritten as

With this notation, the positivity of the solutions reads as follows: For any positive initial vector α⁰, the relation α ⁿ >0 holds for each n. The mass matrix M is a diagonal matrix with positive diagonal entries due to the vertex quadrature rule. Thus, for given α ⁿ⁻¹>0 we have Mα ⁿ⁻¹>0. Clearly, the method (50) preserves the positivity of the solutions if and only if X ⁻¹>0. To study that the method (50) generates positive solutions, we recall some facts from the widely studied theory of M-matrices. We first give the following definitions.

Definition 5.1 ([5])

A real n×n matrix A=a _i, j is said to have a Z _n sign pattern if a _i, j ≤0 for all i≠j.

We are interested in special subclass of matrices with Z _n sign pattern, called M-matrices.

Definition 5.2 [([31, p. 91])]

Let A have a Z _n sign pattern,  then it is an M matrix,  if A is nonsingular and A ⁻¹ ≥0.

Note that if a matrix A has Z _n sign pattern, then it can be expresses as A=s I−B, where B≥0. The matrix A is an M-matrix, if s≥ρ(B), the spectral radius of B.

Note that in one dimension, the stiffness matrix a is an M-matrix. In two dimensions, if all the angles in the triangulation are not greater than π/2, which is called an acute type triangulation, then the matrix is a is an M-matrix 10 32. If all the angles of the triangulation are acute and a vertex quadrature rule is used in the computation of the mass matrix m, then there exists a discrete-maximum principle. Clearly, this is not the case for the standard Galerkin method 30.

Lemma 5.2

We have the following properties for the matrices M and A:

i.	The matrix M is an M-matrix.
ii.	The matrix A is an M-matrix.

Definition 5.3 [([5,14])]

The directed graph,  G(A),  of an n×n matrix A consists of n vertices,  P ₁ , P ₂ , …, P _n where an edge leads from P _i to P _j if and only if a _ij ≠0. The directed graph is called strongly connected if there is a path from each vertex to every other vertex.

Theorem 5.2 [5,14]

A matrix A is irreducible if and only if G(A) is strongly connected.

Proof

See [14, Theorem 3.6] or [5, Theorem 2.7].

Lemma 5.3

We have the following properties for the matrix X:

i.	X has Z n sign pattern.
ii.	X is irreducible.

Proof

i.

The matrix M is a diagonal matrix with positive diagonal entries. The matrices A and −F(α n−1) have Z n sign patterns. So, X has a Z n sign pattern.

ii.

By Theorem 5.2, X is irreducible if and only if G(X) is strongly connected. Clearly, X i, i =M i, i +k A i, i −k F i, i ≠0, and X i, i−1=k A i, i−1≠0, also X i, i+1=k A i, i+1≠0,  for i=1, …, 3N h . Note that the elements of each component matrix a given by a i, j =(∇ϕ j , ∇ϕ i )≠0 if and only if i and j are the neighbouring nodes. Hence, the matrix a is a symmetric matrix. Also, note that if X i, j ≠0, then X j, i ≠0 as well. So, G(X) is strongly connected.

There are many equivalent conditions for M-matrices, among them we mention the following.

Theorem 5.3

Let A be an n×n irreducible matrix with a Z _n sign pattern,  then the following statements are equivalent:

(i)	There exist a vector x>0 such that Ax>0.
(i)	A −1 >0.
(i)	A is an M-matrix.

Proof

See [14, Theorem 5.12].

Theorem 5.4

Let α ⁰ >0,  then α ⁿ >0 for n=1, 2, …, J.

Proof

To show that X is an M-matrix, we apply Theorem 5.3. Take a vector with all components equal to 1. Then, for k small enough, where and , and Hence y X>0, therefore X ^T y ^T >0. By Theorem 5.3, X ^T is an M-matrix, and (X ^T )⁻¹>0. Hence, X ⁻¹>0 and X is an M-matrix.

6. Numerical estimation of the reproduction numbers

6.1. Numerical computation of basic reproduction numbers

In this section we develop a numerical method that will allow us to estimate whether the reproduction numbers , and the invasion numbers , are each larger or smaller than one. We first focus on estimation of this threshold property for the reproduction numbers, since similar analysis is true for the invasion numbers. Recall that the expression for the reproduction number for each strain is implicit. Even if all the parameters are known, the computation of an approximate value is not an easy task. On the other hand, we only need to estimate if or for i=1, 2 to decide what type of dynamical outcome we can expect for each combination of parameters.

We demonstrate the numerical computation of reproduction number for , since the computation of reproduction number is analogous to .

It is discussed in 2 that the reproduction number for strain I ₁ is a positive and monotone decreasing function of d ₁>0. The relationship between and the principal eigenvalue of the following eigenvalue problem can be proved by following a similar argument as in 2

Let λ₁ be the principal eigenvalues of (51), then when λ₁<0, when λ₁=0, and when λ₁>0.

The weak formulation of (51) is, find , and ψ∈H ¹(Ω), ψ≠0 such that

Here and are bilinear, continuous forms given by

The weak formulation (52) has a sequence of eigenvalues which we denote by

and we denote the corresponding eigenfunctions by ψ₁, ψ₂, …. We approximate the eigenvalues of (52) by a finite element method. Let χ _h be a finite dimensional subspace constructed as in Section 4. Consider the following discrete eigenvalue problem, find and ψ ^h ∈χ _h , ψ ^h ≠0 such that

Problem (53) has a sequence of eigenvalues,

and corresponding eigenvectors, . The eigenpairs of (53) are the approximations to the eigenpairs (λ _k , ψ _k ) of (52) k=1, 2, …, n. The eigenvalues λ _k and their approximates satisfy the following well-known minmax principles

where the minimum is taken over all k-dimensional subspaces U _k and M _k , of H ¹(Ω) and χ, respectively. It follows immediately from the minmax principles that every eigenvalue is approximated from above, see 28.

It is also well known that

where ||⋅|| _a denotes the energy norm and is the space of eigenfunctions corresponding to eigenvalue λ _k , see 3 4. Note that satisfy the following minmax principle:

With and v ^h =ϕ _i for i=1, …, n, we obtain the following generalized matrix eigenvalue problem:

where , , and x _i =c _i . The eigenvalues of this generalized, algebraic eigenproblem can be approximated in Matlab. Then the sign of the minimum eigenvalue, , determines if or . Thus, if , then , if , then , and if , then .

06.2. Numerical computation of invasion numbers

We demonstrate the numerical computation of invasion number of strain one, since similar computation is true for In Lemma 3.1, the relationship between and the principal eigenvalue of the following problem is proved:

where and is the equilibrium solution of the following problem:

First, the system (55) and (56) is solved by the numerical method developed in Section 4. We use again a finite element discretization for the space variable, and backward difference for the time discretization. We compute the solution until time large enough so that the solution has numerically stabilized in time. This gives the values of the steady-state equilibrium used in problem (54).

The discrete weak formulation of (54) within the finite dimensional space χ _h is as follows: Find ψ ^h ∈χ _h such that

where and . Let , taking and v ^h =ϕ _i for i=1, …, n, we obtain the following generalized matrix eigenvalue problem:

where , , and x _i =c _i . The eigenvalues of this generalized, algebraic eigenproblem can be approximated in Matlab. The sign of the minimum eigenvalue determines if the invasion number or .

7. Numerical experiments

7.1. Verifying finite element method convergence rate

In this first example, we verify the convergence rates proved in Theorem 5.1.

Example 1

For the numerical computations, we choose d _s =0.5,  d ₁=1, and d ₂=1.5,  use a uniform mesh on the unit square Ω=[0, 1]×[0, 1], set the final time to T=250 and solve the system (1) with the following choices of transmission and recovery rates for strains one and two; β₁=5−5x, γ₁=1, β₂=5x, γ₂=1. Thus as it will be shown in Example 6, these choices of transmission and recovery rates will give coexistence equilibrium. In the error computations in Table 1, exact solution is taken to be the approximate solution at refinement step j=8, that is the approximate solution is computed with n=131, 072 elements, and m=66, 049 nodes. The time step is fixed in all refinements; it is set to k=1. Error is measured with ℓ²(0, T;L ²(Ω)) norm. Thus,

Table 1.  Observed convergence rates, j denotes the refinement step, h denotes mesh size, n denotes the number of elements, and m denotes the number of nodes.

j	h	n	m	||e s ||ℓ^2(0, T;L ^2(Ω))	||e 1||ℓ^2(0, T;L ^2(Ω))	||e 2||ℓ^2(0, T;L ^2(Ω))
1	h 0	8	9	1.75922909516429	1.11674591720160	1.10261347576481
2		32	25	0.45065854583694	0.27681838124441	0.26859338773873
3		128	81	0.11359187391040	0.06890292747305	0.06650989349128
4		512	289	0.02840019069468	0.01715510756730	0.01652957697302
5		2048	1089	0.00702348061909	0.00423712620012	0.00408005466671
6		8192	4225	0.00167301388341	0.00100896077326	9.71368531625e−04
7		32,768	16,641	3.3485e−004	2.0196e−004	1.9443e−004

Looking at Table 1, we see that for each of the columns 5, 6, and 7, the error drops at least 4 times, as the mesh size h drops 2 times, confirming our theoretical result that the convergence rate is of order h ².

In Table 2, we verify the convergence rate for the time step k. In error computations in Table 2, the exact solution is taken to be the approximate solution at refinement step j=8. The approximate solution is computed for J=6400 time steps. Mesh size is kept fixed, and all computations are done with n=25 elements. In Table 2, we observe that the order of convergence for the time step k is approximately 1 as j increases.

Table 2.  Observed convergence rates, j denotes the refinement step, k denotes the time step, n denotes the number of elements, m denotes the number of time steps, is the error computed at the refinement step j, and gives the ratio of the error computed at two consecutive refinement steps.

j	k	n	m	||e s ||ℓ^2(0, T;L ^2(Ω))		||e 1||ℓ^2(0, T;L ^2(Ω))		||e 2||ℓ^2(0, T;L ^2(Ω))
1	k 0	25	50	0.6279	–	0.5780	–	0.4902	–
2		25	100	0.5305	1.18	0.4671	1.23	0.4006	1.22
3		25	200	0.4161	1.27	0.3556	1.31	0.3058	1.31
4		25	400	0.3078	1.35	0.2638	1.34	0.2294	1.33
5		25	800	0.2123	1.45	0.1857	1.42	0.1687	1.35
6		25	1600	0.1319	1.61	0.1169	1.59	0.1103	1.53
7		25	3200	0.0630	2.09	0.0563	2.07	0.0543	2.03

7.2. Verifying numerically some asymptotic properties of system (1)

The reproduction numbers and invasion numbers often (but not always) control the outcome from the competition of the strains. We summarize the expected outcomes based on the values of the reproduction numbers and invasion numbers in Table 3.

Table 3.  List of conditions on reproduction numbers and invasion numbers and potential dynamical outcomes of the competition of the strains. Last column gives the example where the case is numerically illustrated. Case 6 could not be numerically illustrated, possibly because it does not occur in system (1).

Case	Strain 1	Strain two	Expected outcome	Comment
1			I 1→0, I 2→0	Theorem 3.3
2			I 1→0, I 2 persists	Proposition 7.1, Example 2
3			I 1 persists, I 2→0	Proposition 7.1, Example 3
4	,	,	I 1→0, I 2 persists	See Example 4
5	,	,	I 1 persists, I 2→0	See Example 5
6	,	,	init. cond. dep. outcome	–
7	,	,	coexistence; I 1, I 2 persist	See Example 6

Before presenting the numerical examples of some asymptotic properties of the system (1), we first prove the following Proposition, which partially established properties 2 and 3 of (1).

Proposition 7.1

The following statements are true:

(i)	If then .
(i)	If then .

Proof follows from results in 2.

Proving rigorously all properties in Table 3 may not be possible but we check numerically whether they hold at least for arbitrarily chosen parameter values in the examples presented below. For all examples below we choose d _s =0.5, d ₁=1, d ₂=1.5, the domain to be unit square Ω=[0, 1]×[0, 1], and the initial conditions to be as follows:

Initial values are graphed in Figure 1.

Figure 1. Initial values.

(a) Example 2. illustrates Case 2 in Table 3. In this example, we simulate the results of Proposition 7.1(i). Transmission and recovery rate of each strain is chosen as follows:

We then estimate the basic reproduction numbers. We estimate that and . Note that the invasion number of a strain is always less than the reproduction number of the same strain. We estimate the invasion numbers to be and . If , and , then I ₂ persists and . This result is shown in Figure 2. Our numerical experiment agrees with Proposition 7.1(i).

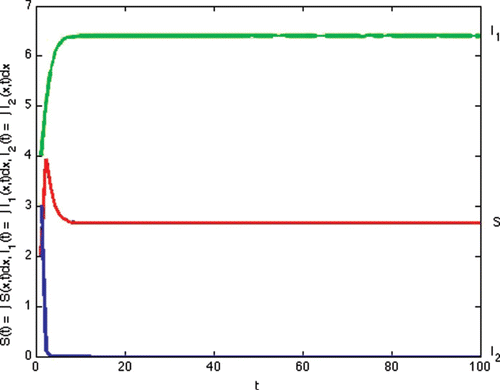
Figure 2. Total densities of susceptible individuals, infected individuals with strain one and two at time t.

(b) Example 3. Example 3 illustrates Case 3 in Table 3. In this example, we also illustrate Proposition 7.1(ii). Transmission and recovery rate of each strain is chosen as follows:

We then estimate the basic reproduction numbers and invasion numbers. We estimate that , , , and . If , , , and , then I ₁ persists and . This result is shown in Figure 3. Our numerical experiment agrees with Proposition 7.1(ii).

Figure 3. Total densities of susceptible individuals, infected individuals with strain one and two at time t.

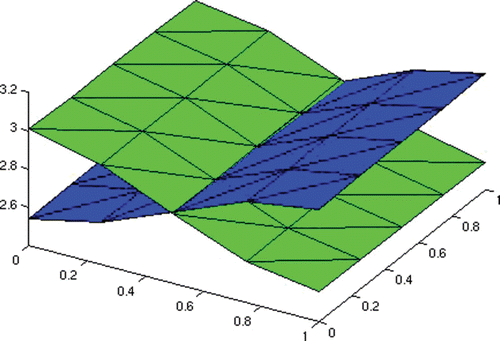
(c) Example 4. If both reproduction numbers are larger than one, as in the remaining examples, none of the strains is automatically eliminated, because it is unfit to the environment. The outcome of the competition between the strains is decided by the invasion numbers. Example 4 illustrates Case 4 in Table 3.

For this example, we chose the transmission and recovery rate of each strain as follows:

With these choices of recovery and transmission rates, we estimate that , , and . As stated in Case 4, I ₂ persists and . We observe this result in Figure 4.

Figure 4. Total densities of susceptible individuals, infected individuals with strain one and two at time t.

(d) Example 5. Example 5 illustrates Case 5 in Table 3, and it is the symmetrical case to Case 4. If , , , and , then I ₁ persists and as shown in Figure 5.

Figure 5. Total densities of susceptible individuals, infected individuals with strain one and two at time t.

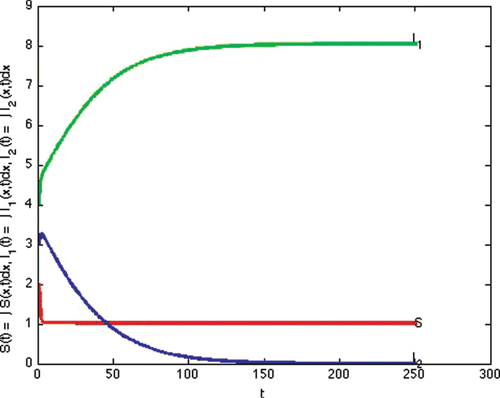
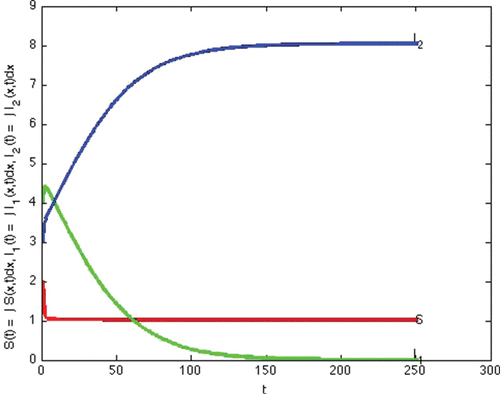
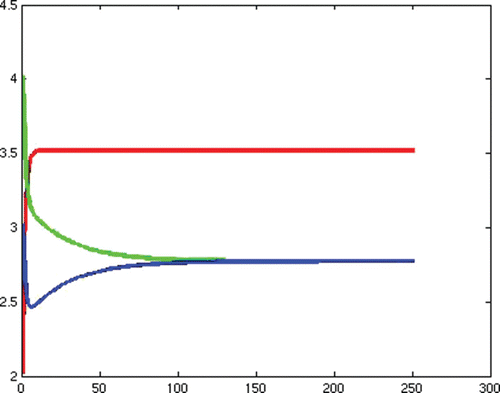
(e) Example 6. Example 6 illustrates Case 7 in Table 3. This is the case that both reproduction numbers are above one, and both invasion numbers are above one. The two strains coexist. We show theoretically that coexistence occurs in Lemma 4.3. In this section we demonstrate that the theoretical possibility of coexistence, actually occurs for some specific values of the parameters. We note that the transmission rate of strain one is quite different from the transmission rate of strain two, giving nontrivial different reproduction numbers.

In this simulation, with the following choices of recovery and transmission rates, we estimate that , , , and , and we observe that coexistence occurs (see Figure 6)

Figure 6. Total densities of susceptible individuals, infected individuals with strain one and two at time t.

In Figure 7, we plot the infected individuals with strain one and two at the final time of interest.

Figure 7. Coexistence equilibrium.

8. Discussion

In this article we introduce a spatially heterogeneous deterministic epidemic model of the SIS type where the pathogen is represented by two strains. We allow for spatially heterogeneous transmission and recovery rates, in contrast with most spatial epidemic models where rates are assumed constant. The model is built on the single-strain model considered in 2.

Fundamentally, our model is very simple – its spatially homogeneous ODE version has dynamics that leads to competitive exclusion. In other words, if any of the reproduction numbers is above one, the strain with the larger reproduction number persists, while the other one dies out (see Appendix). The introduction of space leads to larger variety of outcomes. Intuitively, it seems clear, that when space is taken into account, multiple pathogens could simultaneously persist by partitioning the region into subregions and each occupying separate subdomains. This scenario is known in ecology as ‘niche partitioning’. Here, we hypothesize that space alone may lead to coexistence of the pathogens, and we test this hypothesis both analytically and numerically. In particular, we define spatial reproduction numbers and invasion numbers for both pathogens. We find three types of equilibria: DFE, two dominance equilibria, one corresponding to strain one and the other one corresponding to strain two, and coexistence equilibria. We establish that if the reproduction numbers of both strains are below one, the DFE is globally asymptotically stable. Using the monotonicity of the time-independent problem, we show analytically, that if both invasion numbers are above one, coexistence equilibrium exists (Figure 7).

To check the persistence of both strains in this case, we develop a fully discrete finite element method to simulate the system of partial differential equations in time. The spatial domain is divided into triangles with acute angles. We approximate the integrals with the vertex quadrature rule. Time is discretized with the backward Euler method. Although most finite element methods may not preserve the positivity of the solution, our discretization allows us to show rigorously that the discrete solution is nonnegative, just as the continuous solution it approximates. We also establish both analytically and numerically that the discrete solution converges to the exact solution with an error of order two in space and order one in time.

Finally, we simulate a number of dynamical outcomes of the competition of the strains controlled by different values of the reproduction numbers and invasion numbers. In particular, numerically we show that if one of the reproduction numbers is above one, and the other is below one, then the strain with the larger than one reproduction number persists, while the strain with the smaller than one reproduction number dies out. If both strains have reproduction number above one, then the outcome of the competition depends on the invasion numbers. If exactly one strain has an invasion number above one, that strain persist while the other is eliminated. If both strains have invasion numbers above one, then they both persist.

Acknowledgements

The authors thank two knowledgeable referees and the extremely helpful comments of the handling editor that helped improve the paper. Patrick De Leenheer contributed a great deal to the proof of the coexistence equilibrium. We also benefited from our discussions with Yuan Lou and Georg Hetzer. Maia Martcheva acknowledges NSF support from grant DMS-0817789.

Additional information

Notes on contributors

Necibe Tuncer

Current affiliation: Department of Mathematical and Computer Sciences, University of Tulsa, 800 South Tucker Drive, Tulsa, OK, 74104, USA.

Appendix 1. The ODE model

The ODE version of the model (1) is

with positive initial conditions S(0), I ₁(0), I ₂(0)≥0 and positive recovery and transmission rates β₁, β₂, γ₁, γ₂>0 which are all constants. Let

since (d/dt)(S+I ₁+I ₂)=0, we have S(t)+I ₁(t)+I ₂(t)=N ∀t>0. Since the total population is constant all times, substituting S=N−(I ₁+I ₂) into (1), we obtain the following reduced system of equations:

The steady-state solutions of (A2) are given by

of which only the positive solutions are of interest. Equilibria satisfy the system:

Clearly, the steady states are DFE, (0, 0), -equilibrium, (N(1−γ₁/β₁), 0), and -equilibrium, (0, N(1−γ₂/β₂)). In getting these steady states, we make the assumption γ₁/β₁≠γ₂/β₂. If I*₁≠0 and I*₂≠0, the system above is inconsistent. Small perturbations around the steady state, , satisfy the following linearized system:

where A is the Jacobian matrix given as

The linear stability of is determined by the eigenvalues λ of the stability matrix A. For the DFE, we obtain

Clearly, DFE is stable if β₁−γ₁<0 and β₂−γ₂<0, and unstable if β₁−γ₁>0 or β₂−γ₂>0. Since dI _i /dt=(β _i −γ _i )I _i , for i=1, 2 we set the reproduction numbers of each strain to be R _i =β _i /γ _i ,  i=1, 2.

Let β₁−γ₁>0 and β₂−γ₂>0, so that -equilibrium and -equilibrium exist, then the stability matrices for these equilibria are

-equilibrium is stable if β₁−γ₁>0 and γ₁/β₁−γ₂/β₂<0 and unstable if γ₁/β₁−γ₂/β₂>0. On the other hand, -equilibrium is stable if β₂−γ₂>0 and γ₁/β₁−γ₂/β₂>0 and unstable if γ₁/β₁−γ₂/β₂<0. So, when -equilibrium is stable, -equilibrium is unstable and when -equilibrium is stable, -equilibrium is unstable. Thus, we have competitive exclusion.

To study the global stability of the coexistence equilibrium, set , then

where λ=γ₁γ₂(R ₁−R ₂). Sign of λ will be determined by the sign of R ₁−R ₂. Let R ₁ and R ₂ be both greater than 1, and if R ₁>R ₂, then

If R ₂>R ₁, then