Modelling and optimal control of immune response of renal transplant recipients

Abstract

We consider the increasingly important and highly complex immunological control problem: control of the dynamics of immunosuppression for organ transplant recipients. The goal in this problem is to maintain the delicate balance between over-suppression (where opportunistic latent viruses threaten the patient) and under-suppression (where rejection of the transplanted organ is probable). First, a mathematical model is formulated to describe the immune response to both viral infection and introduction of a donor kidney in a renal transplant recipient. Some numerical results are given to qualitatively validate and demonstrate that this initial model exhibits appropriate characteristics of primary infection and reactivation for immunosuppressed transplant recipients. In addition, we develop a computational framework for designing adaptive optimal treatment regimes with partial observations and low-frequency sampling, where the state estimates are obtained by solving a second deterministic optimal tracking problem. Numerical results are given to illustrate the feasibility of this method in obtaining optimal treatment regimes with a balance between under-suppression and over-suppression of the immune system.

Keywords:

• renal transplant
• human cytomegalovirus
• mathematical model
• optimal feedback control
• state estimation
• model predictive control

AMS Subject Classification :

• 92C50
• 93C10
• 93C15

1. Introduction

According to USRDS latest report 30, there are more than 580 thousands of people in the United States reported as having end-stage renal disease (ESRD). ESRD, also known as kidney failure, is a medical condition in which kidney fails to adequately filter the toxins and waste products from the blood. Renal transplant is often the best way to treat kidney failure, and there were 16,897 kidneys transplanted in the United States during 2010 based on the OPTN data as on 11 March 2011 31.

To reduce the risk of rejection, the standard care for transplant recipients is a life-long pharmacological immunosuppression. However, the immunosuppression therapy can render the transplant recipients susceptible to a broad array of bacterial and viral pathogens, and may reactivate latent viruses such as human cytomegalovirus (HCMV), Epstein-Barr virus (EBV), human herpes virus (HHV)-6, HHV-7 and polyomavirus (e.g., BK virus) preexisting in either the recipient or the donor's organ or both. Viral infection can cause both ‘direct’ and ‘indirect’ effects, including immune suppression predisposing the recipient to other opportunistic infections and oncogenesis. Hence, there is a delicate balance needed so that the immune response is neither over-suppressed (e.g., reactivation of latent virus) nor under-suppressed (rejection of transplanted organ). Currently, there is no consensus regarding how best to use the available and emerging classes of immunosuppressive agents and other therapies, and each transplantation center follows its own guidelines, typically based on local preferences, experience and interpretation of published studies. Thus, there is a critical need for continued research on evidence-based immunosuppressive strategies for long-term management of the transplant recipient population.

Mathematical modelling has been successfully used to understand many complex biological systems. This includes our own efforts in using data-oriented quantitative modelling to design treatment strategies and clinical trials for human immunodeficiency virus (e.g., see 1 2 5 6 10). Our first goal in this paper is to develop an initial mathematical model of immune response in an immunosuppressed transplant recipient based on known and hypothesized mechanisms reported in the literature. It is worth noting that in developing a mathematical model for any complex biological system there is a balance between complexity and utility. In this paper, we do not try to formulate a model that captures all the features of the immune response as well as all viral and genetic factors and their interactions with each other, but rather propose a simple first model that we feel possesses certain features that are relevant in trying to understand quantitative and qualitative aspects of a very complex immunological control process.

In a clinical setting, low-frequency observations are usually the case due to the high financial costs of associated assays as well as emotional/physical costs to the patients. In addition, almost all the modelling for a complex immunological process involves partial observations and/or measurements from combined compartments due to lack of proper technology to quantify all the state variables. This is true for the human immunodeficiency virus (HIV) modeling, where the viral load and total number of CD4+T cells are the two sets of measurements that are routinely collected from a patient (e.g., see 6). Hence, our second goal in this paper is to use the proposed initial model to design adaptive optimal treatment schedules for a transplant recipient to achieve a balance between under-suppression and over-suppression of immune system with partial observations and low-frequency sampling.

The outline of the remainder of this paper is as follows. In Section 2, a mathematical model is developed for describing the immune response to viral infection and a foreign organ transplant, and some simulation results demonstrate that this initial model exhibits appropriate characteristics of primary infection and reactivation for immunosuppressed transplant recipients. In Section 3 a feedback control problem is formulated to derive possible treatment strategies, and numerical results are given to show that this methodology has the potential to produce optimal treatment regimes with a balance between under-suppression and over-suppression. Some concluding remarks and suggestions for future research efforts are then given in Section 4.

2. Model description and analysis

In this initial model, we assume for simplification and to facilitate demonstration of feasibility that only one type of latent virus exists either in the recipient or in the donor's kidney tissue. Since HCMV is the most common infectious pathogen arising in solid organ transplantation, we will take HCMV infection in an immunosuppressed transplant recipient as an example.

HCMV is one of the eight known HHVs which establish life-long latent infection after initial infection. HCMV infection is widespread throughout the world, and the infection is usually asymptomatic in immunocompetent individuals 14. However, during immunosuppression HCMV can reactivate and cause serious medical problems after transplantation, including allograft injury and acute and chronic rejection, post-transplant lymphoproliferative disorder (PTLD) and even death 25. The wide distribution of HCMV-infected cells in the various tissues and organs, such as the bone marrow, liver, kidney, lungs and gastrointestinal tract, permits the efficient transmission of HCMV to susceptible hosts during organ and tissue transplantation 26.

In the absence of any preventive therapy, HCMV infection occurs in approximately 30–75% of transplant recipients, with an incidence of HCMV disease between 8 and 80%, depending on the type of transplantation, immunosuppression, and most importantly, the donor and recipient HCMV serostatus 25. Prophylactic and preemptive antiviral therapy (by use of either valganciclovir or oral ganciclovir) are two commonly used strategies to prevent HCMV infection after organ transplantation. Prophylactic treatment involves the administration of antiviral drugs to all patients at risk for an extended period, while preemptive therapy is specifically directed towards patients identified as having a high risk for HCMV disease to avoid the toxicity of the universally applied antiviral prophylaxis.

2.1. Mathematical model

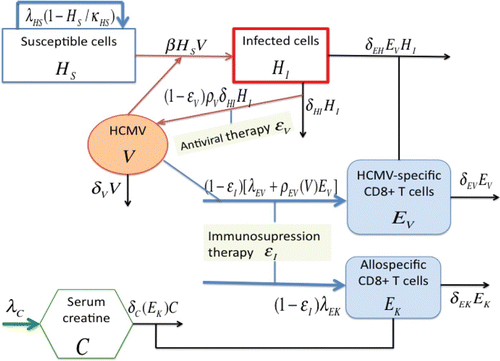
The model we use here is modified and extended from Kepler et al. 20 to include the immune response to the donor kidney. Specifically, we have modified the equation describing the dynamics for the immune response to the HCMV infection for our purpose, and for simplicity we also do not explicitly model the latent infected cells as done in 20. The latent state will be characterized by the stable nonzero equilibrium level of viral load that is below the detection limit, representing an ongoing infection that is controlled by the immune system. Table 1 lists all the state variables that we will use in the model. As in 20, the measurement of free virus is reported in terms of copies/μL-blood in order to be consistent with the units of the cell compartments. To convert from copies/μl-blood to the generally reported unit copies/mL-plasma, we need to know the ratio of the plasma to the blood, and here we set it at 0.57 as in 20.

Table 1. Description of state variables.

States	Description	Units
H S	Concentration of susceptible cells	cells/μl-blood
H I	Concentration of infected cells	cells/μl-blood
V	Concentration of free HCMV	copies/μl-blood
E V	Concentration of HCMV-specific CD8+T cells	cells/μl-blood
E K	Concentration of allospecific CD8+T cells that targets kidney	cells/μl-blood
C	Serum creatine concentration	mg/dl

The model, based on the schematic in Figure 1 and the discussions below, is given by the following set of ordinary differential equations:

with an initial condition vector . Here ε _V and ε _I denote the efficacy of the antiviral drugs and immunosuppressive drugs, respectively, and both are assumed to be scaled to be less than or equal to 1. These two variables serve as the controllers for the system to achieve a balance between under-suppression and over-suppression of the immune system of a transplant recipient. In addition, we observed that Equations (1)–(4) describing the immune response to the viral infection are coupled with Equations (5) and (6) describing the immune response to the transplanted kidney through the controller ε _I , the efficacy (or qualitative effectiveness) of immunosuppressive administered to the patient.

Figure 1. Model schematic.

In the absence of infection, susceptible cells are assumed to proliferate through the term . Once encountering virus, they become infected, and the term β H _S V in Equation (1) represents the loss of susceptible cells due to the infection. For simplification, one copy of virion is assumed to infect only one cell. Hence the term β H _S V in Equation (3) models the loss of virus due to infection of susceptible cells. Infected cells die due to cytopathic effect of HCMV at a rate δ _HI , and are assumed to produce ρ _V virions before death. In addition, infected cells are eliminated by the HCMV-specific effector CD8+T cells, and the term in Equation (2) is used to account for this elimination. The parameter δ _V in Equation (3) denotes the natural clearance rate of virus. It was documented in 26 that acute rejection may increase the risk of HCMV disease. Specifically, the proinflammatory cytokines, such as TNF-α, released during an episode of allograft rejection serve as potent transactivators of HCMV from a state of latency to one of active replication. However, to simplify the initial analysis, this feature is not included in this initial model.

The cellular immune response is the key defense against HCMV infection. We do note that humoral immune response also participates in the control of HCMV infection, and the activation and proliferation of HCMV-specific CD8+T cells may require the help of HCMV-specific CD4+T cells, but for simplification we do not model these in this initial model. The terms λ _EV and in Equation (4) denote the source and death rates, respectively, for the HCMV-specific immune effector cells. The concentration of HCMV-specific immune effector cells increases in response to the presence of free virus through the term in Equation (4), where ρ _EV is a bounded positive increasing function (in this paper, ρ _EV is chosen as the saturating nonlinearity , where ρ¯ _EV and κ _V are some positive constants). In addition, we assume that both the source rate λ _EV and the rate function ρ _EV are affected by the immunosuppressive drug, which is reflected in the term . We note that Equation (4) can be applied to the case with HCMV-seropositive donor/HCMV-seronegative recipient and the case with HCMV-seronegative donor/HCMV-seropositive recipient (but with different interpretation). For the D−/R+ scenario (that is, E _V (0)≠0), the term can be used to serve as the low level of maintenance of (memory) cells, while for the D+/R− case, λ _EV can be used to initiate the immune response during primary infection which begins with E _V (0)=0.

Initially, all T cells are assumed to be naive to the alloantigens on the transplanted kidney, and the alloreactive immune response mounted is most like a response to a viral infection. In Equation (5), E _K is used to denote those effector and memory CD8+T cells that are specific to target the transplant (kidney) with E _K (0)=0. The source rate for E _K is denoted by λ _EK , which is dependent on the human leukocyte antigen (HLA) matching between the donor and recipient. This term can be used to initiate the immune response against the transplanted kidney, and can be affected by the immunosuppressive drugs (through the term ). The death rate for E _K is denoted by δ _EK . Again here we do not model the allospecific CD4+T cells that targets the kidney tissue.

Creatine is a waste product in the blood that comes from muscle activity. Its production is continuous and is proportional to muscle mass, and can be removed from blood by the kidneys. Serum creatine concentration C (described in Equation (6)) is widely used to estimate glomerular filtration rate (GFR), which is considered the best overall index of renal function in health and disease 23. In Equation (6), we use λ _C to denote the production rate for C. Note that when the kidney function is impaired, creatine will not be effectively filtered, and its level will rise. Hence, to account for the negative effect of the alloreactive immune response E _K on the kidney, we use to denote the clearance rate for the creatine, where δ _C is a bounded decreasing function in E _K (in this paper, we choose , where δ _C0 and κ _EK are some positive constants). We observe that active viral replication in the transplanted kidneys might adversely affect their function, and hence impose a risk factor for the occurrence of acute and chronic allograft rejection. Once again, to simplify the analysis, we did not include this feature in this initial model.

2.2. Model analysis

Verification and validation are important steps in the iterative modelling process described in some detail in 4. For validation, one requires sufficient longitudinal data, which are unfortunately not presently available to us for our problem. However, we can pursue qualitative verification by finding rough approximate values of some parameters (e.g., κ _HS , δ _HI , δ _V , β) as well as the relationship between some parameters (e.g., λ _EV and δ _EV ) in model (1)–(6). We can then carry out simulation studies to verify that the model produces qualitative behaviour similar to that observed in clinical reports.

Our parameter values are based on the following known results, which are collected from the literature by the authors in 20.

	(1) Generally, no free virus are detected in healthy HCMV-seropositive individuals. The lower limit of detection for the ultra sensitive assays is 20 copies/ml-plasma (about  copies/μl-blood).
	(2) During HCMV infection, monocytes are considered to be an important target of infection, a site of latency, and vehicles for virus dissemination. The concentration of monocytes in blood is 150–600 cells/μl-blood.
	In the simulation, we choose  cells/μl-blood. During the latent state where the susceptible cells are not significantly depleted, the equilibrium value for the susceptible cells can be approximated by l-blood.
	(3) The measurements of the time to late cytopathology is 120–168 hours for HCMV. Hence, δ HI is about 0.2 per day.
	(4) The exponential decay rate of the HCMV load for patients on effective antiviral treatment has been measured by various researchers, and the measurement of the half-life of the viral load decay t H in the literature range from 1.5 to 11.5 days.
	Hence, under the assumption that the antiviral drug completely blocks the release of new virions (that is, ), the clearance rate of virus (the sum of natural clearance rate δ V and clearance due to the loss of infection of susceptible cells β H S ) ranges from 0.0603 to 0.4621 per day.
	(5) The range of CD8+ cells is 300–900 cells/μl-blood. The total HCMV-specific CD8+T cell response in seropositive healthy (latent-infected) individuals is 4.6% with a range of 0–36% of the overall CD8+ population in blood.
	In the simulations, we set the target value of the equilibrium for E V in the latent state (without any drug therapy, i.e., ) to be . Note that in the latent state the equilibrium of E V can be well approximated by . Hence, in the simulations we set . In addition, we can find a relationship between the parameters β, δ HI , δ EH , δ V and ρ V based on the equilibrium in the latent state, which satisfies Summing Equations (7) and (8), we find that Hence, to have a positive equilibrium value for H I and V we need to have By solving Equations (7) and (8) for [Htilde] I and then setting them equal, we have

In addition, based on 24 we also assume:

	(6) First, the normal range for C is usually 0.6–1.2 mg/dl.
	We furthermore assume that at t=0 the serum creatine for the transplant recipient is at a steady state, that is, . In the simulation, we set C(0)=1, which implies that .

In Table 2, we provide a summary of parameter values which are chosen based on the above analysis as well as the simulations, the requirements of achieving the target values for [Htilde] _S and [Etilde] _V and obtaining reasonable equilibrium values and peak values for the viral load and serum creatine.

Table 2. Parameter values used in the simulations.

Parameters	Value	Parameters	Value
λ HS	10^−3 per day	κ HS	400 cells/μl-blood
β	l-blood/(copies day)	δ HI	0.2 per day
δ EH	l-blood/(cells day)	ρ V	12 copies/cells
δ V	0.2 per day	λ EV	0.5 cells/(μl-blood day)
ρ¯ EV	1 per day	κ V	20 copies/μl-blood
δ EV	0.05 per day	λ EK	0.5 cells/(μl-blood day)
δ EK	0.1 per day	λ C	0.2 mg/(dL day)
δ C0	0.2 per day	κ EK	8 cells/μl-blood

With the parameter values defined in Table 2 and and for different values of ε _I , we find that model (1)–(6) has locally asymptotically stable equilibria given by

•	(immunocompetent: latent state)
•	(immunosuppressed)

This reveals that we have an equilibrium level of viral load for an immunocompetent individual () well below the detection limit, and for an immunosuppressed individual () well above the detection limit (which indicates the possibility to achieve an HCMV complication). In addition, we see that for the case we have H̄ _S close to [Htilde] _S and Ē _V close to [Etilde] _V .

In the following, we will simulate two types of HCMV infection that recipients may acquire after transplantation. One is primary infection, which occurs when a HCMV-seronegative recipient (R−) is first exposed to virus contained within an organ obtained from a HCMV-seropositive donor (D+). The other is reactivation, which occurs when endogenous latent HCMV in a HCMV-seropositive recipients (R+) reactivates during the periods of immunosuppression after transplantation. All the simulations below are carried out by using the parameter values listed in Table 2 with different degree of immunosuppression and different number of days of prophylactic antiviral treatment.

2.2.1. Primary infection

In Figure 2, we present model simulations of primary infections with different levels of efficacy of immunosuppression in the case of no antiviral drug treatment corresponding to initial conditions

Figure 2. Simulations of primary infection with different efficacy levels (ε _I =0, 0.4, 0.8) of immunosuppression in the case of no antiviral drug treatment (ε _V ≡ 0).

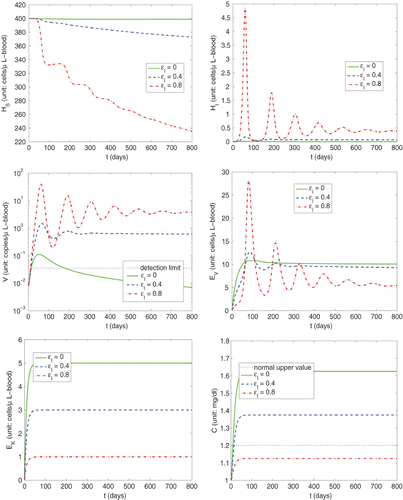
From the bottom right panel of this figure, we observe that without immunosuppression therapy () the serum creatine concentration C is far above the upper normal value, but when a sufficient level of immunosuppression is achieved (e.g., as seen in the figure), we can bring down the serum creatine concentration to within the normal range due to suppression of immune response E _K to the transplanted kidney (as can be seen from the bottom left panel of this figure). Furthermore, we observe from the middle left panel of Figure 2 that the peak viral load is 0.1108 copies/μl-blood (about 63.1560 copies/mL-plasma) for immunocompetent individual (), and increases to 39.42 copies/μl-blood (about  copies/mL-plasma) as immunosuppression increases to 0.8 (which corresponds to a dramatic increase of susceptible cells becoming infected, as observed from the upper panels of this figure). This is in the range of viral load measurements ( copies/mL-plasma) reported in 29 for 24 transplant patients with HCMV infection observed just prior to antiviral treatment. In addition, we see that the time at which the viral load peaks for all the cases occurs before day 70. This is in agreement with the observation in 27 where more than 50% of high-risk kidney allograft recipients (HCMV-seronegative patients receiving organs from HCMV-seropositive donors) developed symptomatic infection during the first 3 months after transplantation. We also observe from the middle right panel of Figure 2 that the immune response E _V to the HCMV infection with is much higher than that with for some time period. This is somehow consistent with observation in 16 that the frequencies of HCMV-specific CD8+T cells are significantly higher in immunosuppressed individuals than those in immunocompetent individuals.

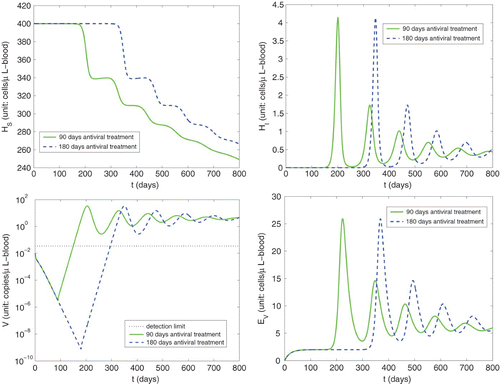
We depict in Figure 3 simulations of primary infection during immunosuppression () with different number of days of prophylactic antiviral treatment (ε _V is set at 0.8 during antiviral treatment) by using initial conditions . From the right column of this figure, we observe that compartments H _I and E _V with 90 days antiviral treatment have similar trends as those with 180 days antiviral treatment except a time lag. In addition, we see from the bottom left panel of Figure 3 that independent of length of administration of the prophylactic antiviral treatment, the viral load will eventually be reaching a similar peak level as in the case without antiviral treatment. This is in agreement with the conclusion obtained in 19. There it was found that HCMV primary infection was common after 6 months of valganciclovir prophylaxis and mostly symptomatic with the viral load at diagnosis in the range 490– copies/ml-plasma and the peak viral load in the range 1250– copies/ml-plasma. In addition, we observed from Figure 3 that the viral load is above the detection limit in 60 days after 90 days prophylaxis ended, and in 115 days after 180 days prophylaxis ended, which is again consistent with the observation in 19 that HCMV infection developed in a mean of 107 days (with a range 26–330 days) after prophylaxis was terminated.

Figure 3. Simulations of primary infection with different numbers of days of prophylactic antiviral treatment (ε _V is set at 0.8 during antiviral treatment) during immunosuppression (ε _I ≡ 0.8).

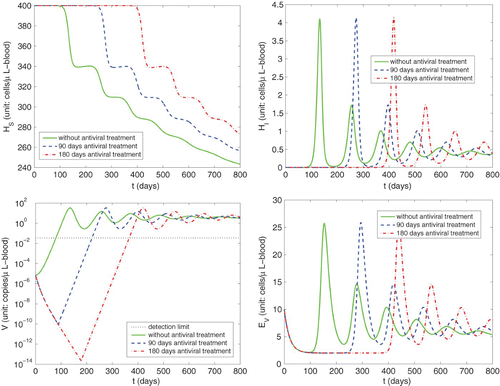
2.2.2. Reactivation

In Figure 4 we graph simulations of the reactivation of HCMV infection during the immunosuppression () of a previously healthy individual with a latent HCMV infection under the case with different numbers of days of prophylactic antiviral treatment. Here the results are obtained by using initial conditions chosen as the equilibrium values (11) during the latent state. From this figure, we see that compartments H _S , H _I , V and E _V have the similar behaviour as those for the primary infection illustrated in Figure 3. For example, we also observe that independent of length of prophylactic antiviral treatment, the viral load will eventually be above the detection limit and reach a similar peak level as in the case without antiviral treatment. However, under the case without antiviral treatment the peak viral load for the reactivation (33.47 copies/μl-blood) is lower than that for primary infection (39.38 copies/μl-blood) during immunosuppression. Moreover, the time at which the viral load peaks for the reactivation (day 135) occurs much later than that for the primary infection (day 62). This is in agreement with the common observations that the degree of HCMV reactivation and replication in HCMV R+ patients is relatively lower when compared to the primary HCMV infection in HCMV D+/R− patients (e.g., see 26).

Figure 4. Simulations of reactivation following immunosuppression (ε _I ≡ 0.8) with different numbers of days of prophylactic antiviral treatment (ε _V is set at 0.8 during antiviral treatment).

3. Optimal control

In this section, we turn to a question of major importance: the feasibility of effective immunosuppression control following organ transplantation. We derive optimal treatment strategies based on the current state of the system by using ideas from model predictive control (MPC), which has been used in 10 12 13 to design adaptive treatment schedules for HIV patients. MPC, also known as receding horizon control (RHC) or moving horizon control (MHC), entails solving a finite horizon open-loop optimal control problem iteratively, where the current state is sampled at measurement times and a control strategy minimizing a cost is computed for a short time interval. We formulate this control problem in the context of our model (1)–(6).

Let and be some positive constants such that and . Then we can rewrite Equations (1)–(6) as a nonlinear vector system

where is the control vector with the aim to achieve a balance between under-suppression and over-suppression of the immune system.

Let ℕ denote the set of all the positive integers, and be a sequence of measurement times with , i=1, 2, …. Note that real-time polymerase chain reaction (PCR) for HCMV DNA quantification in blood are often routinely performed to monitor HCMV infection in renal transplant recipients (e.g., see 21), and serum creatine concentration is used to estimate GFR that are often employed to monitor the kidney function (e.g., see 23). Hence, in our effort here we assume that we can only observe the viral load and serum creatine concentration at each measurement time point, and the simulated observation at measurement time t _i takes the form

where , and [Pcirc] is some positive constant that is used to introduce some noise into the observation. In other words, we have introduced the same level of relative errors for both sets of measurements (with |[Pcirc]−1| being the relative error). Note that the simulated observations z ⁱ generated above are always either bigger than the true values (when [Pcirc]>1) or smaller than the true values (when [Pcirc]<1). Although the errors are not usually represented this way, we do this because we want to test our state-estimation methodology (in Section 3.1) to ascertain the impact of the values of observations on the controls and state estimates.

3.1. Algorithm

Let ℤ⁺ denote all the nonnegative integer numbers, be the control horizon such that , and and are both measurable</texlscub> for any . The cost functional on the finite horizon is defined by

Here C* and V* denote the threshold values for C and V, respectively, such that C≤C* indicates that the functioning of the transplanted kidney is normal, and V≤V* corresponds to no serious viral complications for the transplant recipient. Hence, the third and fourth terms (with weighting terms Q and R) inside the integral of Equation (14) is used to achieve a balance between under-suppression and over-suppression. Here V*/2 and C*/2 are chosen based on the simulation to attempt to control the viral load and serum creatine concentration below their threshold values for different values of [Pcirc].

To initiate the algorithm, we set i=0, and choose initial value x ₀. We then solve the optimal tracking control problem, O _i , ,

subject to Equation (12) over the time interval with initial value x(t _i )=x _i to obtain the optimal control function . We remark that the existence of the optimal control function to each optimal control problem O _i can be readily established by standard arguments given in 15. An optimality system methodology to computationally solve these problems with HIV dynamics was discussed in 1 2 5 and can be applied to the transplant problem formulated here.

After finding the optimal control over the interval , we substitute into Equation (12) to obtain the state trajectory over the time interval [t _i , t _i+1], that is, to solve

Then the simulated measurement z ⁱ⁺¹ at time t _i+1 is given by .

With observation z ⁱ⁺¹ available, we will find a continuous optimal control over the next subinterval . Note that we do not have sufficient observation information for the initial condition, , of this subinterval. Hence, we design a state estimator based on optimization, termed as optimization-based state-estimation (OBSE) in the remainder of this paper, to obtain full knowledge of x _i+1. Our state estimate of x in the subinterval [t _i , t _i+1] (based on observation z ⁱ⁺¹) has the form

Here is obtained by solving a new optimal control problem, Õ _i ,

where is measurable, , and α _i , i=1, 2, …, 6 are some chosen positive constant bounds. After finding w*, we solve Equation (17) to obtain x _e (t _i+1). Setting , we then increment i by 1 and repeat this whole process to find an optimal control and state estimate over the entire interval of interest.

Note that because of Equation (17), the sum in the cost functional in Equation (18) is the same as , which provides our state estimate x _e on the interval [t _i , t _i+1]. In addition, we see that our methodology (referred to as OBSE-MPC in this paper) involves solving two optimization problems in each subinterval: one for the optimal control, and the other for the state estimator. The resulting approximate optimal feedback control function u* is given by for , i=1, 2, …. To determine and , the optimality systems of Equations (15) and (18) are solved numerically using a conjugate gradient algorithm. The interested readers are referred to 11 17 22 28 for more information on this powerful algorithm for solving large-scale minimization problems. In each optimal control problem, the state system with initial conditions is solved forward in time by using an initial guess of the controls and the adjoint system with terminal conditions is solved backward in time. The controls are updated in each iteration by using the conjugate gradient algorithm.

3.2. Numerical simulations

We next summarize results from simulations with the control algorithms described above. All the simulations reported on here were carried out with the values of model parameters given in Table 2 and initial condition at t=0 given by

The maximum efficacy of immunosuppression and antiviral drugs are set to be and , respectively, and the control horizon is chosen to be for any . To balance the differences between the magnitudes of viral load and creatine concentration, the weight constants Q and R in the objective functional (14) are chosen to be Q=1 and R=100. Moreover, we set to place more weight in the tracking terms in the objective functional (18). The maximum amplitude for w _i is chosen to be α _i =1, i=1, 2, …, 6. To test the efficacy of the OBSE methodology, the constant [Pcirc], used to generate the simulated data, is varied from 0.90, 0.95, 1.05, to 1.10, representing several different levels (5%, 10% ) of constant relative error in the observations.

The test in 18 suggests that in solid organ transplant recipients viral loads higher than 5000 copies/ml-plasma (about 8.7719 copies/μl-blood) are associated with a high risk of HCMV disease and that viral loads below 2000 copies/ml-plasma (about 3.5088 copies/μl-blood) are unlikely to be associated with HCMV-related complications. Hence, we set V*=3.5 copies/μl-blood in the simulation. Based on the information in Section 2, we set C*=1.2 mg/dL.

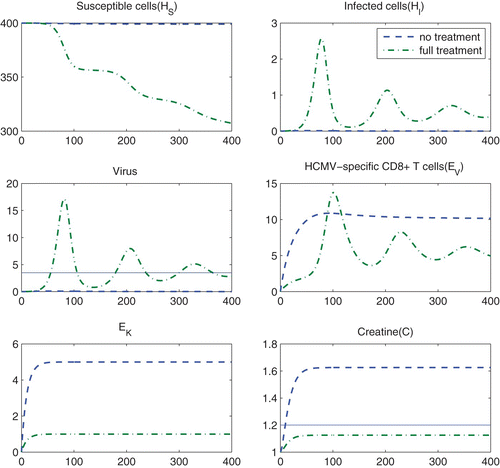
Figure 5 depicts the simulation results obtained with no treatment, i.e., (dashed line) and with full treatment, i.e., and (dash-dot lines) for 400 days. We observe from this figure that the viral load corresponding to no treatment is maintained below the threshold value V*=3.5 while the serum creatine concentration with no treatment is higher than the threshold value C*=1.2. This case corresponds to rejection of transplanted kidney and hence under-suppression of the immune system. On the contrary, the viral load peaks corresponding to full treatment are considerably higher than the threshold value V*=3.5 while the serum creatine concentration with full treatment is maintained below the threshold value C*=1.2. This case suggests over-suppression.

Figure 5. Simulation results obtained with no treatment, i.e., ϵ _I =ϵ _V ≡ 0 (dashed line) and with full treatment, i.e., ϵ _I ≡ 0.8 and ϵ _V ≡ 0.2 (dash-dot lines). The solid lines indicate the threshold quantities, V* and C*.

The solid lines in Figures 6–9 depict the numerical results obtained with measurements 15 days apart for different values of [Pcirc]. To test the efficacy of our state-estimation methodology, we also plot the results (depicted by the dashed lines) obtained with the case where we have full knowledge of all the state variables at each measurement time, that is, the values of the state x at each sampling instant are given by the final values of the state in the previous subinterval, and we call this case simple MPC. Specifically, the optimal feedback control functions u* obtained by the OBSE-MPC (depicted by the solid lines) and the simple MPC (depicted by the dashed lines), referred to as OBSE-MPC control and simple MPC control, respectively, are shown in the top two panels of each figure. The state trajectories obtained with the OBSE-MPC control and the simple MPC control are illustrated in the bottom two panels of each figure, and they are referred to as OBSE-MPC solutions and simple MPC solutions, respectively. To see the effect of sampling frequency on the state estimation, we also demonstrate the results for the case with measurements 20 days apart in Figures 10–13 and the case with measurement 30 days apart in Figures 14–17.

Figure 6. OBSE-MPC controls and solutions (solid line), and simple MPC controls and solutions (dashed line) obtained with [Pcirc]=0.90, |w _i |≤1, Q=1, R=100, [Qcirc]=[Rcirc]=10⁴, , , and t _i+1−t _i =15.

Figure 7. OBSE-MPC controls and solutions (solid line), and simple MPC controls and solutions (dashed line) obtained with [Pcirc]=0.95, |w _i |≤1, Q=1, R=100, [Qcirc]=[Rcirc]=10⁴, , , and t _i+1−t _i =15.

Figure 8. OBSE-MPC controls and solutions (solid line), and simple MPC controls and solutions (dashed line) obtained with [Pcirc]=1.05, |w _i |≤1, Q=1, R=100, [Qcirc]=[Rcirc]=10⁴, , , and t _i+1−t _i =15.

Figure 9. OBSE-MPC controls and solutions (solid line), and simple MPC controls and solutions (dashed line) obtained with [Pcirc]=1.10, |w _i |≤1, Q=1, R=100, [Qcirc]=[Rcirc]=10⁴, , , and t _i+1−t _i =15.

Figure 10. OBSE-MPC controls and solutions (solid line), and simple MPC controls and solutions (dashed line) obtained with [Pcirc]=0.90, |w _i |≤1, Q=1, R=100, [Qcirc]=[Rcirc]=10⁴, , , and t _i+1−t _i =20.

Figure 11. OBSE-MPC controls and solutions (solid line), and simple MPC controls and solutions (dashed line) obtained with [Pcirc]=0.95, |w _i |≤1, Q=1, R=100, [Qcirc]=[Rcirc]=10⁴, , , and t _i+1−t _i =20.

Figure 12. OBSE-MPC controls and solutions (solid line), and simple MPC controls and solutions (dashed line) obtained with [Pcirc]=1.05, |w _i |≤1, Q=1, R=100, [Qcirc]=[Rcirc]=10⁴, , , and t _i+1−t _i =20.

Figure 13. OBSE-MPC controls and solutions (solid line), and simple MPC controls and solutions (dashed line) obtained with [Pcirc]=1.10, |w _i |≤1, Q=1, R=100, [Qcirc]=[Rcirc]=10⁴, , , and t _i+1−t _i =20.

Figure 14. OBSE-MPC controls and solutions (solid line), and simple MPC controls and solutions (dashed line) obtained with [Pcirc]=0.90, |w _i |≤1, Q=1, R=100, [Qcirc]=[Rcirc]=10⁴, , , and t _i+1−t _i =30.

Figure 15. OBSE-MPC controls and solutions (solid line), and simple MPC controls and solutions (dashed line) obtained with [Pcirc]=0.95, |w _i |≤1, Q=1, R=100, [Qcirc]=[Rcirc]=10⁴, , , and t _i+1−t _i =30.

Figure 16. OBSE-MPC controls and solutions (solid line), and simple MPC controls and solutions (dashed line) obtained with [Pcirc]=1.05, |w _i |≤1, Q=1, R=100, [Qcirc]=[Rcirc]=10⁴, , , and t _i+1−t _i =30.

Figure 17. OBSE-MPC controls and solutions (solid line), and simple MPC controls and solutions (dashed line) obtained with [Pcirc]=1.10, |w _i |≤1, Q=1, R=100, [Qcirc]=[Rcirc]=10⁴, , , and t _i+1−t _i =30.

In general, we observe that the shapes of the OBSE-MPC control and the simple MPC control are similar, especially when [Pcirc] is 0.95 or 1.05 (see Figures 7, 8, 11, 12, 15 and 16). This indicates that the state estimator based on our OBSE approach is performing adequately. In perspective, one could conclude from the control functions in Figures 6–17 that full immunosuppressive therapy should be given in the beginning and then the level of drug should taper off around the 40th day. On the other hand, antiviral drugs are only needed at a later time. In addition, we observe that the viral load and the serum creatine concentration are increasing as the value of [Pcirc] increases (which is expected as the values of simulated observations z ⁱ increase as the value of [Pcirc] increases). For example, the calculations show that when [Pcirc]=0.90 or 0.95, the values of the serum creatine concentration is always smaller than the threshold value C* for all the sampling time points (which can also be observed from the figures below after day 100). However, when [Pcirc]=1.05 or 1.10, the values of the serum creatine concentration at some sampling times are greater than the threshold value C*. We also observe that the OBSE-MPC controllers try to reduce the values of the viral load and the serum creatine concentration and keep them below the threshold quantities (see Figure 9, 13 and 17) even when [Pcirc]=1.05 or 1.10. Overall, the viral load and the serum creatine concentration corresponding to the optimal feedback control functions are maintained around their corresponding threshold values. Indeed, our initial numerical results are most promising. They strongly suggest the potential for design of effective and feasible optimal therapeutic regimens that achieve a balance between under- and over-suppression of the immune system during post-organ transplant therapy.

4. Concluding remarks and future research efforts

In this paper, we formulated an initial mathematical model for describing the cellular immune response to HCMV infection and foreign kidney in an immunosuppressed renal transplant recipient, and developed a computational framework for designing optimal feedback treatment regimens with partial state observations that are collected infrequently.

We have used a wide range of clinical findings to qualitatively validate our initial mathematical model. However, to properly calibrate and quantitatively validate our current mathematical model using sophisticated inverse problem methodology 4, we need an informative set of longitudinal data points to permit efficient and accurate estimation of model parameters. One of our immediate research efforts is to apply an optimal design method (SE-optimal design) proposed in 7 8 as well as other methods such as D-optimal and E-optimal discussed in 8 to the statistical model (observation processes) corresponding to this mathematical model to choose optimal sampling time points. These are obtained through minimization of a specific cost function related to the resulting error in parameter estimation. Once we have the clinical data, which are likely to be censored as the assays can only accurately detect to some lower limit, we will apply an inverse problem methodology such as the one employed in 6 (an expectation-maximization algorithm combined with weighted least-squares method) to validate this initial model. If there is substantial discrepancy between the model predication and the data, we plan to examine those simplifying assumptions that we have made in this paper as well as other new hypothesized mechanisms appearing in the literature, and make another iteration of model construction and validation.

A second deterministic optimal tracking problem was used here for state estimation as opposed to commonly used nonlinear filtering approaches such as extended Kalman filter and unscented Kalman filter. The advantage of this OBSE approach over filtering approaches is that one can deal with many types of noise introduced in the observation process (either dependent or independent, either Gaussian distributed or non-Gaussian distributed). This is particularly useful if we have no prior information on the noise. The obvious disadvantage of this OBSE-MPC method is the cost of computation, which is expected to be much higher than that of a filtering-MPC approach as two optimization problems are needed to be solved at each sampling interval as opposed to only one in the filtering-MPC approach. One of our future research efforts is to compare the estimation accuracy of these two approaches.

The numerical results in Section 3.2 suggest that if we have reasonably accurate information on all the states, then we can apply the proposed methodology to design optimal feedback treatment regimens to achieve a balance between under-suppression and over-suppression during post-transplant therapy. However, when the observation is consistently much higher than the actual value, we are unable to control the viral load (V) and serum creatine concentration (C) within the level that we desire. This is primarily because we did not explicitly incorporate the state-constraints into the optimal control process. Hence, another future effort is to develop a framework where one can carry out feasible and efficient computations for feedback control problems with both control and state constraints. We noted earlier that we anticipate that the clinical data will be censored. Hence, another immediate goal is the development of a state-estimation methodology for censored data so that one can carry out an efficient feedback control problem in a clinical setting.

Finally, another future research question is related to our optimal control formulation for Equation (14). As an alternative one could pose our problem as a two-player min–max noncooperative differential game such as used for electromagnetic interrogation/counter-interrogation in 3 9. In this case strategies or controls for under/over suppression would represent opposing ‘player’ therapy strategies and one could seek formulations of the game (controls) that provide value (i.e., controls where the min–max=max–min – see 3 and the references therein) for the corresponding differential game. In this case, one would find the ‘best’ strategies for balancing virus suppression with organ acceptance.

Acknowledgements

This research was supported in part by grant number R01A I071915-07 from the National Institute of Allergy and Infectious Diseases. The work of Hee-Dae Kwon was supported in part by the Korea Research Foundation Grant funded by the Korean Government (KRF-2008-314-C00043) and in part by the Korea Research Foundation Grant funded by the Korean Government (KRF-2008-331-C00053).