Reproduction numbers for infections with free-living pathogens growing in the environment

Abstract

The basic reproduction number ℛ₀ for a compartmental disease model is often calculated by the next generation matrix (NGM) approach. When the interactions within and between disease compartments are interpreted differently, the NGM approach may lead to different ℛ₀ expressions. This is demonstrated by considering a susceptible–infectious–recovered–susceptible model with free-living pathogen (FLP) growing in the environment. Although the environment could play different roles in the disease transmission process, leading to different ℛ₀ expressions, there is a unique type reproduction number when control strategies are applied to the host population. All ℛ₀ expressions agree on the threshold value 1 and preserve their order of magnitude. However, using data for salmonellosis and cholera, it is shown that the estimated ℛ₀ values are substantially different. This study highlights the utility and limitations of reproduction numbers to accurately quantify the effects of control strategies for infections with FLPs growing in the environment.

Keywords:

• SIRSP model
• infection control
• free-living pathogen
• basic reproduction number
• type reproduction number

1. Introduction

The basic reproduction number, ℛ₀, is considered as one of the most practical tools that mathematical thinking has brought to epidemic theory 26. ℛ₀ is defined as the average number of secondary infections produced by a single infectious host introduced into a totally susceptible population 1. In most cases, if , then the outbreak generates an epidemic; whereas, if , then the infection will disappear from the population. Since ℛ₀ synthesizes important elements of the infection transmission process, it identifies the most important factors in the infection transmission cycle. A method often used to derive ℛ₀ expression is the next generation matrix (NGM) approach 18 19.

As noted in previous works 19, depending on the biological interpretations of the disease compartments, different ℛ₀ expressions can be derived for a compartmental model. Our study highlights the issue of calculating a valid ℛ₀ expression for diseases transmitting through the contaminated environment. Previous studies 7 13 41 45 differ fundamentally in the way they treat the environment compartment; therefore, the ℛ₀ expressions derived are substantially different. For instance, in 13 41 45, the derived ℛ₀ is represented as a sum of two separate terms corresponding to the host-to-host and environment-to-host transmission pathways. This may suggest the independence of these pathways in the disease transmission cycle. Whereas the ℛ₀ derived in 7 has a square root term suggesting a more complicated interaction between the host-to-host and environment-to-host transmission pathways. The present work demonstrates the properties and behaviours of possible ℛ₀ expressions resulting from different ways of interpreting the role of the environment in the transmission cycle of infection. To avoid the issue of multiple ℛ₀ expressions, the NGM approach is used to derive a unique threshold quantity known as a type reproduction number 27 43.

Although host-to-host disease transmission has been traditionally considered as the main cause of infection spread, the role of environment-to-host disease transmission is becoming more evident. A contaminated environment such as food, water, soil, objects and contact surfaces may transmit infection to susceptible hosts 6 12 44. Pathogens in a free-living state adapt to the environment by morphological and physiological changes that promote their survival 5 and even growth 36 in the environment. In addition, the presence of a free-living pathogen (FLP) in the environment can be replenished by infectious hosts that excrete the pathogen for a considerable amount of time. In contrast, the natural decay of a pathogen and decontamination practices reduce environmental persistence. By taking into account the above-mentioned factors and waning host immunity typical for certain infections 1, we extend a susceptible–infectious–recovered–susceptible (SIRS) model to an model that includes FLP capable of growth and survival in the environment.

The main objective of this study is to deepen the understanding of how multiple transmission pathways and pathogen growth in the environment affect measures of control efforts required to eradicate or reduce the infection in the host population. Depending on how the pathogen interactions within the environment and between the host and environment are interpreted, different ℛ₀ expressions corresponding to the model are derived. In particular, the pathogen shedding from infectious hosts into the environment and FLP growth in the environment are considered as transition among infectious states of an infectious host, generation of secondary infectious agents or a combination of both. The former is a progression of an already infectious host through the environment (i.e. pathogen shedding and growth represent extensions of the host's infectiousness to the environment). The latter corresponds to the appearance of secondary FLP in the environment generated by an infectious host or through the growth of pathogen in the environment. While the derived ℛ₀ expressions are different, they all intersect at the threshold value 1 and preserve their order of magnitude below and above 1. Although the global stability results obtained in this study are valid for any ℛ₀ expression, the differences between ℛ₀ values can be extremely large depending on the parameter values. This is numerically illustrated using data of salmonellosis and cholera infections. When the pathogen is unable to maintain itself in the environment, the host population becomes disease-free when a type reproduction number is less than 1, thus this number can be used to accurately guide disease control strategies.

2. The model

The model consists of the standard SIRS model 9, where S, I, R denotes the number of susceptible, infectious, and recovered hosts, respectively, and a compartment P that indicates the FLP load in the environment. Susceptible individuals become infectious either by adequate contacts with infectious individuals or the contaminated environment. Infectious individuals contaminate the environment by shedding pathogen that is capable of growth and survival in the environment. Hence, the set of ordinary differential equations (ODEs) representing the SIRSP model is given by

where and g are non-negative and all other parameters are positive. The birth and natural death rates are, respectively, denoted with b and m; parameter μ is the mortality rate due to the infection. Parameters δ and β are, respectively, the transmission coefficients for environment-to-host and host-to-host contacts. The mean infectious period for infectious individuals is 1/ν, and average duration of immunity for recovered individuals is 1/α. For the pathogen, γ represents the shedding rate, r gives the decay rate in the environment, g represents the growth rate, and 1/c is the carrying capacity. Table 1 summarizes the model variables and parameters, and Figure 1 is a compartmental diagram of our model. This model is applicable to a variety of infections such as salmonellosis and cholera, whose causative agents are capable of surviving and growing in the environment. Moreover, the model can be reduced to various forms such as SIRP, SISP, SIR and SIP. For example, when δ→0, the last equation uncouples from the others, yielding a standard SIRS model, which has been studied in the literature; see, for example, [Chapter 2]9.

Figure 1. A schematic representation of the SIRSP model. Solid and dashed lines indicate the dynamics of host and FLP, respectively.

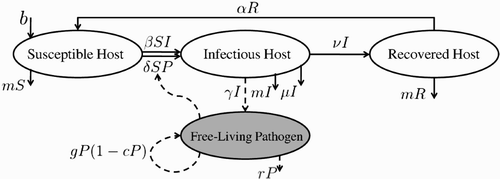
Table 1. Variables and parameters with units for the SIRSP model.

S	Number of susceptible individuals	individuals
I	Number of infectious individuals	individuals
R	Number of recovered individuals	individuals
P	Number of FLP	cells
b	Host birth rate	individuals day^−1
m	Host natural death rate	day^−1
μ	Pathogen-induced host death rate	day^−1
g	Pathogen growth rate	day^−1
1/ν	Infectious period	day
1/α	Immune period	day
1/c	Carrying capacity of FLP	cells
β	Host-to-host transmission	individuals^−1 day^−1
δ	Environment-to-host transmission	cells^−1 day^−1
γ	Pathogen shedding rate	cells day^−1 individuals^−1
r	Pathogen decay rate^a	day^−1
^aPathogen decay rate r corresponds to any reduction of pathogen load (i.e. by decontamination or natural death) in the environment.

3. Host–pathogen dynamics

3.1. Feasible region and the equilibria

For the model (1)–(4), it can be verified that all solutions with non-negative initial conditions remain non-negative. Letting N=S+I+R and adding Equations (1)–(3) gives , which implies that As a consequence, Equation (4) yields , and thus there exists some M>0 such that . The constant M can be chosen as the unique positive zero of the quadratic polynomial . Hence, the feasible region

is positively invariant with respect to model (1)–(4).

The disease-free equilibrium (DFE) is given by (S ₀, 0, 0, 0) with S ₀=b/m. As shown in Section 3.3 and Appendix 1, under a stated condition, there exists a unique endemic equilibrium (EE) with in the interior of Γ, which is denoted by .

3.2. Basic reproduction numbers

Equations (2) and (4) form a subsystem describing the generation and transition of infectious hosts and FLP. The Jacobian matrix associated with the linearized subsystem at the DFE is given by

If g>r, then J _DFE has a positive eigenvalue, and so the DFE is unstable, with the pathogen maintaining itself in the absence of infection from the host (i.e. maintaining itself in the environment). We thus assume in all that follows (unless stated otherwise) that r>g. Thereafter, J _DFE is decomposed as F−V, where F is the transmission matrix describing the generation of secondary infectious hosts (or FLP where applicable), and V is the transition matrix, describing the changes in individual states such as removal by death or recovery. Knowing matrices F and V, ℛ₀ can be simply obtained by calculating the spectral radius of the NGM K=FV ⁻¹. The DFE is locally stable if ; whereas, it is unstable if 18 19. Nonetheless, decomposition of J _DFE is greatly dependent on how the role of the environment is interpreted in transition and transmission of secondary infectious hosts and FLP; this role has been controversial in the literature. Several studies suggest that the environment serves as a reservoir of infectious FLP for infection of humans, animals and plants 8 15 44. Whereas other works conclude that the contaminated environment is only a minor factor within the complicated nature of infectious diseases 2 16 17 29 40. To reflect these diverse opinions, we hypothesize three scenarios where the environment acts as a (I) Transition, (II) Transition–Reservoir and (III) Reservoir. These scenarios include all cases considered in above-mentioned studies. Figure 2 is a conceptual representation of the initial and secondary infections for each of these scenarios. As shown below, each scenario leads to a different ℛ₀ expression.

Figure 2. A conceptual representation of the secondary FLP and infectious hosts generated in the cycle of disease transmission. Here, H ₀ and H ₁ are the initial and secondary infectious host, respectively, while P ₀ and P ₁ are the initial and secondary FLP.

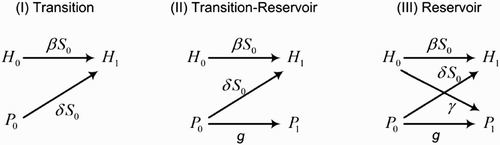
(I) Transition. Assume that the FLP population cannot maintain itself through growth in the environment (i.e. the FLP growth rate g is always less than the FLP decay rate r). Then, the environment is considered as an extended state of host infectiousness, where the pathogen shedding into and growth within the environment are considered as transitions within the initial infectious state of the host population. Therefore, the shedding and growth rate of the pathogen (i.e. γ and g) are placed in the V matrix rather than the F matrix, giving

and the NGM

Since no secondary infectious FLP is generated in the environment, the second rows of F _I and K _I are zero. With our assumption r>g, all entries of matrix K are non-negative and ℛ₀ is given by

This is rewritten

where

The quantities and correspond, respectively, to the average number of secondary infections through host-to-host and environment-to-host transmission caused by one infectious individual in its infectious lifetime. The fraction regulates the magnitude of with respect to FPL growth or decay rates in the environment 23. According to (7), the contribution of each transmission pathway in a disease outbreak is separable. Hence, the control efforts can be focused on infectious hosts or the contaminated environment depending on the amount of effort required to reduce the sum of and to less than 1. Note that is only defined when r>g, and the same expression can be derived by considering an extended NGM approach proposed by Xiao et al. 48.

Although specific forms of and are only related to the model (1)–(4), several studies consider the same scenario and derive an with the same structure as in (7). For example, without pathogen growth in the environment (i.e. g=0), this approach has been used in studies of cholera infection 14 25 45, multi-strain disease transmission 10 and salmonellosis 13.

(II) Transition–Reservoir. Similar to the previous scenario, the environment is assumed to act as an extended state of host infectiousness for pathogen shed by an infected host. However, the environment is assumed to also act as a reservoir of infection. Here, the growth of FLP can be regarded as vertical transmission of infectious pathogen in the environment. Using the extended definition of the F matrix 30, the entry (i, j) of matrix F represents the rate at which secondary individuals appear in class i per individual of type j. Therefore, the FLP growth rate g represents the rate of secondary FLP generated in the environment. Under these assumptions, the F, V and K matrices are changed to

and

Using the and expressions defined in (7), is given by

which indicates a different viewpoint of environment-to-host transmission in the generation of new infections compared to the one presented in (7).

(III) Reservoir. The environment is assumed to act as a reservoir, where secondary FLP are added into the environment both through FLP growth and pathogen shedding by infectious hosts. Hence, both the shedding and growth rates γ and g are placed in the F matrix. Then,

and

give rise to

Without pathogen growth in the environment and host-to-host disease transmission (i.e. g=β=0), the NGM approach presented here has already been used in previous studies. This includes studies of schistosomiasis 21, toxoplasmosis 37 and low-pathogenic avian influenza 7 transmission dynamics.

Assuming r>g, it is fairly straightforward to show that all three basic reproduction numbers agree at the threshold value, i.e. . In particular, for a fixed set of parameter values, they are all greater, equal or less than 1. When a basic reproduction number is greater than 1, provided r>g, it can be shown that they are always in the order . The order is reversed if the basic reproduction number is less than 1. While is limited to the case r>g, and do not have such a limitation and for g>r. The differences between the three reproduction numbers are negligible when is small and . Nonetheless, as numerically illustrated in Sections 3.4 and 4.1, the differences among the reproduction numbers can be large when is large.

3.3. Disease invasion and persistence

Using Theorem 2 of 19, the DFE is locally asymptotically stable if , and unstable if , where ℛ₀ refers to any reproduction number in the form of (6), (8) or (9). Moreover, as indicated in the following theorems, is a necessary and sufficient condition for the existence and uniqueness of the EE, which is then locally asymptotically stable. The proofs of Theorems 3.1 and 3.2 are provided in Appendix 1.

Theorem 3.1

Model (1)–(4) admits a unique EE if and only if .

Theorem 3.2

The EE is locally asymptotically stable if .

Model (1)–(4) is said to be uniformly persistent 11 in if there exists constant c>0 such that

provided that . Biologically, a uniformly persistent system indicates that the infection persists for a long period of time. The next result establishes ℛ₀ as a threshold quantity between the disease dying out or persisting.

Theorem 3.3

The following results hold for model (1)–(4).

	(1) If then the DFE is globally asymptotically stable in Γ.
	(2) If then the DFE is unstable and model (1)–(4) is uniformly persistent in .

As established in the next result, if the infection is assumed to confer permanent immunity, then irrespective of the initial number of infectious hosts, the infection becomes endemic when .

Theorem 3.4

Assume that α=0. If then the unique EE is globally asymptotically stable in .

The proofs of Theorems 3.3 and 3.4 are given in Appendices 2 and 3, respectively. Note that the global stability of the EE remains an open problem when α>0 (i.e. when individuals recovered from infection lose their immunity after an average period 1/α). However, the numerical simulations suggest that the result of Theorem 3.4 remains valid for .

3.4. Examples

We consider two examples of infection: (1) salmonellosis in a dairy herd, and (2) cholera in a large human population. The specific parameter values and references related to the salmonellosis and cholera examples are given in Tables 2 and 3, respectively. Note that these parameters give r>g for both examples. The parameter values related to cholera are mainly taken from 46, which studies the nineteenth century cholera outbreak in London, UK. Note that some of the parameter values have been converted from weeks or years to days. Dynamics of salmonellosis and cholera are explored by numerically solving model (1)–(4) with different initial conditions. Using these parameter values, and the DFE is not achieved for either the salmonellosis or cholera.

Table 2. Model parameters values related to salmonellosis in a dairy herd.

Symbol	Value	References	Remarks
b	0.2	48	^1
m	10^−3	22	^2
μ	10^−3	34 48
g	0.2	39	^3, 4
1/ν	10	48	^3
1/α	10^2	48	^3
1/c	10^6	39	^3, 4
β		48	^3, 5
δ	10^−12	13 48	^3
γ	4×10^8	13 48	^3
r	0.9	28	^6
^1The birth rate value is an assumption.
^2The parameter m represents both natural death rate and the culling rate.
^3The actual value varies among Salmonella serotypes.
^4The parameter value is variable due to environmental conditions and the amount of available nutrients.
^5Compared to 13 48, we consider a smaller value for β.
^6The pathogen decay rate includes both natural death rate and disinfection/removal rate.

Table 3. Model parameters and values related to cholera in humans.

Symbol	Value	References	Remarks
b	12.05	25 46
m		46
μ		46
g	0.3	31	^1
1/ν	3	46
1/α	10^3	33 47	^2
1/c	10^7	31	^1, 3
β		25 46	^3
δ		46	^3
γ	10	31 46	^4
r	0.8	46	^5
^1The parameter value is variable due to environmental conditions and the amount of available nutrients.
^2Cholera does not confer lifetime immunity 47. Duration of immunity after cholera infection is controversial 33.
^3Assumed as the actual value is unknown; we assume the same value as previous studies.
^4The amount is variable due to host's characteristics.
^5The pathogen decay rate includes both natural death rate and disinfection/removal rate.

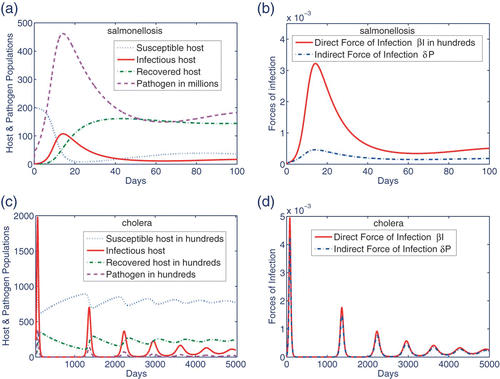
Figure 3(a) refers to salmonellosis, where solutions of model (1)–(4) tend to the EE , . Note that the epidemic peaks of infection in the host population and those of FLP in the environment are synchronized. As shown in Figure 3(b), for these chosen parameter values, the direct force of salmonellosis is much higher than the indirect force. The reproduction numbers for salmonellosis are given by , , , , and , which indicates , agreeing with the direct force being more important. Figure 3(c) shows that the dynamics of cholera tends to the EE in an oscillatory fashion. The epidemic waves become more frequent but with shorter amplitudes as they tend to the EE. Therefore, long-term oscillatory behaviour simulated in 46 may occur without imposing the seasonality in the environment-to-host transmission pathway. In addition, prevalence at the EE could be higher than the previous results [Table 1]46. More importantly, the number of infectious individuals between the first three epidemic waves falls below 1, which highlights the role of the environment as a reservoir of infection and the importance of stochasticity. Figure 3(d) represents the forces of infection with almost equal contributions of infectious host and environment in the generation of secondary infections. Note that for the cholera parameters , , , , and

Figure 3. Using the parameter values indicated in Tables 2 and 3, dynamics of salmonellosis and cholera are numerically simulated. (a) Salmonella infection tends to an EE after the first epidemic wave. (b) Considering the infectious host and environment as generators of salmonellosis, the former corresponds to a force significantly higher than the latter. This is in agreement with . (c) After several epidemic waves, cholera becomes endemic and remains persistent in the host population and the environment. (d) Based on the parameter values, the direct and indirect infection forces play almost equal roles in generation of cholera infection.

As quantified in a previous study 3, reducing the contacts with the infectious host or the contaminated environment can be used as control measures to eradicate or reduce the infection. Specifically for the cholera parameters, when β falls below (or δ is less than 10⁻⁸), ℛ₀ becomes less than 1 and the population becomes disease-free.

4. Control of infection

4.1. Impacts of misinterpretation

The basic reproduction number can be used to measure the control efforts required to reduce or eliminate an infection 1 18. In the event of a disease outbreak, health officials may consider various control measures including (1) more aggressive decontamination of the environment (i.e. increasing the value of r by additional cleaning and disinfecting), (2) antibiotic treatments (i.e. assuming that the pathogen is not resistant to antibiotics, the recovery rate ν is increased and the shedding rate γ is decreased), (3) reducing contacts with infectious host (i.e. the host-to-host transmission rate β is reduced) and (4) reducing contacts with contaminated environment (i.e. the environment-to-host transmission rate δ is reduced) by approaches such as isolation, training and advisory services. Assuming a unique ℛ₀ expression, the efficacy of each control measure can be quantified 3. Specifically, using the partial derivatives of ℛ₀ with respect to the above-mentioned parameters, the rate of reduction in ℛ₀ can be determined for each of these control measures. The issue arises when the ℛ₀ expression is non-unique and therefore partial derivatives of different reproduction numbers may endorse different control measures.

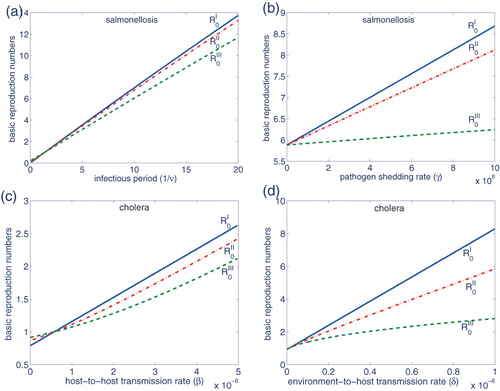
Considering the salmonellosis and cholera examples of Section 3.4, Figure 4 shows the changes in the basic reproduction numbers , and due to changes in 1/ν and γ, for salmonellosis, and changes in β and δ for cholera. All other parameter values are as given in Tables 2 and 3. Note that all reproduction numbers intersect only at 1. As stated in Section 3.2, for values less than 1, , whereas the inequalities are reversed for values greater than 1. Moreover, as shown in Figure 4(b) and (d), the differences between the reproduction numbers can be quite substantial. An overestimated ℛ₀ may give rise to public panic, unnecessary control efforts and economic losses, whereas underestimating ℛ₀ may result in choosing control policies that are not sufficiently intensive. For instance, considering culling as a disease control policy in livestock or poultry, the former may lead to a huge economic loss, whereas the latter may result in culling a proportion of the population that is not sufficient to eradicate the infection.

Figure 4. The top and bottom plots represent, respectively, changes in reproduction numbers for the salmonellosis and cholera parameters. Changes in the parameter values of (a) 1/ν, (b) γ, (c) β and (d) δ may result in substantially different ℛ₀ values.

Under certain conditions, the ℛ₀ expressions are reduced to simpler forms. Nevertheless, they remain substantially different. To show this, we consider three different limiting cases as the following parameter values tend to zero: (a) FLP growth rate g, (b) host-to-host transmission rate β and (c) both g and β.

(a) Neglecting FLP growth. The growth rate of several pathogens such as Salmonella and Vibrio cholerae tends to zero under low temperature conditions (see, for example, 23). In this case, both reproduction numbers and coincide, that is ; whereas,

(b) Neglecting host-to-host transmission. Assuming low mixing in the host population, the value of β can be negligible. Also for several infections, such as Clostridium difficile, vancomycin-resistant enterococci and methicillin-resistant Staphylococcus aureus, the environment-to-host pathway is the predominant route of infection transmission (see, for example, 29). In this case, all three reproduction numbers are substantially different. Specifically, and .

(c) Neglecting FLP growth and host-to-host transmission. Similar to case (a), both reproduction numbers and coincide, that is, , whereas .

Hence, misinterpreting the role of the environment gives rise to an incorrect ℛ₀ expression and possible choice of an inefficient control policy. As shown in the next section, despite initial assumptions about the role of the environment, a unique control measure is obtained when the pathogen is unable to maintain itself in the environment (i.e. r>g).

4.2. Type reproduction number

If the NGM K of order n is known, then using the approach provided in 27 43 a type reproduction number can be calculated. In particular, the disease and the environment compartments may represent different population types. The type reproduction number T _s associated with the population type s has the following expression 27 43

where I is the n×n identity matrix, e _s is an n-dimensional column vector with all entries zero except that the s entry is equal to 1, and P _s is a projection matrix with the (s, s) entry equal to 1 and all other entries equal to zero. As shown in 27 43, provided that the spectral radius of (I−P _s )K is less than 1 (i.e. exists), T _s is well defined and the infection is eradicated by applying different control measures to the population type s such that the T _s value falls below 1.

Suppose that an ODE model has n disease compartments, and that the interactions within and between m disease compartments (m<n) are interpreted differently. The Jacobian matrix is decomposed as in Section 3.2, leading to different NGMs, and . Without loss of generality, assume that V _j =V _i +U _m and F _j =F _i +U _m , where U _m is a matrix with m non-zero rows (say, rows , which correspond with the m disease compartments above) and n−m zero rows. Then, the following result indicates that, regardless of how the interactions are interpreted, the type reproduction number related to any disease compartment other than those m compartments is unique. The proof is provided in Appendix 4.

Theorem 4.1

Let and be the type reproduction numbers associated with population type s defined by (10) and, respectively, derived from the NGMs K _i and K _j . If and both and are well defined, then .

Concerning the SIRSP model, denote the infectious host and FLP populations as type 1 and type 2 population, respectively. Infection can be eradicated by applying a control measure (e.g. vaccination) to type 1 population. If r>g, then is well defined for and III, corresponding to the cases (I), (II) and (III) of Section 3.2. Thus, using Theorem 4.1

for and III. Therefore, no matter what role is considered for the environment, the type reproduction number for type 1 population is unique. The infection will be eliminated when a proportion of type 1 population greater than is permanently vaccinated. Since implies , calculating p ₁ with or results in underestimating the true p ₁ value required for eradication of infection. For example, with cholera parameters given in Table 3, in Figure 4(c) and (d) can be used to accurately estimate p ₁ for control of cholera by vaccination given changes in the direct and indirect transmissions (due to natural or anthropogenic causes).

Now assume that a control measure (e.g. pathogen removal by decontamination) is applied only to type 2 population, then

It follows that

for  and  III, provided that , that is, the host population is not a reservoir of infection. Note that Theorem 4.1 does not apply and as shown below is not unique.

Case j=I is degenerate, since the FLP in the environment is not assumed as an independent population type. Instead, it is considered as an adjunct part of the infectious host population. Therefore, provided that .

For j=II,

provided . Reducing g or increasing r so that the FLP population is reduced by a proportion greater than will cause the infection to die out. Equation (13) indicates a critical role of the FLP growth in the environment without which the pathogen would not be able to maintain itself in the environment (since ). When or , case j=II is reduced to the case j=I.

For j=III,

provided . This represents two separate cycles of infectious agents production via the environment; one directly through FLP growth and the other through indirect transmission and shedding of infectious hosts. To eradicate the infection, both cycles must be suppressed by magnitudes that provide When , it can be shown that and intersect at 1. Moreover, when . Provided , reducing the FLP load to a proportion greater than will result in eradication of infection. With these inequalities, , therefore, p _II is an overestimation of the efforts required for eradication of an infection.

5. Discussion

The present work highlights the utility of the type reproduction number when our knowledge regarding certain disease compartments is limited. For instance, if we are confident that net growth of FLP is negative, the unique expression related to the host of interest (e.g. humans, livestock or wildlife) leads to a correct estimation of the control efforts required to eradicate the infection.

The SIRP model proposed in this study is an extension of the SIR model and considers both host-to-host and environment-to-host disease transmission pathways. The pathogen shed by infectious hosts is assumed to be capable of growth and survival in the environment. Assuming that the environment acts as a transition, transition-reservoir or reservoir of infection, three different ℛ₀ expressions are derived. Several studies 7 13 41 45 consider one of these scenarios and derive ℛ₀ that has the same structure as or . Although all ℛ₀ expressions of the SIRP model intersect at the threshold value 1 and preserve their order of magnitude, the differences between the ℛ₀ values can be large. Therefore, misinterpreting the role of pathogen growth and shedding may result in overestimating or underestimating the control efforts required in eradicating the infection. We showed that the issue is partly resolved when the type reproduction number is used instead of ℛ₀. In particular, regardless of how the pathogen shedding and growth are interpreted in the NGM, the type reproduction number related to the host population is the same. However, this is meaningful only when the environmental decontamination keeps the net FLP growth rate negative (i.e. r>g). Otherwise, the environment becomes a reservoir of the pathogen and targeting the host population will not be sufficient to eradicate the infection.

Noting that all ℛ₀ expressions coincide at the threshold value 1, the local and global stability results presented in this work remain valid for any ℛ₀ expression in the form of (6), (8) or (9). Here, we showed that the DFE is globally stable when and the unique locally (and globally) stable endemic equilibria emerges when ℛ₀ exceeds 1. Furthermore, the system (1)–(4) is uniformly persistent when . The uniqueness of the EE is highly dependent on the pathogen growth and decay behaviours in the environment. In particular, considering a generalized logistic growth 42 of FLP in the environment and limiting the pathogen decay rate to a certain range, there will be multiple EE, leading to rich dynamics of the SIRSP model. For the indirect transmission, a more realistic threshold of pathogen is incorporated in the disease transmission term in 32, but leads to a non-smooth system. This incidence can be approximated by a saturating incidence (rather than mass action) as considered in 14 25. Our methods for the analysis of the DFE can be extended to include such incidence.

In conclusion, the basic reproduction number ℛ₀ provides a reliable threshold for control and prevention of infection. When the interactions between and within the disease compartments are unclear, the NGM approach may lead to a unique expression for the type reproduction number associated with a population type and resolve the issue of multiple ℛ₀ expressions.

Acknowledgements

This work was supported by the National Science Foundation grant NSF-EF-0913367 to RI funded under the American Recovery and Reinvestment Act of 2009. Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation. The research of Zhisheng Shuai and P. van den Driessche is partially supported by an NSERC Postdoctoral Fellowship, an NSERC Discovery Grant and Mprime.

Notes

This is a paper based on an invited talk given at the 3rd International Conference on Math Modeling & Analysis, San Antonio, USA, October 2011.

Appendix 1. Existence and stability of the EE

Proof of Theorem 3.1

The equilibrium equations of model (1)–(4) are given by

It follows that the EE satisfies

and

The existence and number of endemic equilibria can be analysed geometrically through the intersection of the graphs of P=φ(I) and I=ψ(P) in the first quadrant, see Figure A1. It follows that there exists at most one intersection of the graphs of P=φ(I) and I=ψ(P), and thus model (1)–(4) admits at most one EE. In the case that r>g, the intersection exists if and only if , see Figure A1. Calculations yield and , and thus the sufficient and necessary condition becomes . Note that if g≥r, a similar geometric argument shows that system (1)–(4) always has a unique EE.   ▪

Figure A1 The graphs of functions P=φ(I) and I=ψ(P) for r>g.

Proof of Theorem 3.2

Let be the unique EE of model (1)–(4) provided . The linearization at the EE, setting , gives

Following 4, construct a Lyapunov function

where constant a>0 will be determined later. Differentiation L along solutions of (A2) and using equilibrium equations (A1) yield

where

It remains to show that the quadratic A≥0 for some a>0 and all y, w. In fact, it is sufficient to show that there exists some a>0 such that

Simplification yields

where

Since Q>0 and , there exists a>0 such that f(a)=0. As a consequence, A≥0 and L′≤0 for all x, y, z and w. Note that L′=0 implies that x=z=0. It can be verified that the largest invariant set where L′=0 is the singleton . Therefore, by LaSalle's invariance principle 35, the trivial equilibrium of (A2) is asymptotically stable, and thus the EE is locally asymptotically stable for model (1)–(4).   ▪

Appendix 2. Global stability of the DFE

Proof of Theorem 3.3

Let x=(I, P). Since

it follows that

where F and V can be chosen in any of the three forms given in Section 3.2. Notice that, for each choice, both F and V ⁻¹ are non-negative. By the Perron–Frobenius Theorem, the non-negative matrix V ⁻¹ F has a non-negative left eigenvector u≥0 with respect to , that is, . Motivated by 24, consider a Lyapunov function

Differentiating L along solutions of model (1)–(4) gives

If , L′=0 implies that u ^T x=0 by (A6), and thus I=0 or P=0. It follows from (2) and (4) that the largest invariant set where L′=0 satisfies δ SP=0 or γ I=0, respectively; thus, I=P=0 since . Equations (1) and (3) lead to S=S ₀ and R=0 in the above invariant set, that is, the singleton . By LaSalle's invariance principle 35, the DFE is the globally asymptotically stable in Γ if .

If , L′=0 implies that S=S ₀, by (A3), (A5) and the fact that u ^T V ⁻¹>0. Then, Equation (1) gives . Adding Equations (2) and (3) gives , for which the invariant set satisfies I+R=0, and thus I=R=0. Equation (2) gives δ SP=0, and thus P=0. Therefore, the largest invariant set where L′=0 is the singleton , and by LaSalle's invariance principle, the DFE is globally asymptotically stable in Γ if .

If , then by continuity, L′>0 in a neighbourhood of the DFE in . Solutions in sufficiently close to the DFE move away from the DFE, implying that the DFE is unstable. Using a uniform persistence result from 20 and an argument as in the proof of Proposition 3.3 of 38, it can be shown that, when R ₀>1, instability of the DFE implies uniform persistence of model (1)–(4).   ▪

Appendix 3. Global stability of the EE

Proof of Theorem 3.4

If , then by Theorem 3.1, an EE exists, where satisfy the equilibrium equations (A1). Following 45, consider a Lyapunov function

It can be easily verified that V≥0 for all S, I, P>0 and V=0 if and only if S=S*, I=I*  and  P=P*. Differentiating V along solutions of (1)–(4) and using (A1) to simplify give

Here, two inequalities of arithmetic and geometric means have been applied:

and

Using inequalities (A8) and (A9), V′=0 implies that for some positive constant k. Substituting I=kI* into (3) gives , whose invariant set satisfies R=kR*, by (A1). Substituting relations into (1) yields . It follows from the first equation of (A1) that k=1. Therefore, the largest invariant set where V′=0 is the singleton . By LaSalle's invariance principle, the EE is globally asymptotically stable in .   ▪

Appendix 4. Type reproduction number

Proof of Theorem 4.1

Using (10) it follows that

where e _s is a unit column vector with all entries zero except that the s entry is equal to 1, and P _s is an n×n matrix with all entries zero except that the (s, s) entry is equal to 1. From (A10), it follows that

Since s¬=l _w , it follows that and P _s U _m =0, thus

and

Hence,

  ▪