Discrete-time host–parasitoid models with pest control

Abstract

We propose a simple discrete-time host–parasitoid model to investigate the impact of external input of parasitoids upon the host–parasitoid interactions. It is proved that the input of the external parasitoids can eventually eliminate the host population if it is above a threshold and it also decreases the host population level in the unique interior equilibrium. It can simplify the host–parasitoid dynamics when the host population practices contest competition. We then consider a corresponding optimal control problem over a finite time period. We also derive an optimal control model using a chemical as a control for the hosts. Applying the forward–backward sweep method, we solve the optimal control problems numerically and compare the optimal host populations with the host populations when no control is applied. Our study concludes that applying a chemical to eliminate the hosts directly may be a more effective control strategy than using the parasitoids to indirectly suppress the hosts.

AMS Subject Classification::

• 92D25
• 39A30

Keywords:

• biological control
• discrete Hopf bifurcation
• uniform persistence
• optimal control
• Pontryagin's maximum principle

1. Introduction

Biological control is defined as the reduction of pest populations by natural enemies. The natural enemies of pests, also known as biological control agents, include predators, parasitoids, and pathogens. Many species of wasps and some flies are parasitoids and most of the parasitoids have a narrow host range. Very often biological control involves supplemental release of natural enemies. Relatively few natural enemies may be released at a critical time of the season (inoculative release) or literally millions may be released in a single time (inundative release) 6. An example of inoculative release occurs in greenhouse production of several crops. Periodic releases of the parasitoid, Encarsia formosa, are used to control greenhouse whitefly, and the predaceous mite, Phytoseiulus persimilis, is used for the control of the two-spotted spider mite 6.

Grasman et al. 7 use a two-compartment ordinary differential equations model of host–parasitoid interactions to determine the size of an inundative release of parasitoids for effectively controlling a host population. Morton 19 on the other hand formulates a stochastic birth–death process to address the impact of random control on predator–prey interactions. Cavalieri et al. 3 develop a discrete-time model for the study of European Corn Borer (ECB). Their model consisting of four difference equations includes both a natural ECB pathogen and a genetically engineered toxin-producing agent which serves as a biological control agent. Cavalieri et al. 3 conclude that the biological control regime cannot be effective under the conditions that induce chaotic population dynamics. More recently, Kern et al. 14 present a model of ordinary differential equations for population interactions between an invasive and a native species, where the effect of disturbance to the system is modelled as a control variable. Kern et al. 14 provide suggestions for managing the disturbance regime when the invasive species is present. Whittle et al. 25 use a discrete-time optimal control model to provide management for an invasive species consisting of a large main focus and several smaller outlier populations. Other models of pest control can be found in 12,21–23 and references cited therein.

In this study, we propose a simple model of host–parasitoid interactions to study the effects of inoculative release of parasitoids upon host–parasitoid interactions. Our general system is based on the classical Nicholson–Bailey model 20 with density dependence on the per capita growth rate of the host. It is assumed that a constant level of parasitoids is added into the natural host–parasitoid system per generation in order to control the host population. An analysis is carried out for this general system and a more detailed analysis is provided when the host per capita growth rate is modelled either by a Beverton–Holt or Ricker type nonlinearity.

Turchin et al. 24 propose two discrete-time host–parasitoid models to investigate possible cycling mechanisms for the larch budmoth, Zeiraphera diniana, in the Swiss Alps. In these two models studied by Turchin et al., the Ricker type nonlinearity is used as the per capita moth growth rate. See also the analysis carried out on the two models 11. Furthermore, gypsy moth populations in the northeastern US exhibit eruptive population dynamics which result in extensive tree defoliation and ultimately deforestation. Whittle et al. 26 use a discrete-time optimal control model to investigate the effects of the manufactured Nucleopolyhedrosis Virus (NPV) (Gypchek) sprayed on the moth. Whittle et al. 26 also use the Ricker type nonlinearity to model moth's per capita growth rate. On the other hand, since Beverton–Holt nonlinearity frequently appears in the literature and is a classical example for contest intraspecific competition, we also investigate the model with Beverton–Holt growth rate. It can be seen from these two type growth rates that the pest population is harder to control when Ricker type nonlinearity is incorporated.

In particular, we shall derive a threshold in terms of the external parasitoids so that the pest population can be eliminated in the long term. Since insect populations usually have distinct life stages, discrete-time systems are appropriate models for investigating host–parasitoid interactions. We first propose and study a general discrete-time host–parasitoid model where a constant u of external parasitoids is added into the native parasitoid population at each generation. In this model, we prove that the pest population will ultimately go extinct if the constant input u is above a threshold. It is expected that inoculative releases of biological agents will simplify the host–parasitoid interaction, and we shall investigate this question specifically.

In this host–parasitoid model, the cost of implementing the biological control is not incorporated. Moreover, although the biological control can help to eliminate the pests in the long run, it is not practical to perform such a release over a very long period of time. To incorporate this observation, we propose a model of host–parasitoid interactions in which the external input of parasitoids is regarded as a control variable which may vary from generation to generation. We then apply the theory of optimal control to determine the optimal strategy for releasing the biological control agents over a finite time span. We numerically solve the optimal control using the forward–backward sweep method and compare the optimal pest populations with the pest populations when no control is applied. It turns out that the differences between these two populations over the finite time span are small, especially when the cost of control is high. We then propose an optimal control model of host–parasitoid interactions using a chemical agent. We compare and contrast the model with the model of biological control.

In the following section, a general mathematical model of host–parasitoid interactions is proposed, where a constant input u of parasitoids is added to the native parasitoid population at each generation. Section 3 considers a corresponding optimal control problem and also an optimal control problem with a chemical agent. The final section provides a brief summary and discussion.

2. The model and stability analysis

In this section, we first present a general host–parasitoid model and its analysis. Two specific growth rates will be discussed in the subsequent subsections. The host population is regarded as a pest and the parasitoid population is the natural enemy of the host.

2.1. The general model

Let x(t) and y(t) denote the host and parasitoid populations at generation t=0, 1, …, respectively. The host is regarded as a pest and the parasitoid population is treated as an enemy of the host population and is used as a biological control agent against the host population. The parasitoid has a very narrow range of hosts and is specialized to this particular host population. The host–parasitoid interaction without external release of the parasitoids is described by the following system:

In model (1), it is assumed that hosts and parasitoids encounter randomly and the probability of an individual host escaping from being parasitized is modelled by the zero term of a Poisson distribution. Parameter a>0 is the average number of encounters per unit time per parasitoid and is also referred to as the searching efficiency of the parasitoid. The per capita growth rate g of the host population satisfies the following assumptions:

(H1) g∈C ²[0, ∞), g(0)=α>0, g(x)>0, g′(x)<0 for x≥0, lim _x→∞ g(x)=0, and sup<texlscub>xg(x): x≥0</texlscub>=l<∞.

System (1) is a modification of the classical Nicholson–Bailey model 20 in which density dependence of the per capita growth rate of the host population is incorporated. The assumption for x≥0 in (H1) models intraspecific competition of the population. Individuals within the population compete for resources to reproduce when population size or density is large. Since xg(x) is the size of offspring reproduced by all the individuals, we assume that the total offspring, xg(x), remains bounded when the population size x is large due to limited resources. These biological considerations motivate our assumptions imposed for the per capita fertility rate g in (H1).

The classical Beverton–Holt and Ricker type growth rates 1 clearly satisfy all the conditions given in (H1). Furthermore, the growth rate of the Beverton–Holt model has the following monotone property:

The asymptotic dynamics of Equation (1) are simpler if in addition g satisfies Equation (2). Recall that a discrete-time system , where , is said to be uniformly persistent if there exists η>0 such that for all solutions with x _i (0)>0 for i=1, …, n 8. We shall use the concept of uniform persistence to prove long-term coexistence of both populations when appropriate.

The Jacobian matrix J of Equation (1) has the following form

It is clear that system (1) has an extinction steady state where both populations become extinct. Moreover, Equation (1) has another boundary steady state if α>1, where x̄ satisfies g(x)=1. The Jacobian matrices evaluated at these two steady states and are given by

respectively, where by (H1).

To discuss the existence of an interior steady state, notice that the nontrivial x-isocline of Equation (1) is given by y=ln g(x)/a and the y-isocline can be written as

Function h ₀(y) is strictly increasing on [0, ∞) with and . As a result, is well defined, strictly increasing on [0, ∞) with and . Since the x-isocline is strictly decreasing with x and y intercepts given by x̄ and lnα/a, respectively, we conclude that Equation (1) has an interior steady state if and only if 1/a<x̄, that is, if a x̄>1. In such a case, the interior steady state is unique.

The asymptotic dynamics of Equation (1) can be easily obtained and are summarized below. In particular, there exists l>0 given by (H1) such that x(t)≤l for all t≥1 for all solutions (x(t), y(t)) of Equation (1) by (H1). Therefore, we have

for all t≥1 for all solutions of Equation (1). Consider the scalar equation , z(0)≥0. Since the map induced by the scalar equation is continuous and increasing and the scalar equation has no steady state other than 0 when al<1, all solutions of the scalar equation converge to 0. As a result, solutions of Equation (1) satisfy if al<1 (cf. 10 15). The proofs of the following theorem are straightforward and are not provided.

Theorem 2.1

Solutions of Equation (1) remain nonnegative and are bounded for t>0. Steady state always exists and solutions of Equation (1) satisfy if al<1. Moreover, the following statements hold.

	(a) Steady state is globally asymptotically stable in if α<1 and is globally attracting in if α=1.
	(b) Let α>1. Then is unstable and Equation (1) has another boundary steady state , where g(x̄)=1. If a x̄<1 and Equation (2) holds, then is globally asymptotically stable in .
	(c) If α>1 and a x̄>1, then is unstable and Equation (1) has a unique interior steady state where x 0*<x̄. In addition if Equation (2) holds, then Equation (1) is uniformly persistent.

If the assumption (2) given in Theorem 2.1(b) does not hold, then may lose its stability via a period-doubling bifurcation and it is possible for the host population to undergo a cascade of period-doubling bifurcations to chaos. For example, the well known one-dimensional Ricker equation possesses this kind of chaotic behaviour 1. See Figure 1(c) for the bifurcation diagram of a Ricker map.

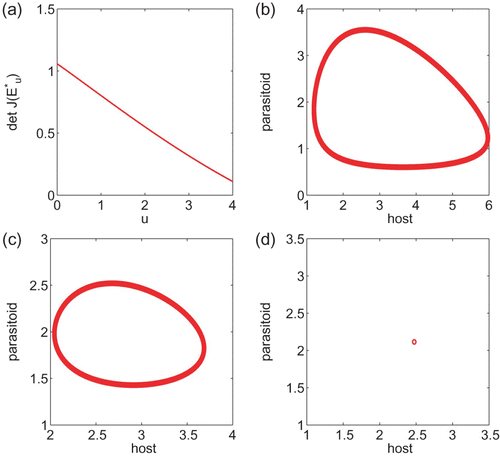
Figure 1. (a) plots components of the interior steady state as a function of u for system (15). (b) plots det J* as a function of u with α=15 and a=0.1. In contrast to Figure 2(a) where det J* is always decreasing, det J* in (b) increases first but it cannot exceed 1, while it is increasing. (c) is the bifurcation diagram for the Ricker equation x(t+1)=x(t) e ^r(1−x(t)) using r as a bifurcation parameter.

Recently, Kang and Chesson 13 use the concept of uniform invasibility to derive a simple sufficient condition for the permanence of a general system of two-interacting populations. When the interaction is of predator–prey type, the sufficient condition [Theorem 5.2]13 is given in terms of the relative nonlinearity of the per capita growth rates of the two populations, that is,

A necessary condition for x>0 immediately follows. When , the Beverton–Holt type nonlinearity, then becomes

which is negative for all x>0. Therefore, the sufficient condition derived by Kang and Chesson does not work well for our system. Similarly, if one uses the Ricker type function and substitutes it into , one arrives at

which is also negative for all x>0. Therefore, the sufficient condition [Theorem 5.2]13 does not work well for system (1) with the modelling assumption of g given in (H1).

Figure 2. This figure provides simulation results for system (15) with α=10 and a=0.5. (a) is the curve of det J(E _u *) as a function of u. (b)–(d) are trajectories when u=0, u=0.2, and u=0.5, respectively.

On the other hand, Kon and Takeuchi [Theorem 3]16 provide a sufficient condition of permanence for the host–parasitoid system (1) for which the host's growth rate is modelled by the Ricker type function. The sufficient condition derived in 16 does include the parameter region for which the host population may be oscillating. Their result [Theorem 3]16 complements Theorem 2.1(c).

One wishes to eliminate the host population or to make the host population below a certain tolerable level for agriculture purpose. One augmentation method is to introduce additional parasitoids into the host–parasitoid community. Suppose now a positive constant u of external parasitoids are added to the native parasitoid population per generation for the control of pest population. The host–parasitoid interaction then becomes

where g satisfies (H1) and a, u>0. It follows that the system has no extinction steady state since there is a constant input of parasitoids added to the interaction per generation. However, system (5) has a boundary steady state of the form E ₂=(0, u). The Jacobian matrix of system (5) is also given by Equation (3). In particular, the Jacobian matrix evaluated at E ₂ has the following form

It follows that E ₂ is locally asymptotically stable if and unstable if . It can be easily shown that E ₂ is globally asymptotically stable in if .

Theorem 2.2

Solutions (x(t), y(t)) of Equation (5) remain nonnegative and are bounded for t>0. Moreover, E ₂=(0, u) is globally asymptotically stable in if and E ₂ is globally attracting in if .

Proof

It is clear that solutions of Equation (5) remain nonnegative and are bounded with x(t)≤l and y(t)≤l+u for t≥1. Notice y(t)≥u for t≥1. To prove E ₂ is globally attracting, we may assume x(0)>0. It follows that x(t)>0 and for t≥1. Therefore, if . If , then is monotonically decreasing and bounded below by 0. Hence, exists. If x ₀>0, then by the continuity of g, we have and obtain a contradiction. Consequently, if . As a result, and the proof is complete.   ▪

Observe that one can use the centre manifold theory to address whether E ₂ is locally asymptotically stable or unstable at the critical value . However, we do not pursue this question since we are more interested in whether the biological control can simply the dynamics.

Let . Then, it is necessary that α>1. It is straightforward to prove that system (5) has a unique interior steady state. Indeed, the x and y components of an interior steady state satisfy

Notice that the x-isocline given by the first equation of (6) as a function of x is strictly decreasing and the graph goes through and (x̄, 0). The y-isocline of Equation (5) is given by

A simple calculation shows that for y>0, , and h(u)=0. It follows that y=h ⁻¹(x) exists and is strictly increasing on [0, ∞), h ⁻¹(0)=u and . We conclude that Equation (6) has a positive solution if and only if , or equivalently, . Moreover, the positive solution is unique if it exists.

Define

Then, the host population will eventually go extinct if u≥u ₀ by Theorem 2.2, where the threshold u ₀ depends on the searching efficiency a of the parasitoids and also on the intrinsic growth rate α of the host. On the other hand, system (5) has a unique interior steady state if 0<u<u ₀. Let denote such a unique interior steady state. Then, u<y*<u ₀ and x* and y* are decreasing and increasing functions of u, respectively, with and as . Moreover, as , either converges to or to (x̄, 0) depending on whether a x̄>1 or a x̄<1, where is the unique interior steady state of Equation (1). We summarize these results into the following lemma.

Lemma 2.1

Let 0<u<u ₀. Then, Equation (5) has a unique interior steady state where x* and y* are decreasing and increasing functions of u, respectively, with . Moreover, if a x̄>1 and if a x̄<1.

Proof

We only prove that x* and y* are decreasing and increasing functions of u, respectively. We differentiate the first equation of (6) with respect to u yielding

We then differentiate the second equation of (6) and substitute the above expression for . It follows that

Since the curve intersects with the bisector z=y from above, the slope of the curve at the intersection is less than the slope of the bisector z=y, that is, . Therefore, x* is a decreasing function of u and y* is an increasing function of u.   ▪

After the existence of interior steady states is resolved, we move on to discuss local stability of such a steady state. Let 0<u<u ₀. The local stability of can be determined by the Jacobian matrix J evaluated at E _u *,

The trace and determinant of J* are given by

and

respectively. The Jury conditions state that the eigenvalues λ _i , i=1, 2, of J* satisfy for i=1, 2, is equivalent to 1. These conditions , , and det J*<1 result in the following three inequalities

and

respectively. The stability of E _u * and its local bifurcations depend on specific function g. However, it can be shown that Equation (11) holds for all g satisfying (H1).

Lemma 2.2

Suppose that the unique interior steady state exists for system (5). Then, inequality holds for all parameters.

Proof

Recall that by the proof of Lemma 2.3. Therefore, Equation (11) holds since g(x*)>1 and .   ▪

Notice that the conclusion of Lemma 2.4 remains valid for u=0. It follows that systems (1) and (5) cannot undergo a transcritical bifurcation when the interior steady state loses its stability. The only possible bifurcation is either a discrete Hopf bifurcation or a period-doubling bifurcation 1. Although solutions of Equation (5) may not always stabilize at the interior steady state, in the following we show that both populations can coexist infinitely if 0<u<u ₀.

Theorem 2.3

Let 0<u<u ₀. Then, system (5) is uniformly persistent.

Proof

Since y(t)≥u for t≥1, it is enough to prove that there exists η>0 such that for all solutions of Equation (5) with positive initial conditions. We apply Theorem 2.2 and Corollary 2.3 of Hutson 9 by letting , the compact global attractor of Equation (5), and let f ^t be the tth iteration of the map induced by system (5). Define , a compact subset of D with empty interior. Then, S and are forward invariant. Let be defined by P(x, y)=x. Then, P(x, y)=0 is equivalent to (x, y)∈S, which satisfies (a) of [Theorem 2.2]9. To verify (b) of [Theorem 2.2]9, we show that the condition of [Corollary 2.3]9 is true for Equation (5). Notice that the ω-limit set of S consists of only a singleton . Then, for any , we have

When X=E ₂, Equation (14) implies

by the assumption 0<u<u ₀. Furthermore, for X∈S, we have x(i)=0 for all i≥0 and y(i)=u for i≥1. Therefore, it follows from Equation (14) that

for X∈S. Consequently, there exists a compact set M⊂D such that the distance between M and S is positive and every solution with initial condition in will enter and remain in M by 9. This completes the proof.   ▪

On the other hand, Theorem 2.2 implies that solutions of Equation (5) satisfying and if u≥u ₀. As a consequence, the pest population can be eliminated if the external input u of parasitoids is large.

In ecology, intraspecific competition refers to competition between individuals within the same population. There are two extreme forms of intraspecific competition, contest and scramble. If there is a rank in the population so that higher rank individuals can obtain resources more easily, then such a competition is called a contest competition. On the other hand, if there is no rank in the population and each individual in the same population competes equally, then the competition is referred to as a scramble competition. In the following subsections, we will use Beverton–Holt and Ricker type functions to study the impact of external release of parasitoids.

2.2. The model with Beverton–Holt growth rate

In this subsection, we assume that individuals in the host population undergoes contest intraspecific competition. The well- known Beverton–Holt growth rate , α, b>0, models such a competition. Let β>0 denote the number of parasitoids produced by each parasitized host that survive to adult. Then, we have the following system

Let , , , , and by ignoring the hats, one can convert the above system into

System (15) is a special case of system (5) with . Consequently, Theorem 2.2 can be applied to system (15) to conclude that E ₂=(0, u) is globally asymptotically stable if and E ₂ is globally attracting if . Assume that , that is, u<u ₀, so that the unique interior steady state E _u * exists. Notice that for x≥0 and thus tr J*>0 and det J*>0 by Equations (9) and (10), respectively.

We can further simply det J* by noting and . Then,

and the derivative of det J* with respect to u is

Since , det J* is a decreasing function of u for and an increasing function of u for .

Theorem 2.4

Let 0≤u<u ₀. Then, inequalities (11) and (12) hold, and a discrete Hopf bifurcation is the only possible bifurcation for Equation (15) when E _u * loses its stability. Moreover, det J* is decreasing at u for which .

Proof

Since tr J*>0, Equations (11) and (12) hold by Lemma 2.4. Therefore, the system cannot undergo either a transcritical or a period-doubling bifurcation when E _u * loses its stability. Notice is equivalent to α≤2. Therefore if α≤2, then and det J* is decreasing for 0≤u<u ₀.

Assume α>2. We prove that if at some , then , or equivalently at the particular u. Observe that the maximum value of det J* occurs when . Substituting α/2 for x* in Equation (16), we have , and hence if then it is necessary that . On the other hand, (cf. proof of Lemma 2.4) implies and thus . One can then easily verify that is equivalent to , which holds trivially since . Therefore, if at some u∈[0, u ₀), then and det J* must be decreasing at u.   ▪

As a consequence of Theorem 2.6, det J* as a function of u is either decreasing for all 0≤u<u ₀ when α≤2 or decreases at a particular u when at the particular u and α>2. It is impossible that while det J* is increasing. Therefore, external input of biological control cannot destabilize the system but may make the system more stable by eliminating quasi-periodic solutions since det J* may exceed 1 when u=0 or small but det J* may decrease to below 1 as u is increased. In particular, it is possible that the interior steady state E ₀* is unstable and E _u * becomes locally asymptotically stable for some u>0.

We use numerical examples and simulations to illustrate our findings. Consider the following parameter values

Then, . Setting g(x̄)=1, we have . Theorem 2.1 and Lemma 2.3 imply that Equation (15) has an interior steady state for 0≤u<u ₀ since . Let E _u * denote the unique interior steady state for 0≤u<u ₀. We compute the determinant of the Jacobian matrix evaluated at the interior steady state. Figure 2(a) demonstrates that the determinant is greater than 1 when u=0 and decreases to below 1 as u is increased. Figure 2(b)–(d) provides trajectories for system (15) with positive initial conditions randomly chosen, where u=0 in(b), u=0.2 in(c), and u=0.5 in (d). The first 6000 iterations are eliminated and the next 2000 iterations are plotted. System (15) has an invariant loop solution when there is no external biological control, u=0. As u is increased, system (15) has only equilibrium dynamics.

Moreover, as indicated in Lemma 2.3, that the host population in the interior steady state is a decreasing function of the external control agent u. Therefore, in addition to simplify the host dynamics, one can also use the control agent to lower the pest population level. See Figure 1(a), where the same parameter values as those in Figure 2 are used. To illustrate Theorem 2.6 we choose different parameter values:

Then, u ₀=27.0805. Figure 1(b) plots det J* as a function of u for . Although the curve increases first as u is increased, det J* always lies below 1.

2.3. The model with Ricker type growth rate

The other extreme of intraspecific competition is the scramble competition with Ricker function being its representative growth rate, where r>0 is the intrinsic growth rate and K>0 is the carrying capacity. The resulting host–parasitoid interactions are then described by the following system

We rescale the variables and parameters by letting , , , and by ignoring the hats, we arrive at

System (19) is a special case of Equation (5) with and . It follows that

Consider first when u=0. The system has two boundary steady states and where x̄=1. Since , (0, 0) is always unstable by Equation (4). Steady state is locally asymptotically stable if r<2 and a<1 and unstable if either r>2 or a>1 by Equation (4). The system has a unique interior steady state if a x̄>1, where . When u>0, then the system has a nontrivial boundary steady state E ₂=(0, u) and Theorem 2.2 applies. In particular, E ₂ is globally asymptotically stable if u>r/a=u ₀. The system has a unique interior steady state for 0<u<u ₀ by Lemma 2.3. However, the monotone property (2) of g does not hold for the model.

Notice , and x*<1. The determinant and trace of the Jacobian matrix evaluated at the interior steady state become

The local stability conditions and det J*<1 reduce to

and

respectively. In particular, it is possible for the system to undergo either a Hopf bifurcation or a period-doubling bifurcation when the interior steady state loses its stability. The following lemma provides a small parameter region for which the interior steady state is locally asymptotically stable.

Lemma 2.3

Let 0<u<u ₀. Then, steady state is locally asymptotically stable if and a<1 hold.

Proof

Since , det J*<1 holds if a<1. On the other hand, is strictly decreasing with minimum 1−r occurring at x*=1. Therefore, the left hand side of Equation (20) is greater than if . If , then since x*<1, if r<2. As a result, holds if . The proof is complete.   ▪

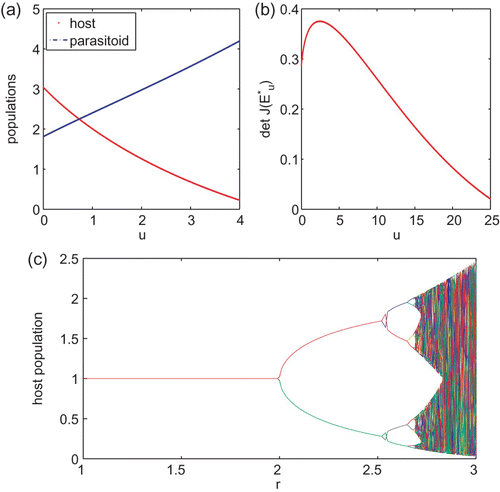
Similar to the discussion of the Beverton–Holt model, we use numerical simulations to study the system with Ricker type growth rate. In addition to u, there are only two parameters r and a. It was noted earlier that the x and y components of the interior steady state are decreasing and increasing functions of u, respectively. We first let r=5 and a=2. Then, u ₀=2.5. Figure 3(a) plots components of the interior steady state as a function of u for 0≤u≤2 and it clearly demonstrates the monotone property. Figure 3(b) plots the left hand sides of Equations (20) and (21) as a function of u with the same parameter values. Plots (c) and (d) of Figure 3 are similar to that of (b) but with different values for r and a. From these plots, it appears that the system undergoes period-doubling bifurcations when the interior steady state loses its stability.

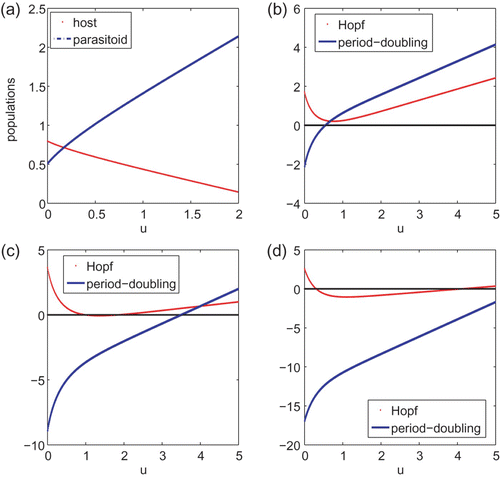
Figure 3. (a) plots components of the interior steady state as a function of u for system (19). (b)–(d) plot curves 1−det J* and 1+tr J*+det J* against u. The interior steady state E _u * is locally asymptotically stable if both curves lie above the horizontal axis. The parameter values are r=5 and a=2 for (a) and (b), r=10, a=2 for (c) and r=20, a=3 for (d).

3. Optimal control problems

In Section 2, a constant level u of parasitoids is added into the natural host–parasitoid community at each generation. It is proved in Theorem 2.2 that if u is large, , then the pest population will eventually go extinct. Moreover, the host population in the interior steady state decreases with increasing u (cf. Lemma 2.3). However, the financial cost of implementing this kind of augmentation is not considered. In addition, it is also not practical to perform such a biological control strategy over a long period of time.

In this section, we shall regard the biological control problem discussed in Section 2 as an optimal control problem over a finite time span. Specifically, we will regard the external input u in system (5) as a control variable u(t) which varies with time t=0, 1, …, T in Subsection 3.1, where T is a fixed positive integer. In Subsection 3.2, we will use a chemical agent as a control that also varies with time. Since the controls are either biological or physical quantities, it is necessary that they be nonnegative. Moreover, the upper bound of the biological control is taken to be u ₀ derived in Section 2, while the upper bound of using a chemical agent is taken to be 1.

Several researchers have studied asymptotic dynamics of populations with time-periodic parameters. See 2 5 18 and references cited therein. Since in reality it is not practical to release external natural enemies into the system or to apply a chemical agent over a long period of time, we do not study the asymptotic dynamics of the corresponding non-autonomous systems as other researchers do. In particular, although the controls are time-dependent, they are not periodic. We look for the controls that will minimize the pest population at the end of the short time period along with the cost of implementing the controls over the entire short time span. We will use the theory of optimal control with numerical simulations to study the pest control problems. We refer the reader to Lenhart and Workman 17 for the theory of optimal control with applications to biological models.

3.1. An optimal control problem with biological control

Parallel to Section 2, we consider the general host–parasitoid model with control

for , where g satisfies (H1). Unlike the constant input u formulated in Section 2, the external input u(t) depends on generation t and is treated as a control variable. In particular, u(t) is not periodic and we do not study the asymptotic dynamics of Equation (22). Since there is usually a cost associated with implementing the control, the objective functional considered is given by

where B>0 is a parameter associated with the cost and the quadratic term u ²(t) is used for simplicity. We wish to minimize the host population at the end of time period T and also minimize the cost of the control over the entire time period. Equivalently, we wish to minimize J(u) over the controls u with bounds and subject to Equation (22), where u ₀ is derived in Section 2 and is defined in Equation (8).

Let

Since the variables are continuous in the state equations and in the objective functional, it is clear that there exists a minimum value of J(u) in 𝒰. Applying an extension of Pontryagin's Maximum Principle 4, we have the following result.

Theorem 3.1

Given an optimal control u* and the corresponding state solutions x and y, there exist adjoint variables λ₁ and λ₂ such that the adjoint variables satisfy the system

for with the transversality conditions

Moreover, the optimal control u* is given by

for .

Proof

Using system (22) and the objective functional J(u), we form the Hamiltonian

Applying an extension of the Pontryagin's Maximum Principle 4 17, we obtain the adjoint equations and for with the transversality conditions and since the payoff term in J(u) involves x(T) but not of y(T). These result in Equations (24) and (25). Using the optimality condition with bounds and solving for u* subject to the bounds we obtain characterization (26).   ▪

3.2. An optimal control model using a chemical agent

Since applying chemical agents to eliminate pests is a common strategy of controlling pests, in this subsection, we use a chemical agent to control the pests instead of the biological control discussed in Section 3.1. We assume that both populations are subject to a chemical which acts as a control for the host population. However, since the parasitoids have the same habitat as the hosts, the parasitoids may also suffer the same negative effects. Specifically, the state equations with the control are given as follows

for , where g satisfies (H1) and v(t) is the amount of population decrease due to the chemical agent at time t, and 0≤c≤1. If c=0, then the chemical agent has no detrimental effect on the parasitoids. The chemical agent has the same negative effects on the parasitoids as on the hosts if c=1. Similar to Section 3.1, we wish to minimize the host population at the end of time period T and also the cost of the control over the entire time period. Therefore, the objective functional is given by Equation (23), where B>0 is a parameter associated with the cost and the quadratic term v ²(t) is used for simplicity. We wish to minimize J(v) over the controls v with bounds .

Similarly, define

Since the variables are continuous in the state equations and in the objective functional, it is clear that there exists a minimum value of J(v) in 𝒱. Using an extension of Pontryagin's Maximum Principle as we did previously, we have similar results parallel to Theorem 3.1. The proof of following theorem is omitted.

Theorem 3.2

Given an optimal control v* and the corresponding state solutions x and y, there exist adjoint variables λ₁ and λ₂ such that the adjoint variables satisfy the following system

for with the transversality conditions

Moreover, the optimal control v* is given by

for .

3.3. Numerical examples

In this subsection, we adopt the forward–backward sweep numerical method 17 with MatLab and Theorems 3.1 and 3.2 to determine the optimal control and its corresponding state variables with different parameter values. Specifically, we start with an initial guess for the control at the first iteration. We then forward solve the state equations (22) and then backward solve the adjoint equations (24). Once these approximations are complete, we update the control by using the characterization (26) derived in Theorem 3.1. We repeat this procedure until convergence of successive iterations is obtained. We plot the host population for which the control is applied (the red curve) and also the host population of no control (the blue curve) over time. We repeat the same procedure for the chemical control problem (27) by using c=1.

Since Beverton–Holt and Ricker nonlinearities have been used frequently in the literature, we shall use these two functions for simulations. Due to the simple asymptotic dynamics of the Beverton–Holt nonlinearity, we obtain consistent results for the optimal control problems. Notice that the Ricker type nonlinearity has been adopted as a gypsy moth's growth rate in a study conducted by Whittle et al. 26, where virus is used as a biological control in their study. For the Ricker nonlinearity, we choose parameter r in regimes corresponding to different dynamical behaviours of the host population in the absence of the parasitoid and the control. In particular, r=1.5 corresponds to the steady-state dynamics, r=2.5 corresponds to the two-cycle dynamics, r=2.6 corresponds to the four-cycle dynamics and r=3.0 is in the chaotic region. See Figure 1(c) for these different parameter regimes.

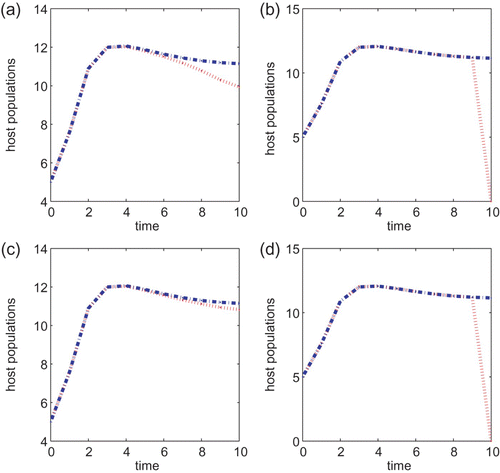
In the following simulations, we let T=10, B=1 or B=5, and the initial condition is taken to be (5, 5) for all simulations. We begin with the biological parameter values: α=5.0 and a=0.1 and . Then, u ₀=16.09. We obtain the optimal control numerically and plot the corresponding pest population over the time period t=0, …, T given in Figures 4 and 5. The plots on the left hand columns are for model (22), while the plots on the right hand columns are for model (27). In each of the figures, B=1 in (a) and (b), and B=5 for (c) and (d). For comparison purpose, we also plot the host population of no control. We can conclude from Figures 4 and 5 that applying a chemical agent is a better control strategy than the biological control since the pest population is at a smaller level when the chemical agent is applied, independent of whether the cost B associated with the control is large or small. This conclusion remains the same if we vary parameter values α and a or vary the initial conditions.

Figure 4. g(x)=α/(1+x) with α=5, a=0.1 and T=10 for models (22) and (27). Control coefficients are B=1 for (a) and (b) and B=5 for (c) and (d). Initial conditions are (x(0), y(0))=(5, 5) for all the plots. The plots (a) and (c) are for (22), while plots (b) and (d) are for model (27).

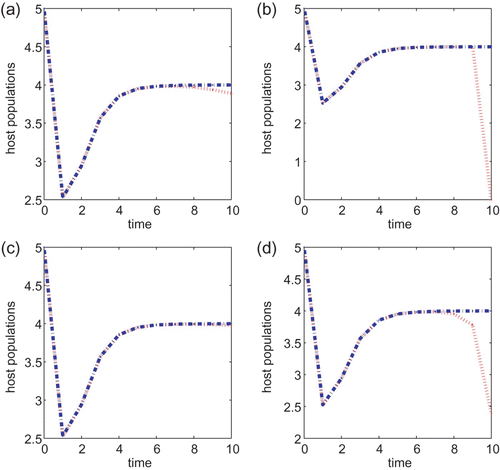
Figure 5. g(x)=α/(1+x) with α=15 and a=0.1 for models (22) and (27). B=1 for (a) and (b), and B=5 in (c) and (d). Initial conditions are (x(0), y(0))=(5, 5) for all these simulations. Plots (a) and (c) are for (22), while (b) and (d) are for (27).

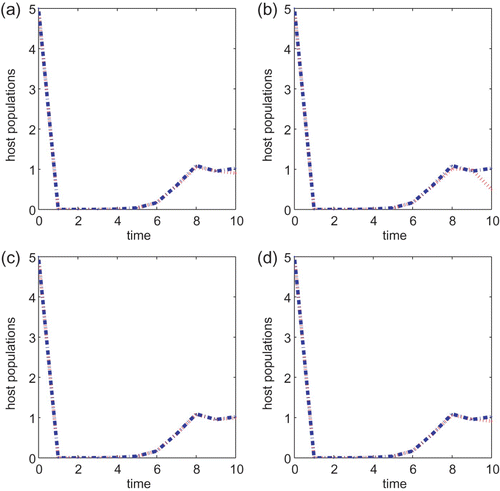
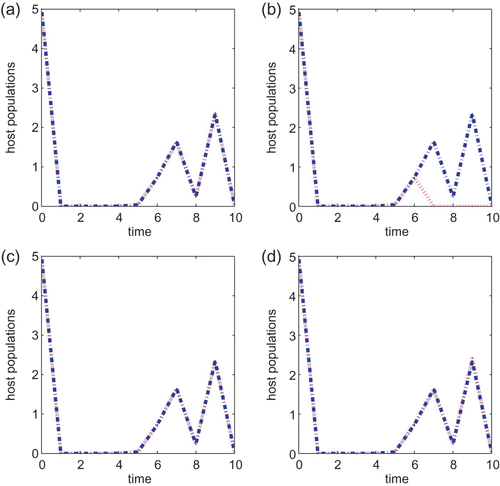
We next turn to the Ricker type growth rate with T=10, a=0.5, B=1 or B=5 and the initial condition also taken to be (5, 5) in all simulations. If r=1.5, then there is a noticeable difference between the two control strategies when the cost B is small. See Figure 6 (a) and (b). As we increase the cost B to 5, it can be seen from Figure 6 (c) and (d) that the chemical control agent only performs a little better than the biological control method. The same observation is obtained when either r=2.5 or r=2.6. The chemical control method is better than the biological control strategy when B=1 but neither method is prominent when the cost B associated with the control is higher. The same conclusion is obtained if we vary the initial conditions or vary r slightly so that r is within the same asymptotic regimes. As we increase r to 3.0, the chemical control is also a better strategy than the biological control method when B=1 but there is no difference between the two strategies when B=5. In particular, neither control method works well when r is large and the cost B is high.

Figure 6. g(x)=e ^r(1−x) with r=1.5, a=0.5 and T=10 for models (22) and (27). B=1 for (a) and (b) and B=5 for (c) and (d). Initial conditions are (x(0), y(0))=(5, 5) for all plots. Plots (a) and (c) are for (22) and (b) and (d) are for (27).

4. Discussion

Pests are animals which are detrimental to humans or to human concerns. They cause damage to agriculture by feeding on crops or parasitizing livestock. Although there are efforts to control or to eliminate pests, pests are still quite prevalent in both agriculture and households. Biological control is the reduction of pest populations by natural enemies that typically involves an active human role. Sometimes biological control involves supplemental release of natural enemies. Relatively few natural enemies may be released at a critical time of the season. Such an augmentation is termed an inoculative release. An example of an inoculative release occurs in greenhouse production of several crops. Periodic releases of the parasitoid, Encarsia formosa, are used to control greenhouse whitefly, and the predaceous mite, Phytoseiulus persimilis, is used for control of the two-spotted spider mite.

Natural enemies of insect pests are often parasitoids. Motivated by this, we use simple discrete-time host–parasitoid models to study the effects of constant external release of parasitoids at each generation upon the host–parasitoid interactions in Section 2. It is proved that the pest population will eventually go extinct if u exceeds the threshold level u ₀ (cf. Theorem 2.2), where u ₀ depends on the searching efficiency of the parasitoids and also on the intrinsic growth rate of the host. Moreover, the constant release of parasitoids can lower the pest population level in the unique coexisting equilibrium (cf. Lemma 2.3). When the per capita growth rate of the pest is modelled by the Beverton–Holt function, it is shown that the constant input of the parasitoids can simplify dynamics of the system (cf. Theorem 2.6) by stabilizing the interior steady state.

Although the constant augmentation of parasitoids can eliminate the pests asymptotically, it is not practical to perform such a control strategy over a long period of time. In addition, the cost of implementing such a control is not considered in Section 2. To incorporate these, we investigate host–parasitoid interactions in the setting of optimal control over a finite time period in Section 3. The constant input of parasitoids is then treated as a control variable which varies from generation to generation and is not periodic. We use the theory of optimal control to minimize the pest population at the final time and the cost of the control over the entire time span. We numerically solve the optimal control problem based on the necessary conditions derived in Theorem 3.1 and compare the optimal pest populations with the host populations when no control is applied. On the other hand, since applying chemical agents to control pests is a common strategy, we also derive an optimal control model with a chemical agent as a control. We solve this optimal control problem numerically using Theorem 3.2. When the pests grow according to the Beverton–Holt mechanism, that is, when the pest population practices contest intraspecific competition, we obtain consistent conclusions that the chemical agent is the more effective control strategy than the biological control, independent of whether the cost associated with the control is small or large. See Figures 4 and 5. On the other hand, this finding is not conclusive when the pest population experiences scramble intraspecific competition. This is probably due to the erratic dynamical behaviour associated with the pest population. One can see from Figures 6–9 that the chemical agent is a more effective control strategy than the biological control when the cost B is small. However, the differences between the two methods are very small if the cost of implementing the control is larger and neither method appears to be efficient.

Figure 7. g(x)=e ^r(1−x), r=2.5, a=0.5 and T=10 for models (22) and (27). B=1 in (a) and (b) and B=5 in (c) and (d). Initial conditions are (x(0), y(0))=(5, 5). Plots (a) and (c) are for model (22) and plots (b) and (d) are for model (27).

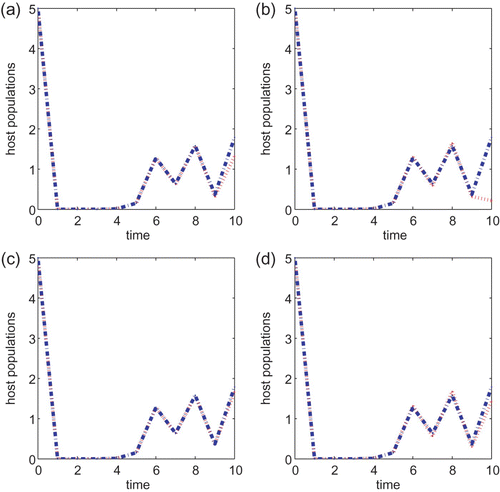
Figure 8. g(x)=e ^r(1−x), r=2.6, a=0.5 and T=10 for models (22) and (27). B=1 in (a) and (b) and B=5 in (c) and (d). Initial conditions are (x(0), y(0))=(5, 5). Plots (a) and (c) are for (22) while (b) and (d) are for (27).

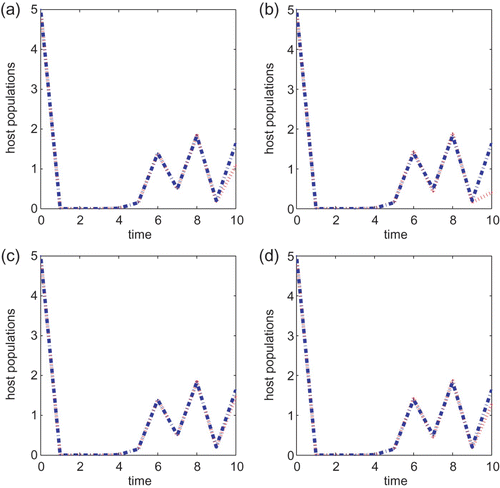
Figure 9. g(x)=e ^r(1−x), r=3.0, a=0.5 and T=10 for models (22) and (27). B=1 in (a) and (b) and B=5 in (c) and (d). Initial conditions are (x(0), y(0))=(5, 5). Plots (a) and (c) are for (22) while (b) and (d) are for (27).

One may conclude from this study that using a chemical control agent is a more effective control strategy than using a biological control. A biological control is more indirect. It relies on the parasitoids to suppress the pest populations. Although using the chemical control agent seems to be a more effective way for controlling the pests, the environment concern is not taken into account. Moreover, our host–parasitoid models are simple mathematical models. The conclusion obtained in this investigation may also depend on specific models and how the biological agents are incorporated into the model. Furthermore, one may also conclude from this investigation that it is harder to control the pests if the pests grow more eruptively.

Acknowledgements

The authors thank both referees for their comments and suggestions for improving the manuscript. S. Jang thanks Suzanne Lenhart for her comments on the original manuscript. S. Jang acknowledges the financial support from Mathematics Research Promotion Center, National Science Council of Taiwan, for her winter 2011–2012 visit to Taiwan.

Additional information

Notes on contributors

Jui-Ling Yu

Author Email: [email protected]