Predicting attenuant and resonant 2-cycles in periodically forced discrete-time two-species population models

Abstract

Periodic environments may either enhance or suppress a population via resonant or attenuant cycles. We derive signature functions for predicting the responses of two competing populations to 2-periodic oscillations in six model parameters. Two of these parameters provide a non-trivial equilibrium and two provide the carrying capacities of each species in the absence of the other, but the remaining two are arbitrary and could be intrinsic growth rates. Each signature function is the sign of a weighted sum of the relative strengths of the oscillations of the perturbed parameters. Periodic environments are favourable for populations when the signature function is positive and are deleterious if the signature function is negative. We compute the signature functions of four classical, discrete-time two-species populations and determine regions in parameter space which are either favourable or detrimental to the populations. The six-parameter models include the Logistic, Ricker, Beverton–Holt, and Hassell models.

Keywords:

• attenuance
• competition
• periodic forcing
• resonance
• signature function

AMS Subject Classifications:

• Primary: 37G15
• 37G35
• 39A28
• Secondary: 39A60
• 92B05

1. Introduction

Populations live naturally in changing environments in which variations caused by food availability, migrations, tidal patterns, and mating habits may be assumed to be cyclic or periodic. As a result, fluctuating environments are of particular interest to population biologists 2 3 6 10 15 16 22. For example, in the 1980 controlled laboratory experiments of flour beetles (Tribolium), Jillson observed that a periodic food supply generated cyclic oscillations within the beetle population. The alternating habitat in fact supported a larger beetle population, more than twice that of a constant environment even though the average flour volume remained the same 17 18. It has since been demonstrated that under certain conditions, periodic environments may be advantageous to a population and yet deleterious under others 5 9 11. In other words, the average of the resulting population oscillations in a periodic environment may either be greater or be less than, respectively, the average of the carrying capacities in an otherwise constant environment.

In constant environments, many discrete-time two-species models are extensions of single-species models that contain at least two parameters, usually the carrying capacity and a demographic characteristic 3–5. Examples of such single-species models include the Logistic, Ricker, Beverton–Holt, and Hassell models. In recent papers, Franke and Yakubu 11 12 have investigated the responses of classical, single-species, discrete-time models to periodic oscillations in two and three parameters. In this paper, we extend their investigations to study the responses of a two-dimensional system to periodic fluctuations in six model parameters and compare them against those elicited by a constant environment. More specifically, we analyse the effects that a 2-periodic forcing of six parameters has on a discretely reproducing two-species population model of a competitive type and investigate a 2-cycle population that bifurcates from the perturbed interior fixed point, which we refer to as the carrying capacity fixed point. We take a special interest in the case where the two species are very similar as might happen when a mutation occurs in a species.

Section 2 introduces a general framework for studying the impact of environmental fluctuations on a discrete-time two-species population model with six oscillating parameters. Here, we provide conditions sufficient for our unforced model to have a stable fixed point. In Sections 3 and 4, we impose 2-periodic forcing on the model and prove that small 2-periodic perturbations support 2-cycle populations. We study the 2-cycle that must, for small forcing, be close to the carrying capacity fixed point defined in Section 2.

In Section 5, we derive a signature function, ℛ _d , for determining whether the average total biomass is suppressed via attenuant stable 2-cycles or augmented via resonant stable 2-cycles. As in 11 12, ℛ _d is the sign of a weighted sum of the relative strengths of the oscillations of the carrying capacities and the remaining parameters. When these oscillations are small and the environment is 2-periodic, we prove that the average total biomass of the two-species system diminishes if ℛ _d is negative and is enhanced when ℛ _d is positive. Also in Section 5, we derive similar signature functions, 𝒮 _d and 𝒯 _d , for each individual species and determine the response that species makes to the periodic environment. We then obtain conditions on the relative strengths of the oscillations sufficient for obtaining positive or negative signature functions.

Furthermore, we establish that the relative strengths of the oscillations of this carrying capacity fixed point and the remaining four model parameters are critical factors in predicting how a two-species population responds to a periodic environment. We observe that changes in the relative strengths of the parameter fluctuations are capable of shifting population dynamics from resonant to attenuant 2-cycles or vice versa. It is known that this dramatic shift is not possible in single-species models with a single oscillating parameter 11 14 15. We illustrate these concepts in Section 6 by computing the signature functions of four discrete-time, competitive, two-species models and provide parameter regimes for the occurrence of stable attenuant and resonant 2-cycles that bifurcate from the carrying capacity fixed point. Finally, the implications of our results are discussed in Section 7, and the derivations of the signature functions are included in Appendix 1.

2. Two-species population models of six parameters

Most single-species ecological models contain two or more model parameters and so, by extension, many two-species ecological models contain at least four parameters 5 23. To study the combined effects of 2-periodic forcing on models with six parameters, we consider two-species population models of the general form

where x(t) and y(t) are the populations of each species at generation t. The per capita growth rates

where and . The parameters L and M play the role of carrying capacities for the system in that we assume that (L, M) is an interior fixed point of Model (1); that is, while S and T represent the boundary equilibrium points in that they are the carrying capacities of each species in the absence of the other; that is, . Finally, B and C are left as arbitrary model parameters, which are intrinsic growth rates in several of the example models given in Section 6. When the rate of change of the growth rate of one species with respect to that of the other species is negative, Model (1) is competitive 3 4 6. We assume that and are both negative at and thus say that our system is competitive at (x, y)=(L, M), the carrying capacity of the system.

To simplify the notation, we let for a pre-selected set of positive parameters . We can then define the function

by

Many of our results involve evaluating the Jacobian determinant of G at some population (x, y). Our notation is where

We frequently refer to the total biomass and the carrying capacity fixed point throughout our discussion. These are defined below.

Definition 2.1

The total biomass of the system defined by Model (1) refers to the sum of the x and y populations at the same generation: x(t)+y(t).

The interior fixed point, (L, M), of Model (1) is often globally attracting in our examples 23. This fixed point thus captures the idea of carrying capacity and we make the following definition.

Definition 2.2

The carrying capacity fixed point is the fixed point population, (L, M), of Model (1).

For each set of six positive constants , we define

by

and

We use these as the component functions for , where

The set of iterates of F is equivalent to the density sequences generated by Model (1).

One way to generate models of the type we are studying is to start with a one-species model:

where α is the intrinsic growth rate and k is the carrying capacity. Since k is the carrying capacity,

Taking as growth rates

induces a two-species system with six parameters that admits the interior point (L, M) as a carrying capacity fixed point. In this model, (S, 0) and (0, T) are also equilibria where it is assumed that S>L and T>M in keeping with a competitive model. This method is used to generate Table 1, which lists four specific classical examples of Model (1) from the literature.

Table 1. Examples of multiparameter population models.

Model number	Model, F(P(x, y))=	References
I		Logistic model 20
II		Ricker 21
III		Beverton–Holt (B, C>1) 1
IV		Hassell 13

The following result provides necessary and sufficient stability conditions whereby the carrying capacity fixed point is locally attracting for Model (1).

Theorem 2.3

The carrying capacity fixed point is a hyperbolic attracting fixed point of Model (1) if and only if

and

where all the partial derivatives are evaluated at P(L, M).

Proof

The derivative matrix of F(P(x, y)) evaluated at the carrying capacity fixed point, , is given by

and its two eigenvalues are found to be

where the partial derivatives are all evaluated at the carrying capacity fixed point. Because Model (1) is competitive at P(L, M), and and there are no complex eigenvalues.

If the carrying capacity fixed point is both hyperbolic and locally attracting, then the eigenvalues of Equation (4) lie entirely inside the unit circle, in which case

or, equivalently,

From this, we immediately obtain which is the first objective of the theorem. For the second objective, using the two inequalities in Equation (6) with −4 yields the two inequalities

Therefore,

After squaring both sides and subtracting, we have

which is . On the other hand, Equation (6) also gives

from which we obtain by squaring and subtracting.

For the reverse direction, first use to obtain

and thus

However, since , and so

Similarly, use to obtain

and therefore

This time use to obtain , and we have

From Equations (7) and (8), we can see that the eigenvalues, λ_{1, 2}, are inside the unit circle and (L, M) is indeed locally attracting.   ▪

A direct application of the inequalities in Theorem 2.3 to the four models in Table 1 yields the necessary and sufficient conditions for (L, M) to be a hyperbolic attracting fixed point presented in Table 2.

Table 2. Stability conditions for the six-parameter two-species models given in Table 1.

	Parameters giving stable carrying capacity, note with
Model number	B, C>1 in Model III
I	4ST>BLT+CMS, LT+MS>ST,
II	4ST>BLT+CMS, LT+MS>ST,
III	, LT+MS>ST,
IV	, LT+MS>ST,

3. 2-Periodic forcing

We introduce 2-periodic forcing into our model by having each parameter oscillate about its original value by fractional amounts. Let a, b, c, d, e, and f be the maximal fractional oscillations of L, M, S, T, B, and C, respectively. Model (1) becomes

To study the changing behaviour of our system as the fractional oscillations of B, C, S, T, L, and M vary from zero to their maximal amounts, we introduce three bifurcation parameters: . We are particularly interested in the case where the two species differ only slightly, as might happen after a mutation has occurred within one species. It is thus reasonable to assume that each term in the pairs (L, M), (S, T), and (B, C) behaves similarly to fluctuations in the environment, and the parameters , and γ are taken to be the fraction of the maximal oscillations of these pairs, respectively. This extends Equation (9) to our general, periodically forced model for this paper, Model (10),

where , , , , , and .

In Section 6, we study the four 2-periodically forced versions of the models listed in Table 1 to illustrate specific examples of Model (10).

When

and

then is a 2-cycle population for Model (10). Depending on the choice of parameters, 2-periodic dynamical systems may support attracting 2-cycles 7. In the next section, we obtain conditions for the asymptotic stability of the 2-cycle of Model (10) under the assumption that the 2-cycle must, for small forcing, be close to the carrying capacity fixed point.

Similar to Franke and Yakubu 7 8 11 12, if the carrying capacity fixed point, (L, M), is the source of a 2-cycle, we use the following definition to compare the average of the 2-cycle with the unforced total biomass.

Definition 3.1

A 2-cycle, of Model (10) is attenuant (resonant) if its average total biomass,

is less (greater) than the unforced total biomass M+L of the system 5 11.

A two-species population cycle of Model (10) is thus attenuant (resonant) if its average total biomass decreases (increases) in the advent of periodic forcing. If is a 2-cycle for Model (10), then and are each 2-cycles for the individual x-species and y-species. Analogous definitions of attenuance and resonance for a single-species 2-cycle of Model (10) are provided below.

Definition 3.2

A 2-cycle, or of a single species of Model (10) is attenuant (resonant) if its average value is less (greater) than L or M, respectively, the corresponding component of the carrying capacity of the system 5 11.

Attenuant and resonant cycles thus refer to a decrease and an increase, respectively, in average total population sizes.

4. 2-cycle population oscillations from unforced carrying capacity

Henson demonstrated that small perturbations of the food supply of a single species can generate 2-periodic population cycles of period two 14. Later, Franke and Yakubu 11 showed that small, 2-periodic perturbations of the carrying capacity and the demographic characteristic of discrete-time, single-species population models produce 2-cycle populations. In this section, we demonstrate that small, 2-periodic fluctuations of the six parameters in Model (1) can produce 2-cycle populations, , with x ₀ and x ₁ near L and y ₀ and y ₁ near M. That is, is near L+M. In a constant environment, this 2-cycle population reduces to the carrying capacity fixed point.

We simplify the notation again and let

in which case we can write . For a given set of perturbation values, maximal fractional oscillations, and parameters, we define

by

and

The orbit of an initial population, (x ₀, y ₀), governed by the 2-periodic model (10) is thus given by

In the absence of periodic forcing, , which is Equation (2). As a result, Model (10) reverts to the unperturbed system governed by Model (1) and the carrying capacity fixed point of Model (1) remains a fixed point of Model (10), provided that , and γ are all zero.

The following theorem provides conditions sufficient for Model (10) to produce a 2-cycle that is perturbed from the carrying capacity fixed point.

Theorem 4.1

Suppose

and

where all the partial derivatives are evaluated at P(L, M). Then, for all sufficiently small and , Model (10) has a 2-cycle population,

Furthermore,

and and are C ³ with respect to and γ. If the carrying capacity fixed point, (L, M), is asymptotically stable, then the 2-cycle is asymptotically stable.

Proof

Let

To prove this result, we must determine the fixed points of the composition map

where , , , , , , , , , and .

Note that . We must establish that when , the eigenvalues of are non-zero where I ₂ is the 2×2 identity matrix. Since Model (10) reduces to the unperturbed system of Model (1),

by the chain rule. In the proof of Theorem 2.3, the two eigenvalues of are found to be

where all the partial derivatives are evaluated at the carrying capacity fixed point. Because Model (1) is competitive, the product is positive and the system does not admit complex eigenvalues.

If is non-zero, then

and hence

From here, we obtain

On the other hand, if , where all the partial derivatives are evaluated at P(L, M), then

This leads to

and it is straightforward to check

Therefore, all of the eigenvalues of lie off the unit circle and the theorem follows from a direct application of the implicit function theorem 19.   ▪

Since the carrying capacity fixed point is a hyperbolic fixed point of F(P(x, y)) when the eigenvalues of its derivative matrix lie off the unit circle, the following consequence of Theorem 4.1 is immediate.

Corollary 4.2

If the carrying capacity fixed point of Model (1) is hyperbolic, then for all sufficiently small and Model (10) has a 2-cycle population,

where

and and are C ³ with respect to and γ. If the carrying capacity fixed point, (L, M), is asymptotically stable, then the 2-cycle is asymptotically stable.

By Corollary 4.2, Table 2 also describes parameter regions for the occurrence of an asymptotically stable 2-cycle in the four population models given in Table 1 under small period-two perturbations of the parameters near the carrying capacity fixed point. In Section 5, we derive an equation for the average total biomass of these 2-cycles.

5. Resonance versus attenuance: 2-cycle bifurcation from unforced carrying capacity

In single-species population models, small perturbations of a single parameter usually generate either attenuant or resonant cycles but not both, whereas small perturbations in single-species population models of two parameters can generate both attenuant and resonant 2-cycles that depend on the relative strengths of the fluctuations 11 14. We demonstrate that small perturbations of the six parameters in Model (1) generate both attenuant and resonant 2-cycles depending on the relative strengths of the fluctuations. As in the previous sections, we assume that the 2-cycle must, for small forcing, be close to the carrying capacity fixed point and that the model is competitive. For this 2-cycle, we derive a signature function, ℛ _d , for determining whether the average total biomass is enhanced via resonance or suppressed via attenuance. We also define signature functions, 𝒮 _d and 𝒯 _d , to determine how each individual species responds to the alternating environment.

When the carrying capacity fixed point, (L, M), of Equation (2) is hyperbolic, Corollary 4.2 guarantees that the 2-cycle solution of Model (10) may be expanded in terms of , and γ as follows:

where

and

are the expansion coefficients and and are the remainder terms. Since x ₀ and y ₀ are C ³ with respect to , and γ,

The expansion of the second point in the 2-cycle with respect to and γ is similar:

where

and

are the expansion coefficients and

The next two lemmas eliminate several of the coefficients in Equations (11) and (12) and establish the following expression for the average total biomass of the 2-cycle:

Similarly, the average biomasses of the individual populations of the x-species and y-species, respectively, are given by

and

Lemma 5.1

In Equations (11) and (12),

Proof

When α=0,

and

However, since α is the fraction of the maximal oscillation of the carrying capacities, the fixed points of and are both (L, M). Thus, for we have , and hence

This forces

  ▪

By this result, the coefficients of the relative strengths of and γ² in Equations (11) and (12) are zero. The next result establishes that the sum of the coefficients of the relative strengths of α in Equations (11) and (12) is also zero.

Lemma 5.2

If , then

Proof

We have

where , , , and . Similarly,

where , , , , , and . Therefore,

and

and we obtain

Adding produces

Likewise,

and

imply that

Adding produces

Solving Equations (13) and (14), we find

Since , we have

A similar calculation yields x ₀₁+x ₁₁=0.   ▪

Let

where

and

ℛ _d is the sign of a weighted sum of the relative strengths of the oscillations of the carrying capacity fixed point, the individual carrying capacities, and the two arbitrary model parameters. When u ₁=w ₁+v ₁, u ₂=w ₂+v ₂, and u ₃=w ₃+v ₃, a compact expression for ℛ _d is

Let

and

Both 𝒮 _d and 𝒯 _d are also the sign functions of a weighted sum of the relative strengths of the oscillations of the carrying capacity fixed point, the individual carrying capacities, and the two arbitrary model parameters. 𝒮 _d and 𝒯 _d may be written compactly as

In the following result, we show that ℛ _d indicates when the 2-cycle is either attenuant or resonant. Analogous results follow for 𝒮 _d and which describe the individual responses of the x-species and y-species, respectively, to a periodic environment.

Theorem 5.3

If the carrying capacity fixed point of Model (1) is hyperbolic, then for sufficiently small and Model (10) has an attenuant (a resonant) 2-cycle if ℛ _d is negative (positive).

Proof

Lemmas 5.1 and 5.2 establish that the average of the 2-cycle predicted in Corollary 4.2 satisfies

Since

and

the sign of

is the same as the sign of , which is ℛ _d . Thus, if

then the 2-cycle is resonant and if

the 2-cycle is attenuant.   ▪

Theorem 5.4

If the carrying capacity fixed point of Model (1) is hyperbolic, then for all sufficiently small and the x -species in Model (10) has an attenuant (a resonant) 2-cycle if 𝒮 _d is negative (positive).

Theorem 5.5

If the carrying capacity fixed point Model (1) is hyperbolic, then for all sufficiently small and the y -species in Model (10) has an attenuant (a resonant) 2-cycle if 𝒯 _d is negative (positive).

As demonstrated in Lemma 5.1, when both the individual carrying capacities, S and T, and the two arbitrary model parameters, B and C, are fluctuating but the parameters L and M are constant (i.e. α=0, β≠0, and γ≠0), the 2-cycle degenerates into a fixed point at the carrying capacity fixed point. However, if the carrying capacity fixed point, (L, M), is fluctuating while the remaining parameters are constant (α≠0, β=0, and γ=0), Theorem 5.3 gives the following result.

Corollary 5.6

If the carrying capacity fixed point of Model (1) is hyperbolic and the individual carrying capacities, S and T, as well as the two arbitrary model parameters, B and C, are all constant then for all sufficiently small

	(i)  and Model (10) has an attenuant (a resonant) 2-cycle if u 1 is negative (positive).
	(ii)  and the x -species in Model (10) has an attenuant (a resonant) 2-cycle if w 1 is negative (positive).
	(iii)  and the y -species in Model (10) has an attenuant (a resonant) 2-cycle if v 1 is negative (positive).

Population models with six parameters which are 2-periodically forced are capable of experiencing both resonance and attenuance. We formalize this in the following result.

Corollary 5.7

If the carrying capacity fixed point of Model (1) is hyperbolic, then for all sufficiently small and Model (10) has an attenuant 2-cycle and a resonant 2-cycle for different choices of and γ, provided that either u ₂ or u ₃ is non-zero.

Proof

If u ₂>0, take α>0, and γ=0. Then, and is negative. The 2-cycle is therefore attenuant. For a resonant 2-cycle, take and γ=0. If u ₂<0, take (), and γ=0 to obtain an attenuant (resonant) 2-cycle. Similar arguments establish the rest of the proof.   ▪

Analogous results hold for Model (10) when considering the x-species or y-species separately. In this case, either substitute w ₁, w ₂, and w ₃ or v ₁, v ₂, and v ₃ for u ₁, u ₂, and u ₃, respectively, in Corollary 5.7 to see that if either w ₂ or w ₃ is non-zero or either v ₂ or v ₃ is non-zero, then Model (10) is capable of generating both attenuant and resonant 2-cycles in the x-species or y-species, respectively.

6. Signature functions for classical models

In this section, we use our theorems to study the impact of the combined effects of fluctuations in the carrying capacities and in the arbitrary model parameters on the average total biomass of each population governed by the models given in Table 1. Appendix 1 provides more specific details for obtaining general formulas for ℛ _d , 𝒮 _d , and 𝒯 _d in terms of g ₁ and g ₂ and the partial derivatives of g ₁ and g ₂, all evaluated at P(L, M). Unfortunately, each of these formulas is much too long to be included, and for these reasons, we instead present some interesting results for the special case where B=C, S=T, and L=M.

Under these conditions, the growth rate functions of Equation (3) reduce to

from which it may be inferred that (S−L)/L must be close to 1 (with S<2L) in order for a subtle mutation to have occurred within the x-species, say. In this situation, the two competing species share many common features, such as carrying capacities and intrinsic growth rates, as could result from one species undergoing a mutation to produce a second competitive species with very similar characteristics. For less subtle mutations, L could increase from below to almost S and still maintain a positive carrying capacity in the model.

We observe what effects fluctuations in the parameters have on the total average biomass of the system as well as on each species. The signature functions are computed in order to investigate regions in the parameter space of attenuance and resonance of the 2-cycle which is perturbed from the carrying capacity fixed point.

In each model, the six constants a, b, c, d, e, and f are the maximal fractional oscillations of the six parameters, while the parameters S, T, L, and M are also consistent with the general periodically forced model (10). The arbitrary parameters B and C are regarded in the Logistic, Ricker, and Beverton–Holt (with B, C>1) models as inherent growth rates, but in the Hassell model, they are more complicated and are taken instead to be demographic parameters.

Recall that each model given in Table 1 is assumed to be competitive at the carrying capacity fixed point. This is realized if and only if and are both negative when evaluated at P(L, L), the carrying capacity in this special case. Finally, we continue with the notation of Model (10) by using

in the models.

6.1. Model I, Logistic

Both the carrying capacities and the inherent growth rates are 2-periodically forced in Model (10). Using the classic Logistic model, we obtain

According to Table 2, the carrying capacity fixed point in a constant environment is asymptotically stable as long as

and

In the special case when B=C, S=T, and L=M, these stability conditions become

Using the fact that C, T, and L are positive gives

For the Logistic model,

and its competitive condition is thus

Integrating this requirement into the above stability conditions gives

Note that 2CL−CT−2T=0 when C=2T/(2L−T) and, since L>2L−T>0, we obtain

Because is a concave up parabola in C, and C is less than the larger horizontal intercept, it must be less than the smaller one as well. Thus, the stability and competition conditions together reduce to simply

Under these conditions, Corollary 4.2 predicts a stable 2-cycle in Model (15).

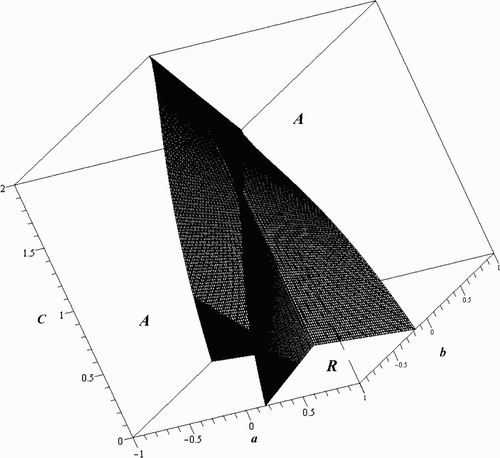
Since we are looking at the scenario where B=C, S=T, and L=M, we begin by considering the case where the maximal oscillations in these pairs of parameters are also equal; that is, when a=b, c=d, and e=f. The calculations discussed in Appendix 1 give

Since , the resonant and attenuant properties of the two individual species are exactly the same. On the stable region, C<2. Thus, if there is no fluctuation in the inherent growth rates (γ=0), then all three of the signature functions are negative on the stable region and we get attenuance of each species as well as of the total biomass. In contrast, we observe a resonant situation in the Logistic model when the fluctuations in the inherent growth rates are strong enough, namely when α>0 and

This is confirmed by Corollary 5.7.

Fluctuations in the components of the carrying capacity for the system (L, M), which is (L, L) in our special case, are of paramount importance and should be investigated if they are fluctuating differently. To study this case, we let c=d and e=f, but allow a and b to vary. This effectively synchronizes the fluctuations of the intrinsic growth rates and of the individual carrying capacities, but not the fluctuations of the carrying capacities of the system. Here,

which forces u ₂=0. This means that the resonance or attenuance of the total biomass is not a function of the fluctuations in the individual carrying capacities. Instead, w ₂ and v ₂ are functions of (a−b) and change sign when a=b. In particular, w ₂>0 when a>b, assuming that we are in the stable region.

When a≠b, the relationship between w ₁ and v ₁ is more complicated. They become 2-forms in a and b and are equal when , which lies inside the stable region. Their difference,

also changes sign when a=±b and has a negative denominator in the stable region.

The quantities w ₁ and v ₁ are functions of a, b, C, T, and L, but if we restrict to a given hyperplane, L=kT, the surface where is only a function of a, b, and C. Taking γ=0 and L=3T/4, the equation of the surface where u ₁=0 is

Figure 1 shows where the total biomass is resonant and attenuant within the stable region. One observation from the graph is that when a and b have opposite signs and C is small, we can be in a resonance region. Another observation is that the attenuance region is larger than the resonance region and includes all of the cases where a and b have the same sign.

Figure 1. Regions of attenuance and resonance in the a, b, and C plane for the 2-periodic Logistic model when γ=0 and L=3T/4.

6.2. Model II, Ricker

When both the carrying capacities and the inherent growth rates are 2-periodically forced as in Model (10), the classic Ricker model becomes

From Table 2, in a constant environment, the conditions needed for the carrying capacity fixed point to be asymptotically stable in the Ricker model are exactly the same as those in the Logistic model. Since the derivatives at the carrying capacity fixed point are also identical, the stable region for our Ricker model at B=C, S=T, and L=M is the same as that for the Logistic model:

To see how two slightly mutated populations governed by a Ricker-type model respond to an alternating environment, we let B=C, S=T, and L=M and then set the maximal oscillations in these pairs of parameters equal; that is, a=b, c=d, and e=f. The calculations obtained from Appendix 1 give

The similarities between the Ricker model and the Logistic model continue with w ₃, v ₃, and u ₃ being the same for both models.

Once more , and the resonant and attenuant dynamics of the two individual species are exactly the same. As with the Logistic model, if there are no oscillations in the inherent growth rates (γ=0), then all three of the signature functions are negative on the stable region (C<2), and we witness attenuance of each species as well as of the total biomass. Resonance is still possible in Model (16), provided the oscillations in the inherent growth rates are strong enough. According to Corollary 5.7, this occurs when α>0 and

Since b is the maximal fractional oscillation and α is the fraction of the maximal oscillation in the carrying capacity of the system, α b is the fractional oscillation in the carrying capacity of the system. Similarly, γ f is the fractional oscillation in the inherent growth rate. Thus, if α>0 and the fractional oscillation in the inherent growth rate is larger than the fractional oscillation in the carrying capacity of the system, then the 2-cycle of the Ricker model is resonant.

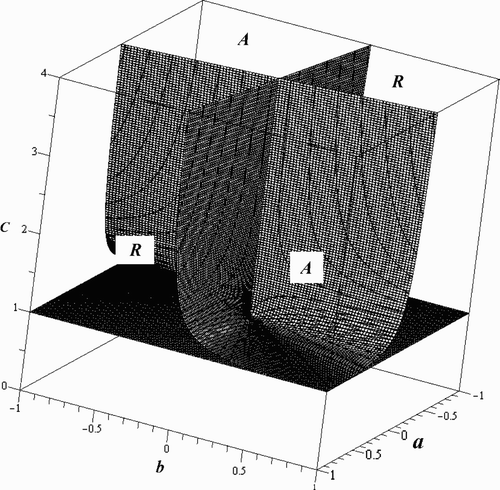
Oscillations in the components of the carrying capacity for this system, which is (L, L) in this scenario, are of particular importance and, if they are fluctuating differently, should be investigated. In this case, we let c=d and e=f but assume that a and b can be different. The formulas for w ₂ and v ₂ turn out the same as those in the Logistic model, where

Hence u ₂=0, and therefore neither the resonance nor the attenuance of the total biomass is a function of the fluctuations in the individual carrying capacities. Note that the denominator is positive in the stable region. From this formula, w ₂ and v ₂ are functions of (a−b) which change sign at a=b, giving w ₂>0 when a>b.

The relationship between w ₁ and v ₁ is no longer straightforward if a≠b. They are 2-forms in a and b and are equal when C=T/L, which belongs to the stable region. Their difference,

also changes sign when a=±b.

As in the Logistic model, w ₁ and v ₁ are the functions of a, b, C, T, and L. Restricting to a given hyperplane, L=kT, again reduces the surface where u ₁=0 to a more manageable function of three parameters, a, b, and C. To stay in the stable region, we must restrict 1/2<k<1, but the surface retains its same basic shape for this range of k. Taking γ=0, there are four distinct regions, two giving attenuance and two giving resonance. Taking γ=0 and L=3T/4, the equation of the surface where u ₁=0 is

Figure 2 illustrates where the total biomass is resonant and attenuant in the stable region. A comparison of Figures 1 and 2 indicates that the regions of attenuance and resonance for the Logistic model and Ricker model are very similar but not completely identical.

Figure 2. Regions of attenuance and resonance in the a, b, and C plane for the 2-periodic Ricker model for γ=0 and L=3T/4.

6.3. Model III, Beverton–Holt

If both the carrying capacities and the inherent growth rates are 2-periodically forced, as in Model (10), the classic Beverton–Holt model becomes

From Table 2, the carrying capacity fixed point, (L, M), is asymptotically stable in a constant environment, provided

and

Taking B=C, S=T, and L=M, these equations reduce to

Since C, T, L>0, we have

Note that the Beverton–Holt model requires L<T for competition because

Hence,

The factors (2C−1) and must have the same sign for stability. In the classic Beverton–Holt model, C>1, which implies or, equivalently, C>(2L−T)/2T. Inside the stable region,

Thus, the stability conditions together with the competition condition simplify to

Under these conditions, Corollary 4.2 predicts a stable 2-cycle in Model (17).

We are investigating the case where B=C, S=T, and L=M, and as before, we start by looking at the situation when the maximal oscillations in these pairs of parameters are also equal (when a=b, c=d, and e=f). The calculations in Appendix 1 give

Again, , and the resonant and attenuant properties of the two individual species are exactly the same. If there are no fluctuations in the inherent growth rates (γ=0), then all three of the signature functions are negative within the stable region (C>1), and we thus observe attenuance in each species as well as in the total biomass. Attenuance is also possible when γ is non-zero, as long as α and γ have the same sign. However, to observe a resonant response, α and γ must have opposite signs with

This is implied by Corollary 5.7.

Next, we consider the situation where the components of the carrying capacity for the system, (L, L) in this special case, might be oscillating differently, but the fluctuations of the remaining parameters are synchronized. We fix c=d and e=f, but allow a and b to differ. The simplest result in this case is

which has a positive denominator in the stable region. This gives u ₂=0, which means that the resonance or attenuance of the total biomass is not a function of the fluctuations in the individual carrying capacities. Instead, w ₂ and v ₂ are functions of (a−b) and change sign at a=b, with w ₂>0 when a>b. This is the same inequality we observe in both the Ricker and Logistic models.

As with Models (15) and (16), the relationship in the Beverton–Holt model between w ₁ and v ₁ is more complicated when a≠b as they are again 2-forms in both a and b. They are equal when , but, unlike the previous two models, this intersection does not lie inside the stable region. Their difference,

changes sign only when a=b or when a=−b. Therefore, the only time w ₁=v ₁ within the stable region is at a=±b.

The quantities w ₁ and v ₁ are still functions of a, b, C, T, and L. By restricting to a given hyperplane, L=kT, the surface where u ₁=0 reduces to one of three variables, a, b, and C. We must restrict 1/2<k<1 in order to remain inside the stable region, but we find that the surface maintains a similar shape for these values of k. If γ=0, there are four distinct regions, two giving attenuance and two giving resonance. Further taking γ=0 and L=3T/4, the equation of the surface where u ₁=0 is

Figure 3 reveals the locations in the stable zone where the total biomass is resonant and attenuant for k=3/4. One observation from the graph is that when a and b have the same sign, we are usually (but not always) in an attenuance region. For instance, when C is close to 1, there are positive values for a and b that give resonance. Another observation is that the resonance region is larger than the attenuance region. This is opposite of what we observe in the Logistic and Ricker models.

Figure 3. Regions of attenuance and resonance in the a, b, and C plane for the 2-periodic Beverton–Holt model with γ=0 and L=3T/4.

6.4. Model IV, Hassell

In the Hassell model, the B and C parameters are exponents. As a consequence, their roles are more complicated than in the previous three models but can be thought of as demographic parameters. When the carrying capacities and the demographic parameters are 2-periodically forced as in Model (10), the classic Hassell model becomes

According to Table 2, the carrying capacity fixed point is asymptotically stable in a constant environment whenever

and

In the special case where B=C, S=T, and L=M, these conditions simplify to

and

Because C, T, and L are positive, these conditions reduce further to

and

For this Hassell model,

and so its competitive condition must be

Hence,

For stability, the factors

must have the same sign, but are zero when C=(2T+2)/T and Since , we have

Each factor in Equation (19) is negative when C is below the two surfaces, but note that C<(2T+2)/L and so we must be below the middle surface. Thus, C< (2T+2)/T, and the stable region is defined by

Since we are considering the special case where B=C, S=T, and L=M, we start by taking the maximal oscillations in these pairs of parameters to be equal (taking a=b, c=d, and e=f). The formulas from Appendix 1 give

Once more , and the resonant and attenuant properties of the two individual species are identical. Note also that no longer is w ₂=0=v ₂.

The signs of w ₁, v ₁, and u ₁ change from negative to positive as C goes from below to above . Since , this sign change occurs inside the stable region. With β=0 and γ=0, we get attenuance in the stable region when C<(T+2)/T and resonance when C>(T+2)/T. This is in marked contrast to what we have seen in the first three models where only attenuance is observed. Since all of the remaining w ₂, v ₂, u ₂, w ₃, v ₃, and u ₃ are positive everywhere on the stable region, we get resonance in the stable region provided that , and γ are all positive and C>(T+2)/T.

Fluctuations in the components of the carrying capacity (L, M), which is (L, L) in our special case, are of particular importance and should be investigated if they are oscillating differently. We thus fix c=d and e=f, but assume that a and b can vary. This Hassell model gives results that are quite different from those obtained for our first three models. In particular, u ₂≠0 since w ₂≠−v ₂. Instead,

which is positive in the stable region if a+b>0 and negative when a+b<0.

The relationship between w ₁ and v ₁ is also more complicated than those of the other three models. This time both are different 2-forms in a and b and are equal on the surface:

which cuts through the model's stable region. Their difference,

also changes sign when a±b, meaning w ₁ and v ₁ are equal in the stable region if a=±b.

Where u ₁ changes sign is a function of a, b, C, T, and L. Unfortunately, when we fix a hyperplane, L=kT, the surface where u ₁=0 is now a function of a, b, C, and T. This would require a four-dimensional graph to illustrate and so we cannot provide one. The equation for the surface is a 2-form in a and b, but cubic in both C and T. One can analyse u ₁ to observe parameter regimes in its stable region inducing both attenuance and resonance.

7. Conclusions

Many experimental and theoretical studies predict that single-species populations may either be enhanced or suppressed by periodic environments 5 9 11 16 18. We derived a discrete, two-species, competitive, six-parameter model to investigate the effects of 2-periodic forcing of the parameters. Our investigation supports these predictions by establishing parameter regions where the total population is enhanced by the periodic forcing and other regions where it is suppressed.

Two of the parameters in the model give an interior fixed point which is globally attracting in many example models and acts as the system carrying capacity. The next two parameters are the carrying capacity of the individual species in the absence of the other. The remaining two parameters can be quite general, but in our specific examples, they are taken either to be intrinsic growth rates or to be more general demographic parameters.

The 2-periodic forcing is first realized by assuming that each of the six parameters has a maximal fractional oscillation. Next, we introduce three bifurcation parameters, in order to investigate the situation where the oscillations in the six model parameters range from zero to plus or minus the maximal oscillation. These three relative strengths of the oscillation parameters organize the six model parameters into three groups: the system carrying capacity, the two individual carrying capacities, and the two arbitrary parameters.

We proved that small 2-periodic fluctuations are capable of supporting 2-cyclic oscillations of the total biomass of the system and also of each species. We derived signature functions, ℛ _d , and for predicting the responses of the total biomass and of each of the two species to 2-periodic fluctuations in the six parameters. Each signature function is the sign of a weighted sum of the three relative strengths of the bifurcation parameters of the oscillations. Periodic environments are deleterious for the total biomass and for each species when the corresponding signature function is negative, but are favourable if the corresponding signature function is positive.

We applied these ideas to four models derived from the classic Logistic, Ricker, Beverton–Holt, and Hassell models and observed both attenuance and resonance in each model. We also observed that changes in the relative strengths of these fluctuations can shift a system from attenuance to resonance or vice versa. The resonance regions in the Logistic and Ricker models are quite similar and considerably smaller than their attenuance regions, as opposed to the Beverton–Holt model where the relative sizes of the regions are interchanged. The resonance and attenuance regions for the Hassell model are more complicated to picture, but in some sense, resonance is a more likely outcome than in the other three models. Special attention is paid to the situation where the terms in each pair of the three groups of model parameters are equal and have the same maximal oscillation. In this case, the two competing species share many common features as could result from one species undergoing a mutation to produce a second competitive species with very similar characteristics.

Our results indicate that the response of a population to a periodic environment is a complex function of the period of the environment, the carrying capacities of the two species, the demographic characteristic, and the type and nature of the fluctuations. These relationships, which affect the dynamics of populations living in periodic environments, are implicitly represented in the signature functions. Further investigations on these relationships and their biological implications are welcome.

Acknowledgements

We are grateful to the referees for the careful reading of this manuscript.

Appendix 1

Here, we outline the derivation of the formulas for w ₁, w ₂, w ₃, v ₁, v ₂, and v ₃ which determine u ₁, u ₂, and u ₃. From these coefficients, one may construct the signature functions derived in Section 5 in terms of , , g ₁, g ₂, and the partial derivatives of g ₁ and g ₂. This appendix ends with proofs for Theorems 5.4 and 5.5.

We apply the implicit function theorem to

as in the proof of Theorem 4.1. The four linear equations found in the proof of Lemma 5.2 are solved to determine the first derivatives of and at , which are

where all partial derivatives are evaluated at the carrying capacity fixed point.

Since

we have

Similarly,

implies

Therefore,

and

where all the partial derivatives are evaluated at P(L, M). Because we already have x ₀₁ and y ₀₁ in terms of , , g ₁, g ₂, and the partial derivatives of g ₁ and g ₂, we can view these as two linear equations in x ₀₁₁+x ₁₁₁ and y ₀₁₁+y ₁₁₁. These are solved to form

Similar procedures are performed to obtain formulas for

as well as

The signature functions can now be expressed in terms of , , g ₁, g ₂, and the partial derivatives of g ₁ and g ₂ via

Proof

[Proof of Theorems 5.4 and 5.5] Lemmas 5.1 and 5.2 establish that the average of the 2-cycle predicted in Corollary 4.2 satisfies the equation

Since

the sign of

is the same as the sign of which is 𝒮 _d . Therefore, if

then the 2-cycle is resonant, and if

then the 2-cycle is attenuant and similarly for Theorem 5.4.\vskip-0.5pc   ▪