Instability in a generalized Keller–Segel model

Abstract

We present a generalized Keller–Segel model where an arbitrary number of chemical compounds react, some of which are produced by a species, and one of which is a chemoattractant for the species. To investigate the stability of homogeneous stationary states of this generalized model, we consider the eigenvalues of a linearized system. We are able to reduce this infinite dimensional eigenproblem to a parametrized finite dimensional eigenproblem. By matrix theoretic tools, we then provide easily verifiable sufficient conditions for destabilizing the homogeneous stationary states. In particular, one of the sufficient conditions is that the chemotactic feedback is sufficiently strong. Although this mechanism was already known to exist in the original Keller–Segel model, here we show that it is more generally applicable by significantly enlarging the class of models exhibiting this instability phenomenon which may lead to pattern formation.

Keywords:

• chemotaxis
• Keller–Segel
• steady state
• stability
• pattern formation
• Turing instability

1. Introduction

Pattern formation is a fascinating area of biology with many unanswered questions. An early example is furnished by morphogenesis, which focuses on the following question: How can an initially spherically symmetric system, such as an embryo in early stages of development, lead to a creature as spherically asymmetric as a person, or an animal with a spotted coat? One of the first attempts to theoretically explain morphogenesis (by means of a mathematical model) was by Alan Turing. In 18, he proposed that an instability mechanism in specific systems of chemical reaction–diffusion systems is the underlying cause of morphogenesis by showing that under certain conditions on both the reaction and diffusion terms, some such systems which are stable without diffusion are destabilized with diffusion 13. Over time, pattern formation in various biological systems has been attributed to such Turing instabilities in systems of reaction–diffusion equations.

The main goal of this article is to present an alternate avenue potentially leading to pattern formation via chemotaxis. The key idea of this mechanism is already present in the well-known Keller–Segel model 11 (reviewed below), as elucidated by Schaaf 17. It relies on the destabilization via a chemotactic term of an otherwise stable uniform steady state. This mechanism of destabilization based on the chemotactic sensitivity is also analysed for the case of the two equation system in one spatial dimension in 19. In this article, we will identify a larger class of systems in higher spatial dimensions where a similar chemotactic destabilization mechanism may lead to pattern formation.

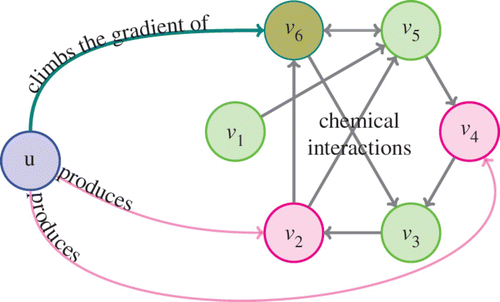
Chemotaxis occurs when the movement of a species is influenced by chemicals in the environment 9. It naturally arises in a wide variety of interesting biological settings, including cancer metastasis, angiogenesis, immune system function and egg fertilization 8. Considering reaction–diffusion systems with chemotactic terms, we show that there are quite general classes of chemical reaction networks (CRNs) which can be destabilized by means of an inherent feedback mechanism. The feedback arises as follows. A population of cells produces a chemical, which in turn participates in a CRN. The CRN leads to one or more chemical products. One of these products serves as the chemotactic signal for the cells, thereby completing the feedback loop. Under certain conditions this feedback loop has unstable homogeneous steady states which, in the absence of the feedback, would be stable. The destabilization of homogeneous stationary states, caused by the feedback mechanism built into the system, may give rise to pattern formation. As mentioned earlier, such a mechanism is already present in a simple CRN appearing in the well-known Keller–Segel model 11. In this model, the signal emitted by the cells is the same as the chemotactic signal, and it is subject only to decay. Since this CRN consists of a single decay reaction, it is perhaps one of the simplest possible CRNs. In this article, we find a larger class of CRNs with destabilizable homogeneous steady states.

To further explain the difference with the traditional destabilization mechanism, let us first review Turing's diffusion-driven instability for a two-species system (generalizations to multi-species systems are also well known), as explained in 14, using a reaction–diffusion system of the form

where d ₁ and d ₂ are positive diffusion coefficients. Here, u _t denotes and n (in ) denotes the outward unit normal on the smooth domain boundary . Assume the existence of a homogeneous steady state (u*, v*) of Equation (1). When the diffusion terms are ignored, we obtain the ordinary differential equation system corresponding to just the reaction terms:

We note that (u*, v*) is also a steady state of Equation (2) and we assume that it is linearly stable, i.e. we assume that the Jacobian matrix

has eigenvalues with a negative real part. (Again, derivatives are indicated by subscripts.)

The question Turing asked is whether (u*, v*), considered as a steady state of Equation (1), can be linearly unstable, even if it is a stable steady state of Equation (2). In other words, is it possible that the eigenvalue problem arising from linearizing Equation (1) at (u*, v*), namely

has an eigenvalue λ with positive real part? It turns out that a first necessary condition for this to happen is that d ₁≠d ₂, implying that both species must move with different diffusion constants. By an appropriate scaling we may assume, without loss of generality, that d ₁=1, and then a second necessary condition is that J has one of the sign patterns

with additional restrictions on d ₂ and Ω. The relevance of this sign pattern is that it imposes certain restrictions on how the species interact. For example, the first matrix implies that the first species activates itself and the second species, and that the second species inhibits itself, as well as the first species. A generalization of Turing-type instabilites to a system modelling an arbitrary number of chemicals can be found in 16.

The model that we propose for pattern formation on the other hand is a fully nonlinear reaction–diffusion system which also contains a nonlinear chemotaxis term. Destabilization of homogeneous steady states in our model does not require any restrictions on the diffusion coefficients, although we do impose some conditions on the sign pattern of the Jacobian corresponding to some of the reaction terms. These may, however, be less crucial than the role played by the chemotactic term.

The Keller–Segel model for chemotaxis is one of the most widely studied models. It was developed focusing on the cellular slime mold Dictyostelium discoideum. As explained in 9 11, the derivation of the Keller–Segel model is based on the aggregation stage of D. discoideum’s life cycle. The unicellular slime mould grows by cell division until it depletes its food source, and begins to enter a starvation mode. After some time, one cell will emit a signal of cyclic adenosine monophosphate (cAMP). The other cells are chemotactically attracted to this signal, and in turn begin to emit cAMP themselves. The cells also produce an enzyme which degrades the cAMP by first binding to it and forming a complex which in turn breaks up into the enzyme plus what we call a ‘degraded product’. To model this, the following assumptions are made in 9 11:

•	Let u(x, t) denote the cell density of the slime mold, v(x, t) the density of the chemoattractant cAMP, η(x, t) the density of the enzyme, c(x, t) the density of the complex formed by the binding of cAMP and the enzyme, and d(x, t) denote the density of the degraded product.
•	The chemoattractant is produced by the amoeba at a rate f(v) per amoeba and the enzyme is produced at a rate g(v, η) per amoeba, which, according to [11 is allowed to vary with both the chemoattractant and enzyme concentrations.
•	The chemoattracant, enzyme, and complex react as shown below. We assume that the reaction rates proceed according to the law of mass action. Accordingly, let the positive rate constants be denoted by r 1 (for the reaction ), r −1 (for the reaction ) and r 2 (for the reaction ).
•	The cAMP, the enzyme and the complex all diffuse according to standard Fick's law.
•	The cell concentration changes by random diffusion, as well by chemotaxis, due to the cells ‘climbing the gradient’ of the chemoattractant cAMP.

The last assumption is again modelled using Fick's law of diffusion, but with the amoebic flux J ^(u) consisting of a purely diffusive part and a chemotactic contribution, namely

for some chemotactic sensitivity function k ₂(u, v) and the diffusion constant k ₁. These assumptions lead to the full Keller–Segel model 9 on a bounded domain Ω for time t>0:

Here, k _v , k _η, and k _c denote the positive diffusion constants for cAMP, enzyme, and complex, respectively.

Keller and Segel 11 use a steady-state assumption to reduce the above set of four equations to a two-equation system which models only the density of the chemoattractant and the cell density. Further simplifications result in the so-called 8 9 ‘minimal system’,

This system has been studied extensively, and there are many results on local and global existence, positivity, and blow-up of solutions as well as steady states 8 9 15 17. Solutions that exhibit blow-up, defined as solutions for which the L ^∞-norm of u or v becomes unbounded in either finite or infinite time, have attracted considerable interest and are reviewed extensively in 9. (The blow-up phenomenon, restricted to a simplified Keller–Segel model, is also featured in [Chapter 5]15, which nicely illustrates the difficulties encountered when dealing with this complex issue in an elementary set-up.) One significant result is that in two dimensions, if then the solution to Equation (5) exists globally in time and its L ^∞-norm is uniformly bounded for all time [Table 5]9. On the other hand, if , then there exist initial data (u ₀, v ₀) for which the solution of Equation (5) blows up at the boundary of Ω in finite or infinite time [Table 5]9. Although the question of blow-up of solutions for our generalization of the Keller–Segel model is interesting, we do not address that issue in this article. Instead, here we focus exclusively on destabilization of homogeneous steady states.

Our work fits in the context of the more recent attempts to investigate multi-species, multi-chemical systems with chemotactic terms 3–6,10 12 20. Just as in the case of the Keller–Segel model, the blow-up phenomenon in these generalized models has received considerable attention 3 5 10 20. Of particular interest to the issue we address here is the recent work by Fasano et al. 6, Horstmann 10, and Liu and Wang 12. All articles consider the existence of non-homogeneous or periodic steady states, a signature of pattern formation for multi species models. In 6, a two-species two-chemical system is proposed where each species produces one of the two chemicals, which in turn serve as attractive chemotactic signals for the species that produce them. In addition, however, these chemicals are also chemotactic repellants for the species that do not produce them. The model is analysed for scalar spatial domains, and focuses on the existence of non-uniform and periodic steady-state patterns. Motivated in part by Fasano et al. 6, Horstmann 10 proposed an n species, m chemicals model where all chemicals are allowed to serve as chemotactic signals for the species, and the species themselves can chemotactically attract or repel each other. In addition, the chemicals may be produced and/or consumed by the species and, in principle, could react with each other in fairly general ways. Several natural questions that have attracted the attention of several researchers in the context of the Keller–Segel model are addressed in 10 for the multi-species, multi-chemical models. They include blow-up, global existence of solutions, existence and non-existence of non-uniform steady states, destabilization of uniform steady states as a way to achieve pattern formation, and the existence of Lyapunov functionals. Although 10 begins with this very general model, the focus of the article quickly turns to specific cases, motivated by the literature, where only a limited number of non-reacting chemicals (often just one or two) appear in the model. One notable exception is in [Section 3.1]10, where a one-species, two chemical system is proposed, where the two chemicals react in a non-trivial way. The model is inspired by work of 2, where an E. coli population is studied in the presence of two chemotactic attractants, namely glucose and oxygen. In 12 a system with two chemical agents is also considered, but in this case one is a chemoattractant while the other acts as a chemorepellent. In contrast, the emphasis of the work presented here is on possible pattern formation in models with several chemicals which react according to fairly general reaction networks, but only a single species that chemotactically responds to one of these chemicals.

In Section 2 of this article, we explain our generalized model and the system of partial differential equations which arises from it. In Section 3, we discuss conditions for the existence of steady-state solutions to the system in a special case. In Section 4 we state our main results, which give sufficient conditions under which steady states are unstable. Section 5 gives examples of theoretical biological systems which meet the conditions of our theorems and also provides a motivating example for generalizing our results.

2. The generalized model

In this section we present a generalization of the Keller–Segel model (5) where the modelled species interacts with several chemical compounds.

As before, consider a population of some species occupying Ω, an open bounded connected n-dimensional domain. Let the population density at a point x in Ω and time t be u(x, t). The population climbs the gradient of a chemical of concentration v _N . To model the more general and the more likely biological scenario, where this chemical is in reaction with several other compounds in the environment, we introduce the concentrations of N−1 other chemicals, denoted by (Figure 1). These chemicals can interact with each other as well as with v _N creating a CRN. Writing , we model the rate of change of due to the CRN by for some function . In applications, this function is often determined by mass action kinetics. Note that in general includes decay of the chemicals.

Figure 1. A schematic of the species (u) and the chemicals (v _i ’s) interacting.

Some of these compounds can also be produced by the species. To model this scenario, consider a general subset and assume that the species produce the chemical v _l at a rate for all l∈S. The remaining compounds are not generated by the species, so we set α _l =0 for l¬∈S. Let be the vector whose ith component is the α _i introduced above. Thus, the rate of change of would be governed by , in the absence of any diffusive effects.

However, we also want to account for spatial diffusion. In general, both the species population and the chemical concentrations diffuse. Assume that the diffusion coefficient for u is given by the constant D>0, and the diffusion coefficients for each v _i are given by the constants [Dtilde] _i >0. Let [Dtilde] be the diagonal matrix whose ith diagonal entry is [Dtilde] _i . Assuming that the chemotactic sensitivity function is χ u, for some constant χ>0, we arrive at our generalized model:

Here, we have assumed zero Neumann boundary conditions. The initial conditions u ₀ and v ₀ are assumed to be non-negative functions on Ω. Notice that upon integrating Equation (6a) over the domain and applying the divergence theorem and boundary conditions, we have

Hence, if u is sufficiently smooth we may interchange the integral with the differentiation with respect to time to conclude that the total population of the amoeba inside the domain is constant in time.

As an immediate example of an application of our generalized model, consider the unreduced Keller–Segel model (4) with the chemotactic sensitivity function and the rates f(v) and g(v, η) assumed to be constant. We change the notation to let v ₁ denote the density of the emitted enzyme, v ₃ the density of the chemoattractant cAMP and v ₂ the density of complex formed from the cAMP and the enzyme. Then setting

and

for constant rates α _i >0, we recover Equation (4) in the framework of our model.

In the following sections, we will examine the constant stationary states of the model (6). We will be especially concerned with conditions for the destabilization of such constant states.

3. Existence of homogeneous steady states

A steady state of our generalized model (6) satisfies

If the steady state is homogeneous, i.e. if it consists of spatially constant functions, then Equation (7c) obviously holds, and Equations (7a)–(7b) reduces to

Recalling that the total population of u is conserved, we note that the initial conditions will predetermine the value of u _*. A basic question is whether such non-negative constant steady states exist. In this section, we will answer this question in the affirmative, assuming a certain linearity condition on .

Before we do so, we need to introduce some terminology from matrix theory that we will use throughout. For any square matrix A, let ρ(A) denote the spectral radius of A. We write A≥0 for a real matrix (or vector) A if each entry of A is non-negative. Similarly, A>0 signifies that every entry of A is positive.

Definition 3.1

A Metzler matrix is a matrix having non-negative off-diagonal entries, i.e.

We will also need M-matrices, which can be defined in many equivalent ways. Following 1, we introduce the definition below.

Definition 3.2

A matrix is an M -matrix if it satisfies

	(1)
	(2) A ii ≥0.
	(3) There exists a non-negative matrix B≥0 and a number such that A=sI−B.

Clearly, if A is an M-matrix, then −A is a Metzler matrix. An M-matrix A is invertible if and only if there exists a B≥0 and s>ρ(B) such that A=sI−B. This is because by the Perron–Frobenius Theorem 1, the spectral radius of a matrix B≥0 is also an eigenvalue of the matrix. We will also need the following well-known result [p. 137]1:

Lemma 3.3

Suppose is non-singular. Then A is an M -matrix if and only if A ⁻¹≥0.

We are now ready to address the above-mentioned question of the existence of homogeneous steady states, under the assumption that each component of is a linear function.

Proposition 3.4

Suppose for some A in and . If A is a non-singular M -matrix, then for every positive constant u _*, there exists a unique non-negative homogeneous stationary solution of Equation (6). Conversely, A is a non-singular M -matrix if Equation (6) has a non-negative homogeneous stationary solution for every u _*>0 and every .

Proof

First, suppose that A is a non-singular M-matrix. Let u _* be any positive constant. Then setting

we observe that satisfies Equation (8). Hence satisfies Equation (7). Furthermore, by virtue of Lemma 3.3, so is a non-negative homogeneous stationary solution. For the given u _*, the component is uniquely determined. Indeed, if were another homogeneous stationary solution, then by Equation (8), . But by the invertibility of A and Equation (9), this implies . This proves the first assertion of the proposition.

Conversely, suppose is a non-negative homogeneous stationary solution obtained using u _*=1 and , the unit vector in the ith coordinate direction. Then, by Equation (8), . Letting C denote the matrix whose ith column is , this implies that AC=I, the identity. Hence A is invertible and, moreover, since , we have A ⁻¹=C≥0. Hence by Lemma 3.3, A is a non-singular M-matrix.   ▪

Having given a sufficient condition under which plenty of non-negative homogeneous steady states exist, we now proceed to study the stability of such states, assuming they exist. Note that we no longer assume that is linear in the ensuing analysis.

4. Instability of homogeneous steady states

In order to analyse the stability of a given homogeneous steady state , we begin by linearizing the spatial partial differential operator in Equation (6) about . Let λ be an eigenvalue of the linearized operator, i.e. λ satisfies

for some non-trivial pair of functions on Ω. Here, the N×N (Jacobian) matrix J denotes the Fréchet derivative of with respect to

i.e. evaluated at . The purpose of this section is to study the eigenvalue problem (10) and thereby find conditions under which the homogeneous state is unstable.

We will use the weak formulation of Equation (10), where u and the components v _i are all sought in the (complex) Sobolev space H ¹(Ω) consisting of square integrable functions whose first-order distributional derivatives are also square integrable. By definition of the weak eigenproblem, the number λ is an eigenvalue of the linearized operator if there exists a non-trivial in satisfying

for and for all ϕ in The integrals are with respect to the standard Lebesgue measure (omitted). The system (12) can be obtained from the classical formulation (10) by multiplying the equations of (10) by a test function ¯ϕ and integrating by parts, provided the boundary of the domain and the eigenfunctions are smooth enough. So as to admit irregular domains with possibly non-smooth eigenfunctions, we adopt the weak formulation (12) as the definition of our eigenproblem.

4.1. Reduction to finite dimensions

The first step in our study of Equation (10) proceeds by generalizing a method of Schaaf 17. This allows us to relate the eigenvalues of the infinite dimensional eigenproblem (12) to a finite dimensional eigenproblem. The latter is easier to analyse. The finite dimensional eigenproblem involves an matrix, written in block form as

where and μ is a real parameter. The parameter μ will always be set to one of the numbers

in the spectrum of the Laplace operator with Neumann boundary conditions, i.e. μ _i satisfies

where ω _i is the corresponding eigenfunction ω _i in H ¹(Ω), normalized to have unit L ²(Ω)-norm. With these notations, the reduction to finite dimension is achieved by the following result.

Theorem 4.1

The number λ solves the eigenproblem (12) if and only if it is an eigenvalue of M(μ _i ) for some integer i≥0.

Proof

Suppose λ satisfies Equation (12) with a non-trivial in . Then, since form a complete orthonormal set in L ²(Ω), it is possible to find an i such that not all of the N+1 numbers

are zero, i.e. the vector is non-trivial. Furthermore, choosing (with the above found i) in Equation (12), using Equation (13), and rewriting the resulting equations in terms of the numbers x _j , we find that

The matrix above is the same as M(μ _i ). Thus, we have shown that λ is an eigenvalue of M(μ _i ) with as its corresponding eigenvector.

To prove the converse, suppose λ satisfies

for some and some i. Then, setting

we find that the equations of (12) hold for any . Thus, λ is an eigenvalue of the linearized operator with the (non-trivial) pair as its corresponding eigenfunction.   ▪

Remark 1 Recalling that the mean of u in Equation (6a) does not vary with t, we may restrict ourselves while linearizing to perturbations U with . Suppose we also restrict the perturbations in V _k to be spatially non-homogeneous by imposing . Then, following the proof of Theorem 4.1, it is easy to see that λ is an eigenvalue of M(μ _i ) for some i≥1 if and only if it solves the eigenproblem (12) with the additional conditions for all k=1, …, N.

4.2. A sufficient condition for destabilization

We now focus on conditions under which the linearized operator has at least one eigenvalue λ in the right half of the complex plane. In such a case, the corresponding stationary state is called linearly unstable. In view of Theorem 4.1, we only need to study the eigenvalues of the parametrized matrix M(μ). Let us begin by reviewing a few useful results from matrix theory that we shall need. The following definitions and the next two theorems are well known – see e.g. [Theorems 1.4 and 2.35 in Chapter 2]1.

Definition 4.2

The directed graph G(A) associated to an N×N matrix A, consists of N vertices where an edge leads from V _i to V _j if and only if a _ij ≠0.

Definition 4.3

A directed graph G is strongly connected if for any ordered pair (V _i , V _j ) of vertices of G (with i≠j), there exists a sequence of edges (a path ) which leads from V _i to V _j .

Definition 4.4

A matrix A is called irreducible if G(A) is strongly connected.

Theorem 4.5 (Perron–Frobenius)

Let A≥0 be a square matrix.

	(1) If A>0, then ρ(A) is a simple eigenvalue of A, greater than the magnitude of any other eigenvalue.
	(2) If A is irreducible, then ρ(A) is a simple eigenvalue, any eigenvalue of A of the same modulus is also simple, A has a positive eigenvector corresponding to ρ(A), and any non-negative eigenvector of A is a multiple of .

Theorem 4.6 (Spectral radius bounds)

Let A≥0 be an irreducible N×N matrix. Letting s _i denote the sum of the elements of the i th row of A, define

Then the spectral radius ρ(A) satisfies

With the help of these well-known results, we can now give a sufficient condition for the destabilization.

Theorem 4.7

Assume that the system (6) has a positive homogeneous steady-state solution and let J be as in Equation (11). Suppose J and satisfy the following conditions:

	(1) There is an i * with such that α i * >0,
	(2) J is irreducible, and
	(3) J is Metzler.

Then, if either χ u _* or α _{i *} is sufficiently large, then is linearly unstable.

Remark 2 The biological interpretation of the first condition is that the organism must produce at least one of the chemicals in the reaction network. The second condition is a technical condition which we will relax in the next theorem. The third condition is the most restrictive of the conditions, but we give an example of a large class of CRNs for which it holds in Corollary 5.2. We also give examples of CRNs which do not meet condition three, but for which a similar result still holds (see Section 5).

Remark 3 For any fixed i _* we may rescale u _* by to rewrite Equation (7a) as

where . Then the condition on χ u _* or α _{i *} in Theorem 4.7 can be interpreted in terms of the single parameter C.

Proof

We use Theorem 4.1. Accordingly, it is enough to prove that M(μ _i ) has a positive eigenvalue λ for some μ _i . We will now show that for any μ<0, the matrix M(μ) has a positive eigenvalue under the given assumptions.

To this end, fix some μ<0, and set . Let

where r>0 is chosen large enough so that B has positive diagonal entries. Note that while both r and K are dependent on μ, r does not depend directly on the value of K (which may be changed by varying parameters other than μ). Note also that r is independent of . Then since J is Metzler, B is a non-negative matrix.

In fact, B is an irreducible non-negative matrix. To see this, consider the directed graph of J made of vertices . The graph G(B) is obtained after augmenting G(J) by a vertex corresponding to the first row and column, say V ₀, and adding vertex loops as needed to account for the positive diagonal of B. Since J is irreducible, G(J) is strongly connected. Moreover, since , we conclude that there is a path from V _j to V ₀ for any j. Similarly, since K>0, there is a path from V ₀ to V _j for any j. Hence, G(B) is strongly connected and B is irreducible.

We now claim that

The theorem follows from the claim. Indeed, since B is a non-negative irreducible matrix, ρ(B) is an eigenvalue of B by Theorem 4.5. Hence, by Equation (14), for large enough K, we can ensure that ρ(B)>r. But then, ρ(B)−r is a positive eigenvalue of M(μ)=B−r I. By the same reasoning, for large enough α _{i *} , the matrix M(μ) has a positive eigenvalue. Thus, in either case, the stationary state is unstable.

In the remainder of this proof, we establish the claim (14). To this end, let us denote by B ^t the transpose of the matrix B and note that for any integer m≥1,

Therefore, to prove that the first limit in Equation (14) is infinite, it suffices to prove that

for some integer m≥1, take the mth root, and use .

To prove Equation (15), we start by observing that the (i, j)th entry of (B ^t) ^m is

where the sums run over the ranges of the matrix indices . We choose these ranges to be 0, 1, …, N (instead of the customary 1, 2, …, N+1) so as to match the indices of the vertices of G(B). Since G(B ^t) is strongly connected, there is a path from V _i to V _j for any i and j of some length (number of connecting edges) l. Since B ^t has positive diagonal entries, each vertex of G(B ^t) has a loop and, consequently, if there is a path of length l, then there is a path of any length longer than l as well. Hence, there is a number m such that every two vertices in G(B ^t) are connected by a path of length m. With this m, consider the (i, 0)th entry of (B ^t) ^m , as given by Equation (16). Since there is a path connecting V _i to V ₀, say with i _m−1=N, we have from Equation (16) that

where is a positive and non-decreasing function of K (in fact a polynomial in K). Let C(K) denote the minimum of such C _i (K) for all 0≤i≤N. Then, the minimal row sum s(B) satisfies

so by Theorem 4.6,

Since C(K) is a non-decreasing positive function of K, letting K→∞, we prove Equation (15).

This proves that the first limit in Equation (14) is infinity. The proof that the second limit is also infinity follows in the same manner by finding, for each 0≤i≤N, a path of length m from V _i to V _i*.   ▪

4.3. Relaxing the irreducibility condition

As in the previous proof, let be the vertices of the G(J). One way to check the second condition (irreducibility) of Theorem 4.7 is to verify that there is a path from any V _i to V _j for all i≠j. In this subsection, we will give another condition involving only one path that is often easier to check.

Let us first recall some further terminology. A strongly connected component of a graph is a maximal strongly connected subgraph. Note that a strongly connected graph consists of exactly one strongly connected component. We consider the following equivalence relation on vertices of a graph: Two vertices V _i and V _j in a graph are equivalent if there is a directed path from V _i to V _j and a path from V _j to V _i . Then, the equivalence classes created by this equivalence relation consist exactly of the vertices of the strongly connected components of the graph. Keeping these in mind, recall the following definition of 1.

Definition 4.8

The classes of an N×N non-negative matrix A are the disjoint subsets corresponding to the vertices of the equivalence classes of G(A). We also identify a class with its strongly connected component.

If A is reducible, then by reordering the vertices, a permutation matrix P can be found so that

is a lower block triangular matrix with the blocks consisting of the classes of A (see 1). Since the classes of A are strongly connected, the diagonal blocks of T are irreducible. Using these facts, we can drop the irreducibility assumption in Theorem 4.7 and replace it with a weaker assumption as follows.

Theorem 4.9

Assume that the system (6) has a positive homogeneous steady-state solution and suppose that J and satisfy the following conditions:

	(1) There is an i * with such that (a) α i * >0, and (b) a directed path from V i * to V N in G(J t) exists.
	(2) J is Metzler.

Then, if either the product χ u _* or α _{i *} is sufficiently large, is linearly unstable.

Proof

As in the proof of Theorem 4.7, fix μ<0, choose r large enough so that B=M(μ)+r I has positive diagonal entries, and consider the graph G(B ^t) with vertices .

We proceed by identifying a cycle in the graph. Since , there is an edge from V ₀ to V _{i *} . Also, by our assumption, there is a path from V _{i *} to V _N . Moreover, since there is an edge from V _N to V ₀, thus completing a cycle. In particular, we have shown that V ₀, V _{i *} , and V _N are part of the same strongly connected component in G(B ^t).

Therefore, finding a permutation matrix P as in Equation (17), we conclude that there is a triangular matrix with a diagonal block T _j corresponding to the strongly connected component containing V ₀, V _{i *} , and V _N . Due to the strong connectivity, T _j is irreducible. Now, we can prove that

by repeating the arguments in the proof of Equation (14), because T _j is a non-negative irreducible matrix with a structure similar to the matrix in Equation (14).

Thus, for sufficiently large K or α _{i *} , the triangular matrix T has an eigenvalue larger than r, and so does B. Hence, M(μ)=B−rI has a positive eigenvalue.   ▪

5. Examples

In this section, we present several examples of how to use the theory developed in the previous sections. We consider the system (6) with a that describes the kinetics of some CRN linking the chemicals . In all the examples, is obtained by the laws of mass action kinetics.

Example

[(The linear case)]5.1 Suppose is linear, i.e.

for some N×N matrix A. This limits the network to reactions of the form v _i →v _j (‘v _i produces v _j ’), or (‘v _i decays’), but these component reactions can be combined arbitrarily.

Let us first observe a consequence of mass action kinetics. The reaction with a rate constant k _ji gives rise to an off-diagonal entry k _ji in the matrix A. Since the rate constants are non-negative, this implies that A must be a Metzler matrix.

If, in addition, we know that −A is a non-singular M-matrix, then Proposition 3.4 can be applied to conclude the existence of non-negative steady states.

To investigate stability, we proceed by studying the paths in the CRN and applying our previous results, as exemplified next.

Corollary 5.2

Assume that Equation (6) has a positive homogeneous steady-state solution . Assume that the kinetics of a CRN on the chemicals is described by a linear function which is obtained by the law of mass action kinetics. If, for some chemical v _{i *} , there is a path in the CRN from v _{i *} to v _N , and α _{i *} >0, then is linearly unstable whenever χ u _* or α _{i *} is sufficiently large.

Proof

We only need to verify the conditions of Theorem 4.9. View the CRN as a directed graph on vertices with an edge from V _i to V _j if and only if there is a reaction producing the chemical v _j from the chemical v _i . This graph, except possibly for diagonal loops, is exactly G(A ^t), where A is as in Equation (18). The linearity of also implies that the Jacobian J in Equation (11) coincides with A. Hence, the given path condition verifies Condition (4.9) of Theorem 4.9. We have already seen above that the assumptions of mass action kinetics imply that J=A is Metzler, thus verifying Condition (4.9) of Theorem 4.9.   ▪

Example

[(Dimerization and decay)]5.3 One of the simplest chemical reactions is dimerization or the reaction

Additionally, suppose the chemicals v ₁ and v ₂ decay at rates and γ₂>0, respectively. Let the rate constant for the forward reaction be k ₁>0, and of the reverse reaction be k ₂≥0. Then, according to the law of mass action kinetics, the function describing the CRN is

Finally, assume that a species of density u produces the chemical v ₁ at a rate of α₁>0, but does not produce v ₂ (α₂=0) and consider Equation (6) in this setting.

Recall from Section 3 that homogeneous steady states are solutions of Equation (8),

Let us verify that this system admits positive steady states. Note that upon adding them, the equations of (20) are equivalent to

Eliminating v ₂ from Equation (21a) using Equation (21b), we find that v ₁ satisfies

a quadratic equation which has a unique positive root whenever u>0. Letting r(u) denote this positive root, we find the family of homogeneous stationary states for this example:

We next turn to determining stability for this example. Clearly is not linear, so we cannot apply Corollary 5.2. However, we can apply Theorem 4.9. The Jacobian of evaluated at a positive homogeneous steady state is

where v _{*, 1} is the first component of . Then J is a Metzler matrix with a path in G(J ^t) from v ₁ to v ₂ since 2k ₁ v _{*, 1}>0. Hence, Theorem 4.9 implies that any positive homogeneous steady state of Equation (6), with the above , can be destabilized for large enough values of χ u _* or α₁.

Notice that the Metzler matrix J above has two negative eigenvalues (since the trace of J is negative, and the determinant is positive). Therefore, the CRN by itself (without the introduction of chemotaxis) is stable. However, once we introduce chemotaxis, the arguments above show that with a high enough chemotactic sensitivity (χ u _*), or a high enough chemical production by the species (α₁), the stable system can be destabilized.

Example 5.4 Now we give an example where a hypothesis of Theorems 4.7 and 4.9 fails. Nonetheless, we can analyse the system by applying Theorem 4.1.

Consider a reaction of the form

where the rate constants of the forward and backward reactions are given by k ₁>0 and k ₂>0, respectively. Again, assume that a species of concentration u produces only the chemical v ₁ at a rate α₁>0 and assume decay rates γ _i and production rates α _i of chemical v _i satisfy

Then the function describing the reaction network is

To verify that positive steady states exist, we look for u>0 and satisfying

Notice that the third equation of is omitted because it is the same as the second up to the sign. By subtracting Equation (23a) from Equation (23b), we obtain the equivalent system

From these equations it is clear that

is a positive solution of Equation (23).

Having verified that positive steady states exist, we turn to determine their stability. The Jacobian of the function evaluated at a positive homogeneous steady state is

Since J is not Metzler (J ₁₂, J ₂₁<0), a hypothesis of Theorems 4.7 and 4.9 fails.

However, by virtue of Theorem 4.1, the linearized stability of steady states is determined by the eigenvalues of the matrix

as μ varies over the spectrum of the Laplace operator. Fix any μ<0 and let .

First consider the case K=0, when there is no chemotactic term. Then, M(μ) is block triangular and its eigenvalues are μ D<0 and those of its next diagonal block, which can be expressed as

using the positive numbers and Its characteristic equation is

We apply the Routh–Hurwitz criterion 7, which says that all solutions of the characteristic equation have negative real part if and only if the following inequalities hold:

The first two are immediate. The third can be verified after some calculations: every term in the product b ₁ b ₂ is positive, and every term in b ₀ cancels some term (but not all terms) in b ₁ b ₂. Hence, for any μ<0 all eigenvalues of M(μ) have negative real part.

We next turn to the case where K>0. Using cofactor expansion along the first row, we can compute det M(μ) to be

where C=−μ D b ₀ is the determinant of the matrix M(μ) in the case K=0. Clearly, C>0 is independent of K. Simplifying and identifying the K dependence,

where . Hence, there is a K ₀>0 such that for all K≥K ₀.

To conclude, we claim that M(μ) must have a negative eigenvalue when K≥K ₀. If all eigenvalues of M(μ) are real, the claim is obvious. If not, complex eigenvalues occur in conjugate pairs, so in order that their product is negative, at least two of the four eigenvalues must be real. Furthermore, these two real eigenvalues must have opposite signs to satisfy .

Therefore, for all sufficiently large values of K, the steady state is linearly unstable.

Acknowledgements

This work was partially supported by the NSF under grants DMS-0818050, DMS-1014817 and DMS-1211635. PDL wishes to thank the VLAC, the Flemish Academic Centre for Science and the Arts, for hosting and supporting him during a sabbatical leave from the University of Florida, the Université Catholique de Louvain-la-Neuve for awarding him a visiting professorship in the fall of 2011, and the University of Florida for a Faculty Enhancement Opportunity (FEO) fund.