Difference equations with the Allee effect and the periodic Sigmoid Beverton–Holt equation revisited

Abstract

In this paper, we investigate the long-term behaviour of solutions of the periodic Sigmoid Beverton–Holt equation

where the a _n and δ _n are p-periodic positive sequences. Under certain conditions, there are shown to exist an asymptotically stable p-periodic state and a p-periodic Allee state with the property that populations smaller than the Allee state are driven to extinction while populations greater than the Allee state approach the stable state, thus accounting for the long-term behaviour of all initial states. This appears to be the first study of the equation with variable δ. The results are discussed with possible interpretations in Population Dynamics with emphasis on fish populations and smooth cordgrass.

Keywords:

• periodic difference equation
• global stability
• Sigmoid Beverton–Holt
• Allee states

AMS Subject Classification :

• 39A23
• 39A30
• 92D25

1. Introduction

In this paper, we investigate the long-term behaviour of solutions of the periodic Sigmoid Beverton–Holt (or Holling Type III, 15) equation

where the a _n and δ _n are p-periodic positive sequences. In a recent ground-breaking publication by Harry et al. 14, an extensive study has been made on the case and a rich source of references on the subject has been presented. Technically, the term ‘Sigmoid’ applies only to the case in which δ>1 where the graph of what we call the Sigmoid Beverton–Holt function,

has the characteristic ‘S’ shape, the slow rise from zero, a rapid rise, and then flattening out for large x. This shape is especially interesting in discrete dynamics when for ‘a’ sufficiently large, it gives rise to the famous Allee effect in which small populations are driven to extinction. This is of paramount importance in the management of fisheries and establishment of safeguards against overfishing 2 19. Stephens and Sutherland 25 described several scenarios that cause the Allee effect in animals. For example, cod and many freshwater fish species have high juvenile mortality when there are fewer adults. Fewer red sea urchins give rise to worsening feeding conditions of their young and less protection from predation. In some mast flowering trees, such as smooth cordgrass, Spartina alterniflora, a low population density results in lower probability of seed production and germination 5. In Section 7, some possible implications of our results in Population Dynamics are given. In particular, our theoretical results are in agreement with the fact that the maximum tolerable depensation can vary with time in the study of fish populations and the observed Allee effect 5 in smooth cordgrass could be modelled with a periodic system such as the one studied here.

See 9 for a discussion of some new examples of models exhibiting the Allee effect and, similar to the Beverton–Holt model, having important biological quantities as parameters, for example, intrinsic growth rate, carrying capacity, Allee threshold, and a new parameter, the shock recovery parameter. Further references pertaining to the Allee effect can be found in 1 3 4 6,10–12,16–18,23 26 31 32, and for references to the general theory of difference equations, see 7 20. For a discussion on the use of the Sigmoid model, see [p. 82]28

In what follows, we show that under certain conditions on the coefficients, Equation (1) has an asymptotically stable p-periodic state and an unstable p-periodic Allee state. With the aid of a Skew-Product Dynamical System, we also show that all initial states smaller than the Allee state go extinct, while all initial states larger than the Allee state approach the asymptotically stable p-periodic state.

Throughout the paper, we use the notation and . Also ‘increasing’ shall always mean strictly increasing and similarly for decreasing. Also, by , we mean the space of continuously differentiable functions from ℝ⁺ to ℝ⁺.

2. Stable periodic orbit

The model that we consider is the p-periodic iterated mapping

on ℝ⁺ where f _n =f _n+p , n=0, 1, …. In particular, we are interested in the case when are Sigmoid Beverton–Holt functions, although we will also have occasion to consider other functions f _n . We are interested in establishing the existence of a positive periodic orbit

that is asymptotically stable and attracts all orbits for which x ₀ lies in some interval (B, ∞). It is well known that this is equivalent to showing the existence of a fixed point s ₀ of the mapping given by

that has the same stability properties.

It is also known 8 21, but not fully appreciated, that the concept of a semigroup plays a key role in the study of periodic difference equations. To illustrate this fact, we begin by disposing of the case in which all .

Theorem 2.1

Suppose in Equation (2) that with and has the property that a _n >1 whenever δ _n =1. Then, there is a periodic orbit (3) that is asymptotically stable and attracts any orbit for which .

Proof

It has been shown in [p. 272]8 that the set of all functions from ℝ⁺ to ℝ⁺ that are continuous, non-decreasing, concave, and whose graph crosses the diagonal on forms a semigroup under composition. Moreover, for any function f in this set, the value of where the graph crosses the diagonal is a fixed point of the iterated mapping that attracts any orbit for which . It is easy to see, under the hypotheses of the theorem, that the functions f _n belong to this set, so, by the semigroup property, their composition must also belong to this set. The positive fixed point of F corresponds to a periodic orbit of Equation (2) that is asymptotically stable and attracts any orbit for which .   ▪

When at least one of the δ _n ’s is greater than 1, the existence of a positive asymptotically stable periodic orbit (3) is more subtle. In order to state conditions on the parameters under which such an orbit is guaranteed to exist, we first explore the nature of the autonomous iterated mapping for different values of the parameters (see also 14 for helpful illustrations).

It is clear that every Sigmoid Beverton–Holt function f _{a, δ} is increasing, goes through the origin, and . When 0<δ<1 and a has any positive value or when δ=1 and a>1, the graph is concave everywhere and there is a unique fixed point that is asymptotically stable on . When δ=1 and 0<a≤1, the graph is concave everywhere but lies below the diagonal, so x=0 is the only fixed point and it is globally asymptotically stable. When δ>1, the function is convex on (0, x ^infl) and concave on where the inflection point is given by

Note that x ^infl depends on δ alone. Also, and as . It has been shown in 14 that there is a critical value of a given by

at which a saddle-node bifurcation takes place. Namely (Figure 1),

	(1) for , the entire graph of , , lies under the diagonal y=x so that the origin is globally asymptotically stable, while
	(2) for , the graph of is tangent to the diagonal at a semi-stable fixed point, and
	(3) for , the graph of intersects the diagonal at two fixed points: the Allee threshold A f and the carrying capacity K f . The origin is exponentially asymptotically stable and attracts all orbits for which x 0∈[0, A f ), the Allee threshold A f is unstable, and K f is exponentially asymptotically stable and attracts all orbits for which .

Figure 1. Bifurcation as a increases for fixed δ>1.

Also of significance is the x value of the bifurcation point as a function of δ, . At the bifurcation point, the graph of f intersects and is tangent to the diagonal. Thus, x ^bif is the solution to the simultaneous equations

Dividing the first by the second and simplifying, we obtain the rather simple expression

Clearly, for all δ>1 and . However, the relative sizes of and A _f depend on the size of a. We denote by the value of a where . At this value, we have

Solving yields

Note that for all δ>1. If , then , and if , then . Figure 2 shows plots of x ^infl and x ^bif as functions of δ and Figure 3 shows plots of and a ^crit as functions of δ.

Figure 2. Bifurcation point: the point x at which the graph of is tangent to the diagonal. Inflection point: the point (independent of a) at which the graph of f _{a, δ} changes from convex to concave. The intervals 1.5 2 3 7 are examples of intervals I such that if δ _n ∈I for all n, then condition 8 of Corollary 2.5 is met.

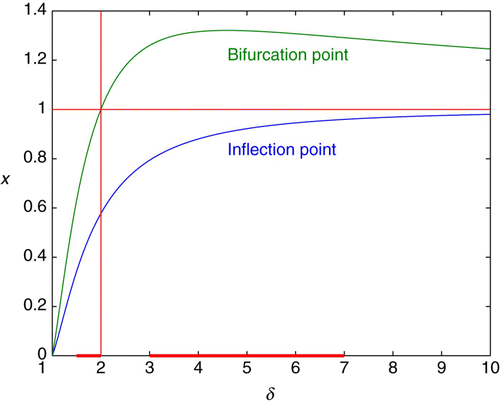
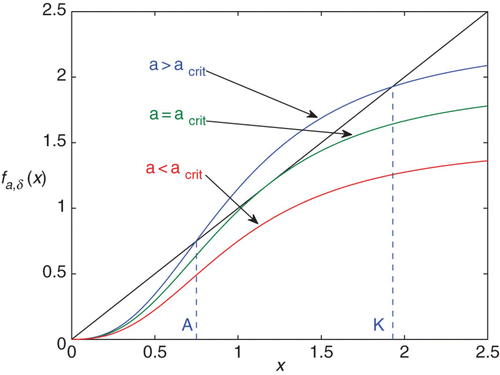
Figure 3. a ^crit: for a>a ^crit, f _{a, δ} has an Allee point A _f and carrying capacity K _f .\newline a ^allee: for a>a ^allee, x ^infl<A _f , so f _{a, δ} is convex on (0, A _f ).

In all of our theorems, we will only be concerned with those Sigmoid Beverton–Holt functions that have a positive asymptotically stable fixed point, in other words those for which δ<1 and a has any value, or δ=1 and a>1, or δ>1 and . To specify these concisely, we define for δ<1 and for δ=1. The maps that we are interested in are then those f _{a, δ} for which .

Harry et al. 14 obtained the following result concerning the existence of a positive asymptotically stable periodic orbit of Equation (2) in the δ _n = constant case.

Theorem 2.2

[14, Theorem 8] Let be fixed and be a p -periodic sequence satisfying . Suppose

Then, there exists and a periodic orbit (3) that is asymptotically stable and attracts all orbits for which .

Since δ>1 is constant in this theorem and , hypothesis (6) is unnecessary. In addition, we will show in Theorem 2.4 that any orbit for which x ₀>A _max is asymptotic to the periodic orbit. Thus, the theorem can be restated as follows.

Theorem 2.3

Let δ>1 be fixed and be a p -periodic sequence satisfying , . Then, there is a periodic orbit (3) that is asymptotically stable and attracts all orbits for which .

In Section 5 we will further improve the condition . We will prove the following theorem in Section 3; it will be a direct consequence of a more general theorem that we prove there. It is considerably stronger than Theorem 2.3, since it allows δ _n to vary.

Theorem 2.4

Let and be p -periodic sequences in such that , for . Let and define

and suppose

Then, there is a periodic orbit (3) that is asymptotically stable and attracts all orbits for which . In addition, the entire orbit (3) lies in the interval .

Since we do not have simple formulae for A _f and K _f , the hypotheses in the theorem given above may need to be verified numerically. The following corollary is weaker than the theorem, but the hypotheses are easily verifiable analytically, since we have formulae for all of the relevant quantities in terms of a _n and δ _n .

Corollary 2.5

Let and be p -periodic sequences in such that δ _n >1 and , for . Define

and assume

Then, there is a periodic orbit (3) that is asymptotically stable and attracts all orbits for which .

Proof

Since δ _n >1 and , we know that for all n. It follows that

and

Thus, by the hypothesis of the corollary, , and the result follows by the theorem.   ▪

Remark 1 Condition (8) in the corollary is a condition on the δ’s alone. This condition says that the δ’s must lie in an interval in which the highest point on the inflection point graph is lower than the lowest point on the bifurcation graph. For example, it is clear from Figure 2 that this condition is satisfied if for all n. As another example, if for all n, then the highest point on the inflection point graph is and the lowest point on the bifurcation graph is , so again this condition is satisfied.

3. A general theorem

In this section, we prove a general theorem that will have Theorem 2.4 as a corollary.

Given r≥0, define ℱ _r as the set of all continuous functions that have the following properties:

	(1) .
	(2) There exists a number B≥r such that f(B)>B and f is increasing and concave on (B, ∞).
	(3) There exists a number x*>B such that f(x*)<x*.

For , define , where the infimum is taken over all B satisfying (2). Note that B _f ≥r, , and f is increasing and concave on .

Lemma 3.1

For each function , the iterated mapping given by

has a unique fixed point K _f on the interval . This point is asymptotically stable and attracts all orbits for which .

Proof

We first prove uniqueness. Suppose x ₁<x ₂ are fixed points on . Choose B such that and f(B)>B. Choose t such that . Since f is concave on (B, x ₂),

a contradiction. The existence follows from (2) and (3) and the intermediate value theorem. To show the asymptotic stability of K _f , note that x<f(x)<K _f for and K _f <f(x)<x for . Thus, the sequence defined by Equation (9) is increasing and bounded above by K _f when and decreasing and bounded below by K _f when . It follows that the sequence converges. By continuity, the limit is a fixed point and by uniqueness it must be K _f .   ▪

There are two important observations to be made about . The first is the role of the number r. Since every function in maps the interval [r, ∞) into itself, the autonomous iterated mapping (9) can be restricted to the set [r, ∞). Moreover, because this interval is common to all the functions in , the p-periodic iterated mapping (2), where , can also be restricted to [r, ∞). Each function also has other intervals that map to themselves, namely [B, ∞) for any number B satisfying (2). However, the p-periodic iterated mapping cannot necessarily be restricted to any subset of [r, ∞), since there may not be a number B that is common to all of the f _n ’s.

The second observation already came out in the proof of Lemma 3.1, but it will be used again, so we point it out explicitly. Given any function , x<f(x)<K _f for and K _f <f(x)<x for .

3.1. A new class of mappings

Given r≥0 and , we define the class

Theorem 3.2

is a semigroup under the operation of composition of maps. Moreover, for any and K _{f ° g} lies on the closed interval with endpoints K _f and K _g .

Proof

Let be given. We first show that f ° g lies in .

	(i) Since f and g both map [r, ∞) to itself, f ° g does as well.
	(ii) Let B be any number such that . Since , g(B)>B, and since f is increasing on [B, ∞), it follows that . Now, since , f(B)>B. Thus, . Moreover, f and g are both increasing and concave on (B, ∞), and since g(B)>B, this interval is invariant under g, so f ° g is also increasing and concave on this interval.
	(iii) We show that there exists a number x*>B such that .
	Case 1: Suppose there exists x>B such that g(x)>K f . Since g is increasing on , this will be true for all sufficiently large x. Choose x* so that g(x*)>K f and x*>K g . Then, x*>B, and since g(x*)>K f , , which, in turn, is less than x*, since x*>K g .
	Case 2: Suppose g(x)≤K f for all x>B. In this case, choose x* to be any number larger than K f . Then, x*>B, and since and f is increasing on (B, ∞), .

Thus, f ° g lies in . Once we have established that and that K _{f ° g} lies between K _f and K _g , it will follow immediately that . The former is immediate because we have seen that any number B that lies between and has the properties in (2). To show the latter, there are three cases.

Case 1

Suppose K _f <K _g . Then, , so . Similarly, , so g(K _f )>K _f , and f is increasing on , so . Thus, .

Case 2

Suppose K _f >K _g . Then, , so . Similarly, , so g(K _f )<K _f , and f is increasing on , so . Thus, .

Case 3

Suppose K _f =K _g . In this case, . Thus, K _f =K _g is a fixed point of f ° g, so by uniqueness it must be K _{f ° g} .   ▪

3.2. Proof of Theorem 2.4

It is easy to see that every Sigmoid Beverton–Holt function with lies in ℱ₀ and B _f =0 if δ≤1 and if δ>1. Choose l so that . This is possible by the hypothesis of the theorem. Then, for all n. It follows by Theorem 3.2 that and that . Thus, by Lemma 3.1, F has a unique fixed point on the interval that is asymptotically stable and attracts all orbits for which . This fixed point corresponds to a periodic orbit of the non-autonomous system (2) with the same stability properties.

Since , it follows immediately that this periodic orbit attracts all orbits for which . However, if , we still need to show that the periodic orbit attracts all orbits for which . To this end, let such a point x ₀ be given and let denote its orbit under Equation (2). To show that this orbit is attracted to the periodic orbit, it suffices to show that there exists such that .

Note first that if x _n >K _min, then , and if x _n ≤K _n , then , and if x _n >K _n , then . Moreover, if , then A _n <x _n <K _n , so . Thus, there are two possibilities: the first is that there exists such that x _n >K _min and the second is that for all n. In the former case, for all m≥n, so the result follows. In the latter case, is an increasing sequence that is bounded above and therefore has a limit. By continuity, the limit is a fixed point of F. But the observations that we have just made show that for any , F(x)>x, so the limit must be and the result follows.

To show that the entire orbit lies in , we use induction. From Theorem 3.2,

Assume, as an induction hypothesis,

Applying Theorem 3.2 to f _m+1 and , we get

From the inductive hypothesis, it follows that

This shows that . To show that the entire periodic orbit lies in , note that and apply a similar argument.

4. Allee periodic orbit

We saw in Theorem 2.4 that inside the envelope of the carrying capacities, there is an asymptotically stable periodic state. A similar result is obtained for the Allee thresholds. For b>0, define

Note that each function has a unique unstable fixed point A _f ∈[0, b) such that any orbit of the autonomous iterated mapping for which x ₀∈[0, A _f ) converges to 0.

Theorem 4.1

Consider a finite collection of functions . Define

The periodic iterated mapping (2) has a positive unstable p -periodic orbit such that all orbits for which are attracted to 0. We call this orbit the Allee periodic orbit of the iterated mapping.

Proof

Define

and let . Note that for all n and recall that U _{0, 0} is a semigroup under composition. (See Section 3.1 for the definition and properties of U _{0, 0}.) Moreover, and . It follows that the iterated mapping has a unique stable periodic orbit that attracts all orbits for which . The fact that follows by an induction argument similar to that used in the proof of Theorem 2.4. Thus, where is an unstable p-periodic orbit of the iterated mapping and any orbit for which is attracted to 0. Since f _n =F _n on [0, b] and for all n, α is also a periodic orbit of and any orbit of this iterated mapping for which is attracted to 0.   ▪

4.1. Application to the Sigmoid Beverton–Holt equation

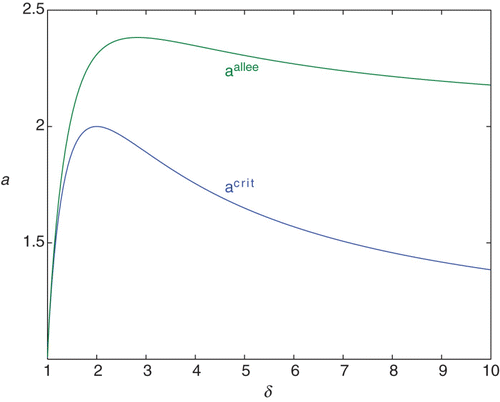
Recall the definition of in Equation (5), the value of a as a function of δ at which the inflection point and Allee threshold coincide. Its graph is shown in Figure 3. If for , each Allee threshold lies on an interval of convexity of the graph of f _n . Thus, if we assume

then each where , see Figure 4. Thus, we have the following.

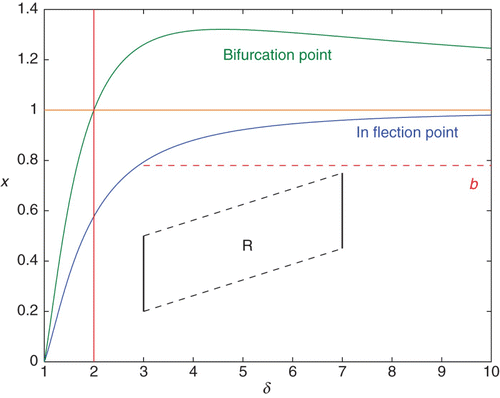
Figure 4. The trapezoidal region R is an example of a region such that if R for all n, then the conditions of Theorem 4.2 are satisfied and there is a unique Allee p-periodic orbit. The point b is the smallest value on the inflection curve and the line at b must be above R.

Theorem 4.2

Let and be p -periodic sequences in such that δ _n >1 and for . Assume

Then, the periodic iterated mapping (2) has a positive unstable p -periodic orbit such that all orbits for which are attracted to 0.

Remark 2 As a increases through with δ fixed, moves upward from the bifurcation graph and moves downward. The trapezoidal region in Figure 4 shows a typical containment region for all the satisfying the hypotheses of the theorem.

5. A new perspective using the Skew-Product space

Certain refinements to the above results can be realized by studying the problem in the Skew-Product setting. In the 1970s, the Skew-Product Dynamical System was introduced and developed by R.J. Sacker and G.R. Sell as a means to analyse time-varying differential equations in a more geometric setting (see 22 and references therein). The concept sprung from an idea in 24 in which the evolution in time of the function on the right-hand side of

is considered along with the evolution of a solution. This is accounted for by embedding f in a certain function space ℱ and introducing the shift flow σ in ℱ whereby the function f, after τ units of time, evolves to , where . In this setting, the orbit under the action of σ of a periodic (in t) f in Equation (12) is a closed Jordan curve in ℱ. Then, an enlarged phase space is introduced and the Skew-Product flow

where is the solution, evaluated at τ, of . It is readily verified that π is indeed a flow in the enlarged state space and thus all the theory of autonomous dynamical systems can be brought to bear.

In the present setting of p-periodic difference equations in one dimension, the situation is much simpler, , , and Equation (13) becomes

In Figure 5, the Skew-Product space is shown for period p=4 along with the stable periodic orbit and the Allee periodic orbit . The following theorem is obtained by a more careful analysis of this figure.

Figure 5. The stable periodic orbit s _j and the Allee periodic orbit α _j in the Skew-Product space. A _M =A _max, the largest of the Allee thresholds A _j of the component functions f _j governing the evolution of the system at time t=j and A _m =A _min. The vertical dashed lines are the regions of extinction at times 0, 1, 2, 3, while the vertical solid lines are the regions of attraction of the periodic orbit s.

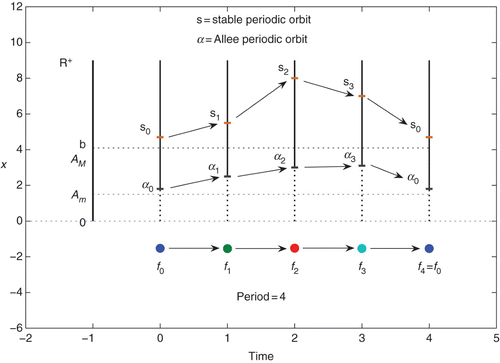
Theorem 5.1

Let and be p -periodic sequences in such that δ _n >1 and for . Suppose that

Then, there are a stable periodic orbit and an Allee periodic orbit . Moreover, we have the following:

	(i) For all the interval (0,α n ) maps homeomorphically onto by f n , and any orbit for which approaches 0 asymptotically.
	(ii) For all the interval maps homeomorphically onto by f n , and any orbit for which is attracted to the stable periodic orbit s.

Proof

The existence of the stable and Allee periodic orbits and their containments within and , respectively, follows directly from Theorems 2.4 and 4.2. Moreover, any orbit for which is attracted to the stable periodic orbit and any orbit for which approach 0 asymptotically. That (0,α _n ) maps homeomorphically to and maps homeomorphically to follows from the fact that f _n is increasing.

It only remains to be shown that any orbit for which is attracted to the stable periodic orbit s. For this, we look more carefully at the proof of Theorem 4.1. The orbit β is globally asymptotically stable under the iterated mapping . In particular, any orbit under this mapping for which , where , is attracted to the periodic orbit β. It follows that there are points arbitrarily close to α _n that are ultimately mapped into the interval (A _max, b) under the mapping . Since F _n =f _n on [0, b), this is also true under the mapping . Since maps homeomorphically to , all points arbitrarily close and greater than α₀ are ultimately mapped to points greater than A _max. The result follows since has already been shown to lie in the basin of attraction of the stable periodic orbit.   ▪

6. Discussion of the conditions in the theorems

Our proof in Theorem 2.4 that the periodic iterated mapping (2) has a stable periodic orbit requires the functions f _n to share an interval [B, ∞) that is invariant under each function and on which each function is concave with a fixed point. The conditions that and that guarantee this. However, they are not necessary conditions. Certainly, if for all of the functions, then every function lies below the diagonal on , so the origin is a globally asymptotically stable fixed point of the iterated mapping and there is no positive stable periodic orbit. However, if some of the functions have and some do not, it is still possible for there to be a positive stable periodic orbit. This is the case, for example, when . If for all of the functions but , then in most cases there is still a stable periodic orbit. However, the following example illustrates that it is not universal: if a ₀=1.2, δ₀=50 and a ₁=1.1, , the condition holds, but the composition f ₁ ° f ₀ has only one fixed point at x=0 to which all solutions are attracted.

Our proof that the periodic iterated mapping (2) has an Allee periodic orbit requires the functions f _n to share an interval (0, b) on which they are each convex with a fixed point. The conditions that and that in Theorem 4.2 guarantee this. As with the stable periodic orbit, these conditions are not necessary. Indeed, near the origin, the composition behaves like

It follows that if , then , so the origin is an unstable fixed point. On the other hand, if , then F′(0)=0, so the origin is a stable fixed point. In this case, if the a _i ’s are large enough, then there is an Allee point; otherwise, the origin is globally asymptotically stable. Finally, if , then . If this product is greater than 1, then the origin is unstable. If it is less than or equal to 1, then the origin is stable, but it is not clear if it is globally asymptotically stable or has an Allee point. What this analysis of the behaviour of the function near the origin lacks is determination of the uniqueness of the Allee and stable periodic orbit. Indeed, it appears to be theoretically possible for the composition to have four (or more) fixed points: the origin, an Allee point, a point that is asymptotically stable on (B, ∞) for some number B and one (or more) point. Under the conditions of Theorem 5.1, this cannot happen and in fact each initial state smaller than the Allee state goes extinct, while each state larger than the Allee state is attracted to the stable periodic state.

7. Implications in Population Dynamics

Fisheries: For a time-independent fish population governed by the autonomous Sigmoid Beverton–Holt equation, it is clear that depensation caused by overfishing or overpredation that drives the population below the Allee threshold will result in extinction even after the depensatory causes are removed. What the results given in the previous sections imply is that the maximum tolerable depensation can vary with time. This is made clear in Figure 5 where it is easily seen that if one has a level of depensation at time 0 that drives the population to a point just above the periodic Allee threshold α₀, then that same level of depensation at time 2 will result in extinction. This could have disastrous outcomes if, for example, all the measurements to determine the maximum allowable harvest are made at the same ‘time’, t=0 each cycle.

This undoubtedly plays a role in the myriad seasonal shellfishing restrictions in coastal waters.

Smooth cordgrass: This species, Spartina alterniflora, spreads by rhizomatous growth and the isolated recruits set one-tenth of the seed of the developed meadow plants and the seeds germinate at only one-third the rate of the meadow plants. In 5, this is attributed to the demographic effects of density and described as an Allee effect. This diminished growth seems to indicate that the colony size resides just above the critical periodic Allee threshold shown in Figure 5. In light of its many predators, for example, blue crab Callinectes sapidus 30, leaf miner parasite Hydrellia valida 27, invertebrate, grass shrimp Palaemonetes pugio, and vertebrate predators, the killifish, mud minnow Fundulus heteroclitus, 13 29, it is conceivable that a fledgling colony of cordgrass could be extinguished.

8. Conclusions

An investigation has been conducted into the long-term behaviour of solutions of the periodic Sigmoid Beverton–Holt equation

where the a _n and δ _n are p-periodic positive sequences. Under certain conditions on the parameters a _n and δ _n , there are shown to exist an asymptotically stable p-periodic state to which all nearby as well as large initial populations approach and a p-periodic Allee state that drives all initially small states to extinction. By employing the Skew-Product Dynamical System, we have shown more, namely every state not equal to the Allee state either goes extinct or is attracted to the stable state. For δ _n independent of n, we obtained a result reported previously in 14 with fewer conditions.

Some possible implications in Population Dynamics are discussed with special emphasis on fish populations and smooth cordgrass.

Acknowledgments

Authors GG, KG, and FG were supported by NSF grant DMS-1045536 as part of the California Research Training Program in Computational and Applied Mathematics. The authors thank Andrea Bertozzi for organizing the Summer Research Experience for Undergraduates at the University of California Los Angeles. CH was supported by the Department of Mathematics and RJS was supported by the Dornsife School of Letters Arts and Sciences Faculty Development Grant, University of Southern California. The authors also thank the referees for their many helpful remarks.

Notes

This is a paper based on an invited talk given at the 3rd International Conference on Math Modeling, Analysis, San Antonio, USA, October 2011