On the global stability of a generalized cholera epidemiological model

Abstract

In this paper, we conduct a careful global stability analysis for a generalized cholera epidemiological model originally proposed in [J. Wang and S. Liao, A generalized cholera model and epidemic/endemic analysis, J. Biol. Dyn. 6 (2012), pp. 568–589]. Cholera is a water- and food-borne infectious disease whose dynamics are complicated by the multiple interactions between the human host, the pathogen, and the environment. Using the geometric approach, we rigorously prove the endemic global stability for the cholera model in three-dimensional (when the pathogen component is a scalar) and four-dimensional (when the pathogen component is a vector) systems. This work unifies the study of global dynamics for several existing deterministic cholera models. The analytical predictions are verified by numerical simulation results.

Keywords:

• cholera modelling
• global asymptotic stability
• geometric approach

1. Introduction

Cholera, a severe water- and food-borne infectious disease caused by the gram negative bacterium Vibrio cholerae, remains a significant public health burden in the developing world, despite a large body of clinical and theoretical studies 1 10 12 20 33,36–38,45 and tremendous efforts in prevention and intervention 48. This is partly due to the limited understanding at present on the complex infection dynamics of cholera, which involve both direct human-to-human and indirect environment-to-human transmission pathways.

Over the last decade, quite a few mathematical models have been published to investigate the transmission dynamics of cholera. For example, Codeço in 2001 proposed a model 5 that explicitly accounted for the environmental component, i.e. the V. cholerae concentration in the water supply, into a regular SIR epidemiological model. The incidence (or the infection force) was modelled by a saturating function aS(B/(K+B)) to represent the effect of saturation, where S is the susceptible population, B is the pathogen concentration, a is the contact rate with contaminated water, and K is the half saturation rate (i.e. the infectious dose in water sufficient to produce disease in 50% of those exposed). Hartley et al. 13 in 2006 extended Codeço's work to include a hyperinfectious (HI) state of the pathogen, representing the ‘explosive’ infectivity of freshly shed V. cholerae, based on the laboratory observations 1 33. They modelled the incidence factor by where β_H and β _L are the HI and less-infectious (LI) ingestion rates, and κ_H and κ _L are the HI and LI half saturation rates. This model was rigorously analysed in 30. Joh et al. 18 in 2009 modified Codeço's model by a threshold pathogen density for infection, with a careful discussion on human–environment contact and in-reservoir pathogen dynamics. More recently, Mukandavire et al. 34 proposed a model to study the 2008–2009 cholera outbreak in Zimbabwe. The model explicitly considered both human-to-human and environment-to-human transmission pathways. The incidence was represented by with I denoting the infected population and β_e and β_h being the rates of vibrio ingestion from the environment and the human–human interaction, respectively. The results in this work demonstrated the importance of the human-to-human transmission in cholera epidemics, especially in such places as Zimbabwe, a land-locked country in the middle of Africa. Moreover, Tien and Earn 44 in 2010 published a water-borne disease model which also included the dual transmission pathways, with bilinear incidence rates employed for both the environment-to-human and human-to-human infection routes. No saturation effect was considered in Tien and Earn's work.

The afore-mentioned work has certainly made important contribution to the understanding of cholera dynamics. Some limitations of these models, however, are that they only considered bilinear or saturating incidence functions, and they all assumed that the bacterial growth outside of human hosts follows linear dynamics. Practically, the multiple interactions between human population, cholera pathogen, and the environment could be much more complicated. For example, in a cholera model published by Jensen et al. 17, the incidence was represented as , a highly nonlinear function, and the growth of V. cholerae was also nonlinear (a quadratic function in B). Also, in a recent paper by Shuai and van den Driessche 39, the incidence function is a summation of the form with nonlinear functions f _j and g _j for different infection stages and pathogen concentrations, and the bacterial growth is determined by a nonlinear shedding rate from the infectious human population.

Building on these studies, Wang and Liao 47 in 2011 proposed a generalized cholera epidemiological model which incorporates general incidence and pathogen functions into the multiple transmission pathways, and which unifies many of the existing cholera models. Careful equilibrium analysis has been conducted in 47 and the results are summarized in Theorem 2.2 in Section 2 of the present paper. In particular, the local and global dynamics of the disease-free equilibrium, as well as the existence, uniqueness, and local dynamics of the endemic equilibrium, have been established.

The global stability of the endemic equilibrium for this general model, however, has not been resolved. In fact, to our knowledge, very few studies on cholera modelling have addressed the endemic global dynamics 43. Thus, some important epidemiological questions, e.g. whether the long-term disease dynamics approaches an equilibrium and how this depends on the initial size of the infection, remain to be answered. The study of the endemic global stability is not only mathematically important, but also essential in predicting the evolution of the disease in the long run so that prevention and intervention strategies can be effectively designed, and public health administrative efforts can be properly scaled. The challenge, however, in the global analysis of cholera models is that due to the incorporation of the environmental components, the models usually constitute high-dimensional nonlinear autonomous systems for which the classical Poincaré–Bendixson theory 14 is no longer valid. The method of monotone flow 23 24,40–42 can be applied to a class of high-dimensional dynamical systems which possesses monotonicity (e.g. competitiveness). Unfortunately, this technique is not applicable to most cholera epidemic models which are non-monotone. The method based on Lyapunov functions 19 21 is well known for stability analysis, though the fact that there is no systematic way to find Lyapunov functions hinders the application of this approach to many nonlinear systems. Finally, the geometric approach for stability analysis, originally developed by Li and Muldowney 9 25 28, has gained much popularity in recent years, especially in dealing with mathematical epidemic models. Nevertheless, the majority of the applications of the geometric approach is concerned with regular epidemiological models such as SIR, SEIR, SIS, SIRS, or the like. In the present paper, we aim to extend this approach to the endemic global stability analysis of the general cholera model, which is a combined human–environment epidemiological model coupling a SIR model with the pathogen components. Such an extension is nontrivial and, to our knowledge, has not been achieved for epidemiological models of this type before.

We organize the remainder of this paper as follows. In Section 2, we briefly present the generalized cholera model and summarize the results established in 47. In Section 3, we apply the geometric approach based on the second compound matrix to analyse the three-dimensional system, where the pathogen component is a scalar. In Section 4, we deal with the four-dimensional model where the pathogen component is a vector. The analysis for higher dimensional system is usually more challenging, and the global stability of our four-dimensional system is established by using the geometric approach based on the third compound matrix. In addition, we verify the analytical predictions in Sections 3 and 4 by numerical simulation results. Finally, we close the paper by conclusions in Section 5.

2. Mathematical model

The model consists of the following differential equations:

together with

Here S, I, and R denote the susceptible, the infected, and the recovered populations, respectively, and B denotes the concentration of the pathogen in the environment (typically the contaminated water). The total population N=S+I+R is assumed to be a constant. The parameter b represents the natural human birth/death rate, and γ represents the rate of recovery from cholera. The function f(I, B) represents the essential part of the incidence which determines the rate of new infection, whereas the function h(I, B) describes the rate of change for the pathogen in the environment which can be either linear or nonlinear. Both f and h are assumed to be sufficiently smooth to ensure the existence and uniqueness of solutions to the system with non-negative initial conditions. In addition, the component B can be either a scalar or a vector. For example, if we consider both the HI and LI states 13 of the vibrios, then we may write .

Based on biological feasibility, the following conditions for f(I, B) and h(I, B) are assumed for I≥0, B≥0:

	(a) f(0, 0)=0, h(0, 0)=0;
	(b) f(I, B)≥0;
	(c) , , , ;
	(d) f(I, B) and h(I, B) are concave; i.e. the matrices D 2 f and D 2 h are negative semi-definite.

Here and in what follows, we write a vector if each component of V is ; we write a matrix if A is positive (negative) semi-definite.

The article 47 conducted some analysis on this model. Based on the next-generation matrix approach 8, the basic reproduction number R ₀ was found by

Remark 2.1 We note that the last inequality in assumption (c) above is based on the experimental observation that the pathogen V. cholerae cannot maintain a stable population in the environment in the absence of the inflow from contaminated sewage 5. This assumption has been used in several existing cholera models (e.g. 5 13 34 44). In addition, when B is a vector, is a matrix. To ensure that R ₀ is positive, we will further assume that is an M-matrix (i.e. a non-singular square matrix with non-positive off-diagonal entries and all principal minors positive). It is known that the inverse of an M-matrix has all its entries being non-negative 2 7.

Under these assumptions, the equation h(I, B)=0 implicitly defines a function B=g(I) with g′(I)≥0, and Equation (5) yields

Biologically speaking, R ₀ measures the average number of secondary infections that occur when one infective is introduced into a completely susceptible host population 8 16 46. Equation (6) shows that R ₀ depends on two factors: one is due to human-to-human transmission () and the other is due to environment-to-human transmission (). The term represents the expected time of the infection, represents the unit human-to-human transmission rate, and measures the total number of secondary infections caused by the human-to-human transmission. Similarly, the product represents the unit environment-to-human transmission rate, and measures the total number of secondary infections caused by the environment-to-human transmission.

It is also shown that there exists a forward transcritical bifurcation at R ₀=1 for this model. Specifically, the following theorem summarizes the dynamics known for the system (1)–(4).

Theorem 2.2

47 When R ₀<1, there is a unique DFE, which is both locally and globally asymptotically stable; when R ₀>1, the DFE becomes unstable, and there is a unique positive endemic equilibrium which is locally asymptotically stable.

3. Three dimensional system

We will now focus our attention on the global asymptotic stability of the endemic equilibrium for R ₀>1. We first consider the case when B is a scalar; i.e. there is only one infectious state (which is assumed to be homogeneous) for the pathogen in the environment. Most cholera models in the literature (e.g. 5 18 34 44) fall into this category. With the pathogen component being a scalar, the system (1)–(3) is three-dimensional.

The assumption implies that the surface h=h(I, B) is below its tangent plane at any point ; that is,

Particularly, setting (I ₀, B ₀)=(0, 0) and using the assumption (a), we obtain

Thus, Equation (3) yields

which implies for any initial value

Therefore, it is clear to see the region

is a positive invariant domain of the system (1)–(3).

We employ the geometric approach based on the second compound matrix 9 25 28 to analyse the endemic global stability of this system. A brief summary of this technique is provided in Appendix A.

Based on Theorem 2.2, the DFE, X ₀=(N, 0, 0), is unstable when R ₀>1. Since the DFE is on the boundary of the domain Δ, this implies the uniform persistence 11; i.e. there exists a constant c>0 such that

Consequently, the uniform persistence and the boundedness of Δ imply that the system has a compact absorbing subset of Δ 4. Together with Theorem 2.2, we obtain the following result:

Proposition 3.1

When R ₀>1, the system (1)–(3) is uniformly persistent, and satisfies the assumptions (H1) and (H2) listed in Appendix A.

We proceed to verify the Bendixson criterion q _2¯<0 (see Theorem A.1). The Jacobian matrix of the system (1)–(3) is

The associated second compound matrix (see Appendix A) is given by

We set the matrix function P by

Then

and

The matrix defined in Equation (A2) can then be written in a block form:

with

Now we define a norm in ℝ³ as

for any vector . Let m denote the Lozinskiǐ measure with respect to this norm. We can then obtain

with

where |Q ₁₂| and |Q ₂₁| are matrix norms induced by the L ₁ vector norm, and m ₁ denotes the Lozinskiǐ measure with respect to the L ₁ norm. Specifically,

and

Note that Equation (3) provides

Also, based on the concavity of h(I, B) (assumption d), it is easy to observe that

at any point (I, B). We thus obtain

provided that

In particular, the condition (13) will be satisfied if

Meanwhile,

Based on Equation (2) and the concavity of f(I, B), we have

and

We then obtain

Therefore,

Since and , there exists T>0 such that when t>T, ; consequently,

which implies .

Hence, we have established the following theorem:

Theorem 3.2

When R ₀>1, the unique endemic equilibrium of the three-dimensional system (1)–(3) is globally asymptotically stable in Δ under the assumptions ( a )– ( d ) and (13).

Remark 3.3 Theorem 3.2 establishes the global endemic stability for the unified three-dimensional cholera model. In particular, the result can be directly applied to several existing cholera models in the literature, such as those in 5 34 44.

To quantify the analysis, we consider the cholera model proposed by Mukandavire et al. 34:

Clearly, this is a special case of the general model (1)–(4). Figure 1 shows a typical phase portrait of S vs I for this model, based on numerical simulation. The parameter values are taken from 34 with . The total population is normalized as N=10, 000, and the initial infection is set as I(0)=1000. We observe a stable spiral and the solution curve eventually converges to the endemic equilibrium at , . We have also tested many different initial conditions including I(0)=1, 10, 100, and 2000, and all these solution curves (not shown here) approach the endemic equilibrium over time, with very similar pattern to that in Figure 1.

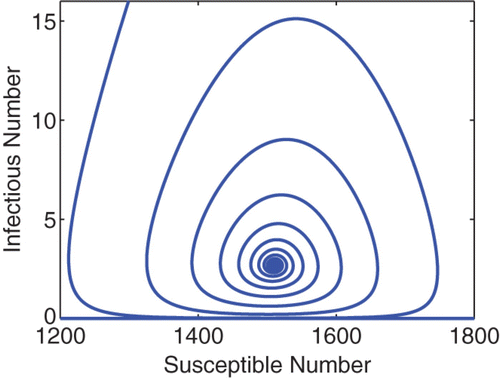
Figure 1. A phase portrait of S vs I for the cholera model (16)–(19). The total population is N=10, 000, and the initial condition is I(0)=1000, S(0)=9000 and R(0)=B(0)=0. The curve converges to the endemic equilibrium at S* ≈ 1510, I* ≈ 2.68. Similar pattern is observed for various different initial conditions.

4. Four-dimensional system

We now consider the model (1)–(3) in the case when B is a vector; i.e. there are heterogeneous and multiple states of infectivity for the pathogen outside the human hosts. The representation of pathogen dynamics in multiple states can possibly provide a deeper insight into the pathogen ecology and the complex interaction between the human hosts and the environment, and reflect better the nature of heterogeneity in disease transmission. Without loss of generality, we assume B=[B ₁, B ₂], where B ₁ and B ₂ represent two different infectious states of the bacterial concentrations. A similar formulation of B was used in 13, where the HI and LI states of the vibrios were modelled. Multiple states of cholera bacterial concentrations were also studied in 39.

We consider the following four-dimensional system corresponding to the model (1)–(3):

The functions f and have to satisfy conditions (a)–(d), noting that and are vectors and that is an M-matrix (see Remark 2.1). It is easy to observe that the mass action bilinear incidence and the saturated incidence satisfy these assumptions. Meanwhile, we note that conditions (c) and (d) imply

for all I, B≥0.

Let

due to fact that is an M-matrix. From Equations (22), (23) and the inequality (24), we see that if , then for all t≥0. Hence, the feasible region

is invariant under the flow of (20)–(23). Moreover, we have

Proposition 4.1

For any and any initial value there is a constant such that

for all t>T.

Similar to Proposition 3.1, the instability of the DFE (N, 0, 0, 0), which is on the boundary of the domain Γ, implies uniform persistence 11. Based on Theorem 2.2, we thus obtain

Proposition 4.2

When R ₀>1, the system (20)–(23) is uniformly persistent.

We now prove the main result in this section, i.e. the global stability of the endemic equilibrium, using the geometric approach based on the third compound matrix (see Appendix B). To simplify our notations, we will adopt the abbreviations

We will also need the following inequalities, which can be easily derived based on the assumptions (a)–(d):

for all I, B≥0. In particular, we have

Theorem 4.3

If R ₀>1 and

then the unique endemic equilibrium of the four-dimensional system (20)–(23) is globally asymptotically stable in Γ provided that the conditions ( a )– ( d ) hold.

Proof

The Jacobian matrix of the system (20)–(23) is given by

The third additive compound matrix of J is

} and the associated linear compound system is

As in 26 27 (also see Appendix B), we need to show the uniform global stability of the linear compound system (33)–(36). To this end, we choose an associated Lyapunov function

where

It is easy to see that the following estimate holds:

Based on Propositions 4.1 and 4.2, we see that there exist positive constants C ₁ and C ₂ such that

Meanwhile, by Equation (32) and the uniform persistence of the system, we can choose a (small) constant k>0 such that

Next, we calculate the total derivative of V along the trajectory of the compound system (33)–(36). We will separate the discussion for the several cases below.

Case I: V=V ₁, then V ₂, V ₃≤V ₁ and

since by Equation (37), by Equation (29) by (31), S f ₀′−b≤0 by Equation (32), and f≥k by Equation (39). Here and in what follows D ₊ denotes the right-hand (total) derivative with respect to t.

Case II: V=V ₂, then V ₁, V ₃≤V ₂. In a way similar to Case I, we can obtain the estimates

where by Equation (30), and by Equation (31).

Case III-a: V=I|W+Z|, then and

since , by Equations (29) and (30), and k≤b by Equation (39).

Case III-b: V=I|W|, then WZ<0, , and

Case III-c: V=I|Z|, then WZ<0, . Using similar estimates and the condition γ≥k, we obtain

Now, let . Then it follows from (40) to (44) that the following estimate holds:

In view of Propositions 4.1 and 4.2, there is a constant C>0 such that

for sufficiently large t. Therefore, we conclude from Equations (38), (45), (46) and Theorem A.2 (see Appendix B) that the endemic equilibrium of the system (20)–(23) is globally asymptotically stable. Indeed, there exists s>0 such that for all t≥s,

implying the uniform global stability of the associated linear compound system. The proof is thus complete.   ▪

Remark 4.4 Theorem 4.3 establishes the global endemic stability for a general four-dimensional cholera model. As a special case, the result can be directly applied to the cholera model in 13. We note, however, that the assumption in (32) is a sufficient condition for the global stability and it might restrict the applicability of the result.

Remark 4.5 The analysis presented here can be easily extended to the case with variable host population, where we incorporate immigration and disease-related mortality into the model (20)– (23). Thus, Equations {\rm (20)} and {\rm (21)} will be replaced by

where N ₀ is the immigration rate and b ₀ is the disease caused death rate (for cholera, this is usually lower than 1% 48). In this case, the total human population N=S+I+R is not a constant but satisfies

If we define

then the feasible domain becomes

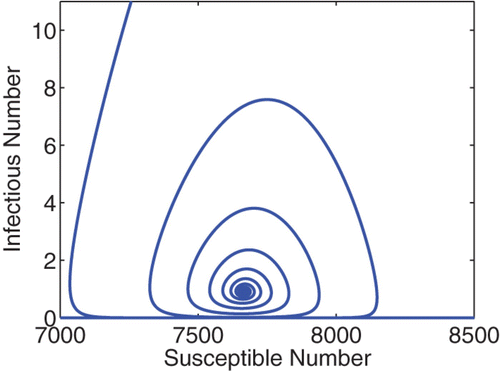
Figure 2. A phase portrait of S vs I for the cholera model (49)–(53). The total population is N=10, 000, and the initial condition is I(0)=1000, S(0)=9000, and R(0)=B _H (0)=B _H(0)=0. The curve converges to the endemic equilibrium at S* ≈ 7666 and I* ≈ 0.92. Similar pattern is observed for various different initial conditions.

Correspondingly, the constraint on f ₀′ in Theorem 4.3 is replaced by

Then the same analysis as presented in this section can be applied to establish the global asymptotic stability of the endemic equilibrium for this variable population model.

Finally, we present an example to verify the analytical prediction in Theorem 4.3. We consider the cholera model of Hartley et al. 13:

Using numerical simulation, we obtain a typical phase portrait of S vs I for this model, shown in Figure 2. The parameter values are taken from 13 30 with . Again the total population is normalized as N=10, 000, and the initial infection is set as I(0)=1000. The solution curve approaches the endemic equilibrium at , over time. It is also observed (though not shown here) that solutions with various different initial conditions converge to the same endemic equilibrium, a verification of its global asymptotical stability.

5. Conclusions

The present work aims to understand the global dynamics of cholera epidemiology in a general mathematical model which has a potential to incorporate different factors of the human host, the environment, and the pathogen ecology into a unified framework. Such an understanding is important for the effective prevention and intervention strategies against cholera outbreak. The unified global stability results established in this paper can be applied to many published cholera models, including (but not limited to) those in 5 13 18 34 44 47.

Due to the incorporation of the environmental component and the coupling of multiple transmission pathways, the cholera model considered in this paper distinguishes itself from regular SIR and SEIR epidemiological models whose global dynamics have been extensively studied 15 16,22–24,27 29 32 49. Using the geometric approach, we have carefully investigated both three-dimensional and four-dimensional systems under general settings. The analysis and results presented in this paper not only extend the application of the geometric approach, but also provide a framework for modelling and analysing other infectious diseases such as typhoid fever, amoebiasis, dracunculiasis, giardia, cryptosporidium, and campylobacter 31 44 which involve environmental components (e.g. water-borne pathogen).

Acknowledgements

J. Wang acknowledges partial support from the National Science Foundation (under Grant No. DMS-0813691) and the Simons Foundation (under Grant No. 208716). The authors thank the two anonymous referees for their helpful comments to improve this paper.

Notes

This paper is based on an invited talk given at the 3rd International Conference on Math Modeling & Analysis, San Antonio, USA, October 2011.

Appendix A

We briefly describe below the geometric approach based on the second additive compound matrix, developed by Li and Muldowney 9 25 28.

For a 3×3 matrix A=[a _ij ], the second additive compound matrix is defined as

We refer to 35 for a survey of general compound matrices.

Now consider the dynamical system

where is a C ¹ function and where is a simply connected open set. Let X(t, X ₀) denote the solution of Equation (A1) with the initial condition X(0)=X ₀. We assume:

	(H1) There exists a compact absorbing set K⊂D;
	(H2) The system (A1) has a unique equilibrium point X* in D.

It is shown in 9 25 28 that X* is globally asymptotically stable if (A1) satisfies (H1)(H2) and a Bendixson criterion that is robust under C ¹ local perturbations of F at all non-equilibrium non-wandering points. This criterion is obtained as follows.

Let be a matrix-valued C ¹ function in D. Set

where P _F is the derivative of P (entry-wise) along the direction of F and J ² is the second compound matrix of the Jacobian J(X)=DF(X). Let m(Q) be the Lozinskiǐ measure of Q with respect to a matrix norm 6, i.e.

Define a quantity q _2¯ as

Then the Bendixson criterion is given by

In summary, we have the following theorem:

Theorem A.1

Assume that D is simply connected and the assumptions {\rm ({ H1})} and {\rm (H2)} hold. Then the unique equilibrium X* of (A1) is globally asymptotically stable in D if q¯₂<0.

Appendix B

In what follows, we outline the geometric approach based on the third additive compound matrix 26 27.

The third additive compound matrix for a 4×4 matrix A=[a _ij ] is defined as

For a solution X(t, X ₀) of any initial value problem of the dynamic system (A1), the linearized system is

and the associated third compound system is

where J ³ is the third compound matrix of the Jacobian J for equation (A1).

Theorem A.2

Assume that {\rm (H1)} and {\rm (H2)} hold and there are a Lyapunov function V(X, Z), a function K(t), and positive constants c, k, and C such that

	(i)
	(ii)

where the total derivative V′ is taken along the direction of Equation (A6), then the interior equilibrium X* of Equation (A1) is globally asymptotically stable.

Proof

If this is the Corollary 3.2 in 27. For a general differentiable function K(t), the conclusion follows from the Corollary 3.2 in 27, since the modified Lyapunov function satisfies all the conditions.   ▪