Desynchronization in synchronous multi-coupled chaotic neurons by mix-adaptive feedback control

Abstract

In this paper, by means of the invariance principle of differential equations, an adaptive feedback scheme is proposed to realize desynchronization in synchronous multi-coupled chaotic neurons by the mix-adaptive feedback effectively. Numerical simulations for the Hindmarsh–Rose neural model with self-coupling are illustrated which agree well with our theoretical analysis. It is observed that the feedback strengths asymptotically converge to a local fixed value in finite time, especially for linear coupling chaotic neurons with self-coupling. Furthermore, robustness of desynchronization in three coupled chaotic neurons on small mismatch of parameters is shown.

Keywords:

• desynchronization
• adaptive delay feedback
• neural activity
• synaptic coupling strengths
• neuronal network
• feedback strength

2000 Mathematics Subject Classifications:

• 92B20
• 93C40

1. Introduction

Neurons and neural networks can be modelled by differential equations and dynamical systems at many different levels, depending upon diverse phenomena and the accuracy desired. They have been gaining increasing attention and recognition as a fundamental tool in understanding dynamical behaviours and response of real systems coming from different fields such as biology, social systems, linguistic networks, and technological systems 1152332. How to understand the synchronous activity in neurons has been an interesting subject in interdisciplinary sciences. Living tissues are complex organizations of individual cells. The activity of each cell within the tissue should be regulated in a coordinated manner to perform their specific functions. Synchronous activities in the central nervous system are the collective behaviours in the process of information transmission, so as to form a coherent and unified perception of the external world 4928. Though the mechanism during the regulation process is very complex, a regular way is to exert control on neural transmission to change the neuron's activity.

The dynamics of neural networks have been widely investigated, with special emphasis on the interplay between the complexity in the overall topology and the local dynamical properties of the coupled nodes 71825. As a typical kind of dynamics, synchronization and desynchronization in neural networks have become of significant interest in recent years. One of particular aims is to understand how synchronization and desynchronization depends on various parameters of the network, such as average distance, clustering coefficient, coupling strength, degree distribution, weight distribution, etc. 23814172629. Different types of synchronization such as complete synchronization 6, phase synchronization 21, lag synchronization 1722, almost synchronization 5, chaotic synchronization 27, and anticipated synchronization 33 have been described. Desynchronization is a process inverse to synchronization, where initially synchronized oscillating systems desynchronize as parameters change or they do so under the influence of an external force or feedback. Desynchronization is important. For example, in neuroscience and medicine, pathologically strong synchronization of neurons may severely impair the brain function as, for example, in Parkinson's disease or epilepsy 20243034. Effective desynchronization has been exploited as a tool for probing the functional significance of synchronized neural activity underlying perceptual and cognitive processes or as a mild treatment for neurological disorders like Parkinson's disease 1319.

Recently, extensive works have been done towards understanding the synchronization of globally coupled phase oscillators, and in particular, possible methods for desynchronizing such systems with short sequences of pulses 113135. In 11, an adaptive feedback scheme was proposed to achieve complete synchronization. Based on this feedback scheme, adaptive synchronizations of neural networks with or without delay were described 3135. This proposed scheme appears simple and is robust against the effect of small noise. It is of great importance for the treatment of neurological disorders like Parkinson's disease and essential tremor, and can also be used to design new psychophysiological and cognitive experimental techniques. In these studies, considering transmission delay in some neural models becomes necessary. In practice, the information is not instantaneous in general because of the finite propagation velocity and delay in the transmission of signal, thus the delay should be an indispensable factor in these circumstances. In our previous works 1729, we once explored synchronization for neural networks with time delay by using the theory of asymptotic stability. In the present paper, we develop an adaptive feedback scheme to study desynchronization in synchronous multi-coupled chaotic neurons.

The rest of the paper is organized as follows. In Section 2, a theoretic result is presented on desynchronization in synchronous multi-coupled chaotic neurons. As an example, a model of three coupled Hindmarsh–Rose (HR) neurons is discussed by the adaptive feedback scheme. Furthermore, we find that small mismatch parameters on the effects of the desynchronization are robust. Section 3 is a brief conclusion.

2. Main results

2.1. Analytical theorem

In this section, based on the invariance principle of differential equations 12, we are concerned with desynchronization in synchronous multi-coupled chaotic neurons with the mix-adaptive delay feedback. Consider the following synchronous multi-coupled chaotic neural system: where , is a nonlinear vector function, and H_i may be linear or nonlinear. We called Equation (1) the reference system.

Let be a chaotic bounded set of system (1), which is globally attractive. In general, we assume that

• (I) the nonlinear vector function f(x_i) is globally Lipschitz with positive constants l>0 such that for any x(t), ;

• (II)  is local Lipschitz with positive constants m_i such that

In what follows, we consider the system of multi-coupled chaotic neurons with the mix-adaptive feedback in the form where y_i represents the response state, u_i represents the feedback control with the delayed state . We called it the controlled system. From 1131, the feedback strength is adapted according to the following scheme 35: where and i≠j.

Let and . Apparently, if τ_i=0, then e_i=x_i−y_i. From Equations (1) and (2) we deduce that

Definition 1

For systems (1) and (2), we say that they possess the property of desynchronization, if there exists as i=1, 2, …, n.

Theorem 1

Assume that conditions (I) and (II) hold, and systems (1) and (2) satisfy the adaptive scheme (3). Then desynchronization in synchronous coupled chaotic neurons can be achieved, that is, .

Proof

[Proof of Theorem 1] According to Equations (3) and (4), we construct a Lyapunov function as where L is a constant and Calculating the derivative of E_h(t) along the trajectory of the error system (4) yields If and only if are all equal to zero, then we have . Thus, we have , that is, , .   ▪

Remark 1 According to above proposed desynchronization scheme, we can obtain desynchronization in synchronous coupled chaotic neurons effectively. The above result appears rather general.

2.2. Applications to HR models

In this section, we consider a model of the HR neurons 10 described by the following equations: where x₁ represents the membrane potential, x₂ represents a recovery variable associated with the fast current, x₃ denotes the adaption current, and and x̄ are real constants. In our previous work 16, we studied the stability by classifying neighbourhood regimes near the Fold-Hopf points and illustrated the complex bursting-spiking firing modes associated with Fold-Hopf bifurcations by numerical simulations. 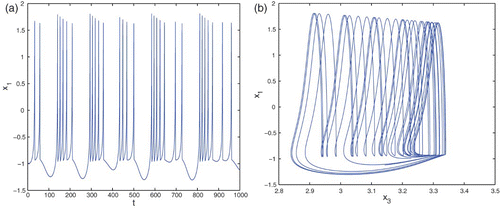Here we take and choose I_x as a control parameter. The change of the value of I_x causes rich firing behaviours. System (5) exhibits multiple time-scale chaotic bursting behaviours for , especially in the case of I_x=3.2 (Figure 1).

Figure 1. (a) Chaotic bursting of HR model at I_x=3.2; (b) chaotic attractor of HR model.

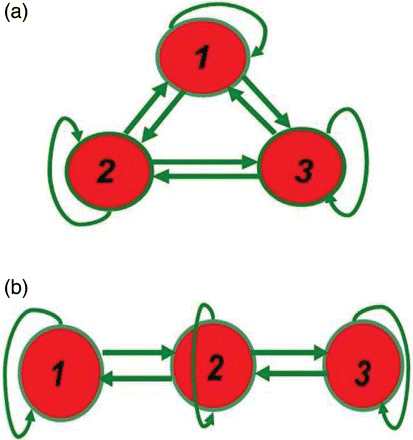
For convenience, we consider the system of three coupled chaotic HR neurons for two cases (Figure 2).

Figure 2. (a) Ring coupling chaotic neurons with self-coupling; (b) linear coupling chaotic neurons with self-coupling.

Case (a): ring coupling chaotic neurons with self-coupling. Consider the system of three ring-coupled chaotic HR neurons with self-coupling: where , relevant parameter values are the same of system (5), and

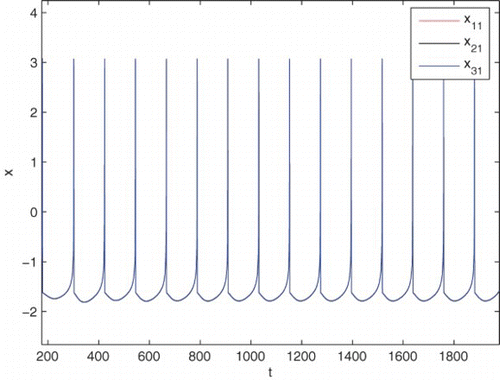
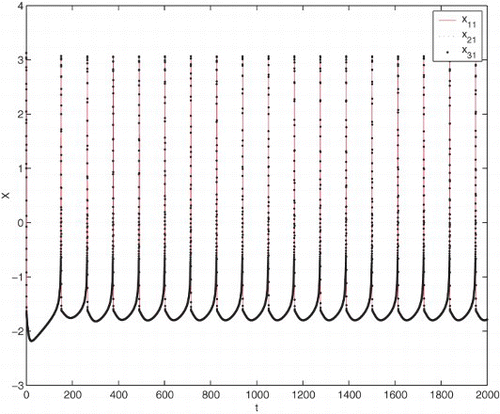
When , synchronization has been achieved, the corresponding numerical results are shown in Figure 3. As real coupled neurons are concerned, the information from the presynaptic neuron is transmitted to the postsynaptic one with certain time delay. Time delays are inherent in neuronal transmissions. Thus it is important to seek the controlling method of synchronous neurons.

Figure 3. The portrait of system (6) with respect to ring coupling chaotic neurons with self-coupling for ϵ=2.0.

In what follows, the corresponding three coupled chaotic neurons are described by the following system: where y_i represents the response state, τ_i represents time delay, and . In order to discuss the synaptic effect to the membrane potential through the gap junction between neurons, we take the synaptic coupling strength as k_i. Here the feedback strength k_i is adapted according to the following scheme: We take parameters , I_x=I_y=3.2, and the initial feedback strength 0.01 to investigate desynchronization in the system of three synchronous coupled chaotic neurons.

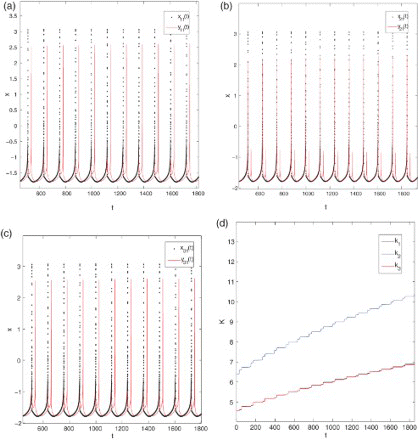
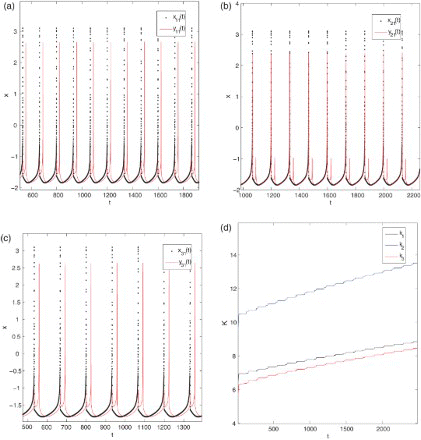
The corresponding numerical simulations are shown in Figure 4. It is shown in Figure 4(a)–(c) with the delay τ₁=25 and τ₃=50, respectively, that the coupled system achieves desynchronization by using the mix-adaptive feedback control. Furthermore, from Figure 4(d), the feedback strength k₁, k₂, and k₃ asymptotically converges to a local fixed value, respectively.

Figure 4. (a)–(c) Desynchronization for three ring-coupled chaotic neurons with the delay τ₁=25 and τ₃=50, respectively; (d) the temporal evolution of k₁, k₂, and k₃ for I_x=I_y=3.2.

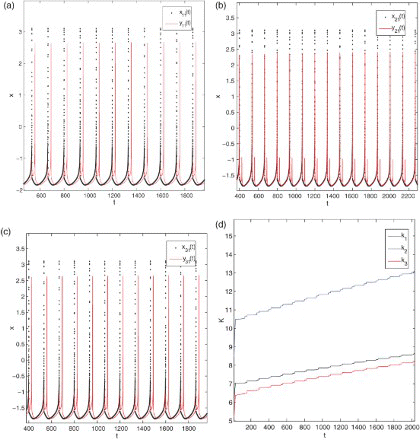
Nonidentity exists everywhere in nature. Thus, it is useful to investigate destructuralization in three coupled HR chaotic neurons with the small mismatch of parameters. We take I_x=3.2 and I_y=3.18, respectively. It is presented in Figure 5(a)–(c) with the delay τ₁=25 and τ₃=50, respectively, that desynchronization of the coupled system can be achieved by using the mix-adaptive feedback control. Furthermore, we can observe the robustness of feedback strength of desynchronization by comparing Figure 4(d) with Figure 5(d).

Figure 5. (a)–(c) Desynchronization for three ring-coupled chaotic neurons with the delay τ₁=25 and τ₃=50, respectively; (d) the temporal evolution of k₁, k₂, and k₃ for I_x=3.2 and I_y=3.18.

Case (b): linear coupling chaotic neurons with self-coupling.

Similar simulations can be obtained for linear coupling chaotic neurons with self-coupling. In Figure 6, simulations for linear coupling chaotic neurons with self-coupling are illustrated. It is shown from Figure 7(a)–(c) with the delay τ₁=25 and τ₃=50, respectively, that desynchronization of the coupled system can be achieved by applying the mix-adaptive feedback control. In particular, the feedback strength can be a stable fix value (Figure 7(d)). Similarly, desynchronization in three linear coupled chaotic neurons on the small mismatch of parameters is also robust.

Figure 6. The synchronization portrait of system (6) with respect to linear coupling chaotic neurons with self-coupling for ϵ=2.0.

Figure 7. (a)–(c) Desynchronization for three linear coupled chaotic neurons with the delay τ₁=25 and τ₃=50, respectively; (d) the temporal evolution of k₁, k₂, and k₃ for I_x=I_y=3.20.

3. Conclusion

In this paper, we applied an adaptive feedback method to determine the desynchronization condition of neural systems, which enables us to observe desynchronization in synchronous multi-coupled chaotic neurons. Based on the invariance principle of differential equations and matrix inequality, applying the mix-adaptive feedback we obtained desynchronization in synchronous multi-coupled chaotic neurons. Numerical simulations are in agreement with our analytical result.

Acknowledgements

This work is supported by the National Natural Science Foundation of China under Grants No. 10972018 and No. 11072013. This work is also partially supported by UTPA Faculty Council Grant under 145MATH04. Authors thank Dr Xiaohui Wang for providing us with the drawing technique.