A didactical note on the advantage of using two parameters in Hopf bifurcation studies

Abstract

In order to maximize the information that a linearized stability analysis provides, one should work with two free parameters rather than one. Moreover, it is recommended to first consider coefficients in the characteristic equation as parameters and in a second step (try to) invert the map that defines the coefficients in terms of the parameters as they occur in the original equation. Our aim is to substantiate these claims by way of a delay equation example taken from the literature.

Keywords:

• stability boundary
• Hopf bifurcation
• long periods
• two parameters

AMS Subject Classification:

• 34K18
• 34K20
• 34K60
• 92C99

1. Introduction

A delay equation is a rule for extending a function of time towards the future on the basis of the (assumed to be) known past. For differential delay equations the rule specifies the derivative at the current time point 13171928, whilst for renewal equations the rule specifies the value of the function itself in the current time point 3111420. Many physiologically structured population models lead to systems of equations that have differential delay as well as renewal components 15.^†

The literature on delay equations is overrun with papers in which a one-parameter Hopf bifurcation analysis is presented for differential equations with discrete delay like And indeed, the Hopf bifurcation theorem itself is usually and conveniently formulated in a one-parameter setting, see, for example, [Theorem X.2.7]13. The aim of this short note is to advocate the use of two parameters rather than one in the following way: first one finds the boundary of the stable region in parameter space characterized by a root of the characteristic equation lying exactly on the imaginary axis (more precisely, a pair of complex conjugate roots). Next, one can apply the Hopf bifurcation theorem to whatever one-dimensional path in the two-parameter plane one is interested in, provided the path intersects the stability boundary transversally.

Our plea, like the one in 4, applies to dynamical systems in general, not just to delay equations. But the approach is somehow more powerful if we deal with a scalar equation (see, e.g. 27 for a similar observation). And first order scalar delay equations can exhibit oscillations whereas first order scalar ordinary differential equations cannot. Likewise the approach is, as a rule, more powerful in case of point delays than when delay is distributed, see the text around Equation (21).

The characteristic equation is one complex equation, so two real equations if we look for roots on the imaginary axis. So if we have a k-dimensional parameter, the equation defines generically a (k+1−2)-dimensional manifold in (parameter, frequency)-space. When k>2 we cannot possibly parametrize this manifold by just ω, but if k=2 we may indeed attempt to use ω to parametrize a curve in the two-dimensional parameter space. For instance, whenever the parameters occur linearly in the equation one can indeed solve for the parameters in terms of the frequency ω. Also note that this yields not just a convenient parametrization but that it does in fact provide very useful information, as the period of the bifurcating periodic solutions is close to 2π/ω. And there is an additional bonus: human beings are particularly good at absorbing two-dimensional visual information!

The coefficients in the characteristic equation are often composite parameters, in the sense that they may relate in complicated, and sometimes implicit, ways to the parameters in the original delay equation. It then makes sense to follow a two-step procedure:

• Step 1: Characterize the stability boundary in coefficient-space.

• Step 2: Try to invert the map from original parameters to coefficients.

The second step is often cumbersome, as there may easily be more parameters than coefficients and hence the inverse is, in general, multi-valued.

In [Chapter XI]13 several examples of this approach are presented. We refer to 29 for general results on characteristic equations. In 10 a numerical variant of our approach is presented. See 2 for a quite different numerical approach and a very nice tool. In 16 the importance of the second step is illustrated by way of an example (showing that a wrong conclusion can arise if one neglects this step). Finally, we note that some time ago Jim Cushing in a sequence of papers 5–9 proved a series of theoretical results showing that one can actually find periodic solutions of the nonlinear problem of fixed period by exploiting the availability of two parameters. Thus the two-parameter plane becomes locally foliated by level curves of the period. Now that numerical bifurcation analysis is becoming more and more powerful, it seems feasible to develop a tool that yields a picture of this foliation.

We aim to substantiate the above general considerations in the next sections by elaborating a well-known example: population dynamics with delayed negative feedback. Here we are motivated by the quest for long period oscillations in the inspiring paper 26 about a model for hematopoietic stem cells. Section 2 deals with Step 1. In essence, we just note that the information we are after is already available in the literature. Section 3 is concerned with a special and rather qualitative variant of Step 2: since we are interested in long periods we want small frequencies, and so we investigate the inverse image of the point on the stability boundary corresponding to ω=0, i.e. we aim to characterize the conditions on the original parameters such that one may expect periodic solutions with long periods. In other words, we perform a systematic search for regions in parameter space where one can expect to see long period oscillations (either damped or sustained). We obtain a diagram showing a transcritical bifurcation curve corresponding to the nontrivial steady state becoming positive, and hence biologically meaningful, as well as a Hopf bifurcation curve at which the nontrivial steady state loses stability and a periodic solution arises. The intersection of these curves is a so-called Takens-Bogdanov singularity.

2. The prototype of delayed negative feedback

In this paper we first of all follow Pujo-Menjouet et al. 26 and consider the delay differential equation for the concentration N of blood production stem cells in the resting phase. Here δ is the rate at which stem cells differentiate into precursor cells of the various types of mature blood cells. At a rate β, which depends smoothly on the prevailing concentration N(t), stem cells enter a proliferation phase of duration τ. As during this phase apoptosis occurs at rate γ, only a fraction of the cells that start the proliferation phase reaches its end. At the end of the proliferation phase the cell divides into two daughter cells, which enter the resting phase.

We assume that feedback is negative: β is a decreasing function of N. It is well-known that the combination of negative feedback and delay can lead to destabilization of a steady state and to oscillations. Often, and also here, this is shown by a Hopf bifurcation analysis.

In Pujo-Menjouet et al. 26, they raise the question: how do short cell cycles give rise to long period oscillations? The aim of the present short note is to show that some of their answers can be obtained rather easily and efficiently by performing a two-parameter analysis of the characteristic equation corresponding to the linearization of Equation (1) around its nontrivial steady state (explicit formulas for α₁ and α₂ are given in the next section). In fact Equation (2) is well-understood, see [Chapter XI]13 for a textbook treatment. And the understanding can be conveniently summarized in the form of the diagram of Figure 1, showing how the -plane is partitioned into regions according to how many roots of Equation (2) lie in the right half-plane.

Figure 1. Bifurcation diagram in the (α₁,α₂)-plane showing a transcritical bifurcation curve (red) and Hopf bifurcation curves (blue) for kπ<ω<(k+1) π with k=0, 1, 2. The numbers of eigenvalues in the right half of the complex plane are indicated in the boxes. Each number (box) corresponds to a region bounded by the bifurcation curves.

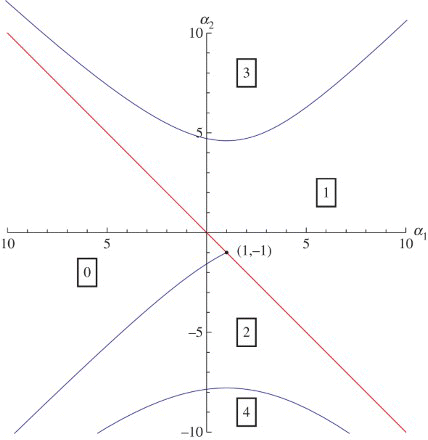
The stability region is characterized by no root at all lying in the right half-plane. Its boundary has two parts:

• The line with (λ=0 is a root of Equation (2)).

• The curve for , corresponding to being a root of Equation (2).

The line and the curve intersect at for which λ=0 is a double root of Equation (2).

A fortunate feature is that the curve is parametrized by the frequency ω of the oscillations of the linearized system at the critical parameter combination. The theory of the Hopf bifurcation, see [Chapter X]13, guarantees that oscillations of the nonlinear system for nearby parameter values have roughly the same frequency. So if we are interested in long periods, we should focus on the curve (3) for small values of ω. For instance, if we consider the part of the curve with , we consider , so periods between 4 and ∞. The nearer we get to (1,−1), the longer the period will be. This point itself is a co-dimension two bifurcation point called ‘double zero eigenvalue’ or Takens-Bogdanov singularity. The unfolding under natural non-degeneracy conditions can be found in [Section 8.4]21. Also see [Section IX.10]13.

But what is the unit of time that we use when we derive Equation (2)? And how do the stylized parameters α₁ and α₂ relate to the parameters occurring in Equation (1)? How do we translate the information contained in Figure 1 and Equation (3) into information about solutions of Equation (1)?

We shall answer these questions in the next section. But before doing so, we draw attention to the fact that exactly the same Equation (2) governs the stability character of a nontrivial steady state of equations corresponding to quite different population dynamical settings. Indeed, the data from the famous blowfly experiments of 2324 are, as far as known today 18, best reproduced by solutions of the delay differential equation where N is the size of the subpopulation of adults (= reproducing individuals), T_D corresponds to the maturation delay, R to reproduction and δ is a per capita adult death rate (note that juvenile survival has to be incorporated in R). In his experiments Nicholson provided limited amount of proteins, an essential ingredient for egg production by adult females. Scramble competition then leads to egg production that is proportional to N for small N, but goes to zero for large N. A convenient function to describe such overcompensation is where P is the maximal per capita egg production rate, corrected for mortality during the juvenile period, and N₀ is a scale parameter for the population level as determined by density dependence. For fish populations one can use the same equation, but interpret the negative density dependence as resulting from ‘egg’ cannibalism 12 (this is reminiscent of the discrete time Ricker equation; see Section VI.3 of http://webarchive.iiasa.ac.at/Research/EEP/Metz2Book.html for a renewal equation variant).

3. Parameter maps

The main aim of this section is to derive the relationship between, on the one hand, α₁, α₂ appearing in Equation (2) and, on the other hand, the parameters δ, γ, τ and the function β appearing in Equation (1).

By introducing we achieve that we can take and The upshot is that Equation (1) now reads with δ, γ and β(N) dimensionless.

We now deduce Equation (2) from Equation (6). Of course we do so in order to go in a next step in the other direction, i.e. from Equation (2) to Equation (6).

The conditions and guarantee that the zero steady state of Equation (6) is unstable and also that Equation (6) has, provided δ>0 and β decreases to a low enough level for large N, a strictly positive steady state N̄ characterized by the equation From Equation (9) we conclude that Equations (7) and (8) are also necessary conditions for the existence of a strictly positive steady state.

We now substitute into Equation (6), Taylor expands β(N)N for small x and ignores higher order terms. This leads to the linearized equation with with

Equation (10) admits a solution of the form if and only if λ satisfies Equation (2). General theory (see, e.g. [Corollary VII.5.12]13) then guarantees that N̄ is stable if all roots of Equation (2) have negative real part and unstable if at least one root has positive real part.

Is it possible to have when α₁ and α₂ are given by Equation (11)? This would require and and hence , which violates Equation (7). So this is not possible when . But this very same calculation also shows that we can come arbitrarily close by letting and whilst making sure that . Or, in other words, a necessary condition for obtaining a Hopf bifurcation of a periodic solution with very long period is that the rate at which stem cells differentiate is very small (when we use the length of the proliferation phase as unit of time) and that the fraction of cells that survives the proliferation phase is only slightly larger than 0.5. In retrospect these are very natural conditions: if we use the length of the proliferation phase as the unit of time, the time scale of population turnover is set by the differentiation rate δ and the reproduction rate .

Thus far the function β is an infinite-dimensional parameter. Sooner or later we need to limit ourselves to a parametrized family such as or with parameters N₀, β₀ and n. (Note that N₀ is called θ in 2526 and note once again that N₀ only sets the scale of N and has no influence on the dynamics. The mathematical requirements on β as well as the biochemical reasons for choosing the decreasing Hill function defined by Equation (13) for this particular model are discussed in 22.)

In any case, we have enough freedom to require, for the time being, that This choice allows us to invert Equation (11) and write By making a Taylor expansion we deduce that for small ω Substituting Equation (16) into Equation (9) we find

It remains to satisfy the condition . For definiteness, let us focus on the family (13) whilst taking without loss of generality N₀=1. One can easily verify that for β given by Equation (13) we have This identity allows us to rewrite in the form which upon substitution of Equation (18) becomes an explicit expression for in terms of ω. For ω=0 we have .

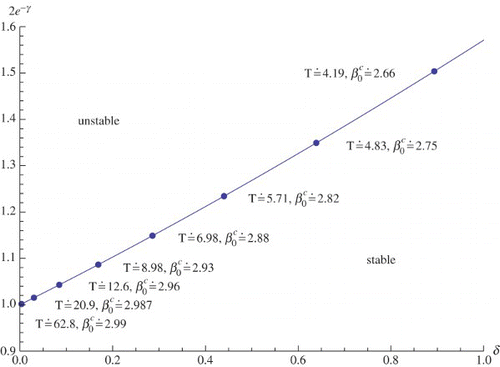
Let us step back and survey the situation. For small values of ω we may choose δ and 2e^−γ according to Equation (16). If we next consider β₀ as a bifurcation parameter, then a Hopf bifurcation with limiting period 2π/ω takes place when β₀ passes the critical value specified by the right hand-side of Equation (20) with given by Equation (18). A graphical representation of the results for n=3 is provided in Figure 2.

Figure 2. Critical values of the parameters δ, 2 e^−γ, and β₀ and the Hopf period T for n=3. The transition from a stable steady state to an unstable steady state happens when we pass from below the curve to above the curve or when β₀ increases from below the critical value to above . For ω=0 we have .

In the case of distributed delay as studied in 1, the characteristic equation reads where the density f(τ) replaces the Dirac measure concentrated, after scaling, in 1. Putting and separating real and imaginary parts, we can rewrite this as

So for given γ and f we can still parametrize a curve in a two-parameter plane by ω, provided we have at our disposal a numerical procedure that evaluates the integrals. (If we do want to consider γ as one of the ‘free’ parameters, there does not seem to be an easy way to organize the calculations.)

For the blowfly (alias egg cannibalism) model the relation between (α₁, α₂) and the parameters P, δ and T_D is given by and we conclude that α₁ needs to be negative in order to correspond to positive P, δ and T_D. This, in turn, corresponds to and hence the period is at most 4 T_D at Hopf bifurcation. We conclude that, even though both the hematopoietic and the ecological problems lead to Equation (2), there is an essential difference in the range of periods at Hopf bifurcation. This clearly illustrates that one cannot just focus on Equation (2), one needs to study the parameter map as well.

4. Conclusion

Figures 2 and 3 become much more informative if along the stability boundary it is indicated whether the Hopf bifurcation is supercritical (implying that the bifurcating periodic solution is stable for parameters close to the bifurcation) or subcritical (implying it is unstable). To decide, one needs to compute the first Lyapunov coefficient and this computation involves higher order terms of the Taylor expansion. So the information is problem specific and it cannot be deduced from just Equation (2). In [Section X.3]13 it is formulated how to compute the direction from linear, second and third order terms. As a rule, the computations require considerable effort, even in the case of a scalar delay equation. To follow the periodic solutions when parameters vary outside a small neighbourhood of the Hopf bifurcation point, one needs sophisticated tools for numerical continuation and bifurcation studies, such as DDE-Biftool (http://twr.cs.kuleuven.be/research/software/delay/ddebiftool.shtml).

Figure 3. Figure 1 repeated with a superimposed curve parametrized by δ in the (α₁,α₂)-plane corresponding to δ∈(0, 3), β₀=1.77, γ=0.2 and n=12.

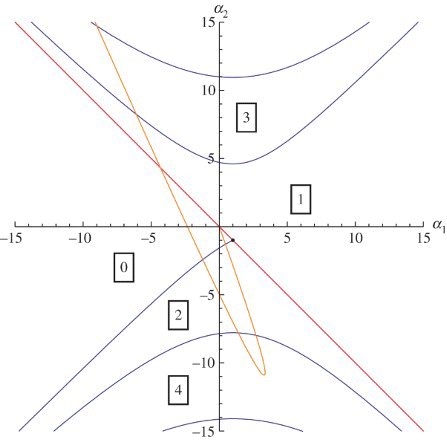
To conclude, let us compare our results with the results presented by Pujo Menjouet et al. in 26 and Pujo-Menjouet and Mackey in 25. First of all we should mention that our analysis is confined to linearized stability and Hopf bifurcation. Consequently it does not give any information about periodic solutions away from the bifurcation point, such as in contrast to the numerical study of 2526. As far as linearized stability and Hopf bifurcation are concerned, our analysis in essence confirms the results of 2526. The gain of our graphical representation of the stability domain in parameter space is that it provides a unifying template. This helps to reveal the precise conditions for long periods. To illustrate this, we show in Figure 3 how the parameters α₁ and α₂ change when, as in 25, we fix , γ=0.2 (i.e. ) and n=12, and consider δ as a bifurcation parameter. The orange δ-parametrized curve is defined by Equation (11) with δ∈(0, 3), , γ=0.2 and n=12. We can clearly see that it crosses the Hopf curve with . At this point, and the relatively long period oscillations are born. When , the nontrivial steady state regains stability and remains stable until the δ-parametrized curve reaches the line where the nontrivial steady state ceases to exist. That happens at approximately .

Since one can plot such a curve in the -plane for any values of the fixed parameters, the method of two-parameter bifurcation analysis using a graphical representation provides a fast and easy way to obtain practical information from the model. Moreover, this approach yields exact information about the linearized model, as opposed to the numerical simulations in 2526. On the other hand, numerical simulations give of course an approximation of the actual solution to the nonlinear equation.

Whenever one studies a complicated problem by implementing numerical solvers, there is the danger of bugs going unnoticed. By implementing both numerical methods to determine stability boundaries and to experimentally determine the dynamical behaviour of solutions of the initial value problem and by confronting the results, one can test the reliability of both.

Acknowledgements

We thank two anonymous referees for constructive criticism which helped to improve the exposition.

Notes

^†Dedicated to Mimmo Iannelli, at the occasion of his 65th birthday, in appreciation of his stimulating friendship, the love for renewal equations that we share.