Optimality of a time-dependent treatment profile during an epidemic

Abstract

The emergence and spread of drug resistance is one of the most challenging public health issues in the treatment of some infectious diseases. The objective of this work is to investigate whether the effect of resistance can be contained through a time-dependent treatment strategy during the epidemic subject to an isoperimetric constraint. We apply control theory to a population dynamical model of influenza infection with drug-sensitive and drug-resistant strains, and solve the associated control problem to find the optimal treatment profile that minimizes the cumulative number of infections (i.e. the epidemic final size). We consider the problem under the assumption of limited drug stockpile and show that as the size of stockpile increases, a longer delay in start of treatment is required to minimize the total number of infections. Our findings show that the amount of drugs used to minimize the total number of infections depends on the rate of de novo resistance regardless of the initial size of drug stockpile. We demonstrate that both the rate of resistance emergence and the relative transmissibility of the resistant strain play important roles in determining the optimal timing and level of treatment profile.

Keywords:

• epidemic modelling
• influenza
• limited antiviral stockpiles
• drug resistance
• control theory

AMS Subject Classification:

• 34
• 49
• 92

1. Introduction

Optimizing intervention strategies is an important policy issue for the management of infectious diseases, in particular when facing an emerging pathogen. In case of influenza, antiviral treatment is a key pharmaceutical measure that reduces illness and duration of infection, and consequently lowers the transmissibility of disease in the population. However, treatment exerts a significant selection pressure that favours resistance and encourages its wide spread in the population [3,8,26,28,31]. The transmissibility of resistance is generally lower than its competitor (sensitive strain) due to a fitness cost associated with de novo resistance emergence. However, since treatment suppresses the growth and spread of the sensitive strain, the relative transmissibility of resistance can be improved through further replication in multiple hosts [3,5,9,26–29]. The effectiveness of antiviral drugs may therefore be trivialized once resistance has developed and spread between individuals. This poses an important question for optimizing treatment strategies in order to reduce the impact of disease on the population, but also minimize the selective pressure of drugs on the evolutionary-epidemiological consequences of resistance emergence.

In the present paper, we extend our previous work [14] on optimal treatment profile during an influenza epidemic by taking into consideration isoperimetric constraints which are imposed on the resources (i.e. the amount of drug stockpile available for treatment). With a limited drug stockpile in the presence of resistance, identifying optimal treatment strategies is a control problem and therefore requires the application of control theory for minimizing the total number of infections during an epidemic episode. To address this problem, we employ an established population dynamical model of influenza infection and investigate analytic solutions for the time-dependent control components. Our objective is to find the optimal treatment profile that minimizes the epidemic final size, resulted from disease transmission through a bilinear mass action incidence. A time-dependent treatment profile was initially introduced by Moghadas et al. [28], proposing a switch in the level of treatment from a low value (at the early stages of disease outset) to a higher value (at a later stage during the epidemic). However, the optimality of this strategy depends on the initial level of treatment and the timing for the switch to a higher level, both of which are important factors for preventing wide-scale resistance spread and reducing the final size.

Using a control theory approach, we analyse different scenarios of optimal treatment profile and investigate how the rate of de novo resistance and its relative transmissibility affect the timing and outcomes of such optimal solutions. We describe the model and its assumptions and constraints, and define the control problem in Section 2. The effect of changes in parameters associated with resistance and the size of drug stockpile will be discussed in Section 3, and simulation results of particular scenarios will be presented. Finally, we close the paper with some concluding remarks and questions to be addressed in future work.

2. The model and control problem

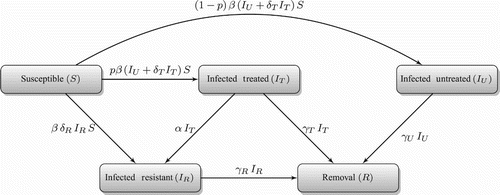
We consider a deterministic model of influenza epidemic [28] that describes the transmission dynamics of drug-sensitive and drug-resistant strains in a host population. The compartmental model divides a randomly mixed population into classes of individuals who are susceptible to infection (S); infected with the sensitive strain (I_U); treated (I_T); and infected with the drug-resistant strain (I_R). Since treatment is effective only against drug-sensitive infection, we combined treated and untreated classes of individuals infected with the drug-resistant strain. The transitions between these classes are represented in Figure 1, and mathematically formulated by the following system of differential equations: where ‘ ′’ is used to show the derivative of the compartments with respect to time (t) and p(t) (as function of time) is the fraction of infected individuals who receive treatment at time t. In this model, β denotes the baseline transmission rate of the drug-sensitive strain; δ_T (≤1) represents the relative infectiousness of treated individuals infected with the drug-sensitive strain (which is reduced compared to untreated infection); δ_R (≤1) is the relative transmissibility of the resistant infection (and is reduced compared to the sensitive infection due to the fitness cost of resistance emergence); α represents the rate of resistance emergence during treatment; and γ_U, γ_T, and γ_R are the recovery rates of untreated, treated, and resistant infections, respectively. The removal compartment consists of recovered individuals (R), and its dynamics are described by the equation We also assume that recovery upon infection provides protection against re-infection. For a single course of an influenza epidemic, natural birth and death rates are neglected. For a limited drug stockpile, the usage can be described by the following equation: with Δ(0)=K, where K represents the initial size of drug stockpile. The function Δ(t) represents the size of drug stockpile available for treatment at time t during the epidemic without replenishment [2,12,22,30]. For simplicity, we rewrite the model in the following form: where X=[S, I_U, I_T, I_R, Δ]^⊤ denotes the state of the control system, and G=[S′, I_U′, I_T′, I_R′, Δ′]^⊤, with S(0)=S₀>0, I_U(0)=I₀>0, I_R(0)=I_T(0)=R(0)=0.

Figure 1. Model diagram for the transitions between sub-populations with emergence of resistance during treatment.

2.1. The control problem

To show the existence of an optimal solution related to the time-dependent treatment level, we define the control problem with the objective of minimizing the total number of infections (epidemic final size). To do so, we express the control problem as where the cost functional is defined by and f(t, X, p)=(γ_UI_U+γ_TI_T+γ_RI_R). For consistency with the published literature [12,13], the upper bound of integration T_f denotes the end of epidemic, where T_f=∈f{t | (I_U+I_T+I_R)(t)=κ≪1}. We also assume that the initial size of drug stockpile is limited and may be exhausted before the end of epidemic (run-out scenario). This corresponds to the situation in which there exists some t_K<T_f, where (I_U+I_T+I_R)(t_K)≥1, but Δ(t)=0 for t≥t_K.

Remark

Let the pair (p*(t), X*(t)) be an optimal control for the corresponding solution of the system (1)–(5). Then, there is a t₁<T_f such that the optimal control value is given by p(t)=0 for t≥t₁.

We consider the effect of treatment as a reduction (by a factor of δ_T≤1) in transmissibility of the disease [28] and assume that recovery rates are the same for all infectious classes (i.e. γ_U=γ_T=γ_R), denoted by γ. In this case, the cost functional reduces to A direct application of Filippov's theorem [1] shows that the pair (p*(t), X*(t)) of admissible optimal control exists for our objective functional. Therefore, in what follows, the existence of an optimal control will be assumed. Now, we discuss the necessary conditions of optimality by introducing the Pontryagin minimum principle (PMP) [11,12,22]. Readers may also consult published literature for further applications of the PMP theorem [10,15–19,21,25]. The main technique in the PMP is to determine an admissible set of necessary conditions for an optimal control problem. This admissible set decreases the cost functional given by Equation (8) provided that the adjoint variable and the corresponding state variables satisfy certain conditions presented by PMP Theorem 2.1 [11,20,22].

Let be a bounded subset of ℝ as the collection of all admissible controls, p, with values in ℝ where admissible controls are measurable functions. We introduce as the set of all bounded measurable functions with values in ℝ for arbitrary positive time T, where T is the time of completion for the control program.

Theorem 2.1

Let the pair (p*(t), X*(t)) be an admissible control for the corresponding solution of system (1)– (4). Then, there exists an absolutely continuous function such that Λ(t)≠0 for t∈[0, T_f] with λ₀∈{0, 1} and for all admissible controls p at time t, where the Hamiltonian function is defined by in which the map ⟨·,·⟩ represents the standard inner product and the adjoint variables are obtained from Furthermore, Λ(T_f) is orthogonal to ker(DΨ(X(T_f))), where DΨ denotes the Jacobian of the set of possible values for the final state values.

The following lemma provides a different way of considering the objective functional and its proof is given in [14].

Lemma 2.2

Minimizing the cost functional given by Equation (9) is equivalent to reducing the influx rates from susceptible class to infection classes, that is, the cost functional can be written as where S_f=S(T_f) and S₀=S(0).

It is worth noting that minimizing the cumulative number of infections (final size of the epidemic) given by Equation (8) is equivalent to maximizing the final number of susceptibles S_f since S₀+I_U(0)−κ is fixed. From now on, we consider the new cost functional for minimizing −S_f resulted from Equation (10).

The function of Hamiltonian for the optimal control theory obtained by the PMP can be expressed by where λ₀∈{0, 1} and f≡0. As a result of the PMP, the adjoint equations corresponding to system (1)–(4) are obtained from where the transversality conditions are given by with q≥0. The Hamiltonian function can then be represented by multiple identities which will be used to study the dynamical model of influenza infection associated with the following system: We consider the maximization of an objective functional over a variable time interval, where the end time T_f is not fixed, and thus based on the PMP, H(t, X, Λ, p)=0 for the entire course of epidemic (t∈[0, T_f]). We note that λ_S(T_f)≠0 (or q≠0); otherwise, using the Hamiltonian at T_f gives q=0 (i.e. λ_S(T_f)=0) which contradicts the fact that Λ(t)≠0 for all t∈[0, T_f] in PMP Theorem 2.1.

2.2. Analysis of treatment profiles

The main challenge in implementing Pontryagin fundamental theory appears in Hamiltonian depending on the linear control p, that is, the function H is generated from the form where the function ψ explicitly consists of only state and adjoint variables, the control component p is constrained to upper and lower bounds 0≤p(t)≤1, and Ψ is the remaining nonlinear terms which depend only on the state and adjoint variables. To reduce the value of Hamiltonian H(t, X, Λ, p) to zero, we need to make the control function p as large or small as possible depending on the sign of ψ(X, Λ, t). The optimality condition represented by the switching time function, ψ, takes positive or negative values at some times and is non-zero with the possible exception of at most a finite number of times t, and the solution to the control problem is easily obtained from Equation (19). In this case, the optimal control is referred to as bang–bang control switches from 0 to 1 at finite number of times corresponding to sign changes in ψ(t) at each switch. However, the case of singularity for control problem arises when ψ(t) continues to be zero on a time interval t₁≤t≤t₂. In this case, the minimization of the Hamiltonian function with respect to the control function p does not provide any informative solution within that time interval. The common technique to explicitly characterize the control function is to recurrently take the derivative of ∂ H/∂ p with respect to time, which guarantees to generate the explicit solution [6]. Setting the expression for ψ(t) to zero, the control p is determined by the requirement that the singularity condition continues to hold. This characterizes the optimal control as follows:

Lemma 2.3

If δ_R=0 or α=0, then a shorter delay in switching the treatment level (from p=0 to p=1) corresponds to a lower epidemic final size regardless of the size of drug stockpile. The minimum cumulative number of infection is achieved when the switch occurs at the onset of epidemic (i.e. t=0). Also, we have ψ≤0 on [0, T_f] when λ_Δ=0.

Proof Case

1: Assume that λ_Δ=0. If α=0, then I_R=0 on [0, T_f]. We first show that the optimal treatment strategy is non-singular. Suppose there exists some interval [t₀, t₁] with t₀≤t₁ such that ψ(t)=0 for all t∈[t₀, t₁]. Thus, we have λ_T(t)=λ_U(t)+λ_Δ and λ′_U(t)=λ′_T(t) for all t∈[t₀, t₁]. Using Equations (13) and (14), it follows that λ_U(t)=λ_S(t)=λ_T(t)−λ_Δ. Considering Equation (12), when λ_Δ=0, we have λ′_U(t)=λ′_T(t)=λ′_S(t)=0, and consequently λ_S(t)=λ_U(t)=λ_T(t)=0 which is a contradiction with Λ(t)≠0. Thus, the optimal control is a bang–bang problem.

Suppose ψ(t₀)=0 and ψ(t)>0 on [0, t₀). Hence, λ′_U(t₀)=0 and we have Solving the above ordinary differential equation gives Since λ_T(0)>λ_U, (λ_T(0)−δ_Tλ_U)>(λ_U−δ_T λ_U); however, evaluating this at t=0 gives , which is a contradiction since .

Now we show that ψ<0 for the entire course of epidemic. For a contrary proposition, assuming that there is a switch before T_f, from the above results, it follows that there exist at least two switches occurring in (0, T_f). Let T₀ be the last switch where T₀<T_f. Since λ_U(T₀)=λ_T(T₀)<λ_S(T₀), there exists some t*∈(T₀, T_f) such that λ_T(t*)=λ_S(t*) and λ′_S(t*)=0<λ′_T(t*). Therefore, t* is an inflection point at which λ″_S(t*)=0, and from Equation (12) it follows that λ′_T(t*)=0, which is a contradiction.

Case

2: Suppose λ_Δ≠0 and that there exists some interval [t₀, t₁]⊂[0, T_f] on which , and therefore λ_U(t)+λ_Δ=λ_T(t) for t∈[t₀, t₁]. Using Equations (13) and (14), it follows that λ_U(t₀)=λ_T(t₀)−λ_Δ<λ_S(t₀) and λ_U(t₁)=λ_T(t₁)−λ_Δ>λ_S(t₁), implying that there exists some t*∈(t₀, t₁) such that λ_T(t*)−λ_Δ=λ_S(t*) and λ′_S(t*)=0<λ′_T(t*). This shows that t* is an inflection point at which λ″_S(t*)=0, and from Equation (12) it follows that λ′_T(t*)=0, again leading to a contradiction.   ▪

Theorem 2.4

Let (p*(t), X*(t)) be an optimal control for the corresponding solution of the system (1)–(5). Then, the adjoint variable corresponding to the isoperimetric constraint (5) is always non-positive.

Proof

Without loss of generality, we assume that the initial size of drug stockpile, K, is smaller than the total number of infections in the absence of any treatment. Otherwise, the adjoint equation λ_Δ=0. With limited drug stockpile over the time period of [0, T_f], there exists t_K<T_f such that the switching time function ψ must be non-negative over [t_K, T_f]. Thus, it follows from Equation (5) that λ_Δ remains either positive or negative constant for the entire epidemic course. Furthermore, taking into account the transversality conditions at T_f, it follows that there exists some t₁<T_f such that for t≥t₁. However, since ψ(t)≥0 on [t_K, T_f], we have If λ_Δ>0, then we have λ_T≥λ_U+λ_Δ>λ_U on [t_K, T_f], which contradicts the inequality (21). Consequently, the adjoint variable corresponding to the isoperimetric constraint (5) is always non-positive.   ▪

Suppose ψ(t)=0 for some interval [t₀, t₁], where 0≤t₀<t₁≤T_f. From the previous results, we have λ_Δ<0 and ( I_U+δ_T I_T−λ_Δδ_RI_R) S>0. Therefore, λ_T=λ_U+λ_Δ and λ′_T=λ′_U on [t₀, t₁] (singularity condition). Substituting this into Equations (13) and (14), we obtain From Equations (23) and (24), we see that

Theorem 2.5

[14] Suppose β S₀>α and p(0)=0, and let (p*(t), X*(t)) be an optimal control for the corresponding solution of the system (1)–(5). Then, a switch in the level of treatment (from p=0 to p>0) must occur before T_f for minimizing the epidemic final size and the expression for the final size relation is given by where N₀=S₀+I_U(0), with equality occurring for the second inequality ‘≤’ only if p(t)=0 for all t.

Remark

We denote the ratio β S₀/γ by R₀, the so-called basic reproduction number. In the epidemiological context, R₀ is defined as the number of secondary infectious cases generated by a single infected case introduced into an entirely susceptible population N₀∼eq S₀ (assuming I_U(0) is small compared to S₀) [7]. If R₀>1, then the outbreak will occur, whereas if R₀<1, then the outbreak is expected to die out.

A switch in the treatment level corresponds to a change of sign in ψ. Now, we show that no singularity can occur at the first switching time and the optimal control is a bang–bang problem.

Theorem 2.6

Suppose δ_T δ_R<1. Let (p*(t), X*(t)) be an optimal control for the corresponding solution of the system (1)–(4). If the switch function ψ remains zero on some interval [t₀, t₁], then

• (1) λ′_U=λ′_T≠0 on the same interval, that is, the adjoint variables λ_U=λ_T+λ_Δ must be either increasing or decreasing on [t₀, t₁ ;

• (2) λ′_R≠0 with opposite sign of λ′_U=λ′_T, that is, λ′_U λ′_R=λ′_T λ′_R<0 on [t₀, t₁].

Furthermore, no singularity occurs at the first switching time.

Proof

Suppose the switching time function ψ is zero on some interval [t₀, t₁] (0≤t₀<t₁≤T_f). Thus, λ_T(t)=λ_U(t)+λ_Δ on [t₀, t₁]. If λ′_T(t)=λ′_U(t)=0 for some t∈[t₀, t₁], then from the Hamiltonian function H(t, X, Λ, p)=−(λ′_U I_U+λ′_T I_T+λ′_R I_R)=0 on [0, T_f], it follows that λ′_U=λ′_T=λ′_R=0 (since I_R≠0). Taking into account Equations (22)–(25), it can be seen that From the first and second equalities, we have which is equivalent to Furthermore, using the equation for the Hamiltonian function, we obtain However from Equation (26) or (28), it follows that Comparing Equation (29) with Equation (30), we have Equality (31) holds only if λ_R≠0 (since otherwise Λ=0). Using Equation (28), it then follows that (1−δ_T)γ=α (δ_R−1), which holds only if δ_T=δ_R=1. In this case, the system (1)–(4) reduces to the basic SIR epidemic model, which essentially eliminates the effect of control problem. If, however, δ_T δ_R<1, we have a contradiction, and therefore when ψ(t) is zero on [t₀, t₁], we get λ′_U=λ′_T≠0 with opposite sign of λ′_R≠0.

Now suppose δ_T δ_R<1 and p*(t)=0 for t∈[0, t₀), where t₀ is the first time at which . Using Equation (23), it is easy to see that λ′_U(t₀⁻)=λ′_U(t₀⁺)=0. At t₀, we must then have . If λ′_T(t₀)<0, then clearly the control is non-singular at the first switch. If λ′_T(t₀)=0, then there are two cases: either ψ(t)≠0 or ψ(t)=0 on (t₀, t*] for some t*>t₀. The first case shows that the first switch is non-singular. The second case may generate a singular control. If ψ(t)=0 on (t₀, t*], then it follows that λ′_U(t)=λ′_T(t)≠0 on (t₀, t*]. Also λ_U(t₀)≠0, since otherwise λ_S(t₀)=λ_U(t₀)=λ_R(t₀)=0>λ_T(t₀)=λ_Δ which is a contradiction based on the previous result. In addition, there exists some t**, where t₀<t**≤t* such that (λ_S−λ_U)β S<γ λ_U(t) on (t₀, t**], and therefore λ′_U(t)=λ′_T(t)<0. This implies that t₀ is an inflection point for λ_U and λ_T at which λ″_U(t₀)=λ″_T(t₀)=0. Using Equations (23) and (24), it follows that which yields λ_R′(t₀)=0. This implies that λ_U′(t₀)=λ_T′(t₀)=λ_R′(t₀)=0, which contradicts the above result for λ_R′(t₀)≠0, and therefore, the optimal control is a bang–bang problem at t₀.   ▪

The following theorem shows the optimal treatment profile to minimize the overall impact of the disease and the total number of drug-resistant infections.

Theorem 2.7

Let (p*(t), X*(t)) be an optimal control for the corresponding solution of the system (1)–(5). Then, there exists some positive interval [0, t₀] (t₀<T_f) such that ψ(t)≠0 on [0, t₀].

Proof

Suppose that there exists some positive interval [0, t₀] on which ψ(t)=0 for the control problem corresponding to solutions of system (1)–(4). Thus, λ_T(t)=λ_U(t)+λ_Δ on the same interval [0, t₀]. Using Equation (12), it follows that From the Hamiltonian condition which shows that H(0)=0, we have Equating the above two equations, we obtain Subtracting the second adjoint equation (23) from the third one in Equation (24) and eliminating the expression for λ_S(0) give Now, by taking the derivative of each expression and then solving for λ_R(t), we have Using the fact that the function of Hamiltonian obtained from the Pontryagin fundamental theory must be zero at any time, that is, H(t, X, Λ, p)=−(λ′_U I_U+λ′_T I_T+λ′_R I_R)=0 for t∈[0, T], in particular, at the start point of time 0, it follows that Applying the same argument as in Theorem 2.6, the above expression is a contradiction, and consequently, we have λ_T(t)≠λ_U(t) on [0, t₀] before the first switch occurs.   ▪

3. Numerical experiments

In this section, we numerically illustrate the optimal scenarios of the treatment profile, when the drug stockpile is limited, and compare the results for variations in the rate of resistance emergence (α) and relative transmissibility of the resistant strain (δ_R). We show that, under some conditions, the system (1)–(4) has an infinite number of solutions generated by the optimal control (19). In all the simulations presented here, we fixed the basic reproduction number of the sensitive strain to be R₀=1.8.

3.1. Run-out scenarios

For a limited drug stockpile sufficient to treat 10% of the population, we simulated the model with the optimal treatment profile when α and δ_R vary in their respective ranges given in Table 1. Figure 2(a) shows the epicurves of untreated, treated, and resistant infections with α=10⁻³ and δ_R=0.9. Since, according to the optimal control, treatment starts with a delay following the onset of epidemic, resistance will be absent in the early stages of the epidemic. Initiation of treatment leads to the rapid suppress of the outbreak caused by the sensitive infection, but leads to the emergence and spread of the resistant outbreak. However, a second wave of infection with the sensitive strain occurs when the drug stockpile is exhausted. When the stockpile is increased (i.e. sufficient to treat 20% of the population), then the optimal control suggests similar delay in the start of treatment in the population; however, the size of drug stockpile is adequate to prevent the second wave of infection by the sensitive strain (Figure 2(b)).

Figure 2. Epidemic profiles with α=10⁻³ and δ_R=0.9 for (a) K=10% and (b) K=20%. Untreated, treated, and resistant infections are illustrated by the solid black, dashed black, and blue curves, respectively. Other parameter values are given in Table 1.

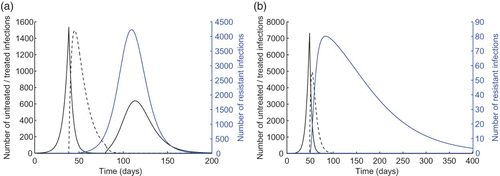
Table 1. Values of the model parameters obtained from the published literature.

Parameter	Value/range	Units	References
β	Variable	people^−1day^−1	[3,8,9,26,28,31]
δT	0.4	–	[3,9,26,28]
δR	[0, 1]	–	[3,8,26,28]
p(t)	[0, 1]	–	Assumption
α	10^−6−10^−1	day^−1	[24,26]
γU	0.244	day^−1	[3,4,9,26,28]
γT	0.244	day^−1	[3,5,9,26,28]
γR	0.244	day^−1	[3,4,9,26,28]

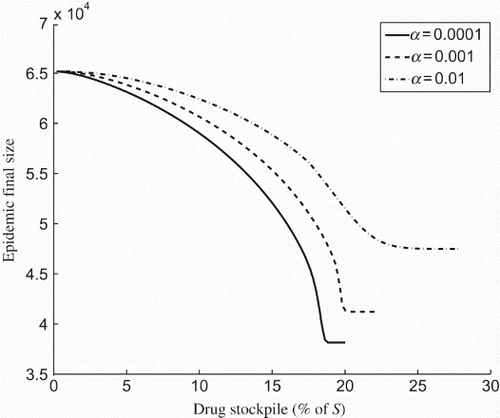
To explore the effect of the size of drug stockpile on the optimal treatment profile, we simulated the model for K=5%, 10%, 15%, 20%. Figure 3 shows the epidemic final size for different amounts of drug stockpile. Clearly, as the size of stockpile increases, a longer delay in start of treatment is required to minimize the total number of infections, which corresponds to a smaller region for optimal profile. It is, however, important to note that the amount of drugs used to minimize the total number of infections (corresponding to the optimal scenario) depends on the rate of resistance emergence regardless of the initial size of drug stockpile. Figure 4 shows the final size as a function of the drug stockpile for different values of α. As α increases, a larger drug stockpile is required to minimize the total number of infections.

Figure 3. Epidemic final size as a function of the treatment level and delay in start of treatment, with α=10⁻³ and δ_R=0.9, for (a) K=5%; (b) K=10%; (c) K=15%; and (d) K=20%. Other parameter values are given Table 1.

Figure 4. Epidemic final size as a function of drug stockpile (K) with δ_R=0.9 for (a) α=0.0001 (solid curve); (b) α=0.001 (dashed curve); and (c) α=0.01 (dot-dashed curve). Other parameter values are given in Table 1.

3.2. Effect of relative transmissibility and resistance development

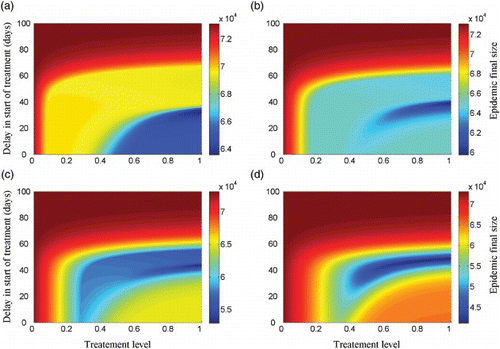
The effect of relative transmissibility of the resistant strain (δ_R) on the optimal treatment level has been investigated in previous work [12–14,23,26,28,31]. However, as shown in our simulations, the rate of resistance emergence (α) also plays a critical role in identifying the optimal treatment profile for a limited drug stockpile. To illustrate the combination effect of α and δ_R, we simulated the model to determine the optimal treatment rate (i.e. time dependent with a switch) for different sizes of drug stockpile (Figure 5(a)–(c)). These simulations indicate that when δ_R is relatively low (i.e. remains below 0.6 in these scenarios), the optimal control suggests that the minimum final size corresponds to the start of treatment at the onset of epidemic without any delay. However, as δ_R increases above a certain threshold, then the resistant strain gains a competitive advantage, and the size of stockpile becomes important in determining the delay in start of treatment. For some values of δ_R (0.6<δ_R<0.8 in these scenarios), as the size of drug stockpile increases, a longer delay is required to minimize the total number of infections (Figure 5(b)–(c)). This delay is shorter for higher values of α. For relatively high values of δ_R (δ_R>0.8 in these scenarios), the rate of resistance emergence (α) has very little impact in determining the optimal timing for switch (regions to the right side of δ_R=0.8 in Figure 5(a)–(c)).

Figure 5. Delay in start of treatment in the time-dependent profile as a function of δ_R and α to minimize the epidemic final size is shown for (a) K=8%; (b) K=12%; and (c) K=16%. Optimal level in the constant treatment profile as a function of δ_R and α to minimize the epidemic final size is shown for (d) K=8%; (e) K=12%; and (f) K=16%. Other parameter values are given in Table 1.

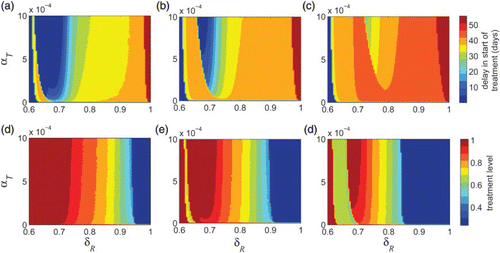
We obtained similar results when treatment profile remains constant throughout the epidemic without any switch (Figure 5(d)–(f)). Figure 5(d) shows that for low values of δ_R (below 0.6), the minimum final size corresponds to the highest treatment level. As δ_R increases, the size of drug stockpile determines the optimal treatment level, and this level decreases as K increases. Similar to the case of time-dependent treatment profile, for some values of δ_R (0.6<δ_R<0.8 in these scenarios), the rate of resistance emergence (α) plays an important role in determining the optimal treatment level. However, for relatively high values of δ_R (above approximately 0.8 in these scenarios), the rate of resistance emergence has very little impact on changing the optimal treatment level, regardless of the size of drug stockpile (Figure 5(d)–(f)).

3.3. Comparison between time-dependent and constant treatment profiles

To compare the outcomes of optimal scenarios in the two treatment profiles simulated in Figure 5, we defined F_op and F_oc to be the final sizes of the epidemic in the time-dependent and constant treatment strategies, respectively. We simulated the model to determine the minimum number of infections as a function of δ_R and α in each strategy. Simulations in Figure 6(a) and 6(b) show contour plots for the ratio F_op/F_oc with two different ranges of α. Simulation results for this ratio indicate that as the transmissibility of the resistant strain increases above a certain threshold, the ratio F_op/F_oc decreases below 1, implying that the optimal time-dependent treatment profile outperforms the optimal constant strategy in reducing the final size. However, the corresponding reduction in the final size depends significantly on the rate of resistance emergence. We also observe that, as δ_R increases, the change in the ratio F_op/F_oc is less pronounced for variation of α in the range 10⁻⁶−10⁻³ (Figure 6(b)) compared to the range 10⁻³−10⁻¹ (Figure 6(a)).

Figure 6. Contour plots for the ratio F_op/F_oc for α in the range (a) 10⁻³−10⁻¹ and (b) 10⁻⁶−10⁻³. Contour plots for the ratio K_op/K_oc for α in the range (c) 10⁻³−10⁻¹ and (d) 10⁻⁶−10⁻³. Other parameter values are given in Table 1.

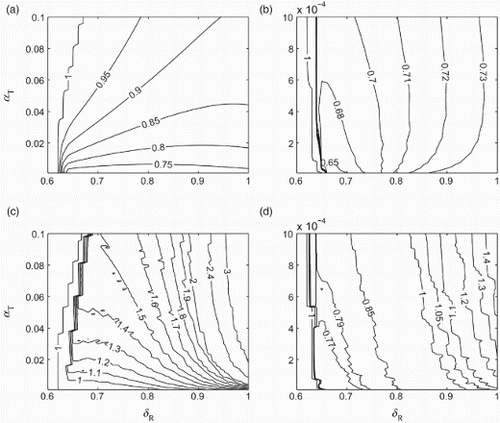
For further comparison, we simulated the model to find the corresponding ratio of K_op/K_oc, where K_op and K_oc are the minimum sizes of drug stockpile to achieve the optimal scenarios in the time-dependent and constant treatment strategies, respectively. Figures 6(c) and 6(d) show contour plots for K_op/K_oc as a function of δ_R and α, corresponding to simulations presented in Figure 6(a) and 6(b). As evident, when F_op/F_oc<1 for α in the range 10⁻³−10⁻¹, a significantly larger drug stockpile may be required in the time-dependent treatment profile (K_op/K_oc>1) as δ increases. However, for low values of α in the range 10⁻⁶−10⁻³ and δ below 0.8, the optimal time-dependent treatment profile outperforms the optimal constant treatment level (Figure 6(b)), with considerably smaller size of the drug stockpile (Figure 6(d)). As δ increases above 0.8, while F_op/F_oc<1, a larger drug stockpile is required in the time-dependent treatment profile compared to the constant treatment strategy. These simulations clearly illustrate the trade-off between minimizing the epidemic final size and the size of drug stockpile in the two scenarios discussed here, and highlight the importance of relative transmissibility and the rate of resistance emergence.

4. Concluding remarks

Summarizing our findings with simulation results, we observed that a time-dependent treatment profile can provide the optimal scenario for minimizing the epidemic final size in the presence of limited drug stockpile. We have shown the effect of two key parameters (i.e. the relative transmissibility of resistance and the rate of resistance emergence) in the optimal control problem. In some scenarios, we found that while the optimal time-dependent treatment strategy outperforms the optimal constant treatment policy, it requires significantly larger drug stockpile, and therefore a cost–benefit analysis would be desirable to inform an antiviral policy with regard to effectiveness and cost-effectiveness of treatment strategies. Combining findings of this study with those of our previous work with no constraint on the size of drug stockpile, Jaberi Douraki et al. [14] provide the grounding for further investigation on the optimal solution of the control problem. Based on the theoretical findings and numerical simulations, we conjecture that for any pair of optimal control (p*(t), X*(t)) corresponding to the solution of the control system (1)–(5), there exists a unique t₀∈[0, t_K) such that the switching function changes its sign at t₀ from positive to negative.

Acknowledgements

The authors would like to thank the reviewers for their insightful comments that have improved the paper. This work was supported in part by Mprime and the Natural Sciences and Engineering Research Council of Canada (NSERC).