Existence of solutions of a two-dimensional boundary value problem for a system of nonlinear equations arising in growing cell populations

Abstract

In the paper [A. Ben Amar, A. Jeribi, and B. Krichen, Fixed point theorems for block operator matrix and an application to a structured problem under boundary conditions of Rotenberg's model type, to appear in Math. Slovaca. (2014)], the existence of solutions of the two-dimensional boundary value problem (1) and (2) was discussed in the product Banach space L_p×L_p for p∈(1, ∞). Due to the lack of compactness on L₁ spaces, the analysis did not cover the case p=1. The purpose of this work is to extend the results of Ben Amar et al. to the case p=1 by establishing new variants of fixed-point theorems for a 2×2 operator matrix, involving weakly compact operators.

Keywords:

• operator matrix
• fixed-point theory
• weak compactness
• growing cell populations

1. Introduction

In this paper, we are concerned with the existence of solutions for the following two-dimensional boundary value problem introduced in [4]:

where , , μ∈[0, 1], with . The functions and are nonlinear and λ is a complex number.

The boundary conditions are given by

where and . We denote by (resp. ) the restriction of ψ_i to Γ₀ (resp. Γ₁), while K_i are nonlinear operators from a suitable function space on Γ₁ to a similar one on Γ₀. The main point in Equation (1) of this model is the nonlinear dependence of the functions on ψ_j. More specifically, we suppose that where f is a measurable function defined by with are measurable functions from to ℂ.

Rotenberg [17] proposed the singular partial differential equation:

which models the evolution of a cell population. Each cell is distinguished by two parameters, the degree of maturity μ and the velocity v.

Latrach and Jeribi [14] examined the existence of Equation (3) supplemented with the boundary conditions

Boulanouar [5] studied the one-dimensional cell proliferating model with linear boundary conditions (3) and (4), which generalize the known biological rules and proved that this model is governed by a strongly continuous semigroup.

Recently, Ben Amar et al. [4] proved an existence result for integrable solutions of the two-dimensional boundary problem (1) and (2) which were obtained in the Banach space for . The analysis was carried out via topological arguments and uses the compactness results established in [14] for a one-dimensional transport equation and the Schauder and Krasnoselskii fixed-point theorems [13,18]. The purpose of this work is to continue this analysis in the Banach space , due to the lack of compactness in L₁ spaces, by using the results concerning the weak compactness in [3]. Our strategy consists in establishing fixed-point theorems for a 2×2 operator matrix on the general product Banach spaces which can be applied directly to solve our problem.

Note that the boundary value problem (1) and (2) may be transformed into the following fixed-point problem: where

is a 2×2 block operator matrix defined on the product Banach space .

The outline of the paper is a follows. In Section 2, we recall some definitions and give basic results for future use. In Section 3, we establish some fixed-point results for the operator matrix (5). In Section 4, we use the results of Section 3 to derive the existence of solutions to problem (1) and (2) in the Banach space . In Theorem 4.1, we consider the special case where each σ_i does not depend on the density of the population i, that is, . The general boundary value problem (1) and (2) (i.e. is a nonlinear function of ) is discussed in Theorem 4.2.

2. Preliminaries

Throughout this section, denotes a Banach space. For any r>0, B_r denotes the closed ball in centred at with radius r. Here ⇀ denotes weak convergence and → denotes strong convergence in , respectively.

is the collection of all nonempty bounded subsets of and is the subset of consisting of all weakly compact subsets of . Recall that the notion of the measure of weak noncompactness was introduced by De Blasi [11]; it is the map defined in the following way: for all . For convenience, we recall some basic properties of needed below [2,11].

Lemma 2.1

Let be two elements of . Then, the following conditions are satisfied:

• (1)  implies .

• (2)  if and only if that is, is the weak closure of .

• (3) .

• (4) .

• (5)  for all .

• (6)  that is, is the convex hull of .

• (7) .

• (8) if is a decreasing sequence of nonempty bounded and weakly closed subsets of with then is nonempty and that is, is relatively weakly compact.

Definition 2.1

A map is said to be weakly compact, if is relatively weakly compact for every bounded subset .

Definition 2.2

A map is said to be ω-contractive (or ω-contraction) if it maps bounded sets into bounded sets, and there exists some α∈[0, 1) such that for all bounded subsets .

Definition 2.3

A map is said to be weakly–strongly sequentially continuous if for every sequence implies .

Let A be a nonlinear operator from into itself. Following Latrach et al. [15], we introduce the following conditions:

Regarding these two conditions, Latrach et al. [15, Remark 2.1] noted the following.

Remark 2.1

• (a) Operators satisfying or are not necessarily weakly continuous.

• (b) Every ω-contractive map satisfies .

• (c) A map A satisfies if and only if it maps relatively weakly compact sets into relatively weakly compact ones (use the Eberlien–Šmulian theorem [12, p. 430]).

• (d) A map A satisfies if and only if it maps relatively weakly compact sets into relatively compact ones.

• (e) The condition holds true for every bounded linear operator.

Moreover, note that is weaker than the weakly–strongly sequentially continuity of the operator A [1]. Now, we shall recall the following well-known results in [15].

Theorem 2.1

Let be a nonempty closed convex subset of a Banach space . Assume that is a continuous map which verifies . If is relatively weakly compact, then there exists such that Ax=x.

Theorem 2.2

Let be a nonempty bounded closed convex subset of a Banach space . Assume that is a continuous map satisfying . If A is ω-contractive, then there exists such that Ax=x.

Remark 2.2 Assume that a mapping is a contraction and satisfies then A is ω-contractive.

Theorem 2.3

Let be a nonempty closed bounded convex subset of a Banach space . Suppose that and such that

• (i) A is continuous, is relatively weakly compact and A satisfies

• (ii) B is a contraction satisfying

• (iii) .

Then, there is such that Ax+Bx=x.

3. Fixed-point theory

Let and be closed convex nonempty subsets of two Banach spaces and . We consider the 2×2 block operator matrix (5) defined on the Banach space , that is, the nonlinear operator A maps into , B from into , C from into and D from into .

Our aim is to develop a general matrix fixed-point theory which allows to treat the biological application described in the introduction. In the following, we discuss the existence of fixed points for the block operator matrix (5) by imposing some conditions on the entries, which are in general nonlinear operators. This discussion is based on the invertibility or not of the diagonal terms of .

First case: I−A and I−D are invertible.

Assume that

•  the operator I−A is invertible and ;

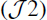• (I−A)⁻¹B is a operator continuous satisfying and is relatively weakly compact;

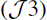• C is a operator continuous satisfying ;

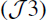• the operator I−D is invertible and their inverse (I−D)⁻¹ is continuous on and satisfies ;

• .

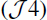
Theorem 3.1

Under assumptions – the block matrix operator (5) has a fixed point in .

Proof Let Γ be the operator defined by . In order to prove the theorem, we have to check that (1) is relatively weakly compact. For this, let be a sequence in , there exists a sequence such that for all , because and is relatively weakly compact then, by Eberlien–Šmulian theorem [12], has a weakly convergent subsequence. On the other hand, using the fact that C and (I−D)⁻¹ verify , the sequence has also a weak converging subsequence, it follows that is relatively weakly compact. (2) Γ satisfies the condition . Let be a weakly convergent sequence of , since (I−A)⁻¹B satisfies and has a strongly convergent subsequence. By the continuity of the operator C and (I−D)⁻¹, has also a strongly convergent subsequence, that is, Γ satisfies . Clearly, Γ is continuous; consequentially, Γ satisfies the hypotheses of Theorem 2.1 as we claimed, and there exists such that Let , hence . ▪

In the other cases, we will assume furthermore that and are bounded.

Second case: I−A or I−D is invertible.

We shall treat only the case of invertibility of I−A, the other case is similar just simply exchanging the roles of A and D and B and C.

Assume that

•  the operator I−A is invertible and ;

• is a contraction satisfying with constant k;

• D is a continuous operator satisfying and ω-α-contractive for some ;

• .

Theorem 3.2

Under assumptions – the block matrix operator (5) has a fixed point in .

Proof Since S is a contraction with a constant k∈(0, 1), the mapping I−S is a homeomorphism from into [18]. Let y′ be fixed in , the map which assigns to each the value Sy+Dy′ defines a contraction from into . Therefore, by the Banach fixed-point theorem, the equation y=Sy+Dy′ has a unique solution in . Therefore, Next, we will prove that satisfies the conditions of Theorem 2.2. It is clear that T is continuous and satisfies . Now, we check that T is ω-β-contractive for some β∈[0, 1). To do so, let be a subset of . Using the following equality: we infer that The properties of in Lemma 2.1 and the assumptions on S and D imply that and therefore, This inequality means that T is ω-β-contractive with . Consequently, T satisfies the hypotheses of Theorem 2.2 as we claimed, and hence, such operator has a fixed point in , so the operator matrix (5) has at least a fixed point in . ▪

Third case: Neither I−A nor I−D is invertible.

Here, we discuss the existence of fixed points for the following perturbed block operator matrix by imposing some conditions on the entries:

Assume that the nonlinear operators A₁ and P₁ maps into , B from into , C from into and D₁ and P₂ from into . Suppose that Equation (6) fulfils the following assumptions:

•  The operator I−A₁ (resp. I−D₁) is invertible from into (resp. from into ).

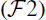• (I−A₁)⁻¹B and (I−D₁)⁻¹C are continuous, weakly compact maps and verify .

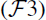
• and are contraction maps and verify .

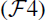
• and .

Theorem 3.3

Under assumptions – the block matrix operator (6) has a fixed point in .

Proof Using assumption the following equation may be transformed into where and Obviously, the operator matrix is continuous. Now, we check that is a weakly compact operator and satisfies . To see this, let be a sequence in ; since (I−A₁)⁻¹B is weakly compact, the sequence has a weakly convergent subsequence, say . On the other hand, the sequence has a weak converging subsequence say , then is a weakly convergent subsequence of ; hence, is a weakly compact operator. Also, we show that the operator matrix verifies and from the operator matrix is a contraction that satisfies . It follows with and Theorem 2.3 that the operator matrix (6) has at least a fixed point in . ▪

4. Application to transport equations

The aim of this section is to apply Theorems 3.1 and 3.3 to discuss existence results for the two-dimensional boundary value problem (1) and (2) in the Banach space . To do so, let us first make precise the functional setting of the problem. Let where . We denote by and the following boundary spaces endowed with their natural norms. Let be the space defined by It is well known [7,8,10] that any ψ in has traces on the spatial boundary {0} and {1} which belong, respectively, to the spaces and .

We define the free streaming operator , i=1, 2, by where , , and K_i, i=1, 2, are the following nonlinear boundary operators

satisfying the following conditions:

 There exists α_i>0 such that

K₂ is a weakly compact operator on .

As an immediate consequences of we have the continuity of the operator K_i from into and Let us consider the equation Our objective is to determine a solution where g is given in and . Let be real defined by For , the solution is formally given by Accordingly, for μ=1, we get

Let the following operators: and finally Clearly, for λ satisfying , the operators P_{i, λ}, Q_{i, λ}, and R_{i, λ}, i=1, 2, are bounded. It is not difficult to check that

and

Moreover, simple calculations show that

and

Thus, Equation (7) may be written abstractly as On the other hand, ψ_i must satisfy the boundary condition (2); thus, we obtain

Observe that the operator in Equation (12) is defined from into .

Let ; from and estimate (8), we have

Consider now the equation

where u is the unknown function and define the operator on by It follows from estimate (13) that Consequently, for the operator is a contraction mapping and therefore Equation (14) has a unique solution Let W_{i, λ} the nonlinear operator defined by

where u_i is the solution of Equation (14). Arguing as the proof of Lemma 2.1 and Proposition 2.1 in [14], we have the following result.

Lemma 4.1

Assume that holds. Then,

(1) for every λ satisfying i=1, 2, the operator W_{i, λ} is continuous and maps bounded sets into bounded ones and satisfies the following estimate

(2) If then the operator is invertible and is given by

Moreover, is continuous on and maps bounded sets into bounded ones.

In what follows and for our subsequent analysis, we need the following hypothesis:

• ( ,

where f is a measurable function defined by with , , is a measurable function from to ℂ which defines a bounded linear operator B_ij by

Definition 4.1 [16]

Let B_ij, be the operator defined by Equation (16). Then, B_ij is said to be a regular operator if is a relatively weakly compact subset of .

Lemma 4.2 [3]

If B_ij, is a regular operator then is weakly compact on for .

Let D be a subset of ℝⁿ. Recall that a function is said to satisfy the Carathéodory conditions on if

Observe that if f is a Carathéodory function, then we can define the operator on the set of functions by for every . The operator is called the Nemytskii operator generated by g.

In L_p spaces, , the Nemytskii operator has been extensively investigated [9,10]. However, we recall the following result which states a basic fact for the theory of these operators on L₁ spaces.

Lemma 4.3 [9]

Assume that g satisfies the Carathéodory conditions. If the operator acts from L₁ into L₁, then is continuous and takes bounded sets into bounded sets.

We shall also assume that

•  f satisfies the Carathéodory conditions and acts from into .

We recall the following lemma established in [15] which will play a crucial role below.

Lemma 4.4

If condition holds true, then satisfies .

We are now ready to state our first existence result.

Theorem 4.1

Assume that – hold. If B₁₂ is a regular collision operator on then for each r>0 there is λ_r>0 such that for each λ satisfying the problem

has at least one solution in .

Proof Let λ be a complex number such that with . Then, according to Lemma 4.1, is invertible and therefore the problem (17) and (18) may be transformed into where Claim 1 Let r>0. We first check that, for suitable λ, leaves B_r invariant. Let ψ∈B_r; therefore, from Lemma 4.1 and the estimates (8)–(11), we have where M(r) is the upper-bound of on B_r. Let . For we have Therefore, Using Equation (15), we have Let , and from the estimate (8) there exists λ₁ such that for any λ satisfying , we have ; then using we obtain It follows that Therefore, where Clearly, Q(·) is continuous strictly decreasing in t>0 and satisfies . Hence, there exists λ₂ such that . Obviously, if , then maps B_r into itself.

Claim 2 It is immediate that the operator S_λ is continuous and weakly compact on . Now, we check that S_λ satisfies the condition . For this, let be a weakly convergent sequence of . Using the fact satisfies , has a weakly convergent subsequence, say . Moreover, using Proposition 2.12 and Lemma 4.7 in [3], we have weakly–strongly sequentially continuous, so converges strongly in . Then, S_λ satisfies .

Claim 3 Clearly is continuous on . Now, we check that satisfies the condition . To do so, let be a weakly convergent sequence of . Using the fact satisfies the condition , has a weakly convergent subsequence, say . Moreover, the continuity of the linear operator B₂₁ implies that it is weakly continuous on [6], so converge weakly in . Then, satisfies .

Claim 4 Clearly from Lemma 4.1, we have that exists and is continuous on . Now, we check that satisfies the condition . For this, let be a weakly convergent sequence of . Using the fact is a bounded sequence and K₂ is a weakly compact operator on , has a weakly convergent subsequence say ; moreover, using the continuity of the linear operators Q_{2, λ} and R_{2, λ}, we have that converge weakly in . Then, the operator satisfies . Arguing as the claim 1 for , there exists λ_r such that for , we have . Finally, Γ has a fixed point in B_r; equivalently the problem (17) and (18) has a solution in . ▪

Now, we discuss the existence of solutions for the more general nonlinear boundary problem (1) and (2). When dealing with this problem, some technical difficulties arise. Therefore, we need the following assumption:

  and for each r>0, the function , i=1, 2, satisfies where denotes the set of all bounded linear operators from into and and acts from into .

Define the free streaming operator , i=1, 2, by

Theorem 4.2

Assume that – hold. If B_ij, are regular collision operators on then for each r>0, there is λ_r>0 such that for each λ satisfying the problem (1) and (2) has at least one solution in .

Proof Since K_i, i=1, 2, is linear, the operator is linear too. Using Lemma 4.1, where denotes the resolvent set of . Let such that . Then, by linearity of the operator , the problem (1) and (2) written in the form where may be transformed into the form where and Claim 1 Check that, for suitable λ, the operator is a contraction mapping. Indeed, let , A simple calculation using the estimates (8)–(11) leads to

where . Moreover, taking into account the assumption on we get where . Using the estimate (19) we have Note that E is a continuous strictly decreasing function in t>0 and Therefore, there exists such that Hence, for is a contraction mapping.

Claim 2 Using Lemma 4.2 and arguing as in the proof of Theorem 4.1, we show that satisfies and is continuous, weakly compact on and satisfies .

Claim 3 Let r>0 and . According to estimation (19), we obtain where T(·) has the same properties as E(·), and M(r) and M′(r) are the upper-bounds of and on B_r. Arguing as above, we show that there exists λ₂ such that, for all λ such that , we have .

By similar reasoning, we prove that there exists λ₃, such that , and we have .

Finally, if , then for all λ satisfying , the operators and satisfy the conditions of Theorem 3.3. Consequently, the problem (1) and (2) has a solution in for all λ such that . ▪