Heterogeneity in multiple transmission pathways: modelling the spread of cholera and other waterborne disease in networks with a common water source

Abstract

Many factors influencing disease transmission vary throughout and across populations. For diseases spread through multiple transmission pathways, sources of variation may affect each transmission pathway differently. In this paper we consider a disease that can be spread via direct and indirect transmission, such as the waterborne disease cholera. Specifically, we consider a system of multiple patches with direct transmission occurring entirely within patch and indirect transmission via a single shared water source. We investigate the effect of heterogeneity in dual transmission pathways on the spread of the disease. We first present a 2-patch model for which we examine the effect of variation in each pathway separately and propose a measure of heterogeneity that incorporates both transmission mechanisms and is predictive of R₀. We also explore how heterogeneity affects the final outbreak size and the efficacy of intervention measures. We conclude by extending several results to a more general n-patch setting.

Keywords:

• epidemiology
• heterogeneity
• cholera
• basic reproduction number
• network
• multiple transmission pathways

1. Introduction

Mathematical models can be used to estimate key quantities related to the spread of infectious disease, such as the basic reproduction number R₀ or the fraction of the population affected by an outbreak, as well as give insight into how best to prevent or control an epidemic. Frequently models make the simplifying assumption that transmission rates are uniform across a population while in reality, heterogeneity is inherent to many epidemiological processes. We expect factors influencing the spread of disease (such as contact rates, susceptibility, or infectivity) to vary both within and across populations even in the absence of external influences such as seasonality. The effects of heterogeneity in transmission have been explored in the classical Susceptible-Infected-Recovered (SIR) model, and can significantly affect the dynamics of a model including estimates of R₀ and final outbreak size [1,7,8,22,43].

While in the SIR model transmission occurs via a single pathway (as a result of contact between susceptible and infected individuals), some waterborne diseases, such as cholera, can be spread through multiple pathways incorporating different timescales of transmission. Cholera is currently a major public health threat, with the World Health Organization estimating 3–5 million cases occur each year resulting in 100–120 thousand deaths [42]. Symptoms include profuse watery diarrhea and in extreme cases can lead to death from dehydration within hours. The treatment for cholera, rehydration via oral salts or intravenous fluids, is extremely effective. However, the case fatality rate for untreated individuals can be as high as 50% [4]. Outbreaks occur regularly in some areas of the world where the causative pathogen Vibrio cholerae is naturally occurring, such as Bangladesh [19]. There have also been recent severe outbreaks in Haiti [38], Zimbabwe [25], Angola [41], and other parts of Africa [12,23]. While isolated cholera cases have been observed in the USA [34], the disease tends to strike hardest in areas with poor economic conditions and limited access to clean water; these areas favour high transmission rates [32].

John Snow's celebrated investigations of London cholera [33] established the connection between contaminated water and cholera transmission. While Vibrio cholerae is an aquatic bacterium that is naturally occuring in brackish water and estuaries, clean water sources can also become contaminated. The cholera bacteria may persist in environmental water reservoirs for a significant amount of time [5], allowing disease transmission to occur through drinking contaminated water. Here, we refer to disease transmission through an environmental reservoir with long pathogen persistence as indirect/delayed transmission. This is in contrast with disease transmission through pathways with shorter pathogen lifetimes, for example through contamination of household water storage containers [35], food preparation [2,18,29], or direct person–person contact [15]. We refer to these latter pathways as direct/fast transmission. The time scales of pathogen persistence and transmission are particularly relevant for cholera, as freshly shed pathogen exists in a highly transmissible hyperinfectious state [16].

The relative importance of direct (fast) and indirect (delayed) transmission is still a major public health question, although both have been shown to be important [10]. The relative contribution of each pathway likely varies from outbreak to outbreak, as well as between different regions in a single outbreak [25,26], since factors affecting both transmission pathways are likely to vary within and across populations. Heterogeneity in direct transmission rates can arise from differences in degree of hand washing, behavioural differences (i.e. shaking hands, avoiding the sick), or kitchen sanitation. Heterogeneity in indirect transmission rates may potentially result from variation in shedding rates, pathogen lifetime, the number of contacts with contaminated water sources (access to clean water), amount of water consumed per contact, and treatment of drinking water prior to consumption (water sanitation).

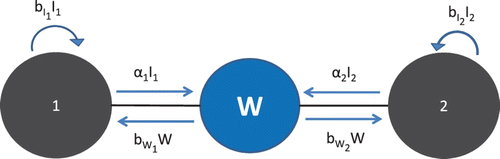
We explore the effect of heterogeneity in dual transmission pathways by adopting a metapopulation approach, where patches can be connected by person–person contacts or by a shared water source. There are a vast number of possible network configurations; specifically, we consider here a network of non-mixing patches with a single common water source, allowing patches to differ in both direct and indirect transmission rates (Figure 1). This simple network is motivated by living conditions in rural Bangladesh, where cholera is endemic [14]. Groups of patrileneally related families may live in multiple household structures known as baris [13], sharing a courtyard and kitchen. Many baris may share a water source such as a tube well for drinking water, or a local stream or lake. Persons from all baris may shed pathogen into the same water source and drink contaminated water from this source; however, transmission through direct contact or contaminated food occurs only within baris. This model can also be applied to villages situated around the perimeter of a lake.

Figure 1. Schematic of metapopulation model: multiple patches and common water source W.\newline Note: Outer arrows represent within patch direct transmission, with red denoting high transmission rates and green low transmission rates. Spokes connecting patches to the shared water source are similarly coloured to represent levels of indirect transmission. Individual patches may have high (low) rates of transmission for both transmission pathways, and are coloured red (green) accordingly. Patches may also have high rates for one type of transmission and low rates for the other; these patches are coloured orange.

In this paper we examine the effect of heterogeneity in one or both transmission pathways on the spread of disease. We first present the ordinary differential equation model that we will use to model the single-patch dynamics of the disease, and then construct a 2-patch model of non-mixing patches with a common water source and derive the basic reproduction number for this model. We examine how heterogeneity in the distribution of transmission in one or both pathways affects R₀, and look at how these results change with the composition of total transmission. We present results for the final outbreak size for the 2-patch model and consider how heterogeneity may affect intervention measures. Finally, we extend the 2-patch model to n patches and present generalizations of several results.

2. The SIWR model

We use the SIWR model of Tien and Earn [36] to describe disease dynamics. We note that although this model has mainly been developed for and applied to cholera (a review of other models used to model cholera can be found in [40]), it can be used to describe the dynamics of any disease spread both directly and indirectly through a reservoir. This model is a modification of the classical SIR model, incorporating an additional compartment W to track the concentration of pathogen in the water, a transition from the susceptible to infected class due to contact with the water source (with transmission rate b_W), and feedback from the infected class into the water (infecteds shed pathogen at rate α). Pathogen in the water decays at a rate ξ. The SIWR model is given by Equations (1), where S, I, and R denote the size of the susceptible, infected, and recovered populations, respectively, μ is the natural birth and death rate of the population, b_I is the direct transmission rate, and γ is the recovery rate.

A non-dimensionalized version of model (1) is given by the following equations:

where s=S/N, i=I/N, r=R/N, , , and .

The basic reproduction number, denoted by R₀, is the expected number of new infections produced by one infected individual introduced into a completely susceptible population over the course of its lifetime. Using the second-generation matrix approach [39] for the scaled SIWR model, . If R₀<1 the disease free equilibrium is globally asymptotically stable, and if R₀>1, the disease free equilibrium is unstable and the unique endemic equilibrium of model (2) is globally asymptotically stable [36]. We note that R₀ can be written as the sum of contributions from the direct transmission pathway, , and the indirect transmission pathway, . Detailed analysis of the SIWR model is given in [36].

3. 2-patch SIWR model with shared water source

Here, we construct a model for two populations (patches) sharing a common water source as shown in Figure 2. Person–person contact (and direct spread of disease) occurs only within each patch, but both patches may contact and shed into the same water source, allowing indirect transmission between patches. Both direct (also referred to as person–person, unshared) and indirect (or water, shared) transmission rates, as well as shedding rates, may vary among patches; the patch number to which a transmission-related parameter refers is denoted by a subscript.

Figure 2. Schematic of 2-patch model.

We denote the (constant) population size of patch i by N_i. The total population size of the system is given by N₁+N₂=N. The 2-patch SIWR model with a shared water source is given by the following equations:

Non-dimensionalizing the model results in the following equations:

where , , , , , , , , , , , and . and are the scaled direct and indirect transmission rates, respectively, for patch i.

The parameter a_j can be interpreted as the proportion of total shedding contributed by patch j (note a₁+a₂=1). Note that the water compartment W and indirect transmission terms are scaled by the total amount of pathogen shed. The product is then equivalent to β_W for the single-patch scaled SIWR model, with parameters from patch j.

The second-generation matrix FV⁻¹ for model (4) is where FV⁻¹(i, j) denotes the expected number of new infections produced in (a completely susceptible) patch i by one infected individual in patch j. R₀ is defined as the spectral radius of FV⁻¹; for the 2-patch model we can calculate R₀ explicitly:

We define to be the ‘patch R₀’ value for patch j, or the R₀ value for the SIWR model for patch j with its own water source. Then the first component of R₀ in Equation (5) can be interpreted as the average of the individual ‘patch R₀’ values, which we can write as

The second term of Equation (5) is the added contribution to R₀ from the shared water source. We note that the quantity under the square root is always non-negative, as

If there is no heterogeneity in transmission (i.e. the two patches have identical parameters, so and ) then the system R₀ is the average of the direct (unshared) transmission components of the patch reproductive numbers plus the sum of the indirect (shared) transmission components:

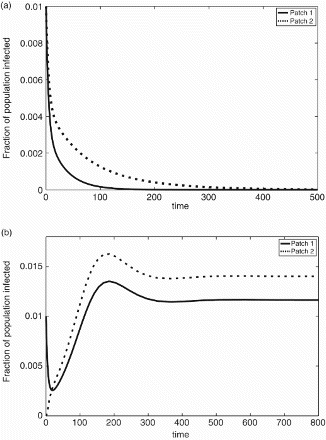
Due to the added contribution to R₀ from shared water transmission, the disease may persist in both patches for parameter values where it would not persist in either isolated patch alone (, system R₀>1; Figure 3).

Figure 3. (a) R₀=0.7407 in patch 1, and R₀=0.9259 in patch 2. The disease dies out in both patches when each patch has its own water source. Patch 1 parameter values: β_W=0.1, β_I=0.1, γ=0.25, ξ=0.1. Patch 2 parameter values: β_W=0.1, β_I=0.15, γ=0.25, ξ=0.1. Initial conditions: 99% of the population susceptible and 1% infected in each patch. (b) R₀=1.2151 for two patch system with shared water source. The disease persists in both patches. 2-patch parameter values: , , , a₁=a₂=0.5, γ=0.25, ξ=0.1. Initial condition: 99% of the population in patch 1 susceptible and 1% infected; patch 2 100% susceptible.

If the two patches differ in their transmission parameters, then R₀ may be either greater than or less than in the homogeneous case (7), depending on the distribution of the two types of transmission across patches. If one patch is higher in direct transmission but lower in indirect transmission compared to the other patch, then the term in Equation (5) will be negative.

R₀ of the system is always greater than or equal to the greater of the individual patch R₀ values. Equality is realized for cases where all the water transmission is on one patch, as the patches decouple and there is no amplification of transmission from sharing. This can occur when one patch either does not contact the water source, or possibly treats all water to prevent becoming sick. Assuming, without loss of generality, that all of the water transmission is on patch 1, R₀ reduces to:

This expression is minimized when the second term is zero, which occurs when total transmission in both patches is equal. If both types of transmission contribute equally, then this means the minimum R₀ occurs when all water transmission is on one patch and all person–person transmission is placed on the other patch. R₀ increases with the difference in total transmission among patches.

3.1 Heterogeneity in individual pathways

We next examine how the basic reproduction number (5) is affected when there is heterogeneity in each individual transmission pathway alone, and then when both are allowed to vary among patches.

Heterogeneity in direct (unshared) transmission only

If there is no variation in indirect transmission (shedding rates or water transmission rates) among populations, so , but populations may differ in factors related to direct transmission, such as hand washing, contacts with infected individuals, or kitchen sanitation, then the basic reproduction number is

In this case the distribution of person–person transmission among patches is important for disease dynamics. For a fixed total person–person transmission for the system (), R₀ will be lowest when this transmission is equal among patches, and increases with the magnitude of the difference between and .

3.1.2 Heterogeneity in indirect (shared) transmission only

Here, we assume there is no variation in direct transmission rates between patches (). Rather, patches may differ only in factors affecting indirect transmission rates, such as the amount of pathogen shed into the water, the rate at which they contact the shared water source, or the degree to which the population in each patch treats/sanitizes their water before drinking it. In this case

The total water transmission determines the value of R₀, and thus whether the disease can invade, and the distribution among patches is irrelevant.

3.1.3 Heterogeneity in both transmission pathways

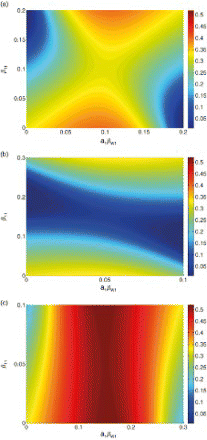
It is likely that both transmission pathways are heterogeneous across patches, and we next examine how the basic reproduction number changes with the distribution of both types of transmission among patches. The results are illustrated in Figure 4(a), which shows R₀ as a function of the amount of each type of transmission on patch 1. We see from Figure 4(a) that if person–person transmission is not homogeneous, then the distribution of water transmission becomes important for determining R₀. There is a trade-off between the two types of transmission – if patch 1 has more person–person transmission than patch 2, R₀ can be reduced by placing less water transmission on patch 1.

Figure 4. R₀ for model (4) as a function of distribution of both types of transmission across patches, for three cases: pathways contribute equally (), direct transmission dominates (, ), and indirect transmission dominates (, ). Axes denote the amount of transmission placed on patch 1, with the remainder placed on patch 2. For all cases, μ=0.02 and γ=0.25. (a) Direct and indirect transmission equal, (b) direct transmission dominant, and (c) indirect transmission dominant.

3.2 Relative contribution of transmission pathways

Since the relative importance of each pathway is likely different for each outbreak, we now investigate how our results depend on the relative contribution of each type of transmission to a fixed total amount of transmission. We consider three cases: direct and indirect transmission have equal importance, direct (unshared) transmission is dominant, and indirect (shared) transmission is dominant.

Figure 4 shows R₀ as a function of the amount of each type of transmission on patch 1 for these three possibilities. In all cases, we see that R₀ is maximized when all transmission (of both types) is placed on a single patch, with the other patch risk free (upper right and bottom left corners of plots in Figure 4, where all transmission is on either patch 1 or patch 2, respectively). The maximum value of R₀ is the same for all three cases, as it depends only on the total amount of transmission and not the relative composition of shared and unshared transmission.

We note that Figure 4 also illustrates the results of Section 3.1, for heterogeneity in only one pathway. R₀ remains constant for a horizontal cross-section through each plot at , showing that if direct (unshared) transmission is equal among patches, heterogeneity in indirect (shared) transmission alone does not affect R₀. Vertical cross-sections at illustrate our finding that when indirect transmission is equal among patches, R₀ is minimized when direct transmission is evenly distributed among patches () and increases with the difference between patches.

We have seen the minimum value of R₀ (for a fixed amount of total transmission) occurs when there is no sharing of indirect transmission (all water transmission is on one patch) and total transmission is equal among patches (c.f. Equation (8)). If the total amount of both types of transmission are equal (Figure 4(a)), then this occurs when transmission is completely segregated among patches. That is, all direct transmission is on one patch and all indirect transmission is on the other. If direct transmission is dominant (Figure 4(b)), then R₀ is no longer minimized when transmission is completely segregated among patches. Rather, the minimum now occurs when all water transmission is on one patch and the total amount of transmission on each patch is equal. The minimum value R₀ can attain is the same as in Figure 4(a). Finally, Figure 4(c) illustrates the third case, where a greater proportion of the total transmission is due to indirect transmission rather than direct transmission. The minimum again occurs when all the water transmission is on either patch 1 or patch 2, with all direct transmission placed on the other patch (note that now there is not enough direct transmission to generate equal total transmission in both patches). However, the minimum value of R₀ is higher than in the other two cases as the total amount of water transmission is higher.

3.3 R₀ and heterogeneity: variance and covariance

A classical result in mathematical epidemiology links the basic reproduction number with the variance in transmission or contact rates between groups [1,7,8]. These results hold for models with a single transmission pathway. In the presence of multiple transmission pathways, each pathway has the possibility of variability in its associated parameters. The variability in each pathway, as well as the interaction between different pathways, may affect the basic reproduction number.

Consider R₀ (Equation (5)) for the 2-patch system as we vary the distribution of shared and unshared transmission among patches, while holding the total amount of each type of transmission fixed. In this case, changes in R₀ stem solely from the last two terms in the radicand, , as the other terms in Equation (5) remain constant for fixed total transmission. This quantity is equal (up to a constant multiple) to the variance of direct transmission plus twice the covariance of direct and indirect transmission.

Therefore, we propose the following measure of heterogeneity:

where var and cov indicate the sample variance and covariance of the patch transmission parameters and , j=1, 2, constrained to have a sum equal to the total amount of direct and indirect transmission, respectively. Plotting R₀ versus our proposed measure of H for all possible distributions of transmission across patches, we see that R₀ is indeed an increasing function of H (Figure 5).

Figure 5. R₀ versus H, where H=var(β_I)+2 cov(a β_W, β_I), for 2-patch system, {with parameters as in Figure 4(a)}. R₀ is an increasing function of heterogeneity. This measure of heterogeneity incorporating the trade-off between different types of transmission is predictive of R₀.

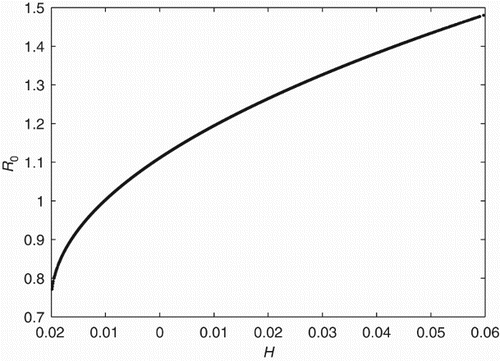
Variation in person–person transmission increases the first component of H (). However, if there is also variation in water transmission, distributing the two types of transmission so that they are negatively correlated may serve to reduce H, and may reduce R₀ even below that for the homogeneous case. If both transmission pathways are equally distributed among patches, then H=0 and R₀>1 for the example in Figure 5. R₀ can be reduced below the threshold of unity by reducing H; this can be done by distributing transmission among patches so direct and indirect transmission are negatively correlated. Increasing heterogeneity in both individual pathways may reduce H by reducing heterogeneity in total transmission among patches and/or reducing the amplification of shared transmission.

3.4 Final outbreak size

While the value of R₀ is important for determining whether or not an outbreak will occur, other measures are also of interest, such as the final outbreak size. For SIR models, as well as many modifications of the classical SIR model, the final outbreak size z is given by the following relation:

where z denotes the proportion of the population who became infected at some point during the outbreak. This relation also applies to many modifications of the SIR model [21], including the SIWR model, provided w(0)=0 [36]. For our 2-patch model, this equation no longer holds.

Proposition 3.1

If μ=0, w(0)=0, and R₀>1, then the final outbreak size in patch 1 (z₁) and patch 2 (z₂) are given by the following equations:

which are equivalent to

Proof The proof is similar to that used for the SIWR model in [36] and staged-progression models in [21]. Let

F₁(t) and F₂(t) are both constant along solution trajectories of model (4). Since μ=0, with no new births to replenish the susceptible population, the outbreak eventually dies out (). The susceptible and recovered populations approach the limits , , , and with and . Then

Also,

Letting , (and thus , , , ) and ,

Since both F₁(t) and F₂(t) are constant along solution trajectories, and , so

and

which give the desired result with and .

The size of the final outbreak in patch 1 is increased by the shedding from patch 2 as long as there is a non-zero amount of water transmission in patch 1, and visa versa. Thus the sharing of a water source increases the final outbreak size compared to when two patches are isolated. If there is no heterogeneity in transmission, then z₁=z₂=z, and the (equal) final outbreak size in each patch i is given by:

for i=1, 2.

Figure 6 shows the final outbreak size as a function of the amount of each type of transmission on patch 1, for the cases where total direct and indirect transmission are equal (Figure 6(a)), direct transmission is dominant (Figure 6(b)), and indirect transmission is dominant (Figure 6(c)). Whereas the maximum R₀ value occurs when all transmission is placed on one patch, we see that the maximum outbreak size does not occur here (although the maximum outbreak size for one patch, and minimum outbreak size for the other, does occur here). Rather, it occurs when all person–person transmission is on one patch, but water transmission is more evenly distributed. Thus, final outbreak size does not necessarily increase with R₀.

Figure 6. Shown are the total outbreak size (z₁+z₂) as a function of the distribution of transmission for three cases: direct and indirect transmission equal ( and , direct transmission dominant ( and ), and indirect transmission dominant ( and ). Axes denote the amount of each type of transmission on patch 1. Here μ=0 and γ=0.25. (a) Direct and indirect transmission equal, (b) direct transmission dominant, and (c) indirect transmission dominant.

3.5 Control

3.5.1 Sensitivity

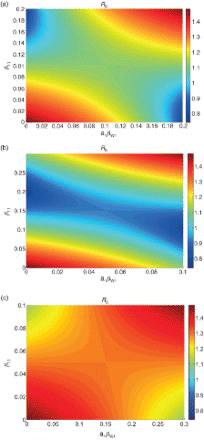
So far we have been looking at how the distribution of transmission among patches affects the spread of disease, while keeping total transmission constant. One of the primary goals of modelling cholera is to gain insight into the most effective intervention mechanisms in order to control the spread of the disease. Assuming we can reduce transmission by a certain percentage, then we can look at the reduction we can achieve in R₀ with a percent reduction in a parameter p, where p will be one of our transmission rates:

If we can only control one type of transmission on one patch, then we can examine how the best choice depends on heterogeneity. While one might expect that the transmission parameter greatest in magnitude should be reduced, we see in Figure 7 that this is not always the most effective choice. Rather, there are situations for which it is most effective to control water (shared) transmission, even though there are other transmission parameters of greater magnitude. It is never the case that controlling unshared transmission is most effective when it is not of greatest magnitude.

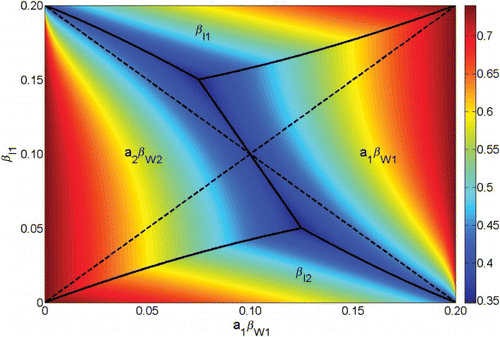
Figure 7. A comparison of the regions where the sensitivity of R₀ to each transmission parameter is greatest and the regions where each transmission parameter is greatest. Shown in colour is max((∂ R₀/∂ p)p) for , , , . The plane is divided into four regions (upper, lower, left, right) where R₀ is most sensitive to , , , and , respectively (boundaries denoted with solid black lines) and where each the value of each transmission parameter is greatest (boundaries denoted with dashed black lines). Here μ=0.02 and γ=0.25.

3.5.2 Type reproduction numbers

For heterogeneous models with different groups of infectious individuals, it may be useful to consider the type reproductive number [3,17,31] rather than the basic reproductive number, where T_i represents the expected number of secondary type i infections produced by an infected type i individual over its lifetime. While T_i<1 (T_i>1) if and only if R₀<1 (R₀>1), it may be the case that we can only implement intervention measures for one type of infected individual, with no control over the other types. Here, type i individuals are those infected individuals in patch i. Without loss of generality, we calculate the type reproduction number for patch 1, T₁, for the 2-patch model (4) (provided , else there is no chance of controlling the outbreak via patch 1 alone):

Note that , so reducing the basic reproduction number for patch 1 alone below 1 may not be sufficient to prevent an outbreak if a water source is shared with another population. We see that controlling the disease in a particular patch may require more effort than is apparent from the single-patch reproduction number. The effect of the adjoining patch via the shared transmission pathway may be enough to allow the disease to flourish (by increasing the type reproductive number above 1), even in cases where the second patch reproduction number is less than 1. We can also write T₁ as follows

From Equation (29), one can see that reducing either person–person or water transmission will reduce T₁, however decreasing water transmission on patch 1 will have a greater effect on T₁ than direct person–person transmission rates due to the shared nature of the water source.

4. n-patch model with shared water source

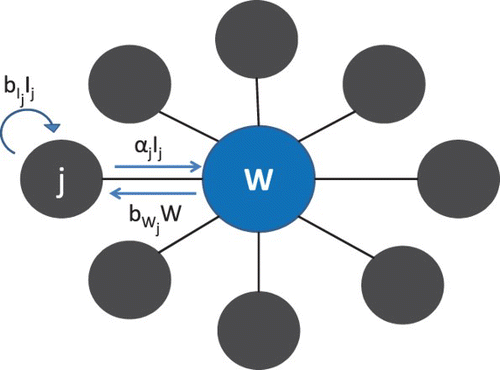
We now extend our model to n non-mixing patches connected only by a common water source (Figure 8).

Figure 8. Schematic of n-patch setup with shared water source.

The equations for the n-patch model (30) follow naturally from those for the 2-patch case (3).

A non-dimensional version is given by the following equations:

where , , , , , , .

Again, is the indirect transmission rate for patch j, scaled by total shedding, and is the indirect transmission rate that patch j would have in isolation with its own water source. R₀, the basic reproductive number of the system, is again given by the spectral radius of the second-generation matrix FV⁻¹, calculated as in [39]: where as in the 2-patch case, however now the dominant eigenvalue cannot be calculated analytically.

4.1 Heterogeneity in individual pathways

As for the 2-patch model, we first consider how the spread of disease is affected by heterogeneity in only one of the two transmission pathways. While we cannot explicitly calculate R₀ in general, we next extend several 2-patch results to the general case of n patches.

4.1.1 Heterogeneity in direct (unshared) transmission only

If shedding rates and transmission through water are the same across all patches, but person–person transmission differs among patches, the second-generation matrix has the following form: R₀ is given by the dominant eigenvalue of the upper n×n matrix. This matrix has the form of a constant matrix plus a diagonal matrix. From [20, p. 417], we know that for a non-negative symmetric matrix perturbed by a diagonal matrix with zero-trace, the minimum eigenvalue of the perturbed matrix occurs when all row-sums are equal. If the row-sums of the unperturbed matrix are already equal (true when all shedding rates, a_i, and water transmission rates , are equal for all patches), then the minimum eigenvalue occurs uniquely for zero-perturbation. Biologically, we can say that for a constant total amount of person–person transmission (β_I), the minimum R₀ occurs when are equal across all patches. This result generalizes our earlier result for the two patch system, that R₀ is minimized when person–person transmission is distributed evenly across patches.

4.1.2 Heterogeneity in indirect (shared) transmission only

If shedding rates are equal and transmission through water varies across all patches, while person–person transmission is equal among patches, the second-generation matrix has the following form: Again, R₀ is given by the spectral radius of the upper n×n matrix. This matrix now has the form of an n×n rank-one matrix (W) plus an n×n constant diagonal matrix (D), where W and D are as follows

Since D can be written as , the eigenvalues of W+D are equal to the eigenvalues of W plus (since

We can also calculate the dominant eigenvalue of W. W can be written as W=xy^T where and . Then the dominant eigenvalue of W is given by . The sum can be interpreted as a weighted average of the . In this case, R₀ is determined by the average of the (with respect to weights a_k); if shedding is equal across patches, then R₀ does not depend upon the variability in the between patches.

4.2 R₀ and heterogeneity: variance and covariance

We cannot find an explicit expression for R₀ of the general n-patch system, and therefore we cannot propose a heterogeneity measure based on an expression for R₀ as we did for the 2-patch case. Instead, we propose a measure of heterogeneity that is a natural extension of that for the 2-patch system, . Figure 9 shows R₀ plotted against this measure of H (blue). We see a cone-like shape rather than a single curve. There is a wide base, as multiple distributions with different values of H result in the same R₀. Yet the maximum R₀ can only be attained in one way (transmission all on one patch). Scatter is reduced if we only consider distributions with randomly chosen symmetric perturbations to the average β_I and a β_W randomly distributed among patches (red). The size of each perturbation is between 0 and the average β_I or a β_W; for each type of transmission, half the patches will be above average and half will be below average. For this case, it appears that R₀ increases if H is increased enough, but R₀ is not a function of H.

Figure 9. R₀ versus H (defined as H=var(β_I)+n cov(a β_W, β_I)) for a 4 patch network with a common water source, with both total water and person–person transmission held constant (, {μ=0.02, γ=0.25}). Shown are results from three simulations. First, transmission values for each patch are drawn from a complete random sampling of β_I, a β_W space (blue points). Next, all transmission values are restricted to symmetric perturbations from the average transmission rates (red points). Third, transmission parameters for each patch only have two possible values, high or low, and these values are determined by a random perturbation from the average transmission rate (yellow curve).

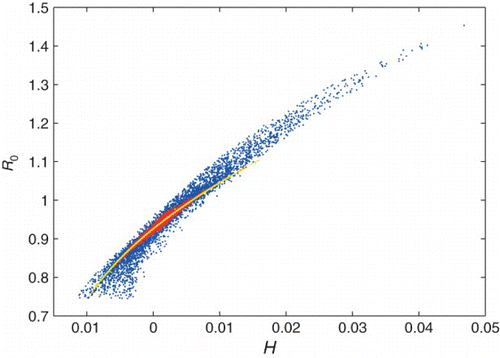
Another natural simplification of the model is to discretize the transmission parameters so that each transmission pathway can have either a high or low value, and patches can either be high (or low) in both types of transmission or high in one type and low in the other type. If we allow only one size perturbation to each type of transmission (so transmission parameters can be high or low), then R₀ is an increasing function of H (yellow). We conjecture that for an even number of patches taking on either high or low values in each type of transmission, R₀ is an increasing function of H. This has been shown directly for n=2, n=4, and n=6.

5. Concluding remarks

Disease spread is often promoted by connection to other regions. Reiner et al. [30] show that in Dhaka, Bangladesh, an urban core region serves to propagate disease to the other areas in the city. In Haiti, the internally displaced person (IDP) camps in the Port au Prince area were largely spared the first wave of the ongoing cholera epidemic in October 2010. This may be due to strong efforts to provision the camps with treated water, thereby ‘disconnecting’ them from the shared water source [9,28]. However, limited resources and the subsequent rainy season (which causes runoff and flooding) led to a resurgence of the disease throughout Haiti, including the (now ‘re-connected’) IDP camps [9].

By considering a network of multiple patches with a common environmental water reservoir, we find that the sharing of a water source by multiple populations always results in an increased R₀ and final outbreak size relative to the case where each population has its own (isolated) water source. In certain cases the connection between patches can allow the disease to persist in communities of multiple populations, where it could not persist in any individual population.

Mukandavire et al. [25] showed that the basic reproduction number for a 2008 and 2009 cholera outbreak in Zimbabwe was highly heterogeneous among provinces, and furthermore the estimates for the contribution of each pathway to the spread of disease also varied greatly. Incorporating heterogeneity in both direct (unshared) and indirect (shared) disease transmission rates into our network model, we found the relative total contribution of shared and unshared transmission, as well as the distribution of each type among patches to affect both the basic reproduction number of the system and the final outbreak size.

A classical result in mathematical epidemiology is that increased heterogeneity in transmission in SIR models increases the ability of disease to invade. One of the insights from this study is that when multiple transmission pathways exist, trade-offs in variability between pathways is also important. For the two patch system considered here, this can be explicitly quantified in terms of the covariance of the transmission parameters. We define a measure of heterogeneity H that is predictive of R₀, and with which R₀ increases. However, we also find that R₀ can be decreased by redistributing transmission so water and person–person transmission are not high or low on the same patches, despite increased variation in individual pathways. Disease spread is reduced when populations with high direct transmission rates are less ‘connected’ to other populations by having low indirect transmission rates, contacting and shedding into the water less. This distribution has a homogenizing effect on total transmission while minimizing the amplification of R₀ from the shared water source.

We find the total amount of transmission (shared plus unshared) across patches to be important for determining the maximum possible R₀. The upper bound on R₀ is realized for a specific distribution pattern – all transmission placed on a single patch, and the other risk free. We can think of this as a case of extreme heterogeneity, maximizing variation in each individual type of transmission across patches, as well as the variation in total patch transmission.

The lower bound on R₀ is determined by the total amount of indirect transmission, and occurs when all indirect transmission is placed on one patch. This means only one patch is contacting the water source, and all others are effectively disconnected. The system R₀ becomes the greatest individual patch R₀. For systems with more than two patches, there are multiple distributions of transmission that result in the same value of R₀. The minimum value is realized as long as the direct transmission on any patch disconnected from the water source does not exceed the indirect transmission rate on the patch using the water source. Therefore multiple distributions of transmissions can have different values of H but the same R₀.

Heterogeneity in transmission also has implications for controlling the spread of waterborne disease; our results demonstrate that a particular patch or pathway contributing more to disease transmission does not necessarily imply that it is the best target for an intervention. Figure 7 shows the most sensitive target for intervention measures may be different than the largest contributing transmission pathway or patch. For example, there may be situations where person–person transmission in patch 1 is greater than all other transmission pathways, but it is more effective to try and reduce water transmission on patch 1 instead (and try to disconnect the patch) rather than control direct transmission.

If we only have control over intervention measures in one patch, considering the type reproduction number gives insight that more effort may be required than considering the basic reproduction number of the patch alone. The form of the type reproductive number shows that reducing shared (indirect) transmission is more effective than reducing unshared (direct) transmission. These issues may be relevant in cases where patches represent adjacent countries or regions with interacting water sources, but where interventions are coordinated in one patch (country). For example, the recent cholera outbreak in Haiti [6,28,38] has spread to the Dominican Republic (21,432 cases and 363 deaths as of December 2011) [24,27], which may be important when designing control measures in Haiti.

The model considered in this paper has the form of multiple patches with a common water source and no person–person mixing. If we instead consider a model where person–person transmission is shared and each patch has its own unshared water source, then R₀ has the same form as Equation (5) with and interchanged. If we consider only the parameter as being allowed to be heterogeneous, then all results presented here are analogous and we can simply think of ‘shared’ and ‘unshared’ transmission. However, if shedding rates or population sizes (a_j) differ as well as contact rates with contaminated water () then it becomes important which transmission pathway is shared.

There is currently no explicit spatial structure incorporated in the model. Patches can be renumbered without affecting the results. Direct transmission between patches is an area for future work, with many possible modelling frameworks and network structures describing the interactions. In this case, the placement of high and low transmission patches within the network may affect the spread of disease (see [11,37] for related work on this topic).

Acknowledgements

We thank Tony Nance for his advice and discussion on this work.

Funding

This work was supported by the National Science Foundation through the Mathematical Biosciences Institute (DMS 0931642) and Grant OCE-1115881.