Abstract
We provide a generalization of the logistic two-sex model with ephemeral pair-bonds and with stable couples without assuming any specific mathematical form for fertility, mortality and the mating function. In particular, we establish a necessary and sufficient condition on the fertility/mortality density-dependent ratio that ensures the existence of the logistic behaviour. Several differences and similarities between the two models are also provided.
Keywords:
AMS Subject Classification:
1. Introduction
Two-sex models are clearly necessary in many models where the sex of individuals is important: demography, epidemics of sexually transmitted diseases, etc. The analysis of these models still faces numerous mathematical and conceptual difficulties. Most of these centre around how one models the pair-formation function. This is an issue of interest for both demographers and ecologists, namely those who are interested in two-sex dynamics from human motivated problems as well as questions arising from the animal world. The mathematical form that one chooses for the mating/pair-formation function is the core of controversy.
Below we summarize several hypotheses imposed on the pair-formation function by modellers with the observation that not all functions currently used satisfy all of these hypotheses. For a comprehensive review of gender-structured population modelling, see [Citation5] and references therein.
Let F and M denote the number of females and males available for pairing. The mating/pair-formation function is denoted by . The conditions usually imposed on
are
positivity:
whenever
,
heterosexuality:
. This indicates that the pair-formation function vanishes if individuals of one gender are absent,
homogeneity:
for every α≥0. This ensures the preservation of sex ratio if the number of singles in each gender changes by the same factor α,
monotonicity:
for every F2≥0 and M2≥0,
consistency:
and
for every F≥0 and M≥0. This condition ensures that the number of pairs is smaller than the number of available singles in each sex category.
Typical examples of functional forms for are
harmonic mean:
,
geometric mean:
,
female/male dominance: ρ F or ρ M,
generalized weighted mean:
,
where ρ denotes the pair-formation rate. The last example above was proposed by Hadeler [Citation3] and, for appropriate values of a and b, it corresponds to the other three examples mentioned above.
We point out that the heterosexuality condition is not satisfied by the female/male-dominated form of . Furthermore, the consistency condition may fail in the case of the geometric mean while it is guaranteed to hold in the case of harmonic mean. This is because
and, consequently,
while
Neither of these forms is universally acceptable by modellers. Furthermore, there is also the issue on how one interprets what the pair-formation actually means in the model. Demographers often use this function to model marriages while the actual birth is given as a rate per-couple which is modelled separately from un-paired (single) individuals. In the ecological models, where the focus of interest is the mating process, this function typically represent actual matings where pairings are made only for copulation. This eliminates the requirement to model couples separately. Of course, this will not be suitable for animals that form stable pairs.
We mention that we do not intend to argue in this paper in favour or against any of these proposed functional forms and their properties. Rather, we acknowledge that, in some cases, a modeller will adopt or reject a certain form and hypothesis. For example, if represents the number of sexual acts (i.e. purely a mating function) then, perhaps, the consistency condition is not mandatory. Conversely, if
is strictly designed to model the formation of stable pairs then consistency conditions become more important and female/male-dominated forms inappropriate. Indeed, as we will show later on, a female/male-dominated function will cause the two-sex model with couples to become biologically unfeasible (solutions starting with positive values become negative).
From these considerations, we believe it is important to establish a general logistic two-sex model (with and without couples) using a generic birth, death and mating function to allow greater flexibility in tackling problems related to gender-structured populations. Another motivation is given by epidemiology. When modelling an infectious disease, it is important to have a well-understood base-line demographic model of the population under study in the absence of the disease upon which to expand and incorporate the disease specific state variables: susceptibles, infected, recovered, etc.
Ideally we want a basic demographic model whose dynamics is completely determined by certain net reproductive numbers. However, most of the existing results are not as straightforward as the well-known Verhulst model [Citation9] for the one-sex case:
where K>0 is the carrying capacity. Here, the sign of the intrinsic growth parameter, r, is the threshold that separates the extinction from persistence of the total population P.
Corresponding two-sex logistic models typically assume specific forms and properties for the pair-formation function or for the fertility and mortality rates. Castillo-Chavez and Huang [Citation1] were the first to introduce a logistic version of the two-sex model with couples by introducing density-dependent birth and divorce rates but assuming constant mortality. They also assumed that the density-dependent birth rate is not only decreasing with the total population but also converging to zero which is a strong and somewhat less realistic assumption. Maxin and Milner [Citation6] analysed a logistic two-sex model with couples assuming a constant birth rate and density-dependent linear mortality forms. Here too we note the assumption of a specific form of the mortality rate and the proofs of the theorems actually depend on this assumption. These models still have open questions that are yet to be solved. Greater generality is achieved by Milner and Yang [Citation8], who analysed a two-sex logistic model with age-structure. However, the mathematical difficulties presented by partial differential equations models required additional technical hypotheses and the threshold between extinction and persistence is still an open problem.
If the couples are not modelled separately, results are, as expected, much stronger due to the fact that these models are planar (i.e. only females and males). In particular, global stability results can be established instead of local ones. Maxin et al. [Citation7] analysed the two-sex model with ephemeral pair-bonds using the harmonic mean mating function and linear density-dependent mortality rates with the same logistic term, i.e. the term b below,
where μf and μm are the background sex-specific mortality rates and P is the total population size. Again, some of the arguments in the proofs provided in [Citation7] depended on that particular choice of mortality rates, i.e. having the same logistic term b, and also made use of some properties of the mating function that are not present in others such as the consistency assumption.
In this paper, our aim is to generalize the current results from the two-sex logistic models without age-structure to a model with arbitrary mating/marriage function and density-dependent fertility and mortality rates. The only assumptions on the mating function will be: heterosexuality, non-negativity, monotonicity and degree-one homogeneity. The consistency assumption will not be needed and neither the heterosexuality in the case of the model without pairs. We will also assume a decreasing birth rate and increasing mortality rate. With this generalization we aim to make precise the threshold for existence of a logistic behaviour in terms of the relative dependence of fertility and mortality rates. This should provide greater flexibility in choosing these rates according to the biological properties of the population under study. In particular, it will be possible to include different logistic effects on the population if the environment affects the two genders in a different way. For example, Edwards and Edwards [Citation2] discuss population limiting factors and provide an example of a species (red deer) where population density effects are stronger in the males leading to skewed sex ratios. Another advantage is that one can use a density-dependent mortality that does not necessarily increases without bound or a density-dependent birth rate that decreases to zero as in the model proposed by Castillo-Chavez and Huang [Citation1].
The paper is structured as follows: in the first section, we introduce and analyse a logistic two-sex model without pair-formation and provide the thresholds described above. In Section 3, we analyse in a similar manner the two-sex model with pair-formation. We conclude with a discussion about the similarities and differences between the two models, directions for further study, as well as some illustrative examples which are provided in the appendix.
2. The two-sex logistic model with ephemeral pair-bonds
Consider the following model of a population where the reproductive individuals form pairs for mating purposes only (no stable couples).
non-increasing and positive birth rate:
non-decreasing and positive mortality rates:
β is the per-mating birth rate and
γf, γm with are the probabilities that a newborn is female or male, respectively.
We now define several important quantities that will be used throughout this section:
The logistic behaviour of solutions depends on the relative density dependence of mortality and fertility. Loosely speaking, the mortality should ‘gain traction’ relative to the birth rate as the population increases. It is not sufficient to simply have a decreasing birth rate and increasing mortality (see also Figure A1). The necessary and sufficient condition that ensures boundedness of solutions is made precise in the following theorem:
Theorem 2.1
If , the solution of Equation (1) is unbounded in the positive quadrant (i.e. no logistic behaviour). If
, the solution of Equation (1) is bounded in the positive quadrant.
In proving our main results, we will use an approach similar to the one used in [Citation1,Citation6].
Specifically, the proofs of all theorems (except the last one) make repeated use of bounding arguments for either the minimum or the maximum of two or three suitable functions. In general, given two differentiable functions, f and g, neither min{f, g} nor max{f, g} are differentiable but only continuous on their domains. This prevents the use of Riemann integrals in several necessary estimates. Nevertheless, the functions used in the proofs are increasing and measurable with respect to the usual Lebesgue measure on the real line. So they are differentiable almost everywhere and one can use the Lebesgue integral instead. In particular, we will use the following weak version of the Fundamental Theorem of Calculus.
Theorem 2.2
Let f be an increasing real-valued function on the interval [a, b]. Then f is differentiable almost everywhere. The derivative f′ is measurable and
We will also use, several times, the following identity:
This follows from differentiating the following identity with respect to α and replacing α with 1 afterwards
Finally, since the bounding arguments are very similar, we will provide full details for the first two proofs and concentrate only on the specific differences for the later ones in hope that this will avoid tedious redundancies when reading the paper.
Before proving the first theorem note that the existence, uniqueness and positivity of solutions of Equation (1) can be derived by standard means.
Proof [Proof of Theorem 2.1] Suppose . This implies
and
. Consider the following function
For every t>0 we distinguish two cases:
. This case implies the following lower bound on the males/females ratio:
We use this inequality in the following estimate:
Notice that the expression in the first square bracket above is always positive since the right side of the inequality is decreasing and bounded below by a positive constant and, letting
, we have
. Similar to the previous case,
which implies
. Then
. In a similar fashion, this case implies
The system (1) always admits the extinction equilibrium (0,0). In order to compute the interior (positive) steady state we see that, when solving for the equilibria,
We use this to substitute M/F in the first equation as follows
Therefore, an interior equilibrium (F*, M*) exists whenever the following function has a positive root P*:
with
Since f(P) is decreasing and and
, it is clear that the interior equilibrium exists if and only if the solutions are bounded, i.e.
and
. The following theorem establishes the limiting behaviour of the solutions of Equation (1) when they are bounded.
Theorem 2.3
Suppose . If
the extinction equilibrium is globally stable. If
there exists a unique positive equilibrium (F*, M*) that is globally stable.
Proof Using the monotonicity of we see that f(P) is decreasing and
This means that, if
then f has no roots and (0, 0) is the only steady state. Otherwise, if
there exists a unique positive equilibrium P*. First we show that
is the threshold between population extinction and persistence. We assume first
and consider the following function
For each t>0, one of the following holds:
implies
implies
. Then
. Then
Note that these results hold without the heterosexuality assumption, , which makes the model suitable for female/male-dominated birth rates, i.e.
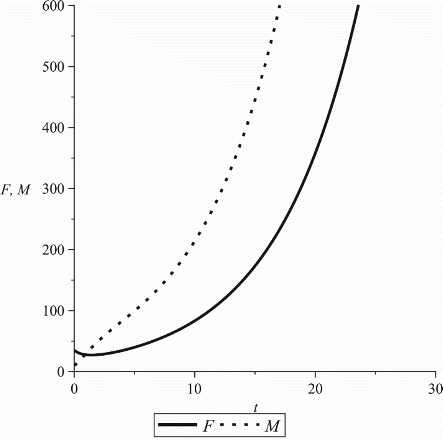
. This will not be the case for the model with pair-formation as seen in Figure A2.
3. The logistic two-sex model with pair-formation
The purpose of this section is to provide a similar generalization for the two-sex model where single individuals form stable pairs and the fertility is modelled as a per-couple birth rate. The meaning of the variables is similar with the difference that F and M represent single females and males, C are the couples and δ is the couple-separation (i.e. divorce) rate. The model is as follows
It is worth mentioning that this condition is essential for a biological feasible solution. Indeed, as seen in Figure A2, if one chooses a female-dominated pair-formation function, i.e. it is possible for M(t) to be negative even if the initial condition is positive. However, this is not an issue since, in the case of Equation (1), one can assume that females control the mating process and, in the absence of males they may find partners outside the community modelled. On the other hand, in the case of Equation (2), the function
does not represent the number of matings but the number of pairs formed per unit of time. So it will not make sense to use a function independent of either males or females.
The model (2) can be better analysed through an equivalent one that follows the dynamics of total females, males and couples (see also [Citation1,Citation4,Citation6]):
The relevant threshold quantities for this model are as follows (note that we preferred to use similar notations as for Equation (1) to maintain the tradition of using when referring to reproductive numbers):
The main results are formulated in the following theorems:
Theorem 3.1
If
and
then the solution of Equation (3) is unbounded. If either
or
the solution of Equation (3) is bounded for all time t.
Proof Due to the similarity of the approach, we will skip some details that are similar to the ones used in the previous sections while still pointing out some key differences. Suppose first ,
and
. We shall prove that the solution of Equation (3) is unbounded. This case requires a stronger estimate on the threshold parameters (and a similar situation will occur when proving the extinction case below). Specifically, we first note that, since the mortality rates are increasing, they either approach a positive limit or infinity. However, since the overall limits above are greater than 1, we must have all mortality rates bounded above and converging to a positive value. From continuity assumptions, we can choose a strictly positive number k>0, small enough, such that:
With this choice for k we now consider the following function
For every t>0, we have the following cases:
. Then
In a similar way, we can show that
 >k if
>k if .
h(t)=C(t). Then
The following theorem establishes the threshold that separates extinction from persistence:
Theorem 3.2
Suppose either
or
. If either
or
then the extinction steady state is globally stable. Otherwise, the solution of Equation (3) is bounded away from zero.
Proof First assume . Then
This implies
and then
since
. Finally from the equation of y′ we also conclude that
.
Similarly, if one can show the entire population goes extinct. We now assume
,
and
. Due to similar continuity assumptions as the ones used in the previous theorems, one can choose a strictly positive number k>0 small enough such that
Now consider the function
Analysing all three possibilities for every t>0 we see that, if
then
Analogously
implies
. Finally if g(t)=C(t), we can see that
Choosing
, the estimates above show that
. From this and Theorem 2.2, we have that
which implies that
. We now assume
,
and
. And we choose P0>0 small enough such that
Consider now the function
Using very similar steps as in Theorem 2.2 (which we prefer to omit at this point), one can show that as soon as P(t)<P0 then h′/h>0 which shows that the population is bounded away from zero.
The existence and uniqueness of the interior steady state is complicated by the fact that, in the model with pair-formation, the monotonicity of may change if its arguments become negative. Specifically, an interior steady state is a solution P* of the following equation
Notice that, under the persistence conditions established in the previous theorem, i.e.
,
and
, we have that f(0)>1, f(P) is initially decreasing and the initial arguments of
are also positive and decreasing. If
and
then f(P) is decreasing on its entire domain. Thus, the existence and uniqueness of P* is equivalent to
,
and
. If either
or
the arguments of
become negative as
. In this case, f(P) crosses the horizontal axis which ensures the existence of P*. Depending on the pair-formation function chosen, f(P) may become negative or undefined after its first crossing. It may also increase as soon as both the arguments of
become negative, as it happens in the case of geometric mean
, which is undefined whenever xy<0. In this case, the existence of a second root for f(P)=1 is possible. However, this second root will satisfy
or
and this is always outside the invariant region of biological feasibility of the solutions of Equation (3). Specifically, all solutions starting in the positive quadrant remain bounded away from zero. This implies that the total number of females and males are at least as large as the number of couples for all time t. It follows that, in the biologically feasible region, an interior steady state satisfies
Therefore, regardless of the choice of the pair-formation function, the existence and uniqueness of the interior steady state P* that is biologically relevant is equivalent to either
,
or
. This is precisely the boundedness condition established in Theorem 3.1. We now show that the interior steady state is locally asymptotically stable by generalizing the similar theorem in [Citation1,Citation6].
Theorem 3.3
Suppose either
or
. If
and
then there exists a unique positive steady state of Equation (3) that is locally asymptotically stable.
Proof The existence and uniqueness of a positive steady state follows from the arguments presented before stating the theorem in the previous section. We denote also
The Jacobian of Equation (3) is
} Note that β′≤0, μf′≥0 and μm′≥0. To simplify the computation of the coefficients of the characteristic polynomial of
we will also use the following identities:
If we denote the characteristic polynomial as
we can now analyse the Routh–Hurwitz conditions for ensuring that all its roots have a negative real part:
A tedious but straightforward computation shows that
as well. Thus,
is locally asymptotically stable.
We believe (as Castillo-Chavez and Huang conjectured in [Citation1]) that this equilibrium is in fact globally stable under the condition of the previous theorem but we still lack a proof of this assertion.
4. Conclusions
We revisited two logistic gender-structured models that have been used in various forms in the literature and generalized them to models using milder conditions on the pair-formation function, fertility and mortality rates. In particular, we established the thresholds between logistic and exponential behaviour as well as the threshold between extinction and persistence. If the population persists, the unique interior equilibrium was found to be globally stable for the model with ephemeral pair-bonds. We believe the same holds for the model with stable couples although we only managed to prove local stability in this case.
The main advantage of this generalization is the possibility of more freedom in choosing the specific mathematical forms for these rates that may be more appropriate depending on the population under study and the environmental effects that impose the logistic behaviour.
From [Citation1,Citation6] and the results in the present paper, we see that, in the case of a population model with stable couples, the solution approaches a positive steady state provided that
Thus, the threshold requires each sex-specific reproductive number to be greater than one, in addition to having enough marriages among the net-offspring population to compensate for the couple removal rate given here by divorce rate (δ) and spousal mortality. This is not needed in the model without pairs for some forms of the mating function. It is true that some mating functions actually imply
and
as we can see in the case of harmonic mean,
with
. Note that
However, other mating functions, such as the geometric mean
, do not require this as we can see in Figure A3.
The results obtained in this paper can be extended in several ways. First, it would be useful to construct a Lyapunov function corresponding to Equation (3) to close the remaining gap in the proof that would guarantee global stability of the interior equilibrium. Secondly, further generality can be attempted in order to include more important types of density dependence such as: Allee effects incorporated in the birth function, density dependence in the separation rate of couples to account for a competitive mating environment, etc. We plan to follow these directions in the near future.
Funding
DM acknowledges funding from Wheat Ridge Ministries – O. P. Kretzmann Grant for Research in the Healing Arts and Sciences.
The authors wish to thank the two reviewers for their detailed reports that helped improve the exposition of the paper.
REFERENCES
- C. Castillo-Chavez and W. Huang, The logistic equation revisited: The two-sex case, Math. Biosc. 128(1–2) (1995), pp. 299–316. doi: 10.1016/0025-5564(94)00077-D
- W.J. Edwards and C.T. Edwards, Population limiting factors, Nature Education Knowledge 3 (2011). Available at http://www.nature.com/scitable/knowledge/library/population-limiting-factors-17059572.
- K.P. Hadeler, Pair formation in age structured populations, Acta Appl. Math. 14 (1989), pp. 91–102. doi: 10.1007/BF00046676
- K.P. Hadeler, R. Waldstätter, and A. Wörz-Busekros, Models for pair formation in bisexual populations, J. Math. Biol. 26 (1988), pp. 635–649. doi: 10.1007/BF00276145
- M. Iannelli, M. Martcheva, and F.A. Milner, Gender-structured population modeling, mathematical methods, numerics and simulations, SIAM, Philadelphia, PA, April 2005.
- D. Maxin and F.A. Milner, The role of sexually abstained groups in two-sex demographic and epidemic logistic models with non-linear mortality, J. Theor. Biol. 258(3) (2009), pp. 389–402. doi: 10.1016/j.jtbi.2008.08.027
- D. Maxin, L. Berec, M. Covello, J. Jessee, and M. Zimmer, The impact of sexually abstaining groups on persistence of sexually transmitted infections in populations with ephemeral pair bonds, J. Theor. Biol. 292 (2012), pp. 1–10. doi: 10.1016/j.jtbi.2011.09.023
- F.A. Milner and K. Yang, The logistic, two-sex, age-structured population model, J. Biol. Dyn. 3 (2009), pp. 252–270. doi: 10.1080/17513750802283261
- P.F. Verhulst, Notice sur la Loi que la Population suit dans son Accroisement, Correspondance mathématique et physique publiée par A. Quételet, Brussels, X (1838), pp. 113–121.
Appendix 1. Examples and figures
In this section, we provide the examples quoted several times in remarks done throughout the paper. We mention again that our choice for the mathematical forms of the birth and death rates are chosen for illustrating purposes only and are not related to real data. Consider the following birth and death rates:
One reason for choosing these forms is to point out that the birth rate need not decrease to zero nor the mortality needs to increase to infinity as
in order to have the logistic behaviour in the model. In Figure A1, we show a case where the model (1) exhibits exponential behaviour despite the fact that the birth rate is decreasing and the death rate increasing. The pair-formation chosen was the harmonic mean,
.
The second example illustrates that male/female dominance in the form of the pair-formation function may lead to a biologically ill-posed model. This happens when one drops the heterosexuality condition in the model (2):
Suppose the pair-formation depends only on females, i.e. . Then, it is possible to obtain negative solutions of M even if M(0)>0 as seen in Figure A2.
Figure A2. The case of a biologically ill posed model (2) with female-dominated pair-formation. Parameter values: β0=1, b=0.3, cf=0.007, cm=0.006, ,
, ρ=2, γf=0.4, γm=0.6.
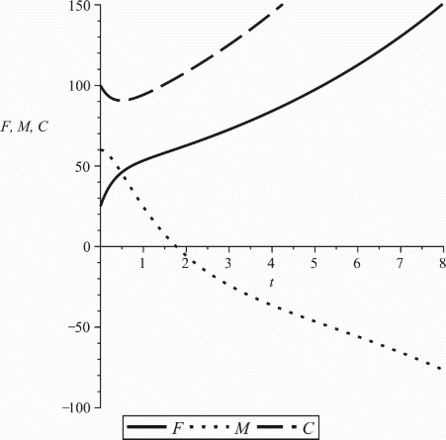
Figure A3. ℛf=8, ℛm=0.86, ℛ=1.83. Parameter values: β0=0.7, b=0.3, cf=0.07, cm=0.06, ,
, ρ=0.7, γf=0.4, γm=0.6.
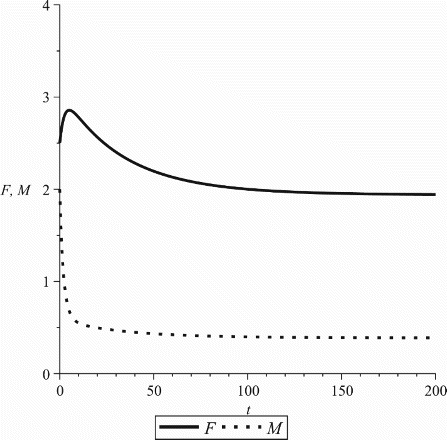
Finally, in the last example (Figure A3), we illustrate that, in the case of the model with ephemeral pair-bonds (1), the population may persist even if one sex-specific reproductive number is less than one. The mating function chosen was the geometric mean, .