Estimating the probability of an extinction or major outbreak for an environmentally transmitted infectious disease

Abstract

Indirect transmission through the environment, pathogen shedding by infectious hosts, replication of free-living pathogens within the environment, and environmental decontamination are suspected to play important roles in the spread and control of environmentally transmitted infectious diseases. To account for these factors, the classic Susceptible–Infectious–Recovered–Susceptible epidemic model is modified to include a compartment representing the amount of free-living pathogen within the environment. The model accounts for host demography, direct and indirect transmission, replication of free-living pathogens in the environment, and removal of free-living pathogens by natural death or environmental decontamination. Based on the assumptions of the deterministic model, a continuous-time Markov chain model is developed. An estimate for the probability of disease extinction or a major outbreak is obtained by approximating the Markov chain with a multitype branching process. Numerical simulations illustrate important differences between the deterministic and stochastic counterparts, relevant for outbreak prevention, that depend on indirect transmission, pathogen shedding by infectious hosts, replication of free-living pathogens, and environmental decontamination. The probability of a major outbreak is computed for salmonellosis in a herd of dairy cattle as well as cholera in a human population. An explicit expression for the probability of disease extinction or a major outbreak in terms of the model parameters is obtained for systems with no direct transmission or replication of free-living pathogens.

Keywords:

• free-living pathogen
• multitype branching process
• Markov chain
• cattle salmonellosis
• cholera

AMS Subject Classification::

• 92D30
• 60J80

1. Introduction

Although direct transmission of infectious diseases from host-to-host is typically considered to be the main route of infection transmission, there are many diseases for which the primary route of transmission is through the environment. Examples of environmentally transmitted infectious agents are Escherichia coli O157:H7 and Salmonella in their animal host populations, and Vibrio cholerae in humans. These environmentally transmitted infectious diseases (ETIDs) can spread through a host population without the need for direct contact between hosts. For example, a susceptible host can become infectious by ingesting a free-living pathogen from the environment. Contaminated food, water, soil, surfaces, and fomites are all possible vehicles for indirect transmission [6,10,14,55]. Some free-living pathogens are capable of long-term survival and even growth within the environment [9,45,58,73]. Moreover, infectious hosts contribute to the load of free-living pathogen in the environment through shedding. This creates a cycle of transmission in which susceptible hosts become infectious by ingesting free-living pathogens from the environment and, in turn, infectious hosts contribute to the level of environmental contamination. On the other hand, the load of free-living pathogens within the environment is reduced by environmental decontamination practices and natural death of the pathogen.

In the theory of infectious disease transmission, a problem of interest is to predict whether the appearance of a small number of infectious individuals (or pathogens) will result in disease extinction or a major outbreak. The basic reproduction number is a well-known threshold which can be used to determine whether an outbreak will occur. The basic reproduction number, denoted by ${\mathcal{R}}_0$, is defined as the expected number of secondary infections produced by a typical infectious individual during its infectious period in a completely susceptible population [20]. In general, if ${\mathcal{R}}_0>1$, there will be an outbreak which results in the disease becoming endemic, and if ${\mathcal{R}}_0<1$, the disease will disappear from the population. Epidemic models for the transmission of ETIDs have been developed in previous studies [see e.g. 5,6,12,18,24,26,43,56,57,62,63,71, and references therein] with particular emphasis on E. coli O157:H7 infection [24], salmonellosis [18,26,43,71], and cholera [56,57,62]. In these studies, the basic reproduction number was used to predict disease persistence or extinction. However, ${\mathcal{R}}_0$ is an expected value and the predictions based on ${\mathcal{R}}_0$ may not be valid for populations with a small initial number of infectious hosts or a low initial level of environmental contamination [2,3,33,48]. For instance, if one infectious host is introduced into a completely susceptible population, that host may die or recover before transmitting the infection to a susceptible host. Similarly, if a small number of free-living pathogens are introduced into the environment with susceptible hosts present, those pathogens may die or be removed from the environment through decontamination prior to an indirect transmission [2,3,33,48]. Therefore, in order to determine the probability of an outbreak or disease extinction for these infections, it is necessary to consider a stochastic model. For more information related to stochastic epidemic modelling and stochastic fade-out of epidemics, see [1–3,7,27,33,41,48].

The stochastic counterpart of an ordinary differential equation (ODE) model, is a continuous-time Markov chain (CTMC) model, where time is continuous and the random variables are discrete. In stochastic epidemic theory, there are also thresholds for a major outbreak or disease extinction [2,3]. These stochastic thresholds are similar to the basic reproduction number, but depend on the initial number of infectious hosts and the initial level of environmental contamination. The theory of multitype branching processes is used to determine the stochastic threshold [2,3]. Whittle [67] showed that for the Susceptible–Infectious–Recovered model with an exponentially distributed infectious period, the probability of disease extinction can be determined by the basic reproduction number. If ${\mathcal{R}}_0>1$, then the probability of disease extinction is approximately $(1/{\mathcal{R}}_0{)}^{i_0}$, where i₀=I(0) is the initial number of infectious hosts [2,67]. In the literature (e.g. [2,3,33]), any event other than disease extinction is loosely referred to as a major outbreak. Thus, the probability of a major outbreak is approximately

$1-{\left(\frac{1}{{\mathcal{R}}_0}\right)}^{i_0}.$

This approximation depends on the assumptions that each infectious host has the same probability of producing a secondary infection, and each infectious host produces secondary infections independent of other infectious hosts. For large populations with a small number of infectious individuals, the expression in Equation (1) is a good approximation [1]. However, this result is only valid for epidemic models with one infectious group. If there are multiple infectious groups (i.e. more than one type of host and/or more than one stage of infectiousness), a major outbreak could emerge from multiple subgroups within the population. In this case, the probability of a major outbreak depends on the initial number of individuals in each infectious group [2]. For infectious diseases that are spread directly via host-to-host contacts and indirectly through the contaminated environment, both infectious hosts and free-living pathogens represent sources of infection for susceptible hosts. Thus, infectious hosts and free-living pathogens can be regarded as distinct infectious groups.

Several stochastic and semi-stochastic epidemic models have been developed for the transmission of ETIDs [8,34,60,72]. However, none of these models account for replication of free-living pathogens within the environment. For pathogens which are able to replicate and persist in the environment, ignoring indirect transmission and free-living pathogen replication in the environment may not adequately reflect the most influential pathway in the transmission process [24]. In addition, the models in [8,34] do not consider the probability of a major outbreak or host demography. Soumpasis and Butler [60] approximate the probability of a major outbreak using many numerical simulations, but their model ignores indirect transmission through the environment and host demography. The model of Xiao et al. [72] includes host demography and indirect transmission, and the probability of a major outbreak is computed using many numerical simulations. However, such numerical simulations can be replaced by more convenient analytical techniques which are computationally efficient and far less time-consuming.

In a previous work, an ODE model was developed by Bani-Yaghoub et al. [6] for ETIDs which includes host demography, direct and indirect transmission, replication of free-living pathogens, and environmental decontamination. However, the model developed by Bani-Yaghoub did not account for stochasticity in the transmission dynamics which is critical for determining the probability of a major outbreak. Therefore, based on the assumptions of the deterministic model in [6], we develop a CTMC model which accounts for the random variations that occur in the transmission process. The objectives of our investigation are to: (1) explore the effects of indirect transmission, pathogen shedding by infectious hosts, free-living pathogen replication, and environmental decontamination on the probability of disease extinction or a major outbreak, and (2) demonstrate an analytically tractable method for approximating the probability of disease extinction or a major outbreak initiated by a small number of infectious individuals or a low level of environmental contamination.

In the next section, the epidemic model of Bani-Yaghoub et al. is introduced and we show that the basic reproduction number determines the dynamics with respect to disease extinction. In Section 3, a CTMC model is formulated based on the assumptions of the ODE model and a multitype branching process approximation of the CTMC is defined. In Section 4, estimates for the probability of disease extinction or a major outbreak are obtained from the branching process approximation when ${\mathcal{R}}_0>1$. These estimates are validated with numerical examples for salmonellosis in a dairy herd and cholera in a human population. For both examples, we investigate the impact of indirect transmission, pathogen shedding by infectious hosts, replication of free-living pathogens, and environmental decontamination on the probability of disease extinction or a major outbreak. The results and their implications for disease control are discussed in Section 5.

2. Deterministic model

2.1. Model development

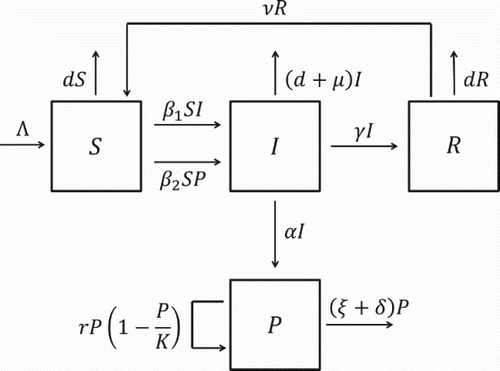
Let S(t), I(t), and R(t) denote the number of susceptible, infectious, and recovered hosts at time t, respectively, with a total host population $N(t)=S(t)+I(t)+R(t)$. Let P(t) denote the number of free-living pathogens in the environment at time t. Suppose that Λ>0 represents the constant recruitment of hosts, d>0 denotes the natural host mortality rate, and μ≥0 denotes the pathogen-induced mortality rate. Susceptible hosts can be infected by contacting infectious hosts (direct transmission) or by ingesting free-living pathogens from the environment (indirect transmission). Both direct and indirect transmission are modelled using mass action incidence with transmission parameters ${\beta }_1\ge 0$ and ${\beta }_2\ge 0$, respectively. Infectious hosts shed pathogen into the environment, typically through their feces. Assume that the shedding rate α≥0 represents the average number of pathogens shed into the environment per infectious host per day. Infectious hosts can recover from infection at rate γ>0, where 1/γ is the average duration of the infectious period. Recovered hosts are temporarily immune from reinfection, but lose their immunity at rate ν>0, where 1/ν is the average duration of immunity. Free-living pathogens are capable of replicating in the environment at rate r≥0, up to some carrying capacity K>0, but also experience natural death at rate ξ>0 and may be removed from the environment through environmental decontamination at rate δ≥0. Figure 1 illustrates the transition dynamics of the model. The corresponding system of differential equations is

$\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}& =\mathrm{\Lambda }-\mathrm{d}S-{\beta }_{1}SI-{\beta }_{2}SP+\nu R,\end{array}$

$\begin{array}{rl}\frac{\mathrm{d}I}{\mathrm{d}t}& ={\beta }_{1}SI+{\beta }_{2}SP-(d+\mu +\gamma )I,\end{array}$

$\begin{array}{rl}\frac{\mathrm{d}R}{\mathrm{d}t}& =\gamma I-(d+\nu )R,\end{array}$

$\begin{array}{rl}\frac{\mathrm{d}P}{\mathrm{d}t}& =\alpha I+rP\left(1-\frac{P}{K}\right)-(\xi +\delta )P,\end{array}$

with non-negative initial conditions S(0), I(0), R(0), P(0). Table 1 summarizes the model variables and parameters.

Figure 1. Compartmental diagram for the model (2)–(5).

Table 1.  Variables and parameters with units for the model (2)–(5).

S	Number of susceptible individuals	Individuals
I	Number of infectious individuals	Individuals
R	Number of recovered individuals	Individuals
P	Number of free-living pathogens	Pathogens
Λ	Recruitment rate	Individuals day^−1
d	Natural death rate	Day^−1
μ	Pathogen-induced death rate	Day^−1
β1	Direct transmission	Individual^−1 day^−1
β2	Indirect transmission	Pathogen^−1 day^−1
1/γ	Average infectious period	Day
1/ν	Average immune period	Day
α	Pathogen shedding rate	Pathogen individual^−1 day^−1
r	Pathogen replication rate	Day^−1
K	Carrying capacity	Pathogens
ξ	Pathogen death rate	Day^−1
δ	Decontamination rate	Day^−1

It can easily be verified that all solutions of Equations (2)–(5) with non-negative initial conditions remain non-negative. Summing Equations (2)–(4) gives the change in the total host population

$\frac{\mathrm{d}N}{\mathrm{d}t}=\mathrm{\Lambda }-\mathrm{d}N-\mu I.$

It follows that $\underset{t\to \mathrm{\infty }}{lim sup}N(t)\le \mathrm{\Lambda }/d$. Thus, Equation (5) gives

$\frac{\mathrm{d}P}{\mathrm{d}t}\le \alpha \left(\frac{\mathrm{\Lambda }}{\mathrm{d}}\right)-(\xi +\delta -r)P-\frac{r}{K}{P}^2,$

and so there exists a constant C>0 such that $\underset{t\to \mathrm{\infty }}{lim sup}P(t)\le C$. In particular, the constant C can be taken as the unique positive zero of the quadratic $\alpha \mathrm{\Lambda }/d-(\xi +\delta -r)P-(r/K)P^2$. Hence, the feasible region

$\mathrm{\Gamma }=\left\{(S,I,R,P)\in {\mathbb{R}}_{+}^4\left|S+I+R\le \frac{\mathrm{\Lambda }}{\mathrm{d}},P\le C\right.\right\}$

is positively invariant with respect to the model (2)–(5).

The unique disease-free equilibrium (DFE) is given by $(\overline{S},0,0,0)$, where $\overline{S}=\mathrm{\Lambda }/d$. The deterministic model (2)–(5) was developed and analysed by the co-authors in a previous work [6]. However, as explained in Section 1, a deterministic model does not account for stochasticity in the transmission dynamics which is critical for determining the probability of disease extinction or a major outbreak. For completeness, a brief review of the analytic results are presented in the following subsection.

2.2. Basic reproduction number

The basic reproduction number, ${\mathcal{R}}_0$, is used to determine the dynamics of the model (2)–(5) regarding disease persistence or extinction. An expression for ${\mathcal{R}}_0$ can be obtained from the next-generation matrix approach [20,22,23]. Let $\overrightarrow{I}(t)=[I(t),P(t){]}^{\mathrm{T}}$ denote the vector of infectious variables. Linearizing Equations (3) and (5) about the DFE gives

$\frac{\mathrm{d}\overrightarrow{I}}{\mathrm{d}t}=J\overrightarrow{I}=(F-V)\overrightarrow{I},$

where J is the Jacobian matrix evaluated at the DFE. Matrix F contains the rates of new infections and matrix V contains all other transition rates.

Following the rationale of [11,26,46], in our model the environment acts as a reservoir for free-living pathogens and so secondary free-living pathogens generated through replication within the environment or shed by infectious hosts are considered as new infectious entities. Thus,

$F=\begin{array}{cc}{\beta }_1\overline{S}& {\beta }_2\overline{S}\\ \alpha & r\end{array}\text{and}V=\begin{array}{cc}d+\mu +\gamma & 0\\ 0& \xi +\delta \end{array}.$

The next-generation matrix is given by

$F{V}^{-1}=\begin{array}{cc}\frac{{\beta }_1\overline{S}}{\mathrm{d}+\mu +\gamma }& \frac{{\beta }_2\overline{S}}{\xi +\delta }\\ \frac{\alpha }{\mathrm{d}+\mu +\gamma }& \frac{r}{\xi +\delta }\end{array},$

and ${\mathcal{R}}_0$ is the spectral radius of this matrix [20,22]. That is,

${\mathcal{R}}_0=\frac{1}{2}[{\mathcal{R}}_{01}+{\mathcal{R}}_{03}+\sqrt{({\mathcal{R}}_{01}-{\mathcal{R}}_{03}{)}^2+4{\mathcal{R}}_{02}}],$

where

${\mathcal{R}}_{01}=\frac{\mathrm{\Lambda }{\beta }_1}{\mathrm{d}(d+\mu +\gamma )},{\mathcal{R}}_{02}=\frac{\mathrm{\Lambda }{\beta }_2\alpha }{\mathrm{d}(\xi +\delta )(d+\mu +\gamma )},{\mathcal{R}}_{03}=\frac{r}{\xi +\delta }.$

The terms ${\mathcal{R}}_{01}$ and ${\mathcal{R}}_{02}$ represent the average number of secondary infections caused by one infectious host during its infectious period through direct and indirect transmission, respectively. Similarly, ${\mathcal{R}}_{03}$ is the average number of secondary free-living pathogens produced through replication by one free-living pathogen during its time in the environment [6].

Since ${\mathcal{R}}_{0j}\ge 0$ for j=1, 2, 3, it follows from Equation (12) that

${\mathcal{R}}_0\ge \frac{1}{2}[{\mathcal{R}}_{01}+{\mathcal{R}}_{03}+\sqrt{({\mathcal{R}}_{01}-{\mathcal{R}}_{03}{)}^2}]=max({\mathcal{R}}_{01},{\mathcal{R}}_{03}),$

and

${\mathcal{R}}_0\ge \frac{1}{2}\sqrt{4{\mathcal{R}}_{02}}=\sqrt{{\mathcal{R}}_{02}}.$

Thus, if ${\mathcal{R}}_{0j}>1$ for j=1, 2, or j=3, then ${\mathcal{R}}_0>1$. This relationship makes sense biologically. If, in the absence of free-living pathogen, there is an outbreak in the host population (${\mathcal{R}}_{01}>1$), then there will certainly be an outbreak in the host-pathogen system with free-living pathogen present (${\mathcal{R}}_0>1$). Similarly, if the free-living pathogen can sustain itself in the environment without the need for hosts (${\mathcal{R}}_{03}>1$), the disease will persist with hosts present.

The basic reproduction number determines the dynamics of the deterministic model regarding disease persistence or extinction. If ${\mathcal{R}}_0\le 1$, then the DFE is globally asymptotically stable in Γ and if ${\mathcal{R}}_0>1$, there exists a unique endemic equilibrium $(S^{\ast },I^{\ast },R^{\ast },P^{\ast })$ which is locally asymptotically stable and the model is uniformly persistent [6]. That is, if ${\mathcal{R}}_0\le 1$ the disease disappears from the population and if ${\mathcal{R}}_0>1$ there is a major outbreak and long-term disease persistence.

3. Stochastic model

The basic reproduction number for the deterministic model introduced in Section 2 can be used to determine, on average, whether the appearance of a small number of infectious hosts or free-living pathogens will result in a major outbreak or disease extinction. However, even if ${\mathcal{R}}_0>1$, it is possible that disease extinction occurs prior to a major outbreak. This is known as the stochastic fade-out of an epidemic [7,33,41,48]. In order to determine the probability of a major outbreak or disease extinction for an ETID, it is necessary to consider a stochastic model. In this section, we consider a continuous-time Markov chain (CTMC) model with a discrete number of hosts and free-living pathogens. The theory of multitype branching processes is used to estimate the probability of disease extinction or a major outbreak.

3.1. CTMC model

Let S(t), I(t), and R(t) denote discrete-valued random variables for the number of susceptible, infectious, and recovered hosts at time t, respectively, with a total host population of $N(t)=S(t)+I(t)+R(t)$. Let P(t) denote a discrete-valued random variable for the number of free-living pathogens in the environment at time t and let

$\overrightarrow{X}(t)=[S(t),I(t),R(t),P(t){]}^{\mathrm{T}}$

be the associated random vector. For simplicity, the same notation is used for the discrete random variables and parameters as for the deterministic model. The state transitions and rates for the CTMC model are given in Table 2. It should be noted that the number of free-living pathogens is only increased by one each time the shedding event occurs. This is in contrast with the way in which shedding occurs for some ETIDs (e.g. cholera). In particular, shedding occurs through discrete events in which large amounts of free-living pathogen are released into the environment. However, the shedding rate α can be adjusted to account for the number of pathogens shed during each shedding event. For example, suppose an infected host sheds an average of 5 times per day, and releases an average of 10⁶ pathogens into the environment during each shedding event. Rather than setting α=5 and increasing the number of free-living pathogens by 10⁶ each time the shedding event occurs (every 1/5 days), we can set $\alpha =5\times {10}^6$ and increase the number of free-living pathogens by one each time the shedding event occurs (every $1/(5\times {10}^6)$ days). In this way, we can use the same parameter value of α for the CTMC model as for the ODE model which assumes shedding occurs continuously. This allows for a more straightforward comparison of the deterministic and stochastic results.

Table 2.  State transitions and rates for the CTMC model.

Description	Transition, $\mathrm{\Delta }\overrightarrow{X}(t)$	Transition rate, p
Recruitment	(1, 0, 0, 0)^T	Λ
Death of S	(−1, 0, 0, 0)^T	dS
Direct transmission	(−1, 1, 0, 0)^T	β1SI
Indirect transmission	(−1, 1, 0, 0)^T	β2SP
Death of I	(0,−1, 0, 0)^T	(d+μ)I
Recovery	(0,−1, 1, 0)^T	γ I
Loss of immunity	(1, 0,−1, 0)^T	ν R
Death of R	(0, 0,−1, 0)^T	dR
Shedding	(0, 0, 0, 1)^T	α I
Pathogen replication	(0, 0, 0, 1)^T	$rP\left(1-{\displaystyle \frac{P}{K}}\right)$
Death of P	(0, 0, 0,−1)^T	ξ P
Decontamination	(0, 0, 0,−1)^T	δ P

Note: The expression $p\mathrm{\Delta }t+o(\mathrm{\Delta }t)$ is the infinitesimal transition probability for the change $\mathrm{\Delta }\overrightarrow{X}(t)=\overrightarrow{X}(t+\mathrm{\Delta }t)-\overrightarrow{X}(t)$.

It follows from the Markov assumption that the time between events is exponentially distributed with parameter

$\omega (\overrightarrow{X})=\mathrm{\Lambda }+\mathrm{d}N+{\beta }_{1}SI+{\beta }_{2}SP+(\mu +\gamma +\alpha )I+\nu R+rP\left(1+\frac{P}{K}\right)+(\xi +\delta )P.$

The theory of multitype branching processes is used to approximate the nonlinear CTMC near the DFE and derive an estimate for the probability of disease extinction or a major outbreak. A multitype branching process assumes that the transition rates are linear with respect to the infectious variables I and P. For example, in Table 2 the transition rates for direct and indirect transmission near the DFE are ${\beta }_1\overline{S}I$ and ${\beta }_2\overline{S}P$, respectively. Moreover, the transition rate for the replication of free-living pathogens near the DFE is rP.

3.2. Branching process approximation

A multitype branching process can be used to approximate the dynamics of the nonlinear CTMC near the DFE [21,29,52]. Since infectious hosts and free-living pathogens are the only sources of infection, the branching process is applied only to these infectious groups and the susceptible hosts are assumed to be at the disease-free state, $\overline{S}=\mathrm{\Lambda }/d$.

Infectious hosts can produce secondary infectious hosts (direct transmission) or free-living pathogens (shedding). Similarly, free-living pathogens are capable of producing infectious hosts (indirect transmission) or additional free-living pathogens (replication). The term ‘offspring’ will be used to describe susceptible hosts that become infectious due to direct or indirect transmission as well as free-living pathogens which are shed into the environment by infectious hosts or secondary pathogens which occur through replication within the environment. Assume that the number of offspring produced by an infectious host or a free-living pathogen does not depend on the number of offspring produced by other infectious hosts or free-living pathogens. Moreover, assume that the initial host population is sufficiently large so that $S(0)\approx N(0)=\overline{S}$. Since the multitype branching process is linear near the DFE, time-homogeneous, and the number of offspring produced by infectious hosts and free-living pathogens is independent, offspring probability generating functions (pgfs) can be defined for the ‘birth’ and ‘death’ of infectious hosts and free-living pathogens. These offspring pgfs can then be used to calculate the probability of disease extinction or a major outbreak [2,4,21,29,40,52].

Additional random variables are defined for the number of infectious hosts or free-living pathogens produced by one infectious host or free-living pathogen. Let Y_ii and Y_pi denote the offspring random variables for infectious hosts. That is, Y_ii and Y_pi denote the number of infectious hosts and free-living pathogens produced by one infectious host, respectively. Similarly, let Y_ip and Y_pp denote the offspring random variables for a free-living pathogen. That is, Y_ip and Y_pp denote the number of infectious hosts and free-living pathogens produced by one free-living pathogen, respectively. The offspring pgf for I defines the probabilities associated with the ‘birth’ of secondary infectious hosts or free-living pathogens, or the ‘death’ of the initial infectious host, given that the process started with only one infectious host, I(0)=1 and P(0)=0. The offspring pgf for I is

$f_1(x_1,x_2)=\sum _{k_1=0}^{\mathrm{\infty }}\sum _{k_2=0}^{\mathrm{\infty }}{P}_1(k_1,k_2)x_1^{k_1}{x}_2^{k_2},$

where

$P_1(k_1,k_2)=\text{Prob}\{Y_{ii}=k_1,Y_{pi}=k_2\}$

(see [4,21,29,40,52]). Similarly, the offspring pgf for P is

$f_2(x_1,x_2)=\sum _{k_1=0}^{\mathrm{\infty }}\sum _{k_2=0}^{\mathrm{\infty }}{P}_2(k_1,k_2)x_1^{k_1}{x}_2^{k_2},$

where

$P_2(k_1,k_2)=\text{Prob}\{Y_{ip}=k_1,Y_{pp}=k_2\}.$

The offspring pgfs for I and P are used to calculate the expected number of offspring produced by a single infectious host or free-living pathogen as well as the probability of disease extinction in the host population or extinction of the free-living pathogen population. The specific offspring pgfs for I and P can be defined using the rates in Table 2 when the initial host population is near the DFE, $S(0)\approx \overline{S}$ [2,21].

The offspring pgf for I is

$f_1(x_1,x_2)=\frac{{\beta }_1\overline{S}{x}_1^2+d+\mu +\gamma +\alpha x_1{x}_2}{{\beta }_1\overline{S}+d+\mu +\gamma +\alpha }.$

The term ${\beta }_1\overline{S}/({\beta }_1\overline{S}+d+\mu +\gamma +\alpha )$ represents the probability that a susceptible host becomes infectious and the initial infectious host does not die which results in two infectious hosts (Y_ii=2 and Y_pi=0). The term $(d+\mu +\gamma )/({\beta }_1\overline{S}+d+\mu +\gamma +\alpha )$ represents the probability that the initial infectious host is lost due to death or recovery resulting in zero infectious hosts and free-living pathogens (Y_ii=Y_pi=0). The term $\alpha /({\beta }_1\overline{S}+d+\mu +\gamma +\alpha )$ represents the probability that pathogen is shed by the infectious host resulting in one infectious host and one free-living pathogen (Y_ii=Y_pi=1).

The offspring pgf for P is

$f_2(x_1,x_2)=\frac{{\beta }_2\overline{S}{x}_1{x}_2+\xi +\delta +r{x}_2^2}{{\beta }_2\overline{S}+\xi +\delta +r}.$

The term ${\beta }_2\overline{S}/({\beta }_2\overline{S}+\xi +\delta +r)$ represents the probability that a susceptible host becomes infectious which results in one infectious host and the original free-living pathogen (Y_ip=Y_pp=1). The term $(\xi +\delta )/({\beta }_2\overline{S}+\xi +\delta +r)$ represents the probability that a pathogen is lost due to decay or decontamination resulting in zero infectious hosts and free-living pathogen (Y_ip=Y_pp=0). The term $r/({\beta }_2\overline{S}+\xi +\delta +r)$ represents the probability that secondary free-living pathogen replicates in the environment resulting in two free-living pathogen cells (Y_ip=0 and Y_pp=2). Typically a susceptible host becomes infectious by ingesting the free-living pathogen. However, the removal of free-living pathogens from the environment through ingestion by a host is negligible when compared to the amount of pathogen shed by infectious hosts and the number of free-living pathogens removed from the environment by natural decay or environmental decontamination. Therefore, the pathogen loss due to ingestion by any host other than the ingestion by susceptible hosts, leading to new infections, can be considered negligible [14].

The offspring pgfs always have one fixed point in [0, 1]², the fixed point (1, 1). If the offspring pgfs are non-singular, then there exists a unique second fixed point in (0, 1)² [4,21,29,52]. A function f_j is called non-singular if it is not a linear function of x₁ and x₂ such that f_j(0, 0)=0. That is, $f_j(x_1,x_2)\ne a_1{x}_1+a_2{x}_2$ [4,29,52].

The expectation matrix of the offspring pgfs is given by

$M={\left.\begin{array}{cc}\frac{\mathrm{\partial }{f}_1}{\mathrm{\partial }{x}_1}& \frac{\mathrm{\partial }{f}_2}{\mathrm{\partial }{x}_1}\\ \frac{\mathrm{\partial }{f}_1}{\mathrm{\partial }{x}_2}& \frac{\mathrm{\partial }{f}_2}{\mathrm{\partial }{x}_2}\end{array}\right|}_{\overrightarrow{x}=\overrightarrow{1}}=\begin{array}{cc}\frac{2{\beta }_1\overline{S}+\alpha }{{\beta }_1\overline{S}+d+\mu +\gamma +\alpha }& \frac{{\beta }_2\overline{S}}{{\beta }_2\overline{S}+\xi +\delta +r}\\ \frac{\alpha }{{\beta }_1\overline{S}+d+\mu +\gamma +\alpha }& \frac{{\beta }_2\overline{S}+2r}{{\beta }_2\overline{S}+\xi +\delta +r}\end{array}.$

The entries m₁₁ and m₂₁ represent the expected number of infectious hosts and free-living pathogens, respectively, produced by one infectious host. Similarly, the entries m₁₂ and m₂₂ represent the expected number of infectious hosts and free-living pathogens, respectively, produced by one free-living pathogen in the environment.

Since the offspring pgfs for I and P are non-singular and the expectation matrix M is irreducible, there are at most two fixed points of the offspring pgfs in [0, 1]² [52]. The spectral radius of the expectation matrix determines the existence of a fixed point in (0, 1)². If the process is subcritical or critical (ρ(M)<1 or ρ(M)=1), then (1, 1) is the only stable fixed point, and if the process is supercritical (ρ(M)>1), then there exists a unique second fixed point $(q_1,q_2)\in (0,1{)}^2$ [4,21,29,52]. This fixed point is used to determine the probability of disease extinction [4,21,29,52]. That is,

${\mathbb{P}}_0=\underset{t\to \mathrm{\infty }}{lim}\mathrm{Prob}\{I(t)=P(t)=0\}=\left\{\begin{array}{ll}1,& \text{if}\rho (M)\le 1,\\ q_1^{i_0}{q}_2^{p_0},& \text{if}\rho (M)>1,\end{array}\right.$

where i₀=I(0) and p₀=P(0). The value of q₁ is the probability of disease extinction in the host population, and q₂ is the probability of extinction for the free-living pathogen. In the case that ρ(M)>1, the probability of a major outbreak is approximately

$1-{\mathbb{P}}_0=1-q_1^{i_0}{q}_2^{p_0}.$

Although the expression in Equation (25) is a limiting result with respect to time, the split between disease extinction or a major outbreak occurs quickly in the branching process approximation [2].

Note that ρ(M) is a threshold for persistence or extinction of the disease in the stochastic model. In particular, if $\rho (M)\le 1$, the disease is eliminated from the host population with probability one and if ρ(M)>1, there is a non-zero probability of a major outbreak. In this way, the value of ρ(M) is similar to the deterministic threshold, ${\mathcal{R}}_0$. Recently an equivalence between the deterministic and stochastic thresholds for disease extinction (${\mathcal{R}}_0<1\iff \rho (M)<1$) was established by Allen and van den Driessche for more general epidemic models [3].

In general, a simple analytical expression for the extinction probabilities q₁ and q₂ cannot be obtained. However, there are special cases for which an analytical expression is possible. If there is no direct transmission or replication of the free-living pathogen (i.e. β₁=r=0), the extinction probabilities q₁ and q₂ are given by

$\begin{array}{rl}{q}_1& =\frac{\alpha }{\alpha +d+\mu +\gamma }\frac{1}{{\mathcal{R}}_{02}}+\frac{\mathrm{d}+\mu +\gamma }{\alpha +d+\mu +\gamma },\\ q_2& =\frac{{\beta }_2\overline{S}}{{\beta }_2\overline{S}+\xi +\delta }\frac{1}{{\mathcal{R}}_{02}}+\frac{\xi +\delta }{{\beta }_2\overline{S}+\xi +\delta }.\end{array}$

The value of q₁ can be interpreted as follows: an infectious host will either shed the pathogen with probability $\alpha /(\alpha +d+\mu +\gamma )$ or die or recover before transmission with probability $(d+\mu +\gamma )/(\alpha +d+\mu +\gamma )$. If the host does shed pathogen into the environment, the probability of transmission through the environment is $1-(1/{\mathcal{R}}_{02})$. Similarly, the value of q₂ can be interpreted as follows: a pathogen in the environment can either infect a susceptible host with probability ${\beta }_2/({\beta }_2+\xi +\delta )$ or disappear from the environment with probability $(\xi +\delta )/({\beta }_2+\xi +\delta )$. If there is an indirect transmission, then the probability a pathogen will produce another pathogen via an infectious host is $1-(1/{\mathcal{R}}_{02})$. In this case, the explicit expression for the probability of disease extinction is

${\mathbb{P}}_0={\left[\frac{\mathrm{d}+\mu +\gamma }{{\beta }_2\overline{S}}\right]}^{i_0}{\left[\frac{\xi +\delta }{\alpha }\right]}^{p_0}{\left[\frac{{\beta }_2\overline{S}+\xi +\delta }{\alpha +d+\mu +\gamma }\right]}^{i_0-p_0}.$

In Section 4, we compute the extinction probabilities q₁ and q₂ numerically and show that the estimate for disease extinction agrees closely with simulations of the CTMC model. A more thorough discussion of multitype branching processes can be found in the literature [4,21,28,29,37,40,42,50].

4. Results

The dynamics of the ODE and CTMC epidemic models are illustrated for salmonellosis in a herd of dairy cattle and cholera in a human population. For each of these examples, we apply the theory of multitype branching processes to estimate the probability of disease extinction or a major outbreak and illustrate the effects of indirect transmission, pathogen shedding by infectious hosts, free-living pathogen replication, and environmental decontamination on the probability of disease extinction or a major outbreak.

4.1. Salmonellosis in dairy cattle

Salmonellosis is the most common bacterial foodborne illness in the USA [15]. It is estimated that in the USA Salmonella causes 1.03 million cases of foodborne disease and 400 deaths annually [54]. There have been numerous research efforts targeted at reducing the number of foodborne Salmonella infections among humans. However, the incidence of foodborne salmonellosis has not changed significantly in the past 15 years [16]. Dairy cattle are one of the major hosts for Salmonella, and control of salmonellosis in dairy herds can lower the risk of contamination of dairy products, thereby reducing the number of cases of human salmonellosis.

Table 3 lists the model parameters related to Salmonella infection in dairy cattle. The values have been scaled so that the unit of time is one day. We assume that Λ=0.1 so that the initial herd size is approximately $\overline{S}=100$, which is the desired herd size indicated by Xiao et al. [71,72]. The rate of environmental decontamination will vary across farms depending on the feces removal system in place. The value of δ=1.2 in Table 3 corresponds to removal of free-living Salmonella from the environment through daily environmental decontamination with a 70% efficacy (see Appendix 1). Due to a lack of data, the true value of the environmental carrying capacity, K, is unknown. We estimate the carrying capacity to be $K=1.95\times {10}^{14}$ (see Appendix 2). Although this value is an estimate, the carrying capacity does not affect the values of ${\mathcal{R}}_0$ or ℙ₀. In [71,72], the direct and indirect transmission rates were assumed to be ${\beta }_1=0.006$ and ${\beta }_2=1.3\times {10}^{-11}$. For these values, ${\mathcal{R}}_{01}\approx 5.88$ and ${\mathcal{R}}_{02}\approx 0.51$ which implies that disease transmission occurs primarily through host-to-host contact. However, it has recently been accepted that transmission of pathogens spreading through the fecal–oral route in their animal host populations occurs primarily indirectly through the contaminated environment and that the direct host-to-host transmission is negligible [11,25,26]. Thus, we assume a smaller value (log10 decrease) of β₁ and larger value (log10 increase) of β₂ compared with [71,72]. The effects of varying the model parameters on the probability of disease extinction or a major outbreak are explored in Section 4.1.1 and Appendix 3.

Table 3.  Model parameters related to salmonellosis in a dairy herd.

Definition	Parameter	Value	References
Recruitment rate	Λ	0.1	[71]
Natural death rate	d	0.001	[18,47]
Direct transmission rate	β1	0.0006	[71,72]
Indirect transmission rate	β2	$1.3\times {10}^{-10}$	[71,72]
Pathogen-induced death rate	μ	0.001	[71,72]
Recovery rate	γ	0.1	[71,72]
Immunity loss rate	ν	0.01	[71,72]
Shedding rate	α	5×10^7	[71,72]
Pathogen replication rate	r	0.2	[6]
Pathogen death rate	ξ	0.051	[44]
Decontamination rate	δ	1.2	[5]
Carrying capacity	K	$1.95\times {10}^{14}$	[58,65]

For the values in Table 3, the reproduction numbers are ${\mathcal{R}}_{01}\approx 0.59$, ${\mathcal{R}}_{02}\approx 5.09$, ${\mathcal{R}}_{03}\approx 0.16$, and ${\mathcal{R}}_0\approx 2.64$. The solution of the ODE model approaches the endemic equilibrium $(S^{\ast },I^{\ast },R^{\ast },P^{\ast })\approx (15,7.7,69.6,3.6\times {10}^8)$ with persistence of the infection. Prior to stabilizing at the endemic equilibrium, there is a major outbreak which exceeds the endemic values. For the CTMC model, there are two outcomes: either disease extinction occurs with only a few infectious cases or there is a major outbreak. The ODE solution and one sample path of the CTMC illustrating a major outbreak are plotted in Figure 2.

Figure 2. Comparison of the ODE solution (dashed) and one sample path of the CTMC (solid) for salmonellosis in a dairy herd illustrating a major outbreak and disease persistence. Parameter values are as in Table 3 with initial conditions S(0)=99, I(0)=1, R(0)=0, and P(0)=0. The basic reproduction number is ℛ₀≈2.64. The probability of a major outbreak is 1−ℙ₀=0.8453 (see Table 4). The locally stable endemic equilibrium for the ODE model is (S*, I*, R*, P*)≈(15, 7.7, 69.6, 3.6×10⁸).

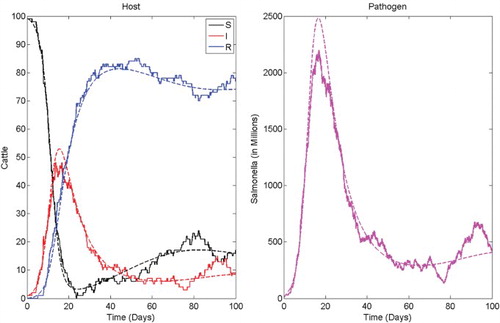
Table 4.  Probability of disease extinction, ℙ₀, for salmonellosis in a dairy herd calculated from the fixed point of the offspring pgfs and an approximation (Approx.) based on the proportion of 10,000 sample paths that hit zero before reaching endemic levels in numerical simulations of the CTMC model.

i0	p0	ℙ0	Approx.
1	0	0.1547	0.1542
2	0	0.0239	0.0239
0	5×10^7	0.5945	0.5921
0	10^8	0.3535	0.3520
1	5×10^7	0.0920	0.0923

Notes: Parameter values are as in Table 3 with initial conditions I(0)=i₀, $S(0)=100-i_0$, R(0)=0, and P(0)=p₀. The basic reproduction number is ${\mathcal{R}}_0\approx 2.6$. Initial conditions $P(0)=5\times {10}^7$ and P(0)=10⁸ correspond to the average amount of Salmonella shed into the environment each day by one or two infectious cattle, respectively.

4.1.1. Probability of disease extinction or a major outbreak

The probability of disease extinction, ℙ₀, is calculated from the branching process approximation and compared to the probability of disease extinction for the CTMC model, obtained from the proportion of 10,000 sample paths for which the sum I(t)+P(t) hits zero before reaching the endemic levels I(t)>8 or $P(t)>3.6\times {10}^8$. Table 4 shows that the value of ℙ₀ is a good estimate of the probability of disease extinction for the CTMC model. The initial conditions $P(0)=\alpha =5\times {10}^7$ and $P(0)=2\alpha ={10}^8$ correspond to the average amount of Salmonella shed into the environment each day by one or two infectious cattle, respectively.

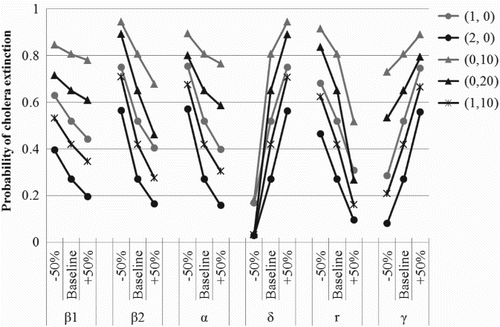
In order to determine the sensitivity of these results to variations in the model parameters, we allow the parameter values to fluctuate by $\pm 50\mathrm{\%}$ of their baseline values in Table 3. Then, the strength of sensitivity to fluctuations is illustrated by the slope of the line representing a relationship between the tested model parameter fluctuations and the corresponding probabilities of disease extinction shown in Figure 3. Notice that the probability of disease extinction is highly sensitive to changes in the indirect transmission rate. Unfortunately, there is a lack of literature regarding the true value of β₂ for salmonellosis among dairy cattle. Thus, determining an accurate estimate for the indirect transmission rate could improve our ability to predict major outbreaks of salmonellosis in dairy herds. The probability of disease extinction is also highly sensitive to changes in the rate of environmental decontamination. This rate will vary between farms depending on the feces removal system in place. The efficacy of pathogen removal (in terms of the proportion of pathogens removed from the environment) can be used to determine the decontamination rate (see Appendix 1). For the parameter values tested in Figure 3 (i.e. $-50\mathrm{\%}$ of the baseline, baseline, and +50% of the baseline) and the corresponding results in Table A2 (cases (d), (e), and (f)), the decontamination rates correspond to daily cleaning of cattle pens with a pathogen removal efficacy of 45%, 70%, and 83%, respectively.

Figure 3. Probability of disease extinction, ℙ₀, for salmonellosis in a dairy herd calculated from the fixed point of the offspring pgfs as the model parameters fluctuate by±50% of their baseline values in Table 3. The five curves indicated in the legend correspond to the five initial conditions considered in Table 4. Initial values P(0)=5×10⁷ and P(0)=10⁸ correspond to the average amount of Salmonella shed into the environment each day by one or two infectious cattle, respectively. Explicit values of ℙ₀ can be found in Tables A1–A4 in Appendix 3.

The results in Figure 3 indicate a moderate influence of the pathogen shedding rate on the probability of disease extinction. However, when interpreting this result one needs to be aware that the Salmonella shedding rate in infected cattle is very high (5×10⁷ pathogens/animal/day) and that a meaningful change in the shedding rate from the epidemiology and control points of view would be on the log10 scale (e.g., reduction by 2–3 log10). Because a 50% change was applied to the non-log transformed baseline parameter value for α, the considered fluctuations of $-50\mathrm{\%}$ and $+50\mathrm{\%}$ meant that we tested the values of $2.5\times {10}^7$ and $7.5\times {10}^7$, respectively which on the log10 scale represent a mere change of approximately $\pm 3\mathrm{\%}$. Therefore, since small tested changes in the value of the shedding rate had moderate effects on the probability of extinction, we expect that a change in α on the epidemiologically more meaningful log10 scale would have a strong effect on the probability of extinction. Table A4 shows the effect of varying the pathogen shedding rate by ±log10 from its baseline value in Table 3. As expected, the pathogen shedding rate has a large impact on the probability of disease extinction.

Although the estimates for the probability of disease extinction are less sensitive to changes in the free-living pathogen replication rate and the rate of recovery, obtaining accurate estimates for these values could improve the ability to predict major outbreaks of salmonellosis in dairy herds and reduce the number of cases of human salmonellosis. Variations in the direct transmission rate have little impact on the probability of disease extinction which reflects the current understanding that indirect transmission through the environment is the primary pathway for transmission of salmonellosis among dairy cattle and supports the findings of Gautam et al. for salmonellosis in pigs [26].

The results in Figure 3 are also relevant for disease control. In particular, the results in Table 4 and Figure 3 show that for the parameter values in Table 3 there is a substantially lower probability of disease extinction if infectious cattle are placed in a susceptible herd compared to the appearance of free-living Salmonella in the environment. This difference highlights the fact that a small amount of free-living Salmonella is likely to be removed from the environment through decontamination or natural decay prior to resulting in secondary infections through indirect transmission, whereas a single infectious cow can transmit the infection directly as well as shed large amounts of Salmonella during the average 10-day infectious period. Moreover, control efforts targeting pathogen shedding and indirect transmission are the most effective, followed by efforts focused on environmental decontamination (compare Table A1 case (d), Table A2 case (f), and Table A4 case (a)). Cleaning cattle fecal waste from the barn surface is a common method of environmental decontamination on dairy farms which can effectively reduce the number of free-living Salmonella and reduce the risk of indirect transmission of infection. Likewise, cattle could be kept in tie stalls, which would reduce the rate of direct and indirect transmission.

Vaccines have been developed to prevent transmission of salmonellosis in cattle [59,70]. Previous studies have indicated that these vaccines have different effects on cattle [32,35,36,53,61,66]. Specifically, some vaccines were shown to decrease host susceptibility [53], while others decreased the shedding level [36] or the duration of infection [53]. An available report indicates that salmonellosis vaccination is used on more than a quarter of Irish dairy farms [49]. We are unaware of published reports for other countries, but it is reasonable to assume that a similar vaccination coverage is present in all countries with intensive dairy production. Thus, we consider the effects of two vaccination strategies on the probability of disease extinction: vaccines which reduce the shedding level of infectious cattle and vaccines that shorten the duration of infectiousness. The results in Figure 3 show that if cattle are vaccinated at the time they are placed in the herd, then the probability of disease extinction increases. Based on the model parameters in Table 3, vaccines which reduce the shedding level of infectious cattle are more effective than vaccines which reduce the duration of infectiousness (compare Table A2 case (a), Table A3 case (f), and Table A4 case (a)).

Direct transmission and replication of free-living Salmonella in cattle pens do not significantly affect the probability of a major outbreak or disease extinction (see Figure 3 and Tables A1 and A3). Letting ${\beta }_1\to 0$, the basic reproduction number approaches a limiting value: $\underset{{\beta }_1\to 0^{+}}{lim}{\mathcal{R}}_0=\frac{1}{2}[{\mathcal{R}}_{03}+\sqrt{{\mathcal{R}}_{03}^2+4{\mathcal{R}}_{02}}].$ For the parameter values in Table 3, the limiting value is $\underset{{\beta }_1\to 0^{+}}{lim}{\mathcal{R}}_0=2.34$ which implies that Salmonella infection in dairy cattle cannot be controlled through direct transmission alone. Similarly, if we let $r\to 0$, the basic reproduction number approaches a limiting value: $\underset{r\to 0^{+}}{lim}{\mathcal{R}}_0=\frac{1}{2}[{\mathcal{R}}_{01}+\sqrt{{\mathcal{R}}_{01}^2+4{\mathcal{R}}_{02}}].$ For the parameter values in Table 3, the limiting value is $\underset{r\to 0^{+}}{lim}{\mathcal{R}}_0=2.57$. This result implies that salmonellosis cannot be controlled solely by inhibiting the replication of free-living Salmonella in cattle pens. In the case that the barn environment is not suitable for the replication of free-living Salmonella (r=0) and the force of infection due to direct transmission is negligible (${\beta }_1\approx 0$), the probability of disease extinction or a major outbreak can be estimated using the explicit expression in Equation (28).

The stochastic results indicate that in order to prevent a major outbreak it is crucial to screen incoming cattle for infection prior to placement in a susceptible herd. Unfortunately, screening cattle for infection can be difficult since they do not typically show clinical signs of infection. The screening process is further complicated by intermittent shedding patterns in which infectious cattle cycle between periods of shedding and non-shedding. If fecal samples are collected during a period of non-shedding, then one or more infectious cattle could be allowed into the herd. Improved methods for the diagnosis of infectious cattle would be valuable in the prevention of outbreaks. Removal of free-living Salmonella from the environment by cleaning cattle pens is an effective outbreak prevention measure. In addition, tie stall management can reduce the risk of direct and indirect transmission and significantly decrease the probability of a major outbreak. Moreover, vaccination of cattle at the time they are placed in the herd can decrease the probability of a major outbreak and vaccines targeting the shedding level of infectious cattle are more promising than vaccines which reduce the duration of host infectiousness. Finally, for the considered parameter values, direct transmission of infection and the replication of free-living Salmonella in cattle pens do not significantly affect the probability of a major outbreak provided that there is a sufficient level of environmental decontamination.

4.2. Cholera

Cholera is an intestinal infection caused by ingestion of food or water contaminated with the pathogen Vibrio cholerae [68]. In most cases, infection causes mild diarrhea but some cases result in severe diarrhea and vomiting which can lead to severe dehydration and death within a few hours if left untreated [30]. In 2008 and 2009, there was an outbreak of cholera in Zimbabwe with 98,585 reported cases and 4287 deaths [51]. Since 2010, there has been a major outbreak of cholera in Haiti with 684,085 reported cases and 8361 deaths [17]. Most recently, Sierra Leone has experienced an outbreak of cholera with more than 19,000 reported cases and 274 deaths [69]. The World Health Organization estimates that there are 3–5 million cases each year with 100,000–120,000 deaths spread over 40–50 countries [30,68].

Table 5 lists the model parameters related to cholera in a human population. The values have been scaled so that the unit of time is one day. We assume that Λ=9.1 so the total host population size is approximately 100, 000 which was the population size considered in [63]. The duration of immunity for cholera infection is controversial. However, Kabir states that the duration of immunity is variable and can be up to 3 years [39]. Thus, we use $\nu =1/(3\times 365)\approx 9.1\times {10}^{-4}$. Although the value of ν is uncertain, it does not affect the values of ${\mathcal{R}}_0$ or ℙ₀. It is possible to treat water wells and latrines by using chemicals such as chlorine or bleach [13]. Although these sanitation methods are highly effective in the removal of free-living V. cholerae from the environment, it is unlikely that widespread sanitation occurs regularly in developing countries where cholera is most prevalent [13]. The decontamination rate will vary between regions and depends on the method of water sanitation and waste treatment being used. Thus, it is difficult to estimate the rate of removal of pathogens from environmental water sources. According to the data in [13], 37% of households in Guinea-Bissau used bleach to disinfect latrines. Thus, we assume removal of free-living V. cholerae from the environment through daily environmental decontamination with a 37% application prevalence in the population (interpreted as efficacy at the population level). Using the formula developed in [5], we estimate the decontamination rate to be δ=0.46 which corresponds to a 37% pathogen removal efficacy (see Appendix 1). Although the decontamination rate is an assumption, the effects of varying the model parameters on the probability of disease extinction or a major outbreak are considered in Section 4.2.1 and Appendix 4.

Table 5.  Model parameters related to cholera in humans.

Definition	Parameter	Value	References
Recruitment rate	Λ	9.1	[63]
Natural death rate	d	$9.1\times {10}^{-5}$	[31,57,63]
Direct transmission rate	β1	$2.5\times {10}^{-6}$	[63]
Indirect transmission rate	β2	$1.07\times {10}^{-7}$	[63]
Pathogen-induced death rate	μ	0.03	[63]
Recovery rate	γ	0.33	[63]
Immunity loss rate	ν	$9.1\times {10}^{-4}$	[39]
Shedding rate	α	10	[19,31,57,63]
Pathogen replication rate	r	0.3	[38]
Pathogen death rate	ξ	0.07	[63]
Decontamination rate	δ	0.46	[13]
Carrying capacity	K	$1.55\times {10}^6$	[64]

For the values in Table 5, the reproduction numbers are ${\mathcal{R}}_{01}\approx 0.69$, ${\mathcal{R}}_{02}\approx 0.56$, ${\mathcal{R}}_{03}\approx 0.57$, and ${\mathcal{R}}_0\approx 1.38$. The solution of the ODE model exhibits dampened oscillations (recurring outbreaks) before stabilizing at the endemic equilibrium $(S^{\ast },I^{\ast },R^{\ast },P^{\ast })\approx (5.04\times {10}^4,75.06,2.47\times {10}^4,3255.3)$ with persistence of the disease. For the CTMC model, either disease extinction occurs with only a few infectious cases or there is a major outbreak. The solution of the ODE and one sample path of the CTMC model are plotted in Figure 4. Note that the solution of the deterministic model exhibits recurring outbreaks while the sample path illustrates a single outbreak followed by disease extinction. This difference is due to the fact that the variables for the ODE model are continuous while the random variables for the CTMC model are discrete-valued. The values of I and P in the deterministic model may take on values less than one and produce secondary outbreaks while disease extinction has occured for the stochastic model. This is often referred to as the stochastic fade-out of an epidemic [7,33,41,48].

Figure 4. Comparison of the ODE solution (dashed) and one sample path of the CTMC model (solid) for cholera illustrating recurring outbreaks and disease persistence. Parameter values are as in Table 5 with initial conditions S(0)=99, 999, I(0)=1, R(0)=0, and P(0)=0. The probability of an outbreak is 1−ℙ₀=0.4804 (see Table 6). The locally stable endemic equilibrium is (S*, I*, R*, P*)≈(5.04×10⁴, 75.06, 2.47×10⁴, 3255.3).

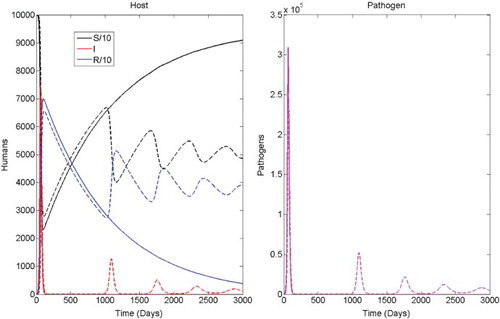
Table 6.  Probability of disease extinction, ℙ₀, for cholera calculated from the fixed point of the offspring pgfs and an approximation (Approx.) based on the proportion of 10,000 sample paths that hit zero before reaching endemic levels in numerical simulations of the CTMC model.

i0	p0	ℙ0	Approx.
1	0	0.5196	0.5220
2	0	0.2700	0.2709
0	10	0.8064	0.8070
0	20	0.6503	0.6498
1	10	0.4190	0.4187

Notes: Parameter values are as in Table 5 with initial conditions I(0)=i₀, S(0)=100, 000−i₀, R(0)=0, and P(0)=p₀. The basic reproduction number is ${\mathcal{R}}_0\approx 1.38$. Initial conditions P(0)=10 and P(0)=20 correspond to the average concentration of V. cholerae shed into the environment each day by one or two infectious individuals, respectively.

4.2.1. Probability of disease extinction or a major outbreak

The probability of disease extinction, ℙ₀, is calculated from the branching process approximation and compared to the estimate obtained from the proportion of 10,000 sample paths of the CTMC model for which the sum I(t)+P(t) hits zero before reaching endemic levels I(t)>75 or P(t)>3255. The value of ℙ₀ is a good estimate of the probability of disease extinction for the CTMC model (see Table 6). The initial conditions $P(0)=\alpha =10$ and $P(0)=2\alpha =20$ correspond to the average concentration of V. cholerae shed into the environment each day by one or two infectious individuals, respectively.

To determine the sensitivity of the model to variations in the model parameters, we allow the parameter values to fluctuate by $\pm 50\mathrm{\%}$ of their baseline values in Table 5. The effects on the probability of disease extinction can be seen in Figure 5. Note that the probability of disease extinction is highly sensitive to changes in the model parameters. The most influential parameter is the environmental decontamination rate. This rate is variable from region to region depending on the methods and frequency of water and/or sewage treatment. The decontamination rates used in Figure 5 and Table A6 cases (d), (e), and (f) correspond to daily treatment of the aquatic reservoir with a pathogen removal efficacy of 21%, 37%, and 50%, respectively. Although the results are most sensitive to changes in the decontamination rate, reducing the indirect transmission rate results in a slightly larger probability of disease extinction (compare Table A5 case (a) and Table A6 case (f)). Variations in the direct transmission rate have the least impact on the estimated probability of disease extinction which reflects the understanding that the primary route of cholera transmission is through the environment. For varying parameter values, there are small changes in the value of the basic reproduction number, ${\mathcal{R}}_0$. However, there are substantial changes in the probability of disease extinction or a major outbreak. For instance, if the indirect transmission rate is reduced by 50%, the basic reproduction number changes from ${\mathcal{R}}_0\approx 1.38$ to ${\mathcal{R}}_0\approx 1.16$. However, the probability of disease extinction increases from ${\mathbb{P}}_0=0.5196$ to ${\mathbb{P}}_0=0.7509$ for I(0)=1 and P(0)=0. The stochastic results provide valuable information about the likelihood of a major outbreak that cannot be obtained from the deterministic model.

Figure 5. Probability of disease extinction, ℙ₀, for cholera in a human population calculated from the fixed point of the offspring pgfs as the model parameters fluctuate by±50% of their baseline values in Table 5. The five curves indicated in the legend correspond to the five initial conditions considered in Table 6. Initial conditions P(0)=10 and P(0)=20 correspond to the average concentration of V. cholerae shed into the environment each day by one or two infectious individuals, respectively. Explicit values of ℙ₀ can be found in Tables A5–A7 in Appendix 4.

By providing a sufficient amount of clean drinking water, the risk of indirect transmission decreases and there is a substantial increase in the probability of disease extinction (see Table A5 case (d)). Similarly, proper disposal of human fecal waste (e.g. use of latrines) results in a large increase in the probability of disease extinction (see Table A6 case (a)). In addition to these control efforts, it is possible to treat water wells and latrines with chemicals to increase the death rate of free-living V. cholerae in the environment [13]. If the decontamination rate is increased, the probability of disease extinction increases significantly (see Table A6 case (f)). Unfortunately, in developing countries it is unlikely that widespread environmental decontamination occurs continually.

Previous epidemic models for cholera have not considered the replication of free-living V. cholerae in the environment. However, the replication rate of free-living pathogen has a substantial effect on the probability of disease extinction (see Figure 5 and Table A7 cases (a) and (c)) as well as the number of infectious hosts at equilibrium. As the replication rate of V. cholerae increases from r=0.3 to r=0.45, the number of infectious hosts at the endemic equilibrium increases from $I^{\ast }\approx 75.1$ to 115.7 whereas if the replication rate is decreased to r=0.15, the endemic level decreases to $I^{\ast }\approx 48.8$. These results suggest that the replication rate of free-living V. cholerae should be considered in cholera models, especially when modelling outbreaks in developing countries where decontamination of the environment is not common and environmental conditions support replication of the free-living pathogen. If we let $r\to 0$, then the basic reproduction number approaches a limiting value: $\underset{r\to 0^{+}}{lim}{\mathcal{R}}_0=\frac{1}{2}[{\mathcal{R}}_{01}+\sqrt{{\mathcal{R}}_{01}^2+4{\mathcal{R}}_{02}}].$ For this example, the limiting value is $\underset{r\to 0^{+}}{lim}{\mathcal{R}}_0=1.17$. This implies that cholera cannot be controlled by solely targeting the replication of free-living V. cholerae in the environment. However, this does not imply that control efforts focused on environmental decontamination are ineffective. In fact, the probability of a major outbreak is most significantly affected by fluctuations in the environmental decontamination rate (see Figure 5).

Other possible control mechanisms are isolation of infectious hosts and rapid treatment of infectious individuals to reduce the duration of infectiousness. Decreasing the duration of infectiousness results in a large increase in the probability of disease extinction. On the other hand, control efforts targeting direct transmission are not as effective since direct transmission of cholera is rare. Letting ${\beta }_1\to 0$, the basic reproduction number approaches a limiting value: $\underset{{\beta }_1\to 0^{+}}{lim}{\mathcal{R}}_0=\frac{1}{2}[{\mathcal{R}}_{03}+\sqrt{{\mathcal{R}}_{03}^2+4{\mathcal{R}}_{02}}].$ For the parameter values in Table 5, the limiting value is $\underset{{\beta }_1\to 0^{+}}{lim}{\mathcal{R}}_0=1.08$. Thus, it is not possible to eliminate cholera from a population by focusing on direct transmission alone. It is interesting to note that the basic reproduction number is ${\mathcal{R}}_0=1.08$ for β₁=0, and ${\mathcal{R}}_0=1.17$ for r=0. This implies that, for the considered parameter values, targeting direct transmission is more effective than targeting the pathogen replication rate. However, the stochastic results illustrate that decreasing the pathogen replication rate has a larger impact on the probability of disease extinction than decreasing the direct transmission rate. Since direct transmission of cholera is not common, some cholera models in the literature ignore direct transmission altogether [31,57]. These models also neglect the replication rate of free-living V. cholerae. For environments which do not support replication of free-living pathogens, the probability of cholera extinction can be estimated using Equation (28). Although the pathogen replication rate was neglected in previous studies on cholera, our results indicate that the replication rate significantly affects the probability of a major outbreak as well as the number of infectious hosts at the equilibrium. Thus, future models for cholera should consider the replication rate of V. cholerae in the aquatic reservoir.

The stochastic results confirm that the control mechanisms recommended by the World Health Organization are effective in preventing cholera outbreaks. Providing clean drinking water and proper disposal of fecal waste result in the largest increases in the probability of disease extinction (see Table A5 case (d) and Table A6 case (a)). Increased sanitation of water wells and latrines to increase the death rate of free-living V. cholerae could be an effective method of outbreak prevention (see Table A6 case (c)). Rapid treatment of infectious hosts to reduce the duration of infectiousness can significantly increase the probability of disease extinction. Control efforts targeting direct transmission or the replication rate of free-living pathogens cannot eliminate cholera unless they are paired with additional control efforts. For the parameter values in Table 5, the value of ${\mathcal{R}}_{01}$ is larger than the values of ${\mathcal{R}}_{02}$ and ${\mathcal{R}}_{03}$. This suggests that direct transmission plays a larger role than indirect transmission, shedding by infectious hosts, or pathogen replication. However, our results indicate that control strategies focused on indirect transmission and decreasing the free-living pathogen load are much more effective than strategies focused on direct transmission (see Figure 5).

5. Discussion

Indirect transmission, pathogen shedding by infectious hosts, replication of free-living pathogens in the environment, and environmental decontamination impact the emergence and spread of ETIDs. We investigated these factors by developing a nonlinear CTMC model based on the assumptions of the deterministic model introduced by Bani-Yaghoub et al. [6]. A multitype branching process was used to approximate the nonlinear CTMC near the disease-free equilibrium and the theory of multitype branching processes was used to estimate the probability of disease extinction or a major outbreak. For the deterministic model (2)–(5), the basic reproduction number determines the dynamics with respect to disease persistence or extinction. In particular, if ${\mathcal{R}}_0\le 1$, the disease-free equilibrium is globally asymptotically stable and if ${\mathcal{R}}_0>1$, the endemic equilibrium is locally asymptotically stable [6]. Using the CTMC model and corresponding branching process approximation, we estimated the probability of disease extinction or a major outbreak for two ETIDs: salmonellosis in a herd of dairy cattle and cholera in a human population. Our results confirm the importance of indirect transmission, pathogen shedding, replication of free-living pathogens, and environmental decontamination to disease transmission and illustrate that there are differences between the deterministic and stochastic models which have major implications for disease control and outbreak prediction.

For salmonellosis in a herd of dairy cattle, our results suggest that screening cattle for infection is the most effective way to prevent a major outbreak. If infectious cattle are placed in a susceptible herd, it is very likely an outbreak will occur (see Table 4 and Figure 3). Unfortunately, cattle often do not show clinical signs of Salmonella infection. The standard method of screening for infectiousness involves collecting fecal samples from cattle and testing these samples for the presence of Salmonella. This process is complicated by the intermittent shedding of pathogen by infectious cattle. If fecal samples are collected from an infected host during a period of non-shedding or shedding below the detection limit, then infected hosts could be allowed into a susceptible herd. Improved methods of screening cattle for Salmonella infection would be valuable for public health, food safety, and farm management. Frequent and thorough decontamination of the barn surface was shown to significantly decrease the probability of a major outbreak. If cattle are kept in tie stalls, the risk of direct and indirect transmission is decreased which results in large decreases in the probability of a major outbreak. Decontamination efforts and tie stall management can be paired with additional control efforts, such as vaccination of cattle, to decrease the probability of a major outbreak. Moreover, our results suggest that vaccines which reduce the shedding level of infectious cattle are more promising than vaccines which reduce the duration of host infectiousness.

For cholera in a human population, our stochastic results support the control efforts recommended by the World Health Organization. Providing clean drinking water to the population and ensuring hygenic disposal of human fecal waste can greatly decrease the probability of a major cholera outbreak. Increased sanitation of water wells and latrines to increase the death rate of free-living pathogens could also be an effective method of outbreak prevention. Unfortunately, regular treatment of water sources is not widespread in developing countries [13]. Although most of the previous models for cholera do not consider the replication of free-living V. cholerae, our results indicate that the pathogen replication rate can significantly impact the probability of a cholera outbreak. Rapid treatment of infectious individuals to reduce their duration of infectiousness significantly decreases the probability of an outbreak. The results indicate that control strategies targeting direct transmission of cholera can decrease the probability of an outbreak, but control efforts targeting indirect transmission are much more effective.

In the case that there is no direct transmission of infection (β₁=0) and no replication of free-living pathogens (r=0), it is possible to obtain a simple analytical expression for the probability of disease extinction or a major outbreak in terms of the model parameters (see Equation (28)). For some ETIDs, such as salmonellosis among pigs and cholera in humans, it is believed that direct transmission of infection is negligible. Moreover, in some regions the environmental conditions may not support replication of free-living pathogens. In such a situation, the expression obtained in Equation (28) provides an estimate for the probability of disease extinction.

There are some limitations of the deterministic and stochastic models presented in this manuscript. In particular, we did not account for removal of free-living pathogens from the environment due to ingestion by hosts. However, the removal of free-living pathogens from the environment through ingestion by a host is negligible when compared to the amount of pathogen shed by infectious hosts and the number of free-living pathogens removed from the environment by natural decay or environmental decontamination. Due to this fact, the majority of previous models for salmonellosis and cholera do not include ingestion of free-living pathogens [18,19,26,43,56,57,62,71]. Additionally, an assumption of our model is that infectious hosts shed pathogens into the environment continuously. However, infectious hosts typically exhibit a pattern of intermittent shedding. Once they become infectious, hosts shed pathogens into the environment at high levels and then cycle between periods of non-shedding or shedding at a lower levels. The next generation of our model will include intermittent pathogen shedding by infectious hosts. In the implementation of the CTMC model, we increase the number of free-living pathogens by one each time the shedding event occurs. However, shedding typically occurs via discrete events in which many pathogens are relased into the environment at one time. To account for this, we include the number of pathogens shed during each event in the shedding rate α. This allowed for a more straightforward comparison of the deterministic and stochastic results. Future stochastic models for ETIDs may consider implementing pathogen shedding as a jump process. Moreover, due to a lack of information regarding the true values of the model parameters, we used estimates or assumptions from previous studies on salmonellosis and cholera. Certain parameters do not affect the value of ${\mathcal{R}}_0$ or ℙ₀ (e.g. ν and K). However, obtaining accurate estimates for parameter values such as the direct and indirect transmission rates or the environmental decontamination rate for cholera could be valuable for outbreak prediction and disease control.

In this manuscript, we considered the examples of salmonellosis in dairy cattle and cholera in a human population. However, the model (2)–(5) and the techniques used to obtain an estimate for the probability of disease extinction of a major outbreak can be applied to other ETIDs such as Escherichia coli O157:H7 in a cattle herd, Salmonella infection in pigs, Avian Influenza in wild birds, Campylobacter infection in chickens, and cryptosporidiosis in cattle.

Funding

This work was supported by the National Science Foundation grant [NSF-EF-0913367] to RI.

Acknowledgements

Any opinions, findings, conclusions, or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation. We would like to thank two anonymous reviewers for their suggestions which improved the paper.

Appendix 1. Estimation of the environmental decontamination rates for salmonellosis and cholera

Using the technique described in [5], the relationship between the decontamination rate δ and the efficacy of environmental decontamination represented as the proportion of free-living pathogens removed from the environment ($P_{\text{Removed}}$) each day is given by $\delta =-\ln \left(1-\frac{P_{\mathrm{Removed}}}{100}\right).$ For salmonellosis, the baseline value of δ=1.2 in Table 3 corresponds to a pathogen removal efficacy of 70% [26]. For cholera, the baseline value of δ=0.46 in Table 5 corresponds to an efficacy of 37% [13].

Appendix 2. Estimation of the carrying capacity of free-living Salmonella in the environment

It follows from Equation (6) that $\underset{t\to \mathrm{\infty }}{lim sup}N(t)\le \mathrm{\Lambda }/d=100$. Thus, there will be no more than 100 cattle in the herd in the long-run. According to Sinton et al. [58], the carrying capacity of free-living Salmonella in cattle fecal debris could be as high as $6.5\times {10}^7$ pathogens per gram of feces. On average, cattle produce 30 kg of feces per day [65]. Thus, if there are 100 cattle, the environmental carrying capacity of free-living Salmonella is approximately $K=30,000\times 100\times 6.5\times {10}^7=1.95\times {10}^{14}$ pathogens. The true value of the environmental carrying capacity is unknown.

Appendix 3. Sensitivity analysis for salmonellosis

Tables A1–A3 illustrate the effects of varying the model parameters by $\pm 50\mathrm{\%}$ of their baseline values in Table 3 on the probability of disease extinction for salmonellosis in a herd of dairy cattle. The results in Table A4 illustrate the effect of varying the pathogen shedding rate α by ±log10 of its baseline value in Table 3.

Appendix 4. Sensitivity analysis for cholera

Tables A5–A7 illustrate the effects of varying the model parameters by $\pm 50\mathrm{\%}$ of their baseline values in Table 5 on the probability of disease extinction for cholera in a human population.

Table A1  Probability of disease extinction, ℙ₀, for salmonellosis in a dairy herd calculated from the fixed point of the offspring pgfs.

		(a)	(b)	(c)
	Initial conditions	50% Decrease ${\beta }_1=0.0003$	Baseline ${\beta }_1=0.0006$	50% Increase ${\beta }_1=0.0009$
i0	p0	ℙ0	ℙ0	ℙ0
1	0	0.1606	0.1547	0.1431
2	0	0.0258	0.0239	0.0205
0	5×10^7	0.5975	0.5945	0.5916
0	10^8	0.3570	0.3535	0.3499
1	5×10^7	0.0959	0.0920	0.0846
		(d)	(e)	(f)
	Initial conditions	50% Decrease ${\beta }_2=6.5\times {10}^{-11}$	Baseline ${\beta }_2=1.3\times {10}^{-10}$	50% Increase ${\beta }_2=1.95\times {10}^{-10}$
i0	p0	ℙ0	ℙ0	ℙ0
1	0	0.3153	0.1547	0.1018
2	0	0.0994	0.0239	0.0104
0	5×10^7	0.8270	0.5945	0.4232
0	10^8	0.6839	0.3535	0.1791
1	5×10^7	0.2607	0.0920	0.0431

Notes: Parameter values are as in Table 3 (except for β₁ in cases (a) and (c) and β₂ in cases (d) and (f)) with initial conditions I(0)=i₀, $S(0)=100-i_0$, R(0)=0, and P(0)=p₀. The basic reproduction number is (a) ${\mathcal{R}}_0\approx 2.48$, (b) ${\mathcal{R}}_0\approx 2.64$, (c) ${\mathcal{R}}_0\approx 2.81$, (d) ${\mathcal{R}}_0\approx 1.98$, (e) ${\mathcal{R}}_0\approx 2.64$, and (f) ${\mathcal{R}}_0\approx 3.15$.

Table A2.  Probability of disease extinction, ℙ₀, for salmonellosis in a dairy herd calculated from the fixed point of the offspring pgfs.

		(a)	(b)	(c)
	Initial conditions	50% Decrease $\alpha =2.5\times {10}^7$	Baseline $\alpha =5\times {10}^7$	50% Increase $\alpha =7.5\times {10}^7$
i0	p0	ℙ0	ℙ0	ℙ0
1	0	0.2779	0.1547	0.1011
2	0	0.0772	0.0239	0.0102
0	5×10^7	0.6408	0.5945	0.5769
0	10^8	0.4107	0.3535	0.3329
1	5×10^7	0.1781	0.0920	0.0583
		(d)	(e)	(f)
	Initial conditions	50% Decrease δ=0.6	Baseline δ=1.2	50% Increase δ=1.8
i0	p0	ℙ0	ℙ0	ℙ0
1	0	0.0698	0.1547	0.2336
2	0	0.0049	0.0239	0.0546
0	5×10^7	0.2645	0.5945	0.7408
0	10^8	0.0721	0.3535	0.5488
1	5×10^7	0.0188	0.0920	0.1731

Notes: Parameter values are as in Table 3 (except for α in cases (a) and (c) and δ in cases (d) and (f)) with initial conditions I(0)=i₀, $S(0)=100-i_0$, R(0)=0, and P(0)=p₀. The basic reproduction number is in (a) ${\mathcal{R}}_0\approx 1.98$, (b) ${\mathcal{R}}_0\approx 2.64$, (c) ${\mathcal{R}}_0\approx 3.15$, (d) ${\mathcal{R}}_0\approx 3.58$, (e) ${\mathcal{R}}_0\approx 2.64$, and (f) ${\mathcal{R}}_0\approx 2.22$.

Table A3  Probability of disease extinction, ℙ₀, for salmonellosis in a dairy herd calculated from the fixed point of the offspring pgfs.

		(a)	(b)	(c)
	Initial conditions	50% Decrease r=0.1	Baseline r=0.2	50% Increase r=0.3
i0	p0	ℙ0	ℙ0	ℙ0
1	0	0.1674	0.1547	0.1413
2	0	0.0280	0.0239	0.0200
0	5×10^7	0.6250	0.5945	0.5599
0	10^8	0.3906	0.3535	0.3135
1	5×10^7	0.1046	0.0920	0.0791
		(d)	(e)	(f)
	Initial conditions	50% Decrease γ=0.05	Baseline γ=0.1	50% Increase γ=0.15
i0	p0	ℙ0	ℙ0	ℙ0
1	0	0.0787	0.1547	0.2312
2	0	0.0062	0.0239	0.0534
0	5×10^7	0.5684	0.5945	0.6250
0	10^8	0.3230	0.3535	0.3906
1	5×10^7	0.0447	0.0920	0.1445

Notes: Parameter values are as in Table 3 (except for r in cases (b) and (c) and γ in cases (e) and (f)) with initial conditions I(0)=i₀, $S(0)=100-i_0$, R(0)=0, and P(0)=p₀. The basic reproduction number is (a) ${\mathcal{R}}_0\approx 2.61$, (b) ${\mathcal{R}}_0\approx 2.64$, (c) ${\mathcal{R}}_0\approx 2.68$, (d) ${\mathcal{R}}_0\approx 3.86$, (e) ${\mathcal{R}}_0\approx 2.64$, and (f) ${\mathcal{R}}_0\approx 2.13$.

Table A4  Probability of disease extinction, ℙ₀, for salmonellosis in a dairy herd calculated from the fixed point of the offspring pgfs.

		(a)	(b)	(c)
	Initial conditions	log10 Decrease $\alpha =5\times {10}^6$	Baseline $\alpha =5\times {10}^7$	log10 Increase $\alpha =5\times {10}^8$
i0	p0	ℙ0	ℙ0	ℙ0
1	0	0.8334	0.1547	0.0162
2	0	0.6946	0.0239	0.0003
0	5×10^7	0.9048	0.5945	0.5461
0	10^8	0.8187	0.3535	0.2982
1	5×10^7	0.7541	0.0920	0.0089

Notes: Parameter values are as in Table 3 (except for α in cases (a) and (c)) with initial conditions I(0)=i₀, $S(0)=100-i_0$, R(0)=0, and P(0)=p₀. The basic reproduction number is (a) ${\mathcal{R}}_0\approx 1.12$, (b) ${\mathcal{R}}_0\approx 2.64$, (c) ${\mathcal{R}}_0\approx 7.51$.

Table A5  Probability of disease extinction, ℙ₀, for cholera calculated from the fixed point of the offspring pgfs.

		(a)	(b)	(c)
	Initial conditions	50% Decrease ${\beta }_1=1.25\times {10}^{-6}$	Baseline ${\beta }_1=2.5\times {10}^{-6}$	50% Increase ${\beta }_1=3.75\times {10}^{-6}$
i0	p0	ℙ0	ℙ0	ℙ0
1	0	0.6287	0.5196	0.4420
2	0	0.3952	0.2700	0.1953
0	10	0.8456	0.8064	0.7800
0	20	0.7151	0.6503	0.6084
1	10	0.5316	0.4190	0.3447
		(d)	(e)	(f)
	Initial conditions	50% Decrease ${\beta }_2=5.35\times {10}^{-8}$	Baseline ${\beta }_2=1.07\times {10}^{-7}$	50% Increase ${\beta }_2=1.605\times {10}^{-7}$
i0	p0	ℙ0	ℙ0	ℙ0
1	0	0.7509	0.5196	0.4048
2	0	0.5638	0.2700	0.1639
0	10	0.9443	0.8064	0.6784
0	20	0.8916	0.6503	0.4602
1	10	0.7090	0.4190	0.2746

Notes: Parameter values are as in Table 5 (except for β₁ in cases (a) and (c) and β₂ in cases (d) and (f)) with initial conditions I(0)=i₀, S(0)=100, 000−i₀, R(0)=0, and P(0)=p₀. The basic reproduction number is in (a) ${\mathcal{R}}_0\approx 1.21$, (b) ${\mathcal{R}}_0\approx 1.38$, (c) ${\mathcal{R}}_0\approx 1.59$, (d) ${\mathcal{R}}_0\approx 1.16$, (e) ${\mathcal{R}}_0\approx 1.38$, and (f) ${\mathcal{R}}_0\approx 1.55$.

Table A6  Probability of disease extinction, ℙ₀, for cholera calculated from the fixed point of the offspring pgfs.

		(a)	(b)	(c)
	Initial conditions	50% Decrease α=5	Baseline α=10	50% Increase α=15
i0	p0	ℙ0	ℙ0	ℙ0
1	0	0.7553	0.5196	0.3971
2	0	0.5705	0.2700	0.1577
0	10	0.8944	0.8064	0.7653
0	20	0.8000	0.6503	0.5856
1	10	0.6756	0.4190	0.3039
		(d)	(e)	(f)
	Initial conditions	50% Decrease δ=0.23	Baseline δ=0.46	50% Increase δ=0.69
i0	p0	ℙ0	ℙ0	ℙ0
1	0	0.1675	0.5196	0.7496
2	0	0.0281	0.2700	0.5618
0	10	0.1789	0.8064	0.9438
0	20	0.0320	0.6503	0.8907
1	10	0.0300	0.4190	0.7074

Notes: Parameter values are as in Table 5 (except for α in cases (a) and (c) and δ in cases (d) and (f)) with initial conditions I(0)=i₀, S(0)=100, 000−i₀, R(0)=0, and P(0)=p₀. The basic reproduction number is in (a) ${\mathcal{R}}_0\approx 1.16$, (b) ${\mathcal{R}}_0\approx 1.38$, (c) ${\mathcal{R}}_0\approx 1.55$, (d) ${\mathcal{R}}_0\approx 1.85$, (e) ${\mathcal{R}}_0\approx 1.38$, and (f) ${\mathcal{R}}_0\approx 1.19$.

Table A7  Probability of disease extinction, ℙ₀, for cholera calculated from the fixed point of the offspring pgfs.

		(a)	(b)	(c)
	Initial conditions	50% Decrease r=0.15	Baseline r=0.3	50% Increase r=0.45
i0	p0	ℙ0	ℙ0	ℙ0
1	0	0.6818	0.5196	0.3074
2	0	0.4649	0.2700	0.0945
0	10	0.9150	0.8064	0.5171
0	20	0.8371	0.6503	0.2674
1	10	0.6239	0.4190	0.1590
		(d)	(e)	(f)
	Initial conditions	50% Decrease $\gamma =0.165$	Baseline γ=0.33	50% Increase $\gamma =0.495$
i0	p0	ℙ0	ℙ0	ℙ0
1	0	0.2855	0.5196	0.7468
2	0	0.0815	0.2700	0.5577
0	10	0.7302	0.8456	0.8910
0	20	0.5331	0.6503	0.7939
1	10	0.2085	0.4190	0.6654

Notes: Parameter values are as in Table 5 (except for r in cases (a) and (c) and γ in cases (d) and (f)) with initial conditions I(0)=i₀, S(0)=100, 000−i₀, R(0)=0, and P(0)=p₀. The basic reproduction number is in (a) ${\mathcal{R}}_0\approx 1.27$, (b) ${\mathcal{R}}_0\approx 1.38$, (c) ${\mathcal{R}}_0\approx 1.52$, (d) ${\mathcal{R}}_0\approx 2$, (e) ${\mathcal{R}}_0\approx 1.38$, and (f) ${\mathcal{R}}_0\approx 1.14$.