A seasonal SIR metapopulation model with an Allee effect with application to controlling plague in prairie dog colonies

Abstract

For wildlife species living among patchy habitats, disease and the Allee effect (reduced per capita birth rates at low population densities) may together drive a patch's population to extinction, particularly if births are seasonal. Yet local extinction may not be indicative of global extinction, and a patch may become recolonized by migrating individuals. We introduce deterministic and stochastic susceptible, infectious, and immune epidemic models with vector species to study disease in a metapopulation with an Allee effect and seasonal birth and dispersal. We obtain conditions for the existence of a strong Allee effect and existence and stability of a disease-free positive periodic solution. These general models have application to many wildlife diseases. As a case study, we apply them to evaluate dynamics of the sylvatic plague in prairie dog colonies interconnected through dispersal. We further evaluate the effects of control of the vector population and control by immunization on plague eradication.

Keywords:

• Allee effect
• stochastic epidemic model
• periodic solutions
• prairie dogs
• vector control

AMS Subject Classification::

• 92D25
• 92D30
• 60H10
• 34C25
• 34C60

1. Introduction

There are many papers discussing disease transmission with population dispersal among patchy or fragmented environments (e.g. [5, 7, 31, 36, 57, 63, 75]). Such studies are important, as changing land usage has resulted in increasingly fragmented habitats for some species, and some other species have naturally patchily distributed habitat or live in colonies (such as butterflies, prairie dogs, field voles, sea urchins, and reef fish [16, 19,43, 52, 54]). If a disease incurs a higher death rate or lower individual fitness compared to a disease-free population, then the disease reduces patch population densities. The Allee effect and seasonal birth rates together may then drive such patches to extinction and population dispersal may govern the recolonization [23, 29, 30,47].

The Allee effect is a positive correlation between population density and mean individual fitness, in which the per capita growth rate of populations at low densities increases with an increase in density [3, 15]. The Allee effect can be caused by several mechanisms that influence reproduction and survival. The most common mechanism is reduced reproduction because of the failure to locate mates [12, 15, 21, 42]. Active dispersal away from low-density populations can also result in stunted population growth rates [10]. Such phenomena affect small populations by reducing the average individual fitness and, hence, the Allee effect is an important phenomenon to include in epidemic models, where epidemics tend to decrease population densities.

Environmental stochasticity is represented by temporal changes in the rates of events, such as the rates of birth, death and dispersal. The effect of environmental stochasticity on the per capita growth rate is nearly independent of the population size [53]. Even when the population is not particularly small, environmental stochasticity contributes to extinction [53]. A stochastic model is required for the study of many problems, such as finding the probability of a major outbreak and the likelihood of disease persistence. To satisfactorily explain the behaviour of the spread of a disease through a population with small or medium size communities, such as through fragmented landscapes, it is important to include both environmental stochasticity and the Allee effect.

The Allee effect and stochasticity are studied together in [22] using diffusion processes that accommodate stochastic fluctuations. Kang and Castillo-Chavez [46] provide a comprehensive literature review and a study of single- and multi-patch SI disease models with the Allee effect and dispersion including the effect of stochasticity. Friedman and Yukabu obtained conditions that guarantee host population persistence (with or without infected individuals) or extinction using a patchy SI epidemic model with the Allee effect [30]. All these results have important implications for predicting the survival of threatened populations, the success of reintroductions, and the control of invasive species. Yet only a few studies have considered a combination of the Allee effect under seasonally dependent rates of change, environmental stochasticity, and dispersal in a multi-patch environment, and then apply the model to evaluate the survival of an actual population. Further, some conservation efforts (such as control of the sylvatic plague within prairie dog colonies) focus on immunization. In this paper, we study a deterministic susceptible, infectious, and immune (SIR) epidemic population model with seasonal and Allee effects in a patchy environment. We discuss how the model can be used to evaluate control methods in wildlife populations and extend the model to include stochasticity. As a case study, we use the model to investigate the sylvatic plague within prairie dog colonies and the effectiveness of existing control methods.

2. Description of the system

The spread of disease within a population residing among p distinct habitable patches is modelled with three classes in each patch for the host species: let $S_i(t)$, $I_i(t)$, and $R_i(t)$ be the number of individuals in patch i at time t in the susceptible, infectious, and immune classes, respectively. Let $N_i(t)$ be the total host population size in patch i at time t: $N_i(t)=S_i(t)+I_i(t)+R_i(t)$. If a vector species spreads the pathogen, vector population dynamics are also important. Some diseases are spread by more than one vector species or transmission method. For example, the Rocky Mountain spotted fever can be transmitted by several different tick species, including Dermacentor variabilis and Dermacentor andersoni [20]. The sylvatic plague in prairie dogs can be transmitted by multiple flea species (Oropsylla hirsuta and Oropsylla tuberculata cynomuris) and through multiple manners (by blocked fleas and also through transition immediately following an infected blood meal) [28, 77, 78]. Let $N_i^{(k)}=Z_i^{(k)}+\sum _l{Y}_i^{(kl)}$ be the number of individuals of the kth vector species in patch i at time t, where $Z_i^{(k)}(t)$ is the number that are susceptible at time t and $Y_i^{(kl)}(t)$ is the number spreading the pathogen at time t in the lth manner.

The dynamics of a population exhibiting the Allee effect are often represented by $\mathrm{d}N/\mathrm{d}t=\gamma N(N-\theta )(\kappa -N),$ where θ is called the Allee threshold (see [29]). This model exhibits a strong Allee effect: populations of size less than threshold θ go extinct. Such representation allows neither for a weak Allee effect nor for distinguishing between birth and death rates, which is important in stochastic models. In this paper, the Allee effect is included as a density-dependent birth rate, representing reduced reproduction levels at lower densities. For a patch i having ${\pi }_i$ individuals of the same species, let $\rho (X_i)=\frac{X_i}{{\pi }_i+1}$ be the proportion of individuals in class ‘$X_i$’. Using this definition, we avoid division by zero in numerical simulations. We make the following assumptions for modelling a vector-spread epidemic within p-distinct patches.

• $\mathcal{A}1$: Birth and dispersal rates are seasonal. Seasonal dependence is incorporated via a function of the form ${\phi }_U\in C(\mathbb{R})$; ${\phi }_U(t+kT)={\phi }_U(t)$ for $k=1,2,\dots ,$ where T is one year; ${\phi }_U(t)\ge 0$; $\parallel {\phi }_U{\parallel }_{\mathrm{\infty }}=1$; and ${\phi }_U(t)\ne 0$ for all $t\in U\subset [0,T]$.

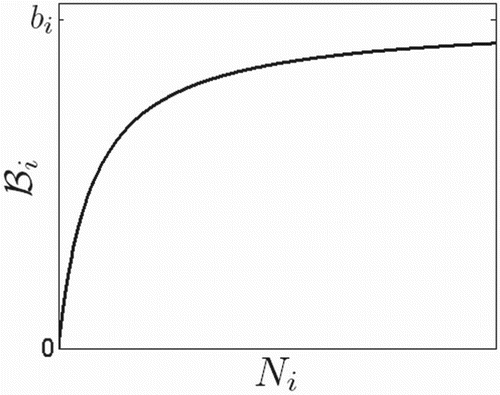
• $\mathcal{A}2$: Newborns of the host species are susceptible at birth. The per capita birth rate is ${\phi }_{U_1}(t){\mathcal{B}}_i(N_i)$, where ${\phi }_{U_1}(t)$ incorporates seasonal dependence and ${\mathcal{B}}_i(N_i)$ is a bounded, continuously differentiable, concave and monotonically increasing function of $N_i$ with $0\le {\mathcal{B}}_i(N_i)\le b_i$ for all $N_i\ge 0$. An example for ${\mathcal{B}}_i$ is given in Figure 1.

• $\mathcal{A}3$: The per capita rate of death is linear and may be higher among infectious individuals: $d_i+c_i{N}_i$ for the susceptible and immune classes and $d_i^I+c_i{N}_i$ for the infectious class, where $d_i,d_i^I,c_i$ are positive constants with $d_i^I\ge d_i$, $i=1,\dots ,p$. Thus, within patch i, the larger the population, the greater the per capita death rate.

• $\mathcal{A}4$: The per capita rate that susceptible individuals become infected is ${\beta }_i{I}_i$ for host-to-host transmission and ${\beta }_i^{(kl)}{Y}_i^{(kl)}/N_i$, $l=1,\dots ,L_k$, $k=1,\dots ,K$, for indirect transmission via vector individuals of the kth species using the lth method. Ratio $Y_i^{(kl)}/N_i$ represents the number of pathogen-carrying vectors of a certain type per host individual (vector abundance) in patch i.

• $\mathcal{A}5$: The per capita rate of recovery is constant within each patch: ${\gamma }_i$. The proportion of recovered individuals that return to the susceptible class is ${\alpha }_1\in [0,1]$ and the remaining recovered individuals become immune to the disease. If infectious individuals are infectious for life, ${\gamma }_i=0$, $i=1,\dots ,p$.

• $\mathcal{A}6$: The per capita rate at which infectious individuals become vaccinated is constant for each patch: $v_i$.

• $\mathcal{A}7$: Immigrants maintain their class (SIR) when migrating between patches. The per capita rate of migration from patch j to patch i varies seasonally: ${\phi }_{U_2}(t)m_{ij}$, where $m_{ij}$ is a positive constant for $i,j=1,\dots ,p$, $i\ne j$, and ${\phi }_{U_2}(t)\in [0,1]$ represents the seasonal dependence.

• $\mathcal{A}8$: The per capita rate of birth among the kth vector species is seasonal: ${\phi }_{U_3^{(k)}}(t){\mathcal{B}}^{(k)}(N_i,N_i^{(k)})$, where ${\phi }_{U_3^{(k)}}(t)$ incorporates seasonal dependence and ${\mathcal{B}}^{(k)}(N_i,N_i^{(k)})$ is a continuous function of $N_i$ and $N_i^{(k)}$, with ${\mathcal{B}}^{(k)}(N_i,N_i^{(k)})\ge 0$ for $N_i,N_i^{(k)}\ge 0$. All vector individuals are born susceptible.

• $\mathcal{A}9$: The per capita death rate of the kth vector species is constant within each patch: $d_i^{(k)}$ and $d_i^{(kl)}$ for classes $Z_i^{(k)}$ and $Y_i^{(kl)}$, respectively, with $d_i^{(k)}\le d_i^{(kl)},$ $i=1,\dots ,p$.

• $\mathcal{A}10$: The per capita rate at which individuals of the kth vector species become pathogen carriers of the lth type depends on the proportion of infectious host individuals: ${\lambda }_i^{(kl)}\rho (I_i)$, where ${\lambda }_i^{(kl)}$ is a positive constant.

• $\mathcal{A}11$: The per capita rate at which pathogen-carrying individuals in the $Y_i^{(kl)}$ class recover may depend on the host population: ${\gamma }_i^{(kl)}h(S_i,I_i,R_i)(t)$, where ${\gamma }_i^{(kl)}$ is a positive constant and $h(S_i,I_i,R_i)$ is a continuous function with respect to $S_i$, $I_i$, and $R_i$, bounded by $\rho (S_i+R_i)\le h(S_i,I_i,R_i)\le 1$. If vector recovery does not depend on host individuals, then $h(S_i,I_i,R_i)=1$ for all t.

• $\mathcal{A}12$: The per capita rate at which infectious vector individuals in class $Y_j^{(kl)}$ move between patches, from patch j to patch i, is seasonal and depends on the proportion of infectious host individuals: ${\phi }_{U_4^{(k)}}(t)m_{ij}^{(kl)}\rho (I_j)$, where $m_{ij}^{(kl)}$ is a positive constant, $i\ne j$. Likewise, susceptible vector individuals in class $Z_j^{(k)}$ move from patch j to patch i with a per capita rate that depends on the proportion of susceptible and immune host individuals, ${\phi }_{U_4^{(k)}}(t)m_{ij}^{(k)}\rho (S_j+R_j)$.

Figure 1. Example curve ${\mathcal{B}}_i(N_i)$ satisfying assumption $\mathcal{A}2$.

In assumption $\mathcal{A}3$, the linear per capita death rate reflects a logistic-type assumption and prevents exponential growth. This death rate, combined with the conditions on the birth rate function in $\mathcal{A}2$, permits the model's intrinsic growth rate to exhibit the Allee effect, as will be shown in Theorem 3.2.

Incorporating ${\phi }_U(t)$ allows the model to capture seasonal trends prevalent among many species, especially in locations with significant changes in weather by season. However, the model can also be applied to species that do not exhibit seasonal changes by setting ${\phi }_U(t)=1$ for all t. Further, seasonal rates need not coincide. Specifically, the migration season(s) for the vector species need not be identical to the migration season(s) for the host species, even though the vector species migration rate does include host variables; that is, $U_4^{(k)}$ need not be identical to $U_2$. Since there may be other, unmodelled species that aid in vector migration, we assume that the prevalence of the disease among other species in a given region is proportional to the prevalence among the host,$\rho (I_i)$.

Assumption $\mathcal{A}11$ accommodates a variety of vector recovery behaviours. If infectious vector individuals remain infectious for life, we set ${\gamma }_i^{(kl)}=0$. If they recover with a constant per capita rate, as assumed in many epidemic models, we set $h(S_i,I_i,R_i)=1$. However, some infectious vector individuals become susceptible again at a rate that depends on the host species. For example, if an insect spreads the pathogen only immediately after a blood meal from an infectious host, then the rate of recovery depends on the proportion of host individuals that are not infectious (see Section 5.1). In this case,$h(S_i,I_i,R_i)=\rho (S_i+R_i)$.

Likewise, by setting host recovery parameter ${\gamma }_i=0$ in assumption $\mathcal{A}5$, the SIR model reduces to an SI model, in which individuals are infectious for life. For ${\gamma }_i>0$, by setting ${\alpha }_1=1$, the SIR model becomes an SIS model, in which recovered individuals are again susceptible.

3. ODE model

The ordinary differential equation (ODE) model is given by $\begin{array}{rl}\frac{\mathrm{d}{S}_i}{\mathrm{d}t}& ={\phi }_{U_1}(t){\mathcal{B}}_i(N_i)N_i-(d_i+c_i{N}_i+v_i+{\beta }_i{I}_i)S_i-\sum _{k=1}^K\sum _{l=1}^{L_k}{\beta }_i^{(kl)}\rho (S_i)Y_i^{(kl)}\\ & +{\alpha }_1{\gamma }_i{I}_i+{\phi }_{U_2}(t)\sum _{j=1}^p[m_{ij}{S}_j-m_{ji}{S}_i],\end{array}$ $\begin{array}{rl}\frac{\mathrm{d}{I}_i}{\mathrm{d}t}& ={\beta }_i{S}_i{I}_i+\sum _{k=1}^K\sum _{l=1}^{L_k}{\beta }_i^{(kl)}\rho (S_i)Y_i^{(kl)}-(d_i^I+c_i{N}_i+{\gamma }_i)I_i+{\phi }_{U_2}(t)\sum _{j=1}^p[m_{ij}^I{I}_j-m_{ji}^I{I}_i],\end{array}$ $\begin{array}{rl}\frac{\mathrm{d}{R}_i}{\mathrm{d}t}& =v_i{S}_i+(1-{\alpha }_1){\gamma }_i{I}_i-(d_i+c_i{N}_i)R_i+{\phi }_{U_2}(t)\sum _{j=1}^p[m_{ij}{R}_j-m_{ji}{R}_i],\end{array}$ $\begin{array}{rl}\frac{\mathrm{d}{Z}_i^{(k)}}{\mathrm{d}t}& ={\phi }_{U_3^{(k)}}(t){\mathcal{B}}^{(k)}(N_i,N_i^{(k)})N_i^{(k)}+\sum _{l=1}^{L_k}{\gamma }_i^{(kl)}h(S_i,I_i,R_i)Y_i^{(kl)}-(d_i^{(k)}+\sum _{l=1}^{L_k}{\lambda }_i^{(kl)}\rho (I_i))Z_i^{(k)}\\ & +{\phi }_{U_4^{(k)}}(t)\sum _{j=1}^p[m_{ij}^{(k)}\rho (S_j+R_j)Z_j-m_{ji}^{(k)}\rho (S_i+R_i)Z_i^{(k)}],\end{array}$ $\begin{array}{rl}\frac{\mathrm{d}{Y}_i^{(kl)}}{\mathrm{d}t}& ={\lambda }_i^{(kl)}\rho (I_i)Z_i^{(k)}-(d_i^{(kl)}+{\gamma }_i^{(kl)}h(S_i,I_i,R_i))Y_i^{(kl)}\\ & +{\phi }_{U_4^{(k)}}(t)\sum _{j=1}^p[m_{ij}^{(kl)}\rho (I_j)Y_j^{(kl)}-m_{ji}^{(kl)}\rho (I_i)Y_i^{(kl)}]\end{array}$ for $i=1,\dots ,p$, $l=1,\dots ,L_k$, $k=1,\dots ,K$.

The model is well posed and biologically well defined. To show this, first define $\begin{array}{rl}\mathit{N}& =[N_1,N_2,\dots ,N_p{]}^{\mathrm{T}},\\ {\mathit{N}}^{(k)}& =[N_1^{(k)},N_2^{(k)},\dots ,N_p^{(k)}{]}^{\mathrm{T}},\\ \mathit{\xi }& =[S_1,\dots ,S_p,I_1,\dots ,I_p,R_1,\dots ,Rp,Z_1^{(1)},\dots ,Z_p^{(K)},Y_1^{(1,1)},\dots ,Y_p^{(K,L_K)}{]}^{\mathrm{T}},\\ {\mathrm{\Sigma }}_{\mathit{N}}& =\sum _{i=1}^p{N}_i,{\mathrm{\Sigma }}_{{\mathit{N}}^{(k)}}=\sum _{i=1}^p{N}_i^{(k)}.\end{array}$ We define a partial order on the n-dimensional Euclidean space ${\mathbb{R}}^n$ by $y\le x$ if $x-y\in {\mathbb{R}}_{+}^n$ and $y<x$ if $x-y\in {\mathbb{R}}_{+}^n\mathrm{\setminus }\{0\}$. Let $\eta =3+K+\sum _{k=1}^K{L}_k,$ the number of classes per patch. Then, System (1$\begin{array}{rl}\frac{\mathrm{d}{S}_i}{\mathrm{d}t}& ={\phi }_{U_1}(t){\mathcal{B}}_i(N_i)N_i-(d_i+c_i{N}_i+v_i+{\beta }_i{I}_i)S_i-\sum _{k=1}^K\sum _{l=1}^{L_k}{\beta }_i^{(kl)}\rho (S_i)Y_i^{(kl)}\\ & +{\alpha }_1{\gamma }_i{I}_i+{\phi }_{U_2}(t)\sum _{j=1}^p[m_{ij}{S}_j-m_{ji}{S}_i],\end{array}$)–(5$\begin{array}{rl}\frac{\mathrm{d}{Y}_i^{(kl)}}{\mathrm{d}t}& ={\lambda }_i^{(kl)}\rho (I_i)Z_i^{(k)}-(d_i^{(kl)}+{\gamma }_i^{(kl)}h(S_i,I_i,R_i))Y_i^{(kl)}\\ & +{\phi }_{U_4^{(k)}}(t)\sum _{j=1}^p[m_{ij}^{(kl)}\rho (I_j)Y_j^{(kl)}-m_{ji}^{(kl)}\rho (I_i)Y_i^{(kl)}]\end{array}$) is of the form $\mathrm{d}{\xi }_j/\mathrm{d}t=g_j({\xi }_1,{\xi }_2,\dots ,{\xi }_{p\eta })$ for $j=1,\dots ,p\eta$. Let $\mathrm{\Omega }=\{\mathit{\xi }\in {\mathbb{R}}_{+}^{p\eta }\}$ and ${\mathrm{\Omega }}_{{\xi }_j}=\{\mathit{\xi }\in \mathrm{\Omega }|{\xi }_j=0\}$. It is straightforward to see that for all $\mathit{\xi }\in {\mathrm{\Omega }}_{{\xi }_j}$, $\mathrm{d}{\xi }_j/\mathrm{d}t\ge 0$. Then, the set Ω is positively invariant for the system.

Theorem 3.1.

Consider model Equations (1$\begin{array}{rl}\frac{\mathrm{d}{S}_i}{\mathrm{d}t}& ={\phi }_{U_1}(t){\mathcal{B}}_i(N_i)N_i-(d_i+c_i{N}_i+v_i+{\beta }_i{I}_i)S_i-\sum _{k=1}^K\sum _{l=1}^{L_k}{\beta }_i^{(kl)}\rho (S_i)Y_i^{(kl)}\\ & +{\alpha }_1{\gamma }_i{I}_i+{\phi }_{U_2}(t)\sum _{j=1}^p[m_{ij}{S}_j-m_{ji}{S}_i],\end{array}$)–(5$\begin{array}{rl}\frac{\mathrm{d}{Y}_i^{(kl)}}{\mathrm{d}t}& ={\lambda }_i^{(kl)}\rho (I_i)Z_i^{(k)}-(d_i^{(kl)}+{\gamma }_i^{(kl)}h(S_i,I_i,R_i))Y_i^{(kl)}\\ & +{\phi }_{U_4^{(k)}}(t)\sum _{j=1}^p[m_{ij}^{(kl)}\rho (I_j)Y_j^{(kl)}-m_{ji}^{(kl)}\rho (I_i)Y_i^{(kl)}]\end{array}$), along with initial conditions ${\mathit{\xi }}^0=\mathit{\xi }(t_0)\in \mathrm{\Omega }$. Suppose assumptions $\mathcal{A}1\text{--}\mathcal{A}12$ are satisfied. If there exists ${\kappa }_i^{(k)}>0$ such that ${\mathcal{B}}^{(k)}(N_i,N_i^{(k)})-d_i^{(k)}<0$ for $N_i^{(k)}/N_i>{\kappa }_i^{(k)}$ for all $k=1,\dots ,K$, $i=1,\dots ,p,$ then the system possesses a unique global solution.

Proof.

Since $\mathrm{\partial }{g}_l/\mathrm{\partial }{\xi }_j$ is continuous for all $\mathit{\xi }\in \mathrm{\Omega }$ and for all $l,j\in \{1,\dots ,p\eta \}$, the system has a unique local solution in Ω. Also, $\frac{\mathrm{d}{\mathrm{\Sigma }}_{\mathit{N}}}{\mathrm{d}t}=\sum _{i=1}^p{\phi }_{U_1}(t){\mathcal{B}}_i(N_i)N_i-d_i(S_i+R_i)-d_i^I{I}_i-c_i{N}_i^2.$ Since ${\mathcal{B}}_i(N_i)\le b_i$, $d_i\le d_i^I$, and $\parallel {\phi }_{U_1}{\parallel }_{\mathrm{\infty }}=1$, $\mathrm{d}{\mathrm{\Sigma }}_{\mathit{N}}/\mathrm{d}t\le \sum _{i=1}^p(b_i-d_i-c_i{N}_i)N_i$, for all $t\in [0,\mathrm{\infty })$. Let $C_1=\underset{i}{max}\{b_i-d_i\}$ and $C_2=\underset{i}{min}{c}_i$. Then, $\mathrm{d}{\mathrm{\Sigma }}_{\mathit{N}}/\mathrm{d}t\le C_1\sum _{i=1}^p{N}_i-C_2\sum _{i=1}^p{N}_i^2\le C_1{\mathrm{\Sigma }}_{\mathit{N}}-p{C}_2{\mathrm{\Sigma }}_{\mathit{N}}^2<0$ for ${\mathrm{\Sigma }}_{\mathit{N}}>C_1/p{C}_2$. Similarly, since $d_i^{(k)}\le d_i^{(kl)}$, then $\mathrm{d}{\mathrm{\Sigma }}_{{\mathit{N}}^{(k)}}/\mathrm{d}t\le \sum _{i=1}^p({\mathcal{B}}^{(k)}(N_i,N_i^{(k)})-d_i^{(k)})N_i^{(k)}$ and, if $N_i^{(k)}>{\kappa }_i^{(k)}{C}_1/p{C}_2$ for $i=1,\dots ,p$, then $\mathrm{d}{\mathrm{\Sigma }}_{{\mathit{N}}^{(k)}}/\mathrm{d}t<0$,$k=1,\dots ,K$. Since ${\mathit{\xi }}^0\in \mathrm{\Omega }$ and Ω is positively invariant for the system, ${\mathrm{\Sigma }}_{\mathit{N}}\ge 0$ and ${\mathrm{\Sigma }}_{{\mathit{N}}^{(k)}}\ge 0$, $k=1,\dots ,K$. Then, ${\mathrm{\Sigma }}_{\mathit{N}}$ and each ${\mathrm{\Sigma }}_{{\mathit{N}}^{(k)}}$ are bounded for all $t\in [0,\mathrm{\infty })$, which concludes the proof.

Note that, if the conditions in Theorem 3.1 are satisfied, then the average number of the kth vector species per host, $N_i^{(k)}/N_i$, remains less than ${\kappa }_i^{(k)}$. One may view ${\kappa }_i^{(k)}$ as the carrying capacity for the kth vector species in the ith patch.

Next we analyse the Allee effect embedded in the system and control of the disease. Consider the disease-free case (i.e. $I_i=0$ and $Y_i^{(kl)}=0$ for all i, k, and l). Define $\mathit{f}(t,\mathit{N})=[f_1,f_2,\dots ,f_p{]}^{\mathrm{T}}$ by $\frac{\mathrm{d}{N}_i}{\mathrm{d}t}=f_i(t,\mathit{N}):={\phi }_{U_1}(t){\mathcal{B}}_i(N_i)N_i-d_i{N}_i-c_i{N}_i^2+{\phi }_{U_2}(t)\sum _{j=1,j\ne i}^p{m}_{ij}{N}_j-m_{ji}{N}_i$ for $i=1,\dots ,p$. A strong Allee effect is given by the existence of a basin of attraction for the trivial equilibrium. Define $\mathbf{B}=\mathrm{diag}(\mathrm{\partial }{\mathcal{B}}_i(N_i)/\mathrm{\partial }{N}_i(0))$ , $\mathbf{D}=\mathrm{diag}(d_1,d_2,\dots ,d_p)$, and $\mathbf{M}=(m_{ij})$ with $m_{ii}=-\sum _{k\ne i}{m}_{ki}$, where $\mathrm{diag}(x_i)$ is a matrix having $x_i$ along the diagonal and zeros elsewhere. For a symmetric matrix $\mathit{A}$, define $\sigma (\mathbf{A})$ to be the largest eigenvalue and, for a given T-periodic integrable function $\phi (t)$, define the average$\tilde{\phi }:=(1/T){\int }_0^T\phi (t)\mathrm{d}t$.

Theorem 3.2.

If $\sigma ({\tilde{\phi }}_{U_1}\mathbf{B}-\mathbf{D}+\frac{1}{2}{\tilde{\phi }}_{U_2}(\mathbf{M}+{\mathbf{M}}^{\mathrm{T}}))<0,$ then $\mathrm{d}\mathit{N}/\mathrm{d}t=\mathit{f}(t,\mathit{N})$ has a nonempty basin of attraction for the trivial equilibrium.

Proof.

Linearizing $\mathrm{d}\mathit{N}/\mathrm{d}t=f(t,\mathit{N})$ about $\mathit{N}=0$ yields $\frac{\mathrm{d}\mathit{N}}{\mathrm{d}t}=({\phi }_{U_1}(t)\mathbf{B}-\mathbf{D}+{\phi }_{U_2}(t)\mathbf{M})\mathit{N}.$ Then, $\begin{array}{rl}\frac{1}{2}\frac{\mathrm{d}{\mathit{N}}^{\mathrm{T}}\mathit{N}}{\mathrm{d}t}& ={\mathit{N}}^{\mathrm{T}}({\phi }_{U_1}(t)\mathbf{B}-\mathbf{D}+{\phi }_{U_2}(t)\mathbf{M})\mathit{N}\\ & ={\mathit{N}}^{\mathrm{T}}\left({\tilde{\phi }}_{U_1}\mathbf{B}-\mathbf{D}+\frac{1}{2}{\tilde{\phi }}_{U_2}(\mathbf{M}+{\mathbf{M}}^{\mathrm{T}})\right)\mathit{N}+{\mathit{N}}^T({\phi }_{U_1}(t)-{\tilde{\phi }}_{U_1})\mathbf{B}\mathit{N}\\ & +\frac{1}{2}{\mathit{N}}^{\mathrm{T}}({\phi }_{U_2}(t)-{\tilde{\phi }}_{U_2})(\mathbf{M}+{\mathbf{M}}^{\mathrm{T}})\mathit{N}+\frac{1}{2}{\phi }_{U_2}(t){\mathit{N}}^T(\mathbf{M}-{\mathbf{M}}^{\mathrm{T}})\mathit{N}.\end{array}$ Let ${\sigma }_0=\sigma ({\tilde{\phi }}_{U_1}\mathbf{B}-\mathbf{D}+\frac{1}{2}{\tilde{\phi }}_{U_2}(\mathbf{M}+{\mathbf{M}}^{\mathrm{T}}))$, ${\sigma }_1=\sigma (\mathbf{B})$, and ${\sigma }_2=\sigma (\frac{1}{2}(\mathbf{M}+{\mathbf{M}}^{\mathrm{T}}))$. Define $u={\mathit{N}}^{\mathrm{T}}\mathit{N}$. Then, $\begin{array}{rl}\frac{\mathrm{d}u}{\mathrm{d}t}& \le \left[2{\sigma }_0+2\sum _{k=1}^2({\phi }_{U_k}(t)-{\tilde{\phi }}_{U_k}){\sigma }_k\right]u,\\ u(t)& \le {\mathrm{e}}^{2{\sigma }_{0}t}{\mathrm{e}}^{2{\int }_0^t\sum _{k=1}^2({\phi }_{U_k}(t)-{\tilde{\phi }}_{U_k}){\sigma }_k\mathrm{d}t}u(0).\end{array}$ Since ${\int }_0^T\sum _{k=1}^2({\phi }_{U_k}(t)-{\tilde{\phi }}_{U_k})=0$, $u(nT+t)\le {\mathrm{e}}^{2{\sigma }_0(nT+t)}{\mathrm{e}}^{2{\int }_0^t\sum _{k=1}^2({\phi }_{U_k}(t)-{\tilde{\phi }}_{U_k}){\sigma }_k\mathrm{d}t}u(0)$ for all $n\in \mathbb{Z}$ and $t\in [0,T]$. Further, ${\sigma }_0<0$ implies that $\underset{n\to \mathrm{\infty }}{lim}u(nT+t)=0$.

Next, we discuss conditions under which a disease-free solution exists. A function $\phi (t,\mathit{x})$ is said to be of type K if, for each t and $i=1,\dots ,p$, ${\phi }_i(t,\mathit{x})\le {\phi }_i(t,\mathit{y})$ for any two points $\mathit{x}=[x_1,x_2,\dots ,x_p{]}^{\mathrm{T}},\mathit{y}=[y_1,y_2,\dots ,y_p{]}^{\mathrm{T}}\in {\mathbb{R}}^p$ satisfying $\mathit{x}\le \mathit{y}$ and $x_i=y_i$ [68]. Notice that $\mathit{f}(t,\mathit{N})$ is of type K. For the next theorem, we assume that ${\phi }_{U_1}$ is as given in Figure 2. Such functions capture the seasonal birth trend of many species, where T represents one year. We also assume that migration is density-dependent and use notation $A_i$ for the area of patch i.

Figure 2. Function ${\phi }_{U_1}(t)$.

Theorem 3.3.

Suppose the conditions in Theorem 3.1 hold and $m_{ij}{A}_j=m_{ji}{A}_i$ for all $i,j=1,\dots ,p$. Suppose $U_1=[0,T_0]\subset [0,T]$ and there exist $z_1,z_2\in \mathbb{R}$ with $0<z_1<z_2<\underset{i}{min}\{(b_i-d_i)/c_i{A}_i\}$ such that, for all i, $(T-T_0)(d_i+c_i{A}_i{z}_2)z_2\le z_2-z_1\le T_0\underset{j=1,2}{min}\{{\mathcal{B}}_i(A_i{z}_j)z_j-(d_i+c_i{A}_i{z}_j)z_j\}.$ Then, the disease-free system possesses a positive periodic solution.

Proof.

Define T-periodic function $\mathit{x}=(x_i)$, where $x_i(t)=\left\{\begin{array}{ll}\left(z_1+\frac{z_2-z_1}{T_0}t\right)A_i,& 0\le t\le T_0,\\ \left(z_1+\frac{z_2-z_1}{T-T_0}(T-t)\right)A_i,& T_0<t\le T,\end{array}\right.$ for all $i=1,\dots ,p$. Let ${\mathit{N}}^{\ast }=[C{A}_1,C{A}_2,\dots ,C{A}_p{]}^{\mathrm{T}}$, where $C=\underset{i}{max}\{(b_i-d_i)/c_i{A}_i\}$. For each i and $t\in [0,T_0]$, $f_i(t,\mathit{x})$ is the difference of two monotone increasing functions of $\mathit{x}$, one of which is concave and the other convex, with $\mathit{f}(t,\mathbf{0})=\mathbf{0}$ and $\mathit{f}(t,{\mathit{N}}^{\ast })<\mathbf{0}$. Then, inequality (6$(T-T_0)(d_i+c_i{A}_i{z}_2)z_2\le z_2-z_1\le T_0\underset{j=1,2}{min}\{{\mathcal{B}}_i(A_i{z}_j)z_j-(d_i+c_i{A}_i{z}_j)z_j\}.$), combined with $z_2-z_1>0$, implies $f_i(t,\mathit{x})\ge (z_2-z_1)A_i/T_0$ for all $t\in [0,T_0]$. Further, for all $i=1,\dots ,p$, $\begin{array}{rl}\frac{\mathrm{d}{x}_i}{\mathrm{d}t}& =\frac{z_2-z_1}{T_0}{A}_i\le f_i(t,\mathit{x})\mathrm{for}0\le t\le T_0,\\ \frac{\mathrm{d}{x}_i}{\mathrm{d}t}& =\frac{z_1-z_2}{T-T_0}{A}_i\le -(d_i+c_i{A}_i{z}_2)z_2{A}_i\le f_i(t,\mathit{x})\mathrm{for}{T}_0<t\le T.\end{array}$ In particular, $D_{+}\mathit{x}(t)\le \mathit{f}(t,\mathit{x})$, where $D_{+}$ is the lower Dini derivative. Also, $\mathit{x}(t)<{\mathit{N}}^{\ast }$ and $\mathit{f}(t,{\mathit{N}}^{\ast })<\mathbf{0}$. For every ${\mathit{N}}_0$ such that $\mathit{x}(0)\le {\mathit{N}}_0\le {\mathit{N}}^{\ast }$, the corresponding solution $\mathit{N}(t,{\mathit{N}}_0)$ satisfies $\mathit{x}(t)\le \mathit{N}(t,{\mathit{N}}_0)\le {\mathit{N}}^{\ast }$ for $0\le t\le T$ (from Theorem B.1 of [68]). Define the map $\mathit{P}:\{{\mathit{N}}_0|\mathit{x}(0)\le {\mathit{N}}_0\le {\mathit{N}}^{\ast }\}\to \{\mathit{N}|\mathit{x}(T)\le \mathit{N}\le {\mathit{N}}^{\ast }\}$ by $\mathit{P}({\mathit{N}}_0)=\mathit{N}(T,{\mathit{N}}_0)$. Notice that $\mathit{x}(0)=\mathit{x}(T)$ and hence $\{\mathit{N}|\mathit{x}(T)\le \mathit{N}\le {\mathit{N}}^{\ast }\}=\{{\mathit{N}}_0|\mathit{x}(0)\le {\mathit{N}}_0\le {\mathit{N}}^{\ast }\}$. Since $\mathit{P}$ is continuous, it follows from Brouwer's Fixed Point Theorem that $\mathit{P}$ has a fixed point.

The necessary condition for inequality (6$(T-T_0)(d_i+c_i{A}_i{z}_2)z_2\le z_2-z_1\le T_0\underset{j=1,2}{min}\{{\mathcal{B}}_i(A_i{z}_j)z_j-(d_i+c_i{A}_i{z}_j)z_j\}.$) is $(T_0/T){\mathcal{B}}_i(z)-(d_i+c_{i}z)\ge 0$ for all $z\in [A_i{z}_1,A_i{z}_2]$. That is, the average growth rate must be nonnegative for a positive solution, as expected.

When an immune class, R, exists, the chance of survival of the species is higher. Without an immune class, persistence depends on disease transmission, death, and recovery rates. The next theorem can be used to evaluate the effect of parameters on disease control for ${\mathit{N}}_0>{\mathit{x}}_0$, where ${\mathit{x}}_0$ is defined in Equation (7$x_i(t)=\left\{\begin{array}{ll}\left(z_1+\frac{z_2-z_1}{T_0}t\right)A_i,& 0\le t\le T_0,\\ \left(z_1+\frac{z_2-z_1}{T-T_0}(T-t)\right)A_i,& T_0<t\le T,\end{array}\right.$).

Theorem 3.4.

Suppose the conditions in Theorem 3.1 hold, ${\alpha }_1=1,$ $v_i=0$ for all i, and ${\mathit{\xi }}^0\in \mathrm{\Omega }$. If there exists a positive parameter set $\{d_i^I,d_i^{(kl)},{\beta }_i,{\beta }_i^{(kl)},{\gamma }_i,{\gamma }_i^{(kl)},c_i,{\lambda }_i^{(kl)}\}$ such that $\delta ({\beta }_i{N}_i-d_i^I-c_i{N}_i-{\gamma }_i)+\sum _{k=1}^K\sum _{l=1}^{L_k}{\lambda }_i^{(kl)}{\kappa }_i^{(k)}<0$ for all i and $t>0,$ where $\delta =\underset{i,k,l}{min}\{(d_i^{(kl)}+{\gamma }_i^{(kl)})/{\beta }_i^{(kl)}\},$ then model (1$\begin{array}{rl}\frac{\mathrm{d}{S}_i}{\mathrm{d}t}& ={\phi }_{U_1}(t){\mathcal{B}}_i(N_i)N_i-(d_i+c_i{N}_i+v_i+{\beta }_i{I}_i)S_i-\sum _{k=1}^K\sum _{l=1}^{L_k}{\beta }_i^{(kl)}\rho (S_i)Y_i^{(kl)}\\ & +{\alpha }_1{\gamma }_i{I}_i+{\phi }_{U_2}(t)\sum _{j=1}^p[m_{ij}{S}_j-m_{ji}{S}_i],\end{array}$–5$\begin{array}{rl}\frac{\mathrm{d}{Y}_i^{(kl)}}{\mathrm{d}t}& ={\lambda }_i^{(kl)}\rho (I_i)Z_i^{(k)}-(d_i^{(kl)}+{\gamma }_i^{(kl)}h(S_i,I_i,R_i))Y_i^{(kl)}\\ & +{\phi }_{U_4^{(k)}}(t)\sum _{j=1}^p[m_{ij}^{(kl)}\rho (I_j)Y_j^{(kl)}-m_{ji}^{(kl)}\rho (I_i)Y_i^{(kl)}]\end{array}$) possesses a stable disease-free solution.

Proof.

Let $I=\sum _{i=1}^p{I}_i$ and $Y=\sum _{i=1}^p\sum _{k=1}^K\sum _{l=1}^{L_k}{Y}_i^{(kl)}$. Then $\begin{array}{rl}\delta \frac{\mathrm{d}I}{\mathrm{d}t}+\frac{\mathrm{d}Y}{\mathrm{d}t}& =\delta \sum _{i=1}^p\left[{\beta }_i{I}_i{S}_i+\sum _{k=1}^K\sum _{l=1}^{L_k}{\beta }_i^{(kl)}\rho (S_i)Y_i^{(kl)}-d_i^I{I}_i-c_i{N}_i{I}_i-{\gamma }_i{I}_i\right]\\ & +\sum _{i=1}^p\sum _{k=1}^K\sum _{l=1}^{L_k}[{\lambda }_i^{(kl)}\rho (I_i)Z_i^{(k)}-d_i^{(kl)}{Y}_i^{(kl)}-{\gamma }_i^{(kl)}h(S_i,I_i,R_i)Y_i^{(kl)}]\end{array}$ Since $h(S_i,I_i,R_i)\ge \rho (S_i+R_i)\ge \rho (S_i)$, $\begin{array}{rl}\delta \frac{\mathrm{d}I}{\mathrm{d}t}+\frac{\mathrm{d}Y}{\mathrm{d}t}& \le \sum _{i=1}^p\left[\delta ({\beta }_i{N}_i-d_i^I-c_i{N}_i-{\gamma }_i)+\sum _{k=1}^K\sum _{l=1}^{L_k}{\lambda }_i^{(kl)}\frac{N_i^{(k)}}{N_i}\right]I_i\\ & +\sum _{i=1}^p\sum _{k=1}^K\sum _{l=1}^{L_k}[\delta {\beta }_i^{(kl)}-d_i^{(kl)}-{\gamma }_i^{(kl)}]Y_i^{(kl)}\rho (S_i).\end{array}$ Since $\delta -(d_i^{(kl)}+{\gamma }_i^{(kl)})/{\beta }_i^{(kl)}\le 0$ for all i, k, and l, if condition (8$\delta ({\beta }_i{N}_i-d_i^I-c_i{N}_i-{\gamma }_i)+\sum _{k=1}^K\sum _{l=1}^{L_k}{\lambda }_i^{(kl)}{\kappa }_i^{(k)}<0$) is satisfied, then $\mathrm{d}I/\mathrm{d}t<0$ for all $t>0$. Since ${\mathit{\xi }}^0\in \mathrm{\Omega },$ then$\underset{t\to \mathrm{\infty }}{lim sup}I=0$.

Note that if ${\mathit{N}}_0>{\mathit{x}}_0$, then from Theorem 3.3, a disease-free solution satisfies ${\mathit{x}}_0<\mathit{N}(t)<{\mathit{N}}^{\ast }$. When considering a neighbourhood around the disease-free solution, we only need Equation (8$\delta ({\beta }_i{N}_i-d_i^I-c_i{N}_i-{\gamma }_i)+\sum _{k=1}^K\sum _{l=1}^{L_k}{\lambda }_i^{(kl)}{\kappa }_i^{(k)}<0$) satisfied for $N_i\in (z_1,N_i^{\ast }]$, $i=1,\dots ,p$. Condition (8$\delta ({\beta }_i{N}_i-d_i^I-c_i{N}_i-{\gamma }_i)+\sum _{k=1}^K\sum _{l=1}^{L_k}{\lambda }_i^{(kl)}{\kappa }_i^{(k)}<0$) explains all possible disease control methods. These include

• reducing transmission rates ${\beta }_i$ and ${\beta }_i^{(kl)}$.

• reducing the maximum possible vector load ${\kappa }_i^{(k)}$.

• increasing death rate parameters $d_i^I$, $c_i$, and $d_i^{(kl)}$.

• increasing recovery rate ${\gamma }_i$.

4. SDE model

Now consider an Itô stochastic differential equation (SDE) model corresponding to the deterministic model, having random variables $\begin{array}{rl}\mathit{X}& =\{X_i{\}}_{i=1}^{p\eta }\\ & =[S_1,I_1,R_1,Z_1^{(1)},Y_1^{(11)},\dots ,Y_1^{(1L_1)},\dots ,Z_1^{(K)},Y_1^{(K1)},\dots ,Y_1^{(K{L}_K)},\dots ,\\ & S_p,I_p,R_p,Z_p^{(1)},Y_p^{(11)},\dots ,Y_p^{(1L_1)},\dots ,Z_p^{(K)},Y_p^{(K1)},\dots ,Y_p^{(K{L}_K)}{]}^{\mathrm{T}},\end{array}$ where $X_i\in {\mathbb{R}}_{+}$ for each i and $\eta =3+K+\sum _{k=1}^K{L}_k$. The transition probabilities are $\mathrm{Prob}\{\mathrm{\Delta }\mathit{X}(t)|\mathit{X}(t)\}$ for transitions $\mathrm{\Delta }\mathit{X}(t)=\mathit{X}(t+\mathrm{\Delta }t)-\mathit{X}(t)$ in small time $\mathrm{\Delta }t$. Transitions $\mathrm{\Delta }\mathit{X}$ and corresponding values $p(\mathrm{\Delta }\mathit{X})=(1/\mathrm{\Delta }t)\mathrm{Prob}\{\mathrm{\Delta }\mathit{X}|\mathit{X}\}$ are given in Table 1.

Table 1. Transitions $\mathrm{\Delta }\mathit{X}(t)=\mathit{X}(t+\mathrm{\Delta }t)-\mathit{X}(t)$, and the respective values $p(\mathrm{\Delta }\mathit{X}(t))=(1/\mathrm{\Delta }t)\mathrm{Prob}\{\mathrm{\Delta }\mathit{X}(t)|\mathit{X}(t)\}$, where vector ${\mathit{e}}_{X_i}$ has unity in the position corresponding to a variable $X_i$ and zeros elsewhere.

$\mathrm{\Delta }\mathit{X}$	$p(\mathrm{\Delta }\mathit{X})$	$\mathrm{\Delta }\mathit{X}$	$p(\mathrm{\Delta }\mathit{X})$
${\mathit{e}}_{S_i}$	${\phi }_{U_1}(t){\mathcal{B}}_i(N_i)N_i$	${\mathit{e}}_{I_i}-{\mathit{e}}_{S_i}$	${\beta }_i{S}_i{I}_i+\rho (S_i)\sum _{k=1}^K\sum _{l=1}^{L_k}{\beta }_i^{(kl)}{Y}_i^{(kl)}$
$-{\mathit{e}}_{S_i}$	$(d_i+c_i{N}_i)S_i$	${\mathit{e}}_{R_i}-{\mathit{e}}_{S_i}$	$v_i{S}_i$
$-{\mathit{e}}_{I_i}$	$(d_i^I+c_i{N}_i)I_i$	${\mathit{e}}_{Z_i^{(k)}}$	${\phi }_{U_3^{(k)}}(t){\mathcal{B}}^{(k)}(N_i,N_i^{(k)})N_i^{(k)}$
$-{\mathit{e}}_{R_i}$	$(d_i+c_i{N}_i)R_i$	$-{\mathit{e}}_{Z_i^{(k)}}$	$d_i^{(k)}{Z}_i^{(k)}$
${\mathit{e}}_{S_i}-{\mathit{e}}_{I_i}$	${\alpha }_1{\gamma }_i{I}_i$	$-{\mathit{e}}_{Y_i^{(kl)}}$	$d_i^{(kl)}{Y}_i^{(kl)}$
${\mathit{e}}_{R_i}-{\mathit{e}}_{I_i}$	$(1-{\alpha }_1){\gamma }_i{I}_i$	${\mathit{e}}_{Y_i^{(kl)}}-{\mathit{e}}_{Z_i^{(k)}}$	${\lambda }_i^{(kl)}\rho (I_i)Z_i^{(kl)}$
${\mathit{e}}_{S_i}-{\mathit{e}}_{S_j}$	${\phi }_{U_2}(t)m_{ij}{S}_j$	${\mathit{e}}_{Z_i^{(k)}}-{\mathit{e}}_{Y_i^{(kl)}}$	${\gamma }_i^{(kl)}h(S_i,I_i,R_i)Y_i^{(kl)}$
${\mathit{e}}_{I_i}-{\mathit{e}}_{I_j}$	${\phi }_{U_2}(t)m_{ij}^I{I}_j$	${\mathit{e}}_{Z_i^{(k)}}-{\mathit{e}}_{Z_j^{(k)}}$	${\phi }_{U_4^{(k)}}(t)m_{ij}^{(k)}\rho (S_j+R_j)Z_j^{(k)}$
${\mathit{e}}_{R_i}-{\mathit{e}}_{R_j}$	${\phi }_{U_2}(t)m_{ij}{R}_j$	${\mathit{e}}_{Y_i^{(kl)}}-{\mathit{e}}_{Y_j^{(kl)}}$	${\phi }_{U_4^{(k)}}(t)m_{ij}^{(kl)}\rho (I_j)Y_j^{(kl)}$

It is assumed that $\mathrm{\Delta }t>0$ is sufficiently small so that $\mathrm{Prob}\{\mathrm{\Delta }\mathit{X}=\mathbf{0}|\mathit{X}(t)\}=\alpha >0$, with α equalling the difference between unity and the sum of all probabilities $\mathrm{Prob}\{\mathrm{\Delta }\mathit{X}(t)|\mathit{X}(t)\}=\mathrm{\Delta }tp(\mathrm{\Delta }X(t))$ for all listed values $p(\mathrm{\Delta }\mathit{X})$ and all appropriate values of $i,j,k,l$:$i,j=1,\dots ,p$, $l=1,\dots ,L_k$, $k=1,\dots ,K$.

The SDE model is formed as [4] $\mathrm{d}\mathit{X}(t)=\mathit{f}(t,\mathit{X})\mathrm{d}t+\mathbf{H}(t,\mathit{X})\mathrm{d}\mathit{W}(t),$ where $\mathit{f}=E(\mathrm{\Delta }\mathit{X})/\mathrm{\Delta }t$, ${\mathbf{H}\mathbf{H}}^{\mathrm{T}}=\mathit{V}$, and $\mathit{V}=E[\mathrm{\Delta }\mathit{X}(\mathrm{\Delta }\mathit{X}{)}^{\mathrm{T}}]/\mathrm{\Delta }t$. The elements of $\mathit{W}(t)$ are Wiener processes: each is normally distributed with mean zero and variance t. For this system, $\mathit{H}$ is $p\eta \times p(\eta (p+1)-K)$ and $\mathit{W}$ has length $p(\eta (p+1)-K)$. Matrix $\mathit{H}$ and vector $\mathit{W}$ are provided in Appendix 1.

The SDE model equations can be expressed component-wise. For $i=1,\dots ,p,l=1,\dots ,L_k,k=1,\dots ,K$:

5. Example: sylvatic plague among black-tailed prairie dog colonies

In this example, we use the deterministic and stochastic models in Sections 3 and4 to evaluate black-tailed prairie dog population dynamics, and possible control methods, in the presence of the sylvatic plague, which is caused by the bacterium Yersinia pestis and spread by fleas. Prairie dogs (Cynomys ludovicianus) are regarded as a keystone species [49, 50, 61, 62], ecosystem engineers [11, 45], and a competition species for cattle [26, 73]. They help sustain many other species, such as endangered black-footed ferrets [17, 60], burrowing owls [25] and tiger salamanders [51]. They alter the ecosystem, affecting a wide array of species found within their habitat range [11, 45, 49, 61, 62]. However, they also act as pests near urban populations. If colonies become very large, they compete with cattle for grass, causing possible loss of livestock [24, 26]. Near urban communities, prairie dog populations present a risk by supporting the transmission of plague to humans [6]. Thus, there is significant value to maintaining a disease-free prairie dog population, while also controlling population densities, making this example particularly meaningful.

There are many factors that govern plague dynamics among prairie dog populations. These include: host factors, such as the spatial distribution of colonies and dispersal between them, population density, susceptibility, food abundance, and the effect of seasonal changes; and vector factors, such as the specific flea species present, transmission potential, population density, effects of seasonal changes on flea populations, and survival rates [8, 18, 34, 56, 78]. The ODE model in Section 3 can incorporate each of these factors to evaluate their importance in an epizootic and in the control thereof.

For sexually reproducing species, it is appropriate to assume that per capita birth rates decline with a reduction in population density; that is, the Allee effect exists [35]. Such behaviour has been observed within prairie dog communities when the population is controlled through hunting. Surviving prairie dogs increase their alertness and reduce both aboveground activity and time spent foraging [64, 74]. Pauli and Baskirk experimentally tested the response of black-tailed prairie dogs to shooting and found that colonies experienced nearly collapsed reproduction the summer after; pregnancy rates declined by 50% and reproductive output fell by 82% [64]. Although few other experiments have been performed on lower densities, there are several publications on prairie dog behavioural traits pertinent to the Allee effect. Prairie dogs in large sub-colonies detect predators quicker, despite devoting proportionately less time to alertness, than do individuals in smaller sub-colonies [39]. The increased vigilance in smaller sub-colonies might result in less time and energy spent foraging, thus reducing individual fitness, resulting an Allee effect. Lower population densities in white-tailed prairie dog colonies than in black-tailed prairie dog colonies [38, 39, 71] may also be a reflection of the existence of an Allee effect. Black-tailed prairie dogs clip vegetation short and depend on communication with other members of the sub-colony to detect predictors [2, 39]. White-tailed prairie dogs are more vigilant, select habitats with more existing cover, and are not as dependent upon other members [39, 59]. These observations demonstrate the appropriateness of including the Allee effect in mathematical models of prairie dog population dynamics. Although there are many epidemic models that include the Allee effect in literature (as mentioned in Section 1), little has been discussed or demonstrated about the consequence of the Allee effect in plague dynamics (see [34] for an exception). In one study, [69], the colony size did not affect its subsequent infectiousness. The Allee effect may not have a significant impact on dynamics for a particularly destructive disease, such as plague; yet it may affect the dynamics under control strategies for the disease, as demonstrated by simulations in Section 6.3.

There are many environmental factors that influence epizootics, such as weather fluctuations and climate change [32, 69, 70]. For example, temperature and soil moisture influence survival and reproduction of vector species and contribute substantially to plague epizootics [70]. Also, the rate of plague transmission between colonies increases with increasing precipitation, while the rate of infection from unknown sources decreases in response to hot weather [69]. Except for periodic seasonality, the model described in Section 3 does not incorporate climate or weather changes, since it is not the focus of this paper to predict epizootics based on such factors. The stochastic model (Section 4) incorporates the effect of environmental stochasticity on susceptible and infectious populations that occur due to variations in related rates. Fluctuations in environmental conditions, including climatic, affect the model parameters and are included via the density-dependent SDE equations, as well as the seasonal terms.

A stochastic model for the plague in spatially distinct but related prairie dog colonies was discussed in [34]. A stochastic patch occupancy model that incorporates colonization, connectivity, and extinction probabilities was used to fit 20 years of data [34]. The colonization probability was modelled as an increasing function of connectivity to existing prairie dog colonies and incorporates an Allee effect. However, this model is species-specific and not suitable for understanding how the spatial arrangement of prairie dog metapopulations could be used to enhance their protection against extinction due to plague or to develop control methods [34]. In this example, we use the deterministic model given in Section 3 to evaluate the effect of the spatial structure and dispersal, and of the Allee effect on extinction and possible control strategies to control the epidemic. We also include stochastic model sample paths for demonstrative purposes.

5.1. Prairie dog model

Many flea species can carry Y. pestis [37]. Among black-tailed prairie dogs, the primarily carriers are O. hirsuta and O. t. cynomuris [78]. Transmission dynamics are not well understood and plague dynamics among prairie dogs do not directly follow plague dynamics among fleas [76]. ‘Blocked’ infected fleas (referred to as such due to the formation of biofilm in their gut) were traditionally believed to be the primary transmission route to prairie dogs [28]. However, the specific flea species commonly found on prairie dogs seldom become blocked (1 out of 10 for O. t. cynomuris and 3 out of 70 for O. hirsuta; see [28]). Another transmission route is through ‘unblocked fleas’, immediately following a blood meal from an infectious prairie dog [78]. In this model, unblocked O. hirsuta and O. t. cynomuris are assumed to be the primary transmission route for Y. pestis. Blocked O. hirsuta are also included for demonstration. A list of variables is given in Table 2.

Table 2. List of variables within patch i, $i=1,\dots ,p$.

Variable	Description
$S_i$	Susceptible hosts (C. ludovicianus)
$I_i$	Infectious hosts
$R_i$	Immune hosts
$N_i$	$S_i+I_i+R_i$
$Z_i^{\mathrm{h}}$	Susceptible O. hirsuta
$Y_i^{\mathrm{h}}$	Infectious unblocked O. hirsuta
$Y_i^{\mathrm{hB}}$	Infectious blocked O. hirsuta
$N_i^{\mathrm{h}}$	$Z_i^{\mathrm{h}}+Y_i^{\mathrm{t}}+Y_i^{\mathrm{tB}}$
$Z_i^{\mathrm{t}}$	Susceptible O. t. cynomuris
$Y_i^{\mathrm{t}}$	Infectious O. t. cynomuris (unblocked)
$N_i^{\mathrm{t}}$	$Z_i^{\mathrm{t}}+Y_i^{\mathrm{h}}$

Density-dependent birth rates among prairie dogs are modelled by ${\mathcal{B}}_i(N_i)=b{N}_i/(N_i+k{A}_i)$, where b and k are positive constants, and $A_i$ is the area of patch i. This form of ${\mathcal{B}}_i(N_i)$ satisfies assumption $\mathcal{A}2$, so that the model exhibits the Allee effect. Assuming that patch carrying capacity depends on patch size and that the rate of migration depends on both prairie dog density and the distance between patches, parameters $c_i=c/A_i$, $m_{ij}=m/(x_{ij}{A}_j)$, and $m_{ij}^I=m^I/(x_{ij}{A}_j)$, where $c,m$, and$m^I$ are positive constants and $x_{ij}$ is the shortest distance between patches i and j.

Variables and parameters specific to unblocked O. hirsuta, blocked O. hirsuta and (unblocked) O. t. cynomuris are denoted by superscripts ‘h’, ‘hB’, and ‘t’, respectively. For example, transmission rates for the three infectious flea classes are denoted by ${\beta }^{\mathrm{h}},{\beta }^{\mathrm{hB}}$, and ${\beta }^{\mathrm{t}}$. Host-to-host transmission between prairie dogs is very unlikely because infectious animals die quickly; hence, we assume no direct transmission, ${\beta }_i=0$. Since recovery is unlikely, ${\gamma }_i=0$. The O. hirsuta per capita birth rate is modelled by ${\mathcal{B}}^{\mathrm{h}}(N_i,N_i^{\mathrm{h}})=b^{\mathrm{h}}{N}_i/(1+N_i+N_i^{\mathrm{h}})$ where $b^{\mathrm{h}}$ is a constant, and the O. t. cynomuris birth rate is modelled similarly. We set the recovery rate for blocked fleas to zero and the recovery rates for unblocked species depend on the proportion of uninfected hosts,$h(S_i,I_i,R_i)=\rho (S_i+R_i)$.

The prairie dog portion of deterministic model (1$\begin{array}{rl}\frac{\mathrm{d}{S}_i}{\mathrm{d}t}& ={\phi }_{U_1}(t){\mathcal{B}}_i(N_i)N_i-(d_i+c_i{N}_i+v_i+{\beta }_i{I}_i)S_i-\sum _{k=1}^K\sum _{l=1}^{L_k}{\beta }_i^{(kl)}\rho (S_i)Y_i^{(kl)}\\ & +{\alpha }_1{\gamma }_i{I}_i+{\phi }_{U_2}(t)\sum _{j=1}^p[m_{ij}{S}_j-m_{ji}{S}_i],\end{array}$)–(5$\begin{array}{rl}\frac{\mathrm{d}{Y}_i^{(kl)}}{\mathrm{d}t}& ={\lambda }_i^{(kl)}\rho (I_i)Z_i^{(k)}-(d_i^{(kl)}+{\gamma }_i^{(kl)}h(S_i,I_i,R_i))Y_i^{(kl)}\\ & +{\phi }_{U_4^{(k)}}(t)\sum _{j=1}^p[m_{ij}^{(kl)}\rho (I_j)Y_j^{(kl)}-m_{ji}^{(kl)}\rho (I_i)Y_i^{(kl)}]\end{array}$) is given by $\begin{array}{rl}\frac{\mathrm{d}{S}_i}{\mathrm{d}t}& ={\phi }_{U_1}(t)\left(\frac{b{N}_i}{N_i+k{A}_i}\right)N_i-\left(d_i+\frac{c{N}_i}{A_i}+v_i\right)S_i\\ & -({\beta }^{\mathrm{h}}{Y}_i^{\mathrm{h}}+{\beta }^{\mathrm{hB}}{Y}_i^{\mathrm{hB}}+{\beta }^{\mathrm{t}}{Y}_i^{\mathrm{t}})\frac{S_i}{N_i+1}+{\phi }_{U_2}(t)\sum _{j=1}^p\frac{m}{x_{ij}}\left(\frac{S_j}{A_j}-\frac{S_i}{A_i}\right),\\ \frac{\mathrm{d}{I}_i}{\mathrm{d}t}& =\left({\beta }^{\mathrm{h}}{Y}_i^{\mathrm{h}}+{\beta }^{\mathrm{hB}}{Y}_i^{\mathrm{hB}}+{\beta }^{\mathrm{t}}{Y}_i^{\mathrm{t}}\right)\frac{S_i}{N_i+1}-\left(d_i^I+\frac{c{N}_i}{A_i}\right)I_i+{\phi }_{U_2}(t)\sum _{j=1}^p\frac{m^I}{x_{ij}}\left(\frac{I_j}{A_j}-\frac{I_i}{A_i}\right),\\ \frac{\mathrm{d}{R}_i}{\mathrm{d}t}& =v_i{S}_i-\left(d_i+\frac{c{N}_i}{A_i}\right)R_i+{\phi }_{U_2}(t)\sum _{j=1}^p\frac{m}{x_{ij}}\left(\frac{R_j}{A_j}-\frac{R_i}{A_i}\right),\end{array}$$i=1,\dots ,p.$ The O. hirsuta portion of model (1$\begin{array}{rl}\frac{\mathrm{d}{S}_i}{\mathrm{d}t}& ={\phi }_{U_1}(t){\mathcal{B}}_i(N_i)N_i-(d_i+c_i{N}_i+v_i+{\beta }_i{I}_i)S_i-\sum _{k=1}^K\sum _{l=1}^{L_k}{\beta }_i^{(kl)}\rho (S_i)Y_i^{(kl)}\\ & +{\alpha }_1{\gamma }_i{I}_i+{\phi }_{U_2}(t)\sum _{j=1}^p[m_{ij}{S}_j-m_{ji}{S}_i],\end{array}$–5$\begin{array}{rl}\frac{\mathrm{d}{Y}_i^{(kl)}}{\mathrm{d}t}& ={\lambda }_i^{(kl)}\rho (I_i)Z_i^{(k)}-(d_i^{(kl)}+{\gamma }_i^{(kl)}h(S_i,I_i,R_i))Y_i^{(kl)}\\ & +{\phi }_{U_4^{(k)}}(t)\sum _{j=1}^p[m_{ij}^{(kl)}\rho (I_j)Y_j^{(kl)}-m_{ji}^{(kl)}\rho (I_i)Y_i^{(kl)}]\end{array}$) is given by $\begin{array}{rl}\frac{\mathrm{d}{Z}_i^{\mathrm{h}}}{\mathrm{d}t}& ={\phi }_{U_3^{\mathrm{h}}}(t)\left(\frac{b^{\mathrm{h}}{N}_i}{1+N_i+N_i^{\mathrm{h}}}\right)N_i^{\mathrm{h}}-\left(d_i^{\mathrm{h}}+{\lambda }^{\mathrm{h}}\left(\frac{I_i}{N_i+1}\right)\right)Z_i^{\mathrm{h}}+{\gamma }^{\mathrm{h}}\left(\frac{S_i+R_i}{N_i+1}\right)Y_i^{\mathrm{h}}\\ & +\sum _{j=1}^p\frac{m}{x_{ij}}\left[\left(\frac{S_j+R_j}{N_j+1}\right)\frac{Z_j^{\mathrm{h}}}{A_j}-\left(\frac{S_i+R_i}{N_i+1}\right)\frac{Z_i^{\mathrm{h}}}{A_i}\right],\\ \frac{\mathrm{d}{Y}_i^{\mathrm{h}}}{\mathrm{d}t}& ={\alpha }_2{\lambda }^{\mathrm{h}}\left(\frac{I_i}{N_i+1}\right)Z_i^{\mathrm{h}}-\left(d_i^{\mathrm{hU}}+{\gamma }^{\mathrm{h}}\left(\frac{S_i+R_i}{N_i+1}\right)\right)Y_i^{\mathrm{h}}\\ & +\sum _{j=1}^p\frac{m^I}{x_{ij}}\left[\left(\frac{I_j}{N_j+1}\right)\frac{Y_j^{\mathrm{h}}}{A_j}-\left(\frac{I_i}{N_i+1}\right)\frac{Y_i^{\mathrm{h}}}{A_i}\right],\\ \frac{\mathrm{d}{Y}_i^{\mathrm{tB}}}{\mathrm{d}t}& =(1-{\alpha }_2){\lambda }^{\mathrm{h}}\left(\frac{I_i}{N_i+1}\right)Z_i^{\mathrm{h}}-d_i^{\mathrm{hB}}{Y}_i^{\mathrm{hB}},\end{array}$$i=1,\dots ,p.$ The O. t. cynomuris portion of model (1$\begin{array}{rl}\frac{\mathrm{d}{S}_i}{\mathrm{d}t}& ={\phi }_{U_1}(t){\mathcal{B}}_i(N_i)N_i-(d_i+c_i{N}_i+v_i+{\beta }_i{I}_i)S_i-\sum _{k=1}^K\sum _{l=1}^{L_k}{\beta }_i^{(kl)}\rho (S_i)Y_i^{(kl)}\\ & +{\alpha }_1{\gamma }_i{I}_i+{\phi }_{U_2}(t)\sum _{j=1}^p[m_{ij}{S}_j-m_{ji}{S}_i],\end{array}$–5$\begin{array}{rl}\frac{\mathrm{d}{Y}_i^{(kl)}}{\mathrm{d}t}& ={\lambda }_i^{(kl)}\rho (I_i)Z_i^{(k)}-(d_i^{(kl)}+{\gamma }_i^{(kl)}h(S_i,I_i,R_i))Y_i^{(kl)}\\ & +{\phi }_{U_4^{(k)}}(t)\sum _{j=1}^p[m_{ij}^{(kl)}\rho (I_j)Y_j^{(kl)}-m_{ji}^{(kl)}\rho (I_i)Y_i^{(kl)}]\end{array}$) is given by $\begin{array}{rl}\frac{\mathrm{d}{Z}_i^{\mathrm{t}}}{\mathrm{d}t}& ={\phi }_{U_3^{\mathrm{t}}}(t)\left(\frac{b^{\mathrm{t}}{N}_i}{1+N_i+N_i^{\mathrm{t}}}\right)N_i^{\mathrm{t}}-\left(d_i^{\mathrm{t}}+{\lambda }^{\mathrm{t}}\left(\frac{I_i}{N_i+1}\right)\right)Z_i^{\mathrm{t}}+{\gamma }^{\mathrm{t}}\left(\frac{S_i+R_i}{N_i+1}\right)Y_i^{\mathrm{t}}\\ & +\sum _{j=1}^p\frac{m}{x_{ij}}\left[\left(\frac{S_j+R_j}{N_j+1}\right)\frac{Z_j^{\mathrm{t}}}{A_j}-\left(\frac{S_i+R_i}{N_i+1}\right)\frac{Z_i^{\mathrm{t}}}{A_i}\right],\\ \frac{\mathrm{d}{Y}_i^{\mathrm{t}}}{\mathrm{d}t}& ={\lambda }^{\mathrm{t}}\left(\frac{I_i}{N_i+1}\right)Z_i^{\mathrm{t}}-\left(d_i^{\mathrm{tU}}+{\gamma }^{\mathrm{t}}\left(\frac{S_i+R_i}{N_i+1}\right)\right)Y_i^{\mathrm{t}}\\ & +\sum _{j=1}^p\frac{m^I}{x_{ij}}\left[\left(\frac{I_j}{N_j+1}\right)\frac{Y_j^{\mathrm{t}}}{A_j}-\left(\frac{I_i}{N_i+1}\right)\frac{Y_i^{\mathrm{t}}}{A_i}\right],\end{array}$$i=1,\dots ,p.$ Prairie dog birth and migration rates are seasonal. The corresponding periodic functions, ${\phi }_{U_1}$ and ${\phi }_{U_2}$, can be represented in Figure 2, where T is one year. Flea birth rates are also assumed to be seasonal, similarly incorporated via periodic functions ${\phi }_{U_3^{\mathrm{h}}}$ and ${\phi }_{U_3^{\mathrm{t}}}$. Since other, unmodelled species also assist in the migration of fleas between patches, flea migration is assumed to occur year-round. Migration of blocked O. hirsuta ($Y_i^{hB}$) is assumed to be negligible.

5.2. Parameters values

Studies of black-tailed prairie dog colonies in Wind Cave National Park, South Dakota, provide data to estimate many parameters. References were obtained through the US Forest Service Database [72].

Birth rates were calculated based on a field study conducted by Hoogland et al. over a period of 14 years in Wind Cave National Park [41]. All the young were weaned at the study colony each year, the mean percentage of males was 53%, the mean percentage of adult females that weaned a litter each year was 47%, and 9% yearling females weaned a litter. The mean ratio between juveniles and the combined group of yearlings and adults was about 2:3; however, Hoogland et al. did not provide the age distribution of the females, specifically. Assuming equal male and female distributions in all the colonies, a uniform age distribution for the combined group of adults and yearlings, and a mean life expectancy of 4.5 years for females who survive the first year (see survivorship data in [40]), the ratio of female yearlings to female adults can be calculated as 2:5. This ratio is comparable to the female age class distribution discussed in [13] for a 1982–1983 population of a southwestern South Dakota prairie dog colony. Only one litter is produced each year and the mean litter size observed above ground was 3–4.9 pups [72]. Using these ratios and an average litter size of four pups, the per capita yearly birthrate is calculated to be 0.434. The mating season occurs late February through April [48] and gestation is 34–35 days [44]. Assuming equal births in March and April and no births in other months, the corresponding monthly per capita birth rate is 0.217 each for March and April and 0 for all other months (i.e. b = 0.217/month and ${\phi }_{U_1}$ is nonzero for March and April).

Using survival data given in [40], one can estimate the overall death rate. The annual total death rate can be calculated by: (total number of deaths)/(total number of animal years). Using the data in Figures 1(a) and 2(a) of [40] and assuming equal males and females at birth, the per capita total death rate can be calculated as 0.428 per year (during the study period). Similar birth and overall death rates suggest a stable population size in Wind Cave National Park, as was suggested in [40]. Using only the mean expected lifespans for male and female adults and a uniform distribution of males and females, the natural death rate $d_i$ is calculated as 0.274 per year. (The mean life expectancy among those who survive their first year is about 3 years for males and about 4.5 years for females.) Hoogland did not discuss the population density in Wind Cave National Park. In 1948–1950, population densities in Wind Cave National Park varied between 5.4 and 15 dogs per acre and some studies estimated population densities of black-tailed prairie dogs as high as 22.7 per acre (see Table 3 of [48]), suggesting that carrying capacities could be higher than 15. However, in wild populations, due to predation, competition with other species, and disease, the mean stable density may not reach the natural carrying capacity. Since the model discussed here includes neither predation nor competition, we assume an effective carrying capacity of 9 individuals per acre, corresponding to $c=0.0178$/year. With this value of c, the mean population density would be $8.65$ for the Hoogland study (i.e. using per capita death rate 0.422/year), which is similar to the mean population density of 8.8 individuals per acre during 1948–1950 [72].

Available dispersal data are insufficient for estimating migration rates. In one study, observations of prairie dogs emigrating from their colonies began in May, reached a peak in early June, and ended by July, and they moved an average distance of 2.4 km from their natal site [33]. In a 2000–2001 genetics test on a sample of 156 black-tailed prairie dogs in Wind Cave National Park, 4 indicated genetic exclusion from their colony of capture [66]. To accommodate such small migration rates, we assume 1% of the population from a colony i with area one hectare disperses to a colony, j, 2.5 km away from the departing colony during May and June. Assuming uniform dispersion during those months, $m=0.002$/month for each of the 2 months and ${\phi }_{U_2}$ is nonzero for April through June.

The size and spatial distribution of 11 black-tailed prairie dog colonies in Wind Cave National Park are given in Tables A1 and A2 and Figure A1. The colony area data from the Hoogland study was obtained from [19] and the distance data is estimated using [19] and from the prairie dog colony map on the US Department of the Interior National Park Service website [65].

The sylvatic plague can quickly eliminate entire black-tailed prairie dog colonies [18]. The bacteria's incubation period is 3–5 days, with death following 2–3 days later, so we assume the per capita death rate of infectious animals is $d_i^I=\frac{1}{6}$ per day [14, 18, 44]. Infectious black-tailed prairie dogs are very unlikely to introduce plague into a colony because they die quickly, such that no migration of such animals can be assumed. However, dispersing black-tailed prairie dogs with plague-ridden fleas can act as a host for transmission. To model this, the migration of infectious animals is assumed to be nonzero. Specifically, it is taken to be 1% of the migration rate of the susceptible class$m^I=m/100$.

Appropriate flea birth, death, and plague transmission parameters are necessary as well. For many flea species, the average lifespan is 1–3 months [28]. For this example, we take the average life expectancy to be 60 days for O. hirsuta ($d_i^{\mathrm{h}}=\frac{1}{60}$). Birth parameters $b^{\mathrm{h}}=0.25$ and $b^{\mathrm{t}}=0.55$ and O. t. cynomuris death rate $d_i^{\mathrm{t}}=\frac{1}{30}$ were obtained by fitting Equations (10$\begin{array}{rl}\frac{\mathrm{d}{Z}_i^{\mathrm{h}}}{\mathrm{d}t}& ={\phi }_{U_3^{\mathrm{h}}}(t)\left(\frac{b^{\mathrm{h}}{N}_i}{1+N_i+N_i^{\mathrm{h}}}\right)N_i^{\mathrm{h}}-\left(d_i^{\mathrm{h}}+{\lambda }^{\mathrm{h}}\left(\frac{I_i}{N_i+1}\right)\right)Z_i^{\mathrm{h}}+{\gamma }^{\mathrm{h}}\left(\frac{S_i+R_i}{N_i+1}\right)Y_i^{\mathrm{h}}\\ & +\sum _{j=1}^p\frac{m}{x_{ij}}\left[\left(\frac{S_j+R_j}{N_j+1}\right)\frac{Z_j^{\mathrm{h}}}{A_j}-\left(\frac{S_i+R_i}{N_i+1}\right)\frac{Z_i^{\mathrm{h}}}{A_i}\right],\\ \frac{\mathrm{d}{Y}_i^{\mathrm{h}}}{\mathrm{d}t}& ={\alpha }_2{\lambda }^{\mathrm{h}}\left(\frac{I_i}{N_i+1}\right)Z_i^{\mathrm{h}}-\left(d_i^{\mathrm{hU}}+{\gamma }^{\mathrm{h}}\left(\frac{S_i+R_i}{N_i+1}\right)\right)Y_i^{\mathrm{h}}\\ & +\sum _{j=1}^p\frac{m^I}{x_{ij}}\left[\left(\frac{I_j}{N_j+1}\right)\frac{Y_j^{\mathrm{h}}}{A_j}-\left(\frac{I_i}{N_i+1}\right)\frac{Y_i^{\mathrm{h}}}{A_i}\right],\\ \frac{\mathrm{d}{Y}_i^{\mathrm{tB}}}{\mathrm{d}t}& =(1-{\alpha }_2){\lambda }^{\mathrm{h}}\left(\frac{I_i}{N_i+1}\right)Z_i^{\mathrm{h}}-d_i^{\mathrm{hB}}{Y}_i^{\mathrm{hB}},\end{array}$) and (11$\begin{array}{rl}\frac{\mathrm{d}{Z}_i^{\mathrm{t}}}{\mathrm{d}t}& ={\phi }_{U_3^{\mathrm{t}}}(t)\left(\frac{b^{\mathrm{t}}{N}_i}{1+N_i+N_i^{\mathrm{t}}}\right)N_i^{\mathrm{t}}-\left(d_i^{\mathrm{t}}+{\lambda }^{\mathrm{t}}\left(\frac{I_i}{N_i+1}\right)\right)Z_i^{\mathrm{t}}+{\gamma }^{\mathrm{t}}\left(\frac{S_i+R_i}{N_i+1}\right)Y_i^{\mathrm{t}}\\ & +\sum _{j=1}^p\frac{m}{x_{ij}}\left[\left(\frac{S_j+R_j}{N_j+1}\right)\frac{Z_j^{\mathrm{t}}}{A_j}-\left(\frac{S_i+R_i}{N_i+1}\right)\frac{Z_i^{\mathrm{t}}}{A_i}\right],\\ \frac{\mathrm{d}{Y}_i^{\mathrm{t}}}{\mathrm{d}t}& ={\lambda }^{\mathrm{t}}\left(\frac{I_i}{N_i+1}\right)Z_i^{\mathrm{t}}-\left(d_i^{\mathrm{tU}}+{\gamma }^{\mathrm{t}}\left(\frac{S_i+R_i}{N_i+1}\right)\right)Y_i^{\mathrm{t}}\\ & +\sum _{j=1}^p\frac{m^I}{x_{ij}}\left[\left(\frac{I_j}{N_j+1}\right)\frac{Y_j^{\mathrm{t}}}{A_j}-\left(\frac{I_i}{N_i+1}\right)\frac{Y_i^{\mathrm{t}}}{A_i}\right],\end{array}$), in the absence of infection and migration, to monthly flea load data, given in [78] (see Figure 3). To match the data, sets $U_3^{\mathrm{h}}$ and $U_3^{\mathrm{t}}$ are chosen to be April–December and January–March, respectively.

Figure 3. Flea parameters $b^{\mathrm{h}}$, $b^{\mathrm{t}}$, and $d^{\mathrm{t}}$ were obtained by fitting Equations (10$\begin{array}{rl}\frac{\mathrm{d}{Z}_i^{\mathrm{h}}}{\mathrm{d}t}& ={\phi }_{U_3^{\mathrm{h}}}(t)\left(\frac{b^{\mathrm{h}}{N}_i}{1+N_i+N_i^{\mathrm{h}}}\right)N_i^{\mathrm{h}}-\left(d_i^{\mathrm{h}}+{\lambda }^{\mathrm{h}}\left(\frac{I_i}{N_i+1}\right)\right)Z_i^{\mathrm{h}}+{\gamma }^{\mathrm{h}}\left(\frac{S_i+R_i}{N_i+1}\right)Y_i^{\mathrm{h}}\\ & +\sum _{j=1}^p\frac{m}{x_{ij}}\left[\left(\frac{S_j+R_j}{N_j+1}\right)\frac{Z_j^{\mathrm{h}}}{A_j}-\left(\frac{S_i+R_i}{N_i+1}\right)\frac{Z_i^{\mathrm{h}}}{A_i}\right],\\ \frac{\mathrm{d}{Y}_i^{\mathrm{h}}}{\mathrm{d}t}& ={\alpha }_2{\lambda }^{\mathrm{h}}\left(\frac{I_i}{N_i+1}\right)Z_i^{\mathrm{h}}-\left(d_i^{\mathrm{hU}}+{\gamma }^{\mathrm{h}}\left(\frac{S_i+R_i}{N_i+1}\right)\right)Y_i^{\mathrm{h}}\\ & +\sum _{j=1}^p\frac{m^I}{x_{ij}}\left[\left(\frac{I_j}{N_j+1}\right)\frac{Y_j^{\mathrm{h}}}{A_j}-\left(\frac{I_i}{N_i+1}\right)\frac{Y_i^{\mathrm{h}}}{A_i}\right],\\ \frac{\mathrm{d}{Y}_i^{\mathrm{tB}}}{\mathrm{d}t}& =(1-{\alpha }_2){\lambda }^{\mathrm{h}}\left(\frac{I_i}{N_i+1}\right)Z_i^{\mathrm{h}}-d_i^{\mathrm{hB}}{Y}_i^{\mathrm{hB}},\end{array}$) and (11$\begin{array}{rl}\frac{\mathrm{d}{Z}_i^{\mathrm{t}}}{\mathrm{d}t}& ={\phi }_{U_3^{\mathrm{t}}}(t)\left(\frac{b^{\mathrm{t}}{N}_i}{1+N_i+N_i^{\mathrm{t}}}\right)N_i^{\mathrm{t}}-\left(d_i^{\mathrm{t}}+{\lambda }^{\mathrm{t}}\left(\frac{I_i}{N_i+1}\right)\right)Z_i^{\mathrm{t}}+{\gamma }^{\mathrm{t}}\left(\frac{S_i+R_i}{N_i+1}\right)Y_i^{\mathrm{t}}\\ & +\sum _{j=1}^p\frac{m}{x_{ij}}\left[\left(\frac{S_j+R_j}{N_j+1}\right)\frac{Z_j^{\mathrm{t}}}{A_j}-\left(\frac{S_i+R_i}{N_i+1}\right)\frac{Z_i^{\mathrm{t}}}{A_i}\right],\\ \frac{\mathrm{d}{Y}_i^{\mathrm{t}}}{\mathrm{d}t}& ={\lambda }^{\mathrm{t}}\left(\frac{I_i}{N_i+1}\right)Z_i^{\mathrm{t}}-\left(d_i^{\mathrm{tU}}+{\gamma }^{\mathrm{t}}\left(\frac{S_i+R_i}{N_i+1}\right)\right)Y_i^{\mathrm{t}}\\ & +\sum _{j=1}^p\frac{m^I}{x_{ij}}\left[\left(\frac{I_j}{N_j+1}\right)\frac{Y_j^{\mathrm{t}}}{A_j}-\left(\frac{I_i}{N_i+1}\right)\frac{Y_i^{\mathrm{t}}}{A_i}\right],\end{array}$), in the absence of infection and migration, to monthly flea load data (marked by +), given in [78].

Table 3. Rate values for calculating ${\beta }^{\mathrm{h}}$ and ${\beta }^{\mathrm{t}}$.

Parameter	O. hirsuta	O. t. cynomuris
Vector efficiency	0.045	0.18
Daily biting rate	0.84	0.82
Unblocked transmission	${\beta }^{\mathrm{h}}=0.006$	${\beta }^{\mathrm{t}}=0.025$

Note: Related reference: [78].

Next we estimate the transmission parameters. The total number of infectious flea bites delivered per day is the product of: the biting rate, the vector efficiency, and the number of infectious fleas. We assume infectious fleas remain on the newly infected host until the host's death; that is, fleas leave the infectious host with probability $\frac{1}{6}$ on any given day. Consequently, the total number of effective infectious bites (those infectious bites that cause a new prairie dog infection) is: (total number of infectious bites)/6. Then, the probability of delivering an effective infectious bite per susceptible prairie dog is: (total effective infectious bites per day)/(total prairie dog population size). Then, ${\beta }^{(kl)}=(\mathrm{biting}\mathrm{rate}\times \mathrm{vector}\mathrm{efficiency})/6.$ Table 3 contains biting rates and vector efficiencies from [78], as well as the resulting values of ${\beta }^{\mathrm{h}}$ and${\beta }^{\mathrm{t}}$.

Using the survival rates given in [78], we set $d_i^{\mathrm{hU}}=0.05$ and $d_i^{\mathrm{tU}}=0.12$. In laboratory tests, it takes 9–28 days for plague infections to become established and form a block in fleas, and fleas die about 2 days thereafter [18, 28, 55]. Since the survival rates in [78] suggest that the post-infection mean life expectancy for O. hirsuta is about 20 days, we assume the incubation period for blocked fleas is two weeks and the mean life expectancy after the block formation is two days. Hence $d_i^{\mathrm{hB}}=0.06$. We assume that, during the incubation period, fleas are not infectious, and then each flea produces one infectious host during the blocked phase. Using a $0.95$ survival rate, the probability of the flea surviving the incubation period is $0.48$. Using the $\frac{3}{70}$ vector efficiency [28], the corresponding transmission rate ${\beta }^{\mathrm{hB}}=0.001$. All parameter values are summarized in Tables 4 and5.

Table 4. Prairie dog parameter values (per year, except for $d_i^I$, which is given per day^*).

Parameter	Value		Description	Reference
b	0.434		Birth parameter,	Calculated,
			$U_1$: Mar–Apr	[40, 41, 44, 48, 72]
$d_i$	0.274	$\mathrm{\forall }i$	Natural mortality	Calculated, [78]
$d_i^I$	0.167^*	$\mathrm{\forall }i$	Infectious mortality	[14, 18, 44]
c	$1.78\times {10}^{-2}$		Crowding	Calculated, [72]
m	$4\times {10}^{-3}$		Migration parameter,	Assumed
			$U_2$: Apr–May
$m^I$	$4\times {10}^{-5}$		Infectious migration parameter	Assumed

Table 5. Flea parameter values (per day).

Parameter	Value		Description	Reference
${\beta }^{\mathrm{h}}$	$6\times {10}^{-3}$		Transmission coefficient	Table 3
${\beta }^{\mathrm{hB}}$	$1\times {10}^{-3}$		Transmission coefficient	Calculated [18, 28, 78]
${\beta }^{\mathrm{t}}$	$2.5\times {10}^{-2}$		Transmission coefficient	Table 3
$b^{\mathrm{h}}$	0.25		Birth parameter,	Figure 3
			$U_3^{\mathrm{h}}$: mid-Apr–mid-Dec
$b^{\mathrm{t}}$	0.55		Birth parameter,	Figure 3
			$U_3^{\mathrm{t}}$: mid-Jan–mid-Mar
$d_i^{\mathrm{h}}$	$1.667\times {10}^{-2}$	$\mathrm{\forall }i$	Natural mortality	Figure 3
$d_i^{\mathrm{t}}$	$3.333\times {10}^{-2}$	$\mathrm{\forall }i$	Natural mortality	Figure 3
$d_i^{\mathrm{hU}}$	0.05	$\mathrm{\forall }i$	Post-infection mortality	[78]
$d_i^{\mathrm{tU}}$	0.12	$\mathrm{\forall }i$	Post-infection mortality	[78]
$d_i^{\mathrm{hB}}$	0.06	$\mathrm{\forall }i$	Blocked mortality	Calculated with 2 weeks incubation [18, 28, 55]
${\lambda }^{\mathrm{h}}$	1		Infection prevalence	[78]
${\lambda }^{\mathrm{t}}$	0.88		Infection prevalence	[78]
${\gamma }^{\mathrm{h}}$	0.2		Recovery	Assumed
${\gamma }^{\mathrm{t}}$	0.2		Recovery	Assumed

Note: Superscripts h and t correspond to species O. hirsuta and O. t. cynomuris, respectively.

6. Simulations

In this section, numerical simulations demonstrate the results of Section 3.

6.1. The Allee effect

To numerically investigate the Allee effect, we consider population dynamics in the absence of infection: $I_i=R_i=0$, $N_i=S_i$ for all patches i.

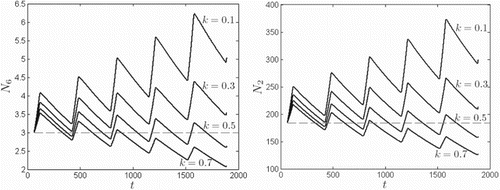
By Theorem 3.2, a strong Allee effect is present if ${\sigma }_0<0$, where ${\sigma }_0=\sigma (\mathrm{diag}({\tilde{\phi }}_{U_1}b/k{A}_i-d_i)+\frac{1}{2}{\tilde{\phi }}_{U_2}(\mathbf{M}+{\mathbf{M}}^{\mathrm{T}})).$ In Figure 4, ${\sigma }_0$ is plotted for various values of k. A nonempty basin of attraction for extinction across the metapopulation (${\sigma }_0<0$) occurs for sufficiently large values of k. In Figure 5, 5-year ODE solution curves for host populations $N_i$ are plotted for $k=0.1,0.3,0.5$ and 0.7, for both the smallest (Rankin Ridge, $i=6$) and largest (Bison Flats, $i=2$) patches. The initial conditions were relatively small: $S_i(t_0)\approx 0.75A_i$ for all patches i and zero for all other classes, and where $t_0$ is the beginning of the prairie dog birth season. For values of k for which ${\sigma }_0<0$ in Figure 4, populations decline each year, $S_i(t+jT)<S_i(t+(j+1)T)$, $j\in {\mathbb{Z}}_{+}$, where period T is one year, indicating the presence of an strong Allee effect. However, the strong Allee effect is absent for values of k for which ${\sigma }_0>0$; populations grow from year to year,$S_i(t+jT)>S_i(t+(j+1)T)$.

Figure 4. Function ${\sigma }_0=\sigma (\mathrm{diag}({\tilde{\phi }}_{U_1}b/k{A}_i-d_i)+\frac{1}{2}{\tilde{\phi }}_{U_2}(\mathbf{M}+{\mathbf{M}}^{\mathrm{T}}))$ for various values of k, where $\sigma (\mathbf{A})$ denotes the largest eigenvalue of a symmetric matrix $\mathit{A}$ and k is the parameter in the birth rate ${\mathcal{B}}_i(N_i)$ which controls the level of the Allee effect. A strong Allee effect exists when ${\sigma }_0<0$.

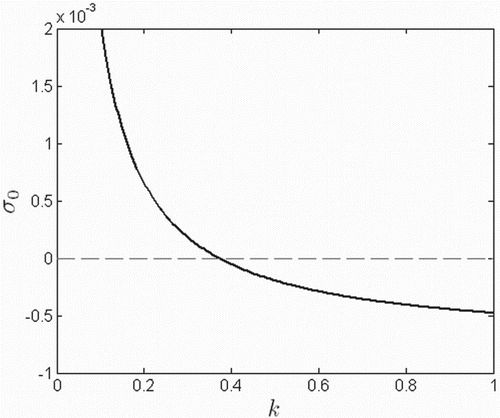
Figure 5. Population size over five years in the absence of disease for the smallest patch ($i=6$, left) and the largest patch ($i=2$, right), for $k=0.1,0.3,0.5,$ and 0.7, according to the ODE model. Time t is given in days. A strong Allee effect is evident for values of k such that ${\sigma }_0<0$.

Henceforth, we use $k=0.7$, such that the model includes a strong Allee effect, ${\sigma }_0<0$.

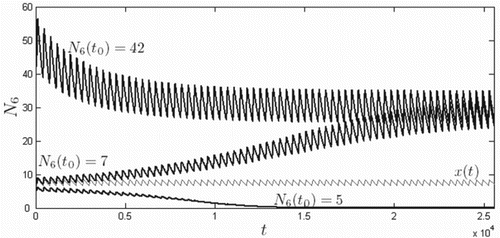
Next, in Figure 6, we numerically demonstrate Theorem 3.4. By letting $z_1=1.6$ and $z_2=2.0$, inequality (6$(T-T_0)(d_i+c_i{A}_i{z}_2)z_2\le z_2-z_1\le T_0\underset{j=1,2}{min}\{{\mathcal{B}}_i(A_i{z}_j)z_j-(d_i+c_i{A}_i{z}_j)z_j\}.$) holds. By Theorem 3.4, for any initial condition $\mathit{N}(t_0)>\mathit{x}(t_0)$, the solution should approach a positive periodic solution, where $\mathit{x}(t)$ is defined in Equation (7$x_i(t)=\left\{\begin{array}{ll}\left(z_1+\frac{z_2-z_1}{T_0}t\right)A_i,& 0\le t\le T_0,\\ \left(z_1+\frac{z_2-z_1}{T-T_0}(T-t)\right)A_i,& T_0<t\le T,\end{array}\right.$). In Figure 6, the light curve is function $x_6(t)$ and the dark curves are 70-year ODE solutions $N_6(t)$ for three sets of initial conditions. The two solutions with initial conditions above $x_i(t_0)$, $i=1,\dots ,p$, approach a positive periodic solution, while the solution with initial conditions below $x_i(t_0)$, $i=1,\dots ,p,$ succumbs to the strong Allee effect.

Figure 6. Seventy-year ODE solution curves for Rankin Ridge, $N_6(t)$, in the absence of infection, with the initial conditions $N_i(t_0)=1.2A_i,1.7A_i,$ and $10A_i$ for all i, where $A_i$ is the area of patch i. Time t is given in days and $t_0$ is the beginning of the prairie dog birth season. Solutions approach a positive periodic solution for initial conditions exceeding periodic threshold $x_i(t)$ for all i.

6.2. Dynamics of disease spread

We now investigate population dynamics in the presence of the plague. In this section, we assume no vaccination, $v_i=0$, such that $R_i(t)=0$ for all $t\ge 0$, $i=1,\dots ,p$.

North Boundary (patch $i=11$) is the northernmost colony, with Sanctuary ($i=7$) and Bison Flats ($i=2$) progressively further south (see Figure A1). To show the progression of the spread of the plague numerically, we introduce two infectious individuals to North Boundary near the beginning of the migration season; that is, we force $I_{11}(120)=2$ in the otherwise disease-free metapopulation.

We first investigate the importance of blocked fleas in plague dynamics. We include O. hirsuta only, and vary the proportion of new infectious fleas that become blocked. The initial conditions are $\begin{array}{r}\begin{array}{rl}{I}_i(0)& =0,Y_i^{\mathrm{h}}(0)=0,Y_i^{\mathrm{hB}}=0,Y_i^{\mathrm{t}}(0)=0,i=1,\dots ,11,\\ N_i(0)& =5A_i,N_i^{\mathrm{h}}(0)=0.675N_i(0),N_i^{\mathrm{t}}(0)=0,i=1,\dots ,11,\end{array}\end{array}$ where $A_i$ is the area of the ith patch in hectares and time $t=0$ corresponds to the beginning of a calendar year. 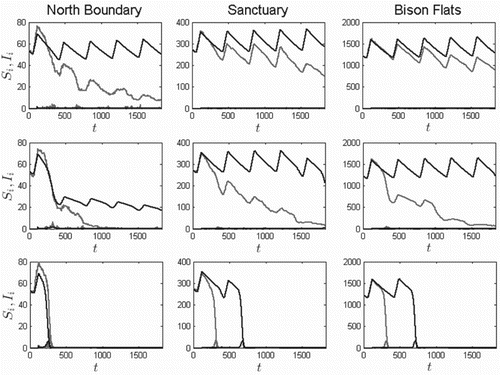Numerical solutions $S_i(t)$ and $I_i(t)$ for the three aforementioned patches are given in Figure 7, with ${\alpha }_2=0,0.5,1$ (i.e. with 0%, 50%, and 100% unblocked fleas). It had once been assumed that blocked fleas were the only significant transmission vector [32]. However, recent research suggests poor vector competence among blocked fleas [55], and some suggest unblocked fleas are the main transmission vector [27]. For the selected transmission rates, when all infectious fleas are blocked (${\alpha }_2=0$), there is no outbreak according to the ODE model, even with the higher transmission rate among blocked fleas. However, for ${\alpha }_2=0.5$ and 1, the greater the proportion of newly infectious unblocked fleas, ${\alpha }_2$, the sooner an outbreak and subsequent population crash occurs, as can be seen in rows 2–3 of Figure 7. We also note the progression of the plague spreading south: the further south the colony, the later the plague affects its population (left to right within each row). Further, the SDE sample path population always crashes, generally sooner than the ODE. The simulations demonstrate the competence of unblocked fleas as vectors.

Figure 7. Five-year solution curves for prairie dog classes $S_i(t)$ and $I_i(t)$ for three patches ($i=11,$ 7, and 2, north to south from left to right) and for unblocked flea proportions ${\alpha }_2=0$ (top row), 0.5 (second row), and 1 (third row), based on the ODE model (dark) and one sample path of the SDE model (light) for the initial conditions given in Equation (12$\begin{array}{r}\begin{array}{rl}{I}_i(0)& =0,Y_i^{\mathrm{h}}(0)=0,Y_i^{\mathrm{hB}}=0,Y_i^{\mathrm{t}}(0)=0,i=1,\dots ,11,\\ N_i(0)& =5A_i,N_i^{\mathrm{h}}(0)=0.675N_i(0),N_i^{\mathrm{t}}(0)=0,i=1,\dots ,11,\end{array}\end{array}$), and introducing two infected prairie dogs in North Boundary on day 120:$I_{11}(120)=2$. For this example, only O. hirsuta is modelled, without O. t. cynomuris. Blocked individuals are not as effective at transmitting plague as unblocked.

Since blocked fleas are not a significant factor in the spread of plague, we set ${\alpha }_2=1$ for the remainder of this paper, with the same initial conditions as Equation (12$\begin{array}{r}\begin{array}{rl}{I}_i(0)& =0,Y_i^{\mathrm{h}}(0)=0,Y_i^{\mathrm{hB}}=0,Y_i^{\mathrm{t}}(0)=0,i=1,\dots ,11,\\ N_i(0)& =5A_i,N_i^{\mathrm{h}}(0)=0.675N_i(0),N_i^{\mathrm{t}}(0)=0,i=1,\dots ,11,\end{array}\end{array}$), except $N_i^{\mathrm{t}}(0)$: $\begin{array}{r}\begin{array}{rl}{I}_i(0)& =0,Y_i^{\mathrm{h}}(0)=0,Y_i^{\mathrm{t}}(0)=0,i=1,\dots ,11,\\ N_i(0)& =5A_i,N_i^{\mathrm{h}}(0)=0.675N_i(0),N_i^{\mathrm{t}}(0)=0.0005N_i(0),i=1,\dots ,11,\end{array}\end{array}$

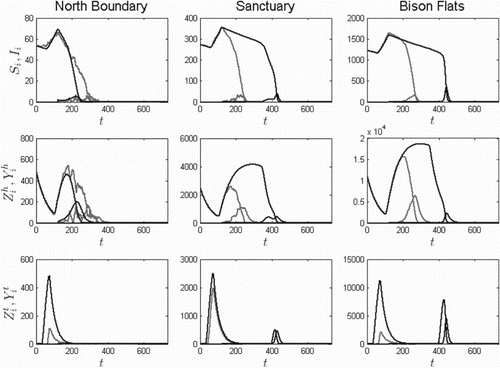
In Figure 8, two-year plague dynamics are given for the two-flea species case. All six classes involved are plotted. In the presence of both species, the plague spreads rapidly, with only a slight delay as the plague travels southward.

Figure 8. Two-year solution curves for three patches (north to south from left to right, $i=11,$ 7, and 2, respectively) for the two-flea species model and ${\alpha }_2=1$ (no blocked O. hirsuta), based on the ODE model (dark) and one sample path of the SDE model (light) for the initial conditions given in Equation (13$\begin{array}{r}\begin{array}{rl}{I}_i(0)& =0,Y_i^{\mathrm{h}}(0)=0,Y_i^{\mathrm{t}}(0)=0,i=1,\dots ,11,\\ N_i(0)& =5A_i,N_i^{\mathrm{h}}(0)=0.675N_i(0),N_i^{\mathrm{t}}(0)=0.0005N_i(0),i=1,\dots ,11,\end{array}\end{array}$). As in Figure 7, two infectious prairie dogs are introduced into North Boundary at time 120 days: $I_{11}(120)=2$. The models predict a much faster spread of plague with both species included.

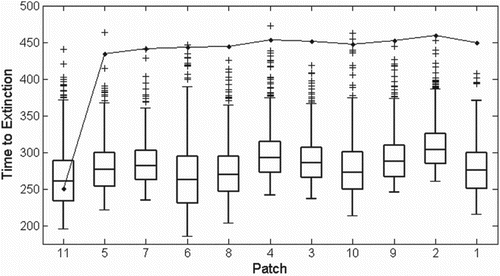
To compare the ODE and SDE dynamics with respect to the spatial distribution, the ODE model and 1000 sample paths of the SDE model were simulated to determine the mean time to extinction for each patch i. We approximate the time of extinction by the first time t for which $N_i(t)<1$. The same two-flea conditions used for Figure 8 are also used here. In Figure 9, the SDE sample path extinction times are represented by box plots and the ODE time to extinction is given by the connected circles. The patches are ordered by distance from the location of initial infection, $i=11$. Except for North Boundary ($i=11$), the ODE model predicts populations will die in the second year, whereas SDE populations generally die in the first year. Since fluctuations in environmental conditions affect the model parameters and are included in the SDE, when parameters are difficult to accurately estimate, the stochastic model behaviours may be more appropriate to consider.

Figure 9. Time (in days) to extinction of each patch for the ODE model (connected circles) and 1000 sample paths of the SDE model (box plots), using initial conditions given by Equation (13$\begin{array}{r}\begin{array}{rl}{I}_i(0)& =0,Y_i^{\mathrm{h}}(0)=0,Y_i^{\mathrm{t}}(0)=0,i=1,\dots ,11,\\ N_i(0)& =5A_i,N_i^{\mathrm{h}}(0)=0.675N_i(0),N_i^{\mathrm{t}}(0)=0.0005N_i(0),i=1,\dots ,11,\end{array}\end{array}$) and introducing $I_{11}(120)=2$. Patches are ordered by distance from North Boundary, from closest (left, North Boundary itself) to furthest (right). See Figure A1 and Table A2 for the spatial arrangement. The ODE model predicts much longer times to extinction for every patch except North Boundary.

6.3. Vector control

Control of the vector species has been considered as a possible method to control plague [9, 67]. Reducing flea density is achieved through periodically applying insecticide in and around prairie dog burrows. In [9], application of insecticide reduced the number of fleas by approximately 95% after one month. At their respective peak seasons, the largest average number of O. hirsuta and O. t. cynomuris per prairie dog is approximately $(b^{\mathrm{h}}-d^{\mathrm{h}})/d^{\mathrm{h}}$ and $(b^{\mathrm{t}}-d^{\mathrm{t}})/d^{\mathrm{t}}$, respectively, for the model investigated here. With respect to the model, applying insecticide is equivalent to imposing a substantially higher flea death rate during the application time. Since the two species modelled here have different abundance patterns, we simulate two insecticide applications annually: one in March and the other in August, each for approximately 10 days, which is consistent with instructions on insecticides such as DeltaDust${}^{\circledR }$ by Bayer^TM. Three insecticide death rates are chosen such that the number of fleas per prairie dog at the end of the simulated insecticide application is reduced by 75%, 85%, and 95% of the level immediately prior to the applications. As in Section 6.2, there are no immune individuals ($v_i=0$) and the initial conditions listed in Equation (13$\begin{array}{r}\begin{array}{rl}{I}_i(0)& =0,Y_i^{\mathrm{h}}(0)=0,Y_i^{\mathrm{t}}(0)=0,i=1,\dots ,11,\\ N_i(0)& =5A_i,N_i^{\mathrm{h}}(0)=0.675N_i(0),N_i^{\mathrm{t}}(0)=0.0005N_i(0),i=1,\dots ,11,\end{array}\end{array}$) are used for numerical simulations. Figure 10 provides five-year numerical solutions for the prairie dog and flea populations for North Boundary ($i=11$), where the infection is first introduced, $I_{11}(120)=2$.

Figure 10. Five-year numerical solutions for prairie dog and flea populations in North Boundary ($i=11$) for control (insecticide) -induced death rates resulting in 75%, 85%, and 95% death at the end of the application compared to levels immediately prior to application, based on the ODE model (dark) and one realization of the SDE model (light). Time t is in days, initial conditions are given by Equation (13$\begin{array}{r}\begin{array}{rl}{I}_i(0)& =0,Y_i^{\mathrm{h}}(0)=0,Y_i^{\mathrm{t}}(0)=0,i=1,\dots ,11,\\ N_i(0)& =5A_i,N_i^{\mathrm{h}}(0)=0.675N_i(0),N_i^{\mathrm{t}}(0)=0.0005N_i(0),i=1,\dots ,11,\end{array}\end{array}$), and $I_{11}(120)=2$. Insecticide is ineffective at 75%, controls the population at 85%, and prevents plague-driven decline in the prairie dog population at 95%.

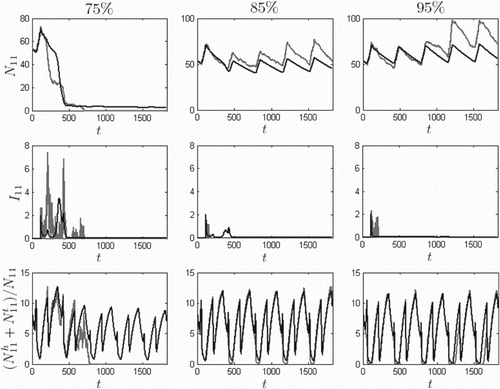
When no vector control was applied, the ODE model predicts extinction (see Figure 8). In Figure 10, removing 75% of the flea population is insufficient for control, but at 85%, the infectious classes decline faster than the susceptible population crash and the prairie dogs avoid extinction. At 95%, the models predict that the prairie dog population avoids plague-driven declines altogether in the first five years.

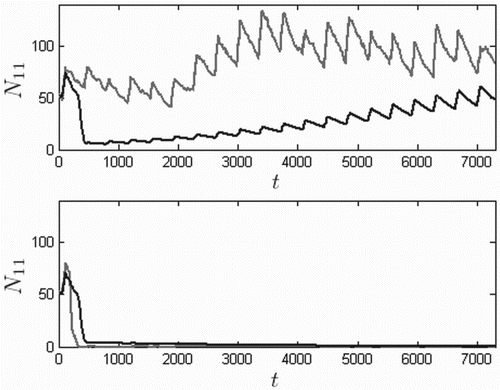
To investigate the influence of the Allee effect on the control method's effectiveness, the 75% flea death control method is again considered. Figure 11 contains solution curves for the model using the control method, both with and without the Allee effect. Specifically, the top plot uses birth rate ${\mathcal{B}}_i(N_i)=b$ (no Allee effect) and the bottom curve is based on the birth rate used elsewhere in this paper, ${\mathcal{B}}_i=b{N}_i/(N_i+k{A}_i)$. Although the prairie dog population suffers a significant initial decline when the plague is introduced, the long-term behaviour in the absence of the Allee effect suggests that the 75% level of flea control is sufficient for population persistence. However, when the Allee effect is included at the same control level, the population never recovers from the initial plague outbreak. The SDE sample path goes to extinction faster in the presence of the Allee effect, and recovers faster in its absence.

Figure 11. Twenty-year solutions $N_{11}$ with (bottom) and without (top) the Allee effect, for vector control using death rates resulting in 75% death at the end of the application compared to levels immediately prior to application, based on the ODE model (dark) and one realization of the SDE model (light). Time t is in days, initial conditions are given by Equation (13$\begin{array}{r}\begin{array}{rl}{I}_i(0)& =0,Y_i^{\mathrm{h}}(0)=0,Y_i^{\mathrm{t}}(0)=0,i=1,\dots ,11,\\ N_i(0)& =5A_i,N_i^{\mathrm{h}}(0)=0.675N_i(0),N_i^{\mathrm{t}}(0)=0.0005N_i(0),i=1,\dots ,11,\end{array}\end{array}$), and $I_{11}(120)=2$. In the absence of the Allee effect, the model predicts eventual recovery of the prairie dog population under this level of vector control, whereas with the Allee effect, the population faces extinction.

6.4. Control by immunization

The possibility of using vaccination to control the plague has been discussed in [1, 58]. These articles consider the use of bait to immunize; however, compared to vector control, this method has not been investigated thoroughly. Here we demonstrate the effect of introducing immunization to the model. For simulations, we use the same initial conditions, listed in Equation (13$\begin{array}{r}\begin{array}{rl}{I}_i(0)& =0,Y_i^{\mathrm{h}}(0)=0,Y_i^{\mathrm{t}}(0)=0,i=1,\dots ,11,\\ N_i(0)& =5A_i,N_i^{\mathrm{h}}(0)=0.675N_i(0),N_i^{\mathrm{t}}(0)=0.0005N_i(0),i=1,\dots ,11,\end{array}\end{array}$), with $R_i(0)=0,i=1,\dots ,p,$ and force $I_{11}(120)=2$. 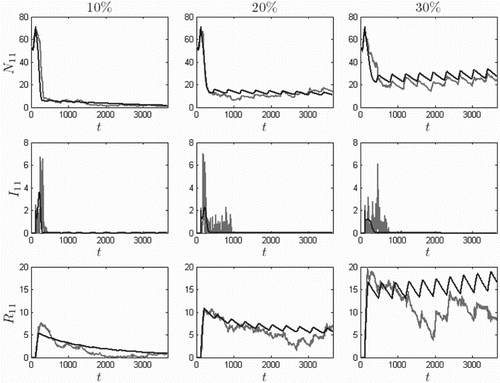Vaccine is given for three months (May–July) at the rates of 0.0012, 0.0025, and 0.0040 per day. These daily rates are sufficient to vaccinate 10%, 20%, and 30% of the May 1 population, respectively. The numerical solutions are provide in Figure 12. At the 10% annual vaccination level, the ODE model predicts that the prairie dog population will approach extinction. At 30%, the population survives, but is significantly lowered by the plague. The SDE model behaves similarly.

Figure 12. Ten-year North Boundary ($i=11$) solution curves $N(t)$, $I(t)$, and $R(t)$ for annual vaccination from May through July, at rates that result in 10% (left), 20% (middle), and 30% (right) vaccinated by the end vaccination period, for the ODE model (dark) and one sample path of the SDE model (light). Time t is in days, initial conditions are given by Equation (13$\begin{array}{r}\begin{array}{rl}{I}_i(0)& =0,Y_i^{\mathrm{h}}(0)=0,Y_i^{\mathrm{t}}(0)=0,i=1,\dots ,11,\\ N_i(0)& =5A_i,N_i^{\mathrm{h}}(0)=0.675N_i(0),N_i^{\mathrm{t}}(0)=0.0005N_i(0),i=1,\dots ,11,\end{array}\end{array}$), and $I_{11}(120)=2$. Although the plague suppresses the population, the patch avoids extinction when vaccination rates are sufficiently high.

7. Conclusion

In this paper, we introduced a deterministic, and corresponding stochastic, vector-driven SIR epidemic model to study the effect of disease on metapopulation dynamics in the presence of the Allee effect and seasonal birth and dispersal rates. The model representation discussed here allows for a weak Allee effect and we obtained conditions for the existence of a strong Allee effect. For a system in which births and migration are seasonal, we obtained conditions for a disease-free positive periodic solution. Next, the stability of the disease-free solution was investigated in the absence of immunization, and possible strategies were explored for the control of a disease spreading within a patch system.

The models were numerically simulated to evaluate the dynamics of a population of prairie dogs living in patch-like colonies and suffering from the slyvatic plague. Existing prairie dog models have not been suitable for studying how the spatial structure of the colonies could be exploited to protect the species against extinction due to the plague or to develop control methods. In the example, we use the deterministic and stochastic SIR models to evaluate the effects of dispersal and the Allee effect on extinction.

Using parameters from field studies, we analysed the effect of birth rate parameter values on the Allee effect (Figure 4). Next we numerically obtained values of $z_1$ and $z_2$ from Theorem 3.4 to demonstrate the positive disease-free solution. The simulations demonstrate the results in Section 3. By introducing disease to one patch, we investigated the spread of disease among patches progressively further away. Simulations demonstrated poor vector competence among blocked fleas and vector competence among unblocked fleas. This is mainly due to high death rates among blocked fleas. Also, the SDE simulations generally exhibited faster extinction under environmental variability.

Finally, we evaluated the effects of control of the flea population, as well as control by immunization, on maintaining a healthy prairie dog population among the patch system interconnected through dispersal. According to ODE simulations, if the control is applied at sufficiently high levels, both methods allow prairie dog persistence. In the case of control, the SDE simulations behaved similar to the ODE solution. Although we have run many simulations, we provided only one sample path for each stochastic simulation in the control section. More study is needed to investigate the probability of an outbreak of the plague for the stochastic model.

Acknowledgments

The authors wish to thank two anonymous reviewers for their helpful comments.

Appendix 1. SDE model formulation

Matrix $\mathit{H}$, a $p\eta \times p(\eta (p+1)-K)$ matrix, is composed of two submatrices $\mathbf{H}=[{\mathbf{H}}_{\mathrm{intra}}|{\mathbf{H}}_{\mathrm{inter}}]$, containing intra-patch and dispersal dynamics, respectively. The rows of $\mathit{H}$ correspond to the entries of $\mathit{X}$, Equation (9$\begin{array}{rl}\mathit{X}& =\{X_i{\}}_{i=1}^{p\eta }\\ & =[S_1,I_1,R_1,Z_1^{(1)},Y_1^{(11)},\dots ,Y_1^{(1L_1)},\dots ,Z_1^{(K)},Y_1^{(K1)},\dots ,Y_1^{(K{L}_K)},\dots ,\\ & S_p,I_p,R_p,Z_p^{(1)},Y_p^{(11)},\dots ,Y_p^{(1L_1)},\dots ,Z_p^{(K)},Y_p^{(K1)},\dots ,Y_p^{(K{L}_K)}{]}^{\mathrm{T}},\end{array}$). Matrix ${\mathbf{H}}_{\mathrm{intra}}=\mathrm{diag}({\mathbf{\Sigma }}_i)$, a matrix having submatrices ${\mathbf{\Sigma }}_i$, $i=1,\dots ,p$, along the diagonal and zeros elsewhere, with ${\mathbf{\Sigma }}_i=\mathrm{diag}([{\mathbf{\Sigma }}_i^{(j1)}|{\mathbf{\Sigma }}_i^{(j2)}])$ for $j=0,\dots ,K$. Using values of $p(\mathrm{\Delta }X)$ in Table 1, the submatricies of ${\mathbf{\Sigma }}_i$ are $\begin{array}{rl}{\mathbf{\Sigma }}_i^{(01)}& =\left[\begin{array}{ccc}\sqrt{p({\mathit{e}}_{S_i})+p(-{\mathit{e}}_{S_i})}& 0& 0\\ 0& \sqrt{p(-{\mathit{e}}_{I_i})}& 0\\ 0& 0& \sqrt{p(-{\mathit{e}}_{R_i})}\end{array}\right],\\ {\mathbf{\Sigma }}_i^{(02)}& =\left[\begin{array}{ccc}-\sqrt{p({\mathit{e}}_{S_i}-{\mathit{e}}_{I_i})+p({\mathit{e}}_{I_i}-{\mathit{e}}_{S_i})}& -\sqrt{p({\mathit{e}}_{R_i}-{\mathit{e}}_{S_i})}& 0\\ \sqrt{p({\mathit{e}}_{S_i}-{\mathit{e}}_{I_i})+p({\mathit{e}}_{I_i}-{\mathit{e}}_{S_i})}& 0& -\sqrt{p({\mathit{e}}_{R_i}-{\mathit{e}}_{I_i})}\\ 0& \sqrt{p({\mathit{e}}_{R_i}-{\mathit{e}}_{S_i})}& \sqrt{p({\mathit{e}}_{R_i}-{\mathit{e}}_{I_i})}\end{array}\right],\end{array}$ for prairie dogs and, for flea species $k=1,\dots ,K$: $\begin{array}{rl}{\mathbf{\Sigma }}_i^{(k1)}& =\left[\begin{array}{cccc}\sqrt{p({\mathit{e}}_{Z_i^{(k)}})+p(-{\mathit{e}}_{Z_i^{(k)}})}& 0& \cdots & 0\\ 0& \sqrt{p(-{\mathit{e}}_{Y_i^{(k1)}})}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & \sqrt{p(-{\mathit{e}}_{Y_i^{(k{L}_k)}})}\end{array}\right],k\\ {\mathbf{\Sigma }}_i^{(k2)}& =\left[\begin{array}{ccccc}\sqrt{q_i^{(k1)}}& \sqrt{q_i^{(k2)}}& \sqrt{q_i^{(k3)}}& \cdots & \sqrt{q_i^{(k{L}_k)}}\\ -\sqrt{q_i^{(k1)}}& 0& 0& \cdots & 0\\ 0& -\sqrt{q_i^{(k2)}}& 0& \cdots & 0\\ ⋮& \ddots & \ddots & \ddots & ⋮\\ 0& \cdots & 0& \cdots & -\sqrt{q_i^{(k{L}_k)}}\end{array}\right],\\ q_i^{(kl)}& =p({\mathit{e}}_{Z_i^{(k)}}-{\mathit{e}}_{Y_i^{(kl)}})+p({\mathit{e}}_{Y_i^{(kl)}}-{\mathit{e}}_{Z_i^{(k)}}).\end{array}$ Thus, matrix ${\mathbf{H}}_{\mathrm{intra}}$ is $p\eta \times p(2\eta -K)$.

Every column of ${\mathbf{H}}_{\mathrm{inter}}$ has two nonzero entries. A column of ${\mathbf{H}}_{\mathrm{inter}}$ corresponding to an individual of class type ‘A’ in patch j migrating to patch i contains entries $\sqrt{p({\mathit{e}}_{A_i}-{\mathit{e}}_{A_j})}$ and $-\sqrt{p({\mathit{e}}_{A_i}-{\mathit{e}}_{A_j})}$ in the rows corresponding to variables $A_i$ and $A_j$, respectively, and zeros elsewhere. Since there are $p(p-1)$ permutations of p patches taken two at a time and η classes per patch, matrix ${\mathbf{H}}_{\mathrm{inter}}$ is$p\eta \times p(p-1)\eta$.

Elements of vector $\mathit{W}(t)=[{\mathit{W}}_1(t),\dots ,{\mathit{W}}_p(t),{\mathit{W}}_{\mathrm{inter}}(t){]}^{\mathrm{T}}$ correspond to columns of $\mathit{H}$: ${\mathit{W}}_{\mathrm{inter}}$ is composed of terms of the form $W_{ij}^A$ corresponding to the column of ${\mathbf{H}}_{\mathrm{inter}}$ representing the migration of an individual of a class type ‘A’ in patch j to another patch i and ${\mathit{W}}_i=[W_{i1},W_{i2},\dots ,W_{i6},W_{i,1,0},W_{i,1,1},\dots ,W_{i,1,2L_1},\dots ,W_{i,K,0},W_{i,K,1},\dots ,W_{i,K,2L_K}],$ where elements $W_{i1},\dots ,W_{i6}$ correspond to the columns of host submatrix $[{\mathbf{\Sigma }}_i^{(01)}|{\mathbf{\Sigma }}_i^{(02)}]$ and elements $W_{i,k,0},W_{i,k,1},\dots ,W_{i,k,2L_k}$ correspond to the columns of kth vector species submatrix $[{\mathbf{\Sigma }}_i^{(k1)}|{\mathbf{\Sigma }}_i^{(k2)}]$, $k=1,\dots ,K$. Vector $\mathit{W}$ has length $p(\eta (p+1)-K)$.

Figure A1. Prairie dog town locations with respect to one another. Related references: [19, 65].

Appendix 2. Prairie dog colony areas, locations, and distances between colonies

Table A1 contains prairie dog colony names and areas, as well as their assigned patch number. Figure A1 approximates the positions of the prairie dog towns relative to one another. Table A2 contains the distances between colonies.

Table A1. Area occupied by prairie dog colonies in Wind Cave National Park, South Dakota.

Number	Name	Area $(\mathrm{in}{10}^4{\mathrm{m}}^2)$
1	Shirttail	14.1
2	Bison Flats	246.4
3	Norbeck	62.5
4	Research Reserve	108.7
5	Pringle	29.0
6	Rankin Ridge	4.2
7	Sanctuary	54.8
8	Highland	12.2
9	Southeast	59.4
10	Northeast	13.8
11	North Boundary	10.7

Related reference: [19].

Table A2. Distances (in 10³m) between closest edges of prairie dog colonies in Wind Cave National Park, South Dakota. Colony names and corresponding patch numbers are given in Table A1.

Colony	1	2	3	4	5	6	7	8	9	10	11
1	0	0.80	4.02	4.83	9.12	9.12	8.85	10.73	9.66	16.09	11.80
2	0.80	0	1.88	2.14	7.77	7.51	6.44	6.97	5.90	11.80	9.66
3	4.02	1.88	0	0.72	4.56	4.56	4.02	5.63	6.44	11.67	6.71
4	4.83	2.14	0.72	0	4.83	4.30	3.09	3.76	4.02	9.66	6.17
5	9.12	7.77	4.56	4.83	0	1.08	1.61	5.63	9.12	11.14	1.07
6	9.12	7.51	4.56	4.30	1.08	0	1.48	5.10	8.32	10.99	2.06
7	8.85	6.44	4.02	3.09	1.61	1.48	0	2.82	6.17	8.85	1.34
8	10.73	6.97	5.63	3.76	5.63	5.10	2.82	0	3.22	5.63	4.56
9	9.66	5.90	6.44	4.02	9.12	8.32	6.17	3.22	0	5.90	8.58
10	16.09	11.80	11.67	9.66	11.14	10.99	8.85	5.63	5.90	0	8.32
11	11.80	9.66	6.71	6.17	1.07	2.06	1.34	4.56	8.58	8.32	0

Related references: [19, 65].