Allee effects and population spread in patchy landscapes

Abstract

Invasion of alien species is one of the major threats for natural community structures, potentially leading to high economic and environmental costs. In this work, we study through a reaction–diffusion model the dynamics of an invasion in a heterogeneous environment and in the presence of a strong Allee effect. We model space as an infinite landscape consisting of periodically alternating favourable and unfavourable patches. In addition, we consider that at the interface between patch types individuals may show preference for more favourable regions. Using homogenization techniques and a classical result for spread with Allee effect in homogeneous landscapes, we derive approximate expressions for the spread speed. When compared with numerical simulations, these expressions prove to be very accurate even beyond the expected small-scale heterogeneity limit of homogenization. We demonstrate how rates of spatial spread depend on demographic and movement parameters as well as on the landscape properties.

Keywords:

• Allee effects
• habitat heterogeneity
• individual movement behaviour
• invasions
• homogenization

AMS Subject Classifications:

• 92D25
• 35K57

1. Introduction

Natural environments are frequently subject to the introduction of new species. In recent years, the rate of new introduction events has even increased as an intense flow of people and products from and to different parts of the globe leads to an increased transport of organisms to new habitats. Non-native or alien species may establish and spread in new habitats, eventually changing existing local food web structure and potentially leading to biodiversity loss [21]. Therefore, understanding the various mechanisms that facilitate or prevent an invasion has become a central point in ecological research [8].

Allee effects, defined as positive density dependence of growth rates at low densities [1], are increasingly being recognized as important factors determining the success of species invasion [26]. Several mechanisms that operate at small population density may induce an Allee effect, for example, reduced fertilization of sessile organisms, reduced mate finding, reduced defence against a predator, reduced hunting efficiency of predators who forage in groups [3]. If these effects induce a negative net population growth rate at low densities, the population is said to suffer a strong Allee effect. A population with a strong Allee effect needs to overcome a given threshold, the Allee threshold, before it becomes viable. Allee effects are believed to operate in many invasion processes since populations in the early stages of an invasion are small. Spatially extended populations require a minimum initial spatial range occupied to successfully invade a region when a strong Allee effect is present [13, 14]. In addition, Allee effects negatively affect the rate of spatial spread [13, 31]. Patchy invasion can also occur when Allee effects are present in predator–prey systems and systems with viral infection [9, 20].

Another factor impacting establishment and spread of an alien species that has gained increased attention in the ecological literature is landscape heterogeneity [5, 10, 23]. Ecosystems become increasingly fragmented due to natural causes or human intervention. Spatial variation in habitat attributes can open niches for alien species to invade, and decreased habitat quality can imperil the persistence of native species. The first study using reaction–diffusion equations to determine population persistence and spread in highly fragmented landscapes dates back to Shigesada et al. [23], who considered a single population without Allee effect in an environment consisting of periodically alternating ‘favourable’ and ‘unfavourable’ patches.

When individuals move within a patchy landscape, they may respond to the presence of boundaries between habitat types by biasing their movement to better quality regions [4, 22]. This aspect of movement was not considered by Shigesada et al. [23], but only recently addressed by Maciel and Lutscher [16]. Based on previous work by Ovaskainen and Cornell [19], we included individual movement behaviour at an interface between two patch types into reaction–diffusion models in heterogeneous landscapes. In the absence of an Allee effect, we found that the degree of bias towards favourable habitats as well as the diffusion coefficient in each habitat type is critical in determining population persistence and rates of spatial spread [16].

For most species invasions then, one needs to understand how Allee effects and movement behaviour in a heterogeneous landscape interact to shape the course of the invasion in order to predict the success of an invader and devise a strategy for its control [27]. A first piece of empirical evidence of spatial variation of the Allee effect comes from recent work on the invasion of gypsy moth in North America [28]. Those authors calculated spread rates for various regions, assuming homogeneous conditions in each, and found that spatial spread can vary significantly. The only theoretical study of the interaction between Allee effects and heterogeneity that we are aware of is by Vergni et al. [30], who studied the downstream spread of an aquatic species from a reservoir. These authors considered movement behaviour to be homogeneous and independent of landscape quality. In particular, there was no behavioural response to interfaces, such as habitat preference and habitat-specific movement rates. The goal of our work is to combine a detailed movement model with a population-level Allee effect and to investigate how different mechanisms affect the population spread rate.

Since the pioneering work by Skellam [24] on the spread of muskrats, reaction–diffusion equations for the density of the invading population $u(x,t)$ of the form (1) $\frac{\mathrm{\partial }u}{\mathrm{\partial }t}=D\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}+f\left(u\right)$(1) have been one of the main theoretical tools for investigating the spread of invading organisms. In this equation, $t>0$ denotes time and $x\in (-\mathrm{\infty },\mathrm{\infty })$ denotes spatial location. In particular, one is interested on the predicted rates of spatial spread these models provide and how they compare with observed rates [2]. In the absence of an Allee effect, the famous formula for the asymptotic spreading speed is $c^{\ast }=2\left[D{f}^{\prime }\right(0){]}^{1/2}.$ In general, there is no explicit formula for the speed with Allee effect, but Hadeler and Rothe [7] showed that for the cubic function $f\left(u\right)=u(1-u)(u-a)$ with $0\le a<1,$ the speed of a decreasing travelling wave connecting the two stable states $u=1$ and $u=0$ is (2) $c=\sqrt{2}\left(\frac{1}{2}-a\right).$(2) In particular, the speed of propagation is positive only if the Allee threshold is small enough ($a<\frac{1}{2}$) and negative otherwise.

In this work, we combine the spatially periodic setting of two patch types as considered by Shigesada et al. [23], together with interface conditions explored in [16], with an Allee effect that can vary spatially in strength. We introduce our reaction–diffusion model in Section 2. Our analysis of the travelling wave speed for this equation is based on various scalings and homogenization techniques and formula (2(2) $c=\sqrt{2}\left(\frac{1}{2}-a\right).$(2) ) in Section 3. In Sections 4 and 5, we illustrate the results from our analysis using two scenarios. In one scenario, the ‘unfavourable’ patches are of such poor quality that the population cannot grow there at all, in the other the population suffers from an Allee effect in both patch types. The expressions that we derive for the travelling wave speeds prove to be good approximations in fine-grained environments, as verified numerically, and reveal the effects demographic and environmental parameters have on the invasion.

2. Model presentation

Our modelling framework is very similar to that in [23], but the population dynamics exhibit an Allee effect, and the interface conditions between patch types allow for patch preference. More precisely, we consider a one-dimensional, infinite periodic landscape consisting of two alternating patch types: ‘favourable’ (of length $l_1$) and ‘unfavourable’ (of length $l_2$). On each patch, movement and population dynamics are described by a reaction–diffusion equation as in Equation (1(1) $\frac{\mathrm{\partial }u}{\mathrm{\partial }t}=D\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}+f\left(u\right)$(1) ), where parameters and functional form are specific to the patch type. Hence, on patch i, we have the equation (3) $\frac{\mathrm{\partial }{u}_i}{\mathrm{\partial }t}=D_i\frac{{\mathrm{\partial }}^2{u}_i}{\mathrm{\partial }{x}^2}+f_i\left(u_i\right),$(3) where $u_i$ and $D_i$ are, respectively, the population density and the diffusion coefficient in patch i. Functions $f_i$ account for births and deaths in the population. We shall always assume that the population is subject to a strong Allee effect on a favourable patch (type 1), where we write $f_1$ as a cubic function, similar to [7]. We consider two scenarios for an unfavourable patch (type 2). These patches may be population dynamic sinks, i.e. $f_2<0$ (see Section 4), or the population may also experience an Allee effect there, but with higher Allee threshold (Section 5).

At the interface between patch types, the population flux has to be continuous to preserve the number of individuals. The population density, on the other hand, is not continuous in general [16, 19]. The diffusion coefficients on either side of the interface, as well as potential preference of one patch type over another influence the jump in density. Specifically, if the interface lies at a point $x_n$ in space with a patch of type 1 to the right and a patch of type 2 to the left, the interface conditions read (4) $\begin{array}{rl}{D}_1\frac{\mathrm{\partial }{u}_1}{\mathrm{\partial }x}(x_n^{+},t)& =D_2\frac{\mathrm{\partial }{u}_2}{\mathrm{\partial }x}(x_n^{-},t),\end{array}$(4) (5) $\begin{array}{rl}{u}_1(x_n^{+},t)& =k{u}_2(x_n^{-},t),\end{array}$(5) where we use the notation $u_i(x_n^{\pm },t)=\underset{x\to x_n^{\pm }}{lim}{u}_i(x,t)$ for one-sided limits. If the locations of the two patch types are reversed, then the signs of one-sided limits must be changed. Parameter k depends on the particular assumptions on species movement.

The expression for k depends subtly on details and modelling assumptions of the random walk [19]. In this work, we use (6) $k=\frac{D_2}{D_1}\frac{\alpha }{(1-\alpha )},$(6) where α denotes the probability that an individual at an interface moves into patch type 1 and, accordingly, $(1-\alpha )$ is the probability that the individual moves to patch type 2. For later reference, we note that continuous interface conditions arise when $\alpha =D_1/(D_1+D_2),$ in particular then there is a preference for the patch type in which movement is faster. This insight will help us interpret some of the results later. For a detailed discussion of the movement assumptions and an alternative expression for k, please see [16].

It might be somewhat surprising that even if there is no preference for one type of habitat (i.e. $\alpha =0.5$), the density is still discontinuous, provided that the diffusion coefficients are different. Here, we give a short heuristic argument for this fact. We present a more detailed derivation that includes habitat preference at an interface in the appendix .

Consider individuals moving randomly in the interval $[-1,1]$ with spatially varying diffusion coefficient (twice differentiable) according to the equation $\mathrm{\partial }/\mathrm{\partial }t\left[u\right(x,t\left)\right]={\mathrm{\partial }}^2/\mathrm{\partial }{x}^2\left[D\right(x\left)u\right(x,t\left)\right]$ [29]. At the boundary points $x=\pm 1,$ we impose no-flux boundary conditions $\mathrm{\partial }/\mathrm{\partial }x\left[D\right(\pm 1\left)u\right(\pm 1,t\left)\right]=0.$ The steady state of this equation with these boundary conditions is $D\left(x\right)u^{\ast }\left(x\right)=$ const. Now, we split the interval into the right half (patch 1) and the left half (patch 2). We choose a smooth, monotone function $D_{ϵ}\left(x\right)$ with $D(x{)}_{ϵ}=D_1$ on $(ϵ,1]$ and $D(x{)}_{ϵ}=D_2$ on $[-1,-ϵ)$ for some $0<ϵ<1.$ In the limit as $ϵ\to 0,$ the function $D_{ϵ}$ approaches a step function. From the steady-state expression, we find that the limit satisfies (7) $u^{\ast }\left(0^{+}\right)=\frac{D_2}{D_1}{u}^{\ast }\left(0^{-}\right).$(7) This expression is precisely the interface condition (6(6) $k=\frac{D_2}{D_1}\frac{\alpha }{(1-\alpha )},$(6) ) for $\alpha =\mathrm{0.5.}$

3. Scaling and homogenization

There are no analytical procedures to find an exact expression for the spreading speed in a model with Allee effect and heterogeneity. Vergni et al. [30] used numerical simulations in their work. We apply a homogenization procedure to gain a better understanding on the effects of habitat heterogeneity on the speed of spread. Previous work in this direction indicates that the results obtained from spatial averaging give a very good approximation to the exact value not only when the scale of dispersal is very large but even when the scale of landscape heterogeneity is on the same order as the scale of dispersal [5, 15].

Following the classic homogenization approach, the growth function in the spatially averaged reaction–diffusion equation is the arithmetic mean of the growth function in the heterogeneous landscape and the diffusion coefficient is the harmonic mean of the diffusivity [18, 23]. However, the classical approach assumes that the density and flux are continuous across an interface, whereas densities in our model are not continuous when $k\ne 1$ in Equation (5(5) $\begin{array}{rl}{u}_1(x_n^{+},t)& =k{u}_2(x_n^{-},t),\end{array}$(5) ). It turns out that we can scale densities and space in such a way that the flux and density are continuous.

Without loss of generality, we may assume that $x=0$ is an interface with a patch of type 1 located to the right and a patch of type 2 to the left. We make the change of variables (8) $\begin{array}{rl}{u}_1(t,x)& =w_1(t,\xi ),\xi =x\in [0,l_1],\end{array}$(8) (9) $\begin{array}{rl}k{u}_2(t,x)& =w_2(t,\xi ),\xi =\frac{x}{k}\in \left[-\frac{l_2}{k},0\right],\end{array}$(9) where, as above, $l_i$ is the size of patch i. All other patches are scaled analogously. In this new scaling, Equation (3(3) $\frac{\mathrm{\partial }{u}_i}{\mathrm{\partial }t}=D_i\frac{{\mathrm{\partial }}^2{u}_i}{\mathrm{\partial }{x}^2}+f_i\left(u_i\right),$(3) ) assumes the form: (10) $\frac{\mathrm{\partial }{w}_i}{\mathrm{\partial }t}={\tilde{D}}_i\frac{{\mathrm{\partial }}^2{w}_i}{\mathrm{\partial }{\xi }^2}+{\tilde{f}}_i\left(w_i\right),$(10) with interface conditions: (11) $\begin{array}{rl}{\tilde{D}}_1\frac{\mathrm{\partial }{w}_1}{\mathrm{\partial }\xi }({\xi }_n^{+},t)& ={\tilde{D}}_2\frac{\mathrm{\partial }{w}_2}{\mathrm{\partial }\xi }({\xi }_n^{-},t),\end{array}$(11) (12) $\begin{array}{rl}{w}_1({\xi }_n^{+},t)& =w_2({\xi }_n^{-},t),\end{array}$(12) when a patch of type 1 is located to the right and a patch of type 2 to the left of ${\xi }_n.$ As in Equations (4(4) $\begin{array}{rl}{D}_1\frac{\mathrm{\partial }{u}_1}{\mathrm{\partial }x}(x_n^{+},t)& =D_2\frac{\mathrm{\partial }{u}_2}{\mathrm{\partial }x}(x_n^{-},t),\end{array}$(4) ) and (5(5) $\begin{array}{rl}{u}_1(x_n^{+},t)& =k{u}_2(x_n^{-},t),\end{array}$(5) ), signs must be changed at interface points where patch locations are reversed. In these expressions ${\tilde{D}}_1=D_1$ and ${\tilde{D}}_2=D_2/k^2$ and ${\tilde{f}}_1\left(w_1\right)=f_1\left(w_1\right)$, ${\tilde{f}}_2\left(w_2\right)=k{f}_2\left(w_2/k\right)$. Note that the scaling of the density in Equation (9(9) $\begin{array}{rl}k{u}_2(t,x)& =w_2(t,\xi ),\xi =\frac{x}{k}\in \left[-\frac{l_2}{k},0\right],\end{array}$(9) ) gives continuous interface conditions and the scaling of space ensures that the flux in the new density is also continuous.

For $\tilde{l}=l_1+l_2/k\ll 1,$ we write the density w with an additional small-scale variable $w(t,\xi ,\xi /\tilde{l})$ of period 1 in the last argument. Inserting the asymptotic expansion of $w(t,\xi ,y)=\sum {ϵ}^m{w}^{\left(m\right)}(t,\xi ,y)$ in $ϵ=\tilde{l}$ into Equation (10(10) $\frac{\mathrm{\partial }{w}_i}{\mathrm{\partial }t}={\tilde{D}}_i\frac{{\mathrm{\partial }}^2{w}_i}{\mathrm{\partial }{\xi }^2}+{\tilde{f}}_i\left(w_i\right),$(10) ) reveals that in the limit $ϵ\to 0$ the lowest order term $w^{\left(0\right)}$ is independent of y and satisfies the equation [18] (13) $\frac{\mathrm{\partial }}{\mathrm{\partial }t}{w}^{\left(0\right)}=⟨D{⟩}_h\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\xi }^2}{w}^{\left(0\right)}+⟨g{⟩}_a\left(w^{\left(0\right)}\right).$(13) The arithmetic mean of the growth function is (14) $⟨g{⟩}_a\left(w\right)=\left[{\int }_0^{l_1/\tilde{l}}{\tilde{f}}_1\left(w\right)\mathrm{d}y+{\int }_{-l_2/k\tilde{l}}^0{\tilde{f}}_2\left(w\right)\mathrm{d}y\right]$(14) and the harmonic mean of diffusivities takes the form: (15) $⟨D{⟩}_h={\left({\int }_0^{l_1/\tilde{l}}\frac{1}{D_1}\mathrm{d}y+{\int }_{-l_2/k\tilde{l}}^0\frac{k^2}{D_2}\mathrm{d}y\right)}^{-1}=\frac{l_1+l_2/k}{l_1/D_1+l_2/k/D_2/k^2}.$(15)

Equation (13(13) $\frac{\mathrm{\partial }}{\mathrm{\partial }t}{w}^{\left(0\right)}=⟨D{⟩}_h\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\xi }^2}{w}^{\left(0\right)}+⟨g{⟩}_a\left(w^{\left(0\right)}\right).$(13) ) is a reaction–diffusion equation of the form in Equation (1(1) $\frac{\mathrm{\partial }u}{\mathrm{\partial }t}=D\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}+f\left(u\right)$(1) ). In the subsequent two sections, we show that for our choices of $f_i,$ the averaged growth function can be written (after scaling) in the form $f\left(u\right)=u(1-u)(u-a)$ so that the expression in Equation (2(2) $c=\sqrt{2}\left(\frac{1}{2}-a\right).$(2) ) gives an explicit expression of the travelling wave speed for this averaged equation.

4. Alternating ‘favourable’ and ‘unfavourable’ patches

We first consider the case in which there is a strong Allee effect in patches of type 1 (favourable patches) and population dies at a constant rate in patches of type 2 (unfavourable patches). We write (16) $f_1\left(u_1\right)=r{u}_1\left(1-\frac{u_1}{K}\right)\left(\frac{u_1}{K}-a\right)\mathrm{and}{f}_2\left(u_2\right)=-m{u}_2.$(16) Parameters r and K stand for the maximum per capita growth rate and the carrying capacity, respectively, in favourable patches. Parameter a is known as the Allee threshold, written in units of carrying capacity in our parametrization. The death rate in unfavourable patches is m. Function $f_1$ induces a bistable behaviour in the system. In the absence of dispersal on a single favourable patch, the population declines to extinction if its initial size, as a fraction of carrying capacity, is below a and approaches K otherwise [12]. Introducing the scaling of parameters and variables $T=rt$, $X=\sqrt{r/D_1}x$, $U_i=u_i/K$, $D=D_2/D_1$, $\tilde{m}=m/r$, we find the non-dimensional equations: (17) $\begin{array}{rl}\frac{\mathrm{\partial }{U}_1}{\mathrm{\partial }T}& =\frac{{\mathrm{\partial }}^2{U}_1}{\mathrm{\partial }{X}^2}+U_1(1-U_1)(U_1-a),\text{in favourable patches, }\end{array}$(17) (18) $\begin{array}{rl}\frac{\mathrm{\partial }{U}_2}{\mathrm{\partial }T}& =D\frac{{\mathrm{\partial }}^2{U}_2}{\mathrm{\partial }{X}^2}-\tilde{m}{U}_2,\text{in unfavourable patches}.\end{array}$(18)

The interface conditions for this system are as in Equations (4(4) $\begin{array}{rl}{D}_1\frac{\mathrm{\partial }{u}_1}{\mathrm{\partial }x}(x_n^{+},t)& =D_2\frac{\mathrm{\partial }{u}_2}{\mathrm{\partial }x}(x_n^{-},t),\end{array}$(4) ) and (5(5) $\begin{array}{rl}{u}_1(x_n^{+},t)& =k{u}_2(x_n^{-},t),\end{array}$(5) ). Rescaling and homogenizing according to the procedure in the previous section, we find the averaged growth rate and diffusion constant for the lowest order term $W=w^{\left(0\right)}/K$. The terms are (19) $\begin{array}{rl}⟨g{⟩}_a\left(W\right)& =\left[{\int }_0^{L_1/\tilde{L}}W(1-W)(W-a)\mathrm{d}Y-{\int }_{-L_2/k\tilde{L}}^0\tilde{m}W\mathrm{d}Y\right]\\ & =pW(1-W)(W-a)-(1-p)\tilde{m}W,\end{array}$(19) where $\tilde{L}=L_1+L_2/k$, $L_i=\sqrt{r/D_1}{l}_i$ are the rescaled sizes of patches i, variable $Y=\sqrt{r/D_1}y$ and $p=L_1/(L_1+L_2/k)$ is the weighted fraction of favourable patches. We can factor this expression into a cubic function of the same form as $f_1$ according to (20) $⟨g{⟩}_a\left(W\right)=p{\tilde{W}}_{+}^{2}W\left(1-\frac{W}{{\tilde{W}}_{+}}\right)\left(\frac{W}{{\tilde{W}}_{+}}-\frac{{\tilde{W}}_{-}}{{\tilde{W}}_{+}}\right),$(20) with constants (21) ${\tilde{W}}_{\pm }=\left[(1+a)\pm \sqrt{{\left(1-a\right)}^2-\frac{4(1-p)\tilde{m}}{p}}\right]/2.$(21)

The non-dimensional harmonic mean of diffusivities, see Equation (15(15) $⟨D{⟩}_h={\left({\int }_0^{l_1/\tilde{l}}\frac{1}{D_1}\mathrm{d}y+{\int }_{-l_2/k\tilde{l}}^0\frac{k^2}{D_2}\mathrm{d}y\right)}^{-1}=\frac{l_1+l_2/k}{l_1/D_1+l_2/k/D_2/k^2}.$(15) ), is (22) $⟨D{⟩}_h=\frac{L_1+L_2/k}{L_1+L_2/k/D/k^2}.$(22)

We can now use the formula in Equation (2(2) $c=\sqrt{2}\left(\frac{1}{2}-a\right).$(2) ), after appropriate scaling of time and space, to derive the following expression for the speed of invasion in the homogenized model: (23) $\tilde{c}=\sqrt{2⟨D{⟩}_{h}p}{\tilde{W}}_{+}\left(\frac{1}{2}-\frac{{\tilde{W}}_{-}}{{\tilde{W}}_{+}}\right).$(23)

Recall, however, that in the homogenization process we scaled space as $S=X/k$ in patches of type 2. If $\overline{T}$ gives the time needed for the population to cross one spatial period, in these units then $\tilde{c}=(L_1+L_2/k)/\overline{T}$. Noting that (24) $\tilde{c}=\frac{L_1+L_2/k}{\overline{T}}\left(\frac{L_1+L_2}{L_1+L_2}\right)=\frac{L_1+L_2}{\overline{T}}\left(\frac{L_1+L_2/k}{L_1+L_2}\right)=c\left(\frac{L_1+L_2/k}{L_1+L_2}\right),$(24) we finally write the actual homogenization approximation for the rate of spatial spread as (25) $c=\sqrt{2⟨D{⟩}_{h}p}{\tilde{W}}_{+}\left(\frac{1}{2}-\frac{{\tilde{W}}_{-}}{{\tilde{W}}_{+}}\right)\left(\frac{L_1+L_2}{L_1+L_2/k}\right).$(25)

As mentioned in the introduction, this expression admits negative speeds when ${\tilde{W}}_{-}/{\tilde{W}}_{+}<1/2$, representing retreating waves in space. The existence of a real-valued speed c further requires the condition (26) $p(1-a{)}^2-4(1-p)\tilde{m}>0,$(26) so that ${\tilde{W}}_{\pm }$ in Equation (21(21) ${\tilde{W}}_{\pm }=\left[(1+a)\pm \sqrt{{\left(1-a\right)}^2-\frac{4(1-p)\tilde{m}}{p}}\right]/2.$(21) ) are real. If ${\tilde{W}}_{\pm }$ are not real, then the population collapses everywhere simultaneously; there is no retreating travelling wave.

We use now Equation (25(25) $c=\sqrt{2⟨D{⟩}_{h}p}{\tilde{W}}_{+}\left(\frac{1}{2}-\frac{{\tilde{W}}_{-}}{{\tilde{W}}_{+}}\right)\left(\frac{L_1+L_2}{L_1+L_2/k}\right).$(25) ) to explore how the speed of invasion depends on the parameters of this system. In addition, we numerically obtain the speed of invasion and compare with the analytical approximation. Numerical solutions were obtained by solving the system of Equations (17(17) $\begin{array}{rl}\frac{\mathrm{\partial }{U}_1}{\mathrm{\partial }T}& =\frac{{\mathrm{\partial }}^2{U}_1}{\mathrm{\partial }{X}^2}+U_1(1-U_1)(U_1-a),\text{in favourable patches, }\end{array}$(17) ) and (18(18) $\begin{array}{rl}\frac{\mathrm{\partial }{U}_2}{\mathrm{\partial }T}& =D\frac{{\mathrm{\partial }}^2{U}_2}{\mathrm{\partial }{X}^2}-\tilde{m}{U}_2,\text{in unfavourable patches}.\end{array}$(18) ) using an implicit Euler scheme [25]. For the implementation of interface conditions, we consider the interface between habitat types as grid points belonging to both patches. Thus, if the interface lies at some point h, say, of our discretized space and a patch of type 1 (type 2) is located to the right (left), we write for every time step (n) of the process: (27) $\begin{array}{rl}{D}_1\frac{(-3{v_1}_h^n+4{v_1}_{h+1}^n-{v_1}_{h+2}^n)}{2\mathrm{\Delta }x}& =D_2\frac{(3{v_2}_h^n-4{v_2}_{h-1}^n+{v_2}_{h-2}^n)}{2\mathrm{\Delta }x},\end{array}$(27) (28) $\begin{array}{rl}{v_1}_h^n& =k{v_2}_h^n,\end{array}$(28) where $v_j^i$ is the value of the density at grid points $(i,j)$. $\mathrm{\Delta }x$ is the spatial step used in calculations. Relations (27(27) $\begin{array}{rl}{D}_1\frac{(-3{v_1}_h^n+4{v_1}_{h+1}^n-{v_1}_{h+2}^n)}{2\mathrm{\Delta }x}& =D_2\frac{(3{v_2}_h^n-4{v_2}_{h-1}^n+{v_2}_{h-2}^n)}{2\mathrm{\Delta }x},\end{array}$(27) ) and (28(28) $\begin{array}{rl}{v_1}_h^n& =k{v_2}_h^n,\end{array}$(28) ) represent, respectively, interface conditions (4(4) $\begin{array}{rl}{D}_1\frac{\mathrm{\partial }{u}_1}{\mathrm{\partial }x}(x_n^{+},t)& =D_2\frac{\mathrm{\partial }{u}_2}{\mathrm{\partial }x}(x_n^{-},t),\end{array}$(4) ) and (5(5) $\begin{array}{rl}{u}_1(x_n^{+},t)& =k{u}_2(x_n^{-},t),\end{array}$(5) ).

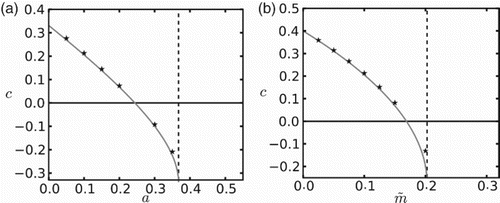
The speed of invasion is a monotonically decreasing function of the Allee threshold, as depicted in Figure 1(a). As the strength of the Allee effect is increased, c eventually becomes negative, representing the retreating population front. The local loss of individuals due to dispersal is so strong that it pushes the population density below the Allee threshold at the leading edge of the wave and this leading edge retreats. For even higher Allee thresholds, no positive steady-state exists and the whole population collapses. The speed of invasion is also a decreasing function of mortality rate ($\tilde{m}$) in ‘unfavourable’ patches (see Figure 1(b)). Again the speed is positive for low mortality rates and becomes negative for a certain range of parameter values. In both figures, the analytical expression (25(25) $c=\sqrt{2⟨D{⟩}_{h}p}{\tilde{W}}_{+}\left(\frac{1}{2}-\frac{{\tilde{W}}_{-}}{{\tilde{W}}_{+}}\right)\left(\frac{L_1+L_2}{L_1+L_2/k}\right).$(25) ) (gray lines) provides a good approximation for the rate of spatial spread when compared with numerically obtained speeds (stars). We only observe a small discrepancy for increased values of mortality rate.

Figure 1. Rates of spatial spread in a heterogeneous environment as a function of the Allee effect threshold in ‘favourable’ patches (a) and the mortality rate in ‘unfavourable’ patches (b). Vertical lines indicate threshold values for c to be real, as obtained from Equation (26(26) $p(1-a{)}^2-4(1-p)\tilde{m}>0,$(26) ). Other parameters are: $D=1$, $L_1=1$ and $L_2=1$. We consider no habitat preference, i.e. $\alpha =0.5$. Furthermore, $\tilde{m}=0.1$ in (a) and $a=0.1$ in (b).

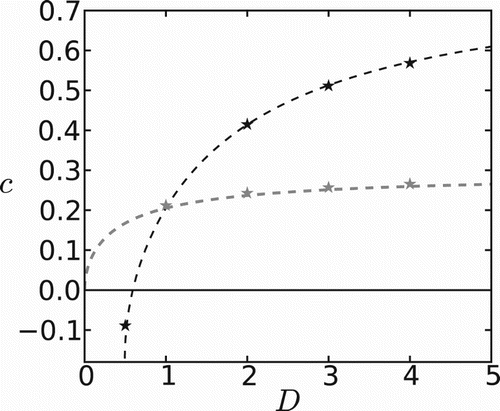
In Figure 2, we show the dependence of invasion speed on the diffusion coefficient in ‘unfavourable’ patches, D. Continuous (i.e. $k=1$ in (5(5) $\begin{array}{rl}{u}_1(x_n^{+},t)& =k{u}_2(x_n^{-},t),\end{array}$(5) ); gray lines) and discontinuous (i.e. k as in Equation (6(6) $k=\frac{D_2}{D_1}\frac{\alpha }{(1-\alpha )},$(6) ); black lines) interface conditions provide strikingly different results. As long as the movement rate is higher in ‘favourable’ patches ($D<1$) speeds are higher for continuous conditions. The order is reversed for $D>1$. For this choice of parameters negative speeds of invasion arise only for discontinuous interface conditions; continuous conditions predict positive speeds for any value of D. We find an excellent agreement between analytical (lines) and numerical (stars) results. The difference between continuous and discontinuous conditions can be explained in terms of individual behaviour at an interface. In the continuous case, individuals move into patch type 1 with higher probability when $D<1.$ Hence, they avoid unfavourable patches, and the population is more likely to persist and spread. This case is unrealistic since individuals should move faster in unfavourable regions, i.e. $D>1,$ yet at the same time choose favourable regions with higher probability. Only the discontinuous interface conditions can incorporate this behaviour, and they show a more realistic dependence of the speed on the diffusion coefficient.

Figure 2. Speed of invasion as a function of diffusion coefficient in ‘unfavourable’ patches. Gray and black lines are obtained using continuous and discontinuous interface conditions, respectively. Numerical calculation of speeds are represented by stars. Fixed parameters are: $a=0.1$, $\tilde{m}=0.1$, $L_1=1$, $L_2=1$ and $\alpha =0.5$.

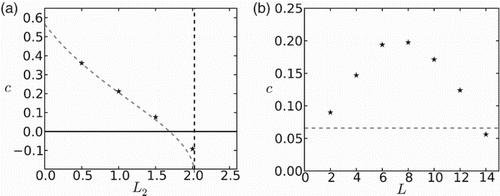
The speed of invasion is also negatively correlated with ‘unfavourable’ patch size. In Figure 3(a), we illustrate the case in which the favourable patch does not support the population when isolated and, hence, population collapses when the separation between favourable patches becomes too large. It is evident in this figure that the goodness of the approximation decreases somewhat as patch sizes increase. Yet, the behaviour of speed with the spatial period $L=L_1+L_2$ presents some subtleties (see Figure 3(b)). As expression (25(25) $c=\sqrt{2⟨D{⟩}_{h}p}{\tilde{W}}_{+}\left(\frac{1}{2}-\frac{{\tilde{W}}_{-}}{{\tilde{W}}_{+}}\right)\left(\frac{L_1+L_2}{L_1+L_2/k}\right).$(25) ) is not valid as L becomes large, the approximated and numerically calculated speeds are markedly different in this case. Although the approximation predicts no variation of the speed with spatial period when a fixed relation between $L_1$ and $L_2$ is set, numerically we obtain a hump-shaped dependence of c on L. When L is small, c is increasing with L as the positive effect of larger favourable patches outweighs the negative effect of larger unfavourable patches. When L is larger, c is decreasing with L as fewer and fewer individuals manage to cross an unfavourable patch.

Figure 3. Dependence of the speed of invasion on the patch sizes. (a) c is a monotonically decreasing function of $L_2$. (b) Numerical calculations (stars) show a non-monotonic dependence of c on the spatial period $L=L_1+L_2$, while analytical approximation for c (Equation (25(25) $c=\sqrt{2⟨D{⟩}_{h}p}{\tilde{W}}_{+}\left(\frac{1}{2}-\frac{{\tilde{W}}_{-}}{{\tilde{W}}_{+}}\right)\left(\frac{L_1+L_2}{L_1+L_2/k}\right).$(25) )) (gray line) shows no dependence on L when a fixed ratio between $L_1$ and $L_2$ is set. Parameter values are $a=0.1$, $\tilde{m}=0.1$ and $L_1=1$ in (a), and $a=0.01$, $\tilde{m}=0.2$ and $L_1=L_2$ in (b). The vertical line in (a) indicates the threshold above which c becomes complex, as obtained from Equation (26(26) $p(1-a{)}^2-4(1-p)\tilde{m}>0,$(26) ). We consider no habitat preference ($\alpha =0.5$) and equal movement rates ($D=1$).

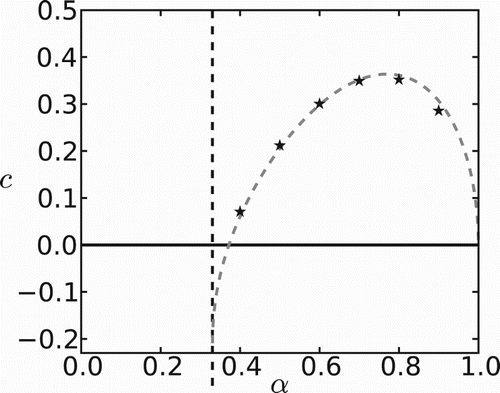
The effect of habitat preference on the invasion speed is twofold. A higher preference for ‘favourable’ patches leads to an increased production of new colonizers and potentially increases the invasion speed. A very large preference, though, prevents individuals from venturing into unfavourable regions and then spread through space. The combined effect produces a hump-shaped curve, as shown in Figure 4, the speed of invasion being maximized at intermediate bias.

Figure 4. The effect of bias towards ‘favourable’ patches on the speed of invasion. The gray dashed curve is drawn from Equation (25(25) $c=\sqrt{2⟨D{⟩}_{h}p}{\tilde{W}}_{+}\left(\frac{1}{2}-\frac{{\tilde{W}}_{-}}{{\tilde{W}}_{+}}\right)\left(\frac{L_1+L_2}{L_1+L_2/k}\right).$(25) ); stars are obtained from numerical solutions. The vertical line shows the threshold habitat preference obtained from Equation (26(26) $p(1-a{)}^2-4(1-p)\tilde{m}>0,$(26) ). Fixed parameters are: $a=0.1$, $\tilde{m}=0.1$, $D=1$ and $L_1=L_2=1$.

5. Geographical variation in the strength of the Allee effect

We consider now the situation that Tobin et al. [28] first documented empirically for Gypsy moth: The species experiences an Allee effect whose strength varies in space. Accordingly, we choose growth functions in both patch types as cubic polynomials with patch-dependent positive parameters (29) $f_i\left(u\right)=r_{i}u\left(1-\frac{u}{K_i}\right)\left(\frac{u}{K_i}-a_i\right),0<a_i<1.$(29)

In line with the distinction of favourable (type 1) and unfavourable (type 2) patches, we assume that the Allee threshold in favourable patches is lower than in unfavourable patches. Defining the rescaled quantities $X=\sqrt{r_1/D_1}$, $T=r_{1}t$, $U_i=u_i/K_1$, $D=D_2/D_1$, $K=K_2/K_1$ and $r=r_2/r_1$, population dynamics are described by the equations: (30) $\begin{array}{rl}\frac{\mathrm{\partial }{U}_1}{\mathrm{\partial }T}& =\frac{{\mathrm{\partial }}^2{U}_1}{\mathrm{\partial }{X}^2}+U_1(1-U_1)(U_1-a_1),\text{in patches of type 1, }\end{array}$(30) (31) $\begin{array}{rl}\frac{\mathrm{\partial }{U}_2}{\mathrm{\partial }T}& =D\frac{{\mathrm{\partial }}^2{U}_2}{\mathrm{\partial }{X}^2}+r{U}_2\left(1-\frac{U_2}{K}\right)\left(\frac{U_2}{K}-a_2\right),\text{in patches of type 2}.\end{array}$(31)

We proceed by homogenization as before. The growth function for the homogenized model in this case is given by (as calculated from Equation (14(14) $⟨g{⟩}_a\left(w\right)=\left[{\int }_0^{l_1/\tilde{l}}{\tilde{f}}_1\left(w\right)\mathrm{d}y+{\int }_{-l_2/k\tilde{l}}^0{\tilde{f}}_2\left(w\right)\mathrm{d}y\right]$(14) )) (32) $⟨g{⟩}_a\left(W\right)=pW(1-W)(W-a_1)+(1-p)rW\left(1-\frac{W}{kK}\right)\left(\frac{W}{kK}-a_2\right),$(32) where p is defined as in Equation (19(19) $\begin{array}{rl}⟨g{⟩}_a\left(W\right)& =\left[{\int }_0^{L_1/\tilde{L}}W(1-W)(W-a)\mathrm{d}Y-{\int }_{-L_2/k\tilde{L}}^0\tilde{m}W\mathrm{d}Y\right]\\ & =pW(1-W)(W-a)-(1-p)\tilde{m}W,\end{array}$(19) ). The harmonic mean of diffusivities is again given by Equation (22(22) $⟨D{⟩}_h=\frac{L_1+L_2/k}{L_1+L_2/k/D/k^2}.$(22) ).

Our next goal is to write the homogenized growth function in Equation (32(32) $⟨g{⟩}_a\left(W\right)=pW(1-W)(W-a_1)+(1-p)rW\left(1-\frac{W}{kK}\right)\left(\frac{W}{kK}-a_2\right),$(32) ) in the standard cubic form Equation (29(29) $f_i\left(u\right)=r_{i}u\left(1-\frac{u}{K_i}\right)\left(\frac{u}{K_i}-a_i\right),0<a_i<1.$(29) ) so that we can apply the wave speed result as before. We begin with three simple cases in which Equation (32(32) $⟨g{⟩}_a\left(W\right)=pW(1-W)(W-a_1)+(1-p)rW\left(1-\frac{W}{kK}\right)\left(\frac{W}{kK}-a_2\right),$(32) ) can be factored and leads to easily interpretable ‘effective’ Allee thresholds.

1. If patches differ only in the strength of the Allee effect, so that $p=0.5$ and r, D, K and k are equal to one, the averaged growth function factors into: (33) $⟨g{⟩}_a\left(W\right)=2W(1-W)\left(W-\frac{a_1+a_2}{2}\right).$(33)

   Consequently, we identify an ‘effective’ Allee threshold given simply by the average of thresholds in each habitat patch.

2. If there is no jump in density at the interface ($k=1$) and both patches have the same growth rate and carrying capacity ($r,K=1$), we obtain an averaged growth function in which the ‘effective’ Allee threshold is given by a weighted average of thresholds $a_1$ and $a_2$: (34) $⟨g{⟩}_a\left(W\right)=W(1-W)(W-(p{a}_1+(1-p)a_2\left)\right),$(34) where now $p=L_1/(L_1+L_2)$.

3. Finally, in the case in which patches differ in all growth parameters, except for the carrying capacity ($K=1$), and again $k=1$, function $⟨g{⟩}_a$ reduces to: (35) $⟨g{⟩}_a\left(W\right)=(p+(1-p\left)r\right)W(1-W)\left(W-\frac{p{a}_1+(1-p)r{a}_2}{p+(1-p)r}\right).$(35)

   Also in this case, the effective Allee threshold is a weighted average of the individual Allee thresholds, but now the weights include both p and r.

In the general case $k\ne 1,$ we can still factor (32(32) $⟨g{⟩}_a\left(W\right)=pW(1-W)(W-a_1)+(1-p)rW\left(1-\frac{W}{kK}\right)\left(\frac{W}{kK}-a_2\right),$(32) ), though the effective Allee threshold is not given by a simple average as in Equations (33(33) $⟨g{⟩}_a\left(W\right)=2W(1-W)\left(W-\frac{a_1+a_2}{2}\right).$(33) )–(35(35) $⟨g{⟩}_a\left(W\right)=(p+(1-p\left)r\right)W(1-W)\left(W-\frac{p{a}_1+(1-p)r{a}_2}{p+(1-p)r}\right).$(35) ). The averaged growth rate can be written in this general case as (36) $⟨g{⟩}_a\left(W\right)=\left(p+(1-p)\frac{r}{k^2{K}^2}\right){\tilde{W}}_{+}^{2}W\left(1-\frac{W}{{\tilde{W}}_{+}}\right)\left(\frac{W}{{\tilde{W}}_{+}}-\frac{{\tilde{W}}_{-}}{{\tilde{W}}_{+}}\right),$(36) where ${\tilde{W}}_{-}$ (${\tilde{W}}_{+}$) is the smaller (larger) root of the quadratic equation: (37) $W^2-\frac{p(1+a_1)+(1-p)(1+a_2)r/kK}{p+(1-p)r/k^2{K}^2}W+\frac{p{a}_1+(1-p)r{a}_2}{p+(1-p)r/k^2{K}^2}=0.$(37) Note that parameter D appears in Equation (36(36) $⟨g{⟩}_a\left(W\right)=\left(p+(1-p)\frac{r}{k^2{K}^2}\right){\tilde{W}}_{+}^{2}W\left(1-\frac{W}{{\tilde{W}}_{+}}\right)\left(\frac{W}{{\tilde{W}}_{+}}-\frac{{\tilde{W}}_{-}}{{\tilde{W}}_{+}}\right),$(36) ) only implicitly in k. Therefore, the effective Allee threshold may be modified by differences in movement rates, D, when discontinuous interface conditions are used, while it does not depend on this parameter when density is continuous across the interface. 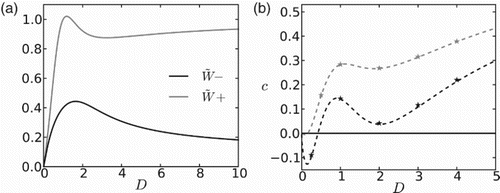We illustrate the effect of D on the homogenized carrying capacity ${\tilde{W}}_{+}$ and Allee threshold ${\tilde{W}}_{-}$ in Figure 5(a). We see that both functions are non-monotone in D. It is the ratio of these two quantities, ${\tilde{W}}_{-}/{\tilde{W}}_{+}$, that will determine the sign of the travelling wave speed.

Figure 5. (a) Homogenized carrying capacity (${\tilde{W}}_{+}$; gray line) and Allee threshold (${\tilde{W}}_{-}$; black line) as a function of movement rates (D) in unfavourable patches. In this case the population experiences a strong Allee effect in both patch types, with strengths $a_1<a_2$. $a_2=0.7$ in this figure. (b) Invasion speed as a function of D. Lines are the approximated speeds obtained from homogenization (Equation (38(38) $c=\sqrt{2⟨D{⟩}_h(p+(1-p\left)r/k^2{K}^2\right)}{\tilde{W}}_{+}\left(\frac{1}{2}-\frac{{\tilde{W}}_{-}}{{\tilde{W}}_{+}}\right)\left(\frac{L_1+L_2}{L_1+L_2/k}\right).$(38) )) and stars are obtained from numerical simulations. The gray line corresponds to $a_2=0.5$ and the black line to $a_2=0.7$. In both figures discontinuous interface conditions are used. Other parameters are: $a_1=0.1$, $r=1$, $K=1$ and $\alpha =0.5$.

As in Section 4, we can use Equation (2(2) $c=\sqrt{2}\left(\frac{1}{2}-a\right).$(2) ) to derive the following expression for the speed of invasion: (38) $c=\sqrt{2⟨D{⟩}_h(p+(1-p\left)r/k^2{K}^2\right)}{\tilde{W}}_{+}\left(\frac{1}{2}-\frac{{\tilde{W}}_{-}}{{\tilde{W}}_{+}}\right)\left(\frac{L_1+L_2}{L_1+L_2/k}\right).$(38) For the more realistic discontinuous interface conditions, with k as in Equation (6(6) $k=\frac{D_2}{D_1}\frac{\alpha }{(1-\alpha )},$(6) ), the speed of invasion presents a curious dependence on the diffusivity in unfavourable patches, D, as shown in Figure 5(b). We suggest that this non-monotonic behaviour arises from a nontrivial interaction between different mechanisms that are influenced by D. Besides acting on the speed per se, by making individuals move faster/slower, D controls the mean residence time [29] of individuals in patches of type 2 and the degree by which dispersal declines the population near the front of invasion. For small D, the residence time in a patch of type 2 is high and the Allee effect induces a high mortality in these patches. As a consequence, the population retreats in space. For small D, speed c is decreasing with D, since higher dispersal rates reduce the density near the edge of invasion and increase the mortality induced by the Allee effect. But larger values of D, in turn, also lead to a lower residence time in patches of type 2, and the Allee effect experienced in these patches is weakened. Hence, after going through a minimum, speed c then grows with D and eventually becomes positive. High movement rates, however, make the population spread more and take the density at the front of the invasion to levels much below the Allee threshold, thereby potentially decreasing the speed. Finally for even larger movement rates, residence times in unfavourable patches become so small that individuals are not much affected by the increased strength of the Allee effects induced by high dispersal rates at the front. The resulting effect is that the speed of invasion is increasing with D for very large diffusivities.

6. Discussion

Invasion of alien species is one of the major causes of biodiversity loss, potentially leading to high environmental and economic costs [21]. In this study, we integrated into a reaction–diffusion model two mechanisms, both of which are expected to be present in real invasions but whose joint consequences for spatial spread had not been explored. We investigated how habitat heterogeneity, individual movement behaviour and an Allee effect impact the speed of an invasion.

Exact expressions for the speed of spread in the presence of an Allee effect are generally not available. Instead, using homogenization techniques allowed us to employ a classical result for spread with Allee effect in homogeneous landscapes. We obtained approximate expressions for the invasion speed that include all the effects mentioned above. Previous studies of spread with Allee effect and heterogeneity did not include movement behaviour at interfaces and were based solely on numerical simulations [30] or on a caricature model for the Allee effect [5]. When we compared our approximate expressions with numerical calculations, the approximation proved to be very accurate even beyond the expected small-scale limits of homogenization, namely also if the spatial period was comparable to the movement scale.

In several aspects, our results resemble those obtained for the invasion in heterogeneous environments in the absence of Allee effects [16, 17, 23, 30]. For example, the speed is decreasing with unfavourable patch size and mortality rates, and it is increasing with diffusivity in these regions if they are sinks. One major difference in the presence of an Allee effect is that a population may retreat, that is,  its ‘invasion’ speed can be negative. For model (1(1) $\frac{\mathrm{\partial }u}{\mathrm{\partial }t}=D\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}+f\left(u\right)$(1) ) in a homogeneous landscape, the sign of the speed can be determined by the sign of the integral ${\int }_0^{K}f\left(u\right)\mathrm{d}u$, where K is the carrying capacity [31]. For the cubic nonlinearity, negative speeds arise when $a>1/2$ in Equation (2(2) $c=\sqrt{2}\left(\frac{1}{2}-a\right).$(2) ). The homogenization procedure then permits us to obtain the sign of the speed in a heterogeneous environment from substituting $⟨g{⟩}_a$ for f. In both scenarios, the sign of the speed is the same as the sign of ${\tilde{W}}_{+}-2{\tilde{W}}_{-}$ (recall that ${\tilde{W}}_{\pm }$ are different in each scenario), see Equations (25(25) $c=\sqrt{2⟨D{⟩}_{h}p}{\tilde{W}}_{+}\left(\frac{1}{2}-\frac{{\tilde{W}}_{-}}{{\tilde{W}}_{+}}\right)\left(\frac{L_1+L_2}{L_1+L_2/k}\right).$(25) ) and (38(38) $c=\sqrt{2⟨D{⟩}_h(p+(1-p\left)r/k^2{K}^2\right)}{\tilde{W}}_{+}\left(\frac{1}{2}-\frac{{\tilde{W}}_{-}}{{\tilde{W}}_{+}}\right)\left(\frac{L_1+L_2}{L_1+L_2/k}\right).$(38) ).

Individual movement behaviour and patch preference enter the equations through different diffusion coefficients ($D_1,D_2$) and through the preference parameter (α). The inclusion of both mechanisms is crucial for correct prediction of the spreading speed. For example, whether the rescaled diffusivity ($D=D_2/D_1$) has an effect on the ‘effective’ Allee threshold or not depends on the interface condition being used. Namely, only for $k\ne 1$ does a difference in diffusivity enter the homogenized expressions. As a consequence, when ‘unfavourable’ patches are sinks we observe negative values of the speed for low diffusivities in these patches when discontinuous conditions are used while the continuous conditions only predict advancing waves for the chosen parameter values (see Figure 2). Clearly, when individuals move extremely slowly in unfavourable patches, they are very likely to die, and therefore the population should not be able to spread. Based on these observations, we argue that the discontinuous interface conditions provide a much more realistic qualitative result than the commonly used continuous interface conditions. For a more detailed ecological discussion of interface conditions in terms of foraging behaviour, we refer to [16].

The nontrivial response of the speed shown in Figure 5(b), when the population suffers from a strong Allee effect in both patch types, emerges only when $k\ne 1$. The somewhat counterintuitive result that at intermediate diffusivities c may be decreasing with D, reveals the potential of dispersal in strengthening an already existing Allee effect by decreasing population levels at the leading edge. At large D, however, the effect of decreasing residence time in ‘unfavourable’ patches dominates, and thereby c increases with D. This intricate behaviour originates from the nonlinear nature of growth in patches of type 2 and therefore is not developed when these patches are sinks, as in the first part of this paper and in [30].

When habitat preference α is a free parameter, the invasion speed is maximized at intermediate levels of bias (see Figure 4). This result had been observed earlier in the absence of an Allee effect [16]. Here, in addition, we observe negative speeds or even population collapse when individuals have a strong preference for unfavourable patches.

When the spatial period gets large so that the homogenization approach fails to predict the speed correctly, different scenarios may arise. When only $L_2$ increases and $L_1$ is too small for a population to be sustained on a favourable patch alone, then the population will simply collapse. When $L=L_1+L_2$ increases with a fixed ratio of $L_1/L_2$, then eventually the unfavourable patches will be too large for individuals to cross in sufficient numbers to overcome the Allee effect in the next favourable patch. But as $L_1$ increases, a single patch will eventually support a population, if the initial conditions are suitable. This phenomenon was termed ‘invasion pinning’ and has been obtained by Keitt et al. [11] in a spatially discrete Allee effect model. Vergni et al. [30] observed a similar ‘localization’ effect numerically in a reaction–diffusion model with Allee growth function.

In a similar context, Fagan et al. [6] used a reaction–diffusion model of favourable and unfavourable patches of varying size to study the expected geographic range of a species. They assumed a strong Allee effect in favourable patches and linear decay in unfavourable patches. They calculated the expected range limit as the expected location of the first unfavourable patch that is too large for the population to cross in sufficient numbers. They used continuous interface conditions. However, due to linearity, their results are unaffected when using the discontinuous interface conditions presented here.

Tobin et al. [28] empirically verified that gypsy moth invasion in the USA is subject to spatial variation in the strength of the Allee effect. They used regional estimates to calculate regional spread rates and found that regions with stronger Allee effects were correlated with lower rates of spatial spread. Our theoretical results are complementary to theirs in that they give a basis to estimate spread rates of invasions with Allee effects varying on a spatial scale comparable to the dispersal scale. Estimating actual parameter values for reaction–diffusion equations is a difficult task, and unfortunately, the Allee threshold parameter is particularly hard to get at. Estimates for all parameters can vary significantly between approaches and regions [9]. Our results give mechanistic explanations of, in some cases, surprising qualitative results. They also suggest spatial scales at which parameter values need to be estimated. The challenge now is to devise experiments from which we can obtain reliable parameter values.

Acknowledgements

We thank Jeff Musgrave for insightful discussions about several phenomena of spatial spread, landscape heterogeneity and Allee effects.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

GAM was supported by a Ph.D. fellowship grant from São Paulo Research Foundation (FAPESP). FL is partially supported by a Discovery grant from the National Science and Engineering Research Council of Canada.

Appendix. Derivation of interface conditions

In this appendix, we provide an heuristic derivation of interface condition (5(5) $\begin{array}{rl}{u}_1(x_n^{+},t)& =k{u}_2(x_n^{-},t),\end{array}$(5) ), with k given by Equation (6(6) $k=\frac{D_2}{D_1}\frac{\alpha }{(1-\alpha )},$(6) ). We use a similar approach to the one by Ovaskainen and Cornell [19]. It is an alternative to the derivation based on modelling of random walks, also presented by these authors.

We consider individuals who move randomly through one-dimensional space and, in general, movement bias may be present. If both movement rate and bias vary in space, we model the population density by the diffusion–advection equation [29]: (A1) $\frac{\mathrm{\partial }u}{\mathrm{\partial }t}(x,t)=\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}\left[D\right(x\left)u\right(x,t\left)\right]-\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left[c\right(x\left)u\right(x,t\left)\right],$(A1) where $D\left(x\right)$ and $c\left(x\right)$ are the diffusion and advection coefficients, respectively. At the steady state $u^{\ast }\left(x\right)$, we set the left-hand side to zero. Integrating the resulting equation over space gives (A2) $\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left[D\right(x\left)u^{\ast }\right(x\left)\right]-\left[c\right(x\left)u^{\ast }\right(x\left)\right]=\mathrm{const}.$(A2)

Multiplying Equation (A2) by the integrating factor $I\left(x\right)=\exp (-{\int }_0^{x}c\left(x^{\prime }\right)/D\left(x^{\prime }\right)\mathrm{d}{x}^{\prime })$ and integrating over an interval $[-ϵ,ϵ]$ leads to: (A3) ${\int }_{-ϵ}^{ϵ}\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left[D\left(x\right)u^{\ast }\left(x\right)\exp \left(-{\int }_0^x\frac{c\left(x^{\prime }\right)}{D\left(x^{\prime }\right)}\mathrm{d}{x}^{\prime }\right)\right]\mathrm{d}x=\mathrm{const}{\int }_{-ϵ}^{ϵ}\exp \left(-{\int }_0^x\frac{c\left(x^{\prime }\right)}{D\left(x^{\prime }\right)}\mathrm{d}{x}^{\prime }\right)\mathrm{d}x$(A3) and hence, (A4) $D\left(ϵ\right)u^{\ast }\left(ϵ\right)\exp \left(-{\int }_0^{ϵ}\frac{c\left(x^{\prime }\right)}{D\left(x^{\prime }\right)}\mathrm{d}{x}^{\prime }\right)-D(-ϵ)u^{\ast }(-ϵ)\exp \left(-{\int }_0^{-ϵ}\frac{c\left(x^{\prime }\right)}{D\left(x^{\prime }\right)}\mathrm{d}{x}^{\prime }\right)=O\left(ϵ\right).$(A4) Rearranging, (A5) $\frac{D\left(ϵ\right)u^{\ast }\left(ϵ\right)}{D(-ϵ)u^{\ast }(-ϵ)}\exp \left(-{\int }_{-ϵ}^{ϵ}\frac{c\left(x^{\prime }\right)}{D\left(x^{\prime }\right)}\mathrm{d}{x}^{\prime }\right)=1+O\left(ϵ\right).$(A5)

Now, we take $x=0$ as the interface between two patch types. We model $D\left(x\right)=D_1$ for $x>ϵ$ and $D\left(x\right)=D_2$ for $x<-ϵ$. In the interval $[-ϵ,ϵ]$, we can always make D a smooth (monotone) function, so that in the limit of $ϵ\to 0$ it approaches a step function. The advection term is chosen to act only in the vicinity of the interface in a way that $c\left(x\right)=0$ for $|x|>ϵ$. By writing the probability of an individual moving right at the interface $R=\alpha$ and the probability of moving left $L=(1-\alpha )$, we have (A6) $c\left(0\right)=\underset{\delta ,\tau \to 0}{lim}\frac{\delta (R-L)}{\tau }=\underset{\delta ,\tau \to 0}{lim}\frac{\delta (2\alpha -1)}{\tau },$(A6) where δ and τ are the characteristic spatial and time steps, respectively. Similarly, we write $D\left(0\right)=\underset{\delta ,\tau \to 0}{lim}{\delta }^2(R+L)/2\tau =\underset{\delta ,\tau \to 0}{lim}{\delta }^2/2\tau$. Taking $ϵ=\delta /2$, in the limit $\delta \to 0$ Equation (A5) reads: (A7) $\frac{D\left(0^{+}\right)u^{\ast }\left(0^{+}\right)}{D\left(0^{-}\right)u^{\ast }\left(0^{-}\right)}\exp [-2(2\alpha -1\left)\right]=1.$(A7)

Noting that $\ln \left(\frac{\alpha }{1-\alpha }\right)=\ln \left(\frac{1+(2\alpha -1)}{1-(2\alpha -1)}\right)$ and using the relation: $\ln \left(\frac{1+y}{1-y}\right)=2\left(y-\frac{y^3}{3}+\frac{y^5}{5}+\cdots \right),$ we approximate $2(2\alpha -1)$ in Equation (A7) by $\ln \left(\alpha /(1-\alpha )\right)$. Finally, we find after rearranging terms (A8) $u^{\ast }\left(0^{+}\right)=\frac{D_2}{D_1}\frac{\alpha }{(1-\alpha )}{u}^{\ast }\left(0^{-}\right),$(A8) which is the relation we wanted to demonstrate.