Bootstrapping least-squares estimates in biochemical reaction networks

Abstract

The paper proposes new computational methods of computing confidence bounds for the least-squares estimates (LSEs) of rate constants in mass action biochemical reaction network and stochastic epidemic models. Such LSEs are obtained by fitting the set of deterministic ordinary differential equations (ODEs), corresponding to the large-volume limit of a reaction network, to network's partially observed trajectory treated as a continuous-time, pure jump Markov process. In the large-volume limit the LSEs are asymptotically Gaussian, but their limiting covariance structure is complicated since it is described by a set of nonlinear ODEs which are often ill-conditioned and numerically unstable. The current paper considers two bootstrap Monte-Carlo procedures, based on the diffusion and linear noise approximations for pure jump processes, which allow one to avoid solving the limiting covariance ODEs. The results are illustrated with both in-silico and real data examples from the LINE 1 gene retrotranscription model and compared with those obtained using other methods.

Keywords:

• reaction network
• density-dependent Markov jump process
• diffusion approximation
• network reverse engineering
• least-squares estimation
• bootstrap monte-carlomethod

AMS Classification:

• 62F
• 60J28
• 92C40
• 92C45

1. Introduction

The rapid advances in modern molecular quantification technology, such as fluorescence microscopy, cellular flow cytometry and high-throughput RNA-seq (see, e.g. [15,26,27]), provide us with an unprecedented opportunity to discover the basic operating principles of molecular systems biology. However, progress seems to largely depend on our ability to bring to bear proper statistical methods capable of separating the biological signal of interest from the vast amount of experimental noise. In order to be effective, such methods must be tailored to the specific experimental tools and data collection mechanisms which, despite continuing improvements, still often provide incomplete and highly noisy information.

In this paper, we are concerned with statistical methods for biochemical reaction rates estimation from the data consisting of one or more time course trajectories of (partial) network species concentrations measured on a pre-defined time grid via, for example, RT-PCR or flow cytometry assays [4,21]. Although this particular problem has been discussed extensively in the computational biology and statistical literature ([9,12] and references therein), its asymptotic analysis was often dismissed due to a small number of longitudinal data points available from typical laboratory experiments. However, as pointed out recently in [11] in many practical situations, it is reasonable to assume that the size of biological system (e.g. cell culture) under consideration is sufficiently large to allow for its large-volume approximation, the technique which is often used in modern population dynamics models, like, for example, epidemic spread studies [1]. The volume limit idea should be particularly appealing to molecular biology experimentalists as it circumvents the problem of small longitudinal sample sizes due to instrumental limitations and cost considerations. The same approach is also applicable (although this is not the focus of current paper) to stochastic epidemic models [1].

Using the large-volume argument Rempala [16] has shown that the popular method of parameter estimation based on the least-squares criterion yields consistent and asymptotically efficient results when fitting the deterministic system of ordinary differential equations (ODEs) to the stochastic data arriving from large collections of molecules (e.g. in the RT-PCR experiments) under the law of mass action kinetics. However, as also pointed out in [16], the practical obstacle to large-volume approximation for the least-square estimates (LSEs) is in the fact that their joined asymptotic covariance structure is given very non-explicitly by a solution to a set of nonlinear differential equations. Consequently, due to often numerically ill-posed inverse problems, it is quite difficult to obtain the asymptotic confidence bounds for the LSEs, even in relatively simple models.

In the current paper, we aim at improving the practical applicability of the results discussed in [16]. First, we consider a slightly more general version of the LSE, the so-called penalized LSE or PLSE. Whereas in many modern statistical analysis problems the penalized methods are used to improve identifiability and decrease variability in the model predictions, in our case the biggest potential gain in their usage is the stabilization of the variance matrix (for the fixed volume) in a way analogous to the ridge model in classical regression analysis [10]. Furthermore, based on the consistency of PLSEs, we derive and illustrate with examples two large-volume parametric bootstrap (Monte-Carlo) procedures which allow for consistent estimation of the covariance structure, possibly under limited and only partially observable trajectory data. In order to improve efficiency in re-computing model trajectories, we propose the usage of diffusion and closely related linear noise approximations (LNAs) [12] with the bootstrap algorithm. We show that the consistency of our procedures follows from the classical large-volume limit theorem for the density-dependent jump process (see, e.g. [7, Chapter 10]). Finally, in order to apply our methods to practical experimental data, we also propose a procedure based on the profile likelihood bootstrap algorithm which allows for a more realistic selection of the effective volume size of the modelled system. In essence, we treat the volume size as an estimable parameter of the model and fit it via the maximal likelihood method.

Beyond this introductory section, the paper is organized as follows. In Section 2, we introduce the concept of a stochastic biochemical network under mass action dynamics, along with the necessary notation. In Section 3, we discuss the least-squares estimation problem for mass action biochemical networks and prove basic consistency and normality results for penalized least-squares estimates (PLSEs). These PLSE results are analogous to those in [16] but form the foundation for our latter analysis and are provided for completeness. As they are consequences of a general law of large numbers and a central limit theorem (CLT) for density-dependent stochastic processes, we provide brief review of the relevant facts about such processes in Appendix 1. In Section 4, our main results on the bootstrap algorithms for estimating LSE distribution are discussed, along with the formulation of the required large-volume consistency and diffusion approximation results. The proofs are deferred to Appendix 2. Finally, in Section 5, we illustrate some of the concepts discussed earlier with the analysis of the LINE 1 retrotransposition model for both synthetic and real data, comparing the latter analysis to the one presented in [16] relying on simple asymptotic LSE bounds. Our conclusions and a brief summary are given in Section 6.

2. Jump processes and mass action kinetics

A reaction system or reaction network is typically defined as a set of d constituent chemical species reacting according to a finite set of equations, each describing the system state change after the occurrence of a particular reaction. For instance, the chemical reaction $A+B\stackrel{\lambda }{⟶}C,$ is interpreted as ‘a molecule of species A combines with a molecule of species B to create a molecule of species C at rate λ’. In this paper, the reaction system is treated as a continuous-time Markov chain, with its state described by a d-dimensional vector $X\left(t\right)$ keeping track of each species molecular counts at time t. The kth reaction is determined by the reaction rate function ${\lambda }_k\left(x\right)$ along with two vectors, ${\nu }_k$ and ${\nu }_k^{\mathrm{\prime }}$ which give, respectively, the number of molecules of each species consumed and produced in the reaction, Both ${\nu }_k$ and ${\nu }_k^{\mathrm{\prime }}$ are the elements of ${\mathbb{Z}}_{\ge 0}^d$ and the corresponding reaction rate is a non-negative scalar. Under the assumptions that the system is well-stirred and thermally equilibrated, the reaction rates take on the classical mass action form and the waiting times between reactions are exponentially distributed (see, e.g. [8]). Intuitively, the mass action form of a kth reaction rate function represents the number of different ways we can choose molecular substrates needed for the reaction k to occur [7, Chapter 10]. Defining $|{\nu }_k|=\sum _i{\nu }_{ik}$, the kth reaction rate function has the form ${\lambda }_k^{\left(n\right)}\left(x\right)=n{\kappa }_k\frac{\prod _i{\nu }_{ik}!\left(\genfrac{}{}{0em}{}{x_i}{{\nu }_{ik}}\right)}{n^{|{\nu }_k|}}.$ Here, the parameter n denotes the effective volume of the system. Whereas in many classical chemistry applications n is simply the physical volume of a container (e.g. cell) multiplied by Avagadro's number, in biological systems, where often the physical units of the parameters are not readily available,¹ it is convenient to consider n simply as a scaling parameter proportionate to the overall system volume [2,3].

The exponential waiting time distribution, along with the probability of a particular reaction [8] justifies the system time-evolution equation (1) $X\left(t\right)=X\left(0\right)+\sum _k{Y}_k\left({\int }_0^t{\lambda }_k^{\left(n\right)}\left(X\right(s\left)\right)\mathrm{d}s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k).$(1) Denoting by $c=n^{-1}x$ the species concentration per unit volume and observing the behaviour of the mass action rate functions in the large-volume limit ($n\to \mathrm{\infty }$) one obtains the approximation (2) ${\lambda }_k^{\left(n\right)}\left(x\right)\approx n{\kappa }_k\prod c_i^{{\nu }_{ik}}=:n{\lambda }_k\left(c\right).$(2) When ${\lambda }_k^{\left(n\right)}\left(x\right)$ is replaced with $n{\lambda }_k\left(x/n\right)$ in Equation (1(1) $X\left(t\right)=X\left(0\right)+\sum _k{Y}_k\left({\int }_0^t{\lambda }_k^{\left(n\right)}\left(X\right(s\left)\right)\mathrm{d}s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k).$(1) ), the process $X\left(t\right)$ becomes a member of a general family of the so-called density-dependent Markov jump processes (DDMJP) described in the appendix. As shown in the appendix (cf. Theorem A.1) the approximation (2(2) ${\lambda }_k^{\left(n\right)}\left(x\right)\approx n{\kappa }_k\prod c_i^{{\nu }_{ik}}=:n{\lambda }_k\left(c\right).$(2) ) ties together the stochastic jump process with its large-volume limit which turns out to be given by the solution of an integral version of the classical law of mass action ODE (the so-called reaction rate equation, cf., e.g. [24]), (3) $\dot{c}\left(t\right)=\sum _k{\kappa }_k\prod c_i^{{\nu }_{ik}}\left(t\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k).$(3) The above ODE is parametrized by a vector of parameters, say β, involving the rate constants ${\kappa }_k$ as well as possibly the initial conditions $c\left(0\right)$. In what follows, we write $c^{\beta }\left(t\right)$ for any such solution to either Equation (3(3) $\dot{c}\left(t\right)=\sum _k{\kappa }_k\prod c_i^{{\nu }_{ik}}\left(t\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k).$(3) ) or to its integral version (see also Appendix 1).

3. Penalized least squares

Let the counts of d species observed at discrete time points, $t_i$, ($i=1,\dots ,T<\mathrm{\infty })$ be denoted by $X_i^{(n,\beta )}\in {\mathbb{Z}}_{\ge 0}^d$ where for now we assume that this observed data arrived from a single trajectory of DDMJP for which the effective system volume n was known. The extension to multiple trajectories is straightforward, but not considered here except for a very simple case of independent observations (see Corollary 3.5 of Theorem 3.3). The case when n is unknown is discussed in Section 5. Following Rempala [16], we denote the scaled molecular counts $C_n\left(t_i\right)=C_n^{\beta }\left(t_i\right)=X^{(n,\beta )}\left(t_i\right)/n$ and assume that ${\beta }^0\in \mathrm{\Theta }\subset {\mathbb{R}}^p$ is the true parameter value we intend to estimate. Throughout the paper, the PLSE is defined as any solution (not necessarily unique) to the optimization problem (4) ${\hat{\beta }}_n={\mathrm{argmin}}_{\beta \in \mathrm{\Theta }}\sum _i|C_n\left(t_i\right)-c^{\beta }\left(t_i\right){|}^2+2{\gamma }_{n}h\left(\beta \right),$(4) where ${\gamma }_n\ge 0$, h is a penalty function and Θ is an open set in ${\mathbb{R}}^p$ containing ${\beta }^0$. Common forms of $h\left(x\right)$ include $|x{|}_2^2=\sum _i{x}_i^2$ for the ridge regression, $|x{|}_1=\sum _i|x_i|$ for the lasso [23], and $|x{|}_2^2+|x{|}_1$ for the elastic net [29]. Note that in our setting we will typically have $\beta \ge 0$ component-wise, in which case the lasso penalty becomes (right) differentiable as it reduces to $h\left(\beta \right)=\sum _i{\beta }_i$

For any matrix A, define $\parallel A\parallel =\sqrt{TrA{A}^{\mathrm{\top }}}$. The following two results extending those in [16] will be useful in the following sections. The first one establishes the strong law of large numbers (SLLN) and the consistency of ${\hat{\beta }}_n$ as $n\to \mathrm{\infty }$.

Theorem 3.1

SLLN

Let ${\mathrm{\partial }}_k{c}^{\beta }$ denote the derivative of $c^{\beta }\in {\mathbb{R}}_{\ge 0}^d$ with respect to the kth coordinate of $\beta \in {\mathbb{R}}^p$ and set $\mathrm{\partial }{c}^{\beta }=\left[{\mathrm{\partial }}_k{c}_j^{\beta }\right]\in {\mathbb{R}}^{p\times d}$. Assume that $\parallel \mathrm{\partial }{c}^{\beta }\parallel <\mathrm{\infty }$ and that the SLLN for DDMJP holds $($cf. Theorem A.1 in the appendix$),$ the subderivatives of the penalty function h are bounded and ${\gamma }_n\to 0$ as $n\to \mathrm{\infty }$. If (5) $\mathrm{\forall }{\beta }_1,{\beta }_2\in \mathrm{\Theta }{c}^{{\beta }_1}\left(t_i\right)=c^{{\beta }_2}\left(t_i\right)\mathrm{for}i=1,\dots ,T\mathrm{implies}{\beta }_1={\beta }_2$(5) and for some $\epsilon >0$ (6) ${\mathrm{\exists }}_k\sum _i{\mathrm{\partial }}_k{c}^{\beta }\left(t_i\right)\left(c^{\beta }\right(t_i)-c^{{\beta }^0}(t_i\left)\right)\ne 0\mathrm{for}\beta \ne {\beta }^0,|\beta -{\beta }^0|<\epsilon$(6) then the penalized LSE ${\hat{\beta }}_n$ given by Equation (4(4) ${\hat{\beta }}_n={\mathrm{argmin}}_{\beta \in \mathrm{\Theta }}\sum _i|C_n\left(t_i\right)-c^{\beta }\left(t_i\right){|}^2+2{\gamma }_{n}h\left(\beta \right),$(4) ) are strongly consistent, that is, ${\hat{\beta }}_n\to {\beta }^0\mathrm{as}n\to \mathrm{\infty }\mathrm{a}.\mathrm{s}.$

Proof.

Let $\theta \in {\mathbb{R}}^p$ denote the vector of subderivatives (the sub-gradient) of $h\left(\beta \right)$. By the so-called KKT necessary optimality conditions (see, e.g. [20], Chapter 3), any solution ${\hat{\beta }}_n$ of the optimization problem (4(4) ${\hat{\beta }}_n={\mathrm{argmin}}_{\beta \in \mathrm{\Theta }}\sum _i|C_n\left(t_i\right)-c^{\beta }\left(t_i\right){|}^2+2{\gamma }_{n}h\left(\beta \right),$(4) ) has to satisfy $-\mathrm{\partial }\sum _i\left(C_n\right(t_i)-c^{{\hat{\beta }}_n}(t_i\left){)}^{\mathrm{\top }}\right(C_n\left(t_i\right)-c^{\hat{\beta }}\left(t_i\right))=2{\gamma }_n\theta$ with $C_n\left(t_i\right)$ and $c^{\hat{\beta }}\left(t_i\right)\in {\mathbb{R}}^d$ denoting, respectively, the observations from d chemical species concentrations measured at $t_i$ and the corresponding deterministic solution of Equation (3(3) $\dot{c}\left(t\right)=\sum _k{\kappa }_k\prod c_i^{{\nu }_{ik}}\left(t\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k).$(3) ) evaluated at $t_i$ and $\hat{\beta }$. This yields $\sum _i\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\left(C_n\right(t_i)-c^{\hat{\beta }}(t_i\left)\right)={\gamma }_n\theta$. Adding and subtracting the deterministic limit gives $\sum _i\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\left(C_n\right(t_i)-c^{{\beta }^0}(t_i)+c^{{\beta }^0}(t_i)-c^{\hat{\beta }}(t_i\left)\right)={\gamma }_n\theta$ or (7) $\sum _i\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\left(c^{\hat{\beta }}\right(t_i)-c^{{\beta }^0}(t_i\left)\right)+{\gamma }_n\theta =\sum _i\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\left(C_n\right(t_i)-c^{{\beta }^0}(t_i\left)\right).$(7) Under the SLLN for DDMJP cited in the appendix (cf. Theorem A.1), the condition ${\gamma }_n\to 0$ and the boundedness of $\mathrm{\partial }{c}^{\beta }\left(t_i\right)$ imply the RHS above converges a.s. to 0 and hence so does the LHS. Consequently, $\underset{n\to \mathrm{\infty }}{lim}\sum _i\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\left(c^{\hat{\beta }}\right(t_i)-c^{{\beta }^0}(t_i\left)\right)=0$. Under the assumptions of the trajectories identifiability (5(5) $\mathrm{\forall }{\beta }_1,{\beta }_2\in \mathrm{\Theta }{c}^{{\beta }_1}\left(t_i\right)=c^{{\beta }_2}\left(t_i\right)\mathrm{for}i=1,\dots ,T\mathrm{implies}{\beta }_1={\beta }_2$(5) ) and non-degeneracy (6(6) ${\mathrm{\exists }}_k\sum _i{\mathrm{\partial }}_k{c}^{\beta }\left(t_i\right)\left(c^{\beta }\right(t_i)-c^{{\beta }^0}(t_i\left)\right)\ne 0\mathrm{for}\beta \ne {\beta }^0,|\beta -{\beta }^0|<\epsilon$(6) ), the asymptotic inversion gives $\underset{n\to \mathrm{\infty }}{lim}{\hat{\beta }}_n={\beta }^0$ a.s.

Remark 3.1.

Note that the conditions (5(5) $\mathrm{\forall }{\beta }_1,{\beta }_2\in \mathrm{\Theta }{c}^{{\beta }_1}\left(t_i\right)=c^{{\beta }_2}\left(t_i\right)\mathrm{for}i=1,\dots ,T\mathrm{implies}{\beta }_1={\beta }_2$(5) ) and (6(6) ${\mathrm{\exists }}_k\sum _i{\mathrm{\partial }}_k{c}^{\beta }\left(t_i\right)\left(c^{\beta }\right(t_i)-c^{{\beta }^0}(t_i\left)\right)\ne 0\mathrm{for}\beta \ne {\beta }^0,|\beta -{\beta }^0|<\epsilon$(6) ) are necessary to guarantee the LSE consistency. The selection of points $\left\{t_i\right\}$ is therefore important to ensure good statistical properties of LSEs, as also seen in our next theorem below. The required boundedness of h subderivatives is, on the other hand, a relatively mild condition and satisfied, e.g. for $h\left(x\right)=|x{|}_1$ and $h\left(x\right)=|x{|}_2$. Indeed, the latter is simply differentiable, and for the former, recall that the subderivative of $\left|x\right|$ is $-1,1$, or any number in $[-1,1]$, respectively, according to $x<0$, $x>0$ or $x=0$.

The second result of this section is the CLT for the scaled PLSEs $\sqrt{n}(\hat{\beta }-{\beta }^0)$. Similarly to the SLLN above, this one is also a consequence of the appropriate result for DDMJP.

Theorem 3.2

CLT

Suppose that the assumptions of the previous theorem hold and additionally ${\gamma }_n=o\left(n^{-1/2}\right)$ and h is twice differentiable in $\mathrm{\Theta }\in {\mathbb{R}}^p$. Furthermore, assume that the hypothesis of CLT for DDMJP holds $($cf. Theorem A.2 in the appendix$)$. Then for any $s\in {\mathbb{R}}^p$ $\underset{x}{sup}|P\left(\sqrt{n}\right(s^{\mathrm{\top }}\hat{\beta }-s^{\mathrm{\top }}{\beta }^0)\le x)-P(s^{\mathrm{\top }}{\mathcal{Z}}_n\le x)|\to 0\mathrm{as}n\to \mathrm{\infty },$ where ${\mathcal{Z}}_n\sim \mathrm{MVN}(0,{\mathrm{\Sigma }}_{\hat{\beta }})$ is a multivariate zero-centred Gaussian distribution with the covariance matrix (8) $\begin{array}{rl}{\mathrm{\Sigma }}_{\hat{\beta }}& =\mathrm{Var}\left(\sum _i(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\sqrt{n}\right(C_n\left(t_i\right)-c^{{\beta }^0}\left(t_i\right))\right)\\ & =\sum _i(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\mathrm{Var}\right(V_i\left)\right[(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i){]}^{\mathrm{\top }}\\ & +\sum _{i\ne j}\left[\right(B_{\hat{\beta }}+{\gamma }_{n}H\left(\hat{\beta }\right){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\mathrm{Cov}(V_i,V_j)\left[\right(B_{\hat{\beta }}+{\gamma }_{n}H\left(\hat{\beta }\right){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\left(t_j\right){]}^{\mathrm{\top }}\\ & +\sum _{i\ne j}(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_j\left)\mathrm{Cov}\right(V_i,V_j\left)\right[(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left){]}^{\mathrm{\top }}\right].\end{array}$(8) Here, $B_{\hat{\beta }}=\sum _i\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\left[\mathrm{\partial }{c}^{{\beta }^0}\right(t_i){]}^{\mathrm{\top }},$ H is the Hessian matrix of the penalty function h and $\mathrm{Cov}(V_i,V_j)=\mathrm{Cov}\left(V\right(t_i),V(t_j\left)\right)$ is given by Equation (23(A5) $\mathrm{Cov}\left(V\right(t),V(r\left)\right)={\int }_0^{r\wedge t}\mathrm{\Phi }(t,s)G\left(c\right(s\left)\right)\mathrm{\Phi }(r,s{)}^{\mathrm{\top }}\mathrm{d}s,$(A5) ) of Theorem A.2 in the appendix.

Proof.

In the notation of the previous proof, under the differentiability assumptions on the penalty function h, in Equation (7(7) $\sum _i\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\left(c^{\hat{\beta }}\right(t_i)-c^{{\beta }^0}(t_i\left)\right)+{\gamma }_n\theta =\sum _i\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\left(C_n\right(t_i)-c^{{\beta }^0}(t_i\left)\right).$(7) ) we may take $\theta =\mathrm{\nabla }h$, the gradient vector of the penalty. Expanding the LHS of Equation (7(7) $\sum _i\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\left(c^{\hat{\beta }}\right(t_i)-c^{{\beta }^0}(t_i\left)\right)+{\gamma }_n\theta =\sum _i\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\left(C_n\right(t_i)-c^{{\beta }^0}(t_i\left)\right).$(7) ) about ${\beta }^0$ gives $\begin{array}{rl}& \sum _i\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\left(C_n\right(t_i)-c^{{\beta }^0}(t_i\left)\right)+{\gamma }_n\mathrm{\nabla }h\left(\hat{\beta }\right)\\ & =\sum _i\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\left(c^{\hat{\beta }}\right(t_i)-c^{{\beta }^0}(t_i\left)\right)+{\gamma }_{n}H\left({\beta }^0\right)(\hat{\beta }-{\beta }^0)+{\gamma }_n\mathrm{\nabla }h\left({\beta }^0\right)+O_p(|\hat{\beta }-{\beta }^0|)(\hat{\beta }-{\beta }^0)\\ & =\sum _i\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\left[\mathrm{\partial }{c}^{{\beta }^0}\right(t_i\left){]}^{\mathrm{\top }}\right(\hat{\beta }-{\beta }^0)+{\gamma }_{n}H({\beta }^0\left)\right(\hat{\beta }-{\beta }^0)+O_p(|\hat{\beta }-{\beta }^0|\left)\right(\hat{\beta }-{\beta }^0)+{\gamma }_n\mathrm{\nabla }h({\beta }^0)\\ & =(B_{\hat{\beta }}+{\gamma }_{n}H({\beta }^0\left)\right)(\hat{\beta }-{\beta }^0)+O_p(|\hat{\beta }-{\beta }^0|)(\hat{\beta }-{\beta }^0)+{\gamma }_n\mathrm{\nabla }h\left({\beta }^0\right).\end{array}$ In view of the theorem assumptions, the higher order terms scaled by $\sqrt{n}$ tend to 0, and therefore (9) $\begin{array}{rl}\sqrt{n}(\hat{\beta }-{\beta }^0)& =(B_{\hat{\beta }}+{\gamma }_{n}H({\beta }^0\left){)}^{-1}\sum _i\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\sqrt{n}\right(C_n\left(t_i\right)-c^{{\beta }^0}\left(t_i\right))\\ & -{\gamma }_n\sqrt{n}(B_{\hat{\beta }}+{\gamma }_{n}H({\beta }^0\left){)}^{-1}\mathrm{\nabla }h\right({\beta }^0)+o_p(1)\\ & =(B_{\hat{\beta }}+{\gamma }_{n}H({\beta }^0\left){)}^{-1}\sum _i\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\sqrt{n}\right(C_n\left(t_i\right)-c^{{\beta }^0}\left(t_i\right))+o_p(1),\end{array}$(9) since the condition ${\gamma }_n=o\left(n^{-1/2}\right)$ implies that the term in the second line above converges to 0. From Theorem A.2 in the appendix, it follows that the d-vectors $\sqrt{n}\left(C_n\right(t_i)-c^{{\beta }^0}(t_i\left)\right)$ $(i=1,\dots ,T$) converge weakly to the d-variate normal variables whose covariance structure is given by $\mathrm{Cov}(V_i,V_j)$ described in Equation (A5(A5) $\mathrm{Cov}\left(V\right(t),V(r\left)\right)={\int }_0^{r\wedge t}\mathrm{\Phi }(t,s)G\left(c\right(s\left)\right)\mathrm{\Phi }(r,s{)}^{\mathrm{\top }}\mathrm{d}s,$(A5) ). Therefore, the relation (9(9) $\begin{array}{rl}\sqrt{n}(\hat{\beta }-{\beta }^0)& =(B_{\hat{\beta }}+{\gamma }_{n}H({\beta }^0\left){)}^{-1}\sum _i\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\sqrt{n}\right(C_n\left(t_i\right)-c^{{\beta }^0}\left(t_i\right))\\ & -{\gamma }_n\sqrt{n}(B_{\hat{\beta }}+{\gamma }_{n}H({\beta }^0\left){)}^{-1}\mathrm{\nabla }h\right({\beta }^0)+o_p(1)\\ & =(B_{\hat{\beta }}+{\gamma }_{n}H({\beta }^0\left){)}^{-1}\sum _i\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\sqrt{n}\right(C_n\left(t_i\right)-c^{{\beta }^0}\left(t_i\right))+o_p(1),\end{array}$(9) ), along with the continuous mapping and Slutsky's theorem arguments (see, e.g. [22], p. 133), implies that $\sqrt{n}(\hat{\beta }-{\beta }^0)\Rightarrow \mathrm{MVN}(0,{\mathrm{\Sigma }}_{{\beta }^0})$ where ⇒ denotes the usual weak convergence of random vectors. Since $\mathrm{MVN}(0,{\mathrm{\Sigma }}_{n,\hat{\beta }})\Rightarrow \mathrm{MVN}(0,{\mathrm{\Sigma }}_{{\beta }^0})$ by Slutsky's theorem, the hypothesis follows via the Cramer–Wold device (see, e.g. [22], p. 56).

Remark 3.2.

Note that the relation (9(9) $\begin{array}{rl}\sqrt{n}(\hat{\beta }-{\beta }^0)& =(B_{\hat{\beta }}+{\gamma }_{n}H({\beta }^0\left){)}^{-1}\sum _i\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\sqrt{n}\right(C_n\left(t_i\right)-c^{{\beta }^0}\left(t_i\right))\\ & -{\gamma }_n\sqrt{n}(B_{\hat{\beta }}+{\gamma }_{n}H({\beta }^0\left){)}^{-1}\mathrm{\nabla }h\right({\beta }^0)+o_p(1)\\ & =(B_{\hat{\beta }}+{\gamma }_{n}H({\beta }^0\left){)}^{-1}\sum _i\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\sqrt{n}\right(C_n\left(t_i\right)-c^{{\beta }^0}\left(t_i\right))+o_p(1),\end{array}$(9) ) indicates that for finite n the penalty term may decrease the variability of the LSE, by stabilizing the inverse of $B_{\hat{\beta }}$ matrix. Indeed, for instance for $h\left(x\right)=|x{|}_2$ this effect is similar to that observed in the ridge regression model. This is further illustrated in the numerical example in Section 5 (cf. Table 1).

Table 1. Penalized vs. ordinary LSEs for L1.

			LSE		PLSE
Coefficient	n	${\gamma }_n$	Mean	Variance	Mean	Variance
${\beta }_1=5$	10	0.18	5.84	55.54	3.95	5.51
${\beta }_2=1$			1.82	47.27	0.96	10.05
${\beta }_3=0.1$			0.10	0.0115	0.13	0.0049
${\beta }_1=5$	100	0.032	5.16	4.09	4.74	2.24
${\beta }_2=1$			1.02	4.18	0.94	3.56
${\beta }_3=0.1$			0.10	0.0013	0.11	0.0010
${\beta }_1=5$	1000	0.0056	5.04	1.18	4.95	1.01
${\beta }_2=1$			0.99	0.67	0.97	0.66
${\beta }_3=0.1$			0.10	0.0005	0.10	0.0004
${\beta }_1=5$	10,000	0.001	5.02	0.89	5.00	0.88
${\beta }_2=1$			1.00	0.25	0.99	0.25
${\beta }_3=0.1$			0.10	0.0003	0.10	0.0004

The comparison of the lasso-penalized and the ordinary LSE estimates in terms of their mean and variance illustrates the reduction in variation due to the presence of penalty term. For smaller system sizes the advantage of the penalized estimates for variance reduction are especially apparent.

In Theorems 3.1 and 3.3, we have assumed that data come from a single trajectory of the jump process. However, the results are obviously immediately extendable to the case of multiple independent trajectories. This special case of independent observations is of interest, for instance, in RT-PCR experiments with multiple cell-culture dishes and therefore deserves a special attention.

Corollary 3.1.

Assume that the trajectory data $X_i^{(n,\beta )}\in {\mathbb{Z}}_{\ge 0}^d$ $(i=1,\dots ,T<\mathrm{\infty })$ are mutually independent, then $\mathrm{Cov}(Z_i,Z_j)=0$ for $i\ne j$ and, assuming that remaining conditions in Theorem 3.3 hold true, its hypothesis also holds with ${\mathrm{\Sigma }}_{\hat{\beta }}=\sum _i(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\mathrm{Var}\right(V_i\left)\right[(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i){]}^{\mathrm{\top }}.$

As already indicated in Section 1, the complicated, non-explicit covariance structure of the collection of random variables $\sqrt{n}\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\left(C_n\right(t_i)-c^{{\beta }^0}(t_i\left)\right)$ $(i=1,\dots ,T$) limits the usefulness of the relation (9(9) $\begin{array}{rl}\sqrt{n}(\hat{\beta }-{\beta }^0)& =(B_{\hat{\beta }}+{\gamma }_{n}H({\beta }^0\left){)}^{-1}\sum _i\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\sqrt{n}\right(C_n\left(t_i\right)-c^{{\beta }^0}\left(t_i\right))\\ & -{\gamma }_n\sqrt{n}(B_{\hat{\beta }}+{\gamma }_{n}H({\beta }^0\left){)}^{-1}\mathrm{\nabla }h\right({\beta }^0)+o_p(1)\\ & =(B_{\hat{\beta }}+{\gamma }_{n}H({\beta }^0\left){)}^{-1}\sum _i\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\sqrt{n}\right(C_n\left(t_i\right)-c^{{\beta }^0}\left(t_i\right))+o_p(1),\end{array}$(9) ) in obtaining asymptotic confidence bounds for the penalized LSE. Although for some simple reaction networks the explicit analytic expression for Equation (8(8) $\begin{array}{rl}{\mathrm{\Sigma }}_{\hat{\beta }}& =\mathrm{Var}\left(\sum _i(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\sqrt{n}\right(C_n\left(t_i\right)-c^{{\beta }^0}\left(t_i\right))\right)\\ & =\sum _i(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\mathrm{Var}\right(V_i\left)\right[(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i){]}^{\mathrm{\top }}\\ & +\sum _{i\ne j}\left[\right(B_{\hat{\beta }}+{\gamma }_{n}H\left(\hat{\beta }\right){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\mathrm{Cov}(V_i,V_j)\left[\right(B_{\hat{\beta }}+{\gamma }_{n}H\left(\hat{\beta }\right){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\left(t_j\right){]}^{\mathrm{\top }}\\ & +\sum _{i\ne j}(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_j\left)\mathrm{Cov}\right(V_i,V_j\left)\right[(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left){]}^{\mathrm{\top }}\right].\end{array}$(8) ) may sometimes exist, in most cases of practical interest it may be only numerically evaluated (cf. Section 5). As such evaluations become more unstable with increasing system complexity (see, e.g. [25]), the methods of approximating the LSEs asymptotic distribution without the need to explicitly evaluate the formula (8(8) $\begin{array}{rl}{\mathrm{\Sigma }}_{\hat{\beta }}& =\mathrm{Var}\left(\sum _i(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\sqrt{n}\right(C_n\left(t_i\right)-c^{{\beta }^0}\left(t_i\right))\right)\\ & =\sum _i(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\mathrm{Var}\right(V_i\left)\right[(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i){]}^{\mathrm{\top }}\\ & +\sum _{i\ne j}\left[\right(B_{\hat{\beta }}+{\gamma }_{n}H\left(\hat{\beta }\right){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\mathrm{Cov}(V_i,V_j)\left[\right(B_{\hat{\beta }}+{\gamma }_{n}H\left(\hat{\beta }\right){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\left(t_j\right){]}^{\mathrm{\top }}\\ & +\sum _{i\ne j}(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_j\left)\mathrm{Cov}\right(V_i,V_j\left)\right[(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left){]}^{\mathrm{\top }}\right].\end{array}$(8) ) are naturally of great interest. This issue is discussed next.

4. Bootstrap algorithms

We present here two resampling algorithms for estimating the distribution of the PLSEs discussed in the previous section. As seen below, this may be done either directly, by considering the appropriate resampling distributions themselves, or indirectly, by considering the resampling estimates of the asymptotic covariance in Theorem 3.3.

4.1. Diffusion approximation

For the purpose of bootstrapping trajectories, it is useful to have an easy to simulate approximation to the concentration process $C_n\left(t\right)=X\left(t\right)/n$ where $X\left(t\right)$ is given by Equation (1(1) $X\left(t\right)=X\left(0\right)+\sum _k{Y}_k\left({\int }_0^t{\lambda }_k^{\left(n\right)}\left(X\right(s\left)\right)\mathrm{d}s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k).$(1) ) (cf. also Equation (A2(A2) $C_n\left(t\right)=C_n\left(0\right)+n^{-1}\sum _k{\hat{Y}}_k\left(n{\int }_0^t{\lambda }_k\left(C_n\right(s\left)\right)\mathrm{d}s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)+{\int }_0^{t}F\left(C_n\right(s\left)\right)\mathrm{d}s.$(A2) ) in the appendix). To this end, consider the following Itô diffusion process $D_n\left(t\right)$ (see, e.g.[2]): (10) $D_n\left(t\right)=D_n\left(0\right)+\sum _k\frac{1}{\sqrt{n}}{\int }_0^t\sqrt{{\lambda }_k\left(D_n\right(s\left)\right)}\mathrm{d}{B}_k\left(s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)+{\int }_0^{t}F\left(D_n\right(s\left)\right)\mathrm{d}s,$(10) where $B_k\left(t\right)$ are independent standard Brownian motions and (11) $F\left(x\right)=\sum _k{\lambda }_k\left(x\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)$(11) is the drift function. Note that under the law of mass action approximation (2(2) ${\lambda }_k^{\left(n\right)}\left(x\right)\approx n{\kappa }_k\prod c_i^{{\nu }_{ik}}=:n{\lambda }_k\left(c\right).$(2) ), $F\left(x\right)$ is asymptotically ($n\to \mathrm{\infty }$) equal to the RHS of the reaction rate equation  (3(3) $\dot{c}\left(t\right)=\sum _k{\kappa }_k\prod c_i^{{\nu }_{ik}}\left(t\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k).$(3) ). As shown in Lemma A.3 in the appendix, the process defined by Equation (10(10) $D_n\left(t\right)=D_n\left(0\right)+\sum _k\frac{1}{\sqrt{n}}{\int }_0^t\sqrt{{\lambda }_k\left(D_n\right(s\left)\right)}\mathrm{d}{B}_k\left(s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)+{\int }_0^{t}F\left(D_n\right(s\left)\right)\mathrm{d}s,$(10) ) approximates $C_n\left(t\right)$ in the sense that both share the same deterministic large-volume limit given by the solution $c\left(t\right)$ of the reaction rate equation (3(3) $\dot{c}\left(t\right)=\sum _k{\kappa }_k\prod c_i^{{\nu }_{ik}}\left(t\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k).$(3) ). Note that there is an obvious computational benefit in considering the process $D_n$ instead of the pure jump process $X\left(t\right)$ which requires an exact (hence expensive) simulation of the trajectory (1(1) $X\left(t\right)=X\left(0\right)+\sum _k{Y}_k\left({\int }_0^t{\lambda }_k^{\left(n\right)}\left(X\right(s\left)\right)\mathrm{d}s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k).$(1) ) [8]. For large systems, the simulation of $D_n$ is typically substantially less computationally intense and may be performed via one of the many standard numerical methods available in the literature [28, Chapter 5].

The considerations above lead to the diffusion bootstrap algorithm (Algorithm 1) for approximating either directly the distribution of the penalized LSE $\hat{\beta }$ or the covariance matrix ${\mathrm{\Sigma }}_{\hat{\beta }}$. The formal justification of Algorithm 1 is given in the following consistency result (Theorem 4.1) stating that as the system volume increases, the bootstrap samples have the asymptotically correct empirical distribution and, consequently, may be used to estimate the covariance structure of the least squares and penalized least-squares estimates with vanishing penalty. The proof is given in Appendix 2.

Theorem 4.1.

Assume $C_n\left(t\right)=X\left(t\right)/n$ is a scaled trajectory from the pure jump process (1(1) $X\left(t\right)=X\left(0\right)+\sum _k{Y}_k\left({\int }_0^t{\lambda }_k^{\left(n\right)}\left(X\right(s\left)\right)\mathrm{d}s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k).$(1) ) with $\beta ={\beta }^0$. Let $\hat{\beta }={\mathrm{argmin}}_{\beta \in \mathrm{\Theta }}\sum _i|C_n\left(t_i\right)-c^{\beta }\left(t_i\right){|}^2+{\gamma }_{n}h\left(\beta \right)$ be associated with the probability space, $(\mathrm{\Omega },\mathcal{F},P)$. Let $D_n^{\ast }\left(t\right)$ denote the diffusion process parametrized by the LSE $\beta =\hat{\beta },$ and let ${\hat{\beta }}^{\ast }={\mathrm{argmin}}_{\beta \in \mathrm{\Theta }}\sum _i|D_n^{\ast }\left(t_i\right)-c^{\beta }\left(t_i\right){|}^2+{\gamma }_{n}h\left(\beta \right)$ be the penalized least-squares estimate associated with the conditional probability space, $({\mathrm{\Omega }}^{\ast },{\mathcal{F}}^{\ast },P_n^{\ast })$ Then, under the assumptions of Theorem 3.3, $\mathrm{\forall }s\in {\mathbb{R}}^p\underset{x}{sup}|P_n^{\ast }\left(\sqrt{n}{s}^{\mathrm{\top }}\right({\hat{\beta }}^{\ast }-\hat{\beta })\le x)-P\left(\sqrt{n}{s}^{\mathrm{\top }}\right(\hat{\beta }-{\beta }^0)\le x)|\to 0\mathrm{a}.\mathrm{s}.n\to \mathrm{\infty }.$

Although in the above theorem we have assumed that the penalty function is differentiable, it should be noted that this is not necessary. Provided that the subderivatives of the penalty term are bounded, the term vanishes asymptotically and the theorem hypothesis still holds.

Remark 4.1.

From the proof of the theorem, it is evident that the hypothesis of Theorem 4.1 extends to the case of independent observations of Corollary 3.5.

4.2. Linear noise approximation

An alternative approximation of Equation (1(1) $X\left(t\right)=X\left(0\right)+\sum _k{Y}_k\left({\int }_0^t{\lambda }_k^{\left(n\right)}\left(X\right(s\left)\right)\mathrm{d}s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k).$(1) ), which is often numerically simpler than $D_n$, may be obtained by directly appealing to the limit theorem for DDMJP, that is, Theorem A.2 in the appendix. Since under the assumptions of Theorem A.2 $\sqrt{n}\left(C_n\right(t)-c^{\beta }(t\left)\right)\Rightarrow V\left(t\right)$ as $n\to \mathrm{\infty }$ where $V\left(t\right)$ is the Gaussian process satisfying the distributionally equivalent diffusion equations  (A3(A3) $V\left(t\right)=v_0+\sum _k{B}_k\left({\int }_0^t{\lambda }_k\left(c\right(s\left)\right)\mathrm{d}s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)+{\int }_0^t\mathrm{\partial }F\left(c\right(s\left)\right)V\left(s\right)\mathrm{d}s,$(A3) ) and (A4(A4) $V\left(t\right)=v_0+\sum _k{\int }_0^t\sqrt{{\lambda }_k\left(c\right(s\left)\right)}\mathrm{d}{B}_k\left(s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)+{\int }_0^t\mathrm{\partial }F\left(c\right(s\left)\right)V\left(s\right)\mathrm{d}s.$(A4) ), the natural approximation of the process $C_n\left(t\right)$ by its limit $V\left(t\right)$ is therefore (12) $L_n\left(t\right)=c^{\beta }\left(t\right)+\frac{V\left(t\right)}{\sqrt{n}}.$(12) where we write β for ${\beta }^0$ for notational convenience. The process $L_n\left(t\right)$ is commonly referred to as the LNA of $C_n\left(t\right)$ [12]. In our present context, it may be also heuristically derived as follows (for another heuristic derivation cf., e.g. [28], Chapter 8). Since $C_n\left(t\right)\approx D_n\left(t\right)$ given by Equation (10(10) $D_n\left(t\right)=D_n\left(0\right)+\sum _k\frac{1}{\sqrt{n}}{\int }_0^t\sqrt{{\lambda }_k\left(D_n\right(s\left)\right)}\mathrm{d}{B}_k\left(s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)+{\int }_0^{t}F\left(D_n\right(s\left)\right)\mathrm{d}s,$(10) ) and $C_n\to c^{\beta }$ a.s. (cf. Theorem A.1), then $C_n\left(t\right)\approx C_n\left(0\right)+\frac{1}{\sqrt{n}}\sum _k{\int }_0^t\sqrt{{\lambda }_k\left(c^{\beta }\right(s\left)\right)}\mathrm{d}{B}_k\left(s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)+{\int }_0^{t}F\left(C_n\right(t\left)\right)\mathrm{d}s.$ Substituting $L_n\left(t\right)$ defined in Equation (12(12) $L_n\left(t\right)=c^{\beta }\left(t\right)+\frac{V\left(t\right)}{\sqrt{n}}.$(12) ) for $C_n\left(t\right)$, and applying Taylor's expansion about $c^{\beta }\left(t\right)$ to the drift function $F\left(x\right)$, one obtains for large n $\begin{array}{rl}{c}^{\beta }\left(t\right)+\frac{1}{\sqrt{n}}V\left(t\right)& =C_n\left(0\right)+\frac{1}{\sqrt{n}}\sum _k{\int }_0^t\sqrt{{\lambda }_k\left(c^{\beta }\right(s\left)\right)}\mathrm{d}{B}_k\left(s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)\\ & +{\int }_0^{t}F\left(c^{\beta }\right(s)+\frac{1}{\sqrt{n}}V(s\left)\right)\mathrm{d}s\\ & \approx C_n\left(0\right)+\frac{1}{\sqrt{n}}\sum _k{\int }_0^t\sqrt{{\lambda }_k\left(c^{\beta }\right(s\left)\right)}\mathrm{d}{B}_k\left(s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)+{\int }_0^{t}F\left(c^{\beta }\right(s\left)\right)\mathrm{d}s\\ & +\frac{1}{\sqrt{n}}{\int }_0^t\mathrm{\partial }F\left(c^{\beta }\right(s\left)\right)V\left(s\right))\mathrm{d}s,\end{array}$ where $[\mathrm{\partial }F{]}_{ij}=[{\mathrm{\partial }}_j{F}_i]$. Assuming that $C_n\left(0\right)=c_0+v_0/\sqrt{n}$, where both $c_0$ and $v_0$ are non-random, and collecting terms of different order in n, the above yields (13) $c^{\beta }\left(t\right)=c_0+{\int }_0^{t}F\left(c^{\beta }\right(s\left)\right)\mathrm{d}s$(13) and (14) $V\left(t\right)=v_0+\sum _k{\int }_0^t\sqrt{{\lambda }_k\left(c^{\beta }\right(s\left)\right)}\mathrm{d}{B}_k\left(s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)+{\int }_0^t\mathrm{\partial }F\left(c^{\beta }\right(s\left)\right)V\left(s\right)\mathrm{d}s,$(14) showing that the quantities $c^{\beta }\left(t\right)$ and $V\left(t\right)$ in Equation (12(12) $L_n\left(t\right)=c^{\beta }\left(t\right)+\frac{V\left(t\right)}{\sqrt{n}}.$(12) ) are indeed (distributionally) the same as those defined in Theorem A.2.

The usage of $L_n\left(t\right)$ in place of $D_n\left(t\right)$ leads to another resampling algorithm similar to the diffusion bootstrap, but potentially exhibiting better numerical stability due to the natural decoupling of the deterministic and stochastic components of the resamples following from Equation (12(12) $L_n\left(t\right)=c^{\beta }\left(t\right)+\frac{V\left(t\right)}{\sqrt{n}}.$(12) ). For the record, we present the second resampling algorithm below as Algorithm 2.

Formally, the validity of Algorithm 2 is derived from the following analogue of Theorem 4.1. The proof is again deferred to the appendix.

Theorem 4.2.

Let $C_n\left(t\right)$ and $\hat{\beta }$ be as in Theorem 4.1. Let $L_n^{\ast }\left(t\right)$ denote the LNA process conditional on $\hat{\beta },$ and let ${\hat{\beta }}^{\ast }={\mathrm{argmin}}_{\beta \in \mathrm{\Theta }}\sum _i|L_n^{\ast }\left(t_i\right)-c^{\beta }\left(t_i\right){|}^2+{\gamma }_{n}h\left(\beta \right)$ be the penalized least-squares estimate associated with the conditional probability space, $({\mathrm{\Omega }}^{\ast },{\mathcal{F}}^{\ast },P_n^{\ast })$. Then, under the assumptions of Theorem 3.3, $\mathrm{\forall }s\in {\mathbb{R}}^p\underset{x}{sup}|P_n^{\ast }\left(\sqrt{n}{s}^{\mathrm{\top }}\right({\hat{\beta }}^{\ast }-\hat{\beta })\le x)-P\left(\sqrt{n}{s}^{\mathrm{\top }}\right(\hat{\beta }-{\beta }^0)\le x)|\to 0\mathrm{a}.\mathrm{s}.n\to \mathrm{\infty }.$

Note that Remark 4.2 following Theorem 4.1 also applies to Theorem 4.3.

4.3. Unobserved species and the EM algorithm

In most practical circumstances, some of the species in the chemical model will be unobservable due to technical or other experimental limitations, like, for instance, the inability to simultaneously record genomic and proteomic data [16]. Let us briefly outline how the inference problem may be handled in such cases. Following the set-up of Section 3, denote by $x_i^j$ the limiting ($n\to \mathrm{\infty }$) scaled concentration of chemical species j at time point $t_i$ (assumed as observed) and let ${\mathit{x}}^j=(x_1^j,\dots ,x_T^j)$ and $\mathit{x}=({\mathit{x}}^1,\dots ,{\mathit{x}}^r{)}^{\mathrm{\top }}\in {\mathbb{R}}^{rT}$. Define in a similar fashion vector $\mathit{y}\in {\mathbb{R}}^{(d-r)T}$ corresponding to the unobserved species, so the full species vector is then $[\mathit{x},\mathit{y}]=({\mathit{x}}^{\mathrm{\top }},{\mathit{y}}^{\mathrm{\top }}{)}^{\mathrm{\top }}$. Under either LNA or the diffusion approximation assumption, the joint limited likelihood of the full data is multivariate normal with its mean ${\mathit{c}}^{\beta }=[{\mathit{c}}_x^{\beta },{\mathit{c}}_y^{\beta }]\in {\mathbb{R}}^{dT}$ being the vector of the ODE solutions to Equation (3(3) $\dot{c}\left(t\right)=\sum _k{\kappa }_k\prod c_i^{{\nu }_{ik}}\left(t\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k).$(3) ) for all d species and its precision matrix ${\mathrm{\Sigma }}^{-1}\left(\beta \right)=\left[\begin{array}{cc}{\tilde{\mathrm{\Sigma }}}_{11}\left(\beta \right)& {\tilde{\mathrm{\Sigma }}}_{12}\left(\beta \right)\\ {\tilde{\mathrm{\Sigma }}}_{21}\left(\beta \right)& {\tilde{\mathrm{\Sigma }}}_{22}\left(\beta \right)\end{array}\right],$ where the partitioning patterns reflects the covariance structure between species vectors $\mathit{x}$ and $\mathit{y}$. In this notation, the expression for the limiting log-likelihood function $\ell (\mathit{x},\mathit{y},|\beta )$ of the full data satisfies $\begin{array}{rl}\ell (\mathit{x},\mathit{y}|\beta )& \propto -\log |\mathrm{\Sigma }\left(\beta \right)|-\left(\right[\mathit{x}\mathbf{,}\mathit{y}]-{\mathit{c}}^{\beta }{)}^{\mathrm{\top }}{\mathrm{\Sigma }}^{-1}(\beta \left)\right(\left[\mathit{x}\mathbf{,}\mathit{y}\right]-{\mathit{c}}^{\beta })\\ & =-\log |\mathrm{\Sigma }\left(\beta \right)|-(\mathit{x}-{\mathit{c}}_x^{\beta }{)}^{\mathrm{\top }}{\tilde{\mathrm{\Sigma }}}_{11}(\beta \left)\right(\mathit{x}-{\mathit{c}}_x^{\beta })-(\mathit{y}-{\mathit{c}}_y^{\beta }{)}^{\mathrm{\top }}{\tilde{\mathrm{\Sigma }}}_{21}\left(\beta \right)(\mathit{x}-{\mathit{c}}_x^{\beta })\\ & -(\mathit{x}-{\mathit{c}}_x^{\beta }{)}^{\mathrm{\top }}{\tilde{\mathrm{\Sigma }}}_{12}(\beta \left)\right(\mathit{y}-{\mathit{c}}_y^{\beta })-(\mathit{y}-{\mathit{c}}_y^{\beta }{)}^{\mathrm{\top }}{\tilde{\mathrm{\Sigma }}}_{22}\left(\beta \right)(\mathit{y}-{\mathit{c}}_y^{\beta }).\end{array}$ With the help of the above, the asymptotic inference on β may be performed via the usual EM algorithm [5]. In particular, it follows that the algorithm's E-step has a closed form expression (see, e.g. [14] Chapter 2) and may be maximized numerically as soon as the Gaussian covariance structure is estimated (e.g. via Algorithm 1 or 2).

5. Example: L1 system

As an example, consider a retrotranscription model of LINE1 or L1 gene introduced and studied earlier in [18]. The system equations given below describe the first stage of the retrotranscription process in which the L1 transcript ($X_1$) production is activated by aggregated amounts of transcription facilitating proteins ($X_2$) that interact with the regulatory region of the gene. The set of chemical equations in the system with effective size n is (15) $\begin{array}{rl}{X}_2& ⟹{\kappa }_1{X}_1+X_2{X}_1⟹{\kappa }_2\phi ,\\ \phi & ⟹n{\kappa }_3{X}_2{X}_2⟹{\kappa }_4\phi .\end{array}$(15) In the above system, the so-called equal dispersal condition (EDC) is often assumed, where ${\kappa }_2={\kappa }_4$. Under EDC the re-parameterized mass action ODE solution $c^{\beta }$ in Equation (13(13) $c^{\beta }\left(t\right)=c_0+{\int }_0^{t}F\left(c^{\beta }\right(s\left)\right)\mathrm{d}s$(13) ) has the closed form (16) $\begin{array}{rl}{c}_1^{\beta }\left(t\right)& ={\beta }_1{\beta }_3[1+{\beta }_5(1+t{\beta }_2\left){\mathrm{e}}^{-{\beta }_{2}t}\right],\\ c_2^{\beta }\left(t\right)& ={\beta }_3(1+{\beta }_5{\mathrm{e}}^{-{\beta }_{2}t}),\end{array}$(16) where ${\beta }_1=\frac{{\kappa }_1}{{\kappa }_2}{\beta }_2={\kappa }_2{\beta }_3=\frac{{\kappa }_3}{{\kappa }_4}{\beta }_4={\beta }_2,$ and ${\beta }_5$ gives the fold change from the initial concentrations [16]. Note that in this parametrization the regularity conditions (5(5) $\mathrm{\forall }{\beta }_1,{\beta }_2\in \mathrm{\Theta }{c}^{{\beta }_1}\left(t_i\right)=c^{{\beta }_2}\left(t_i\right)\mathrm{for}i=1,\dots ,T\mathrm{implies}{\beta }_1={\beta }_2$(5) ) and (6(6) ${\mathrm{\exists }}_k\sum _i{\mathrm{\partial }}_k{c}^{\beta }\left(t_i\right)\left(c^{\beta }\right(t_i)-c^{{\beta }^0}(t_i\left)\right)\ne 0\mathrm{for}\beta \ne {\beta }^0,|\beta -{\beta }^0|<\epsilon$(6) ) are satisfied for L1 system and that the diffusion approximation (10(10) $D_n\left(t\right)=D_n\left(0\right)+\sum _k\frac{1}{\sqrt{n}}{\int }_0^t\sqrt{{\lambda }_k\left(D_n\right(s\left)\right)}\mathrm{d}{B}_k\left(s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)+{\int }_0^{t}F\left(D_n\right(s\left)\right)\mathrm{d}s,$(10) ) specializes to (17) $\begin{array}{rl}{D_n}_1\left(t\right)& ={D_n}_1\left(0\right)+\frac{1}{\sqrt{n}}\left({\int }_0^t\sqrt{{\beta }_1{\beta }_2{D_n}_2\left(s\right)}\mathrm{d}{B}_1\left(s\right)-{\int }_0^t\sqrt{{\beta }_2{D_n}_1\left(s\right)}\mathrm{d}{B}_2\left(s\right)\right)\\ & +{\beta }_1{\beta }_2{\int }_0^t{D_n}_2\left(s\right)\mathrm{d}s-{\beta }_2{\int }_0^t{D_n}_1\left(s\right)\mathrm{d}s,\\ {D_n}_2\left(t\right)& ={D_n}_2\left(0\right)+\frac{1}{\sqrt{n}}\left(\sqrt{{\beta }_3{\beta }_4}{B}_3\left(t\right)-{\int }_0^t\sqrt{{\beta }_2{D_n}_2\left(s\right)}\mathrm{d}{B}_4\left(s\right)\right)+{\beta }_3{\beta }_{2}t-{\beta }_2{\int }_0^t{D_n}_2\left(s\right)\mathrm{d}s,\end{array}$(17) where $B_1,B_2,B_3,B_4$ are independent standard Brownian motions. The LNA for L1 may be derived analogously.

5.1. Asymptotic LSE distribution for L1

In order to illustrate the bootstrap methods from Section 4, we compare the bootstrap estimates of the LSE distributions to their true asymptotic ones in the L1 model under EDC. The mass action ODE for L1 is given by Equation (16(16) $\begin{array}{rl}{c}_1^{\beta }\left(t\right)& ={\beta }_1{\beta }_3[1+{\beta }_5(1+t{\beta }_2\left){\mathrm{e}}^{-{\beta }_{2}t}\right],\\ c_2^{\beta }\left(t\right)& ={\beta }_3(1+{\beta }_5{\mathrm{e}}^{-{\beta }_{2}t}),\end{array}$(16) ). Upon normalizing to the initial concentrations,² ${\beta }_5=1$ and the drift function and its gradient are $\begin{array}{rl}F(x_1,x_2)& =({\beta }_1{\beta }_2{x}_2-{\beta }_2{x}_1,{\beta }_2{\beta }_3-{\beta }_2{x}_2),\\ \mathrm{\partial }F(x_1,x_2)& =\left[\begin{array}{cc}-{\beta }_2& {\beta }_1{\beta }_2\\ 0& -{\beta }_2\end{array}\right].\end{array}$ The matrices Φ and G in the corresponding CLT covariance calculations (Theorem A.2) are, respectively, $\mathrm{\Phi }(t,s)=\left[\begin{array}{cc}{\mathrm{e}}^{{\beta }_2(s-t)}& -{\beta }_1{\beta }_2(s-t){\mathrm{e}}^{{\beta }_2(s-t)}\\ 0& {\mathrm{e}}^{{\beta }_2(s-t)}\end{array}\right]$ and $G\left(x_1\right(s),x_2(s\left)\right)=\left[\begin{array}{cc}{\beta }_1{\beta }_2{x}_2\left(s\right)+{\beta }_2{x}_1\left(s\right)& 0\\ 0& {\beta }_2{\beta }_3+{\beta }_2{x}_2\left(s\right)\end{array}\right].$ Recall that the asymptotic covariance formula for the components $Z_i$ of the scaled limiting process in Theorem 3.2 is $\mathrm{Cov}(Z_i,Z_j)={\int }_0^{t_i\wedge t_j}\mathrm{\Phi }(t_i,s)G\left(c^{\beta }\right(s\left)\right)\left(\mathrm{\Phi }\right(t_j,s){)}^{\mathrm{\top }}\mathrm{d}s$ which may be numerically evaluated along with the remaining terms in the asymptotic variance ${\mathrm{\Sigma }}_{\hat{\beta }}$ expression (8(8) $\begin{array}{rl}{\mathrm{\Sigma }}_{\hat{\beta }}& =\mathrm{Var}\left(\sum _i(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\sqrt{n}\right(C_n\left(t_i\right)-c^{{\beta }^0}\left(t_i\right))\right)\\ & =\sum _i(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\mathrm{Var}\right(V_i\left)\right[(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i){]}^{\mathrm{\top }}\\ & +\sum _{i\ne j}\left[\right(B_{\hat{\beta }}+{\gamma }_{n}H\left(\hat{\beta }\right){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\mathrm{Cov}(V_i,V_j)\left[\right(B_{\hat{\beta }}+{\gamma }_{n}H\left(\hat{\beta }\right){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\left(t_j\right){]}^{\mathrm{\top }}\\ & +\sum _{i\ne j}(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_j\left)\mathrm{Cov}\right(V_i,V_j\left)\right[(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left){]}^{\mathrm{\top }}\right].\end{array}$(8) ). For comparison, we generate the L1 system trajectories with ${\beta }^0=({\beta }_1,{\beta }_2,{\beta }_3)=(5,1,.1)$, ${\beta }_4={\beta }_2$ and ${\beta }_5=1$ and assume the process to be observed at the time points from $0.03$ to $1.00$ in the alternating increments of $0.03$ and $0.04$. For example, the first 5 time points are $0.03,0.07,0.10,0.13,0.17$. The resulting asymptotic covariance matrix for the LSE (with no penalty, ${\gamma }_n=0$) obtained with the help of numerical integration is shown in Figure 1 along with its bootstrap estimates for varying n. For the bootstrap, the diffusion approximation with corresponding ${\beta }^0$ was applied using the Euler–Maruyama method with step size, $dt=0.01$. The number of bootstrap samples was taken as $M=10,000$, for each of the system sizes $n={10}^2,{10}^3,{10}^4$. To additionally graphically illustrate the recovery of the asymptotic covariance structure by the bootstrap algorithms, we show in Figure 2 the theoretical (upper panel) and bootstrap approximated (lower panel) bivariate marginal distributions of the LSE of ${\beta }^0$, denoted $\hat{\beta }$.

Figure 1. Bootstrap estimate of the LSE covariance for the L1 system. True asymptotic LSE covariance matrix vs. diffusion bootstrap covariance matrices for L1 systems with varying n (via Algorithm 1). To facilitate comparisons, the penalty was removed, i.e. ${\gamma }_n=0$ for all cases considered.

Figure 2. LSE covariance recovery via bootstrap for the L1 system. The contour plots for the true asymptotic LSE bivariate marginal distributions (top panel) and their LNA bootstrap estimates (bottom panel) for the LSE in the L1 system with $n=1000$. The recovery of the multivariate Gaussian distribution covariance structure by the bootstrap procedure is clearly visible.

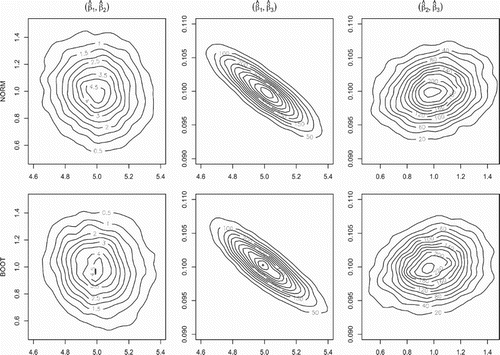
Figures 1 and 2 indicate that the empirical distribution of the bootstrapped LSEs closely approximates that of the theoretical distribution illustrating in practice the application of our Algorithms 1 and 2. Note that obtaining the bootstrap samples only requires the ability to simulate from the diffusion process.

5.2. Penalized LSE for L1

In most practical cases, the data-generating process cannot be measured with arbitrary precision, due to various data collection limitations or errors arising during data processing. In general, such processing errors (see, e.g. [19]) add variation to the LSEs and may compound the problems with formula (8(8) $\begin{array}{rl}{\mathrm{\Sigma }}_{\hat{\beta }}& =\mathrm{Var}\left(\sum _i(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\sqrt{n}\right(C_n\left(t_i\right)-c^{{\beta }^0}\left(t_i\right))\right)\\ & =\sum _i(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\mathrm{Var}\right(V_i\left)\right[(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i){]}^{\mathrm{\top }}\\ & +\sum _{i\ne j}\left[\right(B_{\hat{\beta }}+{\gamma }_{n}H\left(\hat{\beta }\right){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\mathrm{Cov}(V_i,V_j)\left[\right(B_{\hat{\beta }}+{\gamma }_{n}H\left(\hat{\beta }\right){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\left(t_j\right){]}^{\mathrm{\top }}\\ & +\sum _{i\ne j}(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_j\left)\mathrm{Cov}\right(V_i,V_j\left)\right[(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left){]}^{\mathrm{\top }}\right].\end{array}$(8) ) which in practice needs to be evaluated using estimated values of the model parameters in a fixed volume and hence is sensitive to the LSEs lack of precision. The penalty term ${\gamma }_{n}h\left(\beta \right)$ in Equation (4) is intended to improve the LSE estimates precision by giving up some small amount of accuracy (recovering it in the limit, due to ${\gamma }_n\to 0$). Since, as already indicated in Section 3, the penalty term also contributes to stabilizing the inverse matrix in Equation (8(8) $\begin{array}{rl}{\mathrm{\Sigma }}_{\hat{\beta }}& =\mathrm{Var}\left(\sum _i(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\sqrt{n}\right(C_n\left(t_i\right)-c^{{\beta }^0}\left(t_i\right))\right)\\ & =\sum _i(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\mathrm{Var}\right(V_i\left)\right[(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i){]}^{\mathrm{\top }}\\ & +\sum _{i\ne j}\left[\right(B_{\hat{\beta }}+{\gamma }_{n}H\left(\hat{\beta }\right){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\mathrm{Cov}(V_i,V_j)\left[\right(B_{\hat{\beta }}+{\gamma }_{n}H\left(\hat{\beta }\right){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\left(t_j\right){]}^{\mathrm{\top }}\\ & +\sum _{i\ne j}(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_j\left)\mathrm{Cov}\right(V_i,V_j\left)\right[(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left){]}^{\mathrm{\top }}\right].\end{array}$(8) ), the use of penalized formulation (4(8) $\begin{array}{rl}{\mathrm{\Sigma }}_{\hat{\beta }}& =\mathrm{Var}\left(\sum _i(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\sqrt{n}\right(C_n\left(t_i\right)-c^{{\beta }^0}\left(t_i\right))\right)\\ & =\sum _i(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left)\mathrm{Var}\right(V_i\left)\right[(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i){]}^{\mathrm{\top }}\\ & +\sum _{i\ne j}\left[\right(B_{\hat{\beta }}+{\gamma }_{n}H\left(\hat{\beta }\right){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\mathrm{Cov}(V_i,V_j)\left[\right(B_{\hat{\beta }}+{\gamma }_{n}H\left(\hat{\beta }\right){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\left(t_j\right){]}^{\mathrm{\top }}\\ & +\sum _{i\ne j}(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_j\left)\mathrm{Cov}\right(V_i,V_j\left)\right[(B_{\hat{\beta }}+{\gamma }_{n}H(\hat{\beta }\left){)}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left){]}^{\mathrm{\top }}\right].\end{array}$(8) ) for LSEs with fixed sample size may bring considerable benefits.

To illustrate this point, we compare now the bootstrap estimates for the lasso-penalized and ordinary $({\gamma }_n=0)$ LSE in the L1 model with various system sizes. The values of the parameters ${\beta }^0$ are as above. Since the lasso penalty is right-differentiable in our setting, as $\beta \ge 0$ coordinate-wise, all the forms of penalty discussed in Section 3 are smooth and hence roughly equivalent (see, [10]). To account for the observational errors, we also introduce an independent mean 0 Gaussian noise at each observation grid time point. The variance of this noise is set to 5% of the maximum concentration of mRNA L1 transcripts ($X_1$) which is equivalent to approximately 25% of the maximum concentration of the transcription facilitating proteins ($X_2$). The choice of penalty rate is ${\gamma }_n=n^{-3/4}$ for $n=10,{10}^2,{10}^3,$ and ${10}^4$, so as to satisfy the LSE consistency requirements, although in a real data analysis one would typically choose it by some form of a cross-validation procedure (cf. [6]). The results of the analysis for $M=10,000$ resamples are summarized in Table 1. As seen from the table, for the system sizes of $n=10$ and $n=100$ the penalized LSE enjoys, respectively, a 10-fold and 2-fold decrease in variance as compared with the ordinary LSE of ${\beta }_1$, with only modest increase in bias. For the penalized estimate of ${\beta }_2$, there is nearly a 5-fold decrease in variance for $n=10$ but only a moderate decrease for $n\ge 100$, while the variability of the ${\beta }_3$ estimates remaining roughly the same for the LSE and penalized LSE for $n\ge 100$. From the inspection of table entries it should be clear, that with the noisy data the penalized LSE does better in terms of the variance for small system sizes, whereas for larger n the performance of ordinary and penalized LSE is very similar.

5.3. RT-PCR Data for L1

In order to look at a more realistic biological example, in addition to the above synthetic data, we also consider the real time-PCR data from one of the time course experiments analysing L1 system in HeLa cell cultures [13] under external chemical stress, as described in [17]. The data consist of the L1 transcripts values ($X_1$) only, as the protein ($X_2$) is unobservable. The L1 transcript measurements from the experiment are presented in Table 2 taken from Rempala [16] where the LSE-based asymptotic confidence bound for this particular data set was obtained by approximating the overall system size and using the asymptotic distribution of the LSE. The system size approximation in [16] was based on a relatively crude fluorescence conversion method introduced in [17]. We shall illustrate now how the bootstrap approach may be used to help identify most likely system size, without using a (possibly unreliable) method based on fluorescent signal conversion. Note that, unlike in previous examples, the time-course L1 transcript measurements reported in Table 2 were obtained from genetically identical but spatially separated L1 cell cultures (different tissue culture plates) and hence represent not a single one, but rather multiple trajectories of the stochastic system (15(15) $\begin{array}{rl}{X}_2& ⟹{\kappa }_1{X}_1+X_2{X}_1⟹{\kappa }_2\phi ,\\ \phi & ⟹n{\kappa }_3{X}_2{X}_2⟹{\kappa }_4\phi .\end{array}$(15) ), each obtained at different time point . Nonetheless, due to the genetic homogeneity of tissue cultures, the initial conditions for the observed trajectories and the respective experimental system sizes n may be assumed to be approximately equal and Theorems 4.1 and 4.3 (and Algorithms 1 and 2) are still applicable in view of Remark 4.2.

Table 2. Time-course RT-PCR experiment results for L1 gene.

Time (h)	0.16	0.5	1	3	12	24	48	72	96
L1 Rel. Con.	12.583	14.459	12.183	11.985	13.295	12.168	9.584	9.841	6.298

As in our earlier analysis, we took ${\beta }_4={\beta }_2$ and ${\beta }_5=1$ reducing Equation (16(16) $\begin{array}{rl}{c}_1^{\beta }\left(t\right)& ={\beta }_1{\beta }_3[1+{\beta }_5(1+t{\beta }_2\left){\mathrm{e}}^{-{\beta }_{2}t}\right],\\ c_2^{\beta }\left(t\right)& ={\beta }_3(1+{\beta }_5{\mathrm{e}}^{-{\beta }_{2}t}),\end{array}$(16) ) to the following one-dimensional model: (18) $c_1^{\beta }\left(t\right)={\beta }_1{\beta }_3[1+(1+t{\beta }_2\left){\mathrm{e}}^{-{\beta }_{2}t}\right].$(18) Since with the concentration $c_2^{\beta }$ unobserved this model is no longer identifiable, we also fix ${\beta }_3=1$ and hence reduce the initial L1 model to only two parameters $({\beta }_1,{\beta }_2)$. Application of the LNA diffusion approximation and the EM algorithm to the limiting LSE problem, as discussed in Section 4.3 (with no penalty, i.e. ${\gamma }_n=0$),³ gave the following values of the estimates, which are very similar to those obtained in [16] ${\hat{\beta }}_1=6.18,{\hat{\beta }}_2=\mathrm{0.027.}$

Based on these numerical values, the bootstrap algorithm (Algorithm 2) was applied to calculate the confidence bounds for the observed longitudinal trajectory of the L1 transcripts. The bounds depend on the unknown system size n, which was estimated via the method of likelihood profiling as follows. First, for the grid of n values (from $n=500$ to 9000 with 500 step size), the bootstrap approximation based on $M=5000$ resamples was obtained using Algorithm 2 (note that with Algorithm 2 the same set of bootstrap resamples may be used with different n). Next, the actual value of the observed error was compared with the modes of the error distribution for varying n. The best mode-to-data alignment (over the gridded values of n) was obtained at $n=5000$ and hence this value was taken as the estimated effective system size. The process is illustrated in Figure 3. In Figure 4, the 95% confidence envelopes of the original analysis in [16] (where the effective system size was taken as $n=1000$) are compared with the ones obtained from the likelihood profiling ($n=5000$). As may be seen from the plots the new larger estimate of the system size has the effect of shrinking the uncertainty around the observed trajectory due to generally tighter confidence bounds about observed data points. illustrating the advantage of the bootstrap-based analysis for data in Table 2.

Figure 3. Bootstrap likelihood profiling. The LNA bootstrap ($M=5000$) plots approximating for several different n values the residuals distributions for the model (18(18) $c_1^{\beta }\left(t\right)={\beta }_1{\beta }_3[1+(1+t{\beta }_2\left){\mathrm{e}}^{-{\beta }_{2}t}\right].$(18) ) fitted to data in Table 2 and comparing them with the actual observed residuals (grey vertical lines). As seen from the plots, around the value $n=5000$ the mode of the residuals distribution best aligns with the observed value. Note that the alignment is very poor for $n=1000$, which is the estimated volume used in [16].

Figure 4. Confidence envelopes for different n values. The ODE model data (18(18) $c_1^{\beta }\left(t\right)={\beta }_1{\beta }_3[1+(1+t{\beta }_2\left){\mathrm{e}}^{-{\beta }_{2}t}\right].$(18) ) fitted to the trajectory data in Table 2 plotted along with the fits 95% confidence envelopes for two different estimated system sizes. The left panel shows the bounds obtained in [16] for the system size $n=1000$ whereas the right panel shows the bounds obtained by taking $n=5000$.

6. Summary and discussion

We proposed here and justified with the appropriate large-volume limit results some new ways of practically estimating the covariance structure and, in general, improving the performance of LSEs in biochemical network models. We discussed three possible approaches based on (a) the penalized least-squares criterion, (b) the fast bootstrap algorithms for covariance estimation and (c) the bootstrap-based profiling method for the determination of effective system size.

With regard to (a), we have shown that under the vanishing penalty on parameters size, the LSEs continue to be consistent in the limit, but may additionally exhibit much better precision in the small-volume settings. Concerning (b), we have argued that the usage of bootstrap Monte-Carlo algorithms may allow to avoid the often difficult calculations of the LSEs asymptotic covariance structure. To improve efficiency, we proposed the usage of diffusion-based bootstrap methods and shown them to be consistent in the large-volume limit. Two types of diffusion approximation were considered: (i) the classical chemical Langevin equation approximation and (ii) the LNA method directly derived from the CLT for jump processes. The latter one, although slightly more biased in our simulation studies, seems particularly attractive as it allows one to generate resamples which are independent of the system size (volume) n. With regard to (c), this aspect of the LNA-based bootstrap may be used to develop an efficient algorithm for estimating the effective volume of the biochemical model, in essence, by analysing the size of the model fit fluctuations for different volume sizes. We have illustrated the practical applicability of this approach to reducing model uncertainty for partially observed, longitudinal RT-PCR data from the LINE 1 retrotransciption network.

Overall, our current work seems to support the conclusion that the bootstrap methods, although not without limitations, like, for example, the requirement to be able to simulate from the entire reaction network, seem to offer a viable alternative to a direct asymptotic approximation based on the estimated covariance structure. One hopes that the results presented here will encourage further study of the general application of resampling to biochemical network inference problems, both in its theoretical and applied aspects, in particular in the setting specifically not considered here when both $T,n\to \mathrm{\infty }$.

Acknowledgments

Research supported in part by US NIH grant R01CA-152158 (DFL, GAR) and US NSF grant DMS-1106485 (GAR)

Disclosure statement

No potential conflict of interest was reported by the authors.

Notes

1. See Section 5.3.

2. This is done out of convenience to eliminate superfluous parameters. Note that any such renormalization possibly effects the units of system volume n.

3. In the particular case, given the large system size n, the penalty would have only negligible effect.

Appendix 1. Density-dependent Markov jump process

In the following, suppose the state $\left\{X_n\right(t):t\ge 0\}$ is a continuous-time Markov process on the positive orthant of d-dimensional lattice, ${\mathbb{Z}}_{\ge 0}^d$ with jump intensities $q_{x,x+{\nu }_k^{\mathrm{\prime }}-{\nu }_k}^{\left(n\right)}=n{\lambda }_k\left(n^{-1}x\right)$ for $x\in {\mathbb{Z}}_{\ge 0}^d$, ${\nu }_k^{\mathrm{\prime }}-{\nu }_k\in {\mathbb{Z}}^d$ and the transition probabilities $P\left(X_n\right(t+h)=x+{\nu }_k^{\mathrm{\prime }}-{\nu }_k|X_n(t)=x)=hn{\lambda }_k\left(n^{-1}x\right)+o\left(h\right)$ and $P\left(X_n\right(t+h)=x|X_n(t)=x)=1-hn\sum _k{\lambda }_k\left(n^{-1}x\right)+o\left(h\right)$. It is assumed that there are a finite number of vectors, ${\nu }_k^{\mathrm{\prime }}-{\nu }_k\in {\mathbb{Z}}^d$ such that ${\sup }_x{\lambda }_k\left(x\right)>0$ and that ${\lambda }_k\left(x\right)$ is a continuous function of x for each k. Such processes are known as the DDMJPs since their transition rates depend on the density of the process (see, e.g. [16]). Note that under the approximation (2(2) ${\lambda }_k^{\left(n\right)}\left(x\right)\approx n{\kappa }_k\prod c_i^{{\nu }_{ik}}=:n{\lambda }_k\left(c\right).$(2) ) the process given in Equation (1(1) $X\left(t\right)=X\left(0\right)+\sum _k{Y}_k\left({\int }_0^t{\lambda }_k^{\left(n\right)}\left(X\right(s\left)\right)\mathrm{d}s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k).$(1) ) is a special case of the DDMJP. If $Y_l=\left\{Y_k\right(t):t\ge 0\}$ is a collection of independent unit Poisson processes then (A1) $X_n\left(t\right)=X_n\left(0\right)+\sum _k{Y}_k\left(n{\int }_0^t{\lambda }_k\left(n^{-1}{X}_n\right(s\left)\right)\mathrm{d}s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k).$(A1) Define the centred Poisson process ${\hat{Y}}_k\left(nt\right)=Y_k\left(nt\right)-nt$ and $C_n\left(t\right)=X_n\left(t\right)/n$. The corresponding drift function is given by Equation (11(11) $F\left(x\right)=\sum _k{\lambda }_k\left(x\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)$(11) ), that is, $F\left(x\right)=\sum _k{\lambda }_k\left(x\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)$, where for notational simplicity we no longer emphasize the trajectory or rate dependance on any parameters. Then, Equation (A1(A1) $X_n\left(t\right)=X_n\left(0\right)+\sum _k{Y}_k\left(n{\int }_0^t{\lambda }_k\left(n^{-1}{X}_n\right(s\left)\right)\mathrm{d}s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k).$(A1) ) becomes (A2) $C_n\left(t\right)=C_n\left(0\right)+n^{-1}\sum _k{\hat{Y}}_k\left(n{\int }_0^t{\lambda }_k\left(C_n\right(s\left)\right)\mathrm{d}s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)+{\int }_0^{t}F\left(C_n\right(s\left)\right)\mathrm{d}s.$(A2) The following result due to Kurtz [1, Chapter 5] establishes SLLN for $C_n\left(t\right)$.

Theorem A.1

(SLLN)

Let $\underset{n\to \mathrm{\infty }}{lim}{C}_n\left(0\right)=c_0$ and suppose that for any compact $K\in {\mathbb{R}}^d$ there exists a constant $M_K$ such that $|F\left(x\right)-F\left(y\right)|\le M_K|x-y|,\mathrm{\forall }x,y\in K$. Then $\underset{n\to \mathrm{\infty }}{lim}\underset{s\le t}{sup}|C_n\left(s\right)-c\left(s\right)|=0\mathit{a}\mathit{.}\mathit{s}.,$ where $c\left(t\right)$ is the deterministic solution to the integral equation, $c\left(t\right)=c_0\left(t\right)+{\int }_0^{t}F\left(c\right(s\left)\right)\mathrm{d}s.$

For the inferential purposes, it is important to know that the scaled fluctuation of the DDMJP around the deterministic ODE solution, $V_n=\sqrt{n}\left(C_n\right(t)-c(t\left)\right)$ is Gaussian. This fact follows from the following CLT due to Kurtz [1, Chapter 5]. Let $\mathrm{\partial }F\in {\mathbb{R}}^{d\times d}$ such that $[\mathrm{\partial }F{]}_{ij}=[{\mathrm{\partial }}_j{F}_i]$.

Theorem A.2

(CLT)

Suppose $\mathrm{\partial }F$ is continuous and $\underset{n\to \mathrm{\infty }}{lim}{V}_n\left(0\right)=v_0$ is non-random. Then, $V_n=\sqrt{n}\left(C_n\right(t)-c(t\left)\right)\Rightarrow V,$ where the process V is given by (A3) $V\left(t\right)=v_0+\sum _k{B}_k\left({\int }_0^t{\lambda }_k\left(c\right(s\left)\right)\mathrm{d}s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)+{\int }_0^t\mathrm{\partial }F\left(c\right(s\left)\right)V\left(s\right)\mathrm{d}s,$(A3) or, in a distributionally equivalent Itô diffusion form, by (A4) $V\left(t\right)=v_0+\sum _k{\int }_0^t\sqrt{{\lambda }_k\left(c\right(s\left)\right)}\mathrm{d}{B}_k\left(s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)+{\int }_0^t\mathrm{\partial }F\left(c\right(s\left)\right)V\left(s\right)\mathrm{d}s.$(A4) The process V is a Gaussian vector process with covariance (A5) $\mathrm{Cov}\left(V\right(t),V(r\left)\right)={\int }_0^{r\wedge t}\mathrm{\Phi }(t,s)G\left(c\right(s\left)\right)\mathrm{\Phi }(r,s{)}^{\mathrm{\top }}\mathrm{d}s,$(A5) where $\mathrm{\Phi }\in {\mathbb{R}}^{d\times d}$ satisfies $\frac{\mathrm{\partial }}{\mathrm{\partial }s}\mathrm{\Phi }(t,s)=\mathrm{\Phi }(t,s)\mathrm{\partial }F\left(c\right(s\left)\right)\mathrm{\Phi }(s,s)=I$ and $G\left(x\right)=\sum _k({\nu }_k^{\mathrm{\prime }}-{\nu }_k)({\nu }_k^{\mathrm{\prime }}-{\nu }_k{)}^{\mathrm{\top }}{\lambda }_k(x)$.

Appendix 2. Diffusion approximation and the bootstrap

Recall the Itô diffusion process $D_n$ defined by Equation (10(10) $D_n\left(t\right)=D_n\left(0\right)+\sum _k\frac{1}{\sqrt{n}}{\int }_0^t\sqrt{{\lambda }_k\left(D_n\right(s\left)\right)}\mathrm{d}{B}_k\left(s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)+{\int }_0^{t}F\left(D_n\right(s\left)\right)\mathrm{d}s,$(10) ). The following result indicates that $D_n$ has the same consistency property as the scaled pure jump process (A2(A2) $C_n\left(t\right)=C_n\left(0\right)+n^{-1}\sum _k{\hat{Y}}_k\left(n{\int }_0^t{\lambda }_k\left(C_n\right(s\left)\right)\mathrm{d}s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)+{\int }_0^{t}F\left(C_n\right(s\left)\right)\mathrm{d}s.$(A2) ) and may be therefore used as its approximation.

Lemma A.1

Suppose that $\underset{n\to \mathrm{\infty }}{lim}{D}_n\left(0\right)\to c\left(0\right)$ a constant, and that for each compact set $K\in {\mathbb{R}}^d$ we have a Lipschitz constant, $M_K,$ such that $|F\left(x\right)-F\left(y\right)|\le M_K|x-y|,$ $\mathrm{\forall }x,y\in K,$ then $\underset{n\to \mathrm{\infty }}{lim}\underset{s\le t}{sup}|D_n\left(s\right)-c\left(s\right)|=0$ almost surely, where $c\left(t\right)$ is the solution to $c\left(t\right)=c\left(0\right)+{\int }_0^{\mathrm{\top }}F\left(c\right(s\left)\right)\mathrm{d}s$ and $F\left(x\right)=\sum _k({\nu }_k^{\mathrm{\prime }}-{\nu }_k){\lambda }_k\left(x\right),x\in {\mathbb{R}}^d$.

Proof.

By the definition of $D_n\left(t\right)$ given in Equation (10(10) $D_n\left(t\right)=D_n\left(0\right)+\sum _k\frac{1}{\sqrt{n}}{\int }_0^t\sqrt{{\lambda }_k\left(D_n\right(s\left)\right)}\mathrm{d}{B}_k\left(s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)+{\int }_0^{t}F\left(D_n\right(s\left)\right)\mathrm{d}s,$(10) ) $\begin{array}{rl}|D_n\left(s\right)-c\left(s\right)|& =\left|D_n\left(0\right)-c\left(0\right)+\sum _k\frac{1}{\sqrt{n}}{\int }_0^s\sqrt{{\lambda }_k\left(D_n\right(r\left)\right)}\mathrm{d}{B}_k\left(r\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)+\left({\int }_0^s\left(F\right(D_n\left(r\right))-F(c\left(r\right)\left)\right)\mathrm{d}r\right)\right|\\ & \le |D_n\left(0\right)-d\left(0\right)|+\frac{1}{\sqrt{n}}\sum _k|{\nu }_k^{\mathrm{\prime }}-{\nu }_k|\left|{\int }_0^s\sqrt{{\lambda }_k\left(D_n\right(z\left)\right)}\mathrm{d}{B}_k\left(z\right)\right|+{\int }_0^s{M}_K|D_n\left(r\right)-c\left(r\right)|\mathrm{d}r\end{array}$ implying, $\begin{array}{r}|D_n\left(s\right)-c\left(s\right)|\le |D_n\left(0\right)-c\left(0\right)|+\frac{1}{\sqrt{n}}\sum _k|{\nu }_k^{\mathrm{\prime }}-{\nu }_k|\sqrt{{\overline{\lambda }}_k}\underset{0\le r_1\le r_2\le s}{sup}|B_k\left(r_1\right)-B_k\left(r_2\right)|+{\int }_0^s{M}_K|D_n\left(r\right)-c\left(r\right)|\mathrm{d}r,\end{array}$ where ${\overline{\lambda }}_k=\underset{x\in K}{sup}{\lambda }_k\left(x\right)$. For almost all ω, $B_k(\omega ,t)$, is a continuous process, and thus achieves its maximum and minimum on every compact set, implying that $\underset{0\le r_1\le r_2\le s}{sup}|B_k(\omega ,r_1)-B_k(\omega ,r_2)|$ is bounded, except on a set of measure 0. (Note: We have suppressed the inherent sample space notation, ω, except when needed, as is standard for brevity). Then, by Gronwall's inequality (cf. [1], Chapter 5), $|D_n\left(s\right)-c\left(s\right)|\le \left(|D_n\right(0)-c(0)|+\frac{1}{\sqrt{n}}\sum _k|{\nu }_k^{\mathrm{\prime }}-{\nu }_k|\sqrt{{\overline{\lambda }}_k}\underset{0\le r_1\le r_2\le s}{sup}|B_k(r_1)-B_k(r_2\left)|\right){\mathrm{e}}^{M_{K}s}$ yielding $\underset{s\le t}{sup}|D_n\left(s\right)-c\left(s\right)|\le \left(|D_n\right(0)-c(0)|+\frac{1}{\sqrt{n}}\sum _k|{\nu }_k^{\mathrm{\prime }}-{\nu }_k|\sqrt{{\overline{\lambda }}_k}\underset{0\le r_1\le r_2\le t}{sup}|B_k(r_1)-B_k(r_2\left)|\right){\mathrm{e}}^{M_{K}t}.$ As $n\to \mathrm{\infty }$, the first term of the RHS converges almost surely to 0 by the theorem's hypothesis. The second term involves a finite weighted sum of the expressions of type $\underset{0\le r_1\le r_2\le s}{sup}|B_k(\omega ,r_1)-B_k(\omega ,r_2)|$ which are bounded for almost all ω, implying that $\left(1/\sqrt{n}\right)\underset{0\le r_1\le r_2\le s}{sup}|B_k(\omega ,r_1)-B_k(\omega ,r_2)|$ converges to 0 a.s.

The following result shows that the properly centred and scaled diffusion process converges in distribution to the same limit as the centred and scaled pure jump process.

Lemma A.2.

With the assumption $c_n\left(0\right)=\sqrt{n}\left(D_n\right(0)-c(0\left)\right)\to c_0$ a constant, and those of Theorem 2, the process, $V_n^{\mathrm{\prime }}\left(t\right)=\sqrt{n}\left(D_n\right(t)-c(t\left)\right)$ converges in distribution to the process, $V^{\mathrm{\prime }}\left(t\right)$ which is distributionally equivalent to $V\left(t\right)$ defined in Theorem A.2.

Proof.

By definition, $\begin{array}{rl}{V}_n^{\mathrm{\prime }}\left(t\right)& =\sqrt{n}\left(D_n\right(t)-c(t\left)\right)=c_n\left(0\right)+\sum _k{\int }_0^t\sqrt{{\lambda }_k\left(D_n\right(s\left)\right)}\mathrm{d}{B}_k\left(s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)\\ & +{\int }_0^t\mathrm{\partial }F\left(c\right(s\left)\right)V_n^{\mathrm{\prime }}\left(s\right)\mathrm{d}s+{\int }_0^{t}O\left(|D_n\right(s)-c(s\left)|\right)V_n^{\mathrm{\prime }}\left(s\right)\mathrm{d}s.\end{array}$

Define, as before, $\begin{array}{rl}{U}_n\left(t\right)& :=\sum _k{\int }_0^t\sqrt{{\lambda }_k\left(D_n\right(s\left)\right)}\mathrm{d}{B}_k\left(s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)+{\int }_0^{t}O\left(|D_n\right(s)-c(s\left)|\right)V_n^{\mathrm{\prime }}\left(s\right)\mathrm{d}s\\ & =-c_n\left(0\right)+V_n^{\mathrm{\prime }}\left(t\right)-{\int }_0^t\mathrm{\partial }F\left(c\right(s\left)\right)V_n^{\mathrm{\prime }}\left(s\right)\mathrm{d}s.\end{array}$ Since the process $D_n\left(s\right)$ is non-anticipating and converges in probability pointwise to $c\left(s\right)$ by Lemma A.3, the dominated convergence theorem (DCT) for stochastic integrals implies that $\underset{n\to \mathrm{\infty }}{lim}{U}_n\left(t\right)$ can be computed by interchanging the limit with the first integral, and that the classical DCT can be applied to the second. This gives $\begin{array}{rl}{U}_n\left(t\right)& \Rightarrow \sum _k{\int }_0^t\underset{n\to \mathrm{\infty }}{lim}\sqrt{{\lambda }_k\left(D_n\right(s\left)\right)}\mathrm{d}{B}_k\left(s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)+{\int }_0^t\underset{n\to \mathrm{\infty }}{lim}O\left(|D_n\right(s)-c(s\left)|\right)V_n^{\mathrm{\prime }}\left(s\right)\mathrm{d}s\\ & =\sum _k{\int }_0^t\sqrt{{\lambda }_k\left(c\right(s\left)\right)}\mathrm{d}{B}_k\left(s\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)=U\left(t\right).\end{array}$ Again, defining Φ to be the matrix function solution to $\frac{\mathrm{\partial }}{\mathrm{\partial }s}\mathrm{\Phi }(t,s)=-\mathrm{\Phi }(t,s)\mathrm{\partial }F\left(c\right(s\left)\right),\mathrm{\Phi }(s,s)=I,$ we have $\begin{array}{rl}{\int }_0^{\mathrm{\top }}\mathrm{\Phi }(t,s)\mathrm{d}{U}_n\left(s\right)& ={\int }_0^{\mathrm{\top }}\mathrm{\Phi }(t,s)\mathrm{d}{V}_n^{\mathrm{\prime }}\left(s\right)-{\int }_0^{\mathrm{\top }}\mathrm{\Phi }(t,s)\mathrm{\partial }F\left(c\right(s\left)\right)V_n^{\mathrm{\prime }}\left(s\right)\mathrm{d}s\\ & =\mathrm{\Phi }(t,t)V_n^{\mathrm{\prime }}\left(t\right)-\mathrm{\Phi }(t,0)c_n\left(0\right)-{\int }_0^{\mathrm{\top }}{\mathrm{\Phi \prime }}^{}(t,s)V_n^{\mathrm{\prime }}\left(s\right)\mathrm{d}s-{\int }_0^{\mathrm{\top }}\mathrm{\Phi }(t,s)\mathrm{\partial }F\left(c\right(s\left)\right)V_n^{\mathrm{\prime }}\left(s\right)\mathrm{d}s\\ & =V_n^{\mathrm{\prime }}\left(t\right)-\mathrm{\Phi }(t,0)c_n\left(0\right).\end{array}$ Thus, $V_n^{\mathrm{\prime }}\left(t\right)=\mathrm{\Phi }(t,0)c_n\left(0\right)+{\int }_0^{\mathrm{\top }}\mathrm{\Phi }(t,s)\mathrm{d}{U}_n\left(s\right),$ and $U_n\Rightarrow U$ implies $V_n^{\mathrm{\prime }}=h\left(U_n\right)\Rightarrow h\left(U\right)=\mathrm{\Phi }(t,0)c_0+{\int }_0^{\mathrm{\top }}\mathrm{\Phi }(t,s)\mathrm{d}U\left(s\right)=V^{\mathrm{\prime }}$ again by the continuous mapping theorem. This is clearly a Gaussian vector process by definition, with its covariance function given by $\begin{array}{rl}E\left(V^{\mathrm{\prime }}\right(t\left)V^{\mathrm{\prime }}\right(r{)}^{\mathrm{\top }})& =E\left[{\int }_0^{\mathrm{\top }}\mathrm{\Phi }(t,s)\mathrm{d}U\left(s\right){\left({\int }_0^r\mathrm{\Phi }(r,s)\mathrm{d}U\left(s\right)\right)}^{\mathrm{\top }}\right]\\ & =E\underset{|s_{i+1}-s_i|\to 0}{lim}\left(\sum _i\mathrm{\Phi }(t,s_i)\left(U\right(s_{i+1})-U(s_i\left)\right){\left(\sum _i\mathrm{\Phi }(r,s_i)\left(U\right(s_{i+1})-U(s_i\left)\right)\right)}^{\mathrm{\top }}\right)\\ & =E\underset{|s_{i+1}-s_i|\to 0}{lim}\sum _i\mathrm{\Phi }(t,s_i)\sum _k\sqrt{{\lambda }_k\left(c\right(s_i\left)\right)}\left(B_k\right(s_{i+1})-B_k(s_i\left)\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)\\ & \times \left(\sum _i\mathrm{\Phi }(r,s_i)\sum _k\sqrt{{\lambda }_k\left(c\right(s_i\left)\right)}\left(B_k\right(s_{i+1})-B_k(s_i\left)\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k){)}^{\mathrm{\top }}\right)\\ & =\underset{|s_{i+1}-s_i|\to 0}{lim}E\left(\sum _{i,j}\mathrm{\Phi }(t,s_i)\sum _{k,l}({\nu }_k^{\mathrm{\prime }}-{\nu }_k)({\nu }_l^{\mathrm{\prime }}-{\nu }_l{)}^{\mathrm{\top }}\sqrt{{\lambda }_k\left(c\right(s_i\left)\right)}\sqrt{{\lambda }_j\left(c\right(s_j\left)\right)}\right.\\ & \left.\phantom{\sum _{i,j}}\times \left(B_k\right(s_{i+1})-B_k(s_i\left)\right)\left(B_l\right(s_{j+1})-B_l(s_j\left)\right)\mathrm{\Phi }(r,s_j{)}^{\mathrm{\top }}\right).\end{array}$ Since the Brownian motions $B_k$ and $B_l$ are independent, as well as the increments $\left(B_k\right(s_{i+1})-B_k(s_i\left)\right)$ are independent of $\left(B_k\right(s_{j+1})-B_k(s_j\left)\right)$, we have $\begin{array}{rl}E\left(V^{\mathrm{\prime }}\right(t\left)V^{\mathrm{\prime }}\right(r{)}^{\mathrm{\top }})& =\underset{|s_{i+1}-s_i|\to 0}{lim}\sum _i\mathrm{\Phi }(t,s_i)\sum _k\lambda \left(c\right(s_i\left)\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)({\nu }_k^{\mathrm{\prime }}-{\nu }_k{)}^{\mathrm{\top }}E(B_k\left(s_{i+1}\right)-B_k\left(s_i\right){)}^2\mathrm{\Phi }(r,s_i{)}^{\mathrm{\top }}\\ & =\underset{|s_{i+1}-s_i|\to 0}{lim}\sum _i\mathrm{\Phi }(t,s_i)\sum _k\lambda \left(c\right(s_i\left)\right)({\nu }_k^{\mathrm{\prime }}-{\nu }_k)({\nu }_k^{\mathrm{\prime }}-{\nu }_k{)}^{\mathrm{\top }}\mathrm{\Phi }(r,s_i{)}^{\mathrm{\top }}(s_{i+1}-s_i)\\ & ={\int }_0^{t\wedge r}\mathrm{\Phi }(t,s)G\left(c\right(s\left)\right)\mathrm{\Phi }(r,s{)}^{\mathrm{\top }}\mathrm{d}s\end{array}$ and therefore $V^{\mathrm{\prime }}$ and V have the same distribution.

The following observation regarding the LNA process will be useful at this point.

Remark A.1.

In view of the definition of the LNA process $L_n\left(t\right)$ given by Equation (12(12) $L_n\left(t\right)=c^{\beta }\left(t\right)+\frac{V\left(t\right)}{\sqrt{n}}.$(12) ), it is easy to see that the results of Lemmas A.3 and A.4 hold true when $C_n\left(t\right)$ is replaced by $L_n\left(t\right)$.

With the above lemmas, we are finally in a position to prove the bootstrap consistency result of Theorem 4.1.

Proof of Theorem 4.1

Let ${\Rightarrow }^{\ast }$ indicate that the sequence of probability distributions associated with the conditional (bootstrap) space converges to the distribution of a multivariate normal random vector with covariance ${\mathrm{\Sigma }}_{{\beta }^0}$. The notation $\mathrm{a}.\mathrm{s}.\left(\omega \right)$ and $a.s.\left({\omega }^{\ast }\right)$ indicates the property holds for almost every ω and almost every ${\omega }^{\ast }$, respectively. In view of the assumed differentiability of the penalty function h, any minimizing solution, ${\hat{\beta }}^{\ast }$, satisfying ${\hat{\beta }}^{\ast }={\mathrm{argmin}}_{\beta \in \mathrm{\Theta }}\sum _i|D_n^{\ast }\left(t_i\right)-c^{\beta }\left(t_i\right){|}^2+2{\gamma }_{n}h\left(\beta \right)$ must also necessarily satisfy $\sum _i\mathrm{\partial }{c}^{{\hat{\beta }}^{\ast }}\left(t_i\right)\left(D_n^{\ast }\right(t_i)-c^{{\hat{\beta }}^{\ast }}(t_i\left)\right)+{\gamma }_n\mathrm{\nabla }h\left({\hat{\beta }}^{\ast }\right)=0$. Expansion about $\hat{\beta }$ gives $\begin{array}{rl}\sum _i\mathrm{\partial }{c}^{{\hat{\beta }}^{\ast }}\left(t_i\right)\sqrt{n}\left(D_n^{\ast }\right(t_i)-c^{\hat{\beta }}(t_i\left)\right)& =\sum _i\mathrm{\partial }{c}^{{\hat{\beta }}^{\ast }}\left(t_i\right)\sqrt{n}\left(c^{{\hat{\beta }}^{\ast }}\right(t_i)-c^{\hat{\beta }}(t_i\left)\right)+\sqrt{n}{\gamma }_n\mathrm{\nabla }h\left({\hat{\beta }}^{\ast }\right)\\ & =\sum _i\mathrm{\partial }{c}^{{\hat{\beta }}^{\ast }}\left(t_i\right)\left[\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left){]}^{\mathrm{\top }}\sqrt{n}\right({\hat{\beta }}^{\ast }-\hat{\beta })+\sqrt{n}{\gamma }_{n}H({\hat{\beta }}^{\ast }\left)\right({\hat{\beta }}^{\ast }-\hat{\beta })\\ & +O(|{\hat{\beta }}^{\ast }-\hat{\beta }|)\sqrt{n}({\hat{\beta }}^{\ast }-\hat{\beta })\end{array}$ where $H\left(\beta \right)$ is the Hessian of the penalty term evaluated at β. Lemma A.3 gives $O(|{\hat{\beta }}^{\ast }-\hat{\beta }|)\to 0\mathrm{a}.\mathrm{s}.\left({\omega }^{\ast }\right)$ implying that $O(|{\hat{\beta }}^{\ast }-\hat{\beta }|)\sqrt{n}({\hat{\beta }}^{\ast }-\hat{\beta })$ converges to 0 in view of Lemma A.4, validating the removal in the limit of the higher order terms. Setting $B_{{\hat{\beta }}^{\ast }}=\sum _i\mathrm{\partial }{c}^{{\hat{\beta }}^{\ast }}\left(t_i\right)\left[\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i){]}^{\mathrm{\top }}+({\gamma }_n/2\left)H\right({\hat{\beta }}^{\ast })$ we arrive at $\sqrt{n}({\hat{\beta }}^{\ast }-\hat{\beta })=\sum _i{B}_{{\hat{\beta }}^{\ast }}^{-1}\mathrm{\partial }{c}^{{\hat{\beta }}^{\ast }}\left(t_i\right)\sqrt{n}\left(D_n^{\ast }\right(t_i)-c^{\hat{\beta }}(t_i\left)\right).$ By the consistency for the diffusion approximation (Lemma A.3), ${\hat{\beta }}^{\ast }\to \hat{\beta }\mathrm{a}.\mathrm{s}.\left({\omega }^{\ast }\right)$, implying that $\mathrm{\partial }{c}^{{\hat{\beta }}^{\ast }}\left(t_i\right)\to \mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)$ and $B_{{\hat{\beta }}^{\ast }}^{-1}\to B_{\hat{\beta }}^{-1}$ $\mathrm{a}.\mathrm{s}.\left({\omega }^{\ast }\right)$. Since $\sqrt{n}\left(D_n^{\ast }\right(t)-c^{\hat{\beta }}(t\left)\right)$ converges to the same distribution as the Gaussian vector process with mean 0 and covariance function ${\mathrm{\Sigma }}_{\hat{\beta }}^{\ast }(t,r)={\int }_0^{t\wedge r}{\mathrm{\Phi }}^{\hat{\beta }}(t,s)G\left(c^{\hat{\beta }}\right(s\left)\right){\mathrm{\Phi }}^{\hat{\beta }}(r,s{)}^{\mathrm{\top }}\mathrm{d}s,$ where $\frac{\mathrm{\partial }}{\mathrm{\partial }s}{\mathrm{\Phi }}^{\hat{\beta }}(t,s)=-{\mathrm{\Phi }}^{\hat{\beta }}(t,s)\mathrm{\partial }F\left(c^{\hat{\beta }}\right(s\left)\right),{\mathrm{\Phi }}^{\hat{\beta }}(s,s)=I,$ we have (A6) $\mathrm{\forall }s\in {\mathbb{R}}^p\underset{x}{sup}|P_n^{\ast }\left(\sqrt{n}{s}^{\mathrm{\top }}\right({\hat{\beta }}^{\ast }-\hat{\beta })\le x)-P(s^{\mathrm{\top }}{\mathcal{Z}}_n\le x)|\to 0\mathrm{a}.\mathrm{s}.$(A6) where ${\mathcal{Z}}_n\sim \mathrm{MVN}(0,{\mathrm{\Sigma }}_{\hat{\beta }})$ is the zero-centred multivariate normal measure with covariance $\begin{array}{rl}{\mathrm{\Sigma }}_{\hat{\beta }}& =\mathrm{Var}\left(\sum _i{B}_{\hat{\beta }}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\sqrt{n}\left(D_n\right(t_i)-c^{\hat{\beta }}(t_i\left)\right)\right)\\ & =\sum _i{B}_{\hat{\beta }}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right){\mathrm{\Sigma }}_{\hat{\beta }}^{\ast }(t_i,t_i)\left[B_{\hat{\beta }}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i){]}^{\mathrm{\top }}\\ & +\sum _{i\ne j}\left[B_{\hat{\beta }}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i\left){\mathrm{\Sigma }}_{\hat{\beta }}^{\ast }\right(t_i,t_j\left)\right[B_{\hat{\beta }}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\left(t_j\right){]}^{\mathrm{\top }}\\ & +\sum _{i\ne j}{B}_{\hat{\beta }}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\left(t_j\right){\mathrm{\Sigma }}_{\hat{\beta }}^{\ast }(t_i,t_j)\left[B_{\hat{\beta }}^{-1}\mathrm{\partial }{c}^{\hat{\beta }}\right(t_i){]}^{\mathrm{\top }}.\end{array}$ By consistency of the penalized LSE for the pure jump process, $C_n\left(t\right)$, $\hat{\beta }\to {\beta }^0\mathrm{a}.\mathrm{s}.\left(\omega \right)$, implying that $\mathrm{\partial }{c}^{\hat{\beta }}\left(t_i\right)\to \mathrm{\partial }{c}^{{\beta }^0}\left(t_i\right)$ and $B_{\hat{\beta }}^{-1}\to B_{{\beta }^0}^{-1}$ $\mathrm{a}.\mathrm{s}.\left(\omega \right)$. An appeal to Slutsky's theorem gives (A7) $\mathrm{MVN}(0,{\mathrm{\Sigma }}_{\hat{\beta }})\Rightarrow \mathrm{MVN}(0,{\mathrm{\Sigma }}_{{\beta }^0}).$(A7) Asymptotic normality of the penalized LSE for the pure jump process implies (A8) $\sqrt{n}(\hat{\beta }-{\beta }^0)\Rightarrow \mathrm{MVN}(0,{\mathrm{\Sigma }}_{{\beta }^0}).$(A8) Application of the Cramer–Wold device to Equations (A7(A7) $\mathrm{MVN}(0,{\mathrm{\Sigma }}_{\hat{\beta }})\Rightarrow \mathrm{MVN}(0,{\mathrm{\Sigma }}_{{\beta }^0}).$(A7) ) and (A8(A8) $\sqrt{n}(\hat{\beta }-{\beta }^0)\Rightarrow \mathrm{MVN}(0,{\mathrm{\Sigma }}_{{\beta }^0}).$(A8) ), along with Equation (A6(A6) $\mathrm{\forall }s\in {\mathbb{R}}^p\underset{x}{sup}|P_n^{\ast }\left(\sqrt{n}{s}^{\mathrm{\top }}\right({\hat{\beta }}^{\ast }-\hat{\beta })\le x)-P(s^{\mathrm{\top }}{\mathcal{Z}}_n\le x)|\to 0\mathrm{a}.\mathrm{s}.$(A6) ) imply $\mathrm{\forall }s\in {\mathbb{R}}^p\underset{x}{sup}|P_n^{\ast }\left(\sqrt{n}{s}^{\mathrm{\top }}\right({\hat{\beta }}^{\ast }-\hat{\beta })\le x)-P_n\left(\sqrt{n}{s}^{\mathrm{\top }}\right(\hat{\beta }-{\beta }^0)\le x)|\to 0\mathrm{a}.\mathrm{s}.,$ which in turn implies $\sqrt{n}({\hat{\beta }}^{\ast }-\hat{\beta }){\Rightarrow }^{\ast }\mathrm{MVN}(0,{\mathrm{\Sigma }}_{{\beta }^0}).$

Proof of Theorem 4.3

In view of Remark A.5, proof of Theorem 4.1 may be virtually repeated with $L_n\left(t\right)$ in place of $C_n\left(t\right)$ to obtain the hypothesis.