Complex dynamics in biological systems arising from multiple limit cycle bifurcation

ABSTRACT

In this paper, we study complex dynamical behaviour in biological systems due to multiple limit cycles bifurcation. We use simple epidemic and predator–prey models to show exact routes to new types of bistability, that is, bistability between equilibrium and periodic oscillation, and bistability between two oscillations, which may more realistically describe the real situations. Bifurcation theory and normal form theory are applied to investigate the multiple limit cycles bifurcating from Hopf critical point.

KEYWORDS:

• Dynamical system
• epidemic model
• predator–prey model
• stability
• Hopf bifurcation
• limit cycle
• normal form

AMS SUBJECT CLASSIFICATION:

• 92D30
• 37L10
• 37N25

1. Introduction

It is well known that dynamical systems, arising in almost all fields of science and engineering such as physics, mechanics, electronics, ecology, economy, biology, finance, etc. can exhibit self-sustained oscillations, leading to limit cycles. The phenomenon of limit cycle was first discovered by Poincaré [8] in late of the nineteenth century, who developed a breakthrough qualitative theory of differential equations which studies the general behaviours of the system without obtaining a specific solution. In order to determine the existence of limit cycles for a given differential equation and the properties of limit cycles, Poincaré introduced the method of topographical systems, the Poincaré Map, the method of small parameter [9] and the Annular Region Theorem. Ever since, the famous Poincaré Map is still the most basic tool for studying the stability and bifurcations of periodic orbits.

Since the mid of twentieth century, bifurcation theory was developed to promote the study of limit cycles and computational methods were developed to approximate the solution of limit cycles. From the point of view of dynamical system theory, there are four principal bifurcations in producing limit cycles: (i) Multiple Hopf bifurcations from a centre or focus; (ii) Separatrix cycle bifurcations from homoclinic or heteroclinic orbits; (iii) global centre bifurcation from a periodic annuli; and (iv) limit cycle bifurcations from multiple limit cycles. Limit cycles bifurcating from a focus or a centre are called local bifurcations of limit cycles or small-amplitude limit cycles, which are usually studied by using centre manifold theory and normal form theory (e.g. see [4, 5, 7]). Centre manifold and normal form theories may be the two most popular and useful tools for studying local bifurcations, in particular limit cycles of dynamical systems.

One well-known problem closely related to limit cycle theory is Hilbert's 16th problem, which is one of the 23 mathematical problems proposed by D. Hilbert at the Second International Congress of Mathematicians in 1900 [6]. Recently, a modern version of the second part of Hilbert's 16th problem was formulated by S. Smale, and chosen as one of his 18 most challenging mathematical problems for the twenty-first century [11]. This problem is to find an upper bound on the number of limit cycles that a planar polynomial system can have. If the problem is restricted to the vicinity of isolated fixed points, it is equivalent to studying generalized Hopf bifurcations, and the main tasks become computing the focus values (or normal form of Hopf bifurcation) of the point and determining centre conditions. It is now well known that for quadratic systems the maximum number of small-amplitude limit cycles around an isolated singular point is three [1]. However, globally, the problem is unsolved even for quadratic systems. Usually, people thought that Hilbert's 16th problem is an abstract mathematical problem and hard to have any applications.

In order to find multiple limit cycles bifurcating from Hopf singularity, efficient computational methods are essential, particularly in computing higher-order focus values or higher-order normal form coefficients. When the dimension of a dynamical system associated with Hopf bifurcation is more than two, centre manifold theory has to be used together with the normal form computation. In the 1990's computations of centre manifold and normal forms were extensively studied and some efficient computational methods were developed (e.g. see [5] and references therein). This is particularly useful in solving real problems such as those arising in biology. Indeed, recent publications show that even for two-dimensional epidemic model or predator–prey model, determining whether the system can have more than one limit cycle bifurcating from a Hopf critical point is not easy (e.g. see [10, 13, 19–21]). However, studying bifurcation of multiple limit cycles and determining the number of limit cycles are so important for applications. For example, in most disease models, due to difficulty of identifying multiple limit cycles, researchers often merely study bistable states which involve only equilibrium solutions. Nevertheless, in real situations, stable disease-free equilibrium and periodic disease motion may co-exist, and the motion can be generated from Hopf bifurcation. In such a more realistic case, one must investigate bifurcation of limit cycles and determine their stability. More recently, we have found two limit cycles in the vicinity of an equilibrium, with inner unstable and outer stable, showing the interesting bistable phenomenon [18]. The simulation is shown in Figure 1.

Figure 1. Two limit cycles in an HIV model [18]: $\dot{x}=1-Dx-(B+Ay/(y+C))xy,\dot{y}=(B+Ay/(y+C))xy-y$ when B=D=0.057, A=0.01846287, C=0.11969000: (a) three trajectories with moving directions indicated; and (b) two limit cycles with the inner unstable and outer stable.

In this paper, we will apply the method of normal forms to study bifurcation of multiple limit cycles in dynamical systems arising from biology. In particular, we investigate one epidemic model and one predator–prey model, and show that the former can have two limit cycles and the latter can exhibit three limit cycles for certain feasible parameter values. In the next section, we shall present a summary on centre manifold theory and normal form theory and their computations. Then, we consider the epidemic model in Section 3 and the predator–prey model in Section 4. Numerical simulations are given in Section 5 to verify the analytical predictions. Finally, conclusion is drawn in Section 6.

2. Theory, methodology and computation

In this section, we briefly describe centre manifold theory and normal form theory, as well as an efficient computational method. Consider a general nonlinear dynamical system described in the form of (1) $\dot{\mathbf{\text{w}}}=A\mathbf{\text{w}}+\mathbf{\text{F}}\left(\mathbf{\text{w}}\right),\mathbf{\text{w}}\in {\mathbf{\text{R}}}^n,\mathbf{\text{F}}\left(\mathbf{\text{w}}\right):{\mathbf{\text{R}}}^n\to {\mathbf{\text{R}}}^n,$(1) where the dot denotes differentiation with respect to time t, $A\mathbf{\text{w}}$ and $\mathbf{\text{F}}\left(\mathbf{\text{w}}\right)$ represent the linear and nonlinear parts of the system, respectively, and $\mathbf{\text{F}}\left(\mathbf{\text{w}}\right)$ is assumed to be analytic. Here, the matrix A is assumed diagonalizable, implying that the singularity of the system is a semisimple case. Further, suppose $\mathbf{\text{w}}=\mathbf{\text{0}}$ is an equilibrium of the system, leading to $\mathbf{\text{F}}\left(\mathbf{\text{0}}\right)=\mathbf{\text{0}}$ and $D_{\mathbf{\text{w}}}\mathbf{\text{F}}\left(\mathbf{\text{0}}\right)=\mathbf{\text{0}}$. Denote the n eigenvalues of A by ${\lambda }_i$, $i=1,\dots ,n$, and without loss of generality, we assume that there are k eigenvalues ${\lambda }_j$, $j=1,\dots ,k\le n$, having zero real part. This indicates that system (1(1) $\dot{\mathbf{\text{w}}}=A\mathbf{\text{w}}+\mathbf{\text{F}}\left(\mathbf{\text{w}}\right),\mathbf{\text{w}}\in {\mathbf{\text{R}}}^n,\mathbf{\text{F}}\left(\mathbf{\text{w}}\right):{\mathbf{\text{R}}}^n\to {\mathbf{\text{R}}}^n,$(1) ) has a k-dimensional centre manifold.

Then, by using a proper linear transformation $\mathbf{\text{w}}=T\mathbf{\text{z}}$, we can transform system (1(1) $\dot{\mathbf{\text{w}}}=A\mathbf{\text{w}}+\mathbf{\text{F}}\left(\mathbf{\text{w}}\right),\mathbf{\text{w}}\in {\mathbf{\text{R}}}^n,\mathbf{\text{F}}\left(\mathbf{\text{w}}\right):{\mathbf{\text{R}}}^n\to {\mathbf{\text{R}}}^n,$(1) ) into (2) $\dot{\mathbf{\text{z}}}=J\mathbf{\text{z}}+\mathbf{\text{f}}\left(\mathbf{\text{z}}\right),$(2) where J is a diagonal matrix, and $\mathbf{\text{f}}\left(\mathbf{\text{x}}\right)$ is expanded as $\mathbf{\text{f}}\left(\mathbf{\text{z}}\right)=\sum _{m\ge 2}{\mathbf{\text{f}}}_m\left(\mathbf{\text{z}}\right),\mathrm{where}{\mathbf{\text{f}}}_m\left(\mathbf{\text{z}}\right)=\sum _{m\left(n\right)}{\mathbf{\text{f}}}_{m\left(n\right)}{z}_1^{m_1}{z}_2^{m_2}\cdots z_n^{m_n},$ in which $m\left(n\right)$ denotes a vector $(m_1,m_2,\dots ,m_n)$ of n non-negative integers, satisfying $\sum _{j=1}^n{m}_j=m$, and the index $m\left(n\right)$ in the summation denotes that the summation goes over all the sets for $m\ge 2$.

Suppose that the matrix J is given in the form of $J=\text{diag}(J_1,J_2)$, where $J_1=\text{diag}({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_k),J_2=\text{diag}({\lambda }_{k+1},{\lambda }_{k+2},\dots ,{\lambda }_n),$ where $J_1$ contains the eigenvalues with zero real part, while $J_2$ involves the eigenvalues with negative zero real part. This means that the system only contains centre manifold and stable manifold. It should be noted that in general we can treat more general situation mathematically for which J also contains eigenvalues with positive real part, meaning that the system also contains an unstable manifold. However, for real applications a system with unstable manifold is usually unstable and the first task will be stabilizing the system, and therefore, without loss of generality, we assume there is no unstable manifold in the system.

Let $\mathbf{\text{z}}=({\mathbf{\text{x}}}^T,{\mathbf{\text{y}}}^T{)}^T$, where $\mathbf{\text{x}}=(x_1,x_2,\dots ,x_k{)}^T$ and $\mathbf{\text{y}}=(y_1,y_2,\dots ,y_{n-k}{)}^T$. Then, system (2(2) $\dot{\mathbf{\text{z}}}=J\mathbf{\text{z}}+\mathbf{\text{f}}\left(\mathbf{\text{z}}\right),$(2) ) can be rewritten as (3) $\begin{array}{rl}\dot{\mathbf{\text{x}}}& =J_1\mathbf{\text{x}}+{\mathbf{\text{f}}}_1(\mathbf{\text{x}},\mathbf{\text{y}}),\\ \dot{\mathbf{\text{y}}}& =J_2\mathbf{\text{y}}+{\mathbf{\text{f}}}_2(\mathbf{\text{x}},\mathbf{\text{y}}).\end{array}$(3)

2.1. Centre manifold theory

Using the centre manifold theory [2], we can represent the centre manifold of system (3(3) $\begin{array}{rl}\dot{\mathbf{\text{x}}}& =J_1\mathbf{\text{x}}+{\mathbf{\text{f}}}_1(\mathbf{\text{x}},\mathbf{\text{y}}),\\ \dot{\mathbf{\text{y}}}& =J_2\mathbf{\text{y}}+{\mathbf{\text{f}}}_2(\mathbf{\text{x}},\mathbf{\text{y}}).\end{array}$(3) ) as a (local) graph, (4) $W^c=\left\{\right(\mathbf{\text{x}},\mathbf{\text{y}})\mid \mathbf{\text{y}}=\mathbf{\text{H}}(\mathbf{\text{x}}\left)\right\},\mathbf{\text{H}}\left(\mathbf{\text{0}}\right)=D\mathbf{\text{H}}\left(\mathbf{\text{0}}\right)=\mathbf{\text{0}},$(4) where $\mathbf{\text{H}}:\mathbf{\text{U}}\to {\mathbf{\text{R}}}^{n-k}$ is defined on some neighbourhood $\mathbf{\text{U}}\subset {\mathbf{\text{R}}}^k$ of the origin.

We now consider the projection of the vector field on $\mathbf{\text{y}}=\mathbf{\text{H}}\left(\mathbf{\text{x}}\right)$ onto the centre eigenspace, and obtain the differential equation describing the dynamics on the centre manifold, given by (5) $\dot{\mathbf{\text{x}}}=J_1\mathbf{\text{x}}+{\mathbf{\text{f}}}_1(\mathbf{\text{x}},\mathbf{\text{H}}(\mathbf{\text{x}}\left)\right).$(5) Since $\mathbf{\text{H}}\left(\mathbf{\text{x}}\right)$ is tangent to $\mathbf{\text{y}}=\mathbf{\text{0}}$, the solutions of Equation  (5(5) $\dot{\mathbf{\text{x}}}=J_1\mathbf{\text{x}}+{\mathbf{\text{f}}}_1(\mathbf{\text{x}},\mathbf{\text{H}}(\mathbf{\text{x}}\left)\right).$(5) ) provide a good approximation of the flow restricted to the centre manifold $W^c$. More precisely, if the origin $\mathbf{\text{x}}=\mathbf{\text{0}}$ of Equation (5(5) $\dot{\mathbf{\text{x}}}=J_1\mathbf{\text{x}}+{\mathbf{\text{f}}}_1(\mathbf{\text{x}},\mathbf{\text{H}}(\mathbf{\text{x}}\left)\right).$(5) ) is locally asymptotically stable (respectively, unstable), then the origin of system (3(3) $\begin{array}{rl}\dot{\mathbf{\text{x}}}& =J_1\mathbf{\text{x}}+{\mathbf{\text{f}}}_1(\mathbf{\text{x}},\mathbf{\text{y}}),\\ \dot{\mathbf{\text{y}}}& =J_2\mathbf{\text{y}}+{\mathbf{\text{f}}}_2(\mathbf{\text{x}},\mathbf{\text{y}}).\end{array}$(3) ) is also locally asymptotically stable (respectively unstable).

The centre manifold can be found as follows: Substituting $\mathbf{\text{y}}=\mathbf{\text{H}}\left(\mathbf{\text{x}}\right)$ into the second equation of (3(3) $\begin{array}{rl}\dot{\mathbf{\text{x}}}& =J_1\mathbf{\text{x}}+{\mathbf{\text{f}}}_1(\mathbf{\text{x}},\mathbf{\text{y}}),\\ \dot{\mathbf{\text{y}}}& =J_2\mathbf{\text{y}}+{\mathbf{\text{f}}}_2(\mathbf{\text{x}},\mathbf{\text{y}}).\end{array}$(3) ) and using the chain rule yield (6) $\mathcal{N}\left(\mathbf{\text{H}}\right(\mathbf{\text{x}}\left)\right)=D\mathbf{\text{H}}\left(\mathbf{\text{x}}\right)[J_1\mathbf{\text{x}}+{\mathbf{\text{f}}}_1(\mathbf{\text{x}},\mathbf{\text{H}}\left(\mathbf{\text{x}}\right)\left)\right]-J_2\mathbf{\text{H}}\left(\mathbf{\text{x}}\right)-{\mathbf{\text{f}}}_2(\mathbf{\text{x}},\mathbf{\text{H}}(\mathbf{\text{x}}\left)\right)=\mathbf{\text{0}},$(6) with the boundary conditions $\mathbf{\text{H}}\left(\mathbf{\text{0}}\right)=D\mathbf{\text{H}}\left(\mathbf{\text{0}}\right)=\mathbf{\text{0}}$. The nonlinear differential equation for $\mathbf{\text{H}}$ cannot, of course, be solved exactly in most cases (to do so would imply that a solution of the original equation had been found), but its solution can be approximated arbitrarily closely as a Taylor series at $\mathbf{\text{x}}=\mathbf{\text{0}}$, described in the following theorem.

Theorem 2.1

[2]

If a function $\phi \left(\mathbf{x}\right),$ with $\phi \left(\mathbf{0}\right)=D\phi \left(\mathbf{0}\right)=\mathbf{0},$ can be found such that $\mathcal{N}\left(\phi \right(\mathbf{x}\left)\right)=O(\parallel \mathbf{x}{\parallel }^p)$ for some $p>1$ as $\parallel \mathbf{x}\parallel \to 0,$ then it follows that (7) $\mathbf{H}\left(\mathbf{x}\right)=\phi \left(\mathbf{x}\right)+O(\parallel \mathbf{x}{\parallel }^p)\mathrm{as}\parallel \mathbf{x}\parallel \to 0.$(7)

Thus, we can approximate $\mathbf{\text{H}}\left(\mathbf{\text{x}}\right)$ as closely as we wish by seeking series solutions of (6(6) $\mathcal{N}\left(\mathbf{\text{H}}\right(\mathbf{\text{x}}\left)\right)=D\mathbf{\text{H}}\left(\mathbf{\text{x}}\right)[J_1\mathbf{\text{x}}+{\mathbf{\text{f}}}_1(\mathbf{\text{x}},\mathbf{\text{H}}\left(\mathbf{\text{x}}\right)\left)\right]-J_2\mathbf{\text{H}}\left(\mathbf{\text{x}}\right)-{\mathbf{\text{f}}}_2(\mathbf{\text{x}},\mathbf{\text{H}}(\mathbf{\text{x}}\left)\right)=\mathbf{\text{0}},$(6) ). Note that by using centre manifold theory, we have reduced the n-dimensional differential system (3(3) $\begin{array}{rl}\dot{\mathbf{\text{x}}}& =J_1\mathbf{\text{x}}+{\mathbf{\text{f}}}_1(\mathbf{\text{x}},\mathbf{\text{y}}),\\ \dot{\mathbf{\text{y}}}& =J_2\mathbf{\text{y}}+{\mathbf{\text{f}}}_2(\mathbf{\text{x}},\mathbf{\text{y}}).\end{array}$(3) ) to the k-dimensional differential system and keep the local dynamics unchanged.

2.2. Normal form theory

Having applied centre manifold theory to obtain the simple differential system (5(5) $\dot{\mathbf{\text{x}}}=J_1\mathbf{\text{x}}+{\mathbf{\text{f}}}_1(\mathbf{\text{x}},\mathbf{\text{H}}(\mathbf{\text{x}}\left)\right).$(5) ) which describes the dynamical behaviour of the system restricted to the centre manifold, now we want to further simplify the differential system (5(5) $\dot{\mathbf{\text{x}}}=J_1\mathbf{\text{x}}+{\mathbf{\text{f}}}_1(\mathbf{\text{x}},\mathbf{\text{H}}(\mathbf{\text{x}}\left)\right).$(5) ) by applying normal form theory. To achieve this, rewrite Equation (5(5) $\dot{\mathbf{\text{x}}}=J_1\mathbf{\text{x}}+{\mathbf{\text{f}}}_1(\mathbf{\text{x}},\mathbf{\text{H}}(\mathbf{\text{x}}\left)\right).$(5) ) as (8) $\dot{\mathbf{\text{x}}}=J_1\mathbf{\text{x}}+{\mathbf{\text{f}}}_1\left(\mathbf{\text{x}}\right)=J_1\mathbf{\text{x}}+{\mathbf{\text{f}}}_1^2\left(\mathbf{\text{x}}\right)+{\mathbf{\text{f}}}_1^3\left(\mathbf{\text{x}}\right)+\cdots +{\mathbf{\text{f}}}_1^s\left(\mathbf{\text{x}}\right)+O(\parallel \mathbf{\text{x}}{\parallel }^{s+1}),$(8) where ${\mathbf{\text{f}}}_1^s$ denotes the sth-degree homogeneous polynomial in $\mathbf{\text{x}}$. Define ${\mathbf{\text{M}}}_s$ as the linear space of vector fields whose elements are homogeneous polynomials of degree s, and thus ${\mathbf{\text{f}}}_1^s\in {\mathbf{\text{M}}}_s,s=2,3,\dots$. Next, we introduce the near-identity transformation: (9) $\mathbf{\text{x}}=\mathbf{\text{u}}+\mathbf{\text{Q}}\left(\mathbf{\text{u}}\right)=\mathbf{\text{u}}+{\mathbf{\text{q}}}^2\left(\mathbf{\text{u}}\right)+{\mathbf{\text{q}}}^3\left(\mathbf{\text{u}}\right)+\cdots +{\mathbf{\text{q}}}^s\left(\mathbf{\text{u}}\right)+O(\parallel \mathbf{\text{u}}{\parallel }^{s+1}),$(9) where ${\mathbf{\text{q}}}^s\in {\mathbf{\text{M}}}_s,s=2,3,\dots$, into Equation (8(8) $\dot{\mathbf{\text{x}}}=J_1\mathbf{\text{x}}+{\mathbf{\text{f}}}_1\left(\mathbf{\text{x}}\right)=J_1\mathbf{\text{x}}+{\mathbf{\text{f}}}_1^2\left(\mathbf{\text{x}}\right)+{\mathbf{\text{f}}}_1^3\left(\mathbf{\text{x}}\right)+\cdots +{\mathbf{\text{f}}}_1^s\left(\mathbf{\text{x}}\right)+O(\parallel \mathbf{\text{x}}{\parallel }^{s+1}),$(8) ) to obtain the normal form, (10) $\dot{\mathbf{\text{u}}}=J_1\mathbf{\text{u}}+\mathbf{\text{C}}\left(\mathbf{\text{u}}\right)=J_1\mathbf{\text{u}}+{\mathbf{\text{c}}}^2\left(\mathbf{\text{u}}\right)+{\mathbf{\text{c}}}^3\left(\mathbf{\text{u}}\right)+\cdots +{\mathbf{\text{c}}}^s\left(\mathbf{\text{u}}\right)+O(\parallel \mathbf{\text{u}}{\parallel }^{s+1}),$(10) where ${\mathbf{\text{c}}}^s\in {\mathbf{\text{M}}}_s,s=2,3,\dots$. The procedure of normal form method is to use the transformation ${\mathbf{\text{q}}}^s$ to simplify ${\mathbf{\text{c}}}^s$ ‘as simple as possible’ order by order for $s=2,3,\dots$. Note that the s-order transformation ${\mathbf{\text{q}}}^s$ does not affect the lower-order normal form terms ${\mathbf{\text{c}}}^j,j<s$ but affect all higher-order normal form terms ${\mathbf{\text{c}}}^j,j>s$. Therefore, assuming that the normal form reduction up to order s−1 has been preformed, we can introduce the transformation $\mathbf{\text{x}}=\mathbf{\text{u}}+{\mathbf{\text{q}}}^s\left(\mathbf{\text{u}}\right)$, and differentiating it gives (11) $\dot{\mathbf{\text{x}}}=[I+D{\mathbf{\text{q}}}^s(\mathbf{\text{u}}\left)\right]\dot{\mathbf{\text{u}}}.$(11) Now, we introduce the map, called homological operator, as follows: (12) $\mathrm{L}:{\mathbf{\text{M}}}_s\to {\mathbf{\text{M}}}_s,\mathrm{with}\mathrm{L}\left(\mathbf{\text{X}}\right)=[\mathbf{\text{X}},\mathrm{L}]=D\mathrm{L}\mathbf{\text{X}}-D\mathbf{\text{X}}\mathrm{L},\mathrm{\forall }\mathbf{\text{X}}\in {\mathbf{\text{M}}}_s,$(12) where $[\bullet ,\bullet ]$ is called Lie bracket operation, with $\mathrm{L}=J_1\mathbf{\text{x}}$, and define the subspace induced by the map as $\mathrm{L}\left({\mathbf{\text{M}}}_s\right)$. Thus ${\mathbf{\text{M}}}_s=\mathrm{L}\left({\mathbf{\text{M}}}_s\right)\oplus {\mathbf{\text{G}}}_s$, where ${\mathbf{\text{G}}}_s$ is the complement for $\mathrm{L}\left({\mathbf{\text{M}}}_s\right)$ in ${\mathbf{\text{M}}}_s$.

Then, it follows from Equation (11(11) $\dot{\mathbf{\text{x}}}=[I+D{\mathbf{\text{q}}}^s(\mathbf{\text{u}}\left)\right]\dot{\mathbf{\text{u}}}.$(11) ) that (13) $\begin{array}{rl}\dot{\mathbf{\text{u}}}& =[I+D{\mathbf{\text{q}}}^s(\mathbf{\text{u}}\left){]}^{-1}{\mathbf{\text{f}}}_1\right[\mathbf{\text{u}}+{\mathbf{\text{q}}}^s\left(\mathbf{\text{u}}\right)]\\ & =[I-D{\mathbf{\text{q}}}^s(\mathbf{\text{u}})+O(\parallel \mathbf{\text{u}}{\parallel }^{2(s-1)}\left)\right]\left[J_1(\mathbf{\text{u}}+{\mathbf{\text{q}}}^s(\mathbf{\text{u}}\left)\right)+\sum _{k=2}^s{\mathbf{\text{f}}}_1(\mathbf{\text{u}}+{\mathbf{\text{q}}}^s(\mathbf{\text{u}}\left)\right)+O(\parallel y{\parallel }^{s+1})\right]\\ & =J_1\mathbf{\text{u}}+D\mathrm{L}{\mathbf{\text{q}}}^s\left(\mathbf{\text{u}}\right)+{\mathbf{\text{f}}}_1^2\left(\mathbf{\text{u}}\right)+\cdots +{\mathbf{\text{f}}}_1^{s-1}\left(\mathbf{\text{u}}\right)+{\mathbf{\text{f}}}_1^s\left(\mathbf{\text{u}}\right)-D{\mathbf{\text{q}}}^s\left(\mathbf{\text{u}}\right)\mathrm{L}+O(\parallel \mathbf{\text{u}}{\parallel }^{s+1})\\ & =J_1\mathbf{\text{u}}+{\mathbf{\text{c}}}^2\left(\mathbf{\text{u}}\right)+\cdots +{\mathbf{\text{c}}}^{s-1}\left(\mathbf{\text{u}}\right)+{\mathbf{\text{f}}}_1^s\left(\mathbf{\text{u}}\right)+\mathrm{L}{\mathbf{\text{q}}}^s\left(\mathbf{\text{u}}\right)+O(\parallel \mathbf{\text{u}}{\parallel }^{s+1}).\end{array}$(13) Here it should be noted that ${\mathbf{\text{c}}}^j={\mathbf{\text{f}}}_1^j,j=2,3,\dots ,s-1$ since it is assumed that the normal form reduction has been performed up to order s−1. Now, to simplify the s-order term, $\mathrm{\forall }{\mathbf{\text{f}}}_1^s\in {\mathbf{\text{M}}}_s$, we need to find suitable ${\mathbf{\text{q}}}^s\in {\mathbf{\text{M}}}_s$ such that ${\mathbf{\text{f}}}_1^s\left(\mathbf{\text{u}}\right)+\mathrm{L}{\mathbf{\text{q}}}^s\left(\mathbf{\text{u}}\right)={\mathbf{\text{c}}}^s\left(\mathbf{\text{u}}\right)$ becomes as simple as possible, where $\mathrm{L}{\mathbf{\text{q}}}^s\left(\mathbf{\text{u}}\right)\in \mathrm{L}\left({\mathbf{\text{M}}}_s\right)$ and ${\mathbf{\text{c}}}^s\left(\mathbf{\text{u}}\right)\in {\mathbf{\text{G}}}_s$. Therefore, once the basis of $\mathrm{L}\left({\mathbf{\text{M}}}_s\right)$ is found, one can determine the basis of the complementary space ${\mathbf{\text{G}}}_s$ and thus the ‘form’ of the normal form. It is well known that the normal form is not unique since the basis is not unique.

2.3. Normal form computation

From the view point of computation, it seems computing centre manifold and normal form is straightforward. But actually designing an efficient algorithm is not an easy task. As a matter of fact, many researchers have devoted to develop efficient computational methods on normal forms (e.g. see [3, 5, 15, 17]). Recently, an explicit recursive formula has been developed for computing the normal form together with centre manifold for general n-dimensional differential systems associated with semisimple singularities. We briefly outline the approach as follows. Rewrite Equations (9(9) $\mathbf{\text{x}}=\mathbf{\text{u}}+\mathbf{\text{Q}}\left(\mathbf{\text{u}}\right)=\mathbf{\text{u}}+{\mathbf{\text{q}}}^2\left(\mathbf{\text{u}}\right)+{\mathbf{\text{q}}}^3\left(\mathbf{\text{u}}\right)+\cdots +{\mathbf{\text{q}}}^s\left(\mathbf{\text{u}}\right)+O(\parallel \mathbf{\text{u}}{\parallel }^{s+1}),$(9) ) and (10(10) $\dot{\mathbf{\text{u}}}=J_1\mathbf{\text{u}}+\mathbf{\text{C}}\left(\mathbf{\text{u}}\right)=J_1\mathbf{\text{u}}+{\mathbf{\text{c}}}^2\left(\mathbf{\text{u}}\right)+{\mathbf{\text{c}}}^3\left(\mathbf{\text{u}}\right)+\cdots +{\mathbf{\text{c}}}^s\left(\mathbf{\text{u}}\right)+O(\parallel \mathbf{\text{u}}{\parallel }^{s+1}),$(10) ) as (14) $\mathbf{\text{x}}=\mathbf{\text{u}}+\mathbf{\text{Q}}\left(\mathbf{\text{u}}\right)=\mathbf{\text{u}}+\sum _{m\ge 2}\sum _{m\left(k\right)}{\mathbf{\text{q}}}_{m\left(k\right)}{u}_1^{m_1}{u}_2^{m_2}\cdots u_k^{m_k}\equiv \mathbf{\text{q}}\left(\mathbf{\text{u}}\right),$(14) and (15) $\dot{\mathbf{\text{u}}}=J_1\mathbf{\text{u}}+\mathbf{\text{C}}\left(\mathbf{\text{u}}\right)=J_1\mathbf{\text{u}}+\sum _{m\ge 2}\sum _{m\left(k\right)}{\mathbf{\text{c}}}_{m\left(k\right)}{u}_1^{m_1}{u}_2^{m_2}\cdots u_k^{m_k},$(15) respectively, and then the centre manifold can be expressed in the new variable $\mathbf{\text{u}}$ as (16) $\mathbf{\text{y}}=\mathbf{\text{H}}\left(\mathbf{\text{q}}\right(\mathbf{\text{u}}\left)\right)=\sum _{m\ge 2}\sum _{m\left(k\right)}{\mathbf{\text{h}}}_{m\left(k\right)}{u}_1^{m_1}{u}_2^{m_2}\cdots u_k^{m_k}\equiv \mathbf{\text{h}}\left(\mathbf{\text{u}}\right).$(16) Combining the centre manifold and normal form computations yields the following equations, (17) $D_{\mathbf{\text{u}}}\left(\begin{array}{c}\mathbf{\text{Q}}\left(\mathbf{\text{u}}\right)\\ \mathbf{\text{h}}\left(\mathbf{\text{u}}\right)\end{array}\right)J_1\mathbf{\text{u}}-\left(\begin{array}{c}{J}_o\mathbf{\text{Q}}\left(\mathbf{\text{u}}\right)\\ J_r\mathbf{\text{h}}\left(\mathbf{\text{u}}\right)\end{array}\right)=\left(\begin{array}{c}{\mathbf{\text{F}}}_1\left(\mathbf{\text{u}}\right)\\ {\mathbf{\text{F}}}_2\left(\mathbf{\text{u}}\right)\end{array}\right)-D_{\mathbf{\text{u}}}\left(\begin{array}{c}\mathbf{\text{Q}}\left(\mathbf{\text{u}}\right)\\ \mathbf{\text{h}}\left(\mathbf{\text{u}}\right)\end{array}\right)\mathbf{\text{C}}\left(\mathbf{\text{u}}\right)-\left(\begin{array}{c}\mathbf{\text{C}}\left(\mathbf{\text{u}}\right)\\ 0\end{array}\right),$(17) where ${\mathbf{\text{F}}}_1\left(\mathbf{\text{u}}\right)={\mathbf{\text{f}}}_1\left(\mathbf{\text{q}}\right(\mathbf{\text{u}}),\mathbf{\text{h}}(\mathbf{\text{u}}\left)\right)$, ${\mathbf{\text{F}}}_2\left(\mathbf{\text{u}}\right)={\mathbf{\text{f}}}_2\left(\mathbf{\text{q}}\right(\mathbf{\text{u}}),\mathbf{\text{h}}(\mathbf{\text{u}}\left)\right)$. Comparing the coefficients on both sides of Equation (17(17) $D_{\mathbf{\text{u}}}\left(\begin{array}{c}\mathbf{\text{Q}}\left(\mathbf{\text{u}}\right)\\ \mathbf{\text{h}}\left(\mathbf{\text{u}}\right)\end{array}\right)J_1\mathbf{\text{u}}-\left(\begin{array}{c}{J}_o\mathbf{\text{Q}}\left(\mathbf{\text{u}}\right)\\ J_r\mathbf{\text{h}}\left(\mathbf{\text{u}}\right)\end{array}\right)=\left(\begin{array}{c}{\mathbf{\text{F}}}_1\left(\mathbf{\text{u}}\right)\\ {\mathbf{\text{F}}}_2\left(\mathbf{\text{u}}\right)\end{array}\right)-D_{\mathbf{\text{u}}}\left(\begin{array}{c}\mathbf{\text{Q}}\left(\mathbf{\text{u}}\right)\\ \mathbf{\text{h}}\left(\mathbf{\text{u}}\right)\end{array}\right)\mathbf{\text{C}}\left(\mathbf{\text{u}}\right)-\left(\begin{array}{c}\mathbf{\text{C}}\left(\mathbf{\text{u}}\right)\\ 0\end{array}\right),$(17) ), we obtain the recursive formulas for the coefficients of the centre manifold and the normal form as well as the associated nonlinear transformation.

For convenience, we express the powers of $\mathbf{\text{q}}\left(\mathbf{\text{u}}\right)$ and $\mathbf{\text{h}}\left(\mathbf{\text{u}}\right)$, for $j\ge 0$, as (18) $\begin{array}{rl}{\mathbf{\text{q}}}^j\left(\mathbf{\text{u}}\right)& =\sum _{m=j}^{\mathrm{\infty }}\sum _{m\left(k\right)}{\mathbf{\text{q}}}_{m\left(k\right)}^j{u}_1^{m_1}{u}_2^{m_2}\cdots u_k^{m_k},\\ {\mathbf{\text{h}}}^j\left(\mathbf{\text{u}}\right)& =\sum _{m=2j}^{\mathrm{\infty }}\sum _{m\left(k\right)}{\mathbf{\text{h}}}_{m\left(k\right)}^j{u}_1^{m_1}{u}_2^{m_2}\cdots u_k^{m_k}.\end{array}$(18) Then, the following result is obtained.

Theorem 2.2

[12]

For any fixed $s\left(k\right),$ $s\ge 2,$ let $\mathrm{\Lambda }=\sum _{i=1}^k{\lambda }_i{s}_i$. Then the recursive formulas for the coefficients of the nonlinear transformation (14(14) $\mathbf{\text{x}}=\mathbf{\text{u}}+\mathbf{\text{Q}}\left(\mathbf{\text{u}}\right)=\mathbf{\text{u}}+\sum _{m\ge 2}\sum _{m\left(k\right)}{\mathbf{\text{q}}}_{m\left(k\right)}{u}_1^{m_1}{u}_2^{m_2}\cdots u_k^{m_k}\equiv \mathbf{\text{q}}\left(\mathbf{\text{u}}\right),$(14) ), the normal form (15(15) $\dot{\mathbf{\text{u}}}=J_1\mathbf{\text{u}}+\mathbf{\text{C}}\left(\mathbf{\text{u}}\right)=J_1\mathbf{\text{u}}+\sum _{m\ge 2}\sum _{m\left(k\right)}{\mathbf{\text{c}}}_{m\left(k\right)}{u}_1^{m_1}{u}_2^{m_2}\cdots u_k^{m_k},$(15) ) and the centre manifold (16(16) $\mathbf{\text{y}}=\mathbf{\text{H}}\left(\mathbf{\text{q}}\right(\mathbf{\text{u}}\left)\right)=\sum _{m\ge 2}\sum _{m\left(k\right)}{\mathbf{\text{h}}}_{m\left(k\right)}{u}_1^{m_1}{u}_2^{m_2}\cdots u_k^{m_k}\equiv \mathbf{\text{h}}\left(\mathbf{\text{u}}\right).$(16) ) of system (3(3) $\begin{array}{rl}\dot{\mathbf{\text{x}}}& =J_1\mathbf{\text{x}}+{\mathbf{\text{f}}}_1(\mathbf{\text{x}},\mathbf{\text{y}}),\\ \dot{\mathbf{\text{y}}}& =J_2\mathbf{\text{y}}+{\mathbf{\text{f}}}_2(\mathbf{\text{x}},\mathbf{\text{y}}).\end{array}$(3) ), that is, ${\mathbf{q}}_{s\left(k\right)},$ ${\mathbf{c}}_{s\left(k\right)}$ and ${\mathbf{h}}_{s\left(k\right)},$ are given below.

1. For ${\mathbf{q}}_{s\left(k\right)}$ and ${\mathbf{c}}_{s\left(k\right)},$ if $\mathrm{\Lambda }-{\lambda }_j=0,$ $j=1,\dots ,k,$ then $q_{s\left(k\right),j}=0,c_{s\left(k\right),j}=a_{s\left(k\right),j}-b_{s\left(k\right),j},$ otherwise, $q_{s\left(k\right),j}=\frac{a_{s\left(k\right),j}-b_{s\left(k\right),j}}{\mathrm{\Lambda }-{\lambda }_j},c_{s\left(k\right),j}=0.$

2. For ${\mathbf{h}}_{s\left(k\right)}$, the formulas are given by $h_{s\left(k\right),j-k}=\frac{a_{s\left(k\right),j}-b_{s\left(k\right),j}}{\mathrm{\Lambda }-{\lambda }_j},j=k+1,\dots ,n,$ where $\begin{array}{rl}{\mathbf{a}}_{s\left(k\right)}& =\sum _{m=2}^s\sum _{m\left(n\right)}\sum _{j\left(n\right)}^{j=s}\sum _{j_1\left(k\right)}\sum _{j_2\left(k\right)}\cdots \sum _{j_n\left(k\right)}{\mathbf{f}}_{m\left(n\right)}{q}_{j_1\left(k\right),1}^{m_1}\cdots q_{j_k\left(k\right),k}^{m_k}{h}_{j_{k+1}\left(k\right),1}^{m_{k+1}}\cdots h_{j_n\left(k\right),n-k}^{m_n},\\ {\mathbf{b}}_{s\left(k\right)}& =\sum _{i=1}^k\sum _{l=2}^{s-1}\sum _{l\left(k\right)}(s_i+1-l_i)\left(\begin{array}{c}{\mathbf{q}}_{s\left(k\right)-l\left(k\right)+e_i\left(k\right)}\\ {\mathbf{h}}_{s\left(k\right)-l\left(k\right)+e_i\left(k\right)}\end{array}\right)c_{l\left(k\right),i},\\ {\mathbf{q}}_{s\left(k\right)}^j& =\sum _{l=j-1}^{s-1}\sum _{l\left(k\right)\le s\left(k\right)}{\mathbf{q}}_{l\left(k\right)}^{j-1}{\mathbf{q}}_{s\left(k\right)-l\left(k\right)},\\ {\mathbf{h}}_{s\left(k\right)}^j& =\sum _{l=2j-2}^{s-2}\sum _{l\left(k\right)\le s\left(k\right)}{\mathbf{h}}_{l\left(k\right)}^{j-1}{\mathbf{h}}_{s\left(k\right)-l\left(k\right)}.\end{array}$

The proof for this theorem and Maple program can be found in [12].

2.4. Bifurcation of multiple limit cycles

Now we discuss how to determine the maximal number of limit cycles which may bifurcate from a Hopf critical point. Suppose that the normal form of system (1(1) $\dot{\mathbf{\text{w}}}=A\mathbf{\text{w}}+\mathbf{\text{F}}\left(\mathbf{\text{w}}\right),\mathbf{\text{w}}\in {\mathbf{\text{R}}}^n,\mathbf{\text{F}}\left(\mathbf{\text{w}}\right):{\mathbf{\text{R}}}^n\to {\mathbf{\text{R}}}^n,$(1) ) has been obtained in the polar coordinates up to the $(2k+1)$th order term: (19) $\begin{array}{rl}\dot{r}=& r(v_0+v_1{r}^2+v_2{r}^4+\cdots +v_k{r}^{2k}),\\ \dot{\theta }=& {\omega }_c+t_1{r}^2+t_2{r}^4+\cdots +t_k{r}^{2k},\end{array}$(19) where r and θ denote the amplitude and phase of motion, respectively. Both $v_k$ and $t_k$ are explicitly expressed in terms of the original system's coefficients. $v_k$ is called the kth-order focus value of the Hopf-type critical point (the origin). The zero-order focus value $v_0$ is obtained from linear analysis.

The basic idea of finding k small-amplitude limit cycles of system (1(1) $\dot{\mathbf{\text{w}}}=A\mathbf{\text{w}}+\mathbf{\text{F}}\left(\mathbf{\text{w}}\right),\mathbf{\text{w}}\in {\mathbf{\text{R}}}^n,\mathbf{\text{F}}\left(\mathbf{\text{w}}\right):{\mathbf{\text{R}}}^n\to {\mathbf{\text{R}}}^n,$(1) ) around the origin is as follows: First, find the conditions based on the original system's coefficients such that $v_0=v_1=\cdots =v_{k-1}=0$ (note that $v_0=0$ is automatically satisfied at the critical point), but $v_k\ne 0$, and then perform appropriate small perturbations to prove the existence of k limit cycles. This indicates that the procedure for finding multiple limit cycles involves two steps: Computing the focus values (i.e. computing the coefficients of the normal form) and solving multivariate coupled nonlinear polynomial equations: $v_0=v_1=\cdots =v_{k-1}=0$. In the following theorem, we give sufficient conditions for the existence of small-amplitude limit cycles. (The proofs can be found in [16].)

Theorem 2.3.

Suppose that the focus values depend on k parameters, expressed as (20) $v_j=v_j({ϵ}_1,{ϵ}_2,\dots ,{ϵ}_k),j=0,1,\dots ,k,$(20) satisfying (21) $\begin{array}{rl}& v_j(0,\dots ,0)=0,j=0,1,\dots ,k-1,v_k(0,\dots ,0)\ne 0,\\ & \mathrm{and}det\left[\frac{\mathrm{\partial }(v_0,v_1,\dots ,v_{k-1})}{\mathrm{\partial }({ϵ}_1,{ϵ}_2,\dots ,{ϵ}_k)}(0,\dots ,0)\right]\ne 0.\end{array}$(21) Then, for any given ${ϵ}_0>0,$ there exist ${ϵ}_1,$ ${ϵ}_2,\dots ,{ϵ}_k$ and $\delta >0$ with $|{ϵ}_j|<{ϵ}_0,j=1,2,\dots ,k$ such that the equation $\dot{r}=0$ has exactly k real positive roots $($i.e. system (1(1) $\dot{\mathbf{\text{w}}}=A\mathbf{\text{w}}+\mathbf{\text{F}}\left(\mathbf{\text{w}}\right),\mathbf{\text{w}}\in {\mathbf{\text{R}}}^n,\mathbf{\text{F}}\left(\mathbf{\text{w}}\right):{\mathbf{\text{R}}}^n\to {\mathbf{\text{R}}}^n,$(1) ) has exactly k limit cycles) in a δ-ball with its centre at the origin.

3. An epidemic model with a nonlinear incidence rate

The first system we consider in this section for bifurcation of multiple limit cycles is an epidemic model with a nonlinear incidence rate. Detailed dynamical analysis including saddle-node bifurcation, Hopf bifurcation and homoclnic bifurcation was given in [10]. In [10] the critical conditions on Hopf bifurcation are given in terms of system parameters. Moreover, the stability of bifurcating limit cycles is determined by calculating the first focus value. In particular, in Theorem 2.6 of [10], it was mentioned that there are at least two limit cycles if the first focus value vanishes. But no further discussions are given in [10] on how to obtain the conditions for the existence of two limit cycles. Here, we want to show that this epidemic model actually can have maximal two limit cycles due to Hopf bifurcation, and derive the explicit conditions on the existence of two limit cycles. It should be noted that the Hopf bifurcation condition and the first-order focus value obtained in this paper are different from that given [10], though they are equivalent. Our simple formulas help us to compute higher-order focus values for analysing bifurcation of multiple limit cycles. Consider the normalized system (1.3) in [10] describing the epidemic model: (22) $\begin{array}{rl}\dot{I}& =\frac{I^2}{1+p{I}^2}(A-I-R)-mI,\\ \dot{R}& =qI-R,\end{array}$(22) where I and R denote the number of infective individuals and the number of removed individuals, respectively, and all the four parameters, p,A,m and q, take positive values. The system has a disease-free equilibrium ${\mathrm{E}}_0=(0,0)$, which is a stable node, and a disease equilibrium (a positive equilibrium), ${\mathrm{E}}_1=(I_1,R_1)$, where $R_1=q{I}_1$ and $I_1$ is determined by the equation: (23) $(mp+q+1)I_1^2-A{I}_1+m=0.$(23) Therefore,

1. there is no positive equilibrium if $A^2<4m(mp+q+1)$;

2. there is one positive equilibrium if $A^2=4m(mp+q+1)$; and

3. there are two positive equilibria if $A^2>4m(mp+q+1)$.

Regarding the bifurcation of multiple limit cycles in system (22(22) $\begin{array}{rl}\dot{I}& =\frac{I^2}{1+p{I}^2}(A-I-R)-mI,\\ \dot{R}& =qI-R,\end{array}$(22) ), we have the following result.

Theorem 3.1.

For any real values of $I_1\in (0,1/\sqrt{3E}),(E>0),$ if the parameters satisfy $\begin{array}{rl}A& =\frac{4(4-3E{I}_1^2+3I_1^2)}{9E{I}_2^3},p=\frac{1}{3I_1^2}-E,\\ m& =\frac{4-3E{I}_1^2+3I_1^2}{3E{I}_1^2+2},q=\frac{4-3E{I}_1^2}{9E{I}_1^4(2+3E{I}_1^2)(9E^2{I}_1^4+6I_1^2+8)},\end{array}$ then system (22(22) $\begin{array}{rl}\dot{I}& =\frac{I^2}{1+p{I}^2}(A-I-R)-mI,\\ \dot{R}& =qI-R,\end{array}$(22) ) can have two limit cycles due to Hopf bifurcation. The condition under which only one limit cycle exists is also given.

Proof.

To find the maximal number of limit cycles which can bifurcate from a Hopf critical point, we will not explicitly solve the positive equilibrium (like what is done in [10]) since the explicit expression involving square root will cause very messy calculations in computing higher-order focus values. The Jacobian matrix evaluated at the positive equilibrium has the trace, given by (24) $\mathrm{Tr}\left(J\right)=-(3pm+p+2q+3)I_1^2+2A{I}_1-m-1,$(24) Now, linearly solving Equation (23(23) $(mp+q+1)I_1^2-A{I}_1+m=0.$(23) ) and $\mathrm{Tr}\left(J\right)=0$ for m and q yields (25) $m=\frac{1+(1+p)I_1^2}{1-p{I}_1^2}\mathrm{and}q=\frac{A{I}_1(1-p{I}_1^2)-(1+p{I}_1^2{)}^2-2I_1^2}{I_1^2(1-p{I}_1^2)}.$(25) Then, the determinant of the Jacobian matrix becomes (26) $det\left(J\right)=\frac{(1+p{I}_1^2)\left[A{I}_1\right(1-p{I}_1^2)-2(1+p)I_1^2-2]}{1-p{I}_1^2}.$(26) It is obvious that m>0 requires that $1-p{I}_1^2>0$, and a Hopf bifurcation can occur if $A{I}_1(1-p{I}_1^2)>2[1+(1+p\left)I_1^2\right]$ which in turn guarantees q>0. Multiplying $1+p{I}^2$ on both sides of the equations in (22(22) $\begin{array}{rl}\dot{I}& =\frac{I^2}{1+p{I}^2}(A-I-R)-mI,\\ \dot{R}& =qI-R,\end{array}$(22) ) and then introducing the following transformation into the resulting equation, (27) $\left(\begin{array}{c}I\\ R\end{array}\right)=\left(\begin{array}{c}{I}_1\\ q{I}_1\end{array}\right)+\left[\begin{array}{cc}1& 0\\ p+\frac{1}{I_1^2}& \frac{{\omega }_c}{I_1^2}\end{array}\right]\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right),$(27) where ${\omega }_c=\sqrt{(1+p{I}_1^2)\left[A{I}_1\right(1-p{I}_1^2)-2-2(1+p\left)I_1^2\right]/(1-p{I}_1^2)}$, with time scaling $t\to {\omega }_{c}t$, yielding a new system: (28) $\begin{array}{rl}{\dot{x}}_1=& x_2-\frac{1+(1+p)I_1^2}{{\omega }_c{I}_1(1-p{I}_1^2)}{x}_1^2+\frac{2}{I_1}{x}_1{x}_2-\frac{1+(1+p)I_1^2}{{\omega }_c{I}_1(1-p{I}_1^2)}{x}_1^3+\frac{1}{I_1^2}{x}_1^2{x}_2,\\ {\dot{x}}_2=& -x_1-\frac{(1-p{I}_1^2)(1+2pA{I}_1^3)+(1-p)I_1^2-3p(1+p)I_1^4)}{{\omega }_c^2{I}_1(1-p{I}_1^2)}{x}_1^2+\frac{2}{{\omega }_c{I}_1}{x}_1{x}_2\\ & -\frac{(1+AI)p{I}_1^2+I_1^2+1}{{\omega }_c^2{I}_1^2}{x}_1^3+\frac{1}{{\omega }_c{I}_1^2}{x}_1^2{x}_2,\end{array}$(28) whose linear part is in Jordan canonical form.

Next, applying the Maple program [12, 14] to system (28(28) $\begin{array}{rl}{\dot{x}}_1=& x_2-\frac{1+(1+p)I_1^2}{{\omega }_c{I}_1(1-p{I}_1^2)}{x}_1^2+\frac{2}{I_1}{x}_1{x}_2-\frac{1+(1+p)I_1^2}{{\omega }_c{I}_1(1-p{I}_1^2)}{x}_1^3+\frac{1}{I_1^2}{x}_1^2{x}_2,\\ {\dot{x}}_2=& -x_1-\frac{(1-p{I}_1^2)(1+2pA{I}_1^3)+(1-p)I_1^2-3p(1+p)I_1^4)}{{\omega }_c^2{I}_1(1-p{I}_1^2)}{x}_1^2+\frac{2}{{\omega }_c{I}_1}{x}_1{x}_2\\ & -\frac{(1+AI)p{I}_1^2+I_1^2+1}{{\omega }_c^2{I}_1^2}{x}_1^3+\frac{1}{{\omega }_c{I}_1^2}{x}_1^2{x}_2,\end{array}$(28) ) we obtain the first focus value, given by (29) $v_1=\frac{(1+2p)(3pA{I}_1^3+4p{I}_1^2+4I_1^2-A{I}_1+4)}{8(1+p{I}_1^2)\left[A{I}_1\right(1-p{I}_1^2)-2(1+p)I_1^2-2]}.$(29) Note that the denominator of $v_1$ is positive. Solving $v_1=0$ for A yields (30) $A=\frac{4(1+I_1^2+p{I}_1^2)}{I_1(1-3p{I}_1^2)},$(30) which requires $1-3p{I}_1^2>0$ in order for $A>0$. Under the condition (30(30) $A=\frac{4(1+I_1^2+p{I}_1^2)}{I_1(1-3p{I}_1^2)},$(30) ), executing the Maple program yields the second focus value, (31) $v_2=\frac{1+2p}{32I_1^2(1+p{I}_1^2)}$(31) which clearly shows that $v_2>0$ for positive parameter values, implying that system (22(22) $\begin{array}{rl}\dot{I}& =\frac{I^2}{1+p{I}^2}(A-I-R)-mI,\\ \dot{R}& =qI-R,\end{array}$(22) ) can exhibit at most two small-amplitude limit cycles due to Hopf bifurcation, and the outer is unstable (due to $v_2>0$) and the inner is stable. Note that the system contains four free parameters, and so mathematically it may be possible to find at most four limit cycles without the physical restriction on the parameters.

Finally, we want to find the feasible positive parameters for the existence of the two limit cycles. Let (32) $p=\frac{1}{3I_1^2}-E,E>0.$(32) Then, p>0 requires (33) $0<I_1<\frac{1}{\sqrt{3E}},\mathrm{\forall }E>0,$(33) which guarantees A>0 and (34) $m=\frac{4-3E{I}_1^2+3I_1^2}{3E{I}_1^2+2}>0.$(34) Further, under the condition (33(33) $0<I_1<\frac{1}{\sqrt{3E}},\mathrm{\forall }E>0,$(33) ), the q given in Equation (25(25) $m=\frac{1+(1+p)I_1^2}{1-p{I}_1^2}\mathrm{and}q=\frac{A{I}_1(1-p{I}_1^2)-(1+p{I}_1^2{)}^2-2I_1^2}{I_1^2(1-p{I}_1^2)}.$(25) ) becomes (35) $q=\frac{4-3E{I}_1^2}{9E{I}_1^4(2+3E{I}_1^2)(9E^2{I}_1^4+6I_1^2+8)}>0.$(35) Consequently, substituting Equation (32(32) $p=\frac{1}{3I_1^2}-E,E>0.$(32) ) into Equation (31(31) $v_2=\frac{1+2p}{32I_1^2(1+p{I}_1^2)}$(31) ) results in (36) $v_2=\frac{2+3I_1^2-6E{I}_1^2}{32I_1^4(4-3E{I}_1^2)}>0,\text{(due to the condition~(33))}.$(36)

Moreover, we may also discuss the existence of only one limit cycle, for which $v_1\ne 0$, that is, ${\mathrm{One}}_{\mathrm{LC}}:=3pA{I}_1^3+4p{I}_1^2+4I_1^2-A{I}_1+4\ne 0.$ In order to find the above condition given in terms of the system parameters, we eliminate $I_1$ from Equation (23(23) $(mp+q+1)I_1^2-A{I}_1+m=0.$(23) ) and $\mathrm{Tr}\left(J\right)=0$ (see Equation (24(24) $\mathrm{Tr}\left(J\right)=-(3pm+p+2q+3)I_1^2+2A{I}_1-m-1,$(24) )) to obtain the solution for $I_1$, $I_1=\frac{2m^{2}p+mq+2m-q-1}{A(mp+p+1)},$ and a resultant equation, $\begin{array}{rl}\mathrm{Res}& =(1-m)(pm+1+p)A^2+(m-1{)}^2{q}^2+2(m-1\left)\right(2m^{2}p+2m-1)q\\ & +(2m^{2}p+2m-1{)}^2=0.\end{array}$ Then, with $\mathrm{Res}=0$, substituting the solution $I_1$ into $\mathrm{On}{\mathrm{e}}_{\mathrm{LC}}\ne 0$ yields the following condition: $\begin{array}{rl}0\ne & p(1-m)\left[\right(1+m)p+1]A^2+p(1-m{)}^2{q}^2-(1-m\left)\right[2(m^2+m+2)p^2+3(m+1)\\ & p+1]q-(1+2p\left)\right[2m(2m+m^2+2)p^2+(4m^2+5m+2)p+2m+1],\end{array}$ under which there exists only one small-amplitude limit cycle.

It is noted in [10] that one unstable limit cycle is obtained when A=10.02,m=4.0,q=3.6,p=0.2, for which $v_1\approx 0.555787>0$. In fact, for one limit cycle, we can choose some parameter values to obtain a stable limit cycle, since $v_1$ changes its sign around the value of A given in Equation (30(30) $A=\frac{4(1+I_1^2+p{I}_1^2)}{I_1(1-3p{I}_1^2)},$(30) ). For example, by choosing $A=23,m=\frac{11}{4},q=\frac{187}{10},p=\frac{1}{5}$ (which yields $I_1=1$) we obtain $v_1=-\frac{1}{240}<0$, leading to a stable limit cycle; and if taking $A=21,m=\frac{11}{4},q=\frac{167}{10},p=\frac{1}{5}$ (which also yields $I_1=1$) then we have $v_1=\frac{7}{1488}>0$, leading to an unstable limit cycle.

To end this section, we give a set of parameter values for model (22(22) $\begin{array}{rl}\dot{I}& =\frac{I^2}{1+p{I}^2}(A-I-R)-mI,\\ \dot{R}& =qI-R,\end{array}$(22) ) to exhibit two limit cycles as follows: Taking E=1 yields $0<I_1<\frac{1}{\sqrt{3}}\approx 0.577$. Then, choosing $I_1=\frac{1}{2}$ results in (37) $p=\frac{1}{3},A=\frac{128}{9},m=\frac{16}{11},q=\frac{2093}{99},v_0=v_1=0,v_2=\frac{5}{26}.$(37) Hence, proper perturbations on the parameters can be chosen such that $0<v_0\ll -v_1\ll v_2$ to yield two limit cycles, with the outer stable and the inner unstable, both enclosing the stable equilibrium ${\mathrm{E}}_1$. A more detailed numerical example with computer simulation will be given in Section 5.1.

4. A predator–prey model with negative effect of prey on its predator

The next system we consider in this section is a predator–prey model with negative effect of prey on its predator [13], described by (38) $\begin{array}{rl}\dot{X}& =X\left(r_1+\frac{{\alpha }_{12}Y}{b_2+Y}-\frac{{\beta }_{1}Y}{e_1+X}-d_{1}X\right),\\ \dot{Y}& =Y\left(r_2-\frac{{\beta }_{2}X}{e_2+Y}-d_{2}Y\right),\end{array}$(38) where X and Y represent population densities of the predator and prey, respectively. $r_1$ is the intrinsic growth rate of the predator, $d_1$ is the intensity of intraspecific competitions, while $r_1/d_1$ represents the carrying capacity of the predator when in isolation from the prey. Similarly, $r_2$ is the intrinsic growth rate of the prey, $d_2$ is the intensity of intranspecific competition, while $r_2/d_2$ represents the carrying capacity of the prey when in isolation from the predator. When $r_1={\beta }_1=0$, system (38(38) $\begin{array}{rl}\dot{X}& =X\left(r_1+\frac{{\alpha }_{12}Y}{b_2+Y}-\frac{{\beta }_{1}Y}{e_1+X}-d_{1}X\right),\\ \dot{Y}& =Y\left(r_2-\frac{{\beta }_{2}X}{e_2+Y}-d_{2}Y\right),\end{array}$(38) ) becomes the Rosenzweig–MacArthur model. Both cases $r_1={\beta }_1=0$ and $r_1{\beta }_1\ne 0$ were discussed in [13] for a preliminary study of the transition of system states. Complex dynamics and bifurcations such as Hopf bifurcation were not investigated in [13].

In this section, we will consider two cases for bifurcations of multiple limit cycles, one is for $r_1={\beta }_1=0$ and the other for ${\beta }_1=0$, but $r_1\ne 0$. In order to simplify the system and reduce the number of parameters, introducing the following scaling, $\begin{array}{rl}X& =\frac{d_1}{r_2},Y=\frac{d_2}{r_2},\tau =r_{2}t,A=\frac{{\alpha }_{12}}{r_2},r=\frac{r_1}{r_2},\\ B_1& =\frac{{\beta }_1{d}_1}{d_2{r}_2},B_2=\frac{{\beta }_2{d}_2}{d_1{r}_2},E_1=\frac{e_1{d}_1}{r_2},E_2=\frac{e_2{d}_2}{r_2},E_3=\frac{b_2{d}_2}{r_2},\end{array}$ into system (38(38) $\begin{array}{rl}\dot{X}& =X\left(r_1+\frac{{\alpha }_{12}Y}{b_2+Y}-\frac{{\beta }_{1}Y}{e_1+X}-d_{1}X\right),\\ \dot{Y}& =Y\left(r_2-\frac{{\beta }_{2}X}{e_2+Y}-d_{2}Y\right),\end{array}$(38) ), we obtain (still using the notation t for τ) (39) $\begin{array}{rl}\dot{x}& =x\left(r+\frac{Ay}{E_3+y}-\frac{B_{1}y}{E_1+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(39) which now contains only six parameters: $r,A,B_1,B_2,E_2$ and $E_3$. Now, the first case is given by $B_1=r=0$, and the second case is defined by $B_1=0$. In the following, we first consider the first case and then the second case. We will show that there are feasible positive parameter values for both cases such that system (39(39) $\begin{array}{rl}\dot{x}& =x\left(r+\frac{Ay}{E_3+y}-\frac{B_{1}y}{E_1+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(39) ) can have maximal three small-amplitude limit cycles though the second case has less restrictions on the parameters.

4.1. Case $B_1=r=0$

For this case, system (39(39) $\begin{array}{rl}\dot{x}& =x\left(r+\frac{Ay}{E_3+y}-\frac{B_{1}y}{E_1+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(39) ) becomes (40) $\begin{array}{rl}\dot{x}& =x\left(\frac{Ay}{E_3+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(40) which only contains four parameters: $A,B_2,E_2$ and $E_3$. Ideally, four limit cycles might be possible if feasible parameter values exist. However, due to physical limitation on the parameters, we can have three limit cycles for system (40(40) $\begin{array}{rl}\dot{x}& =x\left(\frac{Ay}{E_3+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(40) ), as stated in the following theorem.

Theorem 4.1.

System (40(40) $\begin{array}{rl}\dot{x}& =x\left(\frac{Ay}{E_3+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(40) ) can have three small-amplitude limit cycles bifurcating from the origin due to Hopf bifurcation, with the parameters satisfying the following conditions: $0<y_2<0.266,0<E_2<1-2y_2,E_3>\frac{y_2^2(1-E_2-2y_2)}{E_2+y_2^2},$ where $y_2$ is determined from the equation: $A{B}_2{y}_2-(1-y_2)(E_2+y_2)(E_3+y_2)=0$.

Proof.

First, note that system (40(40) $\begin{array}{rl}\dot{x}& =x\left(\frac{Ay}{E_3+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(40) ) has three equilibrium solutions, two of them are boundary equilibria and one is a positive equilibrium: (41) ${\mathrm{E}}_0:(0,0),{\mathrm{E}}_1:(0,1),{\mathrm{E}}_2:\left(\frac{(1-y_2)(E_2+y_2)}{B_2},y_2\right),$(41) where $y_2$ is determined from the following equation: (42) $A{B}_2{y}_2-(1-y_2)(E_2+y_2)(E_3+y_2)=0.$(42) It can be shown that ${\mathrm{E}}_0$ is a degenerate saddle and ${\mathrm{E}}_1$ is a saddle. For the equilibrium ${\mathrm{E}}_2$, suppose $J_2$ is the Jacobian matrix of system (40(40) $\begin{array}{rl}\dot{x}& =x\left(\frac{Ay}{E_3+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(40) ) evaluated at this positive equilibrium. Then, solving the equation $\mathrm{Tr}\left(J_2\right)=0$ and Equation (42(42) $A{B}_2{y}_2-(1-y_2)(E_2+y_2)(E_3+y_2)=0.$(42) ) for A and $B_2$ yields (43) $A=\frac{(E_3+y_2)(1-E_2-2y_2)}{E_2+y_2},B_2=E_2+\frac{(1-y_2)y_2^2+E_2(E_2+y_2)}{y_2(1-E_2-2y_2)}.$(43) The positivity condition on A and $B_2$ requires that (44) $0<E_2<1-2y_2,0<y_2<\frac{1}{2}.$(44) Next, multiplying $(E_2+y)(E_3+y)$ on both sides of the equations in (40(40) $\begin{array}{rl}\dot{x}& =x\left(\frac{Ay}{E_3+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(40) ) and then introducing the following linear transformation into the resulting equation, (45) $\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}\frac{(1-y_2)(E_2+y_2)}{B_2}\\ y_2\end{array}\right)+\left[\begin{array}{cc}1& 0\\ \frac{(E_3+y_2)(E_2+y_2)}{E_3(1-E_2-2y_2)}& \frac{{\omega }_c(E_2+y_2)}{y_2{E}_3(1-E_2-2y_2{)}^2}\end{array}\right]\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right),$(45) where (46) ${\omega }_c=\sqrt{\left(y_2\right(1-E_2-2y_2\left)\right(E_3+y_2\left)\right[E_3(E_2+y_2^2)-y_2^2(1-E_2-2y_2)]},$(46) with time scaling $t\to {\omega }_{c}t$, yields the system: (47) $\begin{array}{rl}{\dot{x}}_1& =x_2+f_1(x_1,x_2),\\ {\dot{x}}_2& =-x_1+f_2(x_1,x_2),\end{array}$(47) where $f_1$ and $f_2$ are both 4th-degree polynomials. Note that under the conditions given in Equation (44(44) $0<E_2<1-2y_2,0<y_2<\frac{1}{2}.$(44) ), ${\omega }_c^2>0$ requires that (48) $E_3>\frac{y_2^2(1-E_2-2y_2)}{E_2+y_2^2}.$(48) Now, we apply the Maple program in [12, 14] for system (47(47) $\begin{array}{rl}{\dot{x}}_1& =x_2+f_1(x_1,x_2),\\ {\dot{x}}_2& =-x_1+f_2(x_1,x_2),\end{array}$(47) ) to obtain the focus values $v_i,i=1,2,\dots ,4$, all of them are functions of $E_2,E_3$ and $y_2$. $v_1$ is given by (49) $\begin{array}{rl}{v}_1& =\frac{(1-y_2)(E_3+y_2)(E_2+y_2)}{8y_2{E}_3(1-E_2-2y_2{)}^3[2y_2^3+E_2{E}_3+(E_2+E_3-1)y_2^2]}\\ & \times \{2y_2^6+6E_2{y}_2^5+(E_2^2+E_2{E}_3-E_2+E_3\left)\right[3y_2^4-(1-E_3)y_2^3-E_2^2{E}_3]\\ & -6E_2^2{E}_3{y}_2(E_2+y_2)\}.\end{array}$(49) and other lengthy higher-order focus values are not listed here for brevity. Since there are three free parameters, the best result we expect is that we may find conditions such that $v_1=v_2=v_3=0$, but $v_4\ne 0$, possibly yielding four small-amplitude limit cycles.

Since the factor in the script bracket in $v_1$ is not a linear function in any of its variables $E_2,E_3$ and $y_2$, we eliminate $E_3$ from the two pairs of equations $v_1=v_2=0$ and $v_1=v_3=0$, and obtain two solutions for $E_3$: $E_{3a}(E_2,y_2)$ and $E_{3b}(E_2,y_2)$, and two resultant equations. Then, we use the Maple built-in command resultant($R_{12},R_{13},E_2$) to obtain a single-variate resultant equation $R_{123}\left(y_2\right)=0$, which yields 11 real positive solutions such that $R_{12}(E_2,y_2)=R_{13}(E_2,y_2)=0$ with positive solutions of $E_2$. Next, we verify these 11 solutions by checking if the two solutions $E_{3a}$ and $E_{3b}$ are equal, $E_{3a}(E_2,y_2)=E_{3b}(E_2,y_2)$. It is found that there are only two solutions satisfying this condition: $\begin{array}{r}\begin{array}{l}{\mathrm{S}}_1:y_2=0.22599842\dots ,E_2=0.04109062\cdots ,E_3=0.28091409\cdots ,\\ {\mathrm{S}}_2:y_2=0.21468192\cdots ,E_2=0.02586831\cdots ,E_3=0.12300053\cdots .\end{array}\end{array}$ Finally, we want to verify if these two solutions satisfy $A>0,B_2>0$ and ${\omega }_c^2>0$. It is easy to use Equations (54(54) $A=\frac{(E_3+y_3)\left[y_3\right(1-E_2-2y_3)-r(E_2+y_3\left)\right]}{y_3(E_2+y_3)},B_2=\frac{(1-y_3)(E_2+y_3{)}^2}{y_3(1-E_2-2y_3)}.$(54) ) and (57(57) ${\omega }_c=\sqrt{\begin{array}{rl}& (E_3+y_3)\left\{y_3\right(1-E_2-2y_3\left)\right[E_3(E_2+y_3^2)-y_3^2(1-E_2-2y_3)]\\ & -r{E}_3(1-y_3)(E_2+y_3{)}^2\}\end{array}},$(57) ) to obtain that $\begin{array}{rlr}\mathrm{For}{\mathrm{S}}_1:A=0.96207726\cdots ,& B_2=0.48196508\cdots ,& {\omega }_c^2=0,\\ \mathrm{For}{\mathrm{S}}_2:A=0.76474062\cdots ,& B_2=0.38855298\cdots ,& {\omega }_c^2<0,\end{array}$ indicating that no solutions exist for system (40(40) $\begin{array}{rl}\dot{x}& =x\left(\frac{Ay}{E_3+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(40) ) to have four limit cycles. Thus, the next best result could be three limit cycles.

To find feasible parameter values for the existence of three limit cycles, we only need to solve the resultant equation $R_{12}(E_2,y_2)=0$ with $E_3=E_{3a}(E_2,y_2)$. For the convenience of choosing the perturbations later to obtain three limit cycles, we may solve the equation $v_1=0$ ($v_1$ given in Equation (49(49) $\begin{array}{rl}{v}_1& =\frac{(1-y_2)(E_3+y_2)(E_2+y_2)}{8y_2{E}_3(1-E_2-2y_2{)}^3[2y_2^3+E_2{E}_3+(E_2+E_3-1)y_2^2]}\\ & \times \{2y_2^6+6E_2{y}_2^5+(E_2^2+E_2{E}_3-E_2+E_3\left)\right[3y_2^4-(1-E_3)y_2^3-E_2^2{E}_3]\\ & -6E_2^2{E}_3{y}_2(E_2+y_2)\}.\end{array}$(49) )) for $E_3$ to obtain a solution, and then solve the resultant equation $R_{12}(E_2,y_2)=0$. Note that feasible solutions must satisfy the conditions given in Equations (44(44) $0<E_2<1-2y_2,0<y_2<\frac{1}{2}.$(44) ) and (48(48) $E_3>\frac{y_2^2(1-E_2-2y_2)}{E_2+y_2^2}.$(48) ). Now there is one free parameter, we may use a numerical searching in the interval $y_2\in (0,0.5)$ to find feasible solutions from the equation $R_{12}=0$. It can be shown that $R_{12}=0$ has real positive solutions for $y_2\in (0,0.266)$. For example, letting $y_2=0.13$, we have only one feasible solution: (50) $\begin{array}{llll}{\mathrm{S}}_1:& y_2=0.13,& E_2=0.01939683\cdots ,& E_3=0.74997712\cdots ,\\ & A=4.11353863\cdots ,& B_2=0.20728245\cdots ,& {\omega }_c=0.03521529\cdots .\end{array}$(50) for which $v_0=v_1=v_2=0$, but $v_3\ne 0$. Thus, proper perturbations can be chosen on the parameters to obtain three small-amplitude limit cycles.

A more detailed numerical example with computer simulation will be given in Section 5.2.

4.2. Case $B_1=0$

Now we turn to a more general case with only $B_1=0$. For this case, system (39(39) $\begin{array}{rl}\dot{x}& =x\left(r+\frac{Ay}{E_3+y}-\frac{B_{1}y}{E_1+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(39) ) can be rewritten as (51) $\begin{array}{rl}\dot{x}& =x\left(r+\frac{Ay}{E_3+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(51) Ideally, five limit cycles might be possible if feasible parameter values are allowed. However, due to physical limitation on the parameters, we can still have only three small-amplitude limit cycles for system (51(51) $\begin{array}{rl}\dot{x}& =x\left(r+\frac{Ay}{E_3+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(51) ).

Theorem 4.2.

For system (51(51) $\begin{array}{rl}\dot{x}& =x\left(r+\frac{Ay}{E_3+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(51) ), if the following conditions hold: $\begin{array}{rl}0& <y_3<0.21,0<E_2<1-2y_3,E_3>\frac{y_3^2(1-E_2-2y_3)}{E_2+y_3^2},\\ 0& <r<min\left\{\frac{y_3(1-E_2-2y_3)}{E_2+y_3},\frac{y_3(1-E_2-2y_3)\left[E_3\right(E_2+y_3^2)-y_3^2(1-E_2-2y_3\left)\right]}{E_3(E_2+y_3)(1-y_3)(E_2+y_3)}\right\},\end{array}$ then the system can have three small-amplitude limit cycles bifurcating from the origin due to Hopf bifurcation.

Proof.

To prove this result, we first find four equilibrium solutions for system (51(51) $\begin{array}{rl}\dot{x}& =x\left(r+\frac{Ay}{E_3+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(51) ), three of them are boundary equilibria and one is positive equilibrium: (52) ${\mathrm{E}}_0:(0,0),{\mathrm{E}}_1:(r,0),{\mathrm{E}}_2:(0,1),{\mathrm{E}}_3:\left(\frac{(1-y_3)(E_2+y_3)}{B_2},y_3\right),$(52) where $y_3$ is determined from the following equation: (53) $B_2\left[r\right(E_3+y_3)+A{y}_3]-(1-y_3)(E_2+y_3)(E_3+y_3)=0.$(53) Suppose $J_3$ is the Jacobian matrix of system (51(51) $\begin{array}{rl}\dot{x}& =x\left(r+\frac{Ay}{E_3+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(51) ) evaluated at the positive equilibrium ${\mathrm{E}}_3$. Then, solving the equation $\mathrm{Tr}\left(J_3\right)=0$ and Equation (53(53) $B_2\left[r\right(E_3+y_3)+A{y}_3]-(1-y_3)(E_2+y_3)(E_3+y_3)=0.$(53) ) for A and $B_2$ yields (54) $A=\frac{(E_3+y_3)\left[y_3\right(1-E_2-2y_3)-r(E_2+y_3\left)\right]}{y_3(E_2+y_3)},B_2=\frac{(1-y_3)(E_2+y_3{)}^2}{y_3(1-E_2-2y_3)}.$(54) In order to have A>0 and $B_2>0$, it requires that (55) $0<y_3<min\left\{1,\frac{1-(1+r)E_2}{2+r}\right\},\mathrm{for}(1+r)E_2<1.$(55) Next, multiplying $(E_2+y)(E_3+y)$ on both sides of the equations in (51(51) $\begin{array}{rl}\dot{x}& =x\left(r+\frac{Ay}{E_3+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(51) ) and then introducing the following transformation into the resulting equation, (56) $\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}\frac{(1-y_3)(E_2+y_3)}{B_2}\\ y_3\end{array}\right)+\left[\begin{array}{cc}1& 0\\ \frac{-y_3(E_3+y_3)(E_2+y_3)}{{\tilde{E}}_3}& \frac{{\omega }_c(E_2+y_3)}{{\tilde{E}}_3(E_2+2y_3-1)}\end{array}\right]\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right),$(56) where ${\tilde{E}}_3=E_3\left[r\right(E_2+y_3)-y_3(1-E_2-2y_3\left)\right]$ and (57) ${\omega }_c=\sqrt{\begin{array}{rl}& (E_3+y_3)\left\{y_3\right(1-E_2-2y_3\left)\right[E_3(E_2+y_3^2)-y_3^2(1-E_2-2y_3)]\\ & -r{E}_3(1-y_3)(E_2+y_3{)}^2\}\end{array}},$(57) with time scaling $t\to {\omega }_{c}t$, yields the system in the form of (47(47) $\begin{array}{rl}{\dot{x}}_1& =x_2+f_1(x_1,x_2),\\ {\dot{x}}_2& =-x_1+f_2(x_1,x_2),\end{array}$(47) ). Now, similarly, we apply the Maple program in [12, 14] to system (47(47) $\begin{array}{rl}{\dot{x}}_1& =x_2+f_1(x_1,x_2),\\ {\dot{x}}_2& =-x_1+f_2(x_1,x_2),\end{array}$(47) ) to obtain the focus values $v_i,i=1,2,\dots ,5$, all of them are functions of $r,E_2,E_3$ and $y_3$. Thus, the best result we expect is that we may choose them such that $v_1=v_2=v_3=v_4=0$, $v_5\ne 0$, possibly yielding five small-amplitude limit cycles.

First, we try to find if there exist feasible parameter values for the existence of five limit cycles. To achieve this, we need to find feasible parameter values such that $v_1=v_2=v_3=v_4=0$. Solving r from the equation $v_1=0$ we obtain a solution for $r=r_n/r_d$, where (58) $\begin{array}{rl}{r}_n=& y_3\{4y_3^7+2(7E_2-1)y_3^6+6(2E_2^2+E_2{E}_3-2E_2+E_3)y_3^5\\ & +(3E_2+2E_3-5)(E_2^2+E_2{E}_3-E_2+E_3)y_3^4\\ & +(E_2^3{E}_3+E_2^2{E}_3^2-E_2^3-15E_2^2{E}_3+2E_2^2+E_2{E}_3-E_3^2-E_2+E_3)y_3^3\\ & +6E_3{E}_2^2(1-3E_2)y_3^2-2E_3{E}_2^2(4E_2^2+E_2{E}_3-4E_2+E_3)y_3\\ & +E_2^2{E}_3(1-E_2)(E_2^2+E_2{E}_3-E_2+E_3)\},\\ r_d=& E_3\{4y_3^6+(13E_2+2E_3-3)y_3^5+(14E_2^2+7E_2{E}_3-7E_2-E_3+1)y_3^4\\ & +E_2(5E_2^2+8E_2{E}_3-4E_3+3)y_3^3\\ & +E_2(3E_2^2{E}_3+10E_2^2-4E_2{E}_3+2E_2+E_3)y_3^2\\ & +E_2^2(7E_2^2-E_2+2E_3)y_3+E_2^3(E_2^2+E_2{E}_3-E_2+E_3)\},\end{array}$(58) and then $v_2,v_3$ and $v_4$ are expressed in terms of $E_2,E_3$ and $y_3$. The numerators of these equations are respectively 3rd-degree, 8th-degree and 13th-degree polynomials with respect to $E_3$. To solve these equations, we eliminate $E_3$ from the two pairs of equations $v_2=v_3=0$ and $v_2=v_4=0$, and obtain two solutions for $E_3$: $E_{3a}(E_2,y_3)$ and $E_{3b}(E_2,y_3)$, and two resultant equations, $R_{23}(E_2,y_3)=0$ and $R_{24}(E_2,y_3)=0$, where $R_{23}$ and $R_{24}$ are respectively 31th-degree and 79th-degree polynomials with respect to $E_2$. Eliminating $E_2$ from these two equations is difficult. So we use the Maple built-in command resultant($R_{23},R_{24},E_2$) to obtain a single-variate resultant equation $R_{234}\left(y_3\right)=0$. Solving this equation for positive $y_3$ we obtain 62 real positive solutions, among which only 17 solutions lead to $R_{23}(E_2,y_3)=R_{24}(E_2,y_3)=0$ with positive solutions of $E_2$. Next, we verify these 17 solutions by checking if the two solutions $E_{3a}$ and $E_{3b}$ are equal, $E_{3a}(E_2,y_3)=E_{3b}(E_2,y_3)$. We find that there are only 3 solutions satisfying this condition: $\begin{array}{r}{\mathrm{S}}_1:y_3=0.27736160\cdots ,E_2=0.01462471\cdots ,E_3=0.15329046\cdots ,\\ {\mathrm{S}}_2:y_3=0.15343514\cdots ,E_2=0.05932713\cdots ,E_3=0.15470647\cdots ,\\ {\mathrm{S}}_3:y_3=0.32478609\cdots ,E_2=4.51650721\cdots ,E_3=0.08362686\cdots .\end{array}$ Finally, we want to verify if these three solutions satisfy $A>0,B_2>0$ and ${\omega }_c^2>0$. It is easy to use Equations (54(54) $A=\frac{(E_3+y_3)\left[y_3\right(1-E_2-2y_3)-r(E_2+y_3\left)\right]}{y_3(E_2+y_3)},B_2=\frac{(1-y_3)(E_2+y_3{)}^2}{y_3(1-E_2-2y_3)}.$(54) ) and (57(57) ${\omega }_c=\sqrt{\begin{array}{rl}& (E_3+y_3)\left\{y_3\right(1-E_2-2y_3\left)\right[E_3(E_2+y_3^2)-y_3^2(1-E_2-2y_3)]\\ & -r{E}_3(1-y_3)(E_2+y_3{)}^2\}\end{array}},$(57) ) to obtain that $\begin{array}{rl}& \mathrm{For}{\mathrm{S}}_1:A=1.01016268\cdots ,B_2=0.51579028\cdots ,{\omega }_c^2=0,\\ & \mathrm{For}{\mathrm{S}}_2:A=0.66063599\cdots ,B_2=0.39406752\cdots ,{\omega }_c^2<0,\\ & \mathrm{For}{\mathrm{S}}_3:A=-0.00109093\cdots ,B_2=-11.69604925\cdots ,{\omega }_c^2<0.\end{array}$ So, none of the 3 solutions is a candidate for system (51(51) $\begin{array}{rl}\dot{x}& =x\left(r+\frac{Ay}{E_3+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(51) ) to exhibit five limit cycles. Therefore, there do not exist feasible parameter values for the existence of five limit cycles in system (51(51) $\begin{array}{rl}\dot{x}& =x\left(r+\frac{Ay}{E_3+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(51) ). Thus, the next best result could be four limit cycles.

To find feasible parameter values for the existence of four limit cycles, we only need to solve $v_2=v_3=0$ ($v_1=0$ has been solved for r), and thus if there are solutions they should have infinitely many solutions. Now we only need to solve the resultant equation $R_{23}(E_2,y_3)=0$ with $E_3=E_{3a}(E_2,y_3)$. It follows from Equations (54(54) $A=\frac{(E_3+y_3)\left[y_3\right(1-E_2-2y_3)-r(E_2+y_3\left)\right]}{y_3(E_2+y_3)},B_2=\frac{(1-y_3)(E_2+y_3{)}^2}{y_3(1-E_2-2y_3)}.$(54) ) and (57(57) ${\omega }_c=\sqrt{\begin{array}{rl}& (E_3+y_3)\left\{y_3\right(1-E_2-2y_3\left)\right[E_3(E_2+y_3^2)-y_3^2(1-E_2-2y_3)]\\ & -r{E}_3(1-y_3)(E_2+y_3{)}^2\}\end{array}},$(57) ) that $A>0,B_2>0$ and ${\omega }_c>0$ need the following conditions to be satisfied: (59) $\begin{array}{rl}0& <y_3<\frac{1}{2},0<E_2<1-2y_3,E_3>\frac{y_3^2(1-E_2-2y_3)}{E_2+y_3^2},\\ 0& <r<min\left\{\frac{y_3(1-E_2-2y_3)}{E_2+y_3},\frac{y_3(1-E_2-2y_3)\left[E_3\right(E_2+y_3^2)-y_3^2(1-E_2-2y_3\left)\right]}{E_3(E_2+y_3)(1-y_3)(E_2+y_3)}\right\},\end{array}$(59) and $r=r_n/r_d$, where $r_n$ and $r_d$ are given in Equation (58(58) $\begin{array}{rl}{r}_n=& y_3\{4y_3^7+2(7E_2-1)y_3^6+6(2E_2^2+E_2{E}_3-2E_2+E_3)y_3^5\\ & +(3E_2+2E_3-5)(E_2^2+E_2{E}_3-E_2+E_3)y_3^4\\ & +(E_2^3{E}_3+E_2^2{E}_3^2-E_2^3-15E_2^2{E}_3+2E_2^2+E_2{E}_3-E_3^2-E_2+E_3)y_3^3\\ & +6E_3{E}_2^2(1-3E_2)y_3^2-2E_3{E}_2^2(4E_2^2+E_2{E}_3-4E_2+E_3)y_3\\ & +E_2^2{E}_3(1-E_2)(E_2^2+E_2{E}_3-E_2+E_3)\},\\ r_d=& E_3\{4y_3^6+(13E_2+2E_3-3)y_3^5+(14E_2^2+7E_2{E}_3-7E_2-E_3+1)y_3^4\\ & +E_2(5E_2^2+8E_2{E}_3-4E_3+3)y_3^3\\ & +E_2(3E_2^2{E}_3+10E_2^2-4E_2{E}_3+2E_2+E_3)y_3^2\\ & +E_2^2(7E_2^2-E_2+2E_3)y_3+E_2^3(E_2^2+E_2{E}_3-E_2+E_3)\},\end{array}$(58) ). Since now there is one free parameter, we may use a numerical searching for $y_3$ in the interval $y_3\in (0,0.5)$ to find feasible solutions from the equation $R_{23}=0$. It can be shown that $R_{23}=0$ has no real positive solutions which satisfy the conditions in Equation (59(59) $\begin{array}{rl}0& <y_3<\frac{1}{2},0<E_2<1-2y_3,E_3>\frac{y_3^2(1-E_2-2y_3)}{E_2+y_3^2},\\ 0& <r<min\left\{\frac{y_3(1-E_2-2y_3)}{E_2+y_3},\frac{y_3(1-E_2-2y_3)\left[E_3\right(E_2+y_3^2)-y_3^2(1-E_2-2y_3\left)\right]}{E_3(E_2+y_3)(1-y_3)(E_2+y_3)}\right\},\end{array}$(59) ). Hence, there do not exist feasible parameter values for the existence of four limit cycles in system (51(51) $\begin{array}{rl}\dot{x}& =x\left(r+\frac{Ay}{E_3+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(51) ). Thus, the next best result could be three limit cycles.

To find feasible parameter values for the existence of three limit cycles, we only need to solve $v_2=0$ ($v_1=0$ has been solved for r), and thus if there are solutions they should have infinitely many solutions. To achieve this we can numerically search the region in the 2-dimensional parameter space, $0<y_3<\frac{1}{2},0<E_2<1-2y_3$, and we have indeed found the feasible solutions which exist for $0<y_3<0.21$. For example, letting $y_3=0.051$ and $E_2=0.15$, we have two feasible solutions: $\begin{array}{rlrlr}{\mathrm{S}}_1:& E_3=0.26883962\cdots ,& A=0.33314675\cdots ,& B_2=1.00504742\cdots ,r=0.13666915\cdots ,& {\omega }_c=0.00512429\cdots ,\\ {\mathrm{S}}_2:& E_3=0.34246578\cdots ,& A=0.37420939\cdots ,& B_2=1.00504742\cdots ,r=0.141287007\cdots ,& {\omega }_c=0.00502891\cdots ,\end{array}$ for which $v_0=v_1=v_2=0$, but $v_3\ne 0$. Thus, proper perturbations can be chosen on the parameters to obtain three small-amplitude limit cycles.

Remark 1.

Similarly, we may follow the procedure given in Section 3 to discuss the conditions for which the predator–prey model (40(40) $\begin{array}{rl}\dot{x}& =x\left(\frac{Ay}{E_3+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(40) ) or (51(51) $\begin{array}{rl}\dot{x}& =x\left(r+\frac{Ay}{E_3+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(51) ) may have only one or two limit cycles. Since the main purpose of this paper is to show how to get maximal number of limit cycles from Hopf bifurcation, we shall not discuss further on this here.

5. Numerical simulation

In this section, we present numerical simulations for the two models, considered in Sections 3 and 4, to verify the analytical predictions obtained in the previous two sections.

5.1. The endemic model (eqn22)

For the epidemic model (22(22) $\begin{array}{rl}\dot{I}& =\frac{I^2}{1+p{I}^2}(A-I-R)-mI,\\ \dot{R}& =qI-R,\end{array}$(22) ), it has been shown in Section 3 that the maximal number of small-amplitude limit cycles bifurcating from a Hopf critical point is two and the outer is unstable. We take the critical parameter values given in Equation (37(37) $p=\frac{1}{3},A=\frac{128}{9},m=\frac{16}{11},q=\frac{2093}{99},v_0=v_1=0,v_2=\frac{5}{26}.$(37) ), and choose two small perturbations ${\epsilon }_1$ and ${\epsilon }_2$: $p=\frac{1}{3},A=\frac{128}{9}+{\epsilon }_1,m=\frac{16}{11}+{\epsilon }_2,q=\frac{2093}{99},\mathrm{with}{\epsilon }_1=0.5,{\epsilon }_2=0.048,$ for which the first three focus values associated with the disease equilibrium $(I_1,R_1)=(0.52343041,11.06605899)$ are given by $v_0=0.00001744,v_1=-0.00596757,v_2=\mathrm{0.17419119.}$ Therefore, the polynomial equation, $v_0+v_1{r}^2+v_2{r}^4=0$, yields two positive roots: $r_1=0.0568$ and $r_2=0.1762$, which roughly measures the amplitudes of the two bifurcating limit cycles. The simulation is shown in Figure 2. The large limit cycle is unstable with neighbouring trajectories diverging from this limit cycle, as shown in Figure 2(a). For a clear view, Figure 2(b) depicts the two limit cycles, with solid curve and dotted curve to denote the stable and unstable limit cycles, respectively. For this example, it is seen that the analytical predictions agree well with the simulation, predicting the correct dynamical behaviour.

Figure 2. Simulation of the endemic Model (22(22) $\begin{array}{rl}\dot{I}& =\frac{I^2}{1+p{I}^2}(A-I-R)-mI,\\ \dot{R}& =qI-R,\end{array}$(22) ) for $p=0.33333333,A=14.72222222,m=1.50254546,q=21.14141414$, showing the existence of two limit cycles enclosing the disease equilibrium $(I_1,R_1)=(0.52343041,11.06605899)$: (a) trajectories diverging from the outer limit cycle; and (b) two limit cycles, enclosing a stable equilibrium, with the outer unstable (dotted curve) and the inner stable (solid curve).

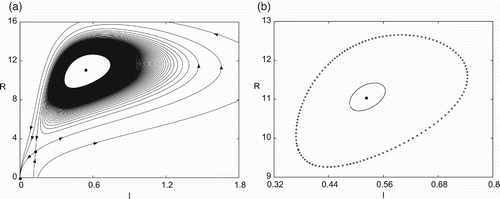
For planar dynamical systems, unstable limit cycles can be identified by using so called time-reversible numerical integration scheme, that is, merely taking negative time steps in a regular numerical integration approach. This technique changes α-limit sets to ω-limit sets and thus unstable limit cycles become ‘stable’ by using this technique. In fact, the unstable limit cycle shown in Figure 2(a) is obtained by using a fourth-order Runge–Kutta method with negative time step. Once the unstable limit cycle is identified, the stable limit cycle can be alternatively determined by checking the eigenvalues of the linearized system at the endemic equilibrium. Indeed, at these perturbed parameter values, the eigenvalues are $0.8720\times {10}^{-5}\pm i2.2650$, implying that the endemic equilibrium is an usable focus, and thus there must exist at least one stable limit cycle between the equilibrium and the unstable limit cycle, as confirmed by the simulation shown in Figure 2(b). However, it should be pointed out that this time-reversible integration technique does not work for dynamical systems with dimension higher than two.

For this endemic model, it is noted that bistable phenomenon appears, with one stable node at the origin and one stable limit cycle enclosing a positive equilibrium solution. The attracting region for the stable limit cycle is inside the unstable limit cycle, while the whole area outside the unstable limit cycle is the attracting region of the stable node (the origin). It should be pointed out that the single unstable limit cycle shown in [10] indicates a bistable phenomenon with purely (two) equilibria. This new type of bistability found in this paper reveals a more complex but more realistic situation: the predicted state may not be necessarily an equilibrium (either the disease-free equilibrium or the disease equilibrium), but may also involve disease periodic oscillation. This implies that the infective individuals and removed individuals are not necessarily fixed, but in a more realistically, mutually stable periodic motion.

5.2. The predator–prey model (eqn38)

In Section 4, we have considered the predator–prey model (38(38) $\begin{array}{rl}\dot{X}& =X\left(r_1+\frac{{\alpha }_{12}Y}{b_2+Y}-\frac{{\beta }_{1}Y}{e_1+X}-d_{1}X\right),\\ \dot{Y}& =Y\left(r_2-\frac{{\beta }_{2}X}{e_2+Y}-d_{2}Y\right),\end{array}$(38) ) for two cases: $B_1=r=0$ and $B_1=0$. Since both the two cases can have maximal three limit cycles, we shall only present a simulation for the first case. That is, we shall use system (40(40) $\begin{array}{rl}\dot{x}& =x\left(\frac{Ay}{E_3+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(40) ) to perform computer simulation. According to Equation (50(50) $\begin{array}{llll}{\mathrm{S}}_1:& y_2=0.13,& E_2=0.01939683\cdots ,& E_3=0.74997712\cdots ,\\ & A=4.11353863\cdots ,& B_2=0.20728245\cdots ,& {\omega }_c=0.03521529\cdots .\end{array}$(50) ), for the critical parameter values: $E_2=0.01939683,E_3=0.74997712,A=4.11353863,B_2=0.20728245,$ the first four focus values are $v_0=v_1=v_2=0,v_3=-0.00604292<0$, implying that the outer limit cycle is stable. We take the following three perturbations: $E_2=0.01939683-{\epsilon }_1,quad{E}_3=0.74997712-{\epsilon }_2,A=4.11353863+{\epsilon }_3,$ with ${\epsilon }_1=0.001,{\epsilon }_2=0.0002$ and ${\epsilon }_3=0.0000001$, for which the positive equilibrium solution is given by ${\mathrm{E}}_2:\left(\frac{(1-y_2)(E_2+y_2)}{B_2},y_2\right)=(0.63214554,0.12999997),$ and the first four focus values become $\begin{array}{rl}& v_0=0.26550341\times {10}^{-8},v_1=-0.76075773\times {10}^{-5},v_2=0.00090754,\\ & v_3=-\mathrm{0.01606573.}\end{array}$ Thus, the equation $v_0+v_1{r}^2+v_2{r}^4+v_3{r}^6=0$ gives the three positive roots: $r_1=0.01909893,r_2=0.09886666,r_3=0.21529098$, which are the approximations of the three limit cycles. The simulation for this case is given in Figure 3, where Figure 3(a) shows the convergence of trajectories to the outer limit cycle; while Figure 3(b) depicts the three limit cycles, with solid curve and dotted curve to represent the stable and unstable limit cycles, respectively. It can be seen that for this example the amplitudes of the simulated limit cycles agree very well with the analytical predictions.

Figure 3. Simulation of the predator–prey model (40(40) $\begin{array}{rl}\dot{x}& =x\left(\frac{Ay}{E_3+y}-x\right),\\ \dot{y}& =y\left(1-\frac{B_{2}x}{E_2+y}-y\right),\end{array}$(40) ) for $E_2=0.01839684,E_3=0.73192174,A=4.19123136,B_2=0.20423339$, showing the existence of three limit cycles enclosing the equilibrium $(x_2,y_2)=(0.63214554,0.12999997)$: (a) trajectories converging to the outer limit cycle; and (b) three limit cycles, enclosing an unstable equilibrium, with the outer and the inner stable (solid curve) and the middle one unstable (dotted curve).

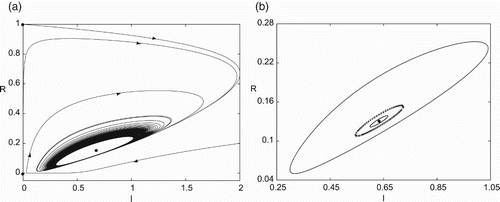
Similarly, for the perturbed parameter values, the Jacobian matrix of the system evaluated at the positive equilibrium has the eigenvalues: $0.7595\times {10}^{-8}\pm i0.0332$, indicating that the positive equilibrium is an unstable focus. Therefore, if there is another stable limit cycle enclosing the equilibrium, then there must also have an unstable limit cycle between the two stable limit cycles. As a matter of fact, the smaller stable limit cycle is confirmed by the simulation, but the convergence speed is extremely slow, while the unstable limit cycle can be identified by using the time-reversible numerical integration scheme.

For this predator–prey model, it is again seen that bistable phenomenon occurs, but now both stable states are limit cycles, with no equilibria, showing a new interesting bistable phenomenon in biological systems. The two attracting regions are separated by an unstable limit cycle. The region inside the unstable limit cycle is the attracting region for the small stable limit cycle, while the region outside the unstable limit cycle is the attracting region for the large stable limit cycle. This implies that in real situation the predator and prey can be balanced on two periodic motions, either a small oscillation or a large oscillation depending upon the initial conditions.

6. Conclusion

In this paper, we have applied normal form theory to investigate bifurcation of multiple limit cycles for one epidemic model and one predator–prey model. New interesting bistable phenomenon has been found, which may involve equilibria and oscillating motions. In particular, for the epidemic model, we have shown that two limit cycles can bifurcate from a Hopf critical point, indicating that the infective individuals and removed individuals are not necessarily fixed, but can be on a mutually stable periodic motion. For the predator–prey model, three limit cycles have been obtained from Hopf bifurcation, which reveals that the predator and prey can be dynamically balanced either on a small oscillation or on a large oscillation depending upon the initial conditions. Moreover, it has been shown that due to physical restriction on system parameters, the maximal number of limit cycles may be hard to reach. However, for some cases, two or three limit cycles are possible to obtain. Hence, the complex dynamical behaviour of a biological system not only depends upon the number of free parameters contained in the system, but also on the physical restriction on those parameters.

Acknowledgment

P. Yu thanks the Key Laboratory of Mathematics for Nonlinear Sciences, Ministry of Education, China for supporting his visit and preparation of this manuscript during the visit.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This research was supported by the Natural Science and Engineering Research Council of Canada [NSERC No. R2686A02], and the National Natural Science Foundation of China [NSFC No. 61273014 and No. 11322111].