Two-sex mosquito model for the persistence of Wolbachia

ABSTRACT

We develop and analyse an ordinary differential equation model to investigate the transmission dynamics of releasing Wolbachia-infected mosquitoes to establish an endemic infection in a population of wild uninfected mosquitoes. Wolbachia is a genus of endosymbiotic bacteria that can infect mosquitoes and reduce their ability to transmit some viral mosquito-transmitted diseases, including dengue fever, chikungunya, and Zika. Although the bacterium is transmitted vertically from infected mothers to their offspring, it can be difficult to establish an endemic infection in a wild mosquito population. Our transmission model for the adult and aquatic-stage mosquitoes takes into account Wolbachia-induced fitness change and cytoplasmic incompatibility. We show that, for a wide range of realistic parameter values, the basic reproduction number, $R_0$, is less than one. Hence, the epidemic will die out if only a few Wolbachia-infected mosquitoes are introduced into the wild population. Even though the basic reproduction number is less than one, an endemic Wolbachia infection can be established if a sufficient number of infected mosquitoes are released. This threshold effect is created by a backward bifurcation with three coexisting equilibria: a stable zero-infection equilibrium, an intermediate-infection unstable endemic equilibrium, and a high-infection stable endemic equilibrium. We analyse the impact of reducing the wild mosquito population before introducing the infected mosquitoes and observed that the most effective approach to establish the infection in the wild is based on reducing mosquitoes in both the adult and aquatic stages.

KEYWORDS:

• Dengue fever
• chikungunya
• Zika
• vertical transmission
• backward bifurcation
• cytoplasmic incompatibility
• basic reproduction number
• threshold condition

AMS SUBJECT CLASSIFICATION:

• 97M10
• 92D30

1. Introduction

We use a disease transmission model to investigate the conditions for releasing Wolbachia-infected mosquitoes that will establish an endemic infection in a population of wild uninfected mosquitoes. The Wolbachia-infected mosquitoes are less able to transmit dengue, chikungunya, or Zika virus [2,10,12,14,16,32,34,39,56]. The goal of the modeling effort is to better understand how this bacterium can be used to control vector-borne diseases. We observed that the basic reproductive number for the Wolbachia model is less than one for typical model parameters, hence small Wolbachia infestations will die out. Our model predicts that there is a critical threshold, and if a sufficient number of infected mosquitoes are released, then an endemic Wolbachia-infected population of mosquitoes can be established. We also investigated how this critical threshold can be reduced by first decreasing the population of wild mosquitoes.

Dengue fever, chikungunya, and Zika are some of the world's most significant and widespread arthropod-borne viral diseases [13,43]. The main vector, Aedes aegypti, is prevalent throughout the world and the secondary vector, Aedes albopictus keeps expanding its geographic distribution [25]. There is no specific therapy available and even though the world first dengue vaccine was licensed for use last year, its efficacy is lower and varied between virus serotype, population age group, and country [4,55]. Traditional control strategies focused on reducing population of Aedes mosquito vectors have failed to significantly slow the current pandemics. There has been 30 fold increase in dengue fever cases over the past 50 years [27]. Each year, approximately 400 million people are infected with dengue virus in more than 100 countries [26], while the other one-third of the world's population is at risk. The ongoing chikungunya epidemics in the Americas, the Pacific Islands, and Indian Ocean Chikungunya causes an estimated three million infections each year [44,47]. Zika has been declared a global health security threat because of the severe birth defects and neurological problems caused by the disease [42]. These diseases are driving a world-wide search for effective approaches to break the transmission cycles in Aedes aegypti and Aedes albopictus mosquitoes [56].

Wolbachia induces resistance to dengue virus in Aedes aegypti [1] and limits transmission of dengue virus in Aedes albopictus [36]. Increasing attention has been paid to controlling the spread of these diseases by targeting mosquito longevity by introducing genetically modified mosquitoes or introducing endosymbiotic Wolbachia bacteria to shorten the mosquito lifespan [2,32,56]. That is, Wolbachia-infected mosquitoes are released to create a sustained infection in the wild (Wolbachia-free) population. If the infection is sustained, then the wild infected mosquitoes will be less effective in transmitting these diseases. We create and analyse a mathematical model to help understand the underlying dynamics of Wolbachia-infected mosquitoes that are needed to create a sustained endemic Wolbachia infection. Once the Wolbachia disease transmission model is well understood, one of our future goals will be to couple this model with a mosquito-human model for the spread of dengue, chikungunya, and Zika.

1.1. Wolbachia bacteria

Wolbachia pipientis bacterium is a maternally inherited endosymbiont infecting more than $60\mathrm{\%}$ of all insect species. The wMel strain of Wolbachia pipientis has the ability to alter host reproduction through parthenogenesis, which results in the development of unfertilized eggs, male killing, feminization, and cytoplasmic incompatibility (CI) [3,40] that prevents the eggs from forming viable offspring. The latter includes strategies for both the suppression and replacement of medically important mosquito populations. Cytoplasmic incompatibility is an incompatibility between the sperm and eggs induced by Wolbachia infection [18] and has received considerable attention as a method to control vector-borne diseases [51].

Uninfected females only mate successfully with uninfected males, while infected females can mate successfully with both uninfected and infected males [8]. If a male fertilizes a female harbouring the same type of infection, the offspring still can survive [32]. When Wolbachia-infected males mate with uninfected females, or females infected with a different Wolbachia strain, then the CI often results in killing the embryos. [18,48,59]. Therefore, infected females have a reproduction advantage over uninfected females due to protection from CI [58].

To successfully transmit the virus, a vector must imbibe virus particles during blood-feeding and survive to the point that the pathogen can be biologically transmitted to the next vertebrate host [41]. This time period, called extrinsic incubation period , varies with ambient temperature, many other climatic factors, and characteristics of the vector-parasite system [57]. Vectors that survive long enough to transmit the pathogen are called effective vectors [41]. Typically, mosquito-borne viral diseases have an incubation period between one and two weeks to transmit through Aedes aegypti populations [13]. A life-shortening strain of Wolbachia may halve the life span of Aedes aegypti [34]. Wolbachia infection may reduce the rate of disease transmission due to the reduction on the lifespan of infected mosquitoes or the interference with mosquito susceptibility to the virus.

1.2. Existing mosquito-Wolbachia models

Ordinary differential equation (ODE) models have been developed to explore key factors that determine the success of applying Wolbachia to control viral diseases. A single-sex model for Wolbachia infection with both age-structured and unstructured models were presented to study the stability and equilibrium based on the assumption that Wolbachia infection leads to increased mortality or reduced birth rate [11]. A model assuming a fixed ratio of females and males addressed how pathogen protection affects Wolbachia invasion [49]. Age-structured and unstructured models combining males and females were found to be different in terms of existence and stability of equilibrium solutions [11]. A stochastic model for female mosquitoes was developed to investigate the impact of introduction frequency on establishment of Wolbachia [22].

Discrete-time models explored the impact of the type of immigration and the temporal dynamics of the host population on the spread of Wolbachia, assuming equal sex ratio between males and females [15]. Discrete generation models for female mosquitoes were built to understand unstable equilibrium produced by reduced lifespan or lengthened development [52]. Reaction–diffusion and integro-difference equation models have been used to analyse the impact of insect dispersal and infection spread on invasion of Wolbachia [5,19,45,49].

An ODE model was developed to evaluate the desirable properties of the Wolbachia strain to be introduced to female mosquitoes, assuming that Wolbachia-infected mosquitoes have reduced lifespan and reduced capability to transmit viral diseases, and an equal fraction of male and female mosquitoes [20]. A continuous time non-spatial model and a reaction–diffusion model incorporating lifespan shortening and CI were developed to study factors that determine the spatial spread of Wolbachia through a population of female Aedes aegypti mosquitoes assuming constant population size and perfect maternal transmission of Wolbachia [46]. A two-sex deterministic model with deterministic immature life stages and stochastic female adult life stage was developed to understand Wolbachia invasion into uninfected host population [6].

A single-strain model, two-strain model, and spatial model were developed to study whether multiple stains of Wolbachia can coexist in a spatial context [23]. A two-sex ODE model taking into account different death rates, but the same egg laying rates of Wolbachia-infected and Wolbachia uninfected mosquitoes [24] showed the basic reproduction number is always less than one, and the complete infection equilibrium (CIE) is locally asymptotically stable (LAS) due to positive determinant of the Jacobian matrix for the system. Simulations showed that dengue epidemics will not occur when Wolbachia infection is sufficiently prevalent [24]. A two-sex mosquito model assuming complete vertical transmission and equal death rates for male and female mosquitoes was developed and four steady states were found [38].

Most of these models consider either a single-sex model for adult mosquitoes, or assume a fixed ratio between the number of male and female mosquitoes. Also, most of the models assume homogeneous death rates and egg laying rates for Wolbachia-free and Wolbachia-infected mosquitoes. Our model addresses both of these issues. Our emphasis is to understand how Wolbachia infection can be established in a wild population of mosquitoes.

1.3. Results

We proposed a compartmental two-sex model to investigate the underlying mechanisms that may contribute to invasion and sustainable establishment of Wolbachia in mosquito populations. We assigned female and male mosquitoes to different classes to understand corresponding roles that they are playing in the spread of Wolbachia in mosquito populations.

We showed that, for a wide range of realistic parameter values, the basic reproduction number, $R_0$, for this model is less than one. Hence, the epidemic will die out if only a few Wolbachia-infected mosquitoes are introduced into the wild population. Even though the basic reproduction number is less than one, an endemic Wolbachia infection can be established if a sufficient number of infected mosquitoes are released. This threshold effect can be explained as a backward bifurcation with three coexisting equilibria: a stable zero-infection equilibrium, an intermediate-infection unstable endemic equilibrium, and a high-infection stable endemic equilibrium.

If the number of infected individuals is below the unstable endemic equilibrium, then the infection decays to the zero-infection equilibrium. Conversely, if the number of infected mosquitoes is greater than unstable endemic equilibrium, then the solution tends to the stable high-infection equilibrium. We identified the relationships between dimensionless combinations of model parameters and the initial conditions for Wolbachia to be attracted to the high-infection state. As expected, the number of infected female mosquitoes needed to be released to establish the infection in a wild Wolbachia-free population decreases as $R_0$ increases to one. We analysed the impact of reducing the wild mosquito population before introducing the infected mosquitoes. We found that the most effective approach of reducing the number of infected mosquitoes needed to establish a wild Wolbachia-infected population requires reducing wild mosquito populations in both the adult and aquatic stages before the release. This could be accomplished by recursive spraying, or a combination of spraying and larvae control [21].

Our main findings are:

1. Three equilibria, the disease-free equilibrium (DFE), the endemic equilibrium (EE), and the CIE coexist when $R_0<1$. The DFE is a steady state where all individuals are Wolbachia-free. The EE is a steady state where some individuals are Wolbachia-free, and the rest are infected with Wolbachia. The CIE is a steady state where all individuals are infected with Wolbachia.

2. The backward bifurcation analysis of our Wolbachia transmission model predicts that if $R_0<1$, then there is a critical threshold for the number of infected mosquitoes released in the wild before the infection can be established. If we release too few Wolbachia-infected mosquitoes, then the Wolbachia infection will die out.

3. Killing both aquatic state (eggs and larvae) and adult mosquitoes before releasing the infected mosquitoes greatly increases the chance that the infection will be established. Our model quantifies what fraction of wild mosquitoes must be killed before releasing Wolbachia-infected mosquitoes.

After introducing the mathematical model, we summarize the key results from the analysis and numerical simulations. We conclude with a discussion of the relevance, importance, and future directions for this work.

2. Description of model framework

We developed an ODE model incorporating adult females (F), adult males (M), and an aggregated aquatic (A) stage that includes the egg, larvae, and pupae stages. The population dynamics of mosquitoes without taking into account Wolbachia is in the appendix, Equation (A1). The vertical transmission of Wolbachia from infected females to their offspring is a key factor in establishing an endemic-infected population.

Mosquitoes are grouped into six compartments: susceptible aquatic stage, $A_u$, infected aquatic stage, $A_w$, susceptible female mosquitoes, $F_u$, infected female mosquitoes, $F_w$, susceptible male mosquitoes, $M_u$, and infected male mosquitoes, $M_w$. The eclosion rates of susceptible female and male mosquitoes hatching from eggs are $\psi \theta A_u$ and $\psi (1-\theta )A_u$, respectively. Similarly, the birth rates of infected female and male mosquitoes are $\psi \theta A_w$ and $\psi (1-\theta )A_w$. Death rates of uninfected male mosquitoes and infected male mosquitoes are ${\mu }_a{A}_u$ and ${\mu }_a{A}_w$. Death rates of uninfected female mosquitoes and infected female mosquitoes are ${\mu }_{fu}{F}_u$ and ${\mu }_{fw}{F}_w$. Death rates of uninfected male mosquitoes and infected male mosquitoes are ${\mu }_{mu}{M}_u$ and ${\mu }_{mw}{M}_w$. Development rates of uninfected aquatic stage and infected aquatic stage of mosquitoes are $\psi A_u$ and $\psi A_w$. The model parameters are described in Table 1.

Table 1. State variables and parameters for the model (1(1a) $\begin{array}{r}\frac{\mathrm{d}{A}_u}{\mathrm{d}t}=B_{uu}+v_u(B_{wu}+B_{ww})-{\mu }_a{A}_u-\psi A_u,\end{array}$(1a) ).

$M_u,F_u,A_u$:	Number of uninfected male, female, and aquatic mosquitoes
$M_w,F_w,A_w$:	Number of male, female, and aquatic mosquitoes infected with Wolbachia
$N_A$:	Total number of aquatic stage of mosquitoes
$K_a$:	Carrying capacity of aquatic stage of mosquitoes
$b_f$:	Fraction of births that are female mosquitoes.
$c_i$:	Fraction of unviable offspring due to cytoplasmic incompatibility.
$b_m$:	Fraction of births that are male mosquitoes $=1-b_f$.
$m_w$:	Fraction of the male mosquitoes that are infected $=M_w/(M_w+M_u)$.
$m_u$:	Fraction of the male mosquitoes that are uninfected $=1-m_w$.
$v_w$:	Fraction of infected mosquito eggs produced by infected female mosquitoes.
$v_u$:	Fraction of uninfected mosquito eggs produced by infected female mosquitoes $=1-v_w$.
${\phi }_u$:	Per capita egg laying rate by Wolbachia-free mosquito eggs. Number of eggs/time
${\phi }_w$:	Per capita egg laying rate by Wolbachia-infected mosquito eggs. Number of eggs/time
ψ:	Per capita development rate of mosquito eggs. Time^−1
${\mu }_a$:	Per capita death rate of aquatic stage of mosquitoes. Time^−1
${\mu }_{fu}$:	Per capita death rate of uninfected female mosquitoes. Time^−1
${\mu }_{fw}$:	Per capita death rate of infected female mosquitoes. Time^−1
${\mu }_{mu}$:	Per capita death rate of uninfected male mosquitoes. Time^−1
${\mu }_{mw}$:	Per capita death rate of infected male mosquitoes. Time^−1

The model (Figure 1) describing population dynamics of aquatic stage, adult male, and adult female mosquitoes is given by (1a) $\begin{array}{r}\frac{\mathrm{d}{A}_u}{\mathrm{d}t}=B_{uu}+v_u(B_{wu}+B_{ww})-{\mu }_a{A}_u-\psi A_u,\end{array}$(1a) (1b) $\begin{array}{r}\frac{\mathrm{d}{A}_w}{\mathrm{d}t}=v_w(B_{wu}+B_{ww})-{\mu }_a{A}_w-\psi A_w,\end{array}$(1b) (1c) $\begin{array}{r}\frac{\mathrm{d}{F}_u}{\mathrm{d}t}=b_f\psi A_u-{\mu }_{fu}{F}_u,\end{array}$(1c) (1d) $\begin{array}{r}\frac{\mathrm{d}{F}_w}{\mathrm{d}t}=b_f\psi A_w-{\mu }_{fw}{F}_w,\end{array}$(1d) (1e) $\begin{array}{r}\frac{\mathrm{d}{M}_u}{\mathrm{d}t}=b_m\psi A_u-{\mu }_{mu}{M}_u,\end{array}$(1e) (1f) $\begin{array}{r}\frac{\mathrm{d}{M}_w}{\mathrm{d}t}=b_m\psi A_w-{\mu }_{mw}{M}_w.\end{array}$(1f)

Figure 1. The birthing rates (2(1b) $\begin{array}{r}\frac{\mathrm{d}{A}_w}{\mathrm{d}t}=v_w(B_{wu}+B_{ww})-{\mu }_a{A}_w-\psi A_w,\end{array}$(1b) ) capture that when the uninfected males mate with uninfected females, they produce uninfected offspring. When infected males mate with uninfected females, then CI causes the embryos to die before hatching. Uninfected males mating with infected females produce a fraction, denoted by $v_w$, of infected offspring by vertical transmission. Cross of infected males with infected females produces a fraction of infected offspring.

Wolbachia can be transmitted vertically from infected parents to their offspring where

• Uninfected males mating with uninfected females produce uninfected offspring.

• Infected males mating with uninfected females leads to death of embryos before hatching due to cytoplasmic incompatibility.

• Uninfected males mating with infected females produce a fraction, $v_w$, of infected offspring by vertical transmission.

• Infected males mating with infected females produces a fraction of infected offspring.

Table

Male	Female	Offspring
Uninfected	Uninfected	Uninfected
Uninfected	Infected	Some offspring are infected
Infected	Uninfected	Unviable
Infected	Infected	Some offspring are infected

Because the vertical transmission and birth rates, $B_{\ast \ast }$, depend on the sex of the infected or uninfected parents, the model included the four egg laying situations (2a) $\begin{array}{r}{B}_{uu}={\phi }_u{F}_u{m}_u\left(1-\frac{N_A}{K_a}\right)\end{array}$(2a) (2b) $\begin{array}{r}{B}_{uw}=(1-c_i){\phi }_u{F}_u{m}_w\left(1-\frac{N_A}{K_a}\right)\end{array}$(2b) (2c) $\begin{array}{r}{B}_{wu}={\phi }_w{F}_w{m}_u\left(1-\frac{N_A}{K_a}\right)\end{array}$(2c) (2d) $\begin{array}{r}{B}_{ww}={\phi }_w{F}_w{m}_w\left(1-\frac{N_A}{K_a}\right).\end{array}$(2d)

Here, $m_u=M_u/(M_w+M_u)$ and $m_w=1-m_u$ are the fractions of uninfected and infected male mosquitoes. $B_{uu}$ is the egg laying rate of uninfected females mating with uninfected males. $B_{uw}$ is the egg laying rate of uninfected females mating with infected males. $B_{wu}$ is the egg laying rate of infected females mating with uninfected males. $N_A$ is the total number of aquatic stage of mosquitoes, and $K_a$ is carrying capacity of aquatic stage of mosquitoes.

3. Stability analysis of the equilibrium solutions

When $R_0<1$, there are three equilibria: the DFE, the EE and the CIE. We analyse the stability of each equilibrium.

3.1. Stability of the DFE

We use the next generation matrix approach to compute the basic reproduction number [53]. Only infected compartments are considered for ease of computation: $\begin{array}{rl}\frac{\mathrm{d}}{\mathrm{d}t}[A_w{F}_w{M}_w{]}^{\mathrm{T}}& =\mathcal{F}-\mathcal{V}\\ & =\left[\begin{array}{c}(v_w{F}_w{\phi }_w{m}_u+v_w{F}_w{\phi }_w{m}_w)\left(1-\frac{N_A}{K_a}\right)\\ b_f\psi A_w\\ b_m\psi A_w\end{array}\right]-\left[\begin{array}{c}{\mu }_a{A}_w+\psi A_w\\ {\mu }_{fw}{F}_w\\ {\mu }_{mw}{M}_w\end{array}\right],\end{array}$

where $\mathcal{F}=\left({\mathcal{F}}_i\right)$ is a vector for new infected, and $\mathcal{V}=\left({\mathcal{V}}_i\right)$ is a vector for transfer between compartments.

Jacobian matrices for transmission, F, and transition, V, [53] are defined as (3) $F=\left[\frac{\mathrm{\partial }{\mathcal{F}}_i\left(x^0\right)}{\mathrm{\partial }{x}_j}\right],V=\left[\frac{\mathrm{\partial }{\mathcal{V}}_i\left(x^0\right)}{\mathrm{\partial }{x}_j}\right],$(3) where $x^0$ represents the DFE, and $x_j$ is the number or proportion of infected individuals in compartment j, $j=1,2,\dots ,m$.

The unique DFE is $\begin{array}{rl}{A}_u^0& =K_a\left(1-\frac{1}{R_{0u}}\right),\\ F_u^0& =b_f\frac{\psi }{{\mu }_{fu}}{A}_u^0,\\ M_u^0& =b_m\frac{\psi }{{\mu }_{mu}}{A}_u^0,\\ A_w^0& =F_w^0=M_w^0=0,\end{array}$ where $R_{0u}=b_f{\phi }_u\psi /({\mu }_a+\psi ){\mu }_{fu}$ is the threshold for Wolbachia-free offspring, $b_f{\phi }_u/{\mu }_{fu}$ is the total number of eggs laid by uninfected female mosquitoes, $\psi /({\mu }_a+\psi )$ is the probability that aquatic stage of mosquitoes survive to the point when they develop into adult mosquitoes. $R_{0u}$ is the number of female eggs that develop into adult mosquitoes. When $R_{0u}>1$, then the mosquito population may grow; otherwise, the population will decrease.

The Jacobian matrix of $\mathcal{F}$ evaluated at DFE is $\begin{array}{rl}F& =\left[\begin{array}{ccc}0& v_w{m}_u^0{\phi }_w\left(1-\frac{N_A^0}{K_a}\right)& 0\\ b_f\psi & 0\\ b_m\psi & 0\end{array}\right]=\left[\begin{array}{ccc}0& \frac{v_w({\mu }_a+\psi ){\mu }_{fu}{\phi }_w}{b_f\psi {\phi }_u}& 0\\ b_f\psi & 0\\ b_m\psi & 0\end{array}\right],\end{array}$ where $m_u^0=M_u^0/(M_w^0+M_u^0)$.

The Jacobian matrix of $\mathcal{V}$ evaluated at DFE is $V=\left[\begin{array}{cc}{\mu }_a+\psi & 0\\ 0& {\mu }_{fw}& 0\\ 0& {\mu }_{mw}\end{array}\right].$

The next generation matrix for infected compartments at DFE is $F{V}^{-1}=\left[\begin{array}{ccc}0& \frac{v_w({\mu }_a+\psi ){\mu }_{fu}{\phi }_w}{b_f\psi {\mu }_{fw}{\phi }_u}& 0\\ \frac{b_f\psi }{{\mu }_a+\psi }& 0\\ \frac{b_m\psi }{{\mu }_a+\psi }& 0\end{array}\right].$

The basic reproduction number is the largest absolute eigenvalue of $F{V}^{-1}$, denoted by $\rho \left(F{V}^{-1}\right)$ (4) $R_0=\rho \left(F{V}^{-1}\right)=\sqrt{v_w\frac{{\phi }_w}{{\mu }_{fw}}{\left(\frac{{\phi }_u}{{\mu }_{fu}}\right)}^{-1}}.$(4)

Wolbachia-infected and Wolbachia-free female mosquitoes produce ${\phi }_w/{\mu }_{fw}$ and ${\phi }_u/{\mu }_{fu}$ eggs during their lifetime, respectively. Hence, $\left({\phi }_w/{\mu }_{fw}\right)({\phi }_u/{\mu }_{fu}{)}^{-1}$ is the ratio of the number of eggs produced by Wolbachia-infected females to the number of eggs produced by Wolbachia-free females during their lifetime. $R_0$ is geometric mean of vertical transmission rate and the ratio of the total number of eggs produced by Wolbachia-infected females to the total number of eggs produced by Wolbachia-free females.

When the variables are ordered as $[A_u{F}_u{M}_u{A}_w{F}_w{M}_w{]}^{\mathrm{T}}$, Jacobian matrix at equilibrium $[A_u^{\ast }{F}_u^{\ast }{M}_u^{\ast }{A}_w^{\ast }{F}_w^{\ast }{M}_w^{\ast }{]}^{\mathrm{T}}$ for system of Equations (1(1a) $\begin{array}{r}\frac{\mathrm{d}{A}_u}{\mathrm{d}t}=B_{uu}+v_u(B_{wu}+B_{ww})-{\mu }_a{A}_u-\psi A_u,\end{array}$(1a) ) is $J=\left[\begin{array}{ccccccc}c& a& b& |& c_2& a_2& b_2\\ b_f\psi & -{\mu }_{fu}& 0& |& 0& 0& 0\\ b_m\psi & 0& -{\mu }_{mu}& |& 0& 0& 0\\ --& --& --& --& --& --& --\\ c_3& 0& b_3& |& c_1& a_1& b_1\\ 0& 0& 0& |& b_f\psi & -{\mu }_{fw}& 0\\ 0& 0& 0& |& b_m\psi & 0& -{\mu }_{mw}\end{array}\right]=\left[\begin{array}{cc}A& C\\ D& B\end{array}\right],$ where $\begin{array}{rl}a& ={\phi }_u{m}_u^{\ast }\left(1-\frac{A_u^{\ast }+A_w^{\ast }}{K_a}\right),\\ b& ={\phi }_u{m}_w^{\ast }\frac{F_u^{\ast }}{M_w^{\ast }+M_u^{\ast }}\left(1-\frac{A_u^{\ast }+A_w^{\ast }}{K_a}\right),\\ c& =-({\mu }_a+\psi )-{\phi }_u{m}_u^{\ast }\frac{F_u^{\ast }}{K_a}-{\phi }_w{v}_u\frac{F_w^{\ast }}{K_a},\\ a_1& =v_w{\phi }_w\left(1-\frac{A_u^{\ast }+A_w^{\ast }}{K_a}\right),\\ b_1& =0,\\ c_1& =-({\mu }_a+\psi )-{\phi }_w{v}_w\frac{F_w^{\ast }}{K_a},\\ a_2& ={\phi }_w{v}_u\left(1-\frac{A_u^{\ast }+A_w^{\ast }}{K_a}\right),\\ b_2& =-{\phi }_u{m}_u^{\ast }\frac{F_u^{\ast }}{M_w^{\ast }+M_u^{\ast }}\left(1-\frac{A_u^{\ast }+A_w^{\ast }}{K_a}\right),\\ c_2& =-{\phi }_u{m}_u^{\ast }\frac{F_u^{\ast }}{K_a}-{\phi }_w{v}_u\frac{F_w^{\ast }}{K_a},\\ b_3& =0,\\ c_3& =-{\phi }_w{v}_w\frac{F_w^{\ast }}{K_a},\end{array}$ At DFE, D=0, then the eigenvalues of J are eigenvalues of A and B. Matrices A and B are $\begin{array}{rl}A& =\left[\begin{array}{ccc}-({\mu }_a+\psi )-{\phi }_u\frac{F_u^0}{K_a}& \frac{{\mu }_{fu}({\mu }_a+\psi )}{b_f\psi }& 0\\ b_f\psi & -{\mu }_{fu}& 0\\ b_m\psi & 0& -{\mu }_{mu}\end{array}\right],\\ B& =\left[\begin{array}{ccc}-({\mu }_a+\psi )& \frac{v_w({\mu }_a+\psi ){\mu }_{fu}{\phi }_w}{b_f\psi {\phi }_u}& 0\\ b_f\psi & -{\mu }_{fw}& 0\\ b_m\psi & 0& -{\mu }_{mw}\end{array}\right].\end{array}$

If $R_{0u}>1$, then all eigenvalues of A are negative. If $R_0<1$, then all eigenvalues of B are negative. Therefore, the system (1(1a) $\begin{array}{r}\frac{\mathrm{d}{A}_u}{\mathrm{d}t}=B_{uu}+v_u(B_{wu}+B_{ww})-{\mu }_a{A}_u-\psi A_u,\end{array}$(1a) ) at DFE is LAS whenever $R_{0u}>1$ and $R_0<1$.

3.2. Stability of the CIE

If $R_0<1$ and $R_{0w}>1$ and the vertical transmission is $100\mathrm{\%}$, ($v_w=1$), then the ratio of the infected to the uninfected aquatic stage mosquitoes, k, is $k=\frac{A_w^{\ast }}{A_u^{\ast }}=\frac{{\mu }_{mw}}{{\mu }_{mu}}\left(R_0^{-2}-1\right),$ and there is a unique EE: (5a) $\begin{array}{r}{A}_u^{\ast }=\frac{K_a}{1+k}(1-R_{0w}^{-1}),\end{array}$(5a) (5b) $\begin{array}{r}{A}_w^{\ast }=k{A}_u^{\ast },\end{array}$(5b) (5c) $\begin{array}{r}{F}_u^{\ast }=b_f\frac{\psi }{{\mu }_{fu}}{A}_u^{\ast },\end{array}$(5c) (5d) $\begin{array}{r}{F}_w^{\ast }=k{F}_u^{\ast },\end{array}$(5d) (5e) $\begin{array}{r}{M}_u^{\ast }=b_m\frac{\psi }{{\mu }_{mu}}{A}_u^{\ast },\end{array}$(5e) (5f) $\begin{array}{r}{M}_{w^{\ast }}=k{M}_u^{\ast },\end{array}$(5f) where $R_{0w}=v_w{b}_f\psi {\phi }_w/({\mu }_a+\psi ){\mu }_{fw}$.

If we further assume that ${\mu }_{mu}={\mu }_{mw}$, then $k=R_0^{-2}-1$ and the unique CIE is $\begin{array}{rl}{A}_u& =0,\\ A_w& =K_a(1-R_{0w}^{-1}),\\ F_u& =0,\\ F_w& =b_f\frac{\psi }{{\mu }_{fw}}{A}_w,\\ M_u& =0,\\ M_w& =b_m\frac{\psi }{{\mu }_{mw}}{A}_w.\end{array}$ Jacobian matrix of system of Equations (1(1a) $\begin{array}{r}\frac{\mathrm{d}{A}_u}{\mathrm{d}t}=B_{uu}+v_u(B_{wu}+B_{ww})-{\mu }_a{A}_u-\psi A_u,\end{array}$(1a) ) at CIE for $v_w=1$ is $\begin{array}{rl}{J}_{cw}& =\left[\begin{array}{ccccccc}-{\mu }_a-\psi & 0& 0& |& 0& 0& 0\\ b_f\psi & -{\mu }_{fu}& 0& |& 0& 0& 0\\ b_m\psi & 0& -{\mu }_{mu}& |& 0& 0& 0\\ --& --& --& --& --& --& --\\ -\frac{b_f\psi (1-R_0^2){\phi }_w}{{\mu }_{fw}}(1-R_{0w}^{-1})& 0& 0& |& -\frac{{\phi }_w{b}_f\psi }{{\mu }_{fw}}& \frac{({\mu }_a+\psi ){\mu }_{fw}}{b_f\psi }& 0\\ 0& 0& 0& |& b_f\psi & -{\mu }_{fw}& 0\\ 0& 0& 0& |& b_m\psi & 0& -{\mu }_{mw}\end{array}\right]\\ & =\left[\begin{array}{cc}A& 0\\ C& B\end{array}\right].\end{array}$

Eigenvalues of $J_{cw}$ are composed of three eigenvalues of A and three eigenvalues of B. The eigenvalues of A are all negative. Characteristic polynomial of B is (6) ${\lambda }^2+\left({\mu }_{fw}+\frac{{\phi }_w{b}_f\psi }{{\mu }_{fw}}\right)\lambda +{\phi }_w{b}_f\psi -({\mu }_a+\psi ){\mu }_{fw}=0.$(6) If $R_{0w}>1$, all eigenvalues of B are negative. Therefore, the CIE is LAS whenever $R_{0w}>1$, as shown in Figure 2(a).

Figure 2. Bifurcation diagrams for Wolbachia vertical transmission. ${\phi }_u$ and ${\mu }_{fu}$ are varying, and other parameter values are the same as those baseline values in Table 2. Denote the intersection of two endemic equilibria, that is, the intersection of the black dashed line and x-axis, as $R_0^{\ast }=\sqrt{4v_w{v}_u}$. When $R_0<1$ and $v_w<0.5$, no endemic equilibria exist. When $R_0<1$ and $v_w>0.5$, as the vertical transmission rate increases so does $R_0^{\ast }$ and the LAS equilibrium approaches a constant. If we increase the number of infected females, then the EE may become stable EE or CIE If we decrease the number of infected females at EE, then the EE may become DFE. WIF denotes Wolbachia-infected female mosquitoes.

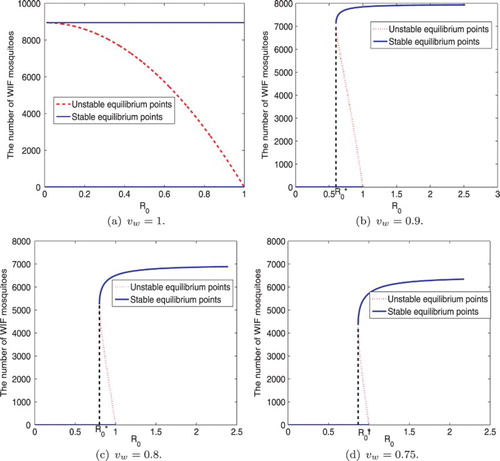
Table 2. Baseline values for parameters in Model (1(1a) $\begin{array}{r}\frac{\mathrm{d}{A}_u}{\mathrm{d}t}=B_{uu}+v_u(B_{wu}+B_{ww})-{\mu }_a{A}_u-\psi A_u,\end{array}$(1a) ).

Parameter	Baseline Value	Ranges	References
$c_i$	1		Assume
$b_f$	0.5	0.34–0.6	[7,29,33]
${\phi }_u$	$50/$day	0–75	[7]
${\phi }_w$	51/day	0–75	[7]
ψ	$0.01/$day		Assume
${\mu }_a$	$0.02/$day		Assume
$v_w$	0.9	0–1	Assume
${\mu }_{fu}$	$0.061/$day	1/55–1/11	[7,31,50]
${\mu }_{fw}$	$0.068/$day	1/55–1/11	[7,31,50]
${\mu }_{mu}$	$0.068/$day	1/31–/7	[7,31,50]
${\mu }_{mw}$	$0.068/$day	1/31–/7	[7,31,50]
$K_a$	100,000		Assume

3.3. Stability of the EE

When vertical transmission is incomplete, i.e. $0<v_w<1$, then at EE, (7) $\frac{A_w^{\ast }}{A_u^{\ast }}=\frac{v_w-v_u\frac{{\mu }_{mw}}{{\mu }_{mu}}\pm \sqrt{{\left(v_u\frac{{\mu }_{mw}}{{\mu }_{mu}}-v_w\right)}^2-4v_u{v}_w(R_0^{-2}-1)\frac{{\mu }_{mw}}{{\mu }_{mu}}}}{2v_u}.$(7) We assume ${\mu }_{mu}={\mu }_{mw}$, and let $k=A_w^{\ast }/A_u^{\ast }$. When $\left(v_u\right({\mu }_{mw}/{\mu }_{mu})-v_w{)}^2>4v_u{v}_w(R_0^{-2}-1\left)\right({\mu }_{mw}/{\mu }_{mu})$, that is, $R_0>2\sqrt{v_w{v}_u}$, then Equation (6(1f) $\begin{array}{r}\frac{\mathrm{d}{M}_w}{\mathrm{d}t}=b_m\psi A_w-{\mu }_{mw}{M}_w.\end{array}$(1f) ) has two roots: $k_1=(2v_w-1+\sqrt{1-4v_w{v}_u{R}_0^{-2}})/2v_u$ and $k_2=(2v_w-1-\sqrt{1-4v_w{v}_u{R}_0^{-2}})/2v_u$.

If $0.5<v_w<1$ and $4v_w(v_w-1)<R_0<1$, two endemic equilibria exist as shown in Figure 2(b), 2(c), and 2(d). When $k=k_1$, the EE is LAS. When $k=k_2$, the equilibrium is not LAS and backward bifurcation occurs. If $v_w\le 0.5$ and $R_0\le 1$, then EE does not exist, only DFE exists. When $k_1=k_2$, then $R_0=2\sqrt{v_w{v}_u}$. Let $R_0^{\ast }=2\sqrt{v_w{v}_u}$, which is the intersection of unstable and stable EE. When $R_0>1$, a unique EE exists with $k=k_1$. It is shown to be LAS by numerical simulations.

4. Bifurcation analysis results

We observed that Wolbachia can persist when $R_0^{\ast }<R_0$, where $R_0^{\ast }$ is the turning point of the backward bifurcation. Three equilibria, namely, DFE, EE, and CIE coexist when $R_0<1$, $R_{0w}>1$, $v_w=1$, and $R_{0u}>1$ as shown in Figure 2(a). The DFE is LAS whenever $R_0<1$ and $R_{0u}>1$, and CIE exists and is LAS as long as $R_{0w}>1$. The unique EE is not LAS, and can become DFE by decreasing the number of infected individuals or become CIE by increasing the number of infected individuals. Figure  2(b)–( d) showed that two endemic equilibria exist when $\sqrt{4v_w{v}_u}<R_0<1$ and $v_w>0.5$, and only one of them is LAS as shown by numerical simulations. When $v_w$ is larger, $R^{\ast }$ is closer to one. The conditions for the existence of the equilibria and their stability are summarized in Table 3.

Table 3. Threshold condition for existence of DFE, EE, and CIE and their stability.

Transmission	DFE	EE	CIE
Complete	$R_0<1$ and $R_{0u}>1$, LAS	$R_0<1$ and $R_{0w}>1$, unstable	$R_{0w}>1$, LAS
Incomplete	$R_0<1$ and $R_{0u}>1$, LAS	$0.5<v_w<1$ and $4v_w(v_w-1)<R_0<1$, when $k=k_1$, LAS, when $k=k_2$, unstable	does not exist

Notes: $R_{0u}$ is the threshold for growth of the Wolbachia-free mosquito population, and $R_{0w}$ is the threshold for growth of the Wolbachia-infected mosquito population. The Wolbachia-free population can grow only when $R_{0u}>1$, and the Wolbachia-infected population can grow only when $R_{0w}>1$.

Initial condition thresholds for an epidemic to occur vary with the vertical transmission rate as shown in Table 4. When $v_w=0.9$, the epidemic will spread if at least $40\mathrm{\%}$ of the population are initially infected. When $v_w=0.95$, the epidemic will spread if at least $34\mathrm{\%}$ of the population are initially infected. When $v_w=1$, the epidemic will spread if at least $28\mathrm{\%}$ of the population are initially infected. When the vertical transmission rate is high, the threshold for the number of initially infected individuals to start Wolbachia epidemic is low.

Table 4. Initial condition thresholds for epidemic to occur with different vertical transmission rates.

Initial condition	$v_w=0.9$	$v_w=0.95$	$v_w=1$
$A_{u0}$	$\le 60\mathrm{\%}{A}_u^0$	$\le 66\mathrm{\%}{A}_u^0$	$\le 72\mathrm{\%}{A}_u^0$
$A_{w0}$	$\ge 40\mathrm{\%}{A}_u^0$	$\ge 34\mathrm{\%}{A}_u^0$	$\ge 28\mathrm{\%}{A}_u^0$
$F_{u0}$	$\le 60\mathrm{\%}{F}_u^0$	$\le 66\mathrm{\%}{F}_u^0$	$\le 72\mathrm{\%}{F}_u^0$
$F_{w0}$	$\ge 40\mathrm{\%}{F}_u^0$	$\ge 34\mathrm{\%}{F}_u^0$	$\ge 28\mathrm{\%}{F}_u^0$
$M_{u0}$	$\le 60\mathrm{\%}{M}_u^0$	$\le 66\mathrm{\%}{M}_u^0$	$\le 72\mathrm{\%}{M}_u^0$
$M_{w0}$	$\ge 40\mathrm{\%}{M}_u^0$	$\ge 34\mathrm{\%}{M}_u^0$	$\ge 28\mathrm{\%}{M}_u^0$

Notes: When the number of Wolbachia-carrying mosquitoes is above the threshold, they can petsit, otherwise, they are wiped out by Wolbachia-free mosquitoes.

The initial condition threshold for an epidemic to occur varies with the ratio of death rates of Wolbachia-infected male mosquitoes to death rates of Wolbachia-free male mosquitoes, ${\mu }_{mw}/{\mu }_{mu}$, while fixing other parameters. The larger ${\mu }_{mw}/{\mu }_{mu}$ is, the larger the initial number of infected individuals required to start a Wolbachia epidemic. With higher vertical transmission rate, a smaller percentage of Wolbachia carriers can invade, as shown in Table 4. Similarly, if we increase ${\phi }_w$ or ${\mu }_{fu}$, or decrease ${\phi }_u$ or ${\mu }_{fw}$, then the threshold for initial infection is smaller. Increasing $\psi /({\mu }_a+\psi )$ will increase the epidemic threshold for initial infection. The thresholds for fraction of initial infections decreasing with the basic reproduction number are shown in Figure 3.

Figure 3. Thresholds for fraction of infected individuals vary with reproduction number. $A_{u0}+A_{w0}=A_u^0$, $F_{u0}+F_{w0}=F_u^0$, $M_{u0}+M_{w0}=M_u^0$. When $R_0<1$, the smaller $R_0$ is, the larger number of infected female mosquitoes are needed to be released for Wolbachia to be endemic. The Wolbachia infection is only sustained if the fraction of WIF mosquitoes is above the red dotted line.

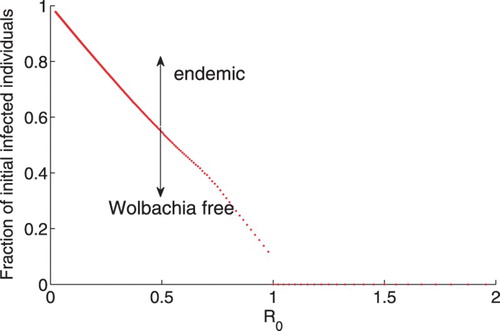
The reproduction number is very sensitive to the vertical transmission rate, egg laying rates of Wolbachia-infected mosquitoes, egg laying rates of Wolbachia-free mosquitoes, and death rates of Wolbachia-infected female mosquitoes and Wolbachia-free female mosquitoes as shown in Equation (4(1d) $\begin{array}{r}\frac{\mathrm{d}{F}_w}{\mathrm{d}t}=b_f\psi A_w-{\mu }_{fw}{F}_w,\end{array}$(1d) ). The reproduction number varies directly with either the vertical transmission rate, the egg laying rates of Wolbachia-infected mosquitoes, or the death rates of Wolbachia-free female mosquitoes. The reproduction number varies inversely with egg laying rates of Wolbachia-free mosquitoes, or the death rates of Wolbachia-infected female mosquitoes.

We compared five strategies before the release of Wolbachia-infected female mosquitoes:

• DFE: releasing Wolbachia-infected female mosquitoes at the DFE,

• KHA: first killing half of the aquatic stage of mosquitoes,

• KHM: first killing half of the wild adult mosquitoes,

• KHM2: first killing half of the wild adult mosquitoes, and then killing half of the adult mosquitoes again after two weeks,

• KHMA: first killing half of the wild mosquitoes and half aquatic stage of mosquitoes.

The ratios of the minimum number of Wolbachia-infected female mosquitoes that can lead to persistence of Wolbachia to the number of female mosquitoes at DFE are listed in Table 5 in decreasing order. Notice that killing the adult mosquitoes only once is not an effective strategy because the aquatic stage mosquitoes hatch and quickly replace the wild uninfected population. Killing both the adult and aquatic (larvae) stage mosquitoes before releasing the infected mosquitoes is the most effective strategy.

Table 5. Different population suppression strategies applied before release of Wolbachia infected female mosquitoes can reduce the minimum number of Wolbachia-infected mosquitoes that can lead to persistence of Wolbachia.

Scenario	Minimum release ratio when $R_0=0.85$	Minimum release ratio when $R_0=0.9$	Minimum release ratio when $R_0=0.95$
DFE	1.007	0.571	0.259
KHA	0.549	0.317	0.151
KHM	0.478	0.244	0.107
KHM2	0.329	0.165	0.072
KHMA	0.210	0.112	0.051

Notes: The top row indicates that you have to release 1.007 times as many wolbachia-infected female mosquitoes as there are wild mosquitoes to establish an infection in the wild that starts at the DFE when $R_0=0.85$. The number of infected mosquitoes that need to be released to establish an infection decreases with the strategies: KHA denotes killing half of the aquatic stage mosquitoes, KHM denotes killing half of adult wild mosquitoes, KHM2 denotes killing half adult of wild mosquitoes once, then kill half adult wild mosquitoes again after two weeks, and finally KHMA denotes killing half adult wild mosquitoes and half aquatic stage of mosquitoes.

The results section should provide details of all of the experiments that are required to support the conclusions of the paper. There is no specific word limit for this section, but details of experiments that are peripheral to the main thrust of the article and that detract from the focus of the article should not be included. The section may be divided into subsections, each with a concise subheading. Large datasets, including raw data, should be submitted as supporting files; these are published online alongside the accepted article. The results section should be written in the past tense.

5. Discussion

We developed a model considering two sex of aquatic stage and adult mosquitoes, diversity in the death rates of Wolbachia-infected mosquitoes and Wolbachia-free mosquitoes, and egg laying rates of Wolbachia-infected female mosquitoes and Wolbachia-free female mosquitoes. The general model is not constrained to particular weather condition, specific Wolbachia strains, or specific mosquito species, and it can be easily adapted to Aedes aegypti or Aedes albopictus at any location with parameters calibrated using realistic environmental factors, such as temperature and rainfall .

We found conditions for the existence of multiple equilibria and backward bifurcation. If vertical transmission is complete, then a unique EE exists and is not LAS when $R_0<1$ and $R_{0u}>1$. A backward bifurcation occurs when EE changes into DFE if we decrease the initial number of infected individuals, or it reaches another LAS equilibrium if we increase the number of initially infected individuals. When vertical transmission is incomplete but more than $50\mathrm{\%}$, and $R_0<1$, two endemic equilibria coexist, but only one EE is LAS such that it becomes DFE or EE by perturbation. Since Wolbachia-infected mosquitoes are less capable of transmitting the virus, complete Wolbachia-infection is the ideal case for disease control.

When $R_0>1$, Wolbachia can spread with a small number of initially infected mosquitoes, although very slowly. Population replacement may occur. When $R_0<1$, Wolbachia can spread if initial number of infected individuals exceeds a threshold, which depends on the vertical transmission rate, ratio of egg laying rates of Wolbachia-infected females to egg laying rates of Wolbachia-free female mosquitoes, and ratio of death rates of infected female mosquitoes to death rates of uninfected female mosquitoes. A smaller number of Wolbachia-infected female mosquitoes is needed to be released for persistence of Wolbachia if a population suppression strategy is implemented before the release.

The reproduction number is the product of the vertical transmission rate, ratio of the egg laying rates of Wolbachia-infected mosquitoes to egg laying rates of Wolbachia-free mosquitoes, and the ratio of death rates of Wolbachia-free mosquitoes to death rates of Wolbachia infected mosquitoes. If the total number of eggs produced by Wolbachia-infected mosquitoes through vertical transmission is more than the total number of eggs produced by Wolbachia-free mosquitoes, then $R_0>1$, such that CIE or EE is LAS.

The number of Wolbachia-infected mosquitoes required for sustained Wolbachia infection depends on vertical transmission rate, $v_w$, the ratio of the number of eggs laid by Wolbachia-infected mosquitoes to the number of eggs laid by Wolbachia-free mosquitoes, ${\phi }_w/{\phi }_u$, the ratio of the death rates of Wolbachia-free females to death rates of Wolbachia-infected females, ${\mu }_{fu}/{\mu }_{fw}$, and the ratio of the death rates of Wolbachia-free males to death rates of Wolbachia-infected males ${\mu }_{mu}/{\mu }_{mw}$. These parameters depend on partculiarWolbachia strain. If the life span of a mosquito is shorter, then the mosquitoes will lay fewer eggs. Once we know the specific Wolbachia strain that a specific mosquito species, such as Aedes aegypti or Aedes albopictus is carrying, we can estimate the number of infected individuals needed to be released for sustainable Wolbachia establishment using this model.

We find that reducing both the aquatic stage and adult uninfected mosquitoes before releasing Wolbachia-infected female mosquitoes is the most effective strategy to reduce the number of Wolbachia-infected female mosquitoes needed for Wolbachia persistence (Table 5). The second most effective strategy was to repeatedly kill the wild uninfected mosquitoes (to reduce both the adult and the aquatic stage mosquitoes) before releasing the infected mosquitoes.

The model and analysis can help in understanding how Wolbachia can invade and persist in mosquito populations. In future research, we will couple our model to a transmission model and analyse the impact that a Wolbachia-infected mosquito population has on the spread of dengue fever, chikungunya, and Zika. Previous studies have shown spatial heterogeneity in the mosquito population can be an important factor in establishing a sustained Wolbachia infected population [5,19,49]. We will also add heterogeneity to our Wolbachia transmission models to better understand the impact of the diffusion of mosquitoes.

The discussion should spell out the major conclusions of the work along with some explanation or speculation on the significance of these conclusions. How do the conclusions affect the existing assumptions and models in the field? How can future research build on these observations? What are the key experiments that must be done? The discussion should be concise and tightly argued. The results and discussion may be combined into one section, if desired.

Acknowledgments

The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Science Foundation or the National Institutes of Health. The authors thank Michael Robert for his many helpful comments.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by the endowment for the Evelyn and John G. Phillips Distinguished Chair in Mathematics at Tulane University, the National Science Foundation (NSF) awards MPS-DMS-1122666, MPS-DMS-156353, DEB-RAPID 1641130, NSF grant CHE-1314029, and the NIH/NIGMS program for Models of Infectious Disease Agent Study (MIDAS) award U01GM097661.

Appendix

The system of equations for mosquito population dynamics is (A1a) $\begin{array}{r}\frac{\mathrm{d}A}{\mathrm{d}t}=\phi F\left(1-\frac{A}{K_a}\right)-{\mu }_{a}A-\psi A,\end{array}$(A1a) (A1b) $\begin{array}{r}\frac{\mathrm{d}F}{\mathrm{d}t}=\theta \psi A-{\mu }_{fu}F,\end{array}$(A1b) (A1c) $\begin{array}{r}\frac{\mathrm{d}M}{\mathrm{d}t}=(1-\theta )\psi A-{\mu }_{mu}M.\end{array}$(A1c) The parameters for this model are described in Table 1.

Theorem A.1

The zero equilibrium for mosquito population dynamics is LAS when $R_{0u}<1,$ while the EE is LAS when $R_{0u}>1,$ where $R_{0u}=\phi \theta \psi /{\mu }_{fu}({\mu }_a+\psi )$.

Proof.

Jacobian matrix of system (A1) is $J=\left[\begin{array}{ccc}-{\mu }_a-\psi -\phi \frac{F}{K_a}& \phi \left(1-\frac{A}{K_a}\right)& 0\\ \theta \psi & -{\mu }_{fu}& 0\\ (1-\theta )\psi & 0& -{\mu }_{mu}\end{array}\right].$ The Jacobian matrix for no-infection equilibrium is $J_0=\left[\begin{array}{ccc}-{\mu }_a-\psi & \phi & 0\\ \theta \psi & -{\mu }_{fu}& 0\\ (1-\theta )\psi & 0& -{\mu }_{mu}\end{array}\right].$ The characteristic polynomial of $J_0$ is (A2) $(\lambda +{\mu }_{mu})\left[\right(\lambda +{\mu }_a+\psi \left)\right(\lambda +{\mu }_{fu})-\phi \theta \psi ]=0.$(A2)

If $R_{0u}<1$, then all eigenvalues are negative, the zero equilibrium is LAS.

The Jacobian matrix at EE is $J_{ss}=\left[\begin{array}{ccc}-{\mu }_a-\psi -\phi \frac{F^{\ast }}{K_a}& \phi \left(1-\frac{A^{\ast }}{K_a}\right)& 0\\ \theta \psi & -{\mu }_{fu}& 0\\ (1-\theta )\psi & 0& -{\mu }_{mu}\end{array}\right].$

Characteristic polynomial of $J_{ss}$ is (A3) $(\lambda +{\mu }_{mu})\left[\lambda +{\mu }_a+\psi +\frac{\phi \theta \psi }{{\mu }_{fu}}\left(1-\frac{({\mu }_a+\psi ){\mu }_{fu}}{\phi \theta \psi }\right)\right](\lambda +{\mu }_{fu})-\phi \theta \psi ]=0.$(A3)

If $R_{0u}>1$, then all eigenvalues of $J_{ss}$ are negative, and the EE is LAS.

Theorem A.2

The zero equilibrium: $(0,0,0)$ is globally asymptotically stable $($GAS$)$ when $R_{0u}<1$. The EE: $\left(K_a\right(1-1/R_{0u}),(K_a\theta \psi /{\mu }_{fu}\left)\right(1-1/R_{0u}),(K_a(1-\theta )\psi /{\mu }_{mu}\left)\right(1-1/R_{0u}\left)\right)$ is GAS when $R_{0u}>1$.

Proof.

We follow the approach in [9]. First, we consider the subsystem: (A4a) $\begin{array}{r}\frac{\mathrm{d}A}{\mathrm{d}t}=\phi F\left(1-\frac{A}{K_a}\right)-{\mu }_{a}A-\psi A,\end{array}$(A4a) (A4b) $\begin{array}{r}\frac{\mathrm{d}F}{\mathrm{d}t}=\theta \psi A-{\mu }_{fu}F,\end{array}$(A4b) where $f=(A,F)$ is $C^1$ on an open set $D\subset {\mathbb{R}}^2$.

Let ${\delta }_1={\delta }_2=1$, ${\delta }_1\left(\mathrm{d}{f}_2/\mathrm{d}{x}_1\right)=\theta \psi >0$, ${\delta }_1\left(\mathrm{d}{f}_1/\mathrm{d}{x}_2\right)=\phi \ge 0$, and ${\delta }_2\left(\mathrm{d}{f}_2/\mathrm{d}{x}_2\right)={\mu }_{fu}>0$. According to the definition of tridiagonal feedback [9], system (A4) is a monotone tridiagonal feedback system with Poincaré–Bendixson property [30].

Recall Theorem 2 in [28]. If the systems of ODEs $\mathrm{d}x/\mathrm{d}t=f\left(x\right),x\subset D$ satisfies:

1. The system exists on a compact absorbing set $K\subset D$.

2. A unique equilibrium point E exists and is LAS.

3. The system has Poincaré–Bendixson property.

4. Each periodic orbit of the system is asymptotically stable.

Then E is globally asymptotically stable in D.

To prove that each periodic orbit $\mathrm{\Omega }=p\left(t\right):0\le t\le w$ of system (A4) is asymptotically stable, we follow [37] and Theorem 3 in [9]. We need to prove that the linear system $\mathrm{d}z\left(t\right)/\mathrm{d}t=J_F^{\left[2\right]}\left(p\right(t\left)\right)z\left(t\right)$ is asymptotically stable, where $J_F^{\left[2\right]}$ is the second additive compound matrix of the Jacobian matrix $J_F$ associated with system (A4). For system (A4), $J_F^{\left[2\right]}=-(\psi +{\mu }_a+(\phi /K_a)F+{\mu }_{fu})$. We build the following linear system with one equation and the right-hand side is the compound matrix of the Jacobian matrix $J_F$. $\frac{\mathrm{d}X}{\mathrm{d}t}=-\left(\psi +{\mu }_a+\frac{\phi }{K_a}F+{\mu }_{fu}\right)X.$ Let Lyapunov function $V(X,A,Y)=|X|$. The right derivative of V along the solution paths (X) and $(A,F)$ is: $D_{+}\left(V\right(t)=-(\psi +{\mu }_a+\left(\phi /K_a\right)F+{\mu }_{fu})|X|$, which implies that $V\left(t\right)\to 0$, and $X\left(t\right)\to 0$ as $t\to \mathrm{\infty }$. Therefore, the linear system (A4) is asymptotically stable, and the solution $(A,F)$ is asymptotically orbitally stable with asymptotic phase.

By the same argument in [9], the system (A4) is uniformly persistent in $D\subset {\mathbb{R}}^2$. The zero equilibrium $(0,0,0)$ is isolated and the largest compact invariant outside D is $(A^{\ast },F^{\ast })$, which is absorbing and the system (A4) is uniformly persistent [17]. The conditions for Theorem 2 in [28] are all satisfied. Therefore, $(0,0)$ is GAS whenever $R_{0u}<1$, and $(A^{\ast },F^{\ast })$ exists and is GAS when $R_{0u}>1$.

Following [54] and Theorem 4 in [9], $(0,0,0)$ is GAS whenever $R_{0u}<1$ and $(A^{\ast },F^{\ast },M^{\ast })$ is GAS whenever $R_{0u}>1$.

Theorem A.3

(A5) $\mathcal{D}=\left\{\left(\begin{array}{c}A\\ F\\ M\end{array}\right)\in {\mathbb{R}}^3\left|\begin{array}{c}0\le A\le K_a,\\ 0\le F\le \frac{\psi \theta K_a}{{\mu }_{fu}},\\ 0\le M\le \frac{\psi (1-\theta )K_a}{{\mu }_{mu}}\end{array}\right.\right\}.$(A5) is an invariant region under the flow induced by Equation (A1).

Proof.

The proof directly follows the proofs for Lemmas  4.2 and 4.3 in [35].