Stability and Hopf bifurcation for a five-dimensional virus infection model with Beddington–DeAngelis incidence and three delays

ABSTRACT

In this paper, the dynamical behaviours for a five-dimensional virus infection model with three delays which describes the interactions of antibody, cytotoxic T-lymphocyte (CTL) immune responses and Beddington–DeAngelis incidence are investigated. The reproduction numbers for virus infection, antibody immune response, CTL immune response, CTL immune competition and antibody immune competition, respectively, are calculated. By using the Lyapunov functionals and linearization method, the threshold conditions on the local and global stability of the equilibria for infection-free, immune-free, antibody response, CTL response and interior, respectively, are established. The existence of Hopf bifurcation with immune delay as a bifurcation parameter is investigated by using the bifurcation theory. Numerical simulations are presented to justify the analytical results.

KEYWORDS:

• Virus infection model
• delay
• CTL and antibody response
• stability
• Hopf bifurcation
• Beddington–DeAngelis incidence

1. Introduction

In recent years, the virus infection models provide comprehensive views for our understanding of diseases, such as HIV, influenza, HBV, Ebola, HTLV and HCV (see [1–21,23,24]). Theoretical analysis for these mathematical models are important to obtain complete insights for the viral dynamics in vivo. In particular, the stability and the bifurcation will provide specific information for our understanding about disease control.

The adaptive immune system reacts against virus and infected cells during virus infections. The antibody and cytotoxic T-lymphocyte (CTL) responses play the significant role in preventing infections. Hence, effective strategies to prevent virus infection need both antibody and CTL responses (see [1,14,17,19]). In [17], Wodarz proposed a basic model to describe the interactions of antibody and CTL immune responses with bilinear incidence which includes uninfected target cells $x\left(t\right)$, productively infected cells $y\left(t\right)$, free virus $v\left(t\right)$, CTL response cells $z\left(t\right)$ and antibody response cells $w\left(t\right)$. Then, Yousfi et al. [20] gave the global analysis for this model. Yan and Wang [19] incorporated an intracellular delay into the infected cell equation in the model and studied the effect of the delay on the global dynamics. However, Wang and Xu [15] suggested that the incidence rate is probably not linear over the large number of virus and susceptible cells. Balasubramaniam et al. [1] developed a HIV model with Beddington–DeAngelis incidence and investigated the global stability and the existence of Hopf bifurcation.

However, only single immune response delay is considered in [1]. We know that there are usually three delays in a virus infection disease with the interactions of antibody and CTL immune responses: the intracellular delay, virus replication delay and immune response delay in the transmission process of virus infection. An important and interesting problem is how dynamical properties in virus infection disease will befallen when three delays exist simultaneously. Particularly, how stability properties will occur at possible equilibrium stations.

Therefore, in this paper we consider a five-dimensional virus infection model with three time delays which describes the interactions of antibody, CTL immune responses and Beddington–DeAngelis incidence rate (1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) where Λ, k, c and g are the birth rate of the uninfected cells, the virus, the CTL responses and the antibody responses, respectively; β is the infection rate; d,r,u,h and α represent the death rate of uninfected target cells, productively infected cells, virus, CTL responses and antibody responses, respectively; p represents the killing rate of infected cells by CTL response cells; q is the B cells neutralize rate; ${\tau }_1$ denotes the intracellular delay, and $e^{-m{\tau }_1}$ denotes the surviving rate of infected cells during delay period $[t-{\tau }_1,t]$ (see [4,7–10,12,19,24]); ${\tau }_2$ is virus replication delay, and $e^{-n{\tau }_2}$ denotes the surviving rate of virus during delay period $[t-{\tau }_2,t]$ (see [5,18]) and ${\tau }_3$ denotes immune response delay which is suggested in [1,8,11,23].

In this paper, our purpose is to investigate the dynamical properties of model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ), expressly the stability of equilibria and the existence of Hopf bifurcation. The organization of our paper is as follows. In Section 2, the basic properties of model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) for the non-negativity and boundedness of solutions, the threshold values and the existence of five equilibria are discussed. In Section 3, the threshold conditions on the global stability and instability for the infection-free equilibrium, infection equilibrium without immune response and infection equilibrium with only antibody response are stated. When ${\tau }_3=0$, the threshold conditions on the global stability and instability for the infection equilibrium with only CTL response and infection equilibrium with both CTL and antibody responses are proved. In Section 4, when ${\tau }_3>0,$ the sufficient conditions on the existence of Hopf bifurcation for the infection equilibrium with only CTL response and infection equilibrium with both CTL and antibody responses are established. In Section 5, the numerical simulations are presented to further illustrate the dynamical behaviour of the model. Finally, we will give a conclusion.

2. Boundedness and equilibrium

Let $\tau =max\left\{{\tau }_1,{\tau }_2,{\tau }_3\right\}$ and $R_{+}^5=\left\{\right(x_1,x_2,x_3,x_4,x_5):x_i\ge 0,i=1,2,3,4,5\}.$ $C\left(\right[-\tau ,0],R_{+}^5)$ denotes the space of continuous functions mapping interval $[-\tau ,0]$ into $R_{+}^5$ with norm $\parallel \phi \parallel =\underset{-\tau \le t\le 0}{sup}\left\{|\phi \right(t\left)|\right\}$ for any $\phi \in C\left(\right[-\tau ,0],R_{+}^5)$.

The initial conditions for model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) are given as follows (2) $\begin{array}{rl}& \left(x\right(\theta ),y(\theta ),v(\theta ),z(\theta ),w(\theta \left)\right)=\left({\phi }_1\right(\theta ),{\phi }_2(\theta ),{\phi }_3(\theta ),{\phi }_4(\theta ),{\phi }_5(\theta \left)\right),\\ & {\phi }_i\left(\theta \right)\ge 0,\theta \in [-\tau ,0),{\phi }_i\left(0\right)>0(i=1,2,3,4,5),\end{array}$(2) where $\left({\phi }_1\right(\theta ),{\phi }_2(\theta ),{\phi }_3(\theta ),{\phi }_4(\theta ),{\phi }_5(\theta \left)\right)\in C\left(\right[-\tau ,0],R_{+}^5).$ By the fundamental theory of functional differential equation [6], It is easy to see that model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) admits a unique solution $\left(x\right(t),y(t),v(t),z(t),w(t\left)\right)$ satisfying initial conditions (2(2) $\begin{array}{rl}& \left(x\right(\theta ),y(\theta ),v(\theta ),z(\theta ),w(\theta \left)\right)=\left({\phi }_1\right(\theta ),{\phi }_2(\theta ),{\phi }_3(\theta ),{\phi }_4(\theta ),{\phi }_5(\theta \left)\right),\\ & {\phi }_i\left(\theta \right)\ge 0,\theta \in [-\tau ,0),{\phi }_i\left(0\right)>0(i=1,2,3,4,5),\end{array}$(2) ). We have the following basic result of model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ).

Theorem 2.1

Let $\left(x\right(t),y(t),v(t),z(t),w(t\left)\right)$ be the solution of model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) satisfying initial conditions (2(2) $\begin{array}{rl}& \left(x\right(\theta ),y(\theta ),v(\theta ),z(\theta ),w(\theta \left)\right)=\left({\phi }_1\right(\theta ),{\phi }_2(\theta ),{\phi }_3(\theta ),{\phi }_4(\theta ),{\phi }_5(\theta \left)\right),\\ & {\phi }_i\left(\theta \right)\ge 0,\theta \in [-\tau ,0),{\phi }_i\left(0\right)>0(i=1,2,3,4,5),\end{array}$(2) ), then $x\left(t\right),y\left(t\right),v\left(t\right),z\left(t\right)$ and $w\left(t\right)$ are positive and ultimately bounded.

Proof.

It is now easy to show that all solutions of model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) with initial conditions (2(2) $\begin{array}{rl}& \left(x\right(\theta ),y(\theta ),v(\theta ),z(\theta ),w(\theta \left)\right)=\left({\phi }_1\right(\theta ),{\phi }_2(\theta ),{\phi }_3(\theta ),{\phi }_4(\theta ),{\phi }_5(\theta \left)\right),\\ & {\phi }_i\left(\theta \right)\ge 0,\theta \in [-\tau ,0),{\phi }_i\left(0\right)>0(i=1,2,3,4,5),\end{array}$(2) ) are defined on $R_{+}^5$ and remain positive for all $t\ge 0$. Denote $N\left(t\right)=e^{-m{\tau }_1}x(t-{\tau }_1)+y\left(t\right)+\frac{r{e}^{n{\tau }_2}}{2k}v(t+{\tau }_2)+\frac{p}{c}z(t+{\tau }_3)+\frac{rq{e}^{n{\tau }_2}}{2kg}w(t+{\tau }_2).$ Calculating the derivative of $N\left(t\right)$ along solutions of model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ), we have $\begin{array}{rl}\dot{N}\left(t\right)& =\mathrm{\Lambda }{e}^{-m{\tau }_1}-d{e}^{-m{\tau }_1}x(t-{\tau }_1)-\frac{r}{2}y\left(t\right)-\frac{ru{e}^{n{\tau }_2}}{2k}v(t+{\tau }_2)\\ & -\frac{ph}{c}z(t+{\tau }_3)-\frac{\alpha rq{e}^{n{\tau }_2}}{2kg}w(t+{\tau }_2)\\ & \le \mathrm{\Lambda }{e}^{-m{\tau }_1}-sN\left(t\right),\end{array}$ where $s=min\{d,r/2,u,h,\alpha \}$. This implies that $N\left(t\right)$ is ultimately bounded for large t. So, $x\left(t\right),y\left(t\right),v\left(t\right),z\left(t\right)$ and $w\left(t\right)$ are also ultimately bounded.

Next, we discuss the existence of equilibria of model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ). Firstly, we directly obtain that model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) always has a unique infection-free equilibrium $E_0=(x_0,0,0,0,0)$ with $x_0=\mathrm{\Lambda }/d.$

The basic reproductive number of viral infection for model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) is $R_0=k\cdot \frac{1}{u}\cdot e^{-n{\tau }_2}\cdot \frac{\beta \frac{\mathrm{\Lambda }}{d}}{(1+a\frac{\mathrm{\Lambda }}{d})}\cdot e^{-m{\tau }_1}\cdot \frac{1}{r}.$ Here, k is the rate of the newly virus produced by infected cells, $1/u$ is the surviving period of virus, $e^{-n{\tau }_2}$ is the surviving rate of newly virus in $[t-{\tau }_2,t]$, $\beta \left(\mathrm{\Lambda }/d\right)/(1+a(\mathrm{\Lambda }/d\left)\right)$ denotes the newly infected cells which are infected by the first virus, $e^{-m{\tau }_1}$ is the the surviving rate of newly infected cells in $[t-{\tau }_1,t]$, and $1/r$ is the surviving period of infected cells. Therefore, we easily see that $R_0$ denotes the average number of the free virus released by the infected cells which are infected by the first virus.

Obviously, $R_0>1$ implies that $k\beta \mathrm{\Lambda }{e}^{-m{\tau }_1-n{\tau }_2}-ur(d+a\mathrm{\Lambda })>0$ and $k(\beta +bd)-aur{e}^{m{\tau }_1+n{\tau }_2}>0.$

When $R_0>1$, model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) has a unique immune-free equilibrium $E_1=(x_1,y_1,v_1,$ $0,0),$ where $\begin{array}{rl}{x}_1& =\frac{\mathrm{\Lambda }kb+ur{e}^{m{\tau }_1+n{\tau }_2}}{k(\beta +bd)-aur{e}^{m{\tau }_1+n{\tau }_2}},y_1=\frac{k\beta \mathrm{\Lambda }{e}^{-m{\tau }_1}-ur{e}^{n{\tau }_2}(d+a\mathrm{\Lambda })}{r\left[k\right(\beta +bd)-aur{e}^{m{\tau }_1+n{\tau }_2}]},\\ v_1& =\frac{\mathrm{\Lambda }{k}^2\beta e^{-m{\tau }_1-n{\tau }_2}-kur(a\mathrm{\Lambda }+d)}{ur\left[k\right(\beta +bd)-aur{e}^{m{\tau }_1+n{\tau }_2}]}.\end{array}$

The antibody immune reproductive number for model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) is $R_1=g\cdot \frac{\mathrm{\Lambda }{k}^2\beta e^{-m{\tau }_1-n{\tau }_2}-kur(a\mathrm{\Lambda }+d)}{ur\left[k\right(\beta +bd)-aur{e}^{m{\tau }_1+n{\tau }_2}]}\cdot \frac{1}{\alpha }.$ Note that when $R_0>1$ model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) has a unique immune-free equilibrium $E_1=(x_1,y_1,v_1,$ $0,0)$. This shows that virus infection is successful and the number of free virus at equilibrium $E_1$ is $\mathrm{\Lambda }{k}^2\beta e^{-m{\tau }_1-n{\tau }_2}-kur(a\mathrm{\Lambda }+d)/ur\left[k\right(\beta +bd)-aur{e}^{m{\tau }_1+n{\tau }_2}]$. Furthermore, we have that $1/\alpha$ is the average life-span of antibody cells, g is birth rate of the antibody response. Hence, $R_1$ denotes the average number of the antibody immune cells activated by virus when virus infection is successful and CTL responses have not been established.

The CTL immune reproductive number for model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) is $R_2=c\cdot \frac{k\beta \mathrm{\Lambda }{e}^{-m{\tau }_1}-ur{e}^{n{\tau }_2}(d+a\mathrm{\Lambda })}{r\left[k\right(\beta +bd)-aur{e}^{m{\tau }_1+n{\tau }_2}]}\cdot \frac{1}{h}.$ Here, $R_2$ denotes the average number of the CTL immune cells activated by infected cells when virus infection is successful and antibody immune responses have not been established. Note that the number of infected cells at equilibrium $E_1$ is $k\beta \mathrm{\Lambda }{e}^{-m{\tau }_1}-ur{e}^{n{\tau }_2}(d+a\mathrm{\Lambda })/r\left[k\right(\beta +bd)-aur{e}^{m{\tau }_1+n{\tau }_2}]$, $1/h$ is the average life-span of CTL cells and c is the rate at which the CTL responses are produced.

We see that $R_1>1$ is equivalent to $\alpha -g{v}_1<0$, and $R_2>1$ is equivalent to $h-c{y}_1<0.$

When $R_1>1$, model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) has a unique infection equilibrium with only antibody response $E_2=(x_2,y_2,v_2,0,w_2)$, where $y_2=\frac{(\mathrm{\Lambda }-\mathrm{d}{x}_2)e^{-m{\tau }_1}}{r},v_2=\frac{\alpha }{g},w_2=\frac{kg{e}^{-m{\tau }_1-n{\tau }_2}(\mathrm{\Lambda }-\mathrm{d}{x}_2)-\alpha ur}{q\alpha r}$ and $x_2$ is the unique positive zero point of the following function $L\left(x\right)=ad{x}^2+\left[d\left(1+\frac{\alpha b}{g}\right)+\frac{\alpha \beta }{g}-a\mathrm{\Lambda }\right]x-\mathrm{\Lambda }\left(1+\frac{\alpha b}{g}\right).$

In fact, from $k\mathrm{\Lambda }{e}^{-m{\tau }_1-n{\tau }_2}/ur>v_1$, by $R_1>1$ we obtain $k\mathrm{\Lambda }g-\alpha ur{e}^{m{\tau }_1+n{\tau }_2}>0$. From the expression of $w_2$ it follows that the existence of equilibrium $E_2$ is equivalent to $x_2\in (0,kg\mathrm{\Lambda }-\alpha ur{e}^{m{\tau }_1+n{\tau }_2}/kgd)$. Noticing that $L\left(x\right)$ is a quadratic function and $L\left(0\right)<0$, we know that the existence and uniqueness of equilibrium $E_2$ is equivalent to $L\left(\frac{kg\mathrm{\Lambda }-\alpha ur{e}^{m{\tau }_1+n{\tau }_2}}{kgd}\right)>0.$ Since $\begin{array}{rl}L\left(\frac{kg\mathrm{\Lambda }-\alpha ur{e}^{m{\tau }_1+n{\tau }_2}}{kgd}\right)& =\frac{-aru\alpha e^{m{\tau }_1+n{\tau }_2}(\mathrm{\Lambda }kg-\alpha ur{e}^{m{\tau }_1+n{\tau }_2})}{k^2{g}^{2}d}\\ & +\frac{k\alpha \beta (\mathrm{\Lambda }kg-\alpha ur{e}^{m{\tau }_1+n{\tau }_2})-(g+\alpha b)e^{m{\tau }_1+n{\tau }_2}\alpha urkd}{k^2{g}^{2}d},\end{array}$ from $R_1>1$, we have $k^2\beta \mathrm{\Lambda }g{e}^{-m{\tau }_1-n{\tau }_2}>urkg(d+a\mathrm{\Lambda })+ur\alpha k(\beta +bd)-aur\alpha ur{e}^{m{\tau }_1+n{\tau }_2}.$ Therefore, when $R_1>1,$ we get $L\left(\frac{kg\mathrm{\Lambda }-\alpha ur{e}^{m{\tau }_1+n{\tau }_2}}{kgd}\right)>0.$

When $R_2>1$, model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) has a unique infection equilibrium with only CTL response $E_3=(x_3,y_3,v_3,z_3,0)$, where $y_3=\frac{h}{c},v_3=\frac{kh{e}^{-n{\tau }_2}}{uc},z_3=\frac{c{e}^{-m{\tau }_1}(\mathrm{\Lambda }-\mathrm{d}{x}_3)-rh}{ph}$ and $x_3$ is the unique positive zero point of the following function $L\left(x\right)=a\mathrm{d}{x}^2+\left[d\left(1+\frac{kbh{e}^{-n{\tau }_2}}{uc}\right)+\frac{k\beta h{e}^{-n{\tau }_2}}{uc}-a\mathrm{\Lambda }\right]x-\mathrm{\Lambda }\left(1+\frac{kbh{e}^{-n{\tau }_2}}{uc}\right).$

In fact, since $\mathrm{\Lambda }{e}^{-m{\tau }_1}/r>y_1$, by $R_2>1$ we obtain $c\mathrm{\Lambda }-rh{e}^{m{\tau }_1}>0$. From the expression of $z_3$ it follows that the existence of CTL-present infection equilibrium $E_3$ is equivalent to $x_3\in (0,c\mathrm{\Lambda }-rh{e}^{m{\tau }_1}/cd)$. Noticing that $L\left(x\right)$ is a quadratic function and $L\left(0\right)<0$, we know that the existence and uniqueness of CTL-present equilibrium $E_3$ is equivalent to $L\left(\frac{c\mathrm{\Lambda }-rh{e}^{m{\tau }_1}}{cd}\right)>0.$ Since $\begin{array}{rl}L\left(\frac{c\mathrm{\Lambda }-rh{e}^{m{\tau }_1}}{cd}\right)& =\frac{-arhu{e}^{m{\tau }_1}(\mathrm{\Lambda }c-rh{e}^{m{\tau }_1})+kh\beta (\mathrm{\Lambda }c-hr{e}^{m{\tau }_1})e^{-n{\tau }_2}}{c^{2}du}\\ & -\frac{(uc+kbh{e}^{-n{\tau }_2})rhd{e}^{m{\tau }_1}}{c^{2}du},\end{array}$

from $R_2>1$, we have $\mathrm{\Lambda }k\beta c{e}^{-m{\tau }_1-n{\tau }_2}>ruc(d+a\mathrm{\Lambda })+hrk(\beta +bd)e^{-n{\tau }_2}-ahu{r}^2{e}^{m{\tau }_1}.$ Therefore, when $R_2>1,$ we get $L\left(\frac{c\mathrm{\Lambda }-rh{e}^{m{\tau }_1}}{cd}\right)>0.$

The CTL immune competitive reproductive number for model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) is $R_3=c\cdot \frac{(\mathrm{\Lambda }-d{x}_2)e^{-m{\tau }_1}}{r}\cdot \frac{1}{h}.$ In fact, when $R_1>1$, model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) has a unique infection equilibrium with only antibody response $E_2=(x_2,y_2,v_2,0,w_2)$. This predicates that CTL immune responses have been established, and the number of infected cells at equilibrium $E_2$ is $(\mathrm{\Lambda }-\mathrm{d}{x}_2)e^{-m{\tau }_1}/r$. Hence, $R_3$ denotes the average number of the CTL immune cells activated by infected cells under the condition that antibody immune responses have been established.

The antibody immune competitive reproductive number for model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) is $R_4=g\cdot \frac{kh{e}^{-n{\tau }_2}}{uc}\cdot \frac{1}{\alpha }.$ In fact, when $R_2>1$, model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) has a unique infection equilibrium with only CTL response $E_3=(x_3,y_3,v_3,z_3,0)$. This predicates that antibody immune responses have been established, and the number of the virus at equilibrium $E_3$ is $kh{e}^{-n{\tau }_2}/uc$. Hence, $R_4$ denotes the average number of the antibody immune cells activated by viruses under the condition that CTL immune responses have been established.

When $R_3>1$ and $R_4>1$, model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) has a unique infection equilibrium with CTL and antibody responses $E_4=(x_4,y_4,v_4,z_4,w_4)$, where $y_4=\frac{h}{c},v_4=\frac{\alpha }{g},z_4=\frac{c{e}^{-m{\tau }_1}(\mathrm{\Lambda }-d{x}_4)-rh}{ph},w_4=\frac{khg{e}^{-n{\tau }_2}-\alpha uc}{\alpha qc}.$

In fact, from the above discussion on the existence of equilibrium $E_2,$ we directly have $v_4=v_2$ and $x_4=x_2.$ From $R_3>1,$ we have $y_2>h/c$. From the expression of $y_2$, we further have $x_4=x_2<(c\mathrm{\Lambda }-rh{e}^{m{\tau }_1})/cd$. Hence, $c{r}^{-m{\tau }_1}(\mathrm{\Lambda }-d{x}_4)-rh>0$, which implies $z_4>0$. Furthermore, from $R_4>1$ we also have $w_4>0$. This shows that equilibrium $E_4$ uniquely exists.

3. Stability analysis

Theorem 3.1

1. If $R_0\le 1,$ then the infection-free equilibrium $E_0$ is globally asymptotically stable.

2. If $R_0>1,$ then the equilibrium $E_0$ is unstable.

Proof.

Consider conclusion (a). Define a Lyapunov functional $\begin{array}{rl}{V}_1\left(t\right)& =\frac{x_0}{1+a{x}_0}\left(\frac{x\left(t\right)}{x_0}-1-\ln \frac{x\left(t\right)}{x_0}\right)+e^{m{\tau }_1}y\left(t\right)+\frac{r{e}^{m{\tau }_1+n{\tau }_2}}{k}v\left(t\right)\\ & +\frac{p{e}^{m{\tau }_1}}{c}z\left(t\right)+\frac{rq{e}^{m{\tau }_1+n{\tau }_2}}{kg}w\left(t\right)+{\int }_{t-{\tau }_1}^t\frac{\beta v\left(\theta \right)x\left(\theta \right)}{1+ax\left(\theta \right)+bv\left(\theta \right)}\mathrm{d}\theta \\ & +p{e}^{m{\tau }_1}{\int }_{t-{\tau }_3}^{t}y\left(\theta \right)z\left(\theta \right)\mathrm{d}\theta +r{e}^{m{\tau }_1}{\int }_{t-{\tau }_2}^{t}y\left(\theta \right)\mathrm{d}\theta .\end{array}$ Calculating the derivative of $V_1\left(t\right)$ along any positive solution of model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) and noting that $x_0=\mathrm{\Lambda }/d$, we can obtain $\begin{array}{rl}\frac{\mathrm{d}{V}_1\left(t\right)}{\mathrm{d}t}& =-\frac{d\left(x\right(t)-x_0{)}^2}{x\left(t\right)(1+a{x}_0)}+\frac{ur{e}^{m{\tau }_1+n{\tau }_2}v\left(t\right)(1+ax(t\left)\right)}{k(1+ax(t)+bv(t\left)\right)}(R_0-1)\\ & -\frac{bur{e}^{m{\tau }_1+n{\tau }_2}{v}^2\left(t\right)}{k(1+ax(t)+bv(t\left)\right)}-\frac{ph{e}^{m{\tau }_1}}{c}z\left(t\right)-\frac{rq\alpha e^{m{\tau }_1+n{\tau }_2}}{kg}w\left(t\right).\end{array}$ If $R_0\le 1$, then $\mathrm{d}{V}_1\left(t\right)/\mathrm{d}t\le 0$ for any $\left(x\right(t),y(t),v(t),z(t),w(t\left)\right)$. We have $\mathrm{d}{V}_1\left(t\right)/\mathrm{d}t=0$ if and only if $x=x_0$, v=0, z=0 and w=0. From the LaSalle's invariance principle [6], we have that $E_0$ is globally asymptotically stable when $R_0\le 1$.

Next, we consider conclusion $\left(b\right)$. The characteristic equation of the linearized system of model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) at the equilibrium $E_0$ is $(s+h)(s+\alpha )(s+d)f\left(s\right)=0,$ where $f\left(s\right)=s^2+(r+u)s+ru-\frac{k\beta \mathrm{\Lambda }}{\mathrm{d}+a\mathrm{\Lambda }}{e}^{-(m+s){\tau }_1-(n+s){\tau }_2}.$ If $R_0>1$, we have $f\left(0\right)=ru-\left(k\beta \mathrm{\Lambda }/(d+a\mathrm{\Lambda })\right)e^{-m{\tau }_1-n{\tau }_2}<0$ and $\underset{s\to +\mathrm{\infty }}{lim}f\left(s\right)=+\mathrm{\infty }$. Hence, there is at least a positive $s^{\ast }$ such that $f\left(s^{\ast }\right)=0$. Therefore, when $R_0>1,$ $E_0$ is unstable. This completes the proof.

Remark 3.2

Theorem 3.1 shows that if only infection-free equilibrium $E_0$ exists, then it is globally asymptotically stable, and delays ${\tau }_1$, ${\tau }_2$ and ${\tau }_3$ do not impact the stability of $E_0.$ Biologically, we see that in this case the virus is cleared up.

Theorem 3.3

Let $R_0>1$.

1. If $R_1\le 1$ and $R_2\le 1,$ then the immune-free equilibrium $E_1$ is globally asymptotically stable.

2. If $R_1>1$ or $R_2>1,$ then the equilibrium $E_1$ is unstable.

Proof.

Let $H\left(\xi \right)=\xi -1-\ln \xi$, we have $H\left(\xi \right)\ge 0$ for all $\xi >0$ and $H\left(\xi \right)=0$ if and only if $\xi =1$. Consider conclusion $\left(a\right)$. Define a Lyapunov functional $\begin{array}{rl}{V}_2\left(t\right)& =e^{-m{\tau }_1}\left(x\right(t)-x_1-{\int }_{x_1}^{x\left(t\right)}\frac{1+a\theta +b{v}_1}{1+a{x}_1+b{v}_1}\frac{x_1}{\theta }\mathrm{d}\theta )+y_{1}H\left(\frac{y\left(t\right)}{y_1}\right)+\frac{p}{c}z\left(t\right)\\ & +\frac{r{e}^{n{\tau }_2}{v}_1}{k}H\left(\frac{v\left(t\right)}{v_1}\right)+r{y}_1\left({\int }_0^{{\tau }_1}H\left(\frac{e^{-m{\tau }_1}\beta x(t-{\theta }_1)v(t-{\theta }_1)}{r{y}_1(1+ax(t-{\theta }_1)+bv(t-{\theta }_1\left)\right)}\right)\mathrm{d}{\theta }_1\right.\\ & \left.+{\int }_{t-{\tau }_2}^{t}H\left(\frac{y\left(\theta \right)}{y_1}\right)\mathrm{d}\theta \right)+p{\int }_{t-{\tau }_3}^{t}y\left(s\right)z\left(s\right)\mathrm{d}s+\frac{rq{e}^{n{\tau }_2}}{kg}w\left(t\right).\end{array}$ Calculating the derivative of $V_2\left(t\right)$ along the solution of model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) gives $\begin{array}{rl}\frac{\mathrm{d}{V}_2\left(t\right)}{\mathrm{d}t}& =-\frac{d{e}^{-m{\tau }_1}\left(x\right(t)-x_1{)}^2(1+b{v}_1)}{x\left(t\right)(1+a{x}_1+b{v}_1)}+\frac{qr{e}^{n{\tau }_2}}{k}\left(v_1-\frac{\alpha }{g}\right)w\left(t\right)+r{y}_1\ln \frac{y(t-{\tau }_2)}{y\left(t\right)}\\ & +r{y}_1\ln \frac{x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}\frac{1+ax\left(t\right)+bv\left(t\right)}{x\left(t\right)v\left(t\right)}\\ & +r{y}_1\left(3-\frac{x_1(1+ax(t)+b{v}_1)}{x\left(t\right)(1+a{x}_1+b{v}_1)}-\frac{y(t-{\tau }_2)v_1}{y_{1}v\left(t\right)}\right.\\ & \left.-\frac{1+a{x}_1+b{v}_1}{x_1{v}_1}\frac{y_1}{y\left(t\right)}\frac{x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}\right)\\ & +r{y}_1\left(\frac{v\left(t\right)}{v_1}\frac{1+ax\left(t\right)+b{v}_1}{1+ax\left(t\right)+bv\left(t\right)}-\frac{v\left(t\right)}{v_1}\right)+pz\left(t\right)\left(y_1-\frac{h}{c}\right)\\ & =-\frac{d{e}^{-m{\tau }_1}\left(x\right(t)-x_1{)}^2(1+b{v}_1)}{x\left(t\right)(1+a{x}_1+b{v}_1)}-r{y}_1\left(H\left(\frac{x_1(1+ax(t)+b{v}_1)}{x\left(t\right)(1+a{x}_1+b{v}_1)}\right)\right.\\ & +H\left(\frac{y(t-{\tau }_2)v_1}{y_{1}v\left(t\right)}\right)+H\left(\frac{1+a{x}_1+b{v}_1}{x_1{v}_1}\frac{y_1}{y\left(t\right)}\frac{x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}\right)\\ & \left.+H\left(\frac{1+ax\left(t\right)+bv\left(t\right)}{1+ax\left(t\right)+b{v}_1}\right)\right)+r{y}_1\left(-1+\frac{1+ax\left(t\right)+bv\left(t\right)}{1+ax\left(t\right)+b{v}_1}-\frac{v\left(t\right)}{v_1}\right.\\ & \left.+\frac{v\left(t\right)}{v_1}\frac{1+ax\left(t\right)+b{v}_1}{1+ax\left(t\right)+bv\left(t\right)}\right)+\frac{p}{c}z\left(t\right)(c{y}_1-h)+\frac{qr{e}^{n{\tau }_2}}{k}\left(v_1-\frac{\alpha }{g}\right)w\left(t\right).\end{array}$ Notice that $\begin{array}{rl}& r{y}_1\left(-1+\frac{1+ax\left(t\right)+bv\left(t\right)}{1+ax\left(t\right)+b{v}_1}-\frac{v\left(t\right)}{v_1}+\frac{v\left(t\right)}{v_1}\frac{1+ax\left(t\right)+b{v}_1}{1+ax\left(t\right)+bv\left(t\right)}\right)\\ & =\frac{-br{y}_1(1+ax(t\left)\right)\left(v\right(t)-v_1{)}^2}{v_1(1+ax(t)+b{v}_1)(1+ax(t)+bv(t\left)\right)}.\end{array}$ Hence, $\mathrm{d}{V}_2\left(t\right)/\mathrm{d}t\le 0$ and $\mathrm{d}{V}_2\left(t\right)/\mathrm{d}t=0$ if and only if $x\left(t\right)=x_1,y\left(t\right)=y_1,v\left(t\right)=v_1$, $z\left(t\right)=0$ and $w\left(t\right)=0.$ From the LaSalle's invariance principle [6], we have that $E_1$ is globally asymptotically stable when $R_0>1$, $R_1\le 1$ and $R_2\le 1$.

Next, we consider conclusion (b). The characteristic equation of the linearized system of model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) at the equilibrium $E_1$ is $(s+\alpha -g{v}_1)f_1\left(s\right)f_2\left(s\right)=0,$ where $\begin{array}{rl}{f}_1\left(s\right)& =s+h-c{y}_1{e}^{-s{\tau }_3},\\ f_2\left(s\right)& =\left|\begin{array}{ccc}s+d+\frac{\beta v_1(1+b{v}_1)}{(1+a{x}_1+b{v}_1{)}^2}& 0& \frac{\beta x_1(1+a{x}_1)}{(1+a{x}_1+b{v}_1{)}^2}\\ -e^{-(m+s){\tau }_1}\frac{\beta v_1(1+b{v}_1)}{(1+a{x}_1+b{v}_1{)}^2}& s+r& -e^{-(m+s){\tau }_1}\frac{\beta x_1(1+a{x}_1)}{(1+a{x}_1+b{v}_1{)}^2}\\ 0& -k{e}^{-(n+s){\tau }_2}& s+u\end{array}\right|.\end{array}$ When $R_1>1$, we have $\alpha -g{v}_1<0$. Hence, there is a positive root $s^{\ast }=g{v}_1-\alpha$. When $R_2>1$, we have $f_1\left(0\right)=h-c{y}_1<0$ and $\underset{s\to +\mathrm{\infty }}{lim}{f}_1\left(s\right)=+\mathrm{\infty }$. Hence, there is at least a positive root $s^{\ast \ast }$ such that $f_1\left(s^{\ast \ast }\right)=0$. Therefore, when $R_1>1$ or $R_2>1$, $E_1$ is unstable. This completes the proof.

Remark 3.4

Theorem 3.3 shows that delays ${\tau }_1$, ${\tau }_2$ and ${\tau }_3$ do not impact the stability of $E_1.$ Biologically, we see that when $R_0>1$, $R_1\le 1$ and $R_2\le 1$ then the establishments of both CTLs and antibody immune responses are unsuccessful.

Theorem 3.5

Let $R_0>1$ and $R_1>1$.

1. If $R_3\le 1,$ then the infection equilibrium $E_2$ with only antibody response is globally asymptotically stable;

2. If $R_3>1,$ then the equilibrium $E_2$ is unstable.

Proof.

Consider conclusion (a). Define a Lyapunov functional $\begin{array}{rl}{V}_3\left(t\right)& =e^{-m{\tau }_1}\left(x\left(t\right)-x_2-{\int }_{x_2}^{x\left(t\right)}\frac{1+a\theta +b{v}_2}{1+a{x}_2+b{v}_2}\frac{x_2}{\theta }\mathrm{d}\theta \right)+\frac{rq{e}^{n{\tau }_2}{w}_2}{kg}H\left(\frac{w\left(t\right)}{w_2}\right)\\ & +y_{2}H\left(\frac{y\left(t\right)}{y_2}\right)+\frac{r{v}_2{e}^{n{\tau }_2}}{k}H\left(\frac{v\left(t\right)}{v_2}\right)+\frac{p}{c}z\left(t\right)+p{\int }_{t-{\tau }_3}^{t}y\left(s\right)z\left(s\right)\mathrm{d}s\\ & +r{y}_2\left({\int }_0^{{\tau }_1}H\left(\frac{e^{-m{\tau }_1}\beta x(t-{\theta }_1)v(t-{\theta }_1)}{r{y}_1(1+ax(t-{\theta }_1)+bv(t-{\theta }_1\left)\right)}\right)\mathrm{d}{\theta }_1+{\int }_{t-{\tau }_2}^{t}H\left(\frac{y\left(\theta \right)}{y_2}\right)\mathrm{d}\theta \right).\end{array}$ Calculating the derivative of $V_3\left(t\right)$ along the solution of model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ), it follows that $\begin{array}{rl}\frac{\mathrm{d}{V}_3\left(t\right)}{\mathrm{d}t}& =-\frac{d{e}^{-m{\tau }_1}\left(x\right(t)-x_2{)}^2(1+b{v}_2)}{x\left(t\right)(1+a{x}_2+b{v}_2)}-r{y}_2\left(H\left(\frac{x_2(1+ax(t)+b{v}_2)}{x\left(t\right)(1+a{x}_2+b{v}_2)}\right)\right.\\ & +H\left(\frac{y(t-{\tau }_2)v_2}{y_{2}v\left(t\right)}\right)+H\left(\frac{1+a{x}_2+b{v}_2}{x_2{v}_2}\frac{y_2}{y\left(t\right)}\frac{x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}\right)\\ & \left.+H\left(\frac{1+ax\left(t\right)+bv\left(t\right)}{1+ax\left(t\right)+b{v}_2}\right)\right)+r{y}_2\left(-1+\frac{1+ax\left(t\right)+bv\left(t\right)}{1+ax\left(t\right)+b{v}_2}-\frac{v\left(t\right)}{v_2}\right.\\ & \left.+\frac{v\left(t\right)}{v_2}\frac{1+ax\left(t\right)+b{v}_2}{1+ax\left(t\right)+bv\left(t\right)}\right)+\frac{p}{c}z\left(t\right)(c{y}_2-h).\end{array}$ Notice that $\begin{array}{rl}& r{y}_2\left(-1+\frac{1+ax\left(t\right)+bv\left(t\right)}{1+ax\left(t\right)+b{v}_2}-\frac{v\left(t\right)}{v_2}+\frac{v\left(t\right)}{v_2}\frac{1+ax\left(t\right)+b{v}_2}{1+ax\left(t\right)+bv\left(t\right)}\right)\\ & =\frac{-br{y}_2(1+ax(t\left)\right)\left(v\right(t)-v_2{)}^2}{v_2(1+ax(t)+b{v}_2)(1+ax(t)+bv(t\left)\right)}.\end{array}$ Hence, $\mathrm{d}{V}_3\left(t\right)/\mathrm{d}t\le 0$ and $\mathrm{d}{V}_3\left(t\right)/\mathrm{d}t=0$ if and only if $x\left(t\right)=x_2,y\left(t\right)=y_2,v\left(t\right)=v_2$ and $z\left(t\right)=0.$ From the LaSalle's invariance principle [6], we have that $E_2$ is globally asymptotically stable when $R_0>1$, $R_1>1$ and $R_3\le 1$.

Next, we consider conclusion $\left(b\right)$. The characteristic equation of the linearized system of model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) at the equilibrium $E_2$ is $f_1\left(s\right)f_2\left(s\right)=0,$ where $\begin{array}{rl}{f}_1\left(s\right)& =s+h-c{y}_2{e}^{-s{\tau }_3},\\ f_2\left(s\right)& =\left|\begin{array}{cccc}{a}_{11}& 0& a_{13}& 0\\ a_{21}& s+r& a_{23}& 0\\ 0& -k{e}^{-(n+s){\tau }_2}& s+u+q{w}_2& q{v}_2\\ 0& 0& -g{w}_2& s+\alpha -g{v}_2\end{array}\right|,\end{array}$ where $\begin{array}{rl}{a}_{11}& =s+d+\frac{\beta v_2(1+b{v}_2)}{(1+a{x}_2+b{v}_2{)}^2},a_{13}=\frac{\beta x_2(1+a{x}_2)}{(1+a{x}_2+b{v}_2{)}^2},\\ a_{21}& =-e^{-(m+s){\tau }_1}\frac{\beta v_2(1+b{v}_2)}{(1+a{x}_2+b{v}_2{)}^2},a_{23}=e^{-(m+s){\tau }_1}\frac{\beta x_2(1+a{x}_2)}{(1+a{x}_2+b{v}_2{)}^2}.\end{array}$ If $R_3>1$, then we have $f_1\left(0\right)=h-c{y}_2<0$ and $\underset{s\to +\mathrm{\infty }}{lim}{f}_1\left(s\right)=+\mathrm{\infty }$. Hence, there is at least a positive root $s^{\ast }$ such that $f_1\left(s^{\ast }\right)=0$. Therefore, when $R_3>1,$ $E_2$ is unstable. This completes the proof.

Remark 3.6

From Theorem 3.5 we see that delays ${\tau }_1$, ${\tau }_2$ and ${\tau }_3$ do not impact the stability of $E_2.$ Biologically, Theorem 3.5 implies that when $R_0>1,$ $R_1>1$ and $R_3\le 1$, the antibody immune response can be established, but the infected cells are too weak so that it can not stimulate CTL immune response.

Theorem 3.7

Let $R_0>1$ and $R_2>1$.

1. If $R_4\le 1$ and ${\tau }_3=0$, then the infection equilibrium $E_3$ with only CTL response is globally asymptotically stable;

2. If $R_4>1,$ then the equilibrium $E_3$ is unstable.

Proof.

Consider conclusion (a). Define a Lyapunov functional $\begin{array}{rl}{V}_4\left(t\right)& =e^{-m{\tau }_1}\left(x\left(t\right)-x_3-{\int }_{x_3}^{x\left(t\right)}\frac{1+a\theta +b{v}_3}{1+a{x}_3+b{v}_3}\frac{x_3}{\theta }\mathrm{d}\theta \right)+y_{3}H\left(\frac{y\left(t\right)}{y_3}\right)\\ & +\frac{(r+p{z}_3)e^{n{\tau }_2}{v}_3}{k}H\left(\frac{v\left(t\right)}{v_3}\right)+\frac{p{z}_3}{c}H\left(\frac{z\left(t\right)}{z_3}\right)+\frac{q(r+p{z}_3)e^{n{\tau }_2}}{kg}w\left(t\right)\\ & +(r+p{z}_3)y_3\left({\int }_0^{{\tau }_1}H\left(\frac{e^{-m{\tau }_1}\beta x(t-{\theta }_1)v(t-{\theta }_1)}{(r+p{z}_3)y_3(1+ax(t-{\theta }_1)+bv(t-{\theta }_1\left)\right)}\right)\mathrm{d}{\theta }_1\right.\\ & \left.+{\int }_{t-{\tau }_2}^{t}H\left(\frac{y\left(\theta \right)}{y_3}\right)\mathrm{d}\theta \right)+p{\int }_{t-{\tau }_3}^{t}y\left(s\right)z\left(s\right)\mathrm{d}s.\end{array}$ Calculating the derivative of $V_4\left(t\right)$ along the solution of model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ), we have $\begin{array}{rl}\frac{\mathrm{d}{V}_4\left(t\right)}{\mathrm{d}t}& =-\frac{d{e}^{-m{\tau }_1}\left(x\right(t)-x_3{)}^2(1+b{v}_3)}{x\left(t\right)(1+a{x}_3+b{v}_3)}-(r+p{z}_3)y_3\left(H\left(\frac{x_3(1+ax(t)+b{v}_3)}{x\left(t\right)(1+a{x}_3+b{v}_3)}\right)\right.\\ & +H\left(\frac{y(t-{\tau }_2)v_3}{y_{3}v\left(t\right)}\right)+H\left(\frac{1+a{x}_3+b{v}_3}{x_3{v}_3}\frac{y_3}{y\left(t\right)}\frac{x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}\right)\\ & \left.+H\left(\frac{1+ax\left(t\right)+bv\left(t\right)}{1+ax\left(t\right)+b{v}_3}\right)\right)+(r+p{z}_3)y_3\left(-1+\frac{1+ax\left(t\right)+bv\left(t\right)}{1+ax\left(t\right)+b{v}_3}-\frac{v\left(t\right)}{v_3}\right.\\ & \left.+\frac{v\left(t\right)}{v_3}\frac{1+ax\left(t\right)+b{v}_3}{1+ax\left(t\right)+bv\left(t\right)}\right)+\frac{q(r+p{z}_3)e^{n{\tau }_2}}{k}\left(v_3-\frac{\alpha }{g}\right)w\left(t\right).\end{array}$ Notice that $\begin{array}{rl}& (r+p{z}_3)y_3\left(-1+\frac{1+ax\left(t\right)+bv\left(t\right)}{1+ax\left(t\right)+b{v}_3}-\frac{v\left(t\right)}{v_3}+\frac{v\left(t\right)}{v_3}\frac{1+ax\left(t\right)+b{v}_3}{1+ax\left(t\right)+bv\left(t\right)}\right)\\ & =\frac{-b(r+p{z}_3)y_3(1+ax(t\left)\right)\left(v\right(t)-v_3{)}^2}{v_3(1+ax(t)+b{v}_3)(1+ax(t)+bv(t\left)\right)}.\end{array}$ Hence, $\mathrm{d}{V}_4\left(t\right)/\mathrm{d}t\le 0$ and $\mathrm{d}{V}_4\left(t\right)/\mathrm{d}t=0$ if and only if $x\left(t\right)=x_3,y\left(t\right)=y_3,v\left(t\right)=v_3$ and $w\left(t\right)=0.$ From the LaSalle's invariance principle [6], we have that the equilibrium $E_3$ is globally asymptotically stable when ${\tau }_3=0$, $R_0>1$, $R_2>1$ and $R_4\le 1$.

Next, we consider conclusion (b). The characteristic equation of the linearization system of model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) at the equilibrium $E_3$ is $(s+\alpha -g{v}_3)f\left(s\right)=0,$ where $f\left(s\right)=\left|\begin{array}{cccc}{a}_{11}& 0& a_{13}& 0\\ a_{21}& s+r+p{z}_3& a_{23}& p{y}_3\\ 0& -k{e}^{-(n+s){\tau }_2}& s+u& 0\\ 0& -c{e}^{-s{\tau }_3}{z}_3& 0& s+h-c{y}_3{e}^{-s{\tau }_3}\end{array}\right|,$ where $\begin{array}{rl}{a}_{11}& =s+d+\frac{\beta v_3(1+b{v}_3)}{(1+a{x}_3+b{v}_3{)}^2},a_{13}=\frac{\beta x_3(1+a{x}_3)}{(1+a{x}_3+b{v}_3{)}^2},\\ a_{21}& =-e^{-(m+s){\tau }_1}\frac{\beta v_3(1+b{v}_3)}{(1+a{x}_3+b{v}_3{)}^2},a_{23}=-e^{-(m+s){\tau }_1}\frac{\beta x_3(1+a{x}_3)}{(1+a{x}_3+b{v}_3{)}^2}.\end{array}$ If $R_4>1$, then we have a positive root $s^{\ast }=g{v}_3-\alpha$. Therefore, when $R_4>1$, $E_3$ is unstable for any ${\tau }_1\ge 0,$ ${\tau }_2\ge 0$ and ${\tau }_3=0$. This completes the proof.

Remark 3.8

Theorem 3.7 shows that delays ${\tau }_1$ and ${\tau }_2$ do not impact the stability of $E_3.$ Biologically, we see that, when ${\tau }_3=0$, for any ${\tau }_1\ge 0$ and ${\tau }_2\ge 0$ as long as $R_0>1$, $R_2>1$, $R_4\le 1$ then the CTL immune response can be determined, but the virus loads are so small that it can not activate the antibody immune responses.

Theorem 3.9

If ${\tau }_3=0,$ $R_0>1,$ $R_1>1,$ $R_3>1$ and $R_4>1,$ then the infection equilibrium $E_4$ with CTL and antibody responses is globally asymptotically stable.

Proof.

Define a Lyapunov functional $\begin{array}{rl}{V}_5\left(t\right)& =e^{-m{\tau }_1}\left(x\right(t)-x_4-{\int }_{x_4}^{x\left(t\right)}\frac{1+a\theta +b{v}_4}{1+a{x}_4+b{v}_4}\frac{x_4}{\theta }\mathrm{d}\theta )+y_{4}H\left(\frac{y\left(t\right)}{y_4}\right)\\ & +\frac{(r+p{z}_4)e^{n{\tau }_2}{v}_4}{k}H\left(\frac{v\left(t\right)}{v_4}\right)+\frac{q(r+p{z}_4)e^{n{\tau }_2}{w}_4}{kg}H\left(\frac{w\left(t\right)}{w_4}\right)+\frac{p{z}_4}{c}H\left(\frac{z\left(t\right)}{z_4}\right)\\ & +(r+p{z}_4)y_4\left({\int }_0^{{\tau }_1}H\left(\frac{e^{-m{\tau }_1}\beta x(t-{\theta }_1)v(t-{\theta }_1)}{(r+p{z}_2)y_2(1+ax(t-{\theta }_1)+bv(t-{\theta }_1\left)\right)}\right)\mathrm{d}{\theta }_1\right.\\ & \left.+{\int }_{t-{\tau }_2}^{t}H\left(\frac{y\left(\theta \right)}{y_4}\right)\mathrm{d}\theta \right)+p{\int }_{t-{\tau }_3}^{t}y\left(s\right)z\left(s\right)\mathrm{d}s.\end{array}$ Calculating the derivative of $V_5\left(t\right)$ along the solution of model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ), it follows that $\begin{array}{rl}\frac{\mathrm{d}{V}_4\left(t\right)}{\mathrm{d}t}& =-\frac{d{e}^{-m{\tau }_1}\left(x\right(t)-x_4{)}^2(1+b{v}_4)}{x\left(t\right)(1+a{x}_4+b{v}_4)}-(r+p{z}_4)y_4\left(H\left(\frac{x_4(1+ax(t)+b{v}_4)}{x\left(t\right)(1+a{x}_4+b{v}_4)}\right)\right.\\ & +H\left(\frac{y(t-{\tau }_2)v_4}{y_{4}v\left(t\right)}\right)+H\left(\frac{1+a{x}_4+b{v}_4}{x_4{v}_4}\frac{y_4}{y\left(t\right)}\frac{x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}\right)\\ & \left.+H\left(\frac{1+ax\left(t\right)+bv\left(t\right)}{1+ax\left(t\right)+b{v}_4}\right)\right)+(r+p{z}_4)y_4\left(-1+\frac{1+ax\left(t\right)+bv\left(t\right)}{1+ax\left(t\right)+b{v}_4}-\frac{v\left(t\right)}{v_4}\right.\\ & \left.+\frac{v\left(t\right)}{v_4}\frac{1+ax\left(t\right)+b{v}_4}{1+ax\left(t\right)+bv\left(t\right)}\right).\end{array}$ Notice that $\begin{array}{rl}& (r+p{z}_4)y_4\left(-1+\frac{1+ax\left(t\right)+bv\left(t\right)}{1+ax\left(t\right)+b{v}_4}-\frac{v\left(t\right)}{v_4}+\frac{v\left(t\right)}{v_4}\frac{1+ax\left(t\right)+b{v}_4}{1+ax\left(t\right)+bv\left(t\right)}\right)\\ & =\frac{-b(r+p{z}_4)y_4(1+ax(t\left)\right)\left(v\right(t)-v_4{)}^2}{v_4(1+ax(t)+b{v}_4)(1+ax(t)+bv(t\left)\right)}.\end{array}$ Hence, $\mathrm{d}{V}_5\left(t\right)/\mathrm{d}t\le 0$ and $\mathrm{d}{V}_5\left(t\right)/\mathrm{d}t=0$ if and only if $x\left(t\right)=x_4,y\left(t\right)=y_4,v\left(t\right)=v_4.$ From the LaSalle's invariance principle [6], we finally have that the equilibrium $E_4$ is globally asymptotically stable when ${\tau }_3=0$, $R_0>1$, $R_1>1$, $R_3>1$ and $R_4>1$. This completes the proof.

Remark 3.10

From Theorem 3.9 we see that delays ${\tau }_1$ and ${\tau }_2$ do not impact the stability of $E_4$ when delay ${\tau }_3=0$. Biologically, Theorem 3.9 implies that, when ${\tau }_3=0$, for any ${\tau }_1\ge 0$ and ${\tau }_2\ge 0$ as long as $R_0>1$, $R_1>1$, $R_3>1$ and $R_4>1$ then the susceptible cells, infected cells, free virus, CTL immune responses and antibody immune responses can coexist in vivo.

4. Hopf bifurcation analysis

We first discuss Hopf bifurcation at the equilibrium $E_3$. By Theorem 3.7, we obtain the globally asymptotically stability of the equilibrium $E_3$ when ${\tau }_1\ge 0,{\tau }_2\ge 0$ and ${\tau }_3=0$. However, what kind of complicated dynamic behaviour will appear at the equilibrium $E_3$ when ${\tau }_3>0$? By computing the characteristic equation for the corresponding linearized system of model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) at the equilibrium $E_3$ is given by (3) $\begin{array}{rl}& s^5+\widetilde{m_1}{s}^4+\widetilde{m_2}{s}^3+\widetilde{m_3}{s}^2+\widetilde{m_4}s+\widetilde{m_5}+(\widetilde{n_1}{s}^4+\widetilde{n_2}{s}^3+\widetilde{n_3}{s}^2+\widetilde{n_4}s+\widetilde{n_5})e^{-s{\tau }_3}\\ & +(\widetilde{p_1}{s}^3+\widetilde{p_2}{s}^2+\widetilde{p_3}s+\widetilde{p_4})e^{-s({\tau }_1+{\tau }_2)}+(\widetilde{q_1}{s}^2+\widetilde{q_2}s+\widetilde{q_3})e^{-s({\tau }_1+{\tau }_2+{\tau }_3)}=0,\end{array}$(3) where $\begin{array}{rl}\widetilde{m_1}& =\alpha -g{v}_3+d+h+u+r+p{z}_3+\frac{\beta v_3(1+b{v}_3)}{(1+a{x}_3+b{v}_3{)}^2},\\ \widetilde{m_2}& =h(u+r+p{z}_3)+(\alpha -g{v}_3)\left(d+h+u+r+p{z}_3+\frac{\beta v_3(1+b{v}_3)}{(1+a{x}_3+b{v}_3{)}^2}\right)\\ & +(r+p{z}_3)u+(h+u+r+p{z}_3)\left(d+\frac{\beta v_3(1+b{v}_3)}{(1+a{x}_3+b{v}_3{)}^2}\right),\\ \widetilde{m_3}& =(\alpha -g{v}_3)\left[h\right(u+r+p{z}_3)+(h+u+r+p{z}_3)\left(d+\frac{\beta v_3(1+b{v}_3)}{(1+a{x}_3+b{v}_3{)}^2}\right)\\ & +(r+p{z}_3)u]+hu(r+p{z}_3)+\left(d+\frac{\beta v_3(1+b{v}_3)}{(1+a{x}_3+b{v}_3{)}^2}\right)[(r+p{z}_3)(u+h)+hu],\end{array}$ $\begin{array}{rl}\widetilde{m_4}& =(\alpha -g{v}_3)\left[hu(r+p{z}_3)+\left(d+\frac{\beta v_3(1+b{v}_3)}{(1+a{x}_3+b{v}_3{)}^2}\right)\left(\right(r+p{z}_3\left)\right(u+h)+hu)\right]\\ & +hu(r+p{z}_3)\left(d+\frac{\beta v_3(1+b{v}_3)}{(1+a{x}_3+b{v}_3{)}^2}\right),\\ \widetilde{m_5}& =\alpha -g{v}_3\left)hu\right(r+p{z}_3)\left(d+\frac{\beta v_3(1+b{v}_3)}{(1+a{x}_3+b{v}_3{)}^2},\right.\\ \widetilde{n_1}& =-h,\widetilde{n_2}=-h\left[\alpha -g{v}_3+u+r+d+\frac{\beta v_3(1+b{v}_3)}{(1+a{x}_3+b{v}_3{)}^2}\right],\end{array}$ $\begin{array}{rl}\widetilde{n_3}& =-h\left\{(\alpha -g{v}_3)\left(u+r+d+\frac{\beta v_3(1+b{v}_3)}{(1+a{x}_3+b{v}_3{)}^2}\right)+ur\right.\\ & \left.+\left(d+\frac{\beta v_3(1+b{v}_3)}{(1+a{x}_3+b{v}_3{)}^2}\right)(u+r)\right\},\\ \widetilde{n_4}& =-h\left\{(\alpha -g{v}_3)\left[ur+\left(d+\frac{\beta v_3(1+b{v}_3)}{(1+a{x}_3+b{v}_3{)}^2}\right)(u+r)\right]\right.\\ & \left.+ur\left(d+\frac{\beta v_3(1+b{v}_3)}{(1+a{x}_3+b{v}_3{)}^2}\right)\right\},\\ \widetilde{n_5}& =-hur(\alpha -g{v}_3)\left(d+\frac{\beta v_3(1+b{v}_3)}{(1+a{x}_3+b{v}_3{)}^2}\right),\widetilde{p_1}=-\frac{k\beta x_3(1+a{x}_3)e^{-m{\tau }_1-n{\tau }_2}}{(1+a{x}_3+b{v}_3{)}^2},\end{array}$ $\begin{array}{rl}\widetilde{p_2}& =-\frac{k\beta x_3(1+a{x}_3)e^{-m{\tau }_1-n{\tau }_2}}{(1+a{x}_3+b{v}_3{)}^2}(\alpha -g{v}_3+h+d),\\ \widetilde{p_3}& =-\frac{k\beta x_3(1+a{x}_3)e^{-m{\tau }_1-n{\tau }_2}}{(1+a{x}_3+b{v}_3{)}^2}[hd+(h+d\left)\right(\alpha -g{v}_3\left)\right],\\ \widetilde{p_4}& =-\frac{k\beta x_3(1+a{x}_3)hd(\alpha -g{v}_3)e^{-m{\tau }_1-n{\tau }_2}}{(1+a{x}_3+b{v}_3{)}^2},\widetilde{q_1}=\frac{k\beta x_{3}h(1+a{x}_3)e^{-m{\tau }_1-n{\tau }_2}}{(1+a{x}_3+b{v}_3{)}^2},\\ \widetilde{q_2}& =\frac{k\beta x_{3}h(1+a{x}_3)e^{-m{\tau }_1-n{\tau }_2}}{(1+a{x}_3+b{v}_3{)}^2}(\alpha -g{v}_3+d),\\ \widetilde{q_3}& =\frac{k\beta x_{3}hd(\alpha -g{v}_3)(1+a{x}_3)e^{-m{\tau }_1-n{\tau }_2}}{(1+a{x}_3+b{v}_3{)}^2}.\end{array}$ However, when ${\tau }_1>0$ or ${\tau }_2>0$ Equation (3(3) $\begin{array}{rl}& s^5+\widetilde{m_1}{s}^4+\widetilde{m_2}{s}^3+\widetilde{m_3}{s}^2+\widetilde{m_4}s+\widetilde{m_5}+(\widetilde{n_1}{s}^4+\widetilde{n_2}{s}^3+\widetilde{n_3}{s}^2+\widetilde{n_4}s+\widetilde{n_5})e^{-s{\tau }_3}\\ & +(\widetilde{p_1}{s}^3+\widetilde{p_2}{s}^2+\widetilde{p_3}s+\widetilde{p_4})e^{-s({\tau }_1+{\tau }_2)}+(\widetilde{q_1}{s}^2+\widetilde{q_2}s+\widetilde{q_3})e^{-s({\tau }_1+{\tau }_2+{\tau }_3)}=0,\end{array}$(3) ) is too complicated so that it can not make a good conclusion. Therefore, in the following discussions, we assume ${\tau }_1={\tau }_2=0.$ For Equation (3(3) $\begin{array}{rl}& s^5+\widetilde{m_1}{s}^4+\widetilde{m_2}{s}^3+\widetilde{m_3}{s}^2+\widetilde{m_4}s+\widetilde{m_5}+(\widetilde{n_1}{s}^4+\widetilde{n_2}{s}^3+\widetilde{n_3}{s}^2+\widetilde{n_4}s+\widetilde{n_5})e^{-s{\tau }_3}\\ & +(\widetilde{p_1}{s}^3+\widetilde{p_2}{s}^2+\widetilde{p_3}s+\widetilde{p_4})e^{-s({\tau }_1+{\tau }_2)}+(\widetilde{q_1}{s}^2+\widetilde{q_2}s+\widetilde{q_3})e^{-s({\tau }_1+{\tau }_2+{\tau }_3)}=0,\end{array}$(3) ), simple manipulation leads to (4) $s^5+m_1{s}^4+m_2{s}^3+m_3{s}^2+m_{4}s+m_5+(n_1{s}^4+n_2{s}^3+n_3{s}^2+n_{4}s+n_5)e^{-s{\tau }_3}=0,$(4) where $\begin{array}{rl}{m}_1& =\widetilde{m_1},m_2=\widetilde{m_2}+\widetilde{p_1},m_3=\widetilde{m_3}+\widetilde{p_2},m_4=\widetilde{m_4}+\widetilde{p_3},m_5=\widetilde{m_5}+\widetilde{p_4},\\ n_1& =\widetilde{n_1},n_2=\widetilde{n_2},n_3=\widetilde{n_3}+\widetilde{q_1},n_4=\widetilde{n_4}+\widetilde{q_2},n_5=\widetilde{n_5}+\widetilde{q_3}.\end{array}$ Let $s=i\omega (\omega >0)$ be a purely imaginary root of (4(4) $s^5+m_1{s}^4+m_2{s}^3+m_3{s}^2+m_{4}s+m_5+(n_1{s}^4+n_2{s}^3+n_3{s}^2+n_{4}s+n_5)e^{-s{\tau }_3}=0,$(4) ). Separating real and imaginary parts, it follows that (5) $\begin{array}{rl}{m}_1{\omega }^4-m_3{\omega }^2+m_5& =-(n_1{\omega }^4-n_3{\omega }^2+n_5)\cos \omega {\tau }_3-(-n_2{\omega }^3+n_4\omega )\sin \omega {\tau }_3,\\ {\omega }^5-m_2{\omega }^3+m_4\omega & =(n_1{\omega }^4-n_3{\omega }^2+n_5)\sin \omega {\tau }_3-(-n_2{\omega }^3+q{n}_4\omega )\cos \omega {\tau }_3.\end{array}$(5) Squaring and adding the two equations of (5(5) $\begin{array}{rl}{m}_1{\omega }^4-m_3{\omega }^2+m_5& =-(n_1{\omega }^4-n_3{\omega }^2+n_5)\cos \omega {\tau }_3-(-n_2{\omega }^3+n_4\omega )\sin \omega {\tau }_3,\\ {\omega }^5-m_2{\omega }^3+m_4\omega & =(n_1{\omega }^4-n_3{\omega }^2+n_5)\sin \omega {\tau }_3-(-n_2{\omega }^3+q{n}_4\omega )\cos \omega {\tau }_3.\end{array}$(5) ), it follows that (6) ${\omega }^{10}+a_0{\omega }^8+b_0{\omega }^6+c_0{\omega }^4+d_0{\omega }^2+e_0=0,$(6) where $\begin{array}{rl}{a}_0& =m_1^2-2m_2-n_1^2,b_0=m_2^2+2m_4-2m_1{m}_3-n_2^2+2n_1{n}_3,\\ c_0& =m_3^2+2m_1{m}_5-2m_4{m}_2-2n_1{n}_5+2n_4{n}_2-n_3^2,\\ d_0& =-2m_3{m}_5+m_4^2+2n_3{n}_5-n_4^2,e_0=m_5^2-n_5^2.\end{array}$ Let $\lambda ={\omega }^2,$ then Equation (6(6) ${\omega }^{10}+a_0{\omega }^8+b_0{\omega }^6+c_0{\omega }^4+d_0{\omega }^2+e_0=0,$(6) ) becomes (7) $H\left(\lambda \right)={\lambda }^5+a_0{\lambda }^4+b_0{\lambda }^3+c_0{\lambda }^2+d_0\lambda +e_0=0.$(7) Denote $\begin{array}{rl}{a}_1^{\ast }& =-\frac{6}{25}{a}_0^2+\frac{3}{5}{b}_0,b_1^{\ast }=-\frac{6}{25}{a}_0{b}_0+\frac{2}{5}{c}_0+\frac{8}{125}{a}_0^3,\\ c_1^{\ast }& =-\frac{3}{625}{a}_0^4+\frac{3}{125}{a}_0^2{b}_0-\frac{2}{25}{a}_0{c}_0+\frac{1}{5}{d}_0,{\mathrm{\Delta }}_0={a_1^{\ast }}^2-4c_1^{\ast },\\ a_2^{\ast }& =-\frac{1}{3}{a_1^{\ast }}^2-4c_1^{\ast },b_2^{\ast }=-\frac{2}{27}{a_1^{\ast }}^3+\frac{8}{3}{a}_1^{\ast }{c}_1^{\ast }-{b_1^{\ast }}^2,\\ {\mathrm{\Delta }}_1& =\frac{1}{27}{a_2^{\ast }}^3+\frac{1}{4}{b_2^{\ast }}^2,d_0^{\ast }=\sqrt[3]{-\frac{b_2^{\ast }}{2}+\sqrt{{\mathrm{\Delta }}_1}}+\sqrt[3]{-\frac{b_2^{\ast }}{2}-\sqrt{{\mathrm{\Delta }}_1}}+\frac{a_1^{\ast }}{3},\\ {\mathrm{\Delta }}_2& =-d_0^{\ast }-a_1^{\ast }+\frac{2b_1^{\ast }}{\sqrt{d_0^{\ast }-a_1^{\ast }}},{\mathrm{\Delta }}_3=-d_0^{\ast }-a_1^{\ast }-\frac{2b_1^{\ast }}{\sqrt{d_0^{\ast }-a_1^{\ast }}}.\end{array}$ Applying the results given in [22] on the distribution of roots for five degree polynomial equation, we have the following results.

Lemma 4.1

For the polynomial equation (7(7) $H\left(\lambda \right)={\lambda }^5+a_0{\lambda }^4+b_0{\lambda }^3+c_0{\lambda }^2+d_0\lambda +e_0=0.$(7) ), the following results are true:

1. If $e_0<0,$ then Equation (7(7) $H\left(\lambda \right)={\lambda }^5+a_0{\lambda }^4+b_0{\lambda }^3+c_0{\lambda }^2+d_0\lambda +e_0=0.$(7) ) has at least one positive root;

2. Assume that $e_0\ge 0$ and $b_1^{\ast }=0,$

   1. If ${\mathrm{\Delta }}_0<0,$ then Equation (7(7) $H\left(\lambda \right)={\lambda }^5+a_0{\lambda }^4+b_0{\lambda }^3+c_0{\lambda }^2+d_0\lambda +e_0=0.$(7) ) has no positive real root;

   2. If ${\mathrm{\Delta }}_0\ge 0,$ $a_1^{\ast }\ge 0$ and $c_1^{\ast }>0,$ then Equation (7(7) $H\left(\lambda \right)={\lambda }^5+a_0{\lambda }^4+b_0{\lambda }^3+c_0{\lambda }^2+d_0\lambda +e_0=0.$(7) ) has no positive real root;

   3. If (a) and (b) are not satisfied, then Equation (7(7) $H\left(\lambda \right)={\lambda }^5+a_0{\lambda }^4+b_0{\lambda }^3+c_0{\lambda }^2+d_0\lambda +e_0=0.$(7) ) has positive real root if and only if there exists at least one ${\lambda }^{\ast }\in \{{\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4\}$ such that ${\lambda }^{\ast }>0$ and $H\left({\lambda }^{\ast }\right)\le 0,$ where ${\lambda }_i={\delta }_i-a_0/5,i=1,2,3,4$ and $\begin{array}{rl}{\delta }_1& =\sqrt{\frac{-a_1^{\ast }+\sqrt{{\mathrm{\Delta }}_0}}{2}},{\delta }_2=-\sqrt{\frac{-a_1^{\ast }+\sqrt{{\mathrm{\Delta }}_0}}{2}},\\ {\delta }_3& =\sqrt{\frac{-a_1^{\ast }-\sqrt{{\mathrm{\Delta }}_0}}{2}},{\delta }_4=-\sqrt{\frac{-a_1^{\ast }-\sqrt{{\mathrm{\Delta }}_0}}{2}}.\end{array}$

   4. Assume that $e_0\ge 0,$ $b_1^{\ast }\ne 0$ and $d_0^{\ast }>b_1^{\ast },$

      1. If ${\mathrm{\Delta }}_2<0$ and ${\mathrm{\Delta }}_3<0,$ then Equation (7(7) $H\left(\lambda \right)={\lambda }^5+a_0{\lambda }^4+b_0{\lambda }^3+c_0{\lambda }^2+d_0\lambda +e_0=0.$(7) ) has no positive real root;

      2. If (a) is not satisfied, then Equation (7(7) $H\left(\lambda \right)={\lambda }^5+a_0{\lambda }^4+b_0{\lambda }^3+c_0{\lambda }^2+d_0\lambda +e_0=0.$(7) ) has positive real root if and only if there exists at least one ${\lambda }^{\ast }\in \{{\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4\}$ such that ${\lambda }^{\ast }>0$ and $H\left({\lambda }^{\ast }\right)\le 0,$ where ${\lambda }_i={\delta }_i-a_0/5,i=1,2,3,4$ and $\begin{array}{rl}{\delta }_1& =\frac{-\sqrt{d_0^{\ast }-a_1^{\ast }}+\sqrt{{\mathrm{\Delta }}_2}}{2},{\delta }_2=\frac{-\sqrt{d_0^{\ast }-a_1^{\ast }}-\sqrt{{\mathrm{\Delta }}_2}}{2},\\ {\delta }_3& =\frac{-\sqrt{d_0^{\ast }-a_1^{\ast }}+\sqrt{{\mathrm{\Delta }}_3}}{2},{\delta }_4=\frac{-\sqrt{d_0^{\ast }-a_1^{\ast }}-\sqrt{{\mathrm{\Delta }}_3}}{2}.\end{array}$

   5. Assume that $e_0\ge 0$ and $b_1^{\ast }\ne 0$ and $d_0^{\ast }<b_1^{\ast },$ then Equation (7(7) $H\left(\lambda \right)={\lambda }^5+a_0{\lambda }^4+b_0{\lambda }^3+c_0{\lambda }^2+d_0\lambda +e_0=0.$(7) ) has positive real root if and only if ${b_1^{\ast }}^2/4(a_1^{\ast }-d_0^{\ast }{)}^2+\frac{1}{2}{d}_0^{\ast }=0$ and $\overline{\lambda }>0$ and $H\left(\overline{\lambda }\right)\le 0,$ where $\overline{\lambda }=b_1^{\ast }/2(a_1^{\ast }-d_0^{\ast })-\frac{1}{5}{a}_0.$

Without loss of generality, we assume that Equation (7(7) $H\left(\lambda \right)={\lambda }^5+a_0{\lambda }^4+b_0{\lambda }^3+c_0{\lambda }^2+d_0\lambda +e_0=0.$(7) ) has m positive roots with $m\in \{1,2,3,4,5\}$, denoted by ${\lambda }_k,k=1,2,\dots m.$ Then Equation (6(6) ${\omega }^{10}+a_0{\omega }^8+b_0{\omega }^6+c_0{\omega }^4+d_0{\omega }^2+e_0=0,$(6) ) has m positive roots, say ${\omega }_k=\sqrt{{\lambda }_k},k=1,2,\dots m.$

From Equation (5(5) $\begin{array}{rl}{m}_1{\omega }^4-m_3{\omega }^2+m_5& =-(n_1{\omega }^4-n_3{\omega }^2+n_5)\cos \omega {\tau }_3-(-n_2{\omega }^3+n_4\omega )\sin \omega {\tau }_3,\\ {\omega }^5-m_2{\omega }^3+m_4\omega & =(n_1{\omega }^4-n_3{\omega }^2+n_5)\sin \omega {\tau }_3-(-n_2{\omega }^3+q{n}_4\omega )\cos \omega {\tau }_3.\end{array}$(5) ) we have (8) $\begin{array}{rl}\sin \omega {\tau }_3& =\frac{({\omega }^5-m_2{\omega }^3+m_4\omega )(n_1{\omega }^4-n_3{\omega }^2+n_5)}{(n_1{\omega }^4-n_3{\omega }^2+n_5{)}^2+(n_2{\omega }^3-n_4\omega {)}^2}\\ & -\frac{(m_1{\omega }^4-m_3{\omega }^2+m_5)(-n_2{\omega }^3+n_4\omega )}{(n_1{\omega }^4-n_3{\omega }^2+n_5{)}^2+(n_2{\omega }^3-n_4\omega {)}^2}\triangleq \gamma \left(\omega \right).\end{array}$(8) Let $\omega ={\omega }_k(k=1,2,\dots ,m)$, we solve ${\tau }_3$ from Equation (8(8) $\begin{array}{rl}\sin \omega {\tau }_3& =\frac{({\omega }^5-m_2{\omega }^3+m_4\omega )(n_1{\omega }^4-n_3{\omega }^2+n_5)}{(n_1{\omega }^4-n_3{\omega }^2+n_5{)}^2+(n_2{\omega }^3-n_4\omega {)}^2}\\ & -\frac{(m_1{\omega }^4-m_3{\omega }^2+m_5)(-n_2{\omega }^3+n_4\omega )}{(n_1{\omega }^4-n_3{\omega }^2+n_5{)}^2+(n_2{\omega }^3-n_4\omega {)}^2}\triangleq \gamma \left(\omega \right).\end{array}$(8) ) to obtain that ${\tau }_k^{\left(j\right)}=\frac{1}{{\omega }_k}\arcsin \gamma \left({\omega }_k\right)+\frac{2\pi j}{{\omega }_k},$ where $k=1,2,\dots ,m,j=0,1,\dots$. Therefore, when $\tau ={\tau }_k^{\left(j\right)},k=1,2,\dots ,m.j=0,1,\dots$, $\pm i{\omega }_k$ is a pair of purely imaginary roots of Equation (4(4) $s^5+m_1{s}^4+m_2{s}^3+m_3{s}^2+m_{4}s+m_5+(n_1{s}^4+n_2{s}^3+n_3{s}^2+n_{4}s+n_5)e^{-s{\tau }_3}=0,$(4) ). Clearly, for every $k=1,2,\dots ,m,$ $\left\{{\tau }_k^{\left(j\right)}\right\}$ is monotonically increasing for $j=0,1,2,\dots$ and $\underset{j\to +\mathrm{\infty }}{lim}{\tau }_k^{\left(j\right)}=\mathrm{\infty }.$ Therefore, there is a $k_0\in \{1,2,\dots ,m\}$ and $j_0\in \{0,1,2,\dots \}$ such that ${\tau }_{k_0}^{\left(j_0\right)}=min\{{\tau }_k^{\left(j\right)}:k=1,2,\dots ,m,j=0,1,2,\dots \}.$ Define (9) ${\tau }_0={\tau }_{k_0}^{\left(j_0\right)},{\omega }_0={\omega }_{k_0},{\lambda }_0={\lambda }_{k_0}.$(9)

Let $s\left({\tau }_3\right)=\xi \left({\tau }_3\right)+i\omega \left({\tau }_3\right)$ be a root of Equation (4(4) $s^5+m_1{s}^4+m_2{s}^3+m_3{s}^2+m_{4}s+m_5+(n_1{s}^4+n_2{s}^3+n_3{s}^2+n_{4}s+n_5)e^{-s{\tau }_3}=0,$(4) ) satisfying $\xi \left({\tau }_0\right)=0,\omega \left({\tau }_0\right)={\omega }_0,{\lambda }_0={\omega }_0^2.$ Differentiating Equation (4(4) $s^5+m_1{s}^4+m_2{s}^3+m_3{s}^2+m_{4}s+m_5+(n_1{s}^4+n_2{s}^3+n_3{s}^2+n_{4}s+n_5)e^{-s{\tau }_3}=0,$(4) ) with respect to ${\tau }_3,$ we get $\begin{array}{rl}& (5s^4+4m_1{s}^3+3m_2{s}^2+2m_{3}s+m_4)\frac{\mathrm{d}s}{\mathrm{d}{\tau }_3}+(4n_1{s}^3+3n_2{s}^2+2n_{3}s+n_4)e^{-s{\tau }_3}\frac{\mathrm{d}s}{\mathrm{d}{\tau }_3}\\ & +(n_1{s}^4+n_2{s}^3+n_3{s}^2+n_{4}s+n_5)\left(-s-{\tau }_3\frac{\mathrm{d}s}{\mathrm{d}{\tau }_3}\right)e^{-s{\tau }_3}=0.\end{array}$ This gives $\begin{array}{rl}{\left(\frac{\mathrm{d}s}{\mathrm{d}{\tau }_3}\right)}^{-1}& =-\frac{5s^4+4m_1{s}^3+3m_2{s}^2+2m_{3}s+m_4}{s(s^5+m_1{s}^4+m_2{s}^3+m_3{s}^2+m_{4}s+m_5)}\\ & +\frac{4n_1{s}^3+3n_2{s}^2+2n_{3}s+n_4}{s(n_1{s}^4+n_2{s}^3+n_3{s}^2+n_{4}s+n_5)}-\frac{{\tau }_3}{s}.\end{array}$ We have $\begin{array}{rl}& \mathrm{sign}{\left.\left\{\frac{\mathrm{d}Re\left(s\right({\tau }_3\left)\right)}{\mathrm{d}{\tau }_3}\right\}\right|}_{{\tau }_3={\tau }_k^{\left(j\right)}}\\ & =\mathrm{sign}{\left.\left\{Re{\left(\frac{\mathrm{d}s}{\mathrm{d}{\tau }_3}\right)}^{-1}\right\}\right|}_{s=i{\omega }_0}\\ & =\mathrm{sign}\left\{\frac{5{\omega }_0^8+{\omega }_0^6(-8m_2+4m_1^2)+{\omega }_0^4(6m_4+3m_2^2-6m_1{m}_3)}{{\omega }_0^2(-{\omega }_0^4+m_2{\omega }_0^2-m_4{)}^2+(m_1{\omega }_0^4-m_3{\omega }_0^2+m_5{)}^2}\right.\\ & +\frac{{\omega }_0^2(-4m_2{m}_4+2m_1{m}_5+2m_3^2)+(m_4^2-2m_3{m}_5)}{{\omega }_0^2(-{\omega }_0^4+m_2{\omega }_0^2-m_4{)}^2+(m_1{\omega }_0^4-m_3{\omega }_0^2+m_5{)}^2}\\ & \left.+\frac{-4n_1^2{\omega }_0^6+(-3n_2^2+6n_1{n}_3){\omega }_0^4+{\omega }_0^2(4n_2{n}_4-4n_1{n}_5-2n_3^2)+(-n_4^2+2n_3{n}_5)}{{\omega }_0^2(n_2{\omega }_0^2-n_4{)}^2+(n_1{\omega }_0^4-n_3{\omega }_0^2+n_5{)}^2}\right\}.\end{array}$ From Equation (6(6) ${\omega }^{10}+a_0{\omega }^8+b_0{\omega }^6+c_0{\omega }^4+d_0{\omega }^2+e_0=0,$(6) ), we get $\begin{array}{rl}& {\omega }_0^2(-{\omega }_0^4+m_2{\omega }_0^2-m_4{)}^2+(m_1{\omega }_0^4-m_3{\omega }_0^2+m_5{)}^2\\ & ={\omega }_0^2(n_2{\omega }_0^2-n_4{)}^2+(n_1{\omega }_0^4-n_3{\omega }_0^2+n_5{)}^2.\end{array}$ It follows that $\mathrm{sign}{\left.\left\{\frac{\mathrm{d}Re\left(s\right({\tau }_3\left)\right)}{\mathrm{d}{\tau }_3}\right\}\right|}_{{\tau }_3={\tau }_k^{\left(j\right)}}=\mathrm{sign}\left[\frac{H^{\prime }\left({\lambda }_k\right)}{{\omega }^2(n_2{\omega }_0^2-n_4{)}^2+(n_1{\omega }_0^4-n_3{\omega }_0^2+n_5{)}^2}\right].$ We conclude that $\mathrm{d}Re\left(s\right({\tau }_3\left)\right)/\mathrm{d}{\tau }_3{|}_{{\tau }_3={\tau }_k^{\left(j\right)}}$ and $H^{\prime }\left({\lambda }_k\right)$ have the same sign. Sum up the above discussion, we get the following conclusion.

Theorem 4.2

Let ${\lambda }_0$ and ${\omega }_0,$ ${\tau }_0$ be defined by Equation (9(9) ${\tau }_0={\tau }_{k_0}^{\left(j_0\right)},{\omega }_0={\omega }_{k_0},{\lambda }_0={\lambda }_{k_0}.$(9) ), respectively.

1. If the following conditions are all not satisfied: (a) $e_0<0;$ (b) $e_0\ge 0$, $b_1^{\ast }=0,$ ${\mathrm{\Delta }}_0\ge 0$ and $a_1^{\ast }<0$ or $c_1^{\ast }\le 0,$ and there exists ${\lambda }^{\ast }\in \{{\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4\}$ such that ${\lambda }^{\ast }>0$ and $H\left({\lambda }^{\ast }\right)\le 0;$ (c) $e_0\ge 0$, $b_1^{\ast }\ne 0,$ $d_0^{\ast }>b_1^{\ast }$ and ${\mathrm{\Delta }}_2\ge 0$ or ${\mathrm{\Delta }}_3\ge 0$ and there exists ${\lambda }^{\ast }\in \{{\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4\}$ such that ${\lambda }^{\ast }>0$ and $H\left({\lambda }^{\ast }\right)\le 0$; (d) $e_0\ge 0$, $b_1^{\ast }\ne 0$, $d_0^{\ast }<b_1^{\ast },$ ${b_1^{\ast }}^2/4(a_1^{\ast }-d_0^{\ast }{)}^2+\frac{1}{2}{d}_0^{\ast }=0$, $\overline{\lambda }>0$ and $H\left(\overline{\lambda }\right)\le 0,$ where $\overline{\lambda }=b_1^{\ast }/2(a_1^{\ast }-d_0^{\ast })-\frac{1}{5}{a}_0,$ then equilibrium $E_3$ is locally asymptotically stable for any ${\tau }_3\ge 0.$

2. If one of the conditions given in (i) is satisfied, then equilibrium $E_3$ is locally asymptotically stable for ${\tau }_3\in [0,{\tau }_0)$.

3. If one of the conditions given in (i) holds and $H^{\prime }\left({\lambda }_0\right)\ne 0,$ then model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) undergoes Hopf bifurcation from equilibrium $E_3$ as ${\tau }_3$ passes through the critical value ${\tau }_0.$

Next, we discuss Hopf bifurcation of the equilibrium $E_4$. By Theorem 3.9, we only obtain the global asymptotic stability of the equilibrium $E_4$ when ${\tau }_1\ge 0,{\tau }_2\ge 0$ and ${\tau }_3=0$. When ${\tau }_3>0$, by the following theoretical analysis we will see that the Hopf bifurcation occurs at the equilibrium $E_4$. Since when ${\tau }_1>0$ or ${\tau }_2>0$ the discussions are very complicated, we here only discuss the case ${\tau }_1={\tau }_2=0$ and ${\tau }_3>0$.

At the equilibrium $E_4$, the characteristic equation for the linearized system of model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) is given by (10) $s^5+p_1{s}^4+p_2{s}^3+p_3{s}^2+p_{4}s+p_5+(q_1{s}^4+q_2{s}^3+q_3{s}^2+q_{4}s+q_5)e^{-s{\tau }_3}=0,$(10) where $\begin{array}{rl}{p}_1& =d+h+r+p{z}_4+u+q{w}_4+\frac{\beta v_4(1+b{v}_4)}{(1+a{x}_4+b{v}_4{)}^2},\\ p_2& =\left(d+\frac{\beta v_4(1+b{v}_4)}{(1+a{x}_4+b{v}_4{)}^2}\right)(h+r+p{z}_4+u+q{w}_4)+h(r+p{z}_4+u+q{w}_4)\\ & +\alpha q{w}_4+(r+p{z}_4)(u+q{w}_4)-\frac{k\beta x_4(1+a{x}_4)}{(1+a{x}_4+b{v}_4{)}^2},\\ p_3& =\left(d+\frac{\beta v_4(1+b{v}_4)}{(1+a{x}_4+b{v}_4{)}^2}\right)\left[h\right(r+p{z}_4+u+q{w}_4)+\alpha q{w}_4\\ & +(r+p{z}_4)(u+q{w}_4)]+h[\alpha q{w}_4+(r+p{z}_4)(u+q{w}_4)]\\ & -(d+h)\frac{k\beta x_4(1+a{x}_4)}{(1+a{x}_4+b{v}_4{)}^2}+\alpha q{w}_4(r+p{z}_4),\\ p_4& =\left(d+\frac{\beta v_4(1+b{v}_4)}{(1+a{x}_4+b{v}_4{)}^2}\right)\left\{\alpha q{w}_4\right(r+p{z}_4)+h[\alpha q{w}_4\\ & +(r+p{z}_4)(u+q{w}_4)\left]\right\}-\frac{hdk\beta x_4(1+a{x}_4)}{(1+a{x}_4+b{v}_4{)}^2}+\alpha qh{w}_4(r+p{z}_4),\\ p_5& =\alpha qh{w}_4(r+p{z}_4)(d+\frac{\beta v_4(1+b{v}_4)}{(1+a{x}_4+b{v}_4{)}^2}),q_1=-h,\\ q_2& =-h(d+r+u+q{w}_4+\frac{\beta v_4(1+b{v}_4)}{(1+a{x}_4+b{v}_4{)}^2}),\\ q_3& =-h\left[(r+u+q{w}_4)\left(d+\frac{\beta v_4(1+b{v}_4)}{(1+a{x}_4+b{v}_4{)}^2}\right)+\alpha q{w}_4\right.\\ & \left.+r(u+q{w}_4)-\frac{k\beta x_4(1+a{x}_4)}{(1+a{x}_4+b{v}_4{)}^2}\right],\\ q_4& =-h\left(d+\frac{\beta v_4(1+b{v}_4)}{(1+a{x}_4+b{v}_4{)}^2}\right)[\alpha q{w}_4+r(u+q{w}_4\left)\right]-\alpha hrq{w}_4\\ & +\frac{hdk\beta x_4(1+a{x}_4)}{(1+a{x}_4+b{v}_4{)}^2},q_5=-\alpha hrq{w}_4\left(d+\frac{\beta v_4(1+b{v}_4)}{(1+a{x}_4+b{v}_4{)}^2}\right).\end{array}$ Let $s=i\omega (\omega >0)$ be a purely imaginary root of (10(10) $s^5+p_1{s}^4+p_2{s}^3+p_3{s}^2+p_{4}s+p_5+(q_1{s}^4+q_2{s}^3+q_3{s}^2+q_{4}s+q_5)e^{-s{\tau }_3}=0,$(10) ). Separating real and imaginary parts, it follows that (11) $\begin{array}{rl}{p}_1{\omega }^4-p_3{\omega }^2+p_5& =-(q_1{\omega }^4-q_3{\omega }^2+q_5)\cos \omega {\tau }_3-(-q_2{\omega }^3+q_4\omega )\sin \omega {\tau }_3,\\ {\omega }^5-p_2{\omega }^3+p_4\omega & =(q_1{\omega }^4-q_3{\omega }^2+q_5)\sin \omega {\tau }_3-(-q_2{\omega }^3+q_4\omega )\cos \omega {\tau }_3.\end{array}$(11) Squaring and adding the two equations of (11(11) $\begin{array}{rl}{p}_1{\omega }^4-p_3{\omega }^2+p_5& =-(q_1{\omega }^4-q_3{\omega }^2+q_5)\cos \omega {\tau }_3-(-q_2{\omega }^3+q_4\omega )\sin \omega {\tau }_3,\\ {\omega }^5-p_2{\omega }^3+p_4\omega & =(q_1{\omega }^4-q_3{\omega }^2+q_5)\sin \omega {\tau }_3-(-q_2{\omega }^3+q_4\omega )\cos \omega {\tau }_3.\end{array}$(11) ), it follows that (12) ${\omega }^{10}+p_0{\omega }^8+q_0{\omega }^6+r_0{\omega }^4+u_0{\omega }^2+{\eta }_0=0,$(12) where $\begin{array}{rl}{p}_0& =p_1^2-2p_2-q_1^2,q_0=-2p_1{p}_3+p_2^2+2p_4+2q_1{q}_3-q_2^2,\\ r_0& =p_3^2+2p_1{p}_5-2p_2{p}_4-q_3^2-2q_1{q}_5+2q_2{q}_4,\\ u_0& =p_4^2-2p_3{p}_5+2q_3{q}_5-q_4^2,{\eta }_0=p_5^2-q_5^2.\end{array}$ Let $\lambda ={\omega }^2,$ then Equation (12(12) ${\omega }^{10}+p_0{\omega }^8+q_0{\omega }^6+r_0{\omega }^4+u_0{\omega }^2+{\eta }_0=0,$(12) ) becomes (13) $F\left(\lambda \right)={\lambda }^5+p_0{\lambda }^4+q_0{\lambda }^3+r_0{\lambda }^2+u_0\lambda +{\eta }_0=0.$(13) Denote $\begin{array}{rl}{p}_1^{\ast }& =-\frac{6}{25}{p}_0^2+\frac{3}{5}{q}_0,q_1^{\ast }=-\frac{6}{25}{p}_0{q}_0+\frac{2}{5}{r}_0+\frac{8}{125}{p}_0^3,\\ r_1^{\ast }& =-\frac{3}{625}{p}_0^4+\frac{3}{125}{q}_0{p}_0^2-\frac{2}{25}{p}_0{r}_0+\frac{1}{5}{u}_0,{\mathrm{\Delta }}_0={p_1^{\ast }}^2-4r_1^{\ast },\\ p_2^{\ast }& =-\frac{1}{3}{p_1^{\ast }}^2-4r_1^{\ast },q_2^{\ast }=-\frac{2}{27}{p_1^{\ast }}^3+\frac{8}{3}{p}_1^{\ast }{r}_1^{\ast }-{q_1^{\ast }}^2,\\ {\mathrm{\Delta }}_1& =\frac{1}{27}{p_2^{\ast }}^3-\frac{1}{4}{q_2^{\ast }}^2,u_0^{\ast }=\sqrt[3]{-\frac{q_2^{\ast }}{2}+\sqrt{{\mathrm{\Delta }}_1}}+\sqrt[3]{-\frac{q_2^{\ast }}{2}-\sqrt{{\mathrm{\Delta }}_1}}+\frac{p_1^{\ast }}{3},\\ {\mathrm{\Delta }}_2& =-u_0^{\ast }-p_1^{\ast }+\frac{2q_1^{\ast }}{\sqrt{u_0^{\ast }-p_1^{\ast }}},{\mathrm{\Delta }}_3=-u_0^{\ast }-p_1^{\ast }-\frac{2q_1^{\ast }}{\sqrt{u_0^{\ast }-p_1^{\ast }}}.\end{array}$

A similar argument as in Lemma 4.1 we can define ${\lambda }_i(i=1,2,3,4)$ for the polynomial equation (13(13) $F\left(\lambda \right)={\lambda }^5+p_0{\lambda }^4+q_0{\lambda }^3+r_0{\lambda }^2+u_0\lambda +{\eta }_0=0.$(13) ), and using the same method as in Equation (9(9) ${\tau }_0={\tau }_{k_0}^{\left(j_0\right)},{\omega }_0={\omega }_{k_0},{\lambda }_0={\lambda }_{k_0}.$(9) ) we can further define ${\tau }_0$, ${\omega }_0$ and ${\lambda }_0$. Therefore, we have the following results.

Theorem 4.3

1. If the following conditions are all not satisfied: (a) ${\eta }_0<0;$ (b) ${\eta }_0\ge 0,$ $q_1^{\ast }=0,$ ${\mathrm{\Delta }}_0\ge 0,$ $p_1^{\ast }<0$ or $r_1^{\ast }\le 0,$ and there exists ${\lambda }^{\ast }\in \{{\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4\}$ such that ${\lambda }^{\ast }>0$ and $F\left({\lambda }^{\ast }\right)\le 0;$ (c) ${\eta }_0\ge 0,$ $q_1^{\ast }\ne 0,$ $u_0^{\ast }>q_1^{\ast },$ ${\mathrm{\Delta }}_2\ge 0$ or ${\mathrm{\Delta }}_3\ge 0$ and there exists ${\lambda }^{\ast }\in \{{\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4\}$ such that ${\lambda }^{\ast }>0$ and $F\left({\lambda }^{\ast }\right)\le 0;$ (d) ${\eta }_0\ge 0,$ $q_1^{\ast }\ne 0,$ $u_0^{\ast }<q_1^{\ast },$ ${q_1^{\ast }}^2/4(p_1^{\ast }-u_0^{\ast }{)}^2+\frac{1}{2}{u}_0^{\ast }=0,$ $\overline{\lambda }>0$ and $F\left(\overline{\lambda }\right)\le 0,$ where $\overline{\lambda }=q_1^{\ast }/2(p_1^{\ast }-u_0^{\ast })-\frac{1}{5}{p}_0,$ then $E_4$ is locally asymptotically stable for any ${\tau }_3\ge 0.$

2. If one of the conditions given in (i) is satisfied, then $E_4$ is locally asymptotically stable for ${\tau }_3\in [0,{\tau }_0)$.

3. If one of the conditions given in (i) holds and $F^{\prime }\left({\lambda }_0\right)\ne 0,$ then model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) undergoes Hopf bifurcation from $E_4$ as ${\tau }_3$ passes through critical value ${\tau }_0.$

Remark 4.4

We here only establish the criteria on the existence of Hopf bifurcations at equilibria $E_3$ and $E_4$ for model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) in the case of delays ${\tau }_1={\tau }_2=0$ and ${\tau }_3>0$. However, when ${\tau }_1>0$ or ${\tau }_2>0$ whether we also can obtain similar results still is a very interesting and estimable problem. In the following section, we will give a discussion by means of the numerical simulations.

5. Numerical simulations

In the above sections, we establish the global asymptotic stability of equilibria $E_3$ and $E_4$ when ${\tau }_1\ge 0,{\tau }_2\ge 0$ and ${\tau }_3=0$, and by using the theory of bifurcation, we obtain the existence of the Hopf bifurcation and stability switches at equilibria $E_3$ and $E_4$ when ${\tau }_1=0,{\tau }_2=0$ and ${\tau }_3\ge 0$. However, aim at the case: ${\tau }_1\ge 0$, ${\tau }_2\ge 0$ and ${\tau }_3\ge 0$, the theoretical analysis is very complicated. In this section, by using the numerical simulation, it is shown that the Hopf bifurcation and stability switches occur at these equilibria as ${\tau }_3$ increases. In model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ), we choose a, α, β, ${\tau }_1,$ ${\tau }_2$ and ${\tau }_3$ as free parameters and fix all other parameters as displayed in Table 1.

Table 1. List of parameters.

Parameter	Definition	Value	Source
Λ	production rate of uninfected cells	$10\mu {\mathrm{l}}^{-1}{\mathrm{day}}^{-1}$	[16]
d	death rate of uninfected cells	$0.01{\mathrm{day}}^{-1}$	[16]
r	death rate of infected cells	$0.5{\mathrm{day}}^{-1}$	[8,16]
p	CTL effectiveness	$1\mu \mathrm{l}{\mathrm{day}}^{-1}$	[8,16]
b	Beddington–DeAngelis coefficient	0.01	Assumed
k	production rate of free virus	0.4 ${\mathrm{cell}}^{-1}{\mathrm{day}}^{-1}$	[8,16]
u	clearance rate of free virus	$3{\mathrm{day}}^{-1}$	[8,17]
q	neutralizing rate of antibody	$1\mu \mathrm{l}{\mathrm{day}}^{-1}$	[1,17]
g	production rate of neutralizing antibodies	$1.5\mu \mathrm{l}{\mathrm{day}}^{-1}$	[1,17]
m	death rate for infected cells during $[t-{\tau }_1,t]$	0.01	Assumed
n	death rate for new virus during $[t-{\tau }_2,t]$	0.01	Assumed
c	proliferation rate of CTL response	$0.1\mu \mathrm{l}{\mathrm{day}}^{-1}$	[8,17]
h	death rate of CTL response	$0.15{\mathrm{day}}^{-1}$	[8,17]

Example 5.1

Take a=0, we have that Beddington–DeAngelis incidence $\beta x\left(t\right)v\left(t\right)/(1+ax(t)+bv(t\left)\right)$ is simplified to saturation incidence $\beta x\left(t\right)v\left(t\right)/(1+bv(t\left)\right)$. Let $\beta =0.5\mathrm{l}{\mathrm{day}}^{-1},\alpha =1{\mathrm{day}}^{-1},{\tau }_1=8.5$ and ${\tau }_2=0.1$. All other parameter values are the same as in Table 1. From Figures 1–4 we see that as ${\tau }_3$ increases the dynamical behaviours of equilibrium $E_3$ will occur: locally asymptotically stable → unstable and Hopf bifurcation appears → locally asymptotically stable → unstable and Hopf bifurcation appears.

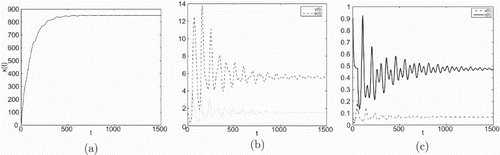
Figure 1. Taking ${\tau }_3=0.02$, we have $R_2=12.1443>1$ and $R_4=0.2997<1$, infection equilibrium with only CTL response $E_3$ is asymptotically stable.

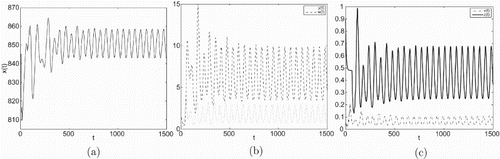
Figure 2. Taking ${\tau }_3=1.2,$ we have $R_2=12.1443>1$ and $R_4=0.2997<1$, infection equilibrium with only CTL response $E_3$ occurs Hopf bifurcation.

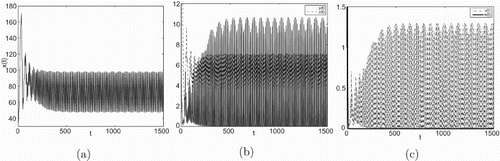
Figure 3. Taking ${\tau }_3=5.8$, we have $R_2=12.1443>1$ and $R_4=0.2997<1$, infection equilibrium with only CTL response $E_3$ is asymptotically stable.

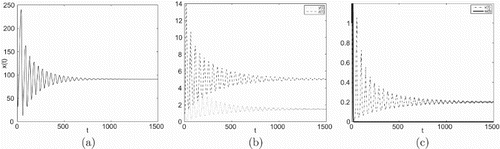
Figure 4. Taking ${\tau }_3=9.5$, we have $R_2=12.1443>1$ and $R_4=0.2997<1$, infection equilibrium with only CTL response $E_3$ occurs Hopf bifurcation.

In Figures 1–8, (a), (b) and (c) are denoted time-series figures of $x\left(t\right)$, $y\left(t\right)$, $v\left(t\right)$, $z\left(t\right)$ and $w\left(t\right)$.

Example 5.2

Consider the Beddington–DeAngelis incidence $\beta x\left(t\right)v\left(t\right)/(1+ax(t)+bv(t\left)\right)$. Let $a=0.01,\beta =0.25\mu \mathrm{l}{\mathrm{day}}^{-1},\alpha =0.1{\mathrm{day}}^{-1},$ ${\tau }_1=2$ and ${\tau }_2=5.$ All other parameter values are the same as in Table 1. From Figures 5–8 we see that as ${\tau }_3$ increases from zero the dynamical behaviours of equilibrium $E_4$ will occur: locally asymptotically stable → unstable and Hopf bifurcation appears → locally asymptotically stable → unstable and Hopf bifurcation appears.

Figure 5. Taking ${\tau }_3=1.285$, we have $R_3=12.8126>1$ and $R_4=2.8537>1$, infection equilibrium with both antibody and CTL responses $E_4$ is asymptotically stable.

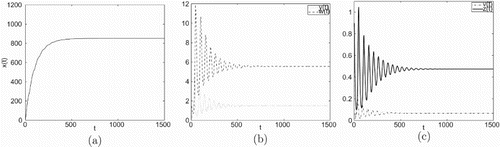
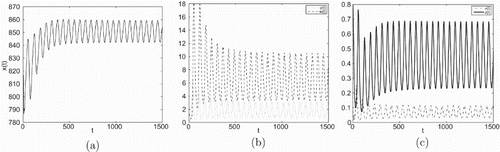
Figure 6. Taking ${\tau }_3=6.365$, we have $R_3=12.8126>1$ and $R_4=2.8537>1$, infection equilibrium with both antibody and CTL responses $E_4$ occurs Hopf bifurcation.

Figure 7. Taking ${\tau }_3=51.578$, we have $R_3=12.8126>1$ and $R_4=2.8537>1$, infection equilibrium with both antibody and CTL responses $E_4$ is asymptotically stable.

Figure 8. Taking ${\tau }_3=65.163$, we have $R_3=12.8126>1$ and $R_4=2.8537>1$, infection equilibrium with both antibody and CTL responses $E_4$ occurs Hopf bifurcation.

6. Discussion

In this paper, we have investigated a virus infection model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) with intracellular delay ${\tau }_1$, virus replication delay ${\tau }_2$ and immune response delay ${\tau }_3$. We assume that the production of CTL immune response depends on the infected cells and CTL cells based above important biological meaning. We see that similar assumption also is given in [1,9,11,12,16,18,24]. Similarly, the production of antibody response depends on the virus and antibody (see [1,13,14,16]). Dynamical analysis shows that ${\tau }_1$, ${\tau }_2$ and ${\tau }_3$ play different roles in the stability of the model.

By the analysis, model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) has five possible equilibria, an infection-free equilibrium $E_0,$ immune-free equilibrium $E_1$, infection equilibrium $E_2$ with only antibody response, infection equilibrium $E_3$ with only CTL response and infection equilibrium $E_4$ with both CTL and antibody responses. A combination of basic reproductive ratio of viral infection $R_0,$ for antibody response $R_1,$ for CTL immune response $R_2,$ for CTL immune response competitive $R_3$ and for antibody response competitive $R_4$ determines the existence of these equilibria. Furthermore, they also determine the global properties of the model. We have shown that when $R_0\le 1$, $E_0$ is globally asymptotically stable, which means that the viruses are cleared and immune is not active. When $R_0>1$, $R_1\le 1$ and $R_2\le 1$, $E_1$ is globally asymptotically stable, which means that the infection becomes chronic but with no persistent CTL immune responses and antibody responses. When $R_1>1$ and $R_3\le 1$, $E_2$ is globally asymptotically stable, which means that the infection becomes chronic with persistent antibody responses, but the infected cells can not stimulate and activate CTL immune responses. As respect to the analysis of $E_3$, we consider special case ${\tau }_1\ge 0$, ${\tau }_2\ge 0$ and ${\tau }_3=0$, when $R_2>1$ and $R_4\le 1$, $E_3$ is globally asymptotically stable, which means that the infection becomes chronic with persistent CTL immune responses, but the virus loads can not activate the antibody responses. About the stability of $E_4$, we have obtained that for special case ${\tau }_1\ge 0$, ${\tau }_2\ge 0$ and ${\tau }_3=0$, when $R_3>1$ and $R_4>1$, $E_4$ is globally asymptotically stable, that is, susceptible cells, infected cells, free virus, antibody responses and CTL responses coexist in vivo. We see that ${\tau }_1$ and ${\tau }_2$ do not affect the stability of the equilibria.

When ${\tau }_3>0$, by using the bifurcation theory, we obtain the sufficient conditions on the existence of Hopf bifurcation at $E_3$ and $E_4$. Meanwhile, by means of numerical simulations, it is shown that the Hopf bifurcation and stability switches occur at $E_3$ and $E_4$ as ${\tau }_3$ increases. Figures 1–4 indicate that $E_3$ remains stable as ${\tau }_3>0$ is small, and along with the increase of ${\tau }_3$, $E_3$ becomes unstable and periodic oscillations appear. It shows that stability switches occur as ${\tau }_3$ increases. Similarly, from Figures 5–8, we see that along with the increase of ${\tau }_3$ the dynamical behaviours of model (1(1) $\begin{array}{rl}\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}& =\mathrm{\Lambda }-dx\left(t\right)-\frac{\beta x\left(t\right)v\left(t\right)}{1+ax\left(t\right)+bv\left(t\right)},\\ \frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}& =\frac{\beta e^{-m{\tau }_1}x(t-{\tau }_1)v(t-{\tau }_1)}{1+ax(t-{\tau }_1)+bv(t-{\tau }_1)}-ry\left(t\right)-py\left(t\right)z\left(t\right),\\ \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}& =k{e}^{-n{\tau }_2}y(t-{\tau }_2)-uv\left(t\right)-qv\left(t\right)w\left(t\right),\\ \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}& =cy(t-{\tau }_3)z(t-{\tau }_3)-hz\left(t\right),\\ \frac{\mathrm{d}w\left(t\right)}{\mathrm{d}t}& =gv\left(t\right)w\left(t\right)-\alpha w\left(t\right),\end{array}$(1) ) at $E_4$ appear very large diversification. Particularly, when ${\tau }_3$ is small enough, $E_4$ is asymptotically stable and when ${\tau }_3$ is increasing, the stability switches occur at $E_4$, and when $E_4$ is unstable, Hopf bifurcation occurs. Finally, when ${\tau }_3$ is large enough, $E_4$ is always unstable. Summarizing these discussions, we point out that ${\tau }_3$ affects markedly the stability of $E_3$ and $E_4.$ This illustrates the fact that ${\tau }_3$ plays a negative part in the disease prevalence and control. Motivated by the above discussion, one can realize that the emergence in the broadly neutralizing antibodies reacted to change in infected cells that could kill viruses. On the whole, this paper somehow provides better understanding about neutralizing antibodies and might help to design a powerful vaccine, which prevents at least uninfected peoples from ever becoming infected with virus. However, by considering some other factors such as the antibody delay, diffusion and a time-varying drug concentration, whether we also can obtain that the global asymptotic stability of equilibria will also be a very estimable and significative subject. This is left to the future research.

Disclosure statement

The authors declare that there is no conflict of interests regarding the publication of this paper.

Additional information

Funding

This work was supported by the Natural Science Foundation of Shanxi University of Finance and Economics Starting Fund for the Shanxi University of Finance and Economics doctoral graduates research [grant No. Z18116], the National Natural Science Foundation of China [grant nos. 11771373 and 11661076], the Natural Science Foundation of Xinjiang [grant no. 2016D03022].