Influence of non-homogeneous mixing on final epidemic size in a meta-population model

ABSTRACT

In meta-population models for infectious diseases, the basic reproduction number ${\mathcal{R}}_0$ can be as much as 70% larger in the case of preferential mixing than that in homogeneous mixing [J.W. Glasser, Z. Feng, S.B. Omer, P.J. Smith, and L.E. Rodewald, The effect of heterogeneity in uptake of the measles, mumps, and rubella vaccine on the potential for outbreaks of measles: A modelling study, Lancet ID 16 (2016), pp. 599–605. doi: 10.1016/S1473-3099(16)00004-9]. This suggests that realistic mixing can be an important factor to consider in order for the models to provide a reliable assessment of intervention strategies. The influence of mixing is more significant when the population is highly heterogeneous. In this paper, another quantity, the final epidemic size ($\mathcal{F}$) of an outbreak, is considered to examine the influence of mixing and population heterogeneity. Final size relation is derived for a meta-population model accounting for a general mixing. The results show that $\mathcal{F}$ can be influenced by the pattern of mixing in a significant way. Another interesting finding is that, heterogeneity in various sub-population characteristics may have the opposite effect on ${\mathcal{R}}_0$ and $\mathcal{F}$.

KEYWORDS:

• Epidemic meta-population models
• non-homogeneous mixing
• final epidemic size

1. Introduction

Epidemiological models can be used to identify key factors affecting disease outbreaks and to evaluate intervention strategies. However, because the model predictions and evaluations can be influenced by assumptions made to simplify the analysis, it is critical to understand how certain simplifying assumptions may affect the model outcomes, particularly if the models are used to inform public health policy-making.

One of the most commonly used assumptions in epidemiological models is the homogeneous, or random, mixing in the whole population, which allows the model to ignore heterogeneity in various sub-population factors including activity (pertinent to disease transmission), susceptibility, preference in contact, group size, etc. Although these simplifying assumptions are reasonable in many cases depending on the questions to be studied, there are cases where these heterogeneous factors cannot be ignored (see e.g. [11–13]).

When epidemic models are used to evaluate strategies for disease control and prevention, the quantities used often include the basic or effective reproduction number (${\mathcal{R}}_0$ or ${\mathcal{R}}_e$), the final epidemic size ($\mathcal{F}$), and the peak size of an outbreak ($\mathcal{P}$). Andreasen [2] studied the role of heterogeneity in susceptibility and infectiousness on final epidemic size for the case of proportionate mixing and discussed the relationship between $\mathcal{F}$ and ${\mathcal{R}}_0$. Tildesley and Keeling [19] considered a model with a spatial structure to discuss the issue of using ${\mathcal{R}}_0$ as a predictor of final epidemic size for the case of foot-and-mouth disease in the UK. Results concerning final epidemic sizes can also be found in other studies including  [1,3,4,10,15,16]. None of these studies considered the influence of heterogeneity on the final size or the relationship between $\mathcal{F}$ and ${\mathcal{R}}_0$ in a meta-population with preferential mixing.

In this paper, we consider an epidemic meta-population model that includes a general mixing function (which includes proportionate, preferential, and homogeneous mixing as special cases). We examine how heterogeneity in various sub-population factors may influence ${\mathcal{R}}_0$, $\mathcal{F}$, and $\mathcal{P}$, and how preferential mixing may affect the relationship between $\mathcal{F}$ and ${\mathcal{R}}_0$. Our results show that models that do not account for heterogeneous mixing may produce biased or even incorrect information.

From previous epidemic models with homogeneous mixing, a general understanding is that $\mathcal{F}$ and ${\mathcal{R}}_0$ are positively related (see Figure 1). We show in this paper that, when preferential mixing is considered in the model with heterogeneity in activity and/or preference, it is possible that $\mathcal{F}$ and ${\mathcal{R}}_0$ are negatively related (see Figures 4 and 5). Moreover, when vaccination is considered, the homogeneous coverage may not be the most effective strategy (see Figures 7 and 8).

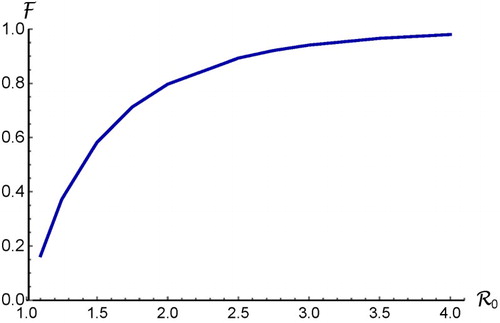
Figure 1. Plot of the final size relation given in (18(18) $Z=S\left(0\right)\left(1-\exp \left[-{\mathcal{R}}_0\frac{Z+I\left(0\right)}{N}\right]\right),$(18) ) for the case of a homogeneous population with random mixing. It shows that $\mathcal{F}$ is an increasing function of ${\mathcal{R}}_0$.

The paper is organized as follows. In Section 2, we present the model with n sub-populations and non-homogeneous mixing. Derivations for the reproduction number and a final epidemic size relation are also included in this section. Section 3 focuses on the investigation of the effects of heterogeneity in various sub-population factors and mixing on the final epidemic size and epidemic peak during an outbreak. Two examples of using the meta-population model to evaluate intervention strategies are also presented in this section. Section 4 includes discussions of the results.

2. The model and final epidemic size

Consider a meta-population with n sub-populations or groups with sizes $N_i$ ($1\le i\le n$). The population in each group i is divided into three epidemiological classes denoted by $S_i$ (susceptible), $I_i$ (infectious), and $R_i$ (recovered and immune due to infection). Thus, $N_i=S_i+I_i+R_i$ ($1\le i\le n$). Because we are concerned with the final epidemic size of a single disease outbreak, births and deaths are ignored. The epidemic model with n sub-groups consists of the following ordinary differential equations: (1) $\begin{array}{rl}{S}_i^{\prime }& =-a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j},\\ I_i^{\prime }& =a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j}-\gamma I_i,\\ R_i^{\prime }& =\gamma I_i,1\le i\le n,\end{array}$(1) with initial conditions: (2) $S_i\left(0\right)=N_i-I_{i0},I_i\left(0\right)=I_{i0},R_i\left(0\right)=0,1\le i\le n.$(2) In model (1(1) $\begin{array}{rl}{S}_i^{\prime }& =-a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j},\\ I_i^{\prime }& =a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j}-\gamma I_i,\\ R_i^{\prime }& =\gamma I_i,1\le i\le n,\end{array}$(1) ), $a_i$ is the per capita contact rate (referred to as activity), ${\beta }_i$ is the probability that a susceptible person in group i becomes infected upon contacting an infectious person, γ denotes the per-capita recovery rate. The contacts between sub-groups are described by the mixing matrix $C=\left(c_{ij}\right)$, where $c_{ij}$ is the proportion of the ith sub-group's contacts that is with members of the jth group, and $I_j/N_j$ is the probability that a randomly encountered member of group j is infectious. As pointed out in Busenberg and Castillo-Chavez [6], a mixing function needs to satisfy the following basic conditions: (3) $\begin{array}{rl}& \left(1\right)c_{ij}\ge 0,\\ & \left(2\right)\sum _{j=1}^n{c}_{ij}=1,\\ & \left(3\right)a_i{N}_i{c}_{ij}=a_j{N}_j{c}_{ji},1\le i,j\le n.\end{array}$(3) One of the commonly used mixing functions, as originally considered by Nold [17] and later extended by Jacquez et al. [14], is the preferential mixing with the form: (4) $c_{ij}={ϵ}_i{\delta }_{ij}+(1-{ϵ}_i)f_j,\text{where}{f}_j=\frac{(1-{ϵ}_j)a_j{N}_j}{\sum _k(1-{ϵ}_k)a_k{N}_k}.$(4) In the preferential mixing (4(4) $c_{ij}={ϵ}_i{\delta }_{ij}+(1-{ϵ}_i)f_j,\text{where}{f}_j=\frac{(1-{ϵ}_j)a_j{N}_j}{\sum _k(1-{ϵ}_k)a_k{N}_k}.$(4) ), ${ϵ}_i$ denotes the fraction of contacts reserved for one's own group (referred to as preferences), and ${\delta }_{ij}$ is the Kronecker delta (1 when i=j and 0 otherwise). The function $f_j$ describes mixing that is random, i.e. proportional to unreserved contacts, $(1-{ϵ}_j)a_j{N}_j$. All parameters are non-negative.

The isolated basic reproduction number for group i is (5) ${\mathcal{R}}_{0i}=\frac{a_i{\beta }_i}{\gamma },1\le i\le n.$(5) The next generation matrix is (6) $K=\left(\begin{array}{cccc}{\mathcal{R}}_{01}{c}_{11}& {\mathcal{R}}_{01}{c}_{12}& \cdots & {\mathcal{R}}_{01}{c}_{1n}\\ {\mathcal{R}}_{02}{c}_{21}& {\mathcal{R}}_{02}{c}_{22}& \cdots & {\mathcal{R}}_{02}{c}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\mathcal{R}}_{0n}{c}_{n1}& {\mathcal{R}}_{0n}{c}_{n2}& \cdots & {\mathcal{R}}_{0n}{c}_{nn}\end{array}\right)=\text{diag}({\mathcal{R}}_{01},{\mathcal{R}}_{02},\dots ,{\mathcal{R}}_{0n})C,$(6) where $C=\left(c_{ij}\right)$ is the mixing matrix. The basic reproduction number for the meta-population is (7) ${\mathcal{R}}_0=\rho \left(K\right),$(7) when $\rho \left(K\right)$ denotes the dominant eigenvalue of K. In general, we can only compute $\rho \left(K\right)$ numerically when n>2. Two special cases are when the mixing is proportionate (i.e. when ${ϵ}_i=0$) or isolated (i.e. when ${ϵ}_i=1$) for all i. In these cases, $\rho \left(K\right)$ is given by either the trace of K or the maximum of ${\mathcal{R}}_{0i}$. That is, the analytic expressions are: (8) $\begin{array}{rl}& {\mathcal{R}}_0=\sum _{i=1}^n{\mathcal{R}}_{0i}{c}_{ii}\text{when}{ϵ}_i=0,1\le i\le n,\\ & {\mathcal{R}}_0=\underset{1\le i\le n}{max}\left\{{\mathcal{R}}_{0i}\right\}\text{when}{ϵ}_i=1,1\le i\le n.\end{array}$(8) If vaccines are available before the epidemic starts, a certain level of population immunity can be achieved via vaccination. Let $p_i$ denote the immunity of sub-population i at time t=0 ($0\le p_i\le 1$). Then the disease dynamics can be modelled by the equations in (1(1) $\begin{array}{rl}{S}_i^{\prime }& =-a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j},\\ I_i^{\prime }& =a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j}-\gamma I_i,\\ R_i^{\prime }& =\gamma I_i,1\le i\le n,\end{array}$(1) ) with modified initial conditions: (9) $S_i\left(0\right)=(1-p_i)(N_i-I_{i0}),I_i\left(0\right)=I_{i0},R_i\left(0\right)=p_i(N_i-I_{i0}),1\le i\le n.$(9) In this case, the isolated effective reproduction number for group i is ${\mathcal{R}}_{ei}=(1-p_i){\mathcal{R}}_{0i}$, and the next generation matrix is $K_e=\text{diag}({\mathcal{R}}_{e1},{\mathcal{R}}_{e2},\dots ,{\mathcal{R}}_{en})C$. The effective reproduction number for the meta-population is ${\mathcal{R}}_e=\rho \left(K_e\right)$.

If the effect of another type of control or intervention programme is to reduce activities $a_i$ and/or probabilities of infection ${\beta }_i$, let ${\mathcal{R}}_{ei}$ denote the isolated effective reproduction number for group i (same formula as for ${\mathcal{R}}_{0i}$ in (5(5) ${\mathcal{R}}_{0i}=\frac{a_i{\beta }_i}{\gamma },1\le i\le n.$(5) ) but with the new values of $a_i$ and ${\beta }_i$), then the effective reproduction number for the meta-population ${\mathcal{R}}_e$ is given by the dominant eigenvalue of the next generation matrix $K_e$, which is the same as K in (6(6) $K=\left(\begin{array}{cccc}{\mathcal{R}}_{01}{c}_{11}& {\mathcal{R}}_{01}{c}_{12}& \cdots & {\mathcal{R}}_{01}{c}_{1n}\\ {\mathcal{R}}_{02}{c}_{21}& {\mathcal{R}}_{02}{c}_{22}& \cdots & {\mathcal{R}}_{02}{c}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\mathcal{R}}_{0n}{c}_{n1}& {\mathcal{R}}_{0n}{c}_{n2}& \cdots & {\mathcal{R}}_{0n}{c}_{nn}\end{array}\right)=\text{diag}({\mathcal{R}}_{01},{\mathcal{R}}_{02},\dots ,{\mathcal{R}}_{0n})C,$(6) ) but with ${\mathcal{R}}_{0i}$ being replaced by ${\mathcal{R}}_{ei}$.

We now use (1(1) $\begin{array}{rl}{S}_i^{\prime }& =-a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j},\\ I_i^{\prime }& =a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j}-\gamma I_i,\\ R_i^{\prime }& =\gamma I_i,1\le i\le n,\end{array}$(1) ) with initial condition (2(2) $S_i\left(0\right)=N_i-I_{i0},I_i\left(0\right)=I_{i0},R_i\left(0\right)=0,1\le i\le n.$(2) ) to derive a relation for the final epidemic size. Note from the $S_i^{\prime }$ and $I_i^{\prime }$ equations in (1(1) $\begin{array}{rl}{S}_i^{\prime }& =-a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j},\\ I_i^{\prime }& =a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j}-\gamma I_i,\\ R_i^{\prime }& =\gamma I_i,1\le i\le n,\end{array}$(1) ) that (10) $(S_i+I_i{)}^{\prime }=-\gamma I_i,1\le i\le n.$(10) Because $S_i\left(t\right)\ge 0$ and $I_i\left(t\right)\ge 0$ for all t>0, $S_i\left(t\right)+I_i\left(t\right)$ is a non-negative decreasing function and hence has a limit as $t\to \mathrm{\infty }$ and ${\int }_{t=0}^{\mathrm{\infty }}{I}_i\left(t\right)dt=0$. It follows that $I_i\left(t\right)\to 0$ as $t\to \mathrm{\infty }$ (see [5], Section 2.4). Thus, $S_i\left(\mathrm{\infty }\right)\doteq \underset{t\to \mathrm{\infty }}{lim}S\left(t\right)$ exists. Using $I_i\left(\mathrm{\infty }\right)=0$ and $S_i\left(0\right)+I_i\left(0\right)=N_i$, and from (10(10) $(S_i+I_i{)}^{\prime }=-\gamma I_i,1\le i\le n.$(10) ) we get (11) $N_i-S_i\left(\mathrm{\infty }\right)=\gamma {\int }_0^{\mathrm{\infty }}{I}_i\left(t\right)\mathrm{d}t,1\le i\le n.$(11) Dividing the $S_i^{\prime }$ equation in (1(1) $\begin{array}{rl}{S}_i^{\prime }& =-a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j},\\ I_i^{\prime }& =a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j}-\gamma I_i,\\ R_i^{\prime }& =\gamma I_i,1\le i\le n,\end{array}$(1) ) by $S_i\left(t\right)$ on both sides, we get (12) $\frac{d{S}_i}{S_i}=-a_i{\beta }_i\sum _{j=1}^n{c}_{ij}\frac{I_j\left(t\right)}{N_j}\mathrm{d}t,1\le i\le n.$(12) Integration of both sides of (12(12) $\frac{d{S}_i}{S_i}=-a_i{\beta }_i\sum _{j=1}^n{c}_{ij}\frac{I_j\left(t\right)}{N_j}\mathrm{d}t,1\le i\le n.$(12) ) from 0 to ∞ yields (13) $\log \frac{S_i\left(0\right)}{S_i\left(\mathrm{\infty }\right)}=\sum _{j=1}^n\frac{a_i{\beta }_i{c}_{ij}}{N_j}{\int }_0^{\mathrm{\infty }}{I}_j\left(t\right)\mathrm{d}t.$(13) From (11(11) $N_i-S_i\left(\mathrm{\infty }\right)=\gamma {\int }_0^{\mathrm{\infty }}{I}_i\left(t\right)\mathrm{d}t,1\le i\le n.$(11) ), (13(13) $\log \frac{S_i\left(0\right)}{S_i\left(\mathrm{\infty }\right)}=\sum _{j=1}^n\frac{a_i{\beta }_i{c}_{ij}}{N_j}{\int }_0^{\mathrm{\infty }}{I}_j\left(t\right)\mathrm{d}t.$(13) ), and ${\mathcal{R}}_{0i}=a_i{\beta }_i/\gamma$, we obtain (14) $\log \frac{S_i\left(0\right)}{S_i\left(\mathrm{\infty }\right)}=\sum _{j=1}^n{\mathcal{R}}_{0i}{c}_{ij}\left(1-\frac{S_j\left(\mathrm{\infty }\right)}{N_j}\right),1\le i\le n.$(14) Let $Z_i=S_i\left(0\right)-S_i\left(\mathrm{\infty }\right)$, then (15) $N_i-S_i\left(\mathrm{\infty }\right)=N_i-\left(S_i\right(0)-Z_i)=I_i\left(0\right)+Z_i,1\le i\le n.$(15) Thus, from (14(14) $\log \frac{S_i\left(0\right)}{S_i\left(\mathrm{\infty }\right)}=\sum _{j=1}^n{\mathcal{R}}_{0i}{c}_{ij}\left(1-\frac{S_j\left(\mathrm{\infty }\right)}{N_j}\right),1\le i\le n.$(14) ) and (15(15) $N_i-S_i\left(\mathrm{\infty }\right)=N_i-\left(S_i\right(0)-Z_i)=I_i\left(0\right)+Z_i,1\le i\le n.$(15) ), we know that $Z_i$ can be determined by a solution of the following set of equations: (16) $Z_i=S_i\left(0\right)\left(1-\exp \left[-\sum _{j=1}^n{\mathcal{R}}_{0i}{c}_{ij}\frac{Z_j+I_j\left(0\right)}{N_j}\right]\right),1\le i\le n.$(16) Let $N=\sum _{i=1}^n{N}_i$ denote the total population size, and let ${\mathcal{F}}_i=Z_i/N$ denote the fraction of infected in group i (over the total N). We define the final epidemic size $\mathcal{F}$ by (17) $\mathcal{F}=\sum _{i=1}^n{\mathcal{F}}_i=\sum _{i=1}^n\frac{Z_i}{N}.$(17) In the special case when the population is considered homogeneous with random mixing, i.e. the parameter values for all sub-groups are identical (e.g. $a_i=a$, ${\beta }_i=\beta$, $N_i=N/n$, $S_i\left(0\right)=S\left(0\right)/N$, $I_i\left(0\right)=I\left(0\right)/N$ are all independent of i and ${ϵ}_i=0$), the final size relation simplifies to (18) $Z=S\left(0\right)\left(1-\exp \left[-{\mathcal{R}}_0\frac{Z+I\left(0\right)}{N}\right]\right),$(18) where $Z=\sum _{i=1}^n{Z}_i$ and ${\mathcal{R}}_0={\mathcal{R}}_{0i}=a\beta /\gamma$. If we vary ${\mathcal{R}}_0$ by varying β while keeping a and γ fixed, the final size relation (18(18) $Z=S\left(0\right)\left(1-\exp \left[-{\mathcal{R}}_0\frac{Z+I\left(0\right)}{N}\right]\right),$(18) ) is illustrated in Figure 1, which shows that $\mathcal{F}$ is an increasing function of ${\mathcal{R}}_0$.

As shown in Feng et al. [11] and Glasser et al. [13], in meta-population models with preferential mixing, even when β and the mean activity $\sum _{i=1}^n{a}_i/n$ are constant (with all other parameter values fixed), ${\mathcal{R}}_0$ may vary with the level of heterogeneity in $a_i$ and preference ${ϵ}_i$. Therefore, the dependence of $\mathcal{F}$ on ${\mathcal{R}}_0$ may not be increasing as exhibited in Figure 1. In the following sections, we will investigate how population heterogeneity in models with non-random mixing may influence the final size $\mathcal{F}$, the relationship between $\mathcal{F}$ and ${\mathcal{R}}_0$, and model evaluations of intervention programmes.

3. Effect of heterogeneity on final size and the relationship between $\mathcal{F}$ and ${\mathcal{R}}_0$

A general understanding based on epidemic models for a homogeneous population with random mixing is that $\mathcal{F}$ is an increasing function of ${\mathcal{R}}_0$, as shown in Figure 1. Recall that the increase in ${\mathcal{R}}_0$ is caused by increasing β. When heterogeneity such as activity ($a_i$), preference of contacts (${ϵ}_i$), and sub-population size ($N_i$) are considered in a meta-population model with preferential mixing, ${\mathcal{R}}_0$ may vary by a significantly magnitude even when ${\beta }_i$ are fixed (see e.g. [13]). In addition, it has been shown in Poghotanyan et al. [18] that, among a large class of mixing matrices $\left(c_{ij}\right)$ including the preferential mixing in (4(4) $c_{ij}={ϵ}_i{\delta }_{ij}+(1-{ϵ}_i)f_j,\text{where}{f}_j=\frac{(1-{ϵ}_j)a_j{N}_j}{\sum _k(1-{ϵ}_k)a_k{N}_k}.$(4) ), ${\mathcal{R}}_0=\rho \left(K\right)$ is bounded below and above by the basic reproduction numbers corresponding to proportionate mixing (${ϵ}_i=0$ for all i) and isolated mixing (${ϵ}_i=1$ for all i), respectively, i.e. (19) $\sum _{i=1}^n{\mathcal{R}}_{0i}{w}_i\le {\mathcal{R}}_0\le \underset{1\le i\le n}{max}{\mathcal{R}}_{0i},$(19) where ${\mathcal{R}}_{0i}=\frac{a_i{\beta }_i}{\gamma },w_i=\frac{a_i{N}_i}{\sum _{j=1}^n{a}_i{N}_j}.$ It is clear from (19(19) $\sum _{i=1}^n{\mathcal{R}}_{0i}{w}_i\le {\mathcal{R}}_0\le \underset{1\le i\le n}{max}{\mathcal{R}}_{0i},$(19) ) that we can keep ${\beta }_i$ fixed and change ${\mathcal{R}}_0$ by varying $a_i$ and $N_i$ while keeping the same mean activity and mean population size. Particularly, different ${ϵ}_i$ values may also affect how ${\mathcal{R}}_0$ and $\mathcal{F}$ may be influenced by heterogeneity in $a_i$ or $N_i$. Thus, the relationship between $\mathcal{F}$ and ${\mathcal{R}}_0$ may be more complex in meta-population models than the one illustrated in Figure 1. This will be explored next.

Results in this section are for the case of n=2 groups, but they can be extended to the case of n>2. Although the equations for $Z_i$ in (16(16) $Z_i=S_i\left(0\right)\left(1-\exp \left[-\sum _{j=1}^n{\mathcal{R}}_{0i}{c}_{ij}\frac{Z_j+I_j\left(0\right)}{N_j}\right]\right),1\le i\le n.$(16) ) cannot be solved analytically, we can explore the dependence of $Z_i$ on other parameters numerically. Rewrite (16(16) $Z_i=S_i\left(0\right)\left(1-\exp \left[-\sum _{j=1}^n{\mathcal{R}}_{0i}{c}_{ij}\frac{Z_j+I_j\left(0\right)}{N_j}\right]\right),1\le i\le n.$(16) ) as (20) $F(Z_1,Z_2)=1,G(Z_1,Z_2)=1,$(20) where (21) $\begin{array}{rl}F(Z_1,Z_2)& =\frac{S_1\left(0\right)}{Z_1}\left(1-\exp \left[-\sum _{j=1}^2{\mathcal{R}}_{01}{c}_{1j}\frac{Z_j+I_j\left(0\right)}{N_j}\right]\right),\\ G(Z_1,Z_2)& =\frac{S_2\left(0\right)}{Z_2}\left(1-\exp \left[-\sum _{j=1}^2{\mathcal{R}}_{02}{c}_{2j}\frac{Z_j+I_j\left(0\right)}{N_j}\right]\right).\end{array}$(21) Figure 2(a) illustrates the final size as an intersection of the curves determined by F=1 and G=1.

Figure 2. (a) The solution $(Z_1,Z_2)$ of the equations (21(21) $\begin{array}{rl}F(Z_1,Z_2)& =\frac{S_1\left(0\right)}{Z_1}\left(1-\exp \left[-\sum _{j=1}^2{\mathcal{R}}_{01}{c}_{1j}\frac{Z_j+I_j\left(0\right)}{N_j}\right]\right),\\ G(Z_1,Z_2)& =\frac{S_2\left(0\right)}{Z_2}\left(1-\exp \left[-\sum _{j=1}^2{\mathcal{R}}_{02}{c}_{2j}\frac{Z_j+I_j\left(0\right)}{N_j}\right]\right).\end{array}$(21) ) is shown as the intersection of the curves $F(Z_1,Z_2)=1$ and $G(Z_1,Z_2)=1$. (b) Cumulative infections during an outbreak in the two groups and the total. The plots are for the case of proportionate mixing (i.e. ${ϵ}_1={ϵ}_2=0$) with $a_1=14,a_2=6$, and $N_1=N_2=5000$.

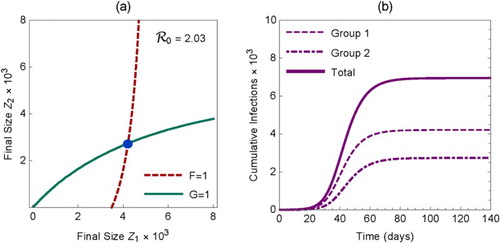
For demonstration purposes, we used the following parameter values in Figure 2 (the time unit is days): ${\beta }_1={\beta }_2=0.035$, $1/\gamma =5$ (infectious period is 5 days), $a_1+a_2=20$ with $a_1=14$ and $a_2=6$ (heterogeneous activity with the mean activity being 10), ${ϵ}_1={ϵ}_2=0$ (proportionate mixing), $N_1+N_2={10}^4$, $\sigma =N_1/N=0.5$ (homogeneous sub-population size with $N_1=N_2=5000$), and $I_1\left(0\right)=I_2\left(0\right)=1$. For these parameter values, the isolated reproduction numbers for sub-populations 1 and 2 are ${\mathcal{R}}_{01}=2.45$ and ${\mathcal{R}}_{02}=1.05$, respectively. The overall effective reproduction number for the meta-population is ${\mathcal{R}}_0=2.03$. From the equations in (16(16) $Z_i=S_i\left(0\right)\left(1-\exp \left[-\sum _{j=1}^n{\mathcal{R}}_{0i}{c}_{ij}\frac{Z_j+I_j\left(0\right)}{N_j}\right]\right),1\le i\le n.$(16) ), we have $Z_1=4210$ and $Z_2=2730$. These values are also consistent with the cumulative infections in groups 1 and 2 presented in Figure 2(b) from numerical simulations of system (1(1) $\begin{array}{rl}{S}_i^{\prime }& =-a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j},\\ I_i^{\prime }& =a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j}-\gamma I_i,\\ R_i^{\prime }& =\gamma I_i,1\le i\le n,\end{array}$(1) ) with the initial condition (2(2) $S_i\left(0\right)=N_i-I_{i0},I_i\left(0\right)=I_{i0},R_i\left(0\right)=0,1\le i\le n.$(2) ).

3.1. Influence of heterogeneity and non-homogeneous mixing

To explore the effect of mixing on model predictions, we consider preferential mixing (4(4) $c_{ij}={ϵ}_i{\delta }_{ij}+(1-{ϵ}_i)f_j,\text{where}{f}_j=\frac{(1-{ϵ}_j)a_j{N}_j}{\sum _k(1-{ϵ}_k)a_k{N}_k}.$(4) ) and examine heterogeneity in various characteristics affecting the mixing function including activity $a_i$, group size $N_i$, and preference ${ϵ}_i$. For demonstration purposes, we fix the same parameter values ${\beta }_1={\beta }_2=0.035$, $N_1=N_2=5000$, and the mean activity $(a_1+a_2)/2=10$. Values for other parameters may vary depending on applications.

3.1.1. Heterogeneity in activity $a_i$

Consider first the case of proportionate mixing (${ϵ}_1={ϵ}_2=0$). The effect of heterogeneity and variability in activity $a_i$ on $\mathcal{F}$ is illustrated in Figure 3, which shows the final sizes for three sets of activities $(a_1,a_2)$. The $a_i$ values used in the three rows from top to bottom are (with increasing variability) $\mathrm{Top}:(a_1,a_2)=(10,10),\mathrm{Middle}:(a_1,a_2)=(14,6),\mathrm{Bottom}:(a_1,a_2)=(18,2).$ The left column shows the values of $Z_i$ determined by equations in (16(16) $Z_i=S_i\left(0\right)\left(1-\exp \left[-\sum _{j=1}^n{\mathcal{R}}_{0i}{c}_{ij}\frac{Z_j+I_j\left(0\right)}{N_j}\right]\right),1\le i\le n.$(16) ), as the intersection of F=1 and G=1 (marked by the dot). The right column shows the epidemic curves based on the simulations of the system (1(1) $\begin{array}{rl}{S}_i^{\prime }& =-a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j},\\ I_i^{\prime }& =a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j}-\gamma I_i,\\ R_i^{\prime }& =\gamma I_i,1\le i\le n,\end{array}$(1) ) with initial condition (2(2) $S_i\left(0\right)=N_i-I_{i0},I_i\left(0\right)=I_{i0},R_i\left(0\right)=0,1\le i\le n.$(2) ). Notice that the number of individuals in the R class represents the cumulative infections at anytime.

Figure 3. Comparison of $\mathcal{F}$, ${\mathcal{R}}_0$, and $\mathcal{P}$ when activity is homogeneous (top) and heterogeneous with increasing variance (middle and bottom). Mixing is proportional (${ϵ}_1={ϵ}_2=0$). The left column shows the final size (marked by the point of intersection of F=1 and G=1 as the solution of (20(20) $F(Z_1,Z_2)=1,G(Z_1,Z_2)=1,$(20) )). The right column shows the the total sizes of S, I, and R as the solution of model (1(1) $\begin{array}{rl}{S}_i^{\prime }& =-a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j},\\ I_i^{\prime }& =a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j}-\gamma I_i,\\ R_i^{\prime }& =\gamma I_i,1\le i\le n,\end{array}$(1) ) with initial condition (2(2) $S_i\left(0\right)=N_i-I_{i0},I_i\left(0\right)=I_{i0},R_i\left(0\right)=0,1\le i\le n.$(2) ).

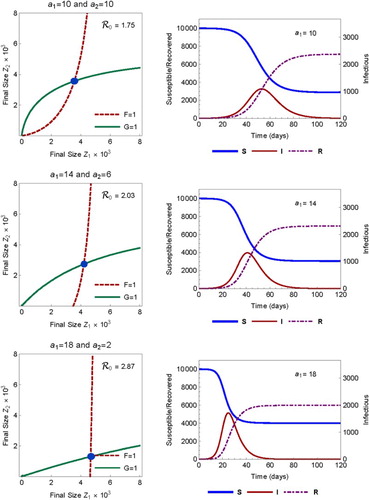
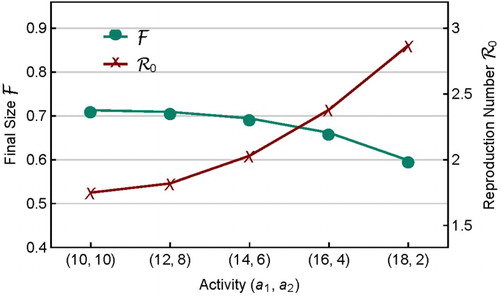
In this case, the basic reproduction numbers are ${\mathcal{R}}_0=1.75,2.03$, and 2.87, respectively, while the final sizes are $\mathcal{F}=0.713,0.695,$ and 0.599, respectively. We observe the following changes as the variability in activity increases

• $\mathcal{F}$ decreases;

• ${\mathcal{R}}_0$ increases;

• $\mathcal{P}$ increases;

• the time to epidemic peak decreases.

To make it more transparent how variability in $a_i$ affects ${\mathcal{R}}_0$, $\mathcal{F}$, and their relationship, Figure 4 plots $\mathcal{F}$ and ${\mathcal{R}}_0$ for several sets of activity $(a_1,a_2)$ that have the same mean. It shows that the homogeneous activity ($a_1=a_2=10$) corresponds to the smallest ${\mathcal{R}}_0=1.75$ and largest $\mathcal{F}=0.713$, while the heterogeneous activity with the highest variability ($a_1=18,a_2=2$) corresponds to the largest ${\mathcal{R}}_0=2.87$ and smallest $\mathcal{F}=0.599$. This provides an example that the final size does not vary with ${\mathcal{R}}_0$ positively. That is, the usual understanding based on models with homogeneous assumption that $\mathcal{F}$ increases with ${\mathcal{R}}_0$ (see Figure 1) may not be true when more realistic mixing functions are incorporated in meta-population models. Such results may have important implications for public health policy-making. For example, when a control programme is aimed at reducing ${\mathcal{R}}_0$, it should also check whether or not it may lead to an increased final epidemic size.

Figure 4. Plots of ${\mathcal{R}}_0$ and $\mathcal{F}$ for contact rates $a_1$ and $a_2$ with the same mean but different variability. When $(a_1,a_2)$ changes from (10,10) to (18,2), ${\mathcal{R}}_0$ increases from 1.75 to 2.87 whereas $\mathcal{F}$ decreases from 0.713 to 0.599.

3.1.2. Preference level in mixing

The examples in Section 3.1.1 are for proportionate mixing (i.e. ${ϵ}_i=0$). A more realistic mixing, in general, is when ${ϵ}_i>0$, representing a preference of contacts with others in the same sub-group. Heterogeneity in factors such as $a_i$ and ${ϵ}_i$ may have an important influence in ${\mathcal{R}}_0$ and $\mathcal{F}$, as suggested in (19(19) $\sum _{i=1}^n{\mathcal{R}}_{0i}{w}_i\le {\mathcal{R}}_0\le \underset{1\le i\le n}{max}{\mathcal{R}}_{0i},$(19) ). We now explore the effect of variability in $a_i$ and the joint effect of $a_i$ and ${ϵ}_i$ on $\mathcal{F}$ and ${\mathcal{R}}_0$. Consider first the simpler case when ${ϵ}_1={ϵ}_2$. Figure 5 provides a similar information as in Figure 4 but includes cases of ${ϵ}_i>0$.

Figure 5. Plots of $\mathcal{F}$ and ${\mathcal{R}}_0$ for various preference level ${ϵ}_i$ and activity variability in $a_i$ (with equal mean $(a_1+a_2)/2=10$), showing that as ${ϵ}_i$ or variability in $a_i$ increases, $\mathcal{F}$ decreases while ${\mathcal{R}}_0$ increases.

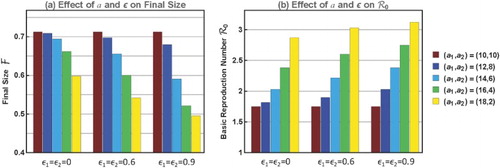
We observe in Figure 5 that (i) for each fixed ${ϵ}_i$ value, ${\mathcal{R}}_0$ increases but $\mathcal{F}$ decreases with the variability in $a_i$, and the changes are more dramatic for higher ${ϵ}_i$; and (ii) for each fixed heterogeneous pair $(a_1,a_2)$, ${\mathcal{R}}_0$ increases and $\mathcal{F}$ decreases with ${ϵ}_i$. Because the bar charts in Figure 5(a,b) are for the same sets of $a_i$ and ${ϵ}_i$, it shows again that $\mathcal{F}$ and ${\mathcal{R}}_0$ are related negatively when heterogeneity in $a_i$ and/or ${ϵ}_i$ is varied. This illustrates again an opposite relationship between $\mathcal{F}$ and ${\mathcal{R}}_0$ to that shown in Figure 1.

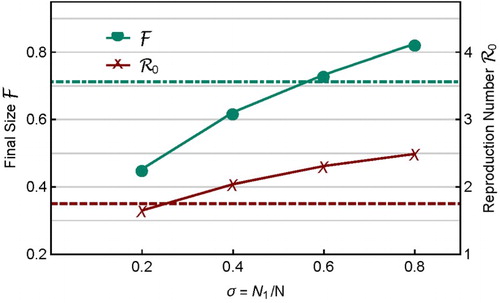
3.1.3. Sub-population size $N_i$

The influence of heterogeneity in $N_i$ can be examined by fixing all other parameter values. For example, Figure 6 shows the case when $a_1=15$, $a_2=5$, ${ϵ}_i=0$, and all other parameter values except $N_i$ are the same as before. The total $N=N_1+N_2={10}^4$ is fixed but $\sigma =N_1/N$ varies. It shows that both $\mathcal{F}$ and ${\mathcal{R}}_0$ increase with σ, and thus, in this case, $\mathcal{F}$ and ${\mathcal{R}}_0$ are positively related. The values of $\mathcal{F}$ and ${\mathcal{R}}_0$ for the homogeneous case ($\sigma =0.5$ and $a_1=a_2=10$) are also shown by the dot-dashed and dashed lines, respectively. Thus, heterogeneity in characteristics including $a_i$ and $N_i$ can either increase or decrease $\mathcal{F}$ and ${\mathcal{R}}_0$.

Figure 6. Changes in $\mathcal{F}$ and ${\mathcal{R}}_0$ with the sub-population sizes $N_i$ ($N_1=\sigma N$ and $N_2=(1-\sigma )N$ for fixed N). The dot-dashed line and dashed line are values of $\mathcal{F}$ and ${\mathcal{R}}_0$, respectively, for homogeneous case in which $\sigma =0.5$ and $a_1=a_2=10$.

3.2. Examples

Because population heterogeneity in factors such as $a_i$ or ${ϵ}_i$ may affect the final size and the basic reproduction number in significant ways, we investigate in this section how the model evaluations of intervention strategies may be affected. Two examples are discussed below.

3.2.1. Heterogeneity in vaccine coverage $p_i$

Consider the model equations in (1(1) $\begin{array}{rl}{S}_i^{\prime }& =-a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j},\\ I_i^{\prime }& =a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j}-\gamma I_i,\\ R_i^{\prime }& =\gamma I_i,1\le i\le n,\end{array}$(1) ) with the initial condition in (9(9) $S_i\left(0\right)=(1-p_i)(N_i-I_{i0}),I_i\left(0\right)=I_{i0},R_i\left(0\right)=p_i(N_i-I_{i0}),1\le i\le n.$(9) ). Assume that the vaccine efficacy is 100% so that the vaccination coverage in group i is the same as the immunity $p_i$, and the total number of vaccine doses is $p_1{N}_1+p_2{N}_2$. When $N_1=N_2$ with fixed total size $N=N_1+N_2$, fixing the total number of vaccine doses is equivalent to fixing the value of $p=p_1+p_2$. Thus, we can examine the effect of heterogeneity in vaccine allocation $(p_1,p_2)$ on $\mathcal{F}$ and ${\mathcal{R}}_e$ for fixed p. Choose parameter values to be the same as before except that ${ϵ}_1={ϵ}_2=0.6$, $\beta =0.05$, $a_1=8$, $a_2=12$, and $1/\gamma =7$. For these parameter values, the basic reproduction numbers for the two groups are ${\mathcal{R}}_{01}=2.8$ and ${\mathcal{R}}_{02}=4.2$ with ${\mathcal{R}}_0=3.8$. For demonstration purpose, let $p_1+p_2=1.32$. For the homogeneous case ($a_1=a_2=10$ and $p_1=p_2=0.66$), the final size is ${\mathcal{F}}^{\left(\mathrm{hom}\right)}=0.1$ and the effective reproduction number is ${\mathcal{R}}_e^{\left(\mathrm{hom}\right)}=1.2$, which are labelled in Figure 7 by the dot-dashed and dashed lines, respectively.

Figure 7. Similar to Figure 6, but this shows the dependence of $\mathcal{F}$ and ${\mathcal{R}}_e$ on heterogeneity in sub-population immunity $p_i$ with $p_1+p_2=1.32$. The dot-dashed line and dashed line are values of ${\mathcal{F}}^{\left(\mathrm{hom}\right)}$ and ${\mathcal{R}}_e^{\left(\mathrm{hom}\right)}$, respectively, for the homogeneous case with $a_1=a_2=10$ and $p_1=p_2=0.66$.

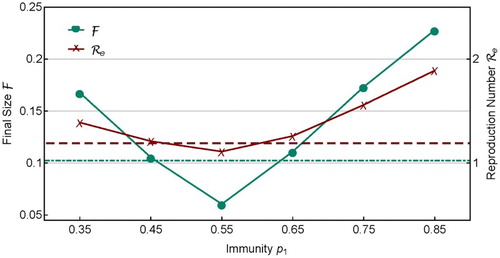
In Figure 7, $\mathcal{F}$ and ${\mathcal{R}}_e$ for several sets of heterogeneous coverage with $p_1+p_2=1.32$ are plotted. It is interesting to notice that for $p_1=0.55$, both $\mathcal{F}$ and ${\mathcal{R}}_e$ are smaller than their corresponding values in the homogeneous case, ${\mathcal{F}}^{\left(\mathrm{hom}\right)}$ and ${\mathcal{R}}_e^{\left(\mathrm{hom}\right)}$ (shown by the dot-dashed and dashed lines). But for other $p_1$ values, $\mathcal{F}>{\mathcal{F}}^{\left(\mathrm{hom}\right)}$ and ${\mathcal{R}}_e>{\mathcal{R}}_e^{\left(\mathrm{hom}\right)}$. This shows that, for a fixed amount of vaccine doses, although the homogeneous coverage $p_1=p_2$ can provide a relatively more effective allocation than many heterogeneous vaccine allocations in reducing ${\mathcal{R}}_e$, it may not be the best choice. This result is consistent with those found in Feng et al. [11], in which it is shown that the optimal vaccine allocation can be determined using a gradient approach based on a Lagrange optimization problem. The results in Feng et al. [11] is formulated in terms of minimizing the effective reproduction number.

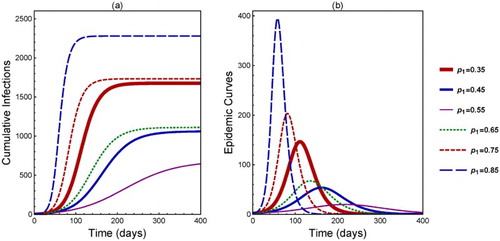
In addition to the final size, the peak size ($\mathcal{P}$) and time to peak ($\mathcal{T}$) are also sensitive to the heterogeneity in $p_i$. This is illustrated in Figure 8 (the $p_1$ values for different curves are labelled in the legend). All parameter values are the same as in Figure 7.

We observe in Figure 8(a) that, as $p_1$ increases from 0.35 to 0.55, the number of cumulative infections decreases (see the solid curves). However, as $p_1$ continues to increase to 0.65 until 0.85, the number of cumulative infections becomes increasing (the dot-dashed to dashed curves). Similarly in Figure 8(b), $\mathcal{P}$ and $\mathcal{T}$ decrease from $p_1=0.35$ to 0.55 (solid curves) but increase from $p_1=0.65$ to 0.85 (dashed curves).

Figure 8. Numerical simulations of system (1(1) $\begin{array}{rl}{S}_i^{\prime }& =-a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j},\\ I_i^{\prime }& =a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j}-\gamma I_i,\\ R_i^{\prime }& =\gamma I_i,1\le i\le n,\end{array}$(1) ) with initial conditions (9(9) $S_i\left(0\right)=(1-p_i)(N_i-I_{i0}),I_i\left(0\right)=I_{i0},R_i\left(0\right)=p_i(N_i-I_{i0}),1\le i\le n.$(9) ) showing (a) the cumulative infections and (b) epidemic curves for various vaccine allocation $(p_1,p_2)$ with $p_1+p_2=1.32$ (the values of $p_1$ for different curves are labelled in the legend).

3.2.2. The 2011 acute haemorrhagic conjunctivitis outbreak in China

In this section, we examine how population heterogeneity in various characteristics may affect model evaluations of control and intervention programmes. We demonstrate this by using an example based on the 2011 outbreak of AHC in Changsha, China. Studies on the efficacy of quarantine during this outbreak is presented in [7,8]. By fitting a homogeneous SIR model to the data from a case report for a school population, they obtained an estimate for the transmission coefficient β. Based on this, we adopt $\beta =0.05$ as a baseline value for the probability of infection on contact with a baseline value for activity to be a=15. The infectious period for this AHC outbreak in China is about 7–10 days, so we choose $1/\gamma$ to be 8 days. Under these parameter values, the baseline value for the reproduction number is ${\mathcal{R}}_0=\beta a/\gamma =6$. This is much higher than the value of the reproduction number ${\mathcal{R}}_0^{\ast }$ presented in [9] for the 2003 AHC outbreak in Mexico, where ${\mathcal{R}}_0^{\ast }=2.64$. The main reason for this difference is in the value of infectious period, which are about 8 and 3 days for the outbreaks in China and Mexico, respectively.

Consider the case when the population is divided into two groups, and individuals in group 1 have a lower risk of being infected due to a reduced contact rate, better health habit (e.g. washing hands to increase protection against infection) or other behavioural changes as suggested by public health officials. Thus, let ${\beta }_2=0.05$ (baseline value) and $N=N_1+N_2={10}^3$ (e.g. a school population) be fixed. Assume that individuals in the low risk group have a reduced activity with $a_1=5$ ($<a_2=15$), and let ${\beta }_1=\delta {\beta }_2\text{with}\delta <1,\sigma =\frac{N_1}{N}\text{with}0\le \sigma \le 1.$ The mixing is assumed to be proportionate. We will examine the changes in $\mathcal{F}$ due to interventions aimed at decreasing δ and increasing σ. The simulation results are presented in Figure 9, which shows the model evaluations for the effect of reducing δ and increasing σ on the final epidemic size $\mathcal{F}$.

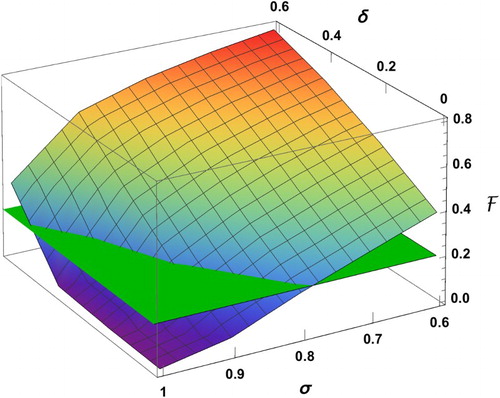
Figure 9. Effect of reducing δ (transmission coefficient) and increasing σ (proportion of the low-risk group) on $\mathcal{F}$.

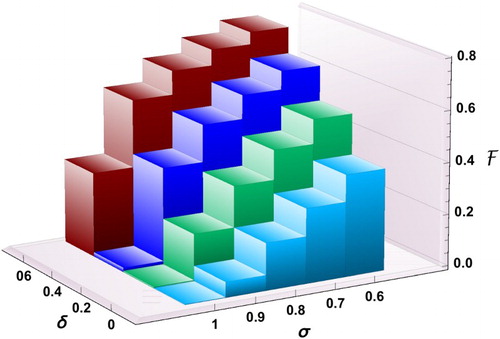
We observe in Figure 9 that increasing σ can be effective in reducing the final size only if δ is sufficiently small. For example, if 60% of individuals are in group 1 ($\sigma =0.6$) and the reduction factor for the risk of infection is $\delta =0.6$, the final size is 0.79. The reason for the high percentage of cumulative infections is because of the high value of the basic reproduction number ${\mathcal{R}}_{20}=6$ for group 2. In fact, in the absence of control, almost the entire population will be infected during the outbreak. For the same value of $\delta =0.6$, even when $\sigma =N_1/N=1$, the final size will still be as high as 32%. The only possibility to have the final size below 10% is when $\delta \le 0.2$ and $\sigma \ge 0.9$. However, as long as $\sigma <1$ (or $N_2/N>0$), there will be a significant number of infections.

Figure 10 plots the surface of the final size as a function of δ and σ, which is obtained by connecting the values of the bar chart. We can identify the region in the ($\delta ,\sigma$) plane in which the final size is below a certain level. For example, the intersection curve of the $\mathcal{F}$ surface with the plane with $\mathcal{F}=0.2$ determines the proportion σ of individuals in group 1 (for a given δ value), above which the final size is below 20%.

Figure 10. The surface is a plot of the final size $\mathcal{F}$ versus δ and σ, and the plane corresponds to $\mathcal{F}=0.2$. The intersection curve identifies the region for $(\delta ,\sigma )$ (where the surface is below the plane) in which the final size is below 20%.

4. Discussion

The results presented in this paper provide another example that incorporation of population heterogeneity and non-homogeneous mixing in epidemic models can generate outcomes that are qualitatively different from that based on models for populations with homogeneous mixing. Particularly, for two of the most important quantities, reproduction number (${\mathcal{R}}_0$ or ${\mathcal{R}}_e$) and final epidemic size ($\mathcal{F}$), we demonstrated how they may be influenced by population heterogeneity in various characteristics and mixing by comparing the results from a meta-population model with and without heterogeneity and non-homogeneous mixing. The final epidemic size relation and the reproduction number derived from the meta-population model (1(1) $\begin{array}{rl}{S}_i^{\prime }& =-a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j},\\ I_i^{\prime }& =a_i{\beta }_i{S}_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j}-\gamma I_i,\\ R_i^{\prime }& =\gamma I_i,1\le i\le n,\end{array}$(1) ) with a general mixing matrix $C=\left(c_{ij}\right)$ allows us to conduct various comparisons (see Sections 3.1.1–3.1.3). We also presented two examples to illustrate the effect of heterogeneity and mixing in the model evaluation of intervention strategies (Section 3.2). An interesting result is that, although homogeneous vaccine coverage may produce higher reduction in $\mathcal{F}$ than many heterogeneous combinations of coverage, it may not be the most effective option (see Figures 7 and 8) if the objective is to maximally reduce $\mathcal{F}$ for a given number of vaccine doses.

Another interesting finding of this study is the correlation between $\mathcal{F}$ and ${\mathcal{R}}_0$. In models with homogeneous mixing, $\mathcal{F}$ and ${\mathcal{R}}_0$ are positively related, as shown in Figure 1. However, this relation may be reversed when heterogeneity is considered in a meta-population model with non-homogeneous mixing, as illustrated in Figures 4 and 5. Particularly, an increase of variability in activity ($a_1-a_2$) or preference level (${ϵ}_i$) can increase ${\mathcal{R}}_0$ but decrease $\mathcal{F}$. Thus, in this case, $\mathcal{F}$ and ${\mathcal{R}}_0$ are negatively related. The finding that ${\mathcal{R}}_0$ can be increased by population heterogeneity in various factors is also supported by the fact pointed out by Tilman and Kareiva [20] that ${\mathcal{R}}_0$ is higher in situations with significant spatial or heterogeneity features.

The final size relation derived in this paper from a meta-population model, which considers n sub-populations, multiple types of heterogeneity, and a general mixing function including preferential mixing, provides a useful evaluation tool for intervention strategies. It also raised the warning issue that, although in many models control measures can be evaluated using the effective reproduction number ${\mathcal{R}}_e$, it should not be the only quantity to consider, especially if a programme reduces ${\mathcal{R}}_e$ but increases $\mathcal{F}$.

Acknowledgements

We thank John Glasser for reading the manuscript and providing many constructive suggestions that improved the presentation of this paper. We thank also the Reviewer for helpful comments.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported partially by the BUCEA Post Graduate Innovation Projects (PG2018094 and PG2018097).