Equilibrium Distributions of Populations of Biological Species on Networks of Social Sites

ABSTRACT

We investigate the problem of how a population of biological species would distribute over a given network of social sites so that their social contacts through the connected sites can be maximized (or minimized). This problem has applications in modelling the behaviours of social (or solitary) species such as the development of social groups in human society and the spread of solitary animals in distant habitats. We show that this problem can be formulated as an evolutionary game, with the equilibrium state of the game corresponding to a strategy for choosing the residing sites, each with a certain probability, or equivalently, to a distribution of the population on these sites. The game has a symmetric payoff matrix, and can therefore be analyzed via the solution of a corresponding quadratic programme: An equilibrium strategy of the game is a KKT point of the quadratic programme, which may be a local maximizer, local minimizer, or saddle point, but it is evolutionarily stable if and only if it is a strict local maximizer. In general, with a goal to maximize the social contacts, the species tend to spread on network sites where there are dense connections such as a complete subnetwork or in other words, a network clique. We show that at equilibrium, the population may or may not distribute on a network clique, but the stability of the equilibrium state does depend on the structure of the selected subnetwork. In particular, we show that the distribution of the population on a maximal network clique is evolutionarily stable unless the clique is ‘attached’ to another clique of the same or larger size, when the population may be able to switch or expand to the neighbouring clique to increase or at least maintain its total amount of contacts. However, the distribution of the population on a non-clique subnetwork is always evolutionarily unstable or weakly evolutionarily stable at the very best, for the population can always move away from its current distribution without decreasing its total amount of contacts. We conclude that the strategies to spread on maximal network cliques are not only equilibrium strategies but also evolutionarily more stable than those on non-clique subnetworks, thus theoretically reaffirming the evolutionary advantages of joining social cliques in social networks for social species.

KEYWORDS:

• Population dynamics
• evolutionary games
• Nash equilibrium
• evolutionary stability
• social networks
• network cliques
• quadratic programming
• necessary and sufficient conditions for constrained optimization

1. Introduction

The social activities of a population can be described by a social network, with the nodes representing the social sites and the links the social channels. The population is distributed over the social sites. The individuals at different social sites may be different species, different cultural groups, different races, or different countries. They make social contacts through the social channels. The types of social contacts may include mating, making friends, communication, sharing knowledge, sharing religious beliefs, or trading. The results from socializing over a social network may include improvement of social connections, increase of genetic and cultural diversities, development of group protection, raise of economic welfare, or spread of rumours or diseases as well [10,17,25,32].

We investigate the problem of how a population of biological species would distribute over a given network of social sites so that their social contacts through the connected sites can be maximized (or minimized). Formally, by a social site i we mean a location where an individual may stay or visit with certain probability or frequency $x_i$; if there is a social link between two social sites, we say the individuals at the two sites can make a social contact; and by the social connection between two individuals at site i and site j with probability $x_i$ and $y_j$, respectively, we mean the average social contact that can be made by the two, i.e. $x_i{A}_{i,j}{y}_j$, where $A_{i,j}=1$ if there is a social link between site i and site j and $A_{i,j}=0$ otherwise.

Let $x=(x_1,\dots ,x_n{)}^T$ be the strategy vector of an individual in the population, with $x_i$ being the probability of staying at social site i, and $y=(y_1,\dots ,y_n{)}^T$ be the distribution of the population, with $y_j$ being the population fraction on social site j, where n is the total number of social sites. Then, the average social contact of the individual of strategy x in the population with y distribution would be $\sum _{i,j}{x}_i{A}_{i,j}{y}_j=x^{T}Ay$, where $A=\left\{A_{i,j}\right\}$. Note that the distribution y of the population depends on the strategy x of every individual in the population or in other words, how the population would spread on the social sites depends on how every individual in the population decides to visit or stay on the social sites.

Let $G=(V,E)$ be a network, where V is a set of nodes representing the social sites, $V=\{1,\dots ,n\}$, and E a set of edges representing the social links between social sites, $E=$ $\{$$(i,j)$: if there is a social link between site i and site j$\}$. Then, A is just the adjacency matrix of network G, and the problem of how a population of biological species may distribute on a given network of social sites to increase their social connections can be modelled as an evolutionary game, where each individual chooses a strategy x against a population of distribution y on a network G so that the social contact $x^{T}Ay$ of the individual can be maximized.

The choice of strategy x by the individual depends on the distribution y of the population, which is in turn the result of the strategies chosen by all the individuals. Therefore, once a decision is made on x, y may be changed due to a change in x, and x needs to be further updated, and so on and so forth. An equilibrium state will eventually be reached in the end, when an ‘optimal’ strategy $x^{\ast }$ is found for the population of distribution $x^{\ast }$, i.e. (1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) where $S=\{x\in R^n:\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\}$. Indeed, in such a state, $x^{\ast }$ is ‘optimal’ for all the individuals and will not change, and thus, the distribution of the population will also remain to be $x^{\ast }$, and the population reaches an equilibrium. 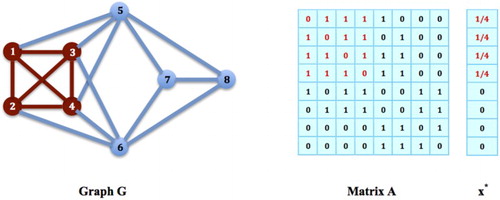We call this game a social networking game and $x^{\ast }$ an equilibrium strategy (for individual species) or an equilibrium distribution (of the population), interchangably. (See Figure 1 for an example.)

Figure 1. Social Networking Game: Given a network of social sites G and its adjacency matrix A as shown in the figure, $x^{\ast }=(1/4,1/4,1/4,1/4,0,0,0,0{)}^T$ is an equilibrium state of the social networking game on G, meaning that $x^{\ast }$ is an equilibrium distribution of the population on G and also an equilibrium strategy for every individual species such that the social contact of each species achieves its maximum $x^{\ast T}A{x}^{\ast }=3/4$.

A social networking game happens in real world. For example, college students want to join or visit social clubs on campus. Assume that some clubs hold events regularly with others so their members can meet. Assume also that the students want to meet people from different clubs as many as possible to increase their social connections. Then, how the students would spread in the clubs can be modelled exactly as a social networking game, with the equilibrium state of the game as a prediction for the distribution of student population in the clubs. Such information for the possible distribution of a population in a given set of socially connected places can be very valuable not only for social studies, but also for other purposes such as placing advertisements for commercial uses, organizing meetings for political campaign, or tracing the spread of certain virus infections, etc. [8,13,14,16].

Contrary to maximizing social contacts, there are also solitary or territorial species in nature who tend to find places where contacts among them may be minimized instead [1]. For example, solitary animals tend to avoid each other when choosing their habitats. Territorial animals may fight fiercely to keep each other away from certain contact distances. However, for such species, their distribution over a set of spatially related habitats may be modelled as an evolutionary game and in particular, a social networking game as well: Let G be the network of habitat sites with the links between two sites referring to certain degree of social or spatial proximity between them. Let B be the adjacency matrix of G. Then, the goal to find a set of sites in G to visit or stay for a solitary or territorial species can be considered as to find an inhabiting strategy $x^{\ast }$ such that the social contact of the species with others can be minimized given population distribution $x^{\ast }$, i.e. $x^{\ast T}B{x}^{\ast }\le x^{T}B{x}^{\ast }$ for all $x\in S$. We name this problem a solitary inhabiting game. Note that to discourage contacts in the same site, we set all the diagonal elements $B_{i,i}=1$ so that the chance for two individuals to bump into each other in the same site can be minimized. Let $A=e{e}^T-B$, where e is a vector of all 1's. It is easy to verify that $x^{\ast T}B{x}^{\ast }\le x^{T}B{x}^{\ast }$ if and only if $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast }$, where A is just the adjacency matrix of the network complementary to G. Thus, the solitary inhabiting game on network G can actually be reduced to a social networking game on the network complementary to G. (See Figure 2 for an example.)

Figure 2. Solitary Inhabiting Game: Given a network of social sites G and its adjacency matrix B with its diagonal elements all set to 1 as shown in the figure, the solitary inhabiting game on G is equivalent to the social networking game on the network complementary to G, which is the same network in Figure 1. Therefore, the equilibrium state of the social networking game in Figure 1, $x^{\ast }=(1/4,1/4,1/4,1/4,0,0,0,0{)}^T$, is also an equilibrium state of the solitary inhabiting game on G in the above figure, meaning that $x^{\ast }$ is an equilibrium distribution of the population on G and also an equilibrium strategy for every individual species in the population such that the social contact of each species achieves its minimum $x^{\ast T}B{x}^{\ast }=1/4$.

We call an evolutionary game symmetric if the payoff matrix A for the game is symmetric. In literature, such a game is also called a double symmetric game since an evolutionary game itself is considered as a symmetric game in the sense that the payoff for player 1 against player 2 is calculated in the same way as player 2 against player 1 [11,33]. Note that the vector function $\pi \left(x\right)=Ax$ for a symmetric evolutionary game is a gradient field. There is a potential function $f\left(x\right)=x^{T}Ax/2$ such that $\mathrm{\nabla }f\left(x\right)=\pi \left(x\right)$. Therefore, a symmetric evolutionary game is also called a potential game, and a corresponding quadratic programming problem, called potential maximization problem, can be defined: $\mathbf{m}\mathbf{a}\mathbf{x}\{x^{T}Ax/2:x\in S\}$ [24]. Consider the social networking game. Since its payoff matrix A is symmetric, the game is a symmetric evolutionary game. We can therefore define a corresponding potential maximization problem: (2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) Since $x^{T}Ax/2$ is half of the social contact an individual of strategy x can make in the population of distribution x, we call the above problem more specifically a contact maximization problem.

It is well known that an equilibrium strategy for a symmetric evolutionary game is a KKT point of the corresponding potential maximization problem, which can be a local maximizer, local minimizer, or saddle point. An equilibrium strategy is evolutionarily stable if and only if it is a strict local maximizer [11,24,33]. Based on this theory, the equilibrium conditions and stabilities of the social networking game can be analyzed via the solution of the corresponding contact maximization problem as shown in [3,12].

Games similar to the one in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ) have been investigated in the past. Vickers and Cannings [27,28,5] studied this class of games for possible numbers of evolutionary stable strategies of evolutionary games. They defined the payoff matrix A such that $A_{i,j}=1$ if there is a link between node i and node j of the corresponding graph G, $A_{i,j}=-1$ if there is no link between node i and node j, and $A_{i,j}=0$ if i=j. As such, the evolutionary stable strategies of the game correspond exactly to the strategies on the maximal cliques of the graph, and thereby, the number of evolutionary stable strategies can be estimated by enumerating all possible numbers of maximal cliques of the graph [27,28,5].

Motzkin and Straus [18] studied exactly the same quadratic programming problem as given in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ). They showed that the global maximum of the problem can be achieved on a solution whose nonzero components are distributed on a maximum clique of the corresponding graph [18]. Pardalos et al. [21] and Bomze [2] later developed algorithms for computing the maximum cliques of a given graph by solving a problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ) globally [2,21]. In particular, Bomze [2] defined the matrix A to be the adjacency matrix of the graph with the diagonal elements of the matrix set to 1/2. He connected the problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ) to a game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ), and showed again that a strategy for the game is evolutionarily stable if and only if it is distributed on a maximal clique of the graph [2].

In this paper, we consider the game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ) with the payoff matrix being exactly the adjacency matrix of the corresponding network, and the diagonal elements of the matrix all set to zero. This can be the case when the contacts in between different sites are encouraged ($A_{i,i}=0$) for the social networking game. It can also be the case when the contacts in the same site is prohibited ($B_{i,i}=1$ and hence $A_{i,i}=0$) for the solitary inhabiting game. For such a game, the strategies on maximal network cliques are not necessarily evolutionarily stable any more, although they are still equilibrium strategies. It is then challenging but interesting to find what network structures the equilibrium strategies may have besides maximal network cliques and under what conditions they may be evolutionarily stable or unstable.

In this paper, based on the relationship between the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ) and the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), we show that an equilibrium distribution for the social networking game may indeed be over a non-clique subnetwork as well as a maximal network clique. Its stability condition, however, can be very different, depending on the structure of the selected subnetwork. We show that the distribution on a maximal network clique usually is evolutionarily stable unless the clique is ‘attached’ to another clique of the same or larger size, when the population may be able to switch or expand to the neighbouring clique to increase or at least maintain its total amount of contacts. On the other hand, the distribution on a non-clique subnetwork is always evolutionarily unstable or weakly evolutionarily stable at the very best, as it does not correspond to a strict local maximizer of the contact maximization problem, and may change without decreasing its total amount of contacts. In this sense, the strategies to spread on maximal network cliques are not only equilibrium but also evolutionarily more stable than those on non-clique subnetworks, and should therefore have greater evolutionary advantages.

More specifically, in Section 2, we describe the relationships between the social networking game and the contact maximization problem, and derive the conditions for equilibrium strategies and their stabilities. In Section 3, we show that strategies choosing maximal network cliques are always equilibrium strategies, while there are equilibrium strategies taking non-clique subnetworks. In Section 4, we discuss the stabilities of strategies on maximal network cliques. We show that such a strategy is evolutionarily stable if and only if there is no clique of the same or larger size ‘attaching’ to its clique. In particular, we show that it is a local contact maximizer and hence is at least weakly evolutionarily stable if and only if there is no neighbouring clique of larger size. In Section 5, we discuss the strategy corresponding to a global maximizer of the contact maximization problem. We show that such a strategy must be on a maximum network clique or a non-clique subnetwork that contains the maximum clique. We prove that the problem to find such a strategy is equivalent to the maximum clique problem and is therefore NP-hard. In Section 6, we discuss the stabilities of strategies on non-clique subnetworks. We show that they are evolutionarily unstable in general and may be weakly evolutionarily stable at the very best. We conclude the paper with a brief summary and several general remarks in Section 7.

2. Equilibrium conditions and stabilities

In this section, we provide a more detailed account on the relationships between the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ) and the corresponding contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), with which a general set of conditions for the equilibrium strategies of the social networking game and their stabilities can be derived. These results come directly from the fact that the social networking game is a symmetric evolutionary game, and its equilibrium strategies can thus be obtained and analyzed via the solution of a corresponding quadratic programming problem [3,12].

2.1. Equilibrium conditions

It is well known, for an evolutionary game, that a strategy $x^{\ast }\in S$ is an equilibrium strategy if and only if it satisfies a set of complementarity conditions: $x^{\ast T}A{x}^{\ast }=(A{x}^{\ast }{)}_i$ for all i such that $x_i^{\ast }>0$ and $x^{\ast T}A{x}^{\ast }\ge (A{x}^{\ast }{)}_i$ for all i such that $x_i^{\ast }=0$ [11,33]. These conditions also apply to any symmetric evolutionary game including the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ), and can be given more specifically in the following form.

Theorem 2.1

A strategy $x^{\ast }\in S$ is an equilibrium strategy for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ) if and only if there is a scalar ${\lambda }^{\ast }$ such that (3) $x_i^{\ast }\ge 0,{\lambda }^{\ast }-(A{x}^{\ast }{)}_i\ge 0$(3) (4) $x_i^{\ast }({\lambda }^{\ast }-(A{x}^{\ast }{)}_i)=0,i=1,\dots ,n.$(4)

The proof for the theorem is straightforward and can be found in any standard textbook on evolutionary games. Since it is helpful for the understanding of the game, we still provide a proof here for the self-containedness of our paper:

Proof.

If $x^{\ast }\in S$ satisfies the conditions in (3(3) $x_i^{\ast }\ge 0,{\lambda }^{\ast }-(A{x}^{\ast }{)}_i\ge 0$(3) ) and (4(4) $x_i^{\ast }({\lambda }^{\ast }-(A{x}^{\ast }{)}_i)=0,i=1,\dots ,n.$(4) ), by adding all equations in (4(4) $x_i^{\ast }({\lambda }^{\ast }-(A{x}^{\ast }{)}_i)=0,i=1,\dots ,n.$(4) ), we then obtain ${\lambda }^{\ast }=x^{\ast T}A{x}^{\ast }$. Let $x\in S$ be an arbitrary strategy. Multiply the second inequality in (3(3) $x_i^{\ast }\ge 0,{\lambda }^{\ast }-(A{x}^{\ast }{)}_i\ge 0$(3) ) by $x_i$. Then, by adding all second inequalities in (3(3) $x_i^{\ast }\ge 0,{\lambda }^{\ast }-(A{x}^{\ast }{)}_i\ge 0$(3) ), we obtain ${\lambda }^{\ast }-x^{T}A{x}^{\ast }\ge 0$, i.e. $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast }$, since ${\lambda }^{\ast }=x^{\ast T}A{x}^{\ast }$. Therefore, $x^{\ast }$ is an equilibrium strategy for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ).

If $x^{\ast }\in S$ is an equilibrium strategy for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ), then $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast }$ for any $x\in S$ and therefore, $x^{\ast T}A{x}^{\ast }\ge e_i^{T}A{x}^{\ast }=(A{x}^{\ast }{)}_i$ for all i. Let ${\lambda }^{\ast }=x^{\ast T}A{x}^{\ast }$. Then, ${\lambda }^{\ast }-(A{x}^{\ast }{)}_i\ge 0$ for all i. Assume that $x_i^{\ast }({\lambda }^{\ast }-(A{x}^{\ast }{)}_i)>0$ for some i. By adding all the left-hand sides of the equations in (4(4) $x_i^{\ast }({\lambda }^{\ast }-(A{x}^{\ast }{)}_i)=0,i=1,\dots ,n.$(4) ), we then obtain ${\lambda }^{\ast }>x^{\ast T}A{x}^{\ast }$, which contradicts to the fact that ${\lambda }^{\ast }=x^{\ast T}A{x}^{\ast }$. Therefore, $x_i^{\ast }({\lambda }^{\ast }-(A{x}^{\ast }{)}_i)=0$ for all i.

As we have introduced in Section 1, the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ) corresponds to a contact maximization problem as given in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ). The latter is a quadratic programming problem or in other words, a constrained optimization problem. Based on the theory for constrained optimization [7,19], an optimal solution (or more accurately, a local optimal solution) to the contact maximization problem must satisfy a set of necessary conditions as can be stated in the following.

Theorem 2.2

If $x^{\ast }\in S$ is an optimal solution to the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), then there must be a scalar ${\lambda }^{\ast }$ such that (5) $x_i^{\ast }\ge 0,{\lambda }^{\ast }-(A{x}^{\ast }{)}_i\ge 0,$(5) (6) $x_i^{\ast }({\lambda }^{\ast }-(A{x}^{\ast }{)}_i)=0,i=1,\dots ,n.$(6)

Proof.

Note that the Lagrangian function for the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ) can be written in the following form: $L(x,\lambda ,\mu )=-x^{T}Ax/2-\lambda (1-\sum _i{x}_i)-{\mu }^{T}x.$ where $x\in R^n,\lambda \in R,\mu \in R^n$. Then, by the first-order necessary conditions for constrained optimization [7,19], if $x^{\ast }\in R^n$ is an optimal solution for the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), there must be a scalar ${\lambda }^{\ast }\in R$ and a vector ${\mu }^{\ast }\in R^n$ such that $\begin{array}{rl}{\mathrm{\nabla }}_{x}L(x^{\ast },{\lambda }^{\ast },{\mu }^{\ast })=-A{x}^{\ast }+{\lambda }^{\ast }e-{\mu }^{\ast }& =0,\\ \sum _i{x}_i^{\ast }& =1,\\ x^{\ast }& \ge 0,\\ {\mu }^{\ast }& \ge 0,\\ x^{\ast T}{\mu }^{\ast }& =0.\end{array}$ By substituting ${\mu }^{\ast }={\lambda }^{\ast }e-A{x}^{\ast }$ in all the formulas, we then have $x^{\ast }\in S$ satisfying $\begin{array}{rl}& x^{\ast }\ge 0,{\lambda }^{\ast }e-A{x}^{\ast }\ge 0,\\ & x^{\ast T}({\lambda }^{\ast }e-A{x}^{\ast })=0,\end{array}$ which are equivalent to the conditions in (5(5) $x_i^{\ast }\ge 0,{\lambda }^{\ast }-(A{x}^{\ast }{)}_i\ge 0,$(5) ) and (6(6) $x_i^{\ast }({\lambda }^{\ast }-(A{x}^{\ast }{)}_i)=0,i=1,\dots ,n.$(6) ).

Note that the conditions in (3(3) $x_i^{\ast }\ge 0,{\lambda }^{\ast }-(A{x}^{\ast }{)}_i\ge 0$(3) ) and (4(4) $x_i^{\ast }({\lambda }^{\ast }-(A{x}^{\ast }{)}_i)=0,i=1,\dots ,n.$(4) ) are the same as those in (5(5) $x_i^{\ast }\ge 0,{\lambda }^{\ast }-(A{x}^{\ast }{)}_i\ge 0,$(5) ) and (6(6) $x_i^{\ast }({\lambda }^{\ast }-(A{x}^{\ast }{)}_i)=0,i=1,\dots ,n.$(6) ). However, it does not imply that the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ) is equivalent to the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), because they are necessary and sufficient for a strategy to be at equilibrium for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ) but only necessary for a solution to be optimal for the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ). We give a clear distinction between the two problems in the following corollary.

Corollary 2.3

An optimal solution $x^{\ast }\in S$ for the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ) must be an equilibrium strategy for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ), while an equilibrium strategy $x^{\ast }\in S$ for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ) is only a KKT point for the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), which is necessary but not sufficient for $x^{\ast }\in S$ to be optimal for the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ).

2.2. Stability conditions

An important concept in evolutionary game theory is the evolutionary stability of an equilibrium strategy or equivalently, equilibrium distribution of the population. It characterizes the ability of a population to resist small changes or invasions when at equilibrium. Consider a general evolutionary game defined by a payoff matrix A. Let $x^{\ast }\in S$ be an equilibrium distribution of the population. Let $x\in S$ be another ‘invading’ distribution. Mix $x^{\ast }$ and $x\ne x^{\ast }$ so that the population changes to distribution, $ϵx+(1-ϵ)x^{\ast }$, for some small fraction $ϵ>0$. Then, $x^{\ast }$ is said to be evolutionarily stable if it remains as a better response to the ‘invaded” population than x. More accurately, we have the following definition.

Definition 2.4

[11,33]

An equilibrium strategy $x^{\ast }\in S$ for an evolutionary game is evolutionarily stable if there is a small number ${ϵ}^{\prime }\in (0,1)$ such that for any $x\in S,x\ne x^{\ast }$, (7) $x^{\ast T}A(ϵx+(1-ϵ\left)x^{\ast }\right)>x^{T}A(ϵx+(1-ϵ\left)x^{\ast }\right)\mathrm{for}\mathrm{all}ϵ\in (0,{ϵ}^{\prime }).$(7)

Usually, it is not easy to prove the evolutionary stability of an equilibrium strategy if just based on its definition. A more straightforward condition is to consider the strategy y in a small neighbourhood U of the equilibrium strategy $x^{\ast }$ and check if no $y\ne x^{\ast }$ prevails $x^{\ast }$ such that $y^{T}Ay\ge x^{\ast T}Ay$. It turns out that this condition is necessary and also sufficient:

Theorem 2.5

[11,33]

An equilibrium strategy $x^{\ast }\in S$ for an evolutionary game is evolutionarily stable if and only if there is a small neighbourhood U of $x^{\ast }$ such that (8) $y^{T}Ay<x^{\ast T}Ay\mathrm{for}\mathrm{all}y\in U\cap S,y\ne x^{\ast }.$(8)

Note that a social networking game is an evolutionary game. Therefore, the condition in (8(8) $y^{T}Ay<x^{\ast T}Ay\mathrm{for}\mathrm{all}y\in U\cap S,y\ne x^{\ast }.$(8) ) also holds for any of its evolutionarily stable strategies $x^{\ast }$. For a social networking game, $x^{\ast T}Ay=y^{T}A{x}^{\ast }$ since A is symmetric. Then, $y^{T}Ay<y^{T}A{x}^{\ast }$ for all $y\in U\cap S$, $y\ne x^{\ast }$. It follows that $y^{T}Ay<x^{\ast T}A{x}^{\ast }$ for all $y\in U\cap S$, $y\ne x^{\ast }$ since $y^{T}A{x}^{\ast }\le x^{\ast T}A{x}^{\ast }$ for all $y\in S$. This implies that if $x^{\ast }$ is an evolutionarily stable strategy for a social networking game, it must be a strict local maximizer of the corresponding contact maximization problem. It turns out that the converse is also true:

Theorem 2.6

An equilibrium strategy $x^{\ast }\in S$ for a social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ) is evolutionarily stable if and only if it is a strict local maximizer of the corresponding contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ).

The above theorem is actually true for any symmetric evolutionary game and its corresponding potential maximization problem, for which a proof can be found in standard textbooks [11,24,33]. Based on this theorem, we can check the stability of an equilibrium strategy for the social networking game more directly from the strictness of the strategy as a local maximizer of the corresponding contact maximization problem. While it is not necessarily a simple matter to see if a local maximizer is strict or not, we provide a set of necessary or sufficient conditions for the strictness of a local maximizer from general optimization theory, which we may need to justify some of our results in later sections.

Theorem 2.7

[3,12]

If $x^{\ast }\in S$ is a local maximizer of the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), then $Z^{T}AZ$ must be negative semidefinite, where Z is the null space matrix of the Jacobian of the active constraints of the contact maximization problem at $x^{\ast }$.

Theorem 2.8

[3,12]

If $x^{\ast }\in S$ is a KKT point of the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ) and $Z^{T}AZ$ is negative definite, where Z is the null space matrix of the Jacobian of the constraints of the contact maximization problem strongly active at $x^{\ast }$, then $x^{\ast }\in S$ must be a strict local maximizer of the contact maximization problem.

3. Equilibrium distributions on network cliques

As we have mentioned in Section 1, with a goal of maximizing the social contact, the population on a network of social sites tends to spread on sites with the most possible connections among them. Such a set of sites corresponds to a subnetwork with a dense set of edges among its nodes. The best one would be a complete subnetwork, i.e. a network clique. However, the population on a network clique is not always an equilibrium distribution. Even when it is, it may not necessarily be evolutionarily stable.

3.1. Is the population on a network clique an equilibrium distribution?

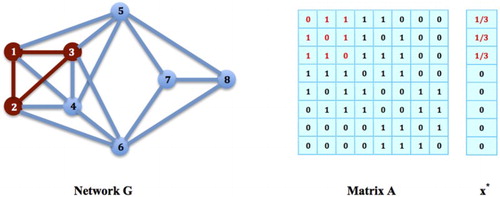
The answer is NOT ALWAYS. See for example the game on network G in Figure 3. Notice that the nodes $\{1,2,3\}$ form a network clique. If it is an equilibrium strategy, the values for $x_1^{\ast }$, $x_2^{\ast }$, and $x_3^{\ast }$ should be the same, i.e. $x_1^{\ast }=x_2^{\ast }=x_3^{\ast }=1/3$, and $x_i^{\ast }=0$ for all $i=4,\dots ,8$. Then, $x^{\ast T}A{x}^{\ast }=(A{x}^{\ast }{)}_i=2/3$ for all i such that $x_i^{\ast }>0$, i.e. i=1, 2, 3. However, $x^{\ast T}A{x}^{\ast }\ge (A{x}^{\ast }{)}_i$ does not hold for all i such that $x_i^{\ast }=0$, i.e. $i=4,\dots ,8$, since $x^{\ast T}A{x}^{\ast }=2/3<(A{x}^{\ast }{)}_4=1$. By Theorem 2.1, $x^{\ast }$ cannot be an equilibrium strategy for the game. In general, let $C=(V_C,E_C)$ be a clique of network $G=(V,E)$, $V_C\subseteq V$ and $E_C=\left\{\right(i,j):i,j\in V_C\}$. We then have the following proposition.

Figure 3. Populations on Cliques: In network G, the nodes $\{1,2,3\}$ form a network clique. Let $x^{\ast }$ be a strategy for choosing this clique, $x_1^{\ast }=x_2^{\ast }=x_3^{\ast }=1/3$ and $x_i^{\ast }=0$ for all $i=4,\dots ,8$. Then, $x^{\ast T}A{x}^{\ast }=(A{x}^{\ast }{)}_i=2/3$ for all i such that $x_i^{\ast }>0$, i.e. $i=1,2,3$. However, $x^{\ast T}A{x}^{\ast }\ge (A{x}^{\ast }{)}_i$ does not hold for all i such that $x_i^{\ast }=0$, i.e. $i=4,\dots ,8$, since $x^{\ast T}A{x}^{\ast }=2/3<(A{x}^{\ast }{)}_4=1$. By Theorem 2.1, $x^{\ast }$ cannot be an equilibrium strategy for the game on G.

Proposition 3.1

Let $x^{\ast }\in S$ be a strategy on a clique C of network G. Then, $x^{\ast }$ cannot be an equilibrium strategy of the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ) if C is contained in a larger clique of G.

Proof.

If $x^{\ast }$ is an equilibrium strategy for the game, then the population must be distributed evenly over C, with $x_i^{\ast }=1/k$ for all $i\in V_C$ and $x_i^{\ast }=0$ for all $i\notin V_C$, where $k=|V_C|$. Since $A_{i,j}=1$ for all $i\ne j\in V_C$ and $A_{i,i}=0$ for all $i\in V_C$, $x^{\ast T}A{x}^{\ast }=\sum _{i,j\in V_C}{x}_i^{\ast }{A}_{i,j}{x}_j^{\ast }=(k-1)/k$. If C is contained in a larger clique of G, there must be a node $l\in V\mathrm{\setminus }{V}_C$ such that $(l,j)\in E$ for all $j\in V_C$. Then,$A_{l,j}=1$ for all $j\in V_C$, and $(A{x}^{\ast }{)}_l=\sum _{j\in V_C}{A}_{l,j}{x}_j^{\ast }=1>x^{\ast T}A{x}^{\ast }$. This would be contradictory to the fact that $(A{x}^{\ast }{)}_i\le x^{\ast T}A{x}^{\ast }$ for all $i\in V$, as implied by Theorem 2.1. Therefore, $x^{\ast }$ cannot be an equilibrium strategy for the game.

The above proposition can also be justified more intuitively as the following: If a clique C is contained in a larger clique of G, we can always find a node, say l, in the larger clique but not in C, and have a strategy x on this node, $x=e_l$, such that $x^{T}A{x}^{\ast }>x^{\ast T}A{x}^{\ast }$, i.e. strategy x to occupy only node l prevails strategy $x^{\ast }$ to occupy all the nodes in C, given the population distributed as $x^{\ast }$ over C. Then, $x^{\ast }$ is not an equilibrium. Moreover, clique C and node l in fact form a larger clique H of size k+1, and strategy $y^{\ast }$ on H has a better payoff than strategy $x^{\ast }$ on C, because $y^{\ast T}A{y}^{\ast }=k/(k+1)$ while $x^{\ast T}A{x}^{\ast }=(k-1)/k$. Therefore, the population would certainly expand from C to H, for higher payoff, and so forth.

3.2. Is the population on a maximal network clique an equilibrium distribution?

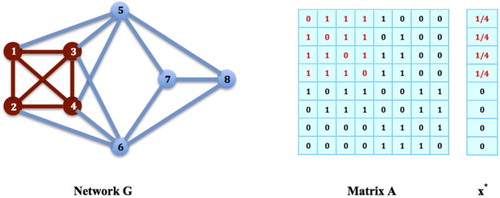
The answer is YES. See for example the game on network G again in Figure 4. The nodes $\{1,2,3,4\}$ form a maximal network clique. It is easy to verify that the strategy $x^{\ast }$ on this clique is an equilibrium: If we let $x_1^{\ast }=x_2^{\ast }=x_3^{\ast }=x_4^{\ast }=1/4$ and $x_i^{\ast }=0$ for all $i=5,\dots ,8$. Then, $x^{\ast T}A{x}^{\ast }=(A{x}^{\ast }{)}_i=3/4$ for all i such that $x_i^{\ast }>0$, i.e. $i=1,2,3,4$, and also, $x^{\ast T}A{x}^{\ast }\ge (A{x}^{\ast }{)}_i$ for all i such that $x_i^{\ast }=0$, i.e. $i=5,\dots ,8$. Then, $x^{\ast }$ satisfies all the conditions in Theorem 2.1, and it must be an equilibrium strategy for the game. In general, we have the following proposition.

Figure 4. Populations on Maximal Cliques: The nodes $\{1,2,3,4\}$ in G form a maximal clique. Let $x^{\ast }$ be a strategy on this clique, $x_1^{\ast }=x_2^{\ast }=x_3^{\ast }=x_4^{\ast }=1/4$ and $x_i^{\ast }=0$ for all $i=5,\dots ,8$. Then, $x^{\ast T}A{x}^{\ast }=(A{x}^{\ast }{)}_i=3/4$ for all i such that $x_i^{\ast }>0$, i.e. $i=1,2,3,4$, and also, $x^{\ast T}A{x}^{\ast }\ge (A{x}^{\ast }{)}_i$ for all i such that $x_i^{\ast }=0$, i.e. $i=5,\dots ,8$. Then, $x^{\ast }$ satisfies all the conditions in Theorem 2.1, and must be an equilibrium strategy for the social networking game on G.

Proposition 3.2

Let C be a clique of network G. Let $x^{\ast }\in S$ be a strategy on C, $x_i^{\ast }=1/k$ for all $i\in V_C,$ $x_i^{\ast }=0$ for all $i\in V\mathrm{\setminus }{V}_C,$ and $k=|V_C|$. If C is a maximal clique, then $x^{\ast }$ is an equilibrium strategy for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ).

Proof.

Since $A_{i,j}=1$ for all $i\ne j\in V_C$ and $A_{i,i}=0$ for all $i\in V_C$, for any $l\in V_C$, $(A{x}^{\ast }{)}_l=\sum _{j\in V_C}{A}_{l,j}{x}_j^{\ast }=(k-1)/k=x^{\ast T}A{x}^{\ast }$. If C is a maximal clique of G, for any $l\in V\mathrm{\setminus }{V}_C$, the number of edges from l to C is fewer than k. In other words, $(l,j)\notin E$ for some $j\in V_C$. Then, $A_{l,j}=0$ for some $j\in V_C$, and $(A{x}^{\ast }{)}_l=\sum _{j\in V_C}{A}_{l,j}{x}_j^{\ast }\le (k-1)/k=x^{\ast T}A{x}^{\ast }$. By Theorem 2.1, $x^{\ast }$ must be an equilibrium strategy for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ).

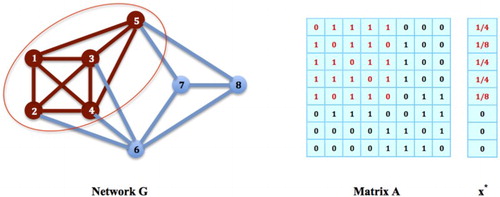
Note that an equilibrium strategy for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ) may not always be on a maximal clique of the network. For example, for the game on network G in Figure 5, the nodes $\{1,2,3,4,5\}$ do not form a network clique, but the strategy $x^{\ast }$, $x_1^{\ast }=x_3^{\ast }=x_4^{\ast }=1/4$, $x_2^{\ast }=x_5^{\ast }=1/8$, and $x_i^{\ast }=0$ for i=6, 7, 8, is in fact an equilibrium strategy: It is easy to verify that $x^{\ast T}A{x}^{\ast }=(A{x}^{\ast }{)}_i=3/4$ for all i such that $x_i^{\ast }>0$, i.e. i=1, 2, 3, 4, 5, and also, $x^{\ast T}A{x}^{\ast }\ge (A{x}^{\ast }{)}_i$ for all i such that $x_i^{\ast }=0$, i.e. i=6, 7, 8. Then, $x^{\ast }$ satisfies all the conditions in Theorem 2.1, and must be an equilibrium strategy for the game. We discuss equilibrium strategies on non-clique subnetworks in greater detail later.

Figure 5. Non-Clique Strategies: The nodes $\{1,2,3,4,5\}$ in G do not form a network clique, but the strategy $x^{\ast }$, $x_1^{\ast }=x_3^{\ast }=x_4^{\ast }=1/4$, $x_2^{\ast }=x_5^{\ast }=1/8$, and $x_i^{\ast }=0$ for $i=6,7,8$, is in fact an equilibrium strategy: It is easy to verify that $x^{\ast T}A{x}^{\ast }=(A{x}^{\ast }{)}_i=3/4$ for all i such that $x_i^{\ast }>0$, i.e. i=1,2,3,4,5, and also, $x^{\ast T}A{x}^{\ast }\ge (A{x}^{\ast }{)}_i$ for all i such that $x_i^{\ast }=0$, i.e. i=6,7,8. Then, $x^{\ast }$ satisfies all the conditions in Theorem 2.1, and must be an equilibrium strategy for the social networking game on G.

4. Stabilities of equilibrium distributions

When reaching equilibrium, whether on a network clique or not, the population may or may not be able to maintain its equilibrium state. It would be if it is evolutionarily stable. As stated in Section 2.2, an equilibrium strategy of the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ) is a KKT point of the corresponding contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), which may be a local minimizer, local maximizer, or saddle point. It is evolutionarily stable if and only if it is a strict local maximizer. We now examine the evolutionary stability of the equilibrium strategies on network cliques in this section and those on non-clique subnetworks in later sections.

4.1. Is the population on a maximal network clique a contact maximizer?

By Theorem 2.6, an equilibrium strategy for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ), with the population distributed on a maximal network clique, is evolutionarily stable if and only if it is a strict local maximizer of the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(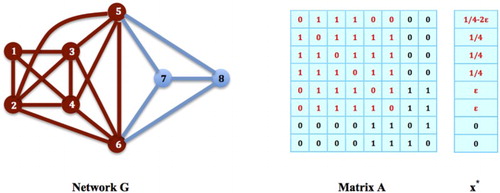2) ). Unfortunately, in some circumstances, such an equilibrium strategy may not even be a local maximizer of the contact maximization problem. For example, for the game on network G in Figure 6, the nodes $\{1,2,3,4\}$ form a maximal clique of G. The population on this clique is an equilibrium distribution, but it is not a local maximizer of the corresponding contact maximization problem: Let $x^{\ast }$ represent the equilibrium distribution on this clique, $x_i^{\ast }=1/4$ for all $i=1,\dots ,4$ and $x_i^{\ast }=0$ for all $i=5,\dots ,8$. Construct a new distribution $x=x^{\ast }+p$, where $p=(-2ϵ,0,0,0,ϵ,ϵ,0,0{)}^T$ for a small $ϵ>0$. Then, it is easy to verify that $x_i\ge 0$ for all $i=1,\dots ,8$, $\sum _i{x}_i=1$, and $x^{T}Ax=x^{\ast T}A{x}^{\ast }+p^{T}Ap=x^{\ast T}A{x}^{\ast }+2{ϵ}^2>x^{\ast T}A{x}^{\ast },$ for all small $ϵ>0$. As ε goes to zero, x is arbitrarily close to $x^{\ast }$, yet $x^{T}Ax>x^{\ast }A{x}^{\ast }$. Therefore, $x^{\ast }$ cannot be a local maximizer for the contact maximization problem. Notice in this example that in G, there is a bigger clique, $\{2,3,4,5,6\}$, attaching to 3 nodes of the clique $\{1,2,3,4\}$, which is in fact a critical factor for why the distribution on the latter clique cannot be a local maximizer for the contact maximization problem. In general we have the following proposition.

Figure 6. Populations on Maximal Cliques vs. Local Contact Maximizers: The nodes $\{1,2,3,4\}$ in G form a maximal network clique. It is an equilibrium strategy for the social networking game on G, but not a local maximizer of the corresponding contact maximization problem: Let $x^{\ast }$ be the equilibrium distribution on this clique, $x_i^{\ast }=1/4$ for all $i=1,\dots ,4$ and $x_i^{\ast }=0$ for all $i=5,\dots ,8$. Construct a new distribution $x=x^{\ast }+p$, where $p=(-2ϵ,0,0,0,ϵ,ϵ,0,0{)}^T$ for a small $ϵ>0$. Then, it is easy to verify that $x_i\ge 0$ for all $i=1,\dots ,8$, $\sum _i{x}_i=1$, and $x^{T}Ax=x^{\ast T}A{x}^{\ast }+2{ϵ}^2>x^{\ast T}A{x}^{\ast }$ for all small $ϵ>0$. As ε goes to zero, x is arbitrarily close to $x^{\ast }$, yet $x^{T}Ax>x^{\ast }A{x}^{\ast }$. Therefore, $x^{\ast }$ cannot be a local maximizer for the corresponding contact maximization problem.

Proposition 4.1

Let C be a maximal clique of network G. Let $x^{\ast }\in S$ be an equilibrium strategy on C for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ), $x_i^{\ast }=1/k$ for all $i\in V_C,$ $x_i^{\ast }=0$ for all $i\in V\mathrm{\setminus }{V}_C$, and $k=|V_C|$. Then, $x^{\ast }$ is a local maximizer for the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), only if there is no any larger clique attaching to k−1 nodes of C.

Proof.

Assume that $x^{\ast }$ is a local maximizer for the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), but there is a larger clique H attaching to k−1 nodes of C. Assume without loss of generality that H is of size k+1. Then, there must be two nodes $i,j\in V_H\mathrm{\setminus }{V}_C$ each connected with the same set of k−1 nodes of C, and both are also connected to each other, i.e. $(i,j)\in E_H$. Let l be the node in C not connected with node i and j. Define a vector $p\in R^n$, with $p_l=-2ϵ$, $p_i=p_j=ϵ$, and $p_r=0$ for all $r\ne i,j,l$, where $0\le ϵ\le 1/2k$. Then, $x=x^{\ast }+p$ satisfies all the constraints for the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ). Note that $(A{x}^{\ast }{)}_l=(A{x}^{\ast }{)}_i=(A{x}^{\ast }{)}_j=(k-1)/k$. Therefore, $p^{T}A{x}^{\ast }=0$. It follows that $x^{T}Ax=x^{\ast T}A{x}^{\ast }+p^{T}Ap=x^{\ast T}A{x}^{\ast }+2{ϵ}^2>x^{\ast T}A{x}^{\ast }$ for all $ϵ>0$. Then, $x^{\ast }$ cannot be a local maximizer of the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ).

In fact, the above condition of not having a larger attached clique is also sufficient for the strategy on a maximal clique for the social network game to be a local maximizer of the corresponding contact maximization problem. However, the proof is more mathematically involved. We provide a detailed justification in the following.

Proposition 4.2

Let C be a maximal clique of network G. Let $x^{\ast }\in S$ be a strategy on C for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ), $x_i^{\ast }=1/k$ for all $i\in V_C,$ $x_i^{\ast }=0$ for all $i\in V\mathrm{\setminus }{V}_C$, and $k=|V_C|$. Then, $x^{\ast }$ is a local maximizer for the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), if there is no any larger clique attaching to k−1 nodes of C.

Proof.

Without loss of generality, let $V_C=\{1,\dots ,k\}$. Then, $x_i^{\ast }=1/k$ for all $i=1,\dots ,k$ and $x_i^{\ast }=0$ for all i>k. We show that there is a small neighbourhood U of $x^{\ast }$ such that $x^{T}Ax\le x^{\ast T}A{x}^{\ast }$ for all x feasible in U.

Let $U=\{x\in R^n:\parallel x-x^{\ast }\parallel <r\}$ for some r>0. If $x\in U$, then $x=x^{\ast }+ϵ$ for some $ϵ\in R^n$, $\parallel ϵ\parallel <r$. Let $S=\{x\in R^n:\sum _i{x}_i=1,x_i\ge 0\}$. If $x\in S$, then $x=x^{\ast }+ϵ$ for some $ϵ\in R^n$, $\sum _i{ϵ}_i=0$, ${ϵ}_i\ge -1/k$ for all $i=1,\dots ,k$, and ${ϵ}_i\ge 0$ for all i>k.

Let $x\in U\cap S$. Define vector $x^{+}\in R^k$, ${ϵ}^{+}\in R^k$, and ${ϵ}^0\in R^{n-k}$, with $x_i^{+}=1/k,i=1,\dots ,k$. We can then write $x^{\ast }=(x^{+},0{)}^T$, $ϵ=({ϵ}^{+},{ϵ}^0{)}^T$, and $x=(x^{+}+{ϵ}^{+},{ϵ}^0{)}^T$, with ${ϵ}_i^{+}\ge -1/k$ for all $i=1,\dots ,k$, ${ϵ}_i^0\ge 0$ for all $i=1,\dots ,n-k$, $\sum _i{ϵ}_i^{+}+\sum _i{ϵ}_i^0=0$, and $\parallel ϵ\parallel <r$ for some r>0.

Let A be decomposed into four submatrices, $\{A^{(i,j)}:i,j=1,2\}$ with $A^{(1,1)}=A_{1:k,1:k}$, $A^{(1,2)}=A_{1:k,k+1:n}$, $A^{(2,1)}=A_{k+1:n,1:k}$, and $A^{(2,2)}=A_{k+1:n,k+1:n}$. Then, $\begin{array}{rl}& x^{T}Ax=x^{+T}{A}^{(1,1)}{x}^{+}+2x^{+T}{A}^{(1,1)}{ϵ}^{+}+{ϵ}^{+T}{A}^{(1,1)}{ϵ}^{+}\\ & +2x^{+T}{A}^{(1,2)}{ϵ}^0+2{ϵ}^{+T}{A}^{(1,2)}{ϵ}^0+{ϵ}^{0T}{A}^{(2,2)}{ϵ}^0.\end{array}$

Since C is a clique of G, the elements in $A^{(1,1)}$ are all equal to 1 except for those along the diagonal, and therefore, $x^{\ast T}A{x}^{\ast }=x^{+T}{A}^{(1,1)}{x}^{+}=(k-1)/k$. So, in order to prove $x^{T}Ax\le x^{\ast T}A{x}^{\ast }$, all we need to do is to show (9) $2x^{+T}{A}^{(1,1)}{ϵ}^{+}+{ϵ}^{+T}{A}^{(1,1)}{ϵ}^{+}+2x^{+T}{A}^{(1,2)}{ϵ}^0+2{ϵ}^{+T}{A}^{(1,2)}{ϵ}^0+{ϵ}^{0T}{A}^{(2,2)}{ϵ}^0\le 0.$(9) or equivalently, (10) ${ϵ}^{+T}{A}^{(1,1)}{ϵ}^{+}+2{ϵ}^{+T}{A}^{(1,2)}{ϵ}^0+{ϵ}^{0T}{A}^{(2,2)}{ϵ}^0\le -2x^{+T}{A}^{(1,1)}{ϵ}^{+}-2x^{+T}{A}^{(1,2)}{ϵ}^0.$(10)

Let $\sum _i{ϵ}_i^0=s_0$. Then, $s_0\ge 0$, and $\sum _i{ϵ}_i^{+}=-s_0$. It follows that $-2x^{+T}{A}^{(1,1)}{ϵ}^{+}=2(k-1)s_0/k$. However, since C is a maximal clique, there are at most k−1 elements equal to 1 in each of the columns of $A^{(1,2)}$. Therefore, $2x^{+T}{A}^{(1,2)}{ϵ}^0\le 2(k-1)s_0/k$. We now consider two cases of this inequality separately, one for strictly less than (<) and another for exactly equal to (=):

(i) First assume $2x^{+T}{A}^{(1,2)}{ϵ}^0<2(k-1)s_0/k$. Then, the right-hand side of inequality (10(10) ${ϵ}^{+T}{A}^{(1,1)}{ϵ}^{+}+2{ϵ}^{+T}{A}^{(1,2)}{ϵ}^0+{ϵ}^{0T}{A}^{(2,2)}{ϵ}^0\le -2x^{+T}{A}^{(1,1)}{ϵ}^{+}-2x^{+T}{A}^{(1,2)}{ϵ}^0.$(10) ) is greater than zero, and $-2x^{+T}{A}^{(1,1)}{ϵ}^{+}-2x^{+T}{A}^{(1,2)}{ϵ}^0=L{s}_0=O\left(s_0\right)=O(\parallel ϵ\parallel ),$ for some constant L>0. On the other hand, the left-hand side of inequality (10(10) ${ϵ}^{+T}{A}^{(1,1)}{ϵ}^{+}+2{ϵ}^{+T}{A}^{(1,2)}{ϵ}^0+{ϵ}^{0T}{A}^{(2,2)}{ϵ}^0\le -2x^{+T}{A}^{(1,1)}{ϵ}^{+}-2x^{+T}{A}^{(1,2)}{ϵ}^0.$(10) ) is basically an expanded form of ${ϵ}^{T}Aϵ$. Therefore, ${ϵ}^{+T}{A}^{(1,1)}{ϵ}^{+}+2{ϵ}^{+T}{A}^{(1,2)}{ϵ}^0+{ϵ}^{0T}{A}^{(2,2)}{ϵ}^0=\lambda \parallel ϵ{\parallel }^2=O(\parallel ϵ{\parallel }^2),$ where λ is a number between the largest and smallest eigenvalues of A. It follows that there must be a number r>0 such that when $\parallel ϵ\parallel \le r$, the left-hand side of (10(10) ${ϵ}^{+T}{A}^{(1,1)}{ϵ}^{+}+2{ϵ}^{+T}{A}^{(1,2)}{ϵ}^0+{ϵ}^{0T}{A}^{(2,2)}{ϵ}^0\le -2x^{+T}{A}^{(1,1)}{ϵ}^{+}-2x^{+T}{A}^{(1,2)}{ϵ}^0.$(10) ) will always be smaller than the right-hand side of (10(10) ${ϵ}^{+T}{A}^{(1,1)}{ϵ}^{+}+2{ϵ}^{+T}{A}^{(1,2)}{ϵ}^0+{ϵ}^{0T}{A}^{(2,2)}{ϵ}^0\le -2x^{+T}{A}^{(1,1)}{ϵ}^{+}-2x^{+T}{A}^{(1,2)}{ϵ}^0.$(10) ).

(ii) Now assume $2x^{+T}{A}^{(1,2)}{ϵ}^0=2(k-1)s_0/k$. Inequality (10(10) ${ϵ}^{+T}{A}^{(1,1)}{ϵ}^{+}+2{ϵ}^{+T}{A}^{(1,2)}{ϵ}^0+{ϵ}^{0T}{A}^{(2,2)}{ϵ}^0\le -2x^{+T}{A}^{(1,1)}{ϵ}^{+}-2x^{+T}{A}^{(1,2)}{ϵ}^0.$(10) ) then becomes (11) ${ϵ}^{+T}{A}^{(1,1)}{ϵ}^{+}+2{ϵ}^{+T}{A}^{(1,2)}{ϵ}^0+{ϵ}^{0T}{A}^{(2,2)}{ϵ}^0\le 0.$(11) Let ${\overline{A}}^{(1,1)}=e{e}^T-A^{(1,1)}$, where e is a vector of all 1's in $R^k$, ${\overline{A}}^{(2,2)}=f{f}^T-A^{(2,2)}$, where f is a vector of all 1's in $R^{n-k}$, and ${\overline{A}}^{(1,2)}=e{f}^T-A^{(1,2)}$. Then, inequality (11(11) ${ϵ}^{+T}{A}^{(1,1)}{ϵ}^{+}+2{ϵ}^{+T}{A}^{(1,2)}{ϵ}^0+{ϵ}^{0T}{A}^{(2,2)}{ϵ}^0\le 0.$(11) ) transforms to (12) $-{ϵ}^{+T}{\overline{A}}^{(1,1)}{ϵ}^{+}-2{ϵ}^{+T}{\overline{A}}^{(1,2)}{ϵ}^0-{ϵ}^{0T}{\overline{A}}^{(2,2)}{ϵ}^0\le 0.$(12)

Since the elements of $A^{(1,1)}$ are all 1's except for those along the diagonal, ${\overline{A}}^{(1,1)}$ is an identity matrix, and (13) $-{ϵ}^{+T}{\overline{A}}^{(1,1)}{ϵ}^{+}=-\sum _i{ϵ}_i^{+2}.$(13)

Also, since $2x^{+T}{A}^{(1,2)}{ϵ}^0=2(k-1)s_0/k$, there must be exactly k−1 elements equal to 1 in each of the columns of $A^{(1,2)}$ and hence one element equal to 1 in each of the columns of ${\overline{A}}^{(1,2)}$. Then, (14) $\begin{array}{rl}-2{ϵ}^{+T}{\overline{A}}^{(1,2)}{ϵ}^0& =-2\sum _i{ϵ}_i^{+}\left(\sum _{j\in D_i}{ϵ}_j^0\right)\le \sum _i{ϵ}_i^{+2}+\sum _i(\sum _{j\in D_i}{ϵ}_j^0{)}^2\\ & =\sum _i{ϵ}_i^{+2}+\sum _j{ϵ}_j^{02}+\sum _l\sum _{i\ne j\in D_l}{ϵ}_i^0{ϵ}_j^0,\end{array}$(14) where $D_l$ is the set of nodes in $V\mathrm{\setminus }{V}_C$ connecting to the same k−1 nodes of C except for node $l\in V_C$.

Now, since there is no any larger clique attaching to k−1 nodes of C, any two nodes $i\ne j\in V\mathrm{\setminus }{V}_C$ connecting to the same k−1 nodes in C do not have a link between them and therefore, $A_{i,j}^{(2,2)}=A_{j,i}^{(2,2)}=0$, and ${\overline{A}}_{i,j}^{(2,2)}={\overline{A}}_{j,i}^{(2,2)}=1$ for all $i\ne j\in D_l,l\in V_C$. Given the fact that all diagonal elements of ${\overline{A}}^{(2,2)}$ are 1's, (15) ${ϵ}^{0T}{\overline{A}}^{(2,2)}{ϵ}^0\ge \sum _j{ϵ}_j^{02}+\sum _l\sum _{i\ne j\in D_l}{ϵ}_i^0{ϵ}_j^0.$(15) By combining (13(13) $-{ϵ}^{+T}{\overline{A}}^{(1,1)}{ϵ}^{+}=-\sum _i{ϵ}_i^{+2}.$(13) ), (14(14) $\begin{array}{rl}-2{ϵ}^{+T}{\overline{A}}^{(1,2)}{ϵ}^0& =-2\sum _i{ϵ}_i^{+}\left(\sum _{j\in D_i}{ϵ}_j^0\right)\le \sum _i{ϵ}_i^{+2}+\sum _i(\sum _{j\in D_i}{ϵ}_j^0{)}^2\\ & =\sum _i{ϵ}_i^{+2}+\sum _j{ϵ}_j^{02}+\sum _l\sum _{i\ne j\in D_l}{ϵ}_i^0{ϵ}_j^0,\end{array}$(14) ), and (15(15) ${ϵ}^{0T}{\overline{A}}^{(2,2)}{ϵ}^0\ge \sum _j{ϵ}_j^{02}+\sum _l\sum _{i\ne j\in D_l}{ϵ}_i^0{ϵ}_j^0.$(15) ), the inequality (12(12) $-{ϵ}^{+T}{\overline{A}}^{(1,1)}{ϵ}^{+}-2{ϵ}^{+T}{\overline{A}}^{(1,2)}{ϵ}^0-{ϵ}^{0T}{\overline{A}}^{(2,2)}{ϵ}^0\le 0.$(12) ) then follows.

As a KKT point for the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), a maximal clique strategy $x^{\ast }$ for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ) may be a local minimizer, saddle point, or local maximizer [7,19]. Only when it is a strict local maximizer, it is evolutionarily stable. When it is just a local maximizer, it is only weakly evolutionarily stable in the sense that it will not be a worse response than any other strategy x in an ‘invaded’ population $ϵx+(1-ϵ)x^{\ast }$ [11,33]. Formally, we have the following definition for weak evolutionary stability:

Definition 4.3

[11,33]

An equilibrium strategy $x^{\ast }\in S$ for an evolutionary game is weakly evolutionarily stable if there is a small number ${ϵ}^{\prime }\in (0,1)$ such that for any $x\in S,x\ne x^{\ast }$, (16) $x^{\ast T}A(ϵx+(1-ϵ\left)x^{\ast }\right)\ge x^{T}A(ϵx+(1-ϵ\left)x^{\ast }\right)\mathrm{for}\mathrm{all}ϵ\in (0,{ϵ}^{\prime }).$(16)

Then, a natural question would be under what condition a maximal clique strategy for the social networking game can be a strict local maximizer of the corresponding contact maximization problem and hence be evolutionarily stable. We answer this question in the following subsection.

4.2. Is the population on a maximal network clique a strict contact maximizer?

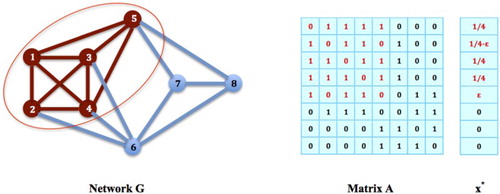
The equilibrium strategy on a maximal network clique for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ) may not necessarily be a strict local maximizer of the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ). For example, in network G in Figure 7, the nodes $\{1,2,3,4\}$ form a maximal network clique. Since it is not attached with any larger clique with any 3 of its nodes, the strategy $x^{\ast }$ on this clique, $x_i^{\ast }=1/4$ for all $i=1,\dots ,4$ and $x_i^{\ast }=0$ for all $i=5,\dots ,8$, is a local maximizer of the contact maximization problem, and $x^{\ast T}A{x}^{\ast }\ge x^{T}Ax$ for any $x\in S$ in a small neighbourhood U of $x^{\ast }$. However, if we choose $x\ne x^{\ast }$ such that $x_1=x_3=x_4=1/4$, $x_2=1/4-ϵ$, $x_5=ϵ$, and $x_i=0$ for i=6,7,8, we see for any U that $x\in S\cap U$ for sufficiently small $ϵ>0$, and $x^{T}Ax=x^{\ast T}A{x}^{\ast }=3/4$. Therefore, $x^{\ast }$ cannot be a strict local maximizer. Notice that in G, node 5 is connected with 3 nodes, node 1, 3, 4, of clique $\{1,2,3,4\}$, which makes it possible to construct the strategy $x\in S\cap U$ on node 1, 2, 3, 4, 5 so that $x^{T}Ax=x^{\ast T}A{x}^{\ast }$. In general, we have the following necessary and sufficient conditions for the equilibrium strategy on a maximal clique to be a strict local maximizer of the contact maximization problem.

Figure 7. Strict Local Maximizer: The nodes $\{1,2,3,4\}$ in G form a maximal clique. The strategy $x^{\ast }$ on this clique for the social networking game on G, $x_i^{\ast }=1/4$ for all $i=1,\dots ,4$ and $x_i^{\ast }=0$ for all $i=5,\dots ,8$, is a local maximizer of the corresponding contact maximization problem, and $x^{\ast T}A{x}^{\ast }\ge x^{T}Ax$ for any $x\in S$ in a small neighbourhood U of $x^{\ast }$. However, if we choose $x\ne x^{\ast }$ such that $x_1=x_3=x_4=1/4$, $x_2=1/4-ϵ$, $x_5=ϵ$, and $x_i=0$ for i=6,7,8, we see for any U that $x\in S\cap U$ for sufficiently small $ϵ>0$, and $x^{T}Ax=x^{\ast T}A{x}^{\ast }=3/4$. Therefore, $x^{\ast }$ is not a strict local maximizer for the contact maximization problem.

Proposition 4.4

Let C be a maximal clique of network G. Let $x^{\ast }\in S$ be an equilibrium strategy on C for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ), $x_i^{\ast }=1/k$ for all $i\in V_C,$ $x_i^{\ast }=0$ for all $i\in V\mathrm{\setminus }{V}_C,$ and $k=|V_C|$. Then, $x^{\ast }$ is a strict local maximizer for the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), only if there is no node in $V\mathrm{\setminus }{V}_C$ connected to k−1 nodes of C.

Proof.

Assume that $x^{\ast }$ is a strict local maximizer for the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), and there is a node $l\in V\mathrm{\setminus }{V}_C$ connected to k−1 nodes of C, i.e. $(l,j)\in E\mathrm{\setminus }{E}_C$ for k−1 node $j\in V_C$. Then, $(A{x}^{\ast }{)}_l=(k-1)/k$. Let $l^{\prime }\in V_C$ be the node that node l is not connected to. Since $l^{\prime }\in V_C$, $(A{x}^{\ast }{)}_{l^{\prime }}=(k-1)/k$. Now, construct a strategy $x=x^{\ast }+p$, with $p_l=ϵ$, $p_{l^{\prime }}=-ϵ$, and $p_i=0$ for all $i\ne l,l^{\prime }$. Then, for a small neighbourhood U of $x^{\ast }$, $x\in S\cap U$ for sufficiently small $ϵ>0$, while $x^{T}Ax=x^{\ast T}A{x}^{\ast }+2p^{T}A{x}^{\ast }+p^{T}Ap=x^{\ast T}A{x}^{\ast },$ since $p^{T}A{x}^{\ast }=ϵ(A{x}^{\ast }{)}_l-ϵ(A{x}^{\ast }{)}_{l^{\prime }}=0$, and $p^{T}Ap=(A_{l,l}-2A_{l,l^{\prime }}+A_{l^{\prime },l^{\prime }}){ϵ}^2=0$. This is contradictory to the assumption that $x^{\ast }$ is a strict local maximizer for the contact maximization problem. So there cannot be a node in $V\mathrm{\setminus }{V}_C$ connected to k−1 nodes of C.

Proposition 4.5

Let C be a maximal clique of network G. Let $x^{\ast }\in S$ be an equilibrium strategy on C for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ), $x_i^{\ast }=1/k$ for all $i\in V_C,$ $x_i^{\ast }=0$ for all $i\in V\mathrm{\setminus }{V}_C,$ and $k=|V_C|$. Then, $x^{\ast }$ is a strict local maximizer for the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), if there is no node in $V\mathrm{\setminus }{V}_C$ connected to k−1 nodes of C.

Proof.

Without loss of generality, let's assume that $V_C=\{1,\dots ,k\}$. Then, $x_i^{\ast }=1/k$ for all $i=1,\dots ,k$ and $x_i^{\ast }=0$ for all i>k. Since there is no node in $V\mathrm{\setminus }{V}_C$ connected to k−1 nodes of C, there is no larger clique attached to any of k−1 nodes of C, either. It follows from Proposition 4.2 that $x^{\ast }$ is a local maximizer of the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ). Since there is no node in $V\mathrm{\setminus }{V}_C$ connected to k−1 nodes of C, the active constraints of the contact maximization problem at $x^{\ast }$ are all strongly active. Therefore, by Theorem 2.8, in order to prove that $x^{\ast }$ is a strict local maximizer of the contact maximization problem, all we need to show is that $Z^{T}AZ$ is negative definite, where Z is a null space matrix of the Jacobian matrix of the active constraints of the contact maximization problem at $x^{\ast }$.

The active constraints of the contact maximization problem at $x^{\ast }$ include all $x_i\ge 0$ for $i>k$ and $\sum _i{x}_i=0$. Then, the null space matrix Z for the Jacobian of this set of constraints is an $n\times (k-1)$ matrix and can be defined as follows: $Z_{1,j}=-1$ and $Z_{j+1,j}=1$ for all $j=1,\dots ,(k-1)$, and all other elements $Z_{i,j}=0$ [12]. Let $\overline{A}$ be the first k rows and k columns of A, and $\overline{Z}$ the first k rows of Z. Then, $Z^{T}AZ={\overline{Z}}^T\overline{A}\overline{Z}$. Since C is a clique, the elements of $\overline{A}$ are all 1's but 0's along the diagonal. Therefore, $\overline{A}=e{e}^T-I$, where $e\in R^k$ is a vector of all 1's and I a $k\times k$ identity matrix. Then, $Z^{T}AZ={\overline{Z}}^T\overline{A}\overline{Z}={\overline{Z}}^T(e{e}^T-I)\overline{Z}=-{\overline{Z}}^T\overline{Z}$ is negative definite, proving that $x^{\ast }$ is a strict local maximizer of the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ).

We have now learned that the population on a maximal network clique C of size k is in equilibrium for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ), when the population is distributed evenly on the clique. Such an equilibrium distribution is at least weakly evolutionarily stable unless there is a larger clique attached to k−1 nodes of C. Otherwise, the population would in some sense be able to migrate easily to the neighbouring larger clique, to achieve a higher payoff. It is evolutionarily stable unless there is a node not in C but connected to k−1 nodes of C or equivalently, there is a clique of size k attached to k−1 nodes of C. Otherwise, again, the population would in some sense be able to shift easily to the neighbouring clique without losing any payoff.

5. Equilibrium distributions on maximum network cliques

Given a network G, the maximum clique is a maximal clique of the largest size in G. Is a strategy on such a clique an equilibrium strategy for the social networking game on G? If yes, is it evolutionarily stable? The answer for the first question is easy: Since the maximum clique is a maximal clique, the strategy is certainly an equilibrium strategy. In addition, since there is no larger clique in G than the maximum clique, there cannot be any larger clique attached to it, and by Proposition 4.1 and 4.2, the strategy must be a local maximizer of the corresponding contact maximization problem and be at least weakly evolutionarily stable. However, there could be a node which is not in the clique, but connects to k−1 nodes of the clique. Therefore, by Proposition 4.4 and 4.5, the strategy can be a strict local maximizer and hence be evolutionarily stable unless there is a node not in the clique but connected to k−1 nodes of the clique. For example, in network G in Figure 7, the nodes $\{1,2,3,4\}$ form a maximum clique. The strategy on this clique is an equilibrium strategy, but it is not a strict local maximizer of the corresponding contact maximization problem, because node 5 connects to 3 nodes of the clique, node 2, 3, 4, and therefore, it is not evolutionarily stable.

In general, let C be a maximum clique of size k of network G. Then, the strategy $x^{\ast }$ on C for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ), $x_i^{\ast }=1/k$ for all $i\in V_C$ and $x_i^{\ast }=0$ for all $i\in V\mathrm{\setminus }{V}_C$, is a local maximizer of the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), with the maximum equal to$x^{\ast T}A{x}^{\ast }/2=(k-1)/2k$. However, Motzkin and Straus [18] showed that the global maximum of the quadratic programme in the form of the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ) is always equal to $(k-1)/2k$, where k is the size of the maximum clique of G [18]. Therefore, $x^{\ast }$ on C must be a global maximizer of the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ). Since these results apply to any quadratic programme in the form of (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ) and its related evolutionary game, we state them as two theorems in the following:

Theorem 5.1

Let H be a subnetwork of G and $x^{\ast }$ a strategy on H, $x^{\ast }>0$ for all $i\in V_H$ and $x^{\ast }=0$ for all $i\in V\mathrm{\setminus }{V}_H$. If $x^{\ast }$ is a global maximizer of the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), then the global maximum $x^{\ast T}A{x}^{\ast }/2$ of the problem must equal to $(k-1)/2k,$ where k is the size of the maximum clique C contained in H.

Theorem 5.2

The strategy $x^{\ast }$ on a maximum clique C of G for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ) is a global maximizer of the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ) with the global maximum equal to $(k-1)/2k,$ where k is the size of C.

Note that the equilibrium strategy corresponding to a global maximizer of the contact maximization problem may not necessarily be on a maximum clique, as implied in the above propositions. In particular, if the size of the maximum clique is k, the strategy can be on a subnetwork of size larger than k. However, once such an equilibrium strategy is obtained, we can always apply a simple procedure, as described below, to recover one on a maximum clique.

Let $x^{\ast }\in S$ be an equilibrium strategy for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ) corresponding to a global maximizer of the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ) with the maximum equal to $(k-1)/2k$, $x_i^{\ast }>0$ for all $i\in V_H$ and $x_i^{\ast }=0$ for all $i\in V\mathrm{\setminus }{V}_H$, where H is a subnetwork of G, and $l=|H|\ge k$. Based on Motzkin and Straus [18], H must contains a maximum clique of size k [18]. If l>k, then H must be incomplete, and there must be $i,j\in V_H$,$(i,j)\notin E_H$.

Define $p\in R^n$, with $p_i=c$, $p_j=-c$, and $p_r=0$ for all $r\ne i,j$, where $-x_i^{\ast }\le c\le x_j^{\ast }$. Then $y^{\ast }=x^{\ast }+p$ remains feasible for all the constraints of the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), and $y^{\ast T}A{y}^{\ast }=(x^{\ast }+p{)}^{T}A(x^{\ast }+p)=x^{\ast T}A{x}^{\ast }+2x^{\ast T}Ap+p^{T}Ap.$

Since $x^{\ast }$ is a global maximizer of the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), it must satisfy the KKT conditions of the problem. In particular, there must be a number ${\lambda }^{\ast }$ such that $(A{x}^{\ast }{)}_r={\lambda }^{\ast }$ for all $r\in V_H$. It follows that $2x^{\ast T}Ap=2{\lambda }^{\ast }(c-c)=0$. Since $(i,j)\notin E_H$, $A_{i,j}=A_{j,i}=0$, and $p^{T}Ap=0$. It follows that $y^{\ast T}A{y}^{\ast }=x^{\ast T}A{x}^{\ast }$, and $y^{\ast }$ remains to be a global maximizer of the contact maximization problem. If we set $c=x_j^{\ast }$ (or $c=-x_i^{\ast }$), we then obtain $y^{\ast }$ with fewer nonzero components, corresponding to a subnetwork of H with node $j\in V_H$ (or $i\in V_H$) and its connected edges eliminated.

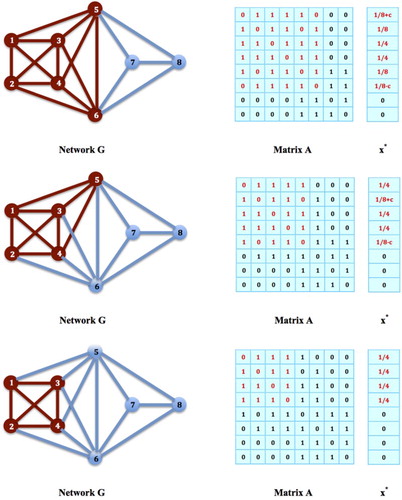
The above procedure can be repeated for the new maximizer $y^{\ast }$ and reduced subnetwork H until a complete subnetwork of size k is reached. The whole process would require only l−k steps, for there are only l−k nodes to be eliminated from a starting subnetwork H. An example is given in Figure 8 to demonstrate how the procedure works. In the first network on the top, the nodes $\{1,2,3,4,5,6\}$ form a subnetwork H, and $x^{\ast }\in S$, $x_i^{\ast }>0$ for all $i\in V_H$ and $x_i^{\ast }=0$ for all $i\in V\mathrm{\setminus }{V}_H$, is a global maximizer for the contact maximization problem. However, H is not a maximum clique. Since node 2 and 6 are not connected, we therefore add 1/8 to $x_2$ but subtract it from$x_6$. We then obtain a reduced subnetwork H, with $V_H=\{1,2,3,4,5\}$, $E_H=\left\{\right(i,j)\in E:i,j\in V_H\}$, as shown in the second network to the top. The solution $x^{\ast }\in S$, $x_i^{\ast }>0$ for all $i\in V_H$ and $x_i^{\ast }=0$ for all $i\in V\mathrm{\setminus }{V}_H$, remains to be a global maximizer for the contact maximization problem. Next, since node 1 and 5 are still not connected, we then add 1/8 to $x_1$ but subtract it from $x_5$ to obtain a further reduced subnetwork H, with $V_H=\{1,2,3,4\}$, $E_H=\left\{\right(i,j)\in E:i,j\in V_H\}$, as shown in the network in the bottom. The solution $x^{\ast }\in S$, $x_i^{\ast }>0$ for all $i\in V_H$ and $x_i^{\ast }=0$ for all $i\in V\mathrm{\setminus }{V}_H$, again remains to be a global maximizer for the contact maximization problem, but this time, H is a maximum clique of G.

Figure 8. Recovering Maximum Clique Strategies: In the network on the top, the nodes $\{1,2,3,4,5,6\}$ form a subnetwork H, and $x^{\ast }\in S$, $x_i^{\ast }>0$ for all $i\in V_H$ and $x_i^{\ast }=0$ for all $i\in V\mathrm{\setminus }{V}_H$, is a global maximizer for the contact maximization problem. However, H is not a maximum clique. Since node 2 and 6 are not connected, we therefore add 1/8 to $x_2$ but subtract it from $x_6$. We then obtain a reduced subnetwork H, with $V_H=\{1,2,3,4,5\}$, $E_H=\left\{\right(i,j)\in E:i,j\in V_H\}$, as shown in the second network to the top. The solution $x^{\ast }\in S$, $x_i^{\ast }>0$ for all $i\in V_H$ and $x_i^{\ast }=0$ for all $i\in V\mathrm{\setminus }{V}_H$, remains to be a global maximizer for the contact maximization problem. Next, since node 1 and 5 are still not connected, we then add 1/8 to $x_1$ but subtract it from $x_5$ to obtain a further reduced subnetwork$H=(V_H,E_H)$, $V_H=\{1,2,3,4\}$, $E_H=\left\{\right(i,j):i,j\in V_H\}$, as shown in the network in the bottom. The solution $x^{\ast }\in S$, $x_i^{\ast }>0$ for all $i\in V_H$ and $x_i^{\ast }=0$ for all $i\in V\mathrm{\setminus }{V}_H$, again remains to be a global maximizer for the contact maximization problem, but this time, H is a maximum clique of G.

Based on Theorem 5.1 and 5.2 and the above network reduction procedure, it is clear that the maximum clique of a given network G can be found by solving a contact maximization problem to its global maximum and then followed by performing a network reduction process. The latter requires only a polynomial time, therefore, solving a contact maximization problem to its global maximum is at least as hard as the problem of finding a maximum clique for a network G. We know that the latter problem is NP-hard [4,9]. It follows that the problem to find a global maximizer for the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ) must be NP-hard. This fact has been aware to some extent in the field of evolutionary game theory, but not been formally justified. We state it as a theorem in the following. The proof follows straightforwardly from our discussion.

Theorem 5.3

The problem to find a global maximizer for the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ) and equivalently, the problem to find an equilibrium strategy of maximum payoff for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ) is NP-hard.

Note that the network reduction procedure described above can also be reversed, i.e. starting from a global maximizer of the contact maximization problem on a maximum clique, we can extend it to a global maximizer on a general subnetwork that contains the clique. Key to this process is to make sure that in every step, an extended subnetwork can be found such that every pairs of unconnected nodes in the subnetwork are connected with the same set of nodes in the subnetwork (as justified in Theorem 5.4 below). For example, in Figure 8, in the network at the bottom, node 1 and 5 are separated but both are connected with the same set of nodes, $\{2,3,4\}$. Let $x^{\ast }$ on $\{1,2,3,4\}$ be the global maximizer for the contact maximization problem for that network. Then, by adding a small number $c=1/8$ to $x_5^{\ast }$ and subtract it from $x_1^{\ast }$, we obtain a global maximizer on the subnetwork formed by the nodes $\{1,2,3,4,5\}$ as shown in the network second to the bottom. Likewise, we can further extend this subnetwork to $\{1,2,3,4,5,6\}$ to obtain another global maximizer as shown in the network at the top of the figure.

Theorem 5.4

Let $x^{\ast }\in S$ be a global maximizer for the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), $x_i^{\ast }>0$ for all $i\in V_H$ and $x_i^{\ast }=0$ for all $i\in V\mathrm{\setminus }{V}_H,$ where H is a subnetwork of G, with node $l,l^{\prime }\in V_H$ not connected. Then, node l and $l^{\prime }$ must connect to the same set of nodes in $V_H$.

Proof.

Since $x^{\ast }$ is a global maximizer for the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), $x^{\ast T}A{x}^{\ast }=(k-1)/2k$, where k is the size of the maximum clique contained in H. Define $p\in R^n$, $p_l=c$, $p_{l^{\prime }}=-c$, and $p_r=0$ for all $r\ne l,l^{\prime }$, with $-x_l\le c\le x_{l^{\prime }}$. Then, $x=x^{\ast }+p$ is also a global maximizer, and $x^{T}Ax=x^{\ast T}A{x}^{\ast }=(k-1)/2k$. Then, by Theorem 2.2, $(Ax{)}_i=x^{T}Ax$ for all $i\in V_H,i\ne l,l^{\prime }$. However, $(Ax{)}_i=\sum _{j\in V_H}{A}_{i,j}{x}_j=\sum _{j\in V_H}{A}_{i,j}{x}_j^{\ast }+A_{i,l}c-A_{i,l^{\prime }}c=x^{\ast T}A{x}^{\ast }+A_{i,l}c-A_{i,l^{\prime }}c.$

It follows that $A_{i,l}c-A_{i,l^{\prime }}c=0$ and $A_{i,l}=A_{i,l^{\prime }}$ for all $i\in V_H,i\ne l,l^{\prime }$, i.e. node l and $l^{\prime }$ are connected to the same set of nodes in H.

6. Equilibrium distributions on non-clique subnetworks

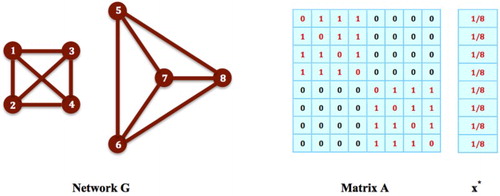
There could be equilibrium strategies on non-clique subnetworks for a given social networking game. Some of them can be derived directly from equilibrium strategies on maximal network cliques. In general, they are not as stable as the strategies on network cliques. For example, in Figure 8, the equilibrium strategies shown in the top two networks are non-clique equilibrium strategies. They are extended from a maximum-clique strategy and are global maximizers of the corresponding contact maximization problem. However, they are not strict maximizers, so they may be weakly evolutionarily stable at the very best. There are also non-clique strategies that are not directly extended from a maximal clique strategy. For example, for the social network game in Figure 9, at equilibrium, the population is distributed on two disconnected cliques, with $x_i^{\ast }=1/8$ for all $i=1,\dots ,8$. Note that at this state, the only active constraint for the corresponding contact maximization problem is the equality constraint, $\sum _i{x}_i=1$. A null space matrix Z for the Jacobian of this constraint can be defined as $\begin{array}{r}Z=\left(\begin{array}{ccccccc}-1& -1& -1& -1& -1& -1& -1\\ 1& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 1\end{array}\right).\end{array}$ Then, it is easy to verify that $\begin{array}{r}{Z}^{T}AZ=\left(\begin{array}{ccccccc}-2& -1& -1& -1& -1& -1& -1\\ -1& -2& -1& -1& -1& -1& -1\\ -1& -1& -2& -1& -1& -1& -1\\ -1& -1& -1& 0& 1& 1& 1\\ -1& -1& -1& 1& 0& 1& 1\\ -1& -1& -1& 1& 1& 0& 1\\ -1& -1& -1& 1& 1& 1& 0\end{array}\right).\end{array}$ Let $u=(1,1,1,-1,-1,-1,-1{)}^T$. Then, $u^T{Z}^{T}AZu=24>0$. Therefore, $Z^{T}AZ$ cannot be negative semidefinite. By the second-order necessary conditions in Theorem 2.7, $x^{\ast }$ cannot be a local maximizer of the contact maximization problem. It follows that $x^{\ast }$ cannot even be weakly evolutionarily stable.

Figure 9. Equilibrium Distributions on Non-clique Subnetworks: One of the equilibrium strategies of the social networking game on network G is when the population is distributed on the two disconnected network cliques, with $x_i^{\ast }=1/8$ for all $i=1,\dots ,8$. It is easy to verify that this strategy is not a local maximizer of the corresponding contact maximization problem and thereby, is not even weakly evolutionarily stable.

In general, the equilibrium strategy on a non-clique subnetwork cannot be evolutionarily stable, and may be weakly evolutionarily stable at the very best, as given in Proposition 6.1. On the other hand, equilibrium strategies on maximal network cliques are evolutionarily stable except for some special circumstances, as we have shown in previous sections. In this sense, the equilibrium strategies on maximal network cliques should have evolutionary advantages over those on non-clique subnetworks.

Proposition 6.1

An equilibrium strategy $x^{\ast }$ on a non-clique subnetwork H of G for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ) cannot be a strict local maximizer of the corresponding contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), and is evolutionarily unstable or weakly evolutionarily stable at the very best.

Proof.

Let $x^{\ast }\in S$ be an equilibrium strategy for the social networking game in (1(1) $x^{\ast T}A{x}^{\ast }\ge x^{T}A{x}^{\ast },\mathrm{\forall }x\in S,$(1) ), $x_i^{\ast }>0$ for all $i\in V_H$ and $x_i^{\ast }=0$ for all $i\in V\mathrm{\setminus }{V}_H$, where H is a non-clique subnetwork of G. If $x^{\ast }$ is not a local maximizer of the corresponding contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), by Theorem 2.6, $x^{\ast }$ is certainly unstable. Assume that $x^{\ast }$ is a local maximizer of the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), i.e. there is a small neighbourhood U of $x^{\ast }$ such that $x^{\ast T}A{x}^{\ast }\ge y^{T}Ay$ for all $y\in U\cap S$. We show that $x^{\ast }$ is not a strict local maximizer, i.e. there is no any neighbourhood U of $x^{\ast }$ such that $x^{\ast T}A{x}^{\ast }>y^{T}Ay$ for all $y\in U\cap S,y\ne x^{\ast }$.

Since H is a non-clique subnetwork, there must be $i,j\in V_H$, $(i,j)\notin E_H$. Define $p\in R^n$, with $p_i=ϵ$, $p_j=-ϵ$, and $p_r=0$ for all $r\ne i,j$. Then, by choosing $ϵ>0$ sufficiently small in between $-x_i^{\ast }$ and $x_j^{\ast }$, we can have $y=x^{\ast }+p\in U\cap S$ for any neighbourhood U of $x^{\ast }$, $y\ne x^{\ast }$. Note that $y^{T}Ay=(x^{\ast }+p{)}^{T}A(x^{\ast }+p)=x^{\ast T}A{x}^{\ast }+2x^{\ast T}Ap+p^{T}Ap.$ Since $x^{\ast }$ is a local maximizer of the contact maximization problem in (2(2) $\begin{array}{rl}& {\max }_{x\in R^n}{x}^{T}Ax/2,\\ & \mathrm{subject}\mathrm{to}\sum _i{x}_i=1,x_i\ge 0,i=1,\dots ,n\end{array}$(2) ), it must satisfy the KKT conditions of the problem. In particular, there must be a number ${\lambda }^{\ast }$ such that $(A{x}^{\ast }{)}_r={\lambda }^{\ast }$ for all $r\in V_H$. It follows that $2x^{\ast T}Ap=2{\lambda }^{\ast }(ϵ-ϵ)=0$. Since $(i,j)\notin E_H$, $A_{i,j}=A_{j,i}=0$, and $p^{T}Ap=0$. It follows that $y^{T}Ay=x^{\ast T}A{x}^{\ast }$. This simply implies that we cannot find any small neighbourhood U of $x^{\ast }$ such that $x^{\ast T}A{x}^{\ast }>y^{T}Ay$ for all $y\in U\cap S,y\ne x^{\ast }$. Therefore, $x^{\ast }$ cannot be a strict local maximizer of the contact maximization problem and is weakly evolutionarily stable at the very best.

7. Concluding remarks

The equilibrium strategies of a social networking game tend to be around network cliques or their extensions. Not all network cliques are optimal choices, however. Only maximal network cliques or some of their extensions are among those selected at equilibrium. Yet, these equilibrium strategies may or may not be evolutionarily stable. There are equilibrium strategies on non-clique subnetworks as well, but they are certainly evolutionarily unstable or weakly evolutionarily stable at the very best. In this paper, we have conducted a detailed analysis on clique and non-clique strategies of social networking games. We have in particular established the equilibrium and stability conditions on these strategies and provided rigorous mathematical justifications.

A social networking game is a symmetric evolutionary game and therefore, corresponds to a special type of quadratic programming problem called contact maximization problem. An equilibrium strategy for the social networking game is a KKT point for the corresponding contact maximization problem, which could be a local maximizer, local minimizer, or saddle point. It is evolutionarily stable if it is a strict local maximizer, and is evolutionarily unstable if it is a local minimizer or saddle point. It is weakly evolutionarily stable if it is a non-strict local maximizer. These properties form the theoretical basis for analyzing the equilibrium strategies of social networking games.

In typical network games, the population is assumed to form a social network, with each node representing an individual and the link between two nodes representing certain social or spatial connections between two individuals. The game is then played among connected individuals. Such a game, often called a social network game, is a little bit different from the game we have studied in this paper. In order to distinguish from it, we have purposely named our game the social networking game, meaning the game for a population to distribute on a given network of social sites for the purpose of ‘social networking’. In other words, general social network games deal with interactions among individuals in social networks, while social networking games deal with distributions of populations on networks of social sites.

Much work has been done in recent years on network games and in particular, on games for evolution of network interaction or cooperation [6,20,22,26,29]. While the nature of interaction or cooperation among the individuals in a given network-structured population can vary, the outcomes of a network game may be affected by the evolution of some general network conditions such as the changes in network structures. The latter is called co-evolution of network games and has been a subject of intensive research in recent years [15,23,30,31]. The problem of how a population would distribute over a social network is in some sense a co-evolutionary game for a network-structured population. The study of this game may therefore contribute to the study of general network games as well.

As we have mentioned in Section 1, social networking games may be applied directly to the studies on the development of social groups in human societies, and to the studies on the behaviours of social, solitary, or territorial animals. In addition, the results from analysis on social networking games, including distributions of populations in given networks of social sites, their equilibrium conditions, and stabilities, can all be valuable inputs for further practical inquiries on related populations, such as how infectious diseases may spread in such network structured populations, where commercial advertisements may be placed, and what social groups should be targeted for effective political campaigns, etc. The focus of our current paper has been only on simple network models and their related theoretical issues. For more general and practical applications, the networks can be more complex, for example, different contact weights may be given to different social links, the weight may not necessarily be symmetric for a given pair of connected nodes, and a social link may be defined in terms of more than one connections, etc. We will extend our work to these more complex cases in our future efforts.

Acknowledgements

The authors would like to thank Dr. Yuanyuan Huang and Dr. Yiping Hao of Iowa State University for participating in the discussions on our work and for the anonymous referees for providing valuable suggestions for the revision of our paper.

Disclosure statement

There is no any potential conflict of interest in this work.

Additional information

Funding

This work is partially supported by the NIH grant R01GM072014 and by the NSF grant DMS0914354.