Dengue in the Philippines: model and analysis of parameters affecting transmission

ABSTRACT

Dengue is endemic in the Philippines and poses a substantial economic burden in the country. In this work, a compartmentalized model which includes healthcare-seeking class is developed. The reproduction number is determined to investigate critical parameters influencing transmission. Partial rank correlation coefficient (PRCC) technique is performed to address how the model output is affected by changes in a specific parameter disregarding the uncertainty over the rest of the parameters. Results show that mosquito biting rate, transmission probability from mosquito to human, respectively, from human to mosquito, and fraction of individuals who seek healthcare at the onset of the disease, posted high PRCC values. In order to obtain the values for the desired parameters, the reported dengue cases by morbidity week in the Philippines for the year 2014 and 2015 are used. The reliability of parameters is then verified via parametric bootstrap.

KEYWORDS:

• Dengue model
• basic reproduction number
• sensitivity analysis
• parameter estimation
• model identification

1. Introduction

Dengue fever is the most important mosquito-borne viral disease in the world [54]. Dengue is a viral disease transmitted primarily by female mosquitoes from the species Aedes aegypti. It is considered as the most common arbovirus (arthropod-borne virus) infection globally, with transmission occurring in at least 128 countries and almost 4 billion people at risk [5]. The number of dengue cases reported annually to the World Health Organization (WHO) has increased significantly from an average of less than a thousand cases globally in the 1950s to more than 3 million cases in 2015 [56]. However, there has been a substantial under-reporting of dengue within the health systems and to WHO [3], which greatly underestimate the apparent global incidence rate estimated at about 50–100 million symptomatic cases per year [4,7,46]. The transmission of dengue viruses is influenced by population growth, urbanization, inadequate public health infrastructure, poor solid waste management, environmental risk factors and inconsistent preventive practices, among others. Dengue virus (DENV) has four different serotypes and thus a person can be infected more than once [44]. Moreover, dengue can evolve into a more complex form of a disease known as dengue haemorrhagic fever (DHF) or dengue shock syndrome, first recognized in the 1950s during dengue epidemics in the Philippines and Thailand [44], which can be fatal [10]. In the Philippines, epidemic dengue is considered one of its eight pervasive infectious diseases [13]. From 2008 to 2012, the country's Department of Health (DOH) reported 585,324 dengue cases, with a case fatality rate (CFR) of 0.55% or 3195 deaths [14] and ranks fourth in the number of dengue cases among the 10 Association of Southeast Asian Nations (ASEAN) [45,49].

Vector control is the predominant strategy for preventing the spread of DENV because there is neither an effective vaccine nor any specific anti-viral treatment for the illness [27,43,50]. However, it has been reported that the attempted prevention strategies have shown a limited effect [35]. This prompted multiple researches focused on identifying and understanding the key determinants in the transmission of dengue virus. Statistical and deterministic mathematical methods have been used to investigate the dynamics of dengue. By using statistical methods, correlations between new incidence cases and climatic variables including temperature, relative humidity, and precipitation have been established and used to predict potential outbreaks in specific areas [1,32,33]. On the other hand, deterministic approaches provide both qualitative and quantitative insights on the transmission dynamics of the disease. In the modelling process, assumptions, variables, and parameters related to dengue transmission are clearly identified to establish, among others, the computation of the basic reproductive number [31]. Most of the deterministic models utilized the ideas underlying the Susceptible–Infected–Recovered (SIR) model developed by Kermack and McKendrick [34]. Several mathematical models for dengue transmission have been investigated to consider constant human population and variable vector population [23]; a variable human population [24]; coexistence of different serotypes [25]; and different stages of vector development such as egg, larva, and pupa [59].

There had been researches on the dengue disease in the Philippines but mostly the nature of investigations is either statistical (dengue incidence), literature reviews, and/or surveillance studies [6,42]. However, there is minimal or no studies that relate the interaction and transmission of the disease between the vector and the host and no dynamical system studies have been made. In addition, a dynamic dengue transmission model using real epidemiological data has not been done where parameter estimation and sensitivity analysis has been examined. Since dengue epidemiology exhibits temporal and geographic variability [36], mathematical models must be fitted using data from specific study region to make them more realistic and relevant; and furthermore, must be validated using real data [37]. For this reason, a compartmental model including human and mosquito populations developed by Derouich et al. [15] is modified to include a healthcare-seeking class depicting the reported dengue cases and a variable human and vector population. In the Philippines, dengue surveillance focuses on hospitalized cases, especially with severe dengue manifestation. It is mainly dependent on disease reporting units (DRUs), including sentinel healthcentres in the smallest government administrative unit (barangay), Rural Health Units (RHUs), municipal or city health offices, local hospitals, private clinics, and human quarantine stations under the Local Government Unit (LGU) surveillance system [41]. All suspected, probable, and confirmed dengue episodes since 2007 are reported to the Philippines Integrated Disease Surveillance and Response System. It is estimated that about 93% of all dengue episodes reported in 2010–2014 were hospitalized patients and, of these, half were reported from private facilities [14,18,48]. A person infected with dengue might get home treatment or self care. However, if one does not seek medical attention, the case will not be reported and no further laboratory test will be done. Inclusion of a healthcare-seeking class in the model gives insights on the influence of the number of individuals who get medical attention and/or treatment, and also captures the impact of under-reported cases due to passive surveillance causing a chronic challenge in endemic countries [3,28,45,47]. The adapted model is investigated to describe the dengue epidemics that occurred in the Philippines in 2014 and 2015. Dengue cases by morbidity week were requested from the Public Health Surveillance Division, Epidemiology Bureau of the Philippine Department of Health. The information is utilized to estimate significant model parameters affecting the spread of the disease, particularly, the dynamics of the healthcare-seeking group. To the authors' best knowledge, a dynamic dengue transmission model using data in the Philippines has not been done where sensitivity analysis and parameter estimation are investigated. The numerical results provide estimates on mosquito biting rate, transmission probability from mosquito to human respectively, from human to mosquito, and fraction of individuals who sought health care.

This paper is organized as follows: Section 2 presents the mathematical model of dengue transmission considered in this work and discusses how the equilibrium points and reproduction number are obtained. Model simulations and sensitivity analysis are examined in Section 3 to determine which parameters are most/least influential to the model output. Parameter estimation and bootstrapping techniques giving the desired parameter values which capture the dynamics of the reported data are provided in Section 4. Discussions and future research directions are summarized in the last section.

2. A model of dengue transmission

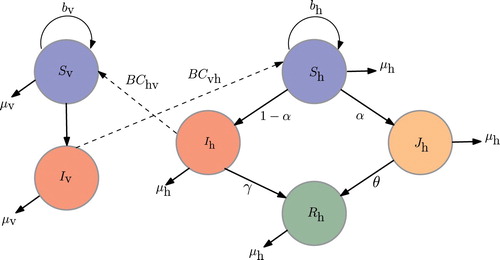
A susceptible–infected–removed (SIR) model developed by Derouich et al. [15] is modified to characterize dengue transmission between the human and vector populations. The model in this work incorporates a healthcare-seeking class to include those infected individuals who seek health care at the onset of the disease. This class constitute both ambulatory and hospitalized patients representing the reported cases. This is logical as in reality, data gathered are only those who are hospitalized and/or has sought medical attention. The human population $\mathit{h}$ is classified into four epidemiological classes, namely, the susceptible ($S_{\mathrm{h}}$), the unhospitalized/unmonitored infectious ($I_{\mathrm{h}}$), the healthcare-seeking infected ($J_{\mathrm{h}}$), and the removed/recovered ($R_{\mathrm{h}}$). The variable vector $\mathrm{v}$ (mosquito) population, on the other hand, is divided into two classes, namely, the susceptible ($S_{\mathrm{v}}$) and the infectious ($I_{\mathrm{v}}$) vectors. The dynamics of the human and vector populations may then be described in the following framework: Susceptible human population $S_{\mathrm{h}}$ increases at a rate of $b_{\text{h}}{N}_{\mathrm{h}}$, where $N_{\mathrm{h}}$ is the total human population. However, being bitten by a (female) mosquito at an average rate of B per week with transmission probability of $C_{\mathrm{vh}}$, susceptible individuals get infected. Of all infected individuals, only a fraction α is reported and included in class $J_{\mathrm{h}}$. A reported dengue case refers to an infected individual who seeks medical consultation and/or care upon experiencing symptoms. An infected individual who did not seek health care is not reported as a dengue case and is included in class $I_{\mathrm{h}}$. In either class, a part recovers and moved in $R_{\mathrm{h}}$ class. Coincidentally, susceptible vectors $S_{\mathrm{v}}$ get infected, at a rate of $C_{\mathrm{hv}}$, by those $I_{\mathrm{h}}$ who do not received hospitalized treatment and thus become part of $I_{\mathrm{v}}$. It should be noted that a single dengue serotype is considered and that immunity is attainable after recovery. Figure 1 illustrates the flow diagram of the dengue transmission involving the host and vector populations.

Figure 1. Model diagram depicting the dengue transmission dynamics.

The birth and death rates of humans are denoted by $b_{\mathrm{h}}$ and ${\mu }_{\mathrm{h}}$, respectively. As noted earlier, only a fraction of infectious individuals seek treatment at a rate of α. Early dengue disease recognition and awareness may enhance prompt attendance to medical care and thereby reduce progression to more severe illness complications and mortality [12,22,51]. Thus, recovery rates for the non- versus healthcare-seeking infected individuals are different since the mode of treatment and monitoring may vary. In addition, individuals who are care-seeking are cognizant to prevent further contact with susceptible mosquitoes. Hence, the recovery rate for unmonitored class γ is assumed to be different from that of the hospitalized group represented by θ. Parameters $b_{\mathrm{v}}$ and ${\mu }_{\mathrm{v}}$ stand for the vector per capita oviposition and mortality rate, respectively. The total vector population at time t is $N_{\mathrm{v}}=S_{\mathrm{v}}+I_{\mathrm{v}}$ with carrying capacity K, while the total human population at time t is $N_{\mathrm{h}}=S_{\mathrm{h}}+I_{\mathrm{h}}+J_{\mathrm{h}}+R_{\mathrm{h}}$.

The dengue transmission dynamics is governed by the following system of ordinary differential equations (ODEs) where the time variable t is measured in weeks: (1) $\begin{array}{rl}\frac{\mathrm{d}{S}_{\mathrm{h}}}{\mathrm{d}t}& =b_{\text{h}}{N}_{\mathrm{h}}-(B{C}_{\mathrm{vh}}\frac{I_{\mathrm{v}}}{N_{\mathrm{h}}}+{\mu }_{\mathrm{h}})S_{\mathrm{h}},\\ \frac{\mathrm{d}{I}_{\mathrm{h}}}{\mathrm{d}t}& =(1-\alpha )B{C}_{\mathrm{vh}}\frac{S_{\text{h}}{I}_{\mathrm{v}}}{N_{\mathrm{h}}}-(\gamma +{\mu }_{\mathrm{h}})I_{\mathrm{h}},\\ \frac{\mathrm{d}{J}_{\mathrm{h}}}{\mathrm{d}t}& =\alpha B{C}_{\mathrm{vh}}{S}_{\mathrm{h}}\frac{I_{\mathrm{v}}}{N_{\mathrm{h}}}-(\theta +{\mu }_{\mathrm{h}})J_{\mathrm{h}},\\ \frac{\mathrm{d}{R}_{\mathrm{h}}}{\mathrm{d}t}& =\gamma I_{\mathrm{h}}+\theta J_{\mathrm{h}}-{\mu }_{\text{h}}{R}_{\mathrm{h}},\\ \frac{\mathrm{d}{S}_{\mathrm{v}}}{\mathrm{d}t}& =b_{\mathrm{v}}{N}_{\mathrm{v}}(1-\frac{N_{\mathrm{v}}}{K})-(B{C}_{\mathrm{hv}}\frac{I_{\mathrm{h}}}{N_{\mathrm{h}}}+{\mu }_{\mathrm{v}})S_{\mathrm{v}},\\ \frac{\mathrm{d}{I}_{\mathrm{v}}}{\mathrm{d}t}& =B{C}_{\mathrm{hv}}{S}_{\mathrm{v}}\frac{I_{\mathrm{h}}}{N_{\mathrm{h}}}-{\mu }_{\text{v}}{I}_{\mathrm{v}},\end{array}$(1) with initial conditions $S_{\mathrm{h}}\left(0\right)$, $I_{\mathrm{h}}\left(0\right)$, $J_{\mathrm{h}}\left(0\right)$, $R_{\mathrm{h}}\left(0\right)$, $S_{\mathrm{v}}\left(0\right)$ and $I_{\mathrm{v}}\left(0\right)$ at time t=0. Model parameters are described in Table 1.

Table 1. Parameters values used in the dengue transmission model.

Parameter	Description	Value per week	Range	References
$b_{\mathrm{h}}$	Birth rate of humans	0.00085	–	Data fitted^a
${\mu }_{\mathrm{h}}$	Mortality rate of humans	0.00045	–	Data fitted^a
B	Vector biting rate	1	[0,4]	[15,37]
$C_{\mathrm{hv}}$	Transmission probability from human to vector	0.75	[0,1]	[15,37]
$C_{\mathrm{vh}}$	Transmission probability from vector to human	0.375	[0,1]	[15,37]
γ	Non-seeking healthcare recovery rate	0.5	[0.5,1.75]	[37]
θ	Healthcare-seeking recovery rate	1	[0.5,1.75]	[37]
$b_{\mathrm{v}}$	Per capita oviposition rate	75	[55,165]	[37]
${\mu }_{\mathrm{v}}$	Mortality rate of vectors	0.1	[0.06,0.20]	[37]
K	Vector carrying capacity	300,000,000	–	Estimated
α	Transition rate from infected to hospitalized humans	0.2	–	Estimated

^aEstimated from the Philippine population data.

2.1. Equilibrium points

We first analyse the system through its equilibrium points. Equilibrium points are the values of $S_{\mathrm{h}},I_{\mathrm{h}},J_{\mathrm{h}},R_{\mathrm{h}},S_{\mathrm{v}}$ and $I_{\mathrm{v}}$ that remain constant over time. The equilibrium points of system (1(1) $\begin{array}{rl}\frac{\mathrm{d}{S}_{\mathrm{h}}}{\mathrm{d}t}& =b_{\text{h}}{N}_{\mathrm{h}}-(B{C}_{\mathrm{vh}}\frac{I_{\mathrm{v}}}{N_{\mathrm{h}}}+{\mu }_{\mathrm{h}})S_{\mathrm{h}},\\ \frac{\mathrm{d}{I}_{\mathrm{h}}}{\mathrm{d}t}& =(1-\alpha )B{C}_{\mathrm{vh}}\frac{S_{\text{h}}{I}_{\mathrm{v}}}{N_{\mathrm{h}}}-(\gamma +{\mu }_{\mathrm{h}})I_{\mathrm{h}},\\ \frac{\mathrm{d}{J}_{\mathrm{h}}}{\mathrm{d}t}& =\alpha B{C}_{\mathrm{vh}}{S}_{\mathrm{h}}\frac{I_{\mathrm{v}}}{N_{\mathrm{h}}}-(\theta +{\mu }_{\mathrm{h}})J_{\mathrm{h}},\\ \frac{\mathrm{d}{R}_{\mathrm{h}}}{\mathrm{d}t}& =\gamma I_{\mathrm{h}}+\theta J_{\mathrm{h}}-{\mu }_{\text{h}}{R}_{\mathrm{h}},\\ \frac{\mathrm{d}{S}_{\mathrm{v}}}{\mathrm{d}t}& =b_{\mathrm{v}}{N}_{\mathrm{v}}(1-\frac{N_{\mathrm{v}}}{K})-(B{C}_{\mathrm{hv}}\frac{I_{\mathrm{h}}}{N_{\mathrm{h}}}+{\mu }_{\mathrm{v}})S_{\mathrm{v}},\\ \frac{\mathrm{d}{I}_{\mathrm{v}}}{\mathrm{d}t}& =B{C}_{\mathrm{hv}}{S}_{\mathrm{v}}\frac{I_{\mathrm{h}}}{N_{\mathrm{h}}}-{\mu }_{\text{v}}{I}_{\mathrm{v}},\end{array}$(1) ) can be obtained by equating the derivatives to zero, yielding three points: (2) $E^{\left(1\right)}=(S_{\mathrm{h}}^{\left(1\right)},I_{\mathrm{h}}^{\left(1\right)},J_{\mathrm{h}}^{\left(1\right)},R_{\mathrm{h}}^{\left(1\right)},S_{\mathrm{v}}^{\left(1\right)},I_{\mathrm{v}}^{\left(1\right)})=(\frac{N_{\mathrm{h}}{b}_{\mathrm{h}}}{{\mu }_{\mathrm{h}}},0,0,0,0,0),$(2) (3) $E^{\left(2\right)}=(S_{\mathrm{h}}^{\left(2\right)},I_{\mathrm{h}}^{\left(2\right)},J_{\mathrm{h}}^{\left(2\right)},R_{\mathrm{h}}^{\left(2\right)},S_{\mathrm{v}}^{\left(2\right)},I_{\mathrm{v}}^{\left(2\right)})=(\frac{N_{\mathrm{h}}{b}_{\mathrm{h}}}{{\mu }_{\mathrm{h}}},0,0,0,\frac{(b_{\mathrm{v}}-{\mu }_{\mathrm{v}})K}{{\mu }_{\mathrm{v}}},0),$(3) and $E^{\ast }=(S_{\mathrm{h}}^{\ast },I_{\mathrm{h}}^{\ast },J_{\mathrm{h}}^{\ast },R_{\mathrm{h}}^{\ast },S_{\mathrm{v}}^{\ast },I_{\mathrm{v}}^{\ast })$ where $\begin{array}{rl}{S}_{\mathrm{h}}^{\ast }& =\frac{N_{\mathrm{h}}^2{b}_v\left[\right(1-\alpha )B{C}_{\mathrm{hv}}{b}_{\mathrm{h}}+{\mu }_{\mathrm{v}}({\mu }_{\mathrm{h}}+\gamma \left)\right]}{(1-\alpha )B{C}_{\mathrm{hv}}[{\mu }_{\mathrm{h}}{b}_{\text{v}}{N}_{\mathrm{h}}+B{C}_{\mathrm{vh}}K(b_{\mathrm{v}}-{\mu }_{\mathrm{v}}\left)\right]},\\ I_{\mathrm{h}}^{\ast }& =\frac{(1-\alpha )B^2{C}_{\mathrm{hv}}{C}_{\mathrm{vh}}K{N}_{\mathrm{h}}{b}_{\mathrm{h}}(b_{\mathrm{v}}-{\mu }_{\mathrm{v}})-{\mu }_{\mathrm{v}}{N}_{\mathrm{h}}^2{b}_{\mathrm{v}}{\mu }_{\mathrm{h}}({\mu }_{\mathrm{h}}+\gamma )}{({\mu }_{\mathrm{h}}+\gamma )[B{C}_{\mathrm{hv}}{N}_{\mathrm{h}}{b}_{\mathrm{v}}{\mu }_{\mathrm{h}}+B^2{C}_{\mathrm{hv}}{C}_{\mathrm{vh}}K(b_{\mathrm{v}}-{\mu }_{\mathrm{v}}\left)\right]},\\ J_{\mathrm{h}}^{\ast }& =\frac{\alpha \left[\right(1-\alpha \left)B^2{C}_{\mathrm{hv}}{C}_{\mathrm{vh}}K{N}_{\mathrm{h}}{b}_{\mathrm{h}}\right(b_{\mathrm{v}}-{\mu }_{\mathrm{v}})-{\mu }_{\mathrm{v}}{N}_{\mathrm{h}}^2{b}_{\mathrm{v}}{\mu }_{\mathrm{h}}({\mu }_{\mathrm{h}}+\gamma \left)\right]}{(1-\alpha )(\theta +{\mu }_{\mathrm{h}})[B{C}_{\mathrm{hv}}{N}_{\mathrm{h}}{b}_{\mathrm{v}}{\mu }_{\mathrm{h}}+B^2{C}_{\mathrm{hv}}{C}_{\mathrm{vh}}K(b_{\mathrm{v}}-{\mu }_{\mathrm{v}}\left)\right]},\\ R_{\mathrm{h}}^{\ast }& =\frac{\begin{array}{c}{N}_{\mathrm{h}}\left[\theta \right({\mu }_{\mathrm{h}}+\gamma )+\gamma {\mu }_{\mathrm{h}}(1-\alpha \left)\right]\left[\right(1-\alpha \left)B^2{C}_{\mathrm{hv}}{C}_{\mathrm{vh}}K{b}_{\mathrm{h}}\right(b_{\mathrm{v}}-{\mu }_{\mathrm{v}})\\ -{\mu }_{\text{v}}{N}_{\mathrm{h}}{b}_{\mathrm{v}}{\mu }_{\mathrm{h}}({\mu }_{\mathrm{h}}+\gamma )]\end{array}}{(1-\alpha )({\mu }_{\mathrm{h}}+\gamma )({\mu }_{\mathrm{h}}+\theta )B{C}_{\mathrm{hv}}{\mu }_{\mathrm{h}}[N_{\mathrm{h}}{b}_{\mathrm{v}}{\mu }_{\mathrm{h}}+B{C}_{\mathrm{vh}}K(b_{\mathrm{v}}-{\mu }_{\mathrm{v}}\left)\right]},\\ S_{\mathrm{v}}^{\ast }& =\frac{{\mu }_{\mathrm{v}}({\mu }_{\mathrm{h}}+\gamma )[{\mu }_{\mathrm{h}}{b}_{\text{v}}{N}_{\mathrm{h}}+B{C}_{\mathrm{vh}}K(b_{\mathrm{v}}-{\mu }_{\mathrm{v}}\left)\right]}{B{C}_{\mathrm{vh}}{b}_{\mathrm{v}}\left[\right(1-\alpha )B{C}_{\mathrm{hv}}{b}_{\mathrm{h}}+{\mu }_{\mathrm{v}}({\mu }_{\mathrm{h}}+\gamma \left)\right]},\\ I_{\mathrm{v}}^{\ast }& =\frac{(1-\alpha )B^2{C}_{\mathrm{hv}}{C}_{\mathrm{vh}}K{b}_{\mathrm{h}}(b_{\mathrm{v}}-{\mu }_{\mathrm{v}})-{\mu }_{\text{v}}{N}_{\mathrm{h}}{b}_{\mathrm{v}}{\mu }_{\mathrm{h}}({\mu }_{\mathrm{h}}+\gamma )}{B{C}_{\mathrm{vh}}{b}_{\mathrm{v}}\left[\right(1-\alpha )B{C}_{\mathrm{hv}}{b}_{\mathrm{h}}+{\mu }_{\mathrm{v}}({\mu }_{\mathrm{h}}+\gamma \left)\right]}.\end{array}$ The first two points $E^{\left(1\right)}$ and $E^{\left(2\right)}$ are called disease-free equilibrium points. They are called so because components $I_{\mathrm{h}}$ and $I_{\mathrm{v}}$ are zero which means that transmission of disease cannot persist. The third point $E^{\ast }$ is called an endemic equilibrium point, and for $E^{\ast }$ to be biologically meaningful, we need to impose that all coordinates are positive. Clearly, $S_{\mathrm{h}}^{\ast }$ are $S_{\mathrm{v}}^{\ast }$ are postive. For the other components, $I_{\mathrm{v}}^{\ast }>0$, $I_{\mathrm{h}}^{\ast }>0$, $J_{\mathrm{h}}^{\ast }>0$, and $R_{\mathrm{h}}^{\ast }>0$ if $\frac{(1-\alpha )B^2{C}_{\mathrm{hv}}{C}_{\mathrm{vh}}K{b}_{\mathrm{h}}(b_{\mathrm{v}}-{\mu }_{\mathrm{v}})}{N_{\mathrm{h}}{b}_{\mathrm{v}}{\mu }_{\mathrm{v}}{\mu }_{\mathrm{h}}({\mu }_{\mathrm{h}}+\gamma )}>1.$

2.2. The reproduction number

The reproduction number ${\mathcal{R}}_0$ is a metric that determines whether an epidemic will ensue or not [29]. It denotes the average number of secondary cases of infection caused by a single case introduced into an otherwise disease-free susceptible population. Thus, we need to perturb the system from its disease-free equilibrium. The equilibrium point $E^{\left(2\right)}$ is used since both susceptible populations exist. If ${\mathcal{R}}_0<1$, then the epidemic dies out. Otherwise, if ${\mathcal{R}}_0>1$, then the epidemic will ensue. The following theorem is stated.

Theorem 2.1

The reproduction number for system (1(1) $\begin{array}{rl}\frac{\mathrm{d}{S}_{\mathrm{h}}}{\mathrm{d}t}& =b_{\text{h}}{N}_{\mathrm{h}}-(B{C}_{\mathrm{vh}}\frac{I_{\mathrm{v}}}{N_{\mathrm{h}}}+{\mu }_{\mathrm{h}})S_{\mathrm{h}},\\ \frac{\mathrm{d}{I}_{\mathrm{h}}}{\mathrm{d}t}& =(1-\alpha )B{C}_{\mathrm{vh}}\frac{S_{\text{h}}{I}_{\mathrm{v}}}{N_{\mathrm{h}}}-(\gamma +{\mu }_{\mathrm{h}})I_{\mathrm{h}},\\ \frac{\mathrm{d}{J}_{\mathrm{h}}}{\mathrm{d}t}& =\alpha B{C}_{\mathrm{vh}}{S}_{\mathrm{h}}\frac{I_{\mathrm{v}}}{N_{\mathrm{h}}}-(\theta +{\mu }_{\mathrm{h}})J_{\mathrm{h}},\\ \frac{\mathrm{d}{R}_{\mathrm{h}}}{\mathrm{d}t}& =\gamma I_{\mathrm{h}}+\theta J_{\mathrm{h}}-{\mu }_{\text{h}}{R}_{\mathrm{h}},\\ \frac{\mathrm{d}{S}_{\mathrm{v}}}{\mathrm{d}t}& =b_{\mathrm{v}}{N}_{\mathrm{v}}(1-\frac{N_{\mathrm{v}}}{K})-(B{C}_{\mathrm{hv}}\frac{I_{\mathrm{h}}}{N_{\mathrm{h}}}+{\mu }_{\mathrm{v}})S_{\mathrm{v}},\\ \frac{\mathrm{d}{I}_{\mathrm{v}}}{\mathrm{d}t}& =B{C}_{\mathrm{hv}}{S}_{\mathrm{v}}\frac{I_{\mathrm{h}}}{N_{\mathrm{h}}}-{\mu }_{\text{v}}{I}_{\mathrm{v}},\end{array}$(1) ) is (4) ${\mathcal{R}}_0={\left(\frac{(1-\alpha )B^2{C}_{\mathrm{hv}}{C}_{\mathrm{vh}}K{b}_{\mathrm{h}}(b_{\mathrm{v}}-{\mu }_{\mathrm{v}})}{N_{\mathrm{h}}{b}_{\mathrm{v}}{\mu }_{\mathrm{v}}{\mu }_{\mathrm{h}}({\mu }_{\mathrm{h}}+\gamma )}\right)}^{1/2},$(4) and that system (1(1) $\begin{array}{rl}\frac{\mathrm{d}{S}_{\mathrm{h}}}{\mathrm{d}t}& =b_{\text{h}}{N}_{\mathrm{h}}-(B{C}_{\mathrm{vh}}\frac{I_{\mathrm{v}}}{N_{\mathrm{h}}}+{\mu }_{\mathrm{h}})S_{\mathrm{h}},\\ \frac{\mathrm{d}{I}_{\mathrm{h}}}{\mathrm{d}t}& =(1-\alpha )B{C}_{\mathrm{vh}}\frac{S_{\text{h}}{I}_{\mathrm{v}}}{N_{\mathrm{h}}}-(\gamma +{\mu }_{\mathrm{h}})I_{\mathrm{h}},\\ \frac{\mathrm{d}{J}_{\mathrm{h}}}{\mathrm{d}t}& =\alpha B{C}_{\mathrm{vh}}{S}_{\mathrm{h}}\frac{I_{\mathrm{v}}}{N_{\mathrm{h}}}-(\theta +{\mu }_{\mathrm{h}})J_{\mathrm{h}},\\ \frac{\mathrm{d}{R}_{\mathrm{h}}}{\mathrm{d}t}& =\gamma I_{\mathrm{h}}+\theta J_{\mathrm{h}}-{\mu }_{\text{h}}{R}_{\mathrm{h}},\\ \frac{\mathrm{d}{S}_{\mathrm{v}}}{\mathrm{d}t}& =b_{\mathrm{v}}{N}_{\mathrm{v}}(1-\frac{N_{\mathrm{v}}}{K})-(B{C}_{\mathrm{hv}}\frac{I_{\mathrm{h}}}{N_{\mathrm{h}}}+{\mu }_{\mathrm{v}})S_{\mathrm{v}},\\ \frac{\mathrm{d}{I}_{\mathrm{v}}}{\mathrm{d}t}& =B{C}_{\mathrm{hv}}{S}_{\mathrm{v}}\frac{I_{\mathrm{h}}}{N_{\mathrm{h}}}-{\mu }_{\text{v}}{I}_{\mathrm{v}},\end{array}$(1) ) is asymptotically stable when ${\mathcal{R}}_0<1$. Otherwise, if ${\mathcal{R}}_0\ge 1$, then the system is unstable.

Note that when ${\mathcal{R}}_0>1$, the result is consistent with the condition for the existence of the endemic equilibrium $E^{\ast }$.

Proof.

In order to find the reproduction number, we use the next generation matrix method, introduced by Diekmann et al. [16]. We form the matrices F and V where F is the matrix of rates of appearance of new infections and V is the matrix of rates of transfer of individuals out of the compartments. These are taken from partial derivatives of the right-side expressions of $I_{\mathrm{h}}^{\ast }$, $J_{\mathrm{h}}^{\ast }$ and $I_{\mathrm{v}}^{\ast }$ in system (1(1) $\begin{array}{rl}\frac{\mathrm{d}{S}_{\mathrm{h}}}{\mathrm{d}t}& =b_{\text{h}}{N}_{\mathrm{h}}-(B{C}_{\mathrm{vh}}\frac{I_{\mathrm{v}}}{N_{\mathrm{h}}}+{\mu }_{\mathrm{h}})S_{\mathrm{h}},\\ \frac{\mathrm{d}{I}_{\mathrm{h}}}{\mathrm{d}t}& =(1-\alpha )B{C}_{\mathrm{vh}}\frac{S_{\text{h}}{I}_{\mathrm{v}}}{N_{\mathrm{h}}}-(\gamma +{\mu }_{\mathrm{h}})I_{\mathrm{h}},\\ \frac{\mathrm{d}{J}_{\mathrm{h}}}{\mathrm{d}t}& =\alpha B{C}_{\mathrm{vh}}{S}_{\mathrm{h}}\frac{I_{\mathrm{v}}}{N_{\mathrm{h}}}-(\theta +{\mu }_{\mathrm{h}})J_{\mathrm{h}},\\ \frac{\mathrm{d}{R}_{\mathrm{h}}}{\mathrm{d}t}& =\gamma I_{\mathrm{h}}+\theta J_{\mathrm{h}}-{\mu }_{\text{h}}{R}_{\mathrm{h}},\\ \frac{\mathrm{d}{S}_{\mathrm{v}}}{\mathrm{d}t}& =b_{\mathrm{v}}{N}_{\mathrm{v}}(1-\frac{N_{\mathrm{v}}}{K})-(B{C}_{\mathrm{hv}}\frac{I_{\mathrm{h}}}{N_{\mathrm{h}}}+{\mu }_{\mathrm{v}})S_{\mathrm{v}},\\ \frac{\mathrm{d}{I}_{\mathrm{v}}}{\mathrm{d}t}& =B{C}_{\mathrm{hv}}{S}_{\mathrm{v}}\frac{I_{\mathrm{h}}}{N_{\mathrm{h}}}-{\mu }_{\text{v}}{I}_{\mathrm{v}},\end{array}$(1) ): $F=\left[\begin{array}{ccc}0& 0& \frac{(1-\alpha )B{C}_{\mathrm{vh}}{S}_{\mathrm{h}}}{N_{\mathrm{h}}}\\ 0& 0& \frac{\alpha B{C}_{\mathrm{vh}}{S}_{\mathrm{h}}}{N_{\mathrm{h}}}\\ \frac{B{C}_{\mathrm{hv}}{S}_{\mathrm{v}}}{N_{\mathrm{h}}}& 0& 0\end{array}\right]\text{and}V=\left[\begin{array}{ccc}\gamma +{\mu }_{\mathrm{h}}& 0& 0\\ 0& \theta +{\mu }_{\mathrm{h}}& 0\\ 0& 0& {\mu }_{\mathrm{v}}\end{array}\right].$ The matrices are then evaluated at the disease-free equilibrium, $E^{\left(2\right)}$, yielding $\begin{array}{rl}F\left(E^{\left(2\right)}\right)& =\left[\begin{array}{ccc}0& 0& \frac{(1-\alpha )B{C}_{\mathrm{vh}}{b}_{\mathrm{h}}}{{\mu }_{\mathrm{h}}}\\ 0& 0& \frac{\alpha B{C}_{\mathrm{vh}}{b}_{\mathrm{h}}}{{\mu }_{\mathrm{h}}}\\ \frac{B{C}_{\mathrm{hv}}K(b_{\mathrm{v}}-{\mu }_{\mathrm{v}})}{N_{\mathrm{h}}{b}_{\mathrm{v}}}& 0& 0\end{array}\right]\text{and}\\ V\left(E^{\left(2\right)}\right)& =\left[\begin{array}{ccc}\gamma +{\mu }_{\mathrm{h}}& 0& 0\\ 0& \theta +{\mu }_{\mathrm{h}}& 0\\ 0& 0& {\mu }_{\mathrm{v}}\end{array}\right].\end{array}$ The product of $F\left(E^{\left(2\right)}\right)$ and inverse of $V\left(E^{\left(2\right)}\right)$ can then be obtained as $F\left(E^{\left(2\right)}\right)V^{-1}\left(E^{\left(2\right)}\right)=\left[\begin{array}{ccc}0& 0& \frac{(1-\alpha )B{C}_{\mathrm{vh}}{b}_{\mathrm{h}}}{{\mu }_{\mathrm{h}}{\mu }_{\mathrm{v}}}\\ 0& 0& \frac{\alpha B{C}_{\mathrm{vh}}{b}_{\mathrm{h}}}{{\mu }_{\mathrm{h}}{\mu }_{\mathrm{v}}}\\ \frac{B{C}_{\mathrm{hv}}K(b_{\mathrm{v}}-{\mu }_{\mathrm{v}})}{N_{\mathrm{h}}{b}_{\mathrm{v}}(\gamma +{\mu }_{\mathrm{h}})}& 0& 0\end{array}\right].$ The reproduction number is the spectral radius of $F\left(E^{\left(2\right)}\right)V^{-1}\left(E^{\left(2\right)}\right)$, that is, we take the largest eigenvalue of the matrix. This gives (5) ${\mathcal{R}}_0={\left(\frac{(1-\alpha )B^2{C}_{\mathrm{hv}}{C}_{\mathrm{vh}}K{b}_{\mathrm{h}}(b_{\mathrm{v}}-{\mu }_{\mathrm{v}})}{N_{\mathrm{h}}{b}_{\mathrm{v}}{\mu }_{\mathrm{v}}{\mu }_{\mathrm{h}}({\mu }_{\mathrm{h}}+\gamma )}\right)}^{1/2}.$(5) The reproduction number also gives an idea of which parameters in our model may be significant in our dynamics. In our proposition, the parameters $\alpha ,B,C_{\mathrm{vh}},$ and $C_{\mathrm{hv}}$ directly affect ${\mathcal{R}}_0$. We shall verify their significance in the next section.

3. Simulations and sensitivity analysis

3.1. Parameter values and initial conditions

Model parameters are estimated based on the available data [55]. The human mortality rate ${\mu }_{\mathrm{h}}$ is calculated as the inverse of the life expectancy reported in [53] relative to 1990–2014. The computed value is ${\mu }_{\mathrm{h}}\approx 0.00045$ per week. Using the Philippine population data from WHO [55] and the computed ${\mu }_{\mathrm{h}}$, human birth rate $b_{\mathrm{h}}$ can be estimated from the exact solution of the differential equation $d{N}_{\mathrm{h}}/dt=(b_{\mathrm{h}}-{\mu }_{\mathrm{h}})N_{\mathrm{h}}$ which is $N_{\mathrm{h}}\left(0\right)\exp \left(\right(b_{\mathrm{h}}-{\mu }_{\mathrm{h}}\left)t\right)$, where t spans the years from 1990 to 2014. The MATLAB optimization routine nonlinear least-squares solver, lsqcurvefit, is used to estimate $b_{\mathrm{h}}\approx 0.00085$ per week. Table 1 provides the list of model parameters, its description, values, ranges, and references.

In the absence of available and more specific information, the following conservative estimates are used as initial conditions for the model defined in (1(1) $\begin{array}{rl}\frac{\mathrm{d}{S}_{\mathrm{h}}}{\mathrm{d}t}& =b_{\text{h}}{N}_{\mathrm{h}}-(B{C}_{\mathrm{vh}}\frac{I_{\mathrm{v}}}{N_{\mathrm{h}}}+{\mu }_{\mathrm{h}})S_{\mathrm{h}},\\ \frac{\mathrm{d}{I}_{\mathrm{h}}}{\mathrm{d}t}& =(1-\alpha )B{C}_{\mathrm{vh}}\frac{S_{\text{h}}{I}_{\mathrm{v}}}{N_{\mathrm{h}}}-(\gamma +{\mu }_{\mathrm{h}})I_{\mathrm{h}},\\ \frac{\mathrm{d}{J}_{\mathrm{h}}}{\mathrm{d}t}& =\alpha B{C}_{\mathrm{vh}}{S}_{\mathrm{h}}\frac{I_{\mathrm{v}}}{N_{\mathrm{h}}}-(\theta +{\mu }_{\mathrm{h}})J_{\mathrm{h}},\\ \frac{\mathrm{d}{R}_{\mathrm{h}}}{\mathrm{d}t}& =\gamma I_{\mathrm{h}}+\theta J_{\mathrm{h}}-{\mu }_{\text{h}}{R}_{\mathrm{h}},\\ \frac{\mathrm{d}{S}_{\mathrm{v}}}{\mathrm{d}t}& =b_{\mathrm{v}}{N}_{\mathrm{v}}(1-\frac{N_{\mathrm{v}}}{K})-(B{C}_{\mathrm{hv}}\frac{I_{\mathrm{h}}}{N_{\mathrm{h}}}+{\mu }_{\mathrm{v}})S_{\mathrm{v}},\\ \frac{\mathrm{d}{I}_{\mathrm{v}}}{\mathrm{d}t}& =B{C}_{\mathrm{hv}}{S}_{\mathrm{v}}\frac{I_{\mathrm{h}}}{N_{\mathrm{h}}}-{\mu }_{\text{v}}{I}_{\mathrm{v}},\end{array}$(1) ). The size of the susceptible human population at the onset of the epidemic is assumed to be 50,000,000 which is about 50% of the total human population. For the infectious human population, an estimate of 15,000 is considered. Due to inadequate public health infrastructure and under-reporting, initial number of hospitalized individuals is taken to be 1500 which is only 9% of the total infected population. It is further assumed that initial number of recovered or those individuals who developed immunity is 5000. With regard to mosquito population, only 20,000,000 is considered as susceptible mosquitoes and 2,000,000 are dengue virus carriers. Summary of the initial conditions is provided in Table 2.

Table 2. Initial conditions used in the dengue transmission model.

Parameter	Description	Value
$S_{\mathrm{h}}\left(0\right)$	Initial condition for susceptible humans	50,000,000
$I_{\mathrm{h}}\left(0\right)$	Initial condition for infected humans	15,000
$J_{\mathrm{h}}\left(0\right)$	Initial condition for healthcare-seeking humans	1500
$R_{\mathrm{h}}\left(0\right)$	Initial condition for recovered humans	5000
$S_{\mathrm{v}}\left(0\right)$	Initial condition for susceptible mosquitoes	20,000,000
$I_{\mathrm{v}}\left(0\right)$	Initial condition for infected mosquitoes	2,000,000

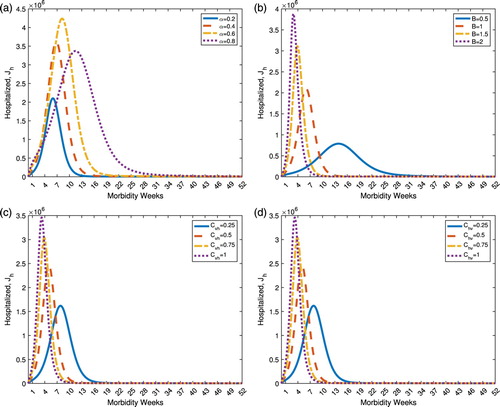
3.2. Effect of varying model parameters

The dynamics of dengue transmission is reliably dependent on the values of the model parameters. Here, the healthcare-seeking class $J_{\mathrm{h}}$ is considered as the reference model output and the parameters in consideration are $\alpha ,B,C_{\mathrm{vh}},$ and $C_{\mathrm{hv}}$. The parameter α refers to the rate at which infected individuals seek immediate medical attention and care. When $\alpha =0$, all suspected dengue-infected humans do not seek health care and treatment, and are not reported dengue cases. On the other hand, when $\alpha =1$, all infected individuals seek medical care and the cases are recorded. Varying parameter α shifts the curve (time occurrence of the disease), changes the peak (maximum number of reported cases) and alters the width (duration and number of cases) of the healthcare-seeking dynamics. As it can be observed from Figure 2(a), there is no apparent trend when α is varied. The other parameters that influence the dynamics of the healthcare-seeking class are the mosquito biting rate B, transmission probability from human to vector $C_{\mathrm{hv}}$, respectively, vector to human $C_{\mathrm{vh}}$. As these three parameters are varied to increasing values, number of healthcare-seeking individuals raises and the instance of peak values occur earlier from the onset of the disease. The number of new infections is given by $B{C}_{\mathrm{vh}}{I}_{\mathrm{v}}{S}_{\mathrm{h}}/N_{\mathrm{h}}$; therefore, higher B increases disease incidence given that $I_{\mathrm{v}}>0$. Thus, higher cases of healthcare-seeking dengue patients are to be expected. This is depicted in Figure 2(b). Increasing values of $C_{\mathrm{vh}}$ and $C_{\mathrm{hv}}$ are expected to increase number of dengue cases as shown in Figure 2(c ,d).

Figure 2. Dynamics of the healthcare-seeking class under varying model parameters. (a) Effect of varying α on the healthcare-seeking class, $J_{\mathrm{h}}$. (b) Effect of varying B on the healthcare-seeking class, $J_{\mathrm{h}}$. (c) Effect of varying $C_{\mathrm{vh}}$ on the healthcare-seeking class, $J_{\mathrm{h}}$. (d) Effect of varying $C_{\mathrm{hv}}$ on the healthcare-seeking class, $J_{\mathrm{h}}$.

3.3. Sensitivity analysis

Sensitivity analysis is used to assess the degree of adequacy of models and determine which parameters influence the model output the most or the least. Consequently, influential parameters on the model output need to be assigned accurate values while less influential parameters suffice to have rough estimate. In this study, partial rank correlation coefficient (PRCC), a global sensitivity analysis technique proven to be most reliable and efficient among sampling-based methods, is utilized. The PRCC addresses the effect of changes in a specific parameter (linearly discounting the influences over the other parameters) on the reference model output [38]. In order to obtain the PRCC values, Latin Hypercube Sampling (LHS) is chosen for the input parameters where a stratified sampling without replacement is performed. In the current study, a uniform distribution is assigned to each model parameter and sampling is done independently. The range for each parameter is initially set to $\pm 20\mathrm{\%}$ of the nominal values given in Table 1, however, it can be noted that $\pm 50\mathrm{\%}$ to $\pm 90\mathrm{\%}$ do not change the qualitative behaviour of the sensitivities. A total of 1000 simulations are considered, wherein a set of parameter values are selected from the uniform distribution. Time points of interest are designated to examine how the changes in the parameter affect the model output. Thus, the PRCCs of the model output at particular instances are obtained with respect to each parameter. Here, the healthcare-seeking class is considered as the model output and the time points of interests correspond to every two weeks from week 2 to 20 and, two and a half weeks from week 20 to 30.

Note that the PRCC values lie between –1 and 1. Positive (negative) values indicate a positive (negative) correlation of the parameter with the model output. A positive (negative) correlation implies that a positive (negative) change in the parameter will increase (decrease) the model output. The larger the absolute value of the PRCC, the greater the correlation of the parameter with the output. The PRCC values are depicted as bar graphs in Figure 3(a) and its time evolution is illustrated in Figure 3(b). Each coloured bar in the figure corresponds to a particular time instance at which sensitivity is assessed. The dummy variable is included to show the consistency and robustness of the method. That is, introduction of a dummy variable will not affect the sampling procedure and obtaining the PRCC values. It can be seen that sensitivities of parameters might change over time. Note that some parameters influence the model output positively during the onset of the disease and negatively towards the end of the epidemics. In particular, the parameters $B,C_{\mathrm{vh}},$ and $C_{\mathrm{hv}}$ have stronger positive correlations on the target model output which is the healthcare-seeking class $J_{\mathrm{h}}$ at the start of the disease. As the disease progresses and $J_{\mathrm{h}}$ class increases, these parameters will have negative impact on the target output. In effect, as more care-seeking individuals become aware of their conditions, preventive measures avoiding severe complications will be taken, thereby, restraining further mosquito bites and transmission of the disease. As expected, α has a positive impact on the model output because it represents the rate at which an infectious individual transfer to the healthcare-seeking class. Table 3 lists the PRCC values of the model parameters at different time points of interest. Residual scatter plots are also shown in Figure 4 illustrating the respective correlations of the parameters under consideration with the target output which is the healthcare-seeking class, $J_{\mathrm{h}}$, at different time points.

Figure 3. (a) Bar graphs and (b) time course plots of the partial rank correlation coefficients (PRCCs) of the model parameters at 14 different time points (week 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22.5, 25, 27.5, 30) having the healthcare-seeking class as the reference model output. Model parameters were sampled 1000 times. (a) PRCC of the model parameters. (b) PRCC plotted over time.

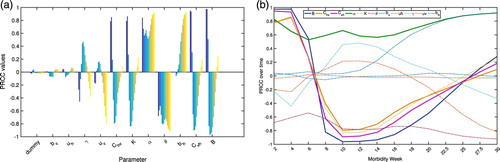
Figure 4. Scatter plots of the residuals of linear regressions of the parameter ($\alpha ,B,C_{\mathrm{vh}},C_{\mathrm{hv}}$) versus all the parameters of the dengue model (abscissa) and the residuals of the regression of the model output ($J_h$) versus the parameter ($\alpha ,B,C_{\mathrm{vh}},C_{\mathrm{hv}}$) (ordinate). Corresponding PRCCs and p-values are obtained at different time points (week 4, 8, 12, 20). (a) Residual scatter plots for α. (b) Residual scatter plots for B. (c) Residual scatter plots for $C_{\mathrm{vh}}$. (d) Residual scatter plots for $C_{\mathrm{hv}}$.

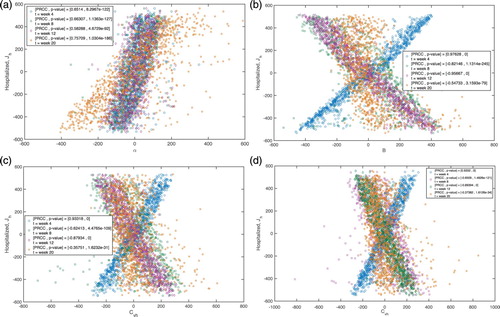
Table 3. Partial rank correlation coefficients (PRCCs) of the model parameters at different time points (week 4, 8, 12, 20) having the healthcare-seeking class as the reference model output.

Parameter	Week 4	Week 8	Week 12	Week 20
$b_{\mathrm{h}}$	0.03326074	0.02634555	0.08166479	0.72440299
${\mu }_{\mathrm{h}}$	−0.01840611	0.01096615	−0.01404464	−0.01795374
B	0.97627901	−0.82145934	−0.95667317	−0.54733113
$C_{\mathrm{hv}}$	0.85555312	−0.40982824	−0.78205065	−0.28843513
$C_{\mathrm{vh}}$	0.93318314	−0.62412762	−0.87934455	−0.35750878
γ	−0.44204164	0.13901939	0.47879786	0.09163382
θ	−0.61020623	−0.62432293	−0.78287610	−0.77245147
$b_{\mathrm{v}}$	0.01916402	−0.05545822	−0.00994370	0.03836683
${\mu }_{\mathrm{v}}$	−0.23054657	0.09739979	0.21898691	−0.16647739
K	0.86682594	−0.46992403	−0.82512793	−0.28395440
α	0.65139711	0.59061355	0.58288276	0.75708901
Dummy	0.03317500	−0.02123174	−0.05246864	−0.01376391

4. Parameter estimation and bootstrapping

4.1. Epidemiological data

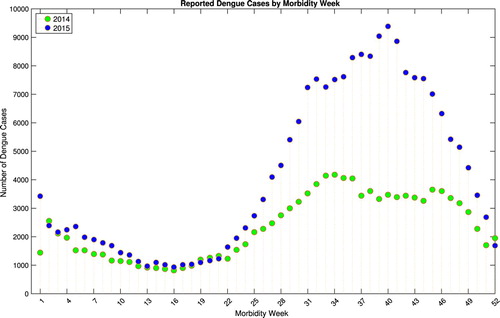
In this study, dengue cases by morbidity week for the year 2014 and 2015 were requested from Epidemiology Bureau, Public Health Surveillance Division of the Department of Health, Philippines. The information was collected from the Philippine Integrated Disease Surveillance and Response System (PIDSR) National Database. Figure 5 depicts the reported dengue cases by morbidity week in the Philippines for the year 2014 and 2015. The graph shows a decreasing trend of reported cases during the first 16 weeks. Observe that for both years, data show increasing pattern of dengue cases from the second quarter (around week 16), attaining a peak on the third quarter and decreasing towards the end of the year. Due to the data profile of annual dengue morbidity cases in the Philippines, two phases are considered. Phase 1 includes data from week 1–15 and phase 2 consists of week 16–52. A smaller peak is observed from the beginning of phase 1 while a significant number of cases is noticeable around the midst of phase 2.

Figure 5. The reported Philippine dengue cases by morbidity week in 2014 and 2015.

4.2. Model identification

To ascertain the identifiability of the dengue model, parameters are determined from the reported data. Model identifiability refers to the goal of verifying unambiguous and accurate parameter estimation in which a parameter set is determined such that the model output is as close as possible to the corresponding set of observations [2]. Parameter estimation involves minimizing a measure of error for the difference between model output and measurements. It should be noted that the quality of the parameter estimates depends on the error criterion, model structure and fidelity of the available data [30].

The adaptability of the dengue model is tested using the reported dengue cases by morbidity week in the Philippines for the year 2014 and 2015. Dengue outbreaks in the country are largely seasonal, with most episodes occurring during the wet season (June–February) [19]. Hence, only phase 2 data (week 16–52) are considered for identification. In the present study, $\left(\alpha B{C}_{\mathrm{vh}}{S}_{\text{h}}{I}_{\mathrm{v}}\right)/N_{\mathrm{h}}$ representing the number of individuals who progresses to the healthcare-seeking compartment is considered as the ‘model data’ and the reported weekly dengue cases as the ‘measurement data’. The parameters $\alpha ,B,C_{\mathrm{vh}}$, and $C_{\mathrm{hv}}$ are identified by minimizing the mean of squared differences between model and measurement data using Matlab's built-in function fminsearch. The achieved parameter values are then used to solve model equation (1(1) $\begin{array}{rl}\frac{\mathrm{d}{S}_{\mathrm{h}}}{\mathrm{d}t}& =b_{\text{h}}{N}_{\mathrm{h}}-(B{C}_{\mathrm{vh}}\frac{I_{\mathrm{v}}}{N_{\mathrm{h}}}+{\mu }_{\mathrm{h}})S_{\mathrm{h}},\\ \frac{\mathrm{d}{I}_{\mathrm{h}}}{\mathrm{d}t}& =(1-\alpha )B{C}_{\mathrm{vh}}\frac{S_{\text{h}}{I}_{\mathrm{v}}}{N_{\mathrm{h}}}-(\gamma +{\mu }_{\mathrm{h}})I_{\mathrm{h}},\\ \frac{\mathrm{d}{J}_{\mathrm{h}}}{\mathrm{d}t}& =\alpha B{C}_{\mathrm{vh}}{S}_{\mathrm{h}}\frac{I_{\mathrm{v}}}{N_{\mathrm{h}}}-(\theta +{\mu }_{\mathrm{h}})J_{\mathrm{h}},\\ \frac{\mathrm{d}{R}_{\mathrm{h}}}{\mathrm{d}t}& =\gamma I_{\mathrm{h}}+\theta J_{\mathrm{h}}-{\mu }_{\text{h}}{R}_{\mathrm{h}},\\ \frac{\mathrm{d}{S}_{\mathrm{v}}}{\mathrm{d}t}& =b_{\mathrm{v}}{N}_{\mathrm{v}}(1-\frac{N_{\mathrm{v}}}{K})-(B{C}_{\mathrm{hv}}\frac{I_{\mathrm{h}}}{N_{\mathrm{h}}}+{\mu }_{\mathrm{v}})S_{\mathrm{v}},\\ \frac{\mathrm{d}{I}_{\mathrm{v}}}{\mathrm{d}t}& =B{C}_{\mathrm{hv}}{S}_{\mathrm{v}}\frac{I_{\mathrm{h}}}{N_{\mathrm{h}}}-{\mu }_{\text{v}}{I}_{\mathrm{v}},\end{array}$(1) ) and consequently, the estimated/identified model data. Plotting the result will obtain the model simulation. Taking the cumulative sum of the estimated model data gives the fit for the model's cumulative sum. 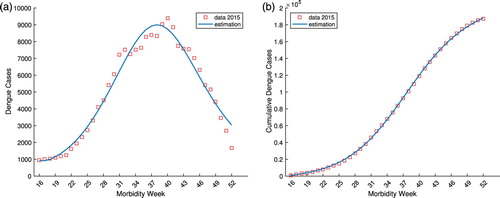Note that $\alpha ,B$ and $C_{\mathrm{vh}}$ directly influences the healthcare-seeking group while $C_{\mathrm{hv}}$ affects the vector first which could have a later consequence on the $J_{\mathrm{h}}$ compartment. Figure 6(a) depicts the reported dengue cases by morbidity week 16–52 in 2014 (red squares) and the model estimation (blue curve). The cumulative sum of the dengue cases (red squares) and the corresponding cumulative model estimation (blue curve) is shown in Figure 6(b). Similarly, Figure 7(a,b) illustrates the model identification using dengue cases by morbidity week 16–52 and the cumulative cases for the year 2015, respectively. As shown in the figures, the model provided a good fit for the data using the estimated parameters both for weekly and cumulative sum of reported dengue cases.

Figure 6. The reported dengue cases by morbidity week and cumulative sum in the Philippines from week 16 to 52 of 2014 and the corresponding model identification. (a) The reported 2014 Philippine dengue cases by morbidity week and the model estimation. (b) The reported 2014 cumulative Philippine dengue cases and the model estimation.

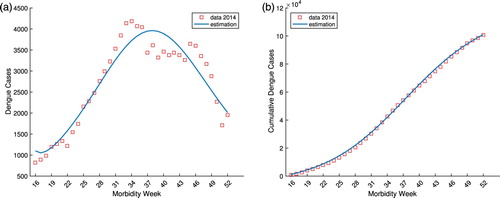
Figure 7. The reported dengue cases by morbidity week and cumulative sum in the Philippines from week 16 to 52 of 2015 and the corresponding model identification. (a) The reported 2015 Philippine dengue cases by morbidity week and the model estimation. (b) The reported 2015 cumulative Philippine dengue cases and the model estimation.

4.3. Bootstrapping

Bootstrapping is a statistical method that relies on building a distribution for a statistic by random sampling with replacement from a given available data. The term bootstrap is derived from the expression pulling oneself up by ones bootstrap, implying that a sample data is used as a population from which repeated samples are drawn. This method allows assigning accuracy measures to the sample estimates and enables to compute the estimated standard errors, confidence intervals, and hypothesis testing [20,26].

In order to quantify the uncertainty of the parameter estimates, parameter bootstrapping approach is utilized to generate multiple samples from the best-fit model [9]. First, parameters are identified through least square fitting the model to the data to obtain the best-fit model (see Section 4.2). Then simulated data sets are generated from the best-fit model by assuming a Poisson error structure. Next, parameters are re-estimated from each of the synthetic datasets/simulated realization to derive a new set of parameter estimates. The set of re-estimated parameters can then be used to characterize their empirical distribution, correlations and construct confidence intervals. The detailed step-by-step algorithm to quantify parameter uncertainty is presented in [8]. The distribution of parameter estimates obtained from 1000 generated datasets are shown in Figures 8 and 9 for 2014 and 2015 Philippine dengue data morbidity week 16 to week 52, respectively. Table 4 provides the initial parameter estimates, estimated value obtained by fminsearch and the corresponding mean, standard deviation (std. dev.) and 95% confidence interval (conf. int.) from bootstrapping method for two data sets. The results provided a certain confidence level of the estimated parameters.

Figure 8. Bootstrap distributions of the parameter estimates $\alpha ,B,C_{\mathrm{vh}},$ and $C_{\mathrm{hv}}$ obtained from 1000 resampling Poisson distribution of 2014 Philippine dengue data by morbidity week.

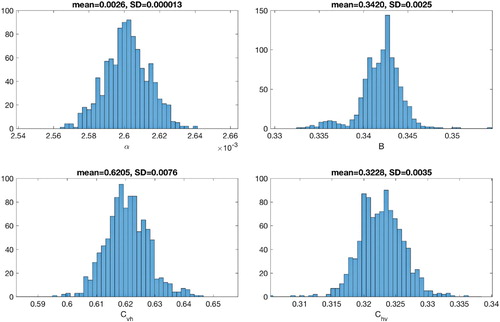
Figure 9. Bootstrap distributions of the parameter estimates $\alpha ,B,C_{\mathrm{vh}},$ and $C_{\mathrm{hv}}$ obtained from 1000 resampling Poisson distribution of 2015 Philippine dengue data by morbidity week.

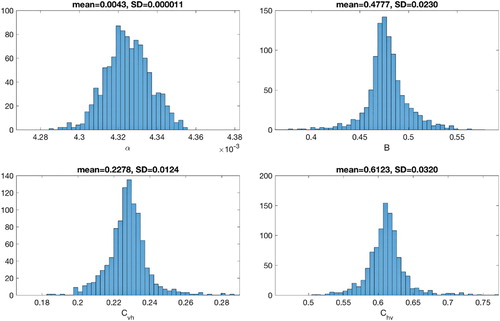
Table 4. Estimated parameter values obtained using 2014 and 2015 Philippine dengue data by morbidity week.

Year	Parameter	Initial	Estimated	Mean	Std. dev.	Conf. int.
2014	α	0.2000	0.0026	0.002608	0.000013	$(0.002584,0.002633)$
	B	1.0000	0.3438	0.342435	0.005263	$(0.332120,0.352750)$
	$C_{\mathrm{vh}}$	0.3750	0.6133	0.615811	0.010432	$(0.595365,0.636256)$
	$C_{\mathrm{hv}}$	0.7500	0.3228	0.324225	0.005208	$(0.314017,0.334433)$
2015	α	0.2000	0.0043	0.004336	0.000011	$(0.004313,0.004358)$
	B	1.0000	0.5176	0.489219	0.031219	$(0.428030,0.550408)$
	$C_{\mathrm{vh}}$	0.3750	0.2069	0.219819	0.016182	$(0.188103,0.251536)$
	$C_{\mathrm{hv}}$	0.7500	0.5713	0.607557	0.044691	$(0.519964,0.695150)$

5. Discussion

Dengue is endemic in all regions of the Philippines with four serotypes circulating in the country causing it a major public health concern [6,18]. In southeast Asia, Philippines ranks among the countries with highest number of dengue episodes [17,49]. In practice, dengue surveillance in the Philippines relies almost entirely on disease reporting units (DRUs), including sentinel hospitals, private clinics, rural health units (RHUs), municipal or city health offices, and human quarantine stations to report all suspected, probable, and confirmed dengue episodes since 2007 to the Philippines Integrated Disease Surveillance and Response System [6,40]. The current surveillance system largely focuses on hospitalized cases, particularly those with severe dengue manifestations. The complexity of illness limits the accuracy of reporting leading to substantial share of unrecorded and under-reported dengue episodes [18,49].

In this work, a model of dengue epidemic based on differential equations is modified and adapted to fit reported dengue cases in the Philippines in 2014 and 2015. A distinct healthcare-seeking compartment is incorporated in the model to represent a class of reported cases who seek immediate medical attention and treatment. Sensitivity of the model parameters is determined to assess those with significant influence on the model output. Some parameters positively affect the model output at the onset of the disease and have negative impact towards the end of the epidemics. See for instances, parameters in a tuberculosis model changing their impacts over time with respect to specific output(s) [38,39], a mechanism in cholera model is time-dependent as system dynamic progresses [57], and variable sensitivities of parameters in calcium dynamics model [11]. Parameters including the mosquito biting rate B, transmission probability from mosquito to human $C_{\mathrm{vh}}$, respectively, from human to mosquito $C_{\mathrm{hv}}$, and fraction of individuals who seek healthcare α, are identified using the reported data. The parameter estimates for morbidity week 16–52 of 2014 and 2015 are obtained with certain degree of accuracy and provided good fitting results. In particular, the obtained values for the parameter α is too small. This could be indicative that very few dengue-infected individuals seek treatment and/or there is an inadequate public health facility which eventually lead to unreported cases. Hence, it is suggested that efforts on dengue surveillance should be intensified in order to eventually control dengue virus transmission and better assess the burden estimate of the disease in the country. This under-reporting is consistent with the results obtained in other studies (see for instance, [18,48,49]). The estimated value for the reporting rate α is comparable to the average dengue hospitalization rate in Malaysia for year 2010 to 2013 which is 2.6 and 3.075 per 1000 population based on privately insured population and total population of Malaysia, respectively [52]. The identified value for B is relatively small which can be accounted for lack of sufficient information on human and vector population. This limitation requires collection of additional data. The uncertainties in parameter estimation are influenced, among others, by model structure and data fidelity. These uncertainties limit the confidence that the models accurately capture disease transmission dynamics in a specific location. The model cannot be used to make explicit predictions, however, it provides information on relative effects of different perturbations in both human and vector population dynamics and could aid in developing more informed decisions on specific local control strategies [21,58]. Based on the obtained values of the parameter estimates, the reproduction number ${\mathcal{R}}_0^{2014}\approx 2.30$ and ${\mathcal{R}}_0^{2015}\approx 2.67$ are determined for year 2014 and 2015, respectively. Even if the actual population size for years 2014 and 2015 are used, ${\mathcal{R}}_0$ will remain greater than 1 (${\mathcal{R}}_0^{2014}\approx 1.62$, ${\mathcal{R}}_0^{2015}\approx 1.87$) enough to sustain an epidemic in the country.

Most mathematical models are sensitive to initial conditions. In the current investigation, hypothetical conservative estimates on initial conditions are considered due to unavailability of sufficient information. Data collected from experimental assays on mosquito population would give improved estimate on vector parameters [37]. These specific information can better characterize dengue occurrence and transmission dynamics in the Philippines. Furthermore, to have a more holistic view on the biological range of the model parameters, extensive identification using data sets from different year should be performed. This would aide in understanding the spread of the disease in the country and eventually provide confidence in the prediction of the disease transmission for the succeeding year. Model can also be improved by including different serotypes and various level of mosquito development. However, this would likewise entail more data from different sources to validate the model. Another important research direction is formulation of an optimal control problem to determine strategies for mitigating the spread of the disease. One can address, among others, which strategies (human and/or vector controls) significantly reduce dengue cases; when to implement these strategies; and which is the most cost-efficient strategy.

Acknowledgements

The authors acknowledge the Institute of Mathematics, University of the Philippines for the research load credit given in order to conduct this research. Gratitude is also due to the Department of Health Philippines, Epidemiology Bureau, Public Health Surveillance Division for providing the reported dengue cases by morbidity week in the Philippines from year 2014 to 2015. The authors would also like to thank the reviewers for the thoughtful comments and constructive suggestions, which help to improve the quality of this manuscript.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

Aurelio A. de los Reyes V  http://orcid.org/0000-0001-5418-4579

Jose Maria L. Escaner IV http://orcid.org/0000-0002-8724-0036

Additional information

Funding

This research was supported by the National Research Council of the Philippines (NRCP) with Project No. P-008.