Onchocerciasis dynamics: modelling the effects of treatment, education and vector control

Abstract

A deterministic model of onchocerciasis disease dynamics is considered in a community partitioned into compartments based on the disease status. Public health education is offered in the community during the implementation of mass treatment using ivermectin drugs. Also, larviciding and trapping strategies are implemented in the vector population with the aim of controlling population growth of black flies. We fit the model to the data to check the suitability of the model. Expressions are derived for the influence on the reproduction numbers of these strategies. Numerical results show that the dynamics of onchocerciasis and the growth of black flies are best controlled when the four strategies are implemented simultaneously. Also, the results suggest that for the elimination of the disease in the society there is a need for finding another drug which will be implemented to ineligible human as well as killing the adult worms instead of ivermectin.

Keywords:

• Onchocerciasis
• ivermectin
• public health education
• larviciding
• trapping

1. Introduction

Onchocerciasis is one of the neglected tropical diseases caused by the parasite Onchocerca Volvulus, a filarial nematode [2]. The disease is transmitted from one person to another by repeated bites of black flies which often breed in fast flowing rivers, and the parasitic infection can result in skin disease, impaired vision and blindness. The blindness and severity of skin lesions have adverse social-economic consequences leading to desertion of large areas of fertile land adjacent to vector breeding sites, impeding the economic development of affected countries [33]. Although, some of the countries (e.g. Colombia, Equador and Mexico) have been declared to be free from the disease, but onchocerciasis is still endemic in 31 countries in Sub-saharan Africa, three countries in Latin America and in Yemen in the middle East.

Control strategies of morbidity of onchocerciasis have included removal of nodules (nodulectomy), vector control and more recently mass drug administration (MDA) with ivermectin [10,11]. For instance, the vector control and distribution of ivermectin which was administered by the Onchocerciasis Control Programme (OCP) (1974–2002) were implemented in 11 West African countries to control the spread of disease [4]. Since there were other countries where the disease is endemic, African Programme for Onchocerciasis Control (APOC) was initiated in 1995 for the purpose of eliminating the disease in these African countries, by using ivermectin drugs [9]. The drug is administered annually to eligible population regardless of their disease status [5]. The drug kills the produced microfilariae which cause the disease and temporarily sterilizes adult worm [3]. From the report by [34] the disease is still endemic in African countries despite of the continued use of ivermectin, e.g. see [13] for details). This may be a result of low coverage of distribution of ivermectin to the community due to lack of broad knowledge on the disease, negative attitude towards the ivermectin drug,and disbelief the technique of determining the dosage of drug. Also the recent study by Hendy et al. [13] has suggested that Ivermectin alone may not be sufficient to eliminate onchocerciasis. For this case, there is a need of taking into account other control strategies which together with ivermectin treatment may attain the goal of onchocerciasis elimination.

Various studies have been conducted on the role of intervention strategies against the spread of onchocerciasis. For instance, Remme et al. [28] used skin snip survey in West Africa to investigate the impact of controlling black flies by larviciding. Plaisier et al. [27] used micro simulation model to determine the period required for combining annual ivermectin treatment and vector control in the onchocerciasis Control Programme in West Africa. Alley et al. [1] used a computer simulation model to study prevention of onchocerciasis by using macrofilaricide which kills the adult worms. Udall [30] studied the diagnosis and treatment of onchocerciasis by using ivermectin. JibriL and Ibrahim [18], Oguoma and Acho [23] investigated the spread and control of onchocerciasis by using ivermectin treatment. Also, Omondi et al. [24] developed a deterministic model to investigate the impact of mass administration of ivermectin by creating a class of individuals who are temporarily protected from infection in the first half of the year and the protection wanes out in the second half of the year. In another study, Omondi et al. [25] investigated the effect of mass administration by using impulsive differential equations.

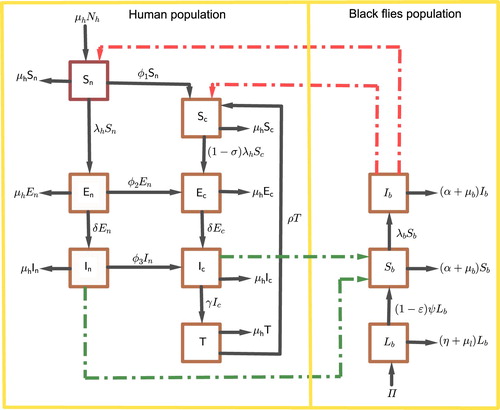
In the present paper we consider a deterministic model of susceptible $\to$ exposed $\to$ infectious $\to$ susceptible (SEIS) in two populations of human and blackfly as a vector. For this model we investigate the effects of four control strategies, namely; mass drug treatment with ivermectin and public health education are implemented in the human community, while larviciding and trapping technique are implemented in the vector population as a move to control the population growth of the vector. Public health education campaign intends to provide comprehensive knowledge about the disease, how to protect themselves using insect repellent and proper clothing, and how medication is provided to the community to increase compliance on human individuals. Larviciding is the process of applying larvicides on the breeding sites of black flies to kill larvae in order to reduce the number of matured adult. Trapping is the process of collecting adult female black flies using different types of traps and baits which attract vectors and remove them from the population [22].

For this model we derive the reproduction number in the presence of the four interventions. By the reproduction we will, in this paper, mean the number of people infected by a (typical) infected person in a totally susceptible population. The rest of the paper is organized as follows. In Section 2 we describe the model formulation and model analysis is done in Section 3. Simulation and numerical results are given in Sections 4 and 5 contains concluding remarks.

2. Model formulation

Two populations namely human host and black flies are considered in the model. The human host population is divided into non-compliant (persons who have negative attitude to the mass treatment (ivermectin) and those who are ineligible to the ivermectin drug) and compliant population (persons who are aware of the disease and comply with ivermectin). From these two groups of human hosts, the model will have seven compartments at any time t namely: susceptible human individuals who are at risk of getting infections denoted by $S_i$, exposed human individuals who are infected but not infectious denoted by $E_i$, infected human individuals who are infectious and can transmit the disease represented by $I_i$, and human individuals treated for microfilariae and remain with the adult worms denoted by T, for $i=(c,n)$ where c stands for compliant individuals and n stands for non-compliant individuals.

Furthermore, black flies (vector) population start with larvae denoted by $L_b$ and the adult female black flies population is divided into susceptible and infected black flies denoted by $S_b$ and $I_b$ respectively.

It is assumed that human population is constant (birth rate = death rate) because the disease does not induce death but the population of black flies vary. Also it is assumed that susceptible human individuals increase from new born depending on the total population of human at a rate ${\mu }_h{N}_h$. Although Ivermectin kills microfilariae and reduce fertility to the adult female worms, but the drug is distributed to all human individuals aged five years old and above regardless of their disease status except ineligible individuals such as children under five years, pregnant women and serious sick human [3]. Therefore, education about onchocerciasis (symptoms, treatment and how to prevent themselves from black flies) is provided to the susceptible non-compliant in which the person who comply with ivermectin and protect themselves from black flies move to susceptible compliant human individuals at a rate ${\phi }_1$. In addition to that, exposed and infected non-compliant individuals become educated at rates ${\phi }_2$ and ${\phi }_3$ respectively and move to their respective compartments. However, susceptible non-compliant and compliant individuals may get infected after being bitten by infectious female black flies at the rate ${\lambda }_h$ and move to their corresponding exposed classes. The parameter ${\lambda }_h$ is the force of infection for human which is denoted by (1) ${\lambda }_h=\frac{\theta {\text{β}}_h{I}_b}{N_h},$(1) where θ is the biting rate of black flies, ${\text{β}}_h$ is the probability that contact between infected back flies and susceptible human cause infections to human.

Furthermore, public health education can be used to control the spread of onchocerciasis within the hardest hit communities. The disease can be prevented by avoiding being bitten by black flies and this may include making people aware on the use of insect repellent and proper clothing [7]. For that case, it is assumed that susceptible compliant individuals are aware of the disease and they know how to protect themselves from female black flies and their rate of transmission is reduced by $(1-\sigma )$, where $0<\sigma <1$ is the efficacy of public health education [17]. After a given period of time, exposed compliant and non-compliant individuals develop symptoms of onchocerciasis and move to their respective infectious compartments at the rate δ. Since ivermectin kills microfilariae and not the macrofilariae, the infectious compliant human will be treated for microfilariae at a rate γ and move to the treated compartment. The treated human will recover from onchocerciasis after being cleared the macrofilariae parasites due to their natural death [20] at a rate ρ and move to susceptible compliant human individuals.

On the other hand, it is assumed that the growth of larvae depends on hatched eggs laid by susceptible and infected black flies taking into account the carrying capacity of the breeding site given by $\pi (S_b+I_b)(1-L_b/K)$, where π is the number of laid eggs and K is the carrying capacity depending on the space available, food and fresh air. The larvae population decreases by natural death at a rate ${\mu }_l$ and death due to larviciding at a rate η. The surviving larvae will mature at a rate ψ and move to susceptible adult female black flies. But the maturation rate is reduced by a rate $(1-ϵ)$, where ε is the efficacy of larvicide. We do not consider male black flies as susceptible because they are not playing any role in the transmission of onchocerciasis. Susceptible female black flies get infections when taking blood meal from infectious human individuals (compliant, non-compliant or treated human) at a rate ${\lambda }_b$. The parameter ${\lambda }_b$ is the force of infection for black flies given by (2) ${\lambda }_b=\frac{\theta {\text{β}}_b({\nu }_1{I}_c+I_n+{\nu }_{2}T)}{N_h},$(2) where ${\text{β}}_b$ is the probability that contact between susceptible black flies and infectious human cause infections to black flies, ${\nu }_1$ and ${\nu }_2$ are modification parameters which reduce transmission on infectious compliant and Treated humans respectively.

Using trapping as a strategy of reducing the number of black flies, susceptible and infected black flies are trapped at a rate α. The model assumes that the infected black flies do not recover. The susceptible and infected female black flies (vector) die naturally at a rate ${\mu }_b$. The interaction between host and vector populations is illustrated in Figure 1.

Figure 1. Schematic presentation of the transmission dynamics of Onchocerciasis.

2.1. Equations of the model

From the model description and underlying assumptions the following system of ordinary differential equations is obtained: (3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) where (4) $\begin{array}{rl}{y}_1& =({\phi }_1+{\mu }_h),y_2=(\delta +{\phi }_2+{\mu }_h),y_3=(\delta +{\mu }_h),y_4=({\phi }_3+{\mu }_h),\\ y_5& =(\gamma +{\mu }_h),y_6=(\rho +{\mu }_h),y_7=\left(\right(1-ϵ)\psi +\eta +{\mu }_l),y_8=(\alpha +{\mu }_b).\end{array}$(4) The initial conditions of the model system  (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) are $S_n\left(0\right)>0,S_c\left(0\right)>0,E_n\left(0\right)\ge 0,E_c\left(0\right)\ge 0,I_n\left(0\right)\ge 0,I_c\left(0\right)\ge 0,T\left(0\right)\ge 0,L_b\left(0\right)>0,S_b\left(0\right)>0$ and $I_b\left(0\right)\ge 0$.

2.2. Basic properties of the model

In this part, positivity of the solution and invariant region (boundedness) as well as the existence and stability of equilibrium points of the model system  (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) are analysed qualitatively.

2.2.1. Positivity and boundedness of the solution

In order to show that the model (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) is biologically meaningful and well posed it is enough to prove that the solution of all state variables are positive all the time. This is done by using the approach employed by Huo and Qiu [15] and Huo et al. [16]. Consider the following lemma:

Lemma 2.1

The solution of all state variables of the model system (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) with positive initial values are positive for all $t>0$.

Proof.

According to Huo and Qiu [15] and Huo et al. [16] we prove the positivity by contradiction as follows: Given the non-negative initial conditions $S_n\left(0\right),S_c\left(0\right),E_n\left(0\right),E_c\left(0\right),I_n\left(0\right),I_c\left(0\right),L_b\left(0\right),S_b\left(0\right)$ and $I_b\left(0\right)$, the positivity of the model system  (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) can be proved. If not, we prove by contradiction by assuming that there exist a slightly time $t_0$ such that $\begin{array}{rl}& S_n\left(0\right)>0,S_n\left(t_0\right)=0,S_n^{\mathrm{\prime }}\left(t_0\right)\le 0,S_c\left(t\right)>0,E_n\left(t\right)>0,E_c\left(t\right)>0,I_n\left(t\right)>0,\\ & I_c\left(t\right)>0,L_b\left(t\right)>0,S_b\left(t\right)>0,I_b\left(t\right)>0,0\le t<t_0.\end{array}$ But in our case, from the first equation of the model system (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) we have $\frac{d{S}_n\left(t_0\right)}{dt}={\mu }_h{N}_h-({\lambda }_h+y_1)S_n\left(t_0\right)$ It implies that $\frac{d{S}_n\left(t_0\right)}{dt}={\mu }_h{N}_h>0,$ which contradict with our assumption and this means that $S_n\left(t\right)>0$ for all t>0. Also, it is assumed that there exist a slightly time $t_1$ such that $\begin{array}{rl}& S_c\left(0\right)>0,S_c\left(t_1\right)=0,S_c^{\mathrm{\prime }}\left(t_1\right)\le 0,S_n\left(t\right)>0,E_n\left(t\right)>0,E_c\left(t\right)>0,I_n\left(t\right)>0,\\ & I_c\left(t\right)>0,L_b\left(t\right)>0,S_b\left(t\right)>0,I_b\left(t\right)>0,0\le t<t_1.\end{array}$ From the second equation of the model system (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) we have $\frac{d{S}_c\left(t_1\right)}{dt}={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c\left(t_1\right),$ which gives $\frac{d{S}_c\left(t_1\right)}{dt}={\phi }_1{S}_n+\rho T>0.$ And this contradicts with our assumption therefore it means that $S_c\left(t\right)>0$ for all t>0 Now following the same procedures, it can be shown that $E_n\left(t\right)\ge 0,E_c\left(t\right)\ge 0,I_n\left(t\right)\ge 0,I_c\left(t\right)\ge 0,L_b\left(t\right)\ge 0,S_b\left(t\right)\ge 0,I_b\left(t\right)\ge 0$ for all $t>0$.

Thus the solution of all state variables of the model system (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) are non-negative.

2.2.2. Invariant region

In this part the region at which the solution of the model has biological meaning is obtained. Since we have two populations we let the feasible region be $\mathrm{\Theta }={\mathrm{\Theta }}_h\cup {\mathrm{\Theta }}_b\in {\mathbb{R}}_{+}^7\times {\mathbb{R}}_{+}^3$ where ${\mathrm{\Theta }}_h=\{S_n,S_c,E_n,E_c,I_n,I_c,T\in {\mathbb{R}}_{+}^7:S_n+S_c+E_n+E_c+I_n+I_c+T=N_h\}$ and ${\mathrm{\Theta }}_b=\{L_b,S_b,I_b\in {\mathbb{R}}_{+}^3:L_b\le K,S_b+I_b=N_b\le \frac{(1-ϵ)K}{y_8}\}.$

To prove the feasible region, the first seven and the last two equations of the model system  (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) are added to obtain $d{N}_h/dt={\mu }_h{N}_h-{\mu }_h(S_n+S_c+E_n+E_c+I_n+I_c+T)$ which gives (5) $\frac{d{N}_h}{dt}={\mu }_h{N}_h-{\mu }_h{N}_h=0\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}\mathrm{p}\mathrm{o}\mathrm{p}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\right)$(5) and for black fly population we have $\frac{d{N}_b}{dt}=(1-ϵ)K-y_8(S_b+I_b)$ implying that (6) $\frac{d{N}_b}{dt}=(1-ϵ)K-y_8{N}_b.$(6) Equation (5(5) $\frac{d{N}_h}{dt}={\mu }_h{N}_h-{\mu }_h{N}_h=0\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}\mathrm{p}\mathrm{o}\mathrm{p}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\right)$(5) ) shows that the human population is constant that is $S_n+S_c+E_n+E_c+I_n+I_c+T=N_h$ which implies that $S_n\le N_h,S_c\le N_h,E_n\le N_h,E_c\le N_h,I_n\le N_h{I}_c\le N_h,T\le N_h.$ Solving for $N_b$ from Equation (6(6) $\frac{d{N}_b}{dt}=(1-ϵ)K-y_8{N}_b.$(6) ) it gives (7) $N_b\left(t\right)\le \frac{(1-ϵ)K}{y_8}+\left(N_b\left(0\right)-\frac{(1-ϵ)K}{y_8}\right){\mathrm{e}}^{-y_{8}t}$(7) Using the differential inequality theorem in [6] from Equation (7(7) $N_b\left(t\right)\le \frac{(1-ϵ)K}{y_8}+\left(N_b\left(0\right)-\frac{(1-ϵ)K}{y_8}\right){\mathrm{e}}^{-y_{8}t}$(7) ) we get $0\le N_b\left(t\right)\le \frac{(1-ϵ)K}{y_8}$ as t goes to infinity.

Therefore, the solution on human and black flies population enters the invariant regions ${\mathrm{\Theta }}_h=\left\{\right(S_n,S_c,E_n,E_c,I_n,I_c,T)\in {\mathbb{R}}_{+}^7:S_n+S_c+E_n+E_c+I_n+I_c+T=N_h\}$ and ${\mathrm{\Theta }}_b=\left\{\right(L_b,S_b,I_b)\in {\mathbb{R}}_{+}^3:L_b\le K,N_b\le \frac{(1-ϵ)K}{y_8}\}$.

This result shows that the region is bounded and it attracts all solutions in $\mathrm{\Theta }={\mathrm{\Theta }}_h\cup {\mathrm{\Theta }}_b$ and therefore the model formulated can be considered in Θ and we can say that the model is biologically meaningful and well posed.

3. Model analysis

3.1. Disease-free equilibrium point

Disease-free equilibrium point is a steady-state solution of the model when there is no disease in both human host and black fly vector populations. That is at disease-free equilibrium, $E_n=E_c=I_n=I_c=T=I_b=0.$. Putting all infected classes equal to zero in the model system  (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) and solve, we get two equilibrium points. Trivial disease-free equilibrium point is obtained when black flies population does not exist which is not realistic because it is not possible to eliminate all black flies and this is given by $E^0=(S_n^{\ast },S_c^{\ast },0,0,0,0,0,0,0,0)=\left(\frac{{\mu }_h{N}_h}{y_1},\frac{{\phi }_1{N}_h}{y_1},0,0,0,0,0,0,0,0\right).$ The second disease-free equilibrium point which has a biological meaning is given by $E^1=(S_n^{\ast },S_c^{\ast },0,0,0,0,0,L_b^{\ast },S_b^{\ast },0),$ where $S_n^{\ast }={\mu }_h{N}_h/y_1,S_c^{\ast }={\phi }_1{N}_h/y_1,L_b^{\ast }=\frac{K{y}_7{y}_8(M-1)}{\pi (1-ϵ)\psi },S_b^{\ast }=\frac{K{y}_7(M-1)}{\pi },$ and (8) $M=\frac{(1-ϵ)\pi \psi }{y_7{y}_8}.$(8)

3.2. Effective reproduction number

Here we compute the reproduction number when the intervention strategies are in place. The reproduction number is a useful quantity that governs the dynamics of disease in epidemiology. It helps to predict whether the disease will persist in the society or will die out. The reproductive number can be calculated by using next generation method as illustrated by Van den Driessche and Watmough [31]. The matrices which describe the rate of new infection terms and transfer terms (evaluated at disease-free equilibrium) are, respectively, given by $\begin{array}{rl}F& =\left(\begin{array}{cccccc}0& 0& 0& 0& 0& \frac{\theta S_n^{\ast }{\text{β}}_h}{N_h}\\ 0& 0& 0& 0& 0& \frac{(1-\sigma )\theta S_c^{\ast }{\text{β}}_h}{N_h}\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& \frac{\theta S_b^{\ast }{\text{β}}_b}{N_h}& \frac{\theta S_b^{\ast }{\text{β}}_b{\nu }_1}{N_h}& \frac{\theta S_b^{\ast }{\text{β}}_b{\nu }_2}{N_h}& 0\end{array}\right)and\\ V& =\left(\begin{array}{cccccc}{y}_2& 0& 0& 0& 0& 0\\ -{\phi }_2& y_3& 0& 0& 0& 0\\ -\delta & 0& y_4& 0& 0& 0\\ 0& -\delta & -{\phi }_3& y_5& 0& 0\\ 0& 0& 0& -\gamma & y_6& 0\\ 0& 0& 0& 0& 0& y_8\end{array}\right).\end{array}$

Thus the effective reproduction number denoted by $R_{\mathrm{e}\mathrm{f}\mathrm{f}}$ which is the dominant eigenvalue of the matrix $F{V}^{-1}$ is given by $R_{\mathrm{e}\mathrm{f}\mathrm{f}}=\sqrt{\frac{\delta {\theta }^{2}K(M-1)y_7{\text{β}}_b{\text{β}}_h\left(d_1{y}_4\right({\phi }_2{\mu }_h+k{y}_2{\phi }_1)+y_3{\mu }_h(d_1{\phi }_3+y_5{y}_6\left)\right)}{\pi y_1{y}_2{y}_3{y}_4{y}_5{y}_6{y}_8{N}_h}},$ where $d_1=\gamma {\nu }_2+{\nu }_1{y}_6,$ $y_1,y_2,y_3,y_4,y_5,y_7,$ and $y_8$ have the same meaning as in (4(4) $\begin{array}{rl}{y}_1& =({\phi }_1+{\mu }_h),y_2=(\delta +{\phi }_2+{\mu }_h),y_3=(\delta +{\mu }_h),y_4=({\phi }_3+{\mu }_h),\\ y_5& =(\gamma +{\mu }_h),y_6=(\rho +{\mu }_h),y_7=\left(\right(1-ϵ)\psi +\eta +{\mu }_l),y_8=(\alpha +{\mu }_b).\end{array}$(4) ) and M is the same as in (8(8) $M=\frac{(1-ϵ)\pi \psi }{y_7{y}_8}.$(8) ).

The effective reproduction number determines whether onchocerciasis will vanish or exist in the two populations (human and black flies) when four interventions are implemented in a move to eradicate the disease. The effective reproduction number is thus the average number of new cases produced by a single onchocerciasis infectious person in a society at which intervention strategies (mass treatment with ivermectin, public health education campaign, larviciding and trapping) are implemented.

According to the obtained reproductive number we can say that when $M\le 1$ the trivial equilibrium point $E^0$ becomes stable, and when M>1 the trivial equilibrium point $E^0$ becomes unstable while the disease-free equilibrium point $E^1$ becomes stable. In this paper we assume that black flies exit therefore M>1.

Thus, applying theorem (2) of [31] the following result is established:

Lemma 3.1

The disease-free equilibrium is locally asymptotically stable when $R_{\mathrm{e}\mathrm{f}\mathrm{f}}<1$ and unstable if $R_{\mathrm{e}\mathrm{f}\mathrm{f}}>1$.

When $R_{\mathrm{e}\mathrm{f}\mathrm{f}}<1$ (in Lemma 2), it implies that the disease will extinct in the society because an infectious individual entered in the society can produce small number of secondary infected individuals. On the other hand if $R_{\mathrm{e}\mathrm{f}\mathrm{f}}>1$ the disease will persist in the society because when an infectious individual entered in the society can produce a large number of new infected individuals.

3.3. Global stability of the disease-free equilibrium

In this part, we investigate the global stability of Disease-Free Equilibrium using the approach demonstrated by Dumont et al. [12] and Kamgang and Sallet [19]. In this approach the model system (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) is written as: (9) $\begin{array}{rl}& \frac{d{Y}_s}{dt}=B_1(Y_s-Y_{E^1\left(0\right)})+B_{12}{Y}_i\\ & \frac{d{Y}_i}{dt}=B_2{Y}_i,\end{array}$(9) where $Y_s$ stand for classes of individuals who do not transmit onchocerciasis, in our case $Y_s=(S_n,S_c,T,L_b,S_b{)}^{Tr}$, $Y_i$ stand for classes of individuals who can transmit onchocerciasis, that is $Y_i=(E_n,E_c,I_n,I_c,I_b{)}^{Tr}$, $Y=(Y_s,Y_i)$, $E^1=(S_n^{\star },S_c^{\star },0,0,0,0,0,L_b^{\star },S_b^{\star },0{)}^{Tr}$ and Tr stand for Transpose. The matrix $B_1$ and $B_{12}$ are obtained by differentiating the non-transmitting equations in the model system (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) with respect to non-transmitting and transmitting state variables respectively at disease-free equilibrium point.

The Disease-Free Equilibrium is globally asymptotically stable if the eigenvalues of $B_1$ are real non-positive, and $B_2$ is a Metzler matrix (that is, the off-diagonal elements of $B_2$ are positive).

Thus, from the model system (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) we have $\begin{array}{rl}{B}_1& =\left(\begin{array}{cccc}-y_1& 0& 0& 0\\ {\phi }_1& -{\mu }_h& 0& 0\\ 0& 0& -\frac{g\pi \psi }{y_8}& \frac{y_7{y}_8}{g\psi }\\ 0& 0& g\psi & -y_8\end{array}\right),\\ B_{12}& =\left(\begin{array}{cccccc}0& 0& 0& 0& 0& -R_1\\ 0& 0& 0& 0& \rho & -R_2\\ 0& 0& 0& 0& 0& \frac{y_7{y}_8}{(1-ϵ)\psi }\\ 0& 0& -R_3& -{\nu }_1{R}_3& -{\nu }_2{R}_3& 0\end{array}\right),\end{array}$ where $R_1=\theta {\text{β}}_h{\mu }_h/y_1,R_2=\frac{\theta (1-\sigma ){\text{β}}_h{\phi }_1}{y_1},R_3=\frac{K(M-1)\theta y_7{\text{β}}_b}{\pi N_h}$ and M is the same as in (8(8) $M=\frac{(1-ϵ)\pi \psi }{y_7{y}_8}.$(8) )

Also, the matrix $B_2$ is obtained by differentiating the transmitting equations in the model system (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) with respect to transmitting state variables which gives, $B_2=\left(\begin{array}{cccccc}-y_2& 0& 0& 0& 0& \frac{\theta {\text{β}}_h{\mu }_h}{y_1}\\ {\phi }_2& -y_3& 0& 0& 0& \frac{(1-\sigma )\theta {\text{β}}_h{\phi }_1}{y_1}\\ \delta & 0& -y_4& 0& 0& 0\\ 0& \delta & {\phi }_3& -y_5& 0& 0\\ 0& 0& 0& \gamma & -y_6& 0\\ 0& 0& \frac{K(M-1)\theta y_7{\text{β}}_b}{\pi N_h}& \frac{K(M-1)\theta y_7{\text{β}}_b{\nu }_1}{\pi N_h}& \frac{K(M-1)\theta y_7{\text{β}}_b{\nu }_2}{\pi N_h}& -y_8\end{array}\right).$ On computing the real parts of eigenvalues of $B_1$ we get $-y_1,-y_1,-(1-ϵ)\psi \left(\pi \right(1-ϵ)\psi +y_8^2),-(1-ϵ)\psi \left(\pi \right(1-ϵ)\psi +y_8^2),-{\mu }_h$ which shows that all are non-positive and real. This indicates that at disease free the system $\frac{d{Y}_s}{dt}=B_1(Y_s-Y_{E^1\left(0\right)})+B_{12}{Y}_i$ is globally asymptotically stable. Again we need to test if $B_2$ is a Metzler stable matrix by applying the proposition 3.1 in [19] which restate that:

Lemma 3.2

Let P be a Metzler matrix, which can be arranged in block form as $P=\left(\begin{array}{cc}{P}_1& P_2\\ P_3& P_4\end{array}\right)$ where $P_1$ and $P_4$ are square matrices. Then P is Metzler stable if and only if $P_4$ and $P_1-P_2{P}_4^{-1}{P}_3$ or $P_1$ and $P_4-P_3{P}_1^{-1}{P}_2$ are Metzler stable.

Proof.

Firstly, matrix $B_2$ is compared with P which gives $\begin{array}{rl}{P}_1& =\left(\begin{array}{cc}-y_2& 0\\ {\phi }_2& -y_3\end{array}\right),P_2=\left(\begin{array}{cccc}0& 0& 0& \frac{\theta {\text{β}}_h{\mu }_h}{y_1}\\ 0& 0& 0& \frac{(1-\sigma )\theta {\text{β}}_h{\phi }_1}{y_1}\end{array}\right),\\ P_3& =\left(\begin{array}{cc}\delta & 0\\ 0& \delta \\ 0& 0\\ 0& 0\end{array}\right),P_4=\left(\begin{array}{cccc}-y_4& 0& 0& 0\\ {\phi }_3& -y_5& 0& 0\\ 0& \gamma & -y_6& 0\\ \frac{K(M-1)\theta y_7{\text{β}}_b}{\pi N_h}& \frac{K(M-1)\theta y_7{\text{β}}_b{\nu }_1}{\pi N_h}& \frac{K(M-1)\theta y_7{\text{β}}_b{\nu }_2}{\pi N_h}& -y_8\end{array}\right).\end{array}$ After some calculations we get: $P_1-P_2{P}_4^{-1}{P}_3=\left(\begin{array}{cc}\frac{\delta \theta R_1{\text{β}}_h{\mu }_h(y_5{y}_6+d_1{\phi }_3)}{y_1{y}_4{y}_5{y}_6{y}_8}-y_2& \frac{\delta \theta d_1{R}_1{\text{β}}_h{\mu }_h}{y_1{y}_5{y}_6{y}_8}\\ \\ {\phi }_2+\frac{k\delta \theta R_1{\text{β}}_h{\phi }_1(y_5{y}_6+d_1{\phi }_3)}{y_1{y}_4{y}_5{y}_6{y}_8}& \frac{k\delta \theta d_1{R}_1{\text{β}}_h{\phi }_1}{y_1{y}_5{y}_6{y}_8}-y_3\end{array}\right)$ Therefore, $P_1-P_2{P}_4^{-1}{P}_3$ will be Metzler stable matrix if and only if $y_2{y}_3-\frac{\delta {\theta }^{2}K(M-1)y_7{\text{β}}_b{\text{β}}_h\left(d_1{y}_4\left({\phi }_2{\mu }_h+k{y}_2{\phi }_1\right)+y_3{\mu }_h\left(d_1{\phi }_3+y_5{y}_6\right)\right)}{\pi y_1{y}_4{y}_5{y}_6{y}_8{N}_h}\ge 0.$ That is $\frac{\delta {\theta }^{2}K(M-1)y_7{\text{β}}_b{\text{β}}_h\left(d_1{y}_4\left({\phi }_2{\mu }_h+(1-\sigma )y_2{\phi }_1\right)+y_3{\mu }_h\left(d_1{\phi }_3+y_5{y}_6\right)\right)}{\pi y_1{y}_2{y}_3{y}_4{y}_5{y}_6{y}_8{N}_h}\le 1,$ which implies that $R_{\mathrm{e}\mathrm{f}\mathrm{f}}\le 1.$ Thus, the Disease-Free Equilibrium is globally asymptotically stable when $R_{\mathrm{e}\mathrm{f}\mathrm{f}}\le 1$, otherwise it is unstable.

3.4. Endemic equilibrium point

Endemic equilibrium point is a steady-state solution which shows the existence of the disease in the society. It is calculated by putting the left hand side of the system (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) equals to zero and solve for all state variables in terms of force of infection ${\lambda }_h^{\ast \ast }$ or ${\lambda }_b^{\ast \ast }$ to obtain (10) $\begin{array}{rl}& S_n^{\ast \ast }=\frac{{\mu }_h{N}_h}{{\lambda }_h^{\ast \ast }+y_1},S_c^{\ast \ast }=\frac{{\mu }_h{N}_h\left(\gamma \delta m_1\rho {\lambda }_h^{\ast \ast }+y_2{y}_3{y}_4{y}_5{y}_6{\phi }_1\right)}{y_2{y}_4\left({\lambda }_h^{\ast \ast }+y_1\right)\left(y_3{y}_5{y}_6\left((1-\sigma ){\lambda }_h^{\ast \ast }+{\mu }_h\right)-\gamma \delta (1-\sigma )\rho {\lambda }_h^{\ast \ast }\right)}\\ & E_n^{\ast \ast }=\frac{{\lambda }_h^{\ast \ast }{S}_n^{\ast \ast }}{y_2},E_c^{\ast \ast }=\frac{(1-\sigma )y_2{S}_c{\lambda }_h^{\ast \ast }+{\phi }_2{\lambda }_h^{\ast \ast }{S}_n^{\ast \ast }}{y_2{y}_3},\\ & I_c^{\ast \ast }=\frac{\delta \left((1-\sigma )y_2{y}_4{S}_c^{\ast \ast }{\lambda }_h^{\ast \ast }+m_1{\lambda }_h^{\ast \ast }{S}_n^{\ast \ast }\right)}{y_2{y}_3{y}_4{y}_5},\\ & I_n^{\ast \ast }=\frac{\delta {\lambda }_h^{\ast \ast }{S}_n^{\ast \ast }}{y_2{y}_4},T^{\ast \ast }=\frac{\gamma \delta \left((1-\sigma )y_2{y}_4{S}_c^{\ast \ast }{\lambda }_h^{\ast \ast }+m_1{\lambda }_h^{\ast \ast }{S}_n^{\ast \ast }\right)}{y_2{y}_3{y}_4{y}_5{y}_6},L_b^{\ast \ast }=\frac{K{y}_7{y}_8(M-1)}{(1-ϵ)\pi \psi },\\ & S_b^{\ast \ast }=\frac{K{y}_7{y}_8(M-1)}{\pi \left({\lambda }_b^{\ast \ast }+y_8\right)},I_b^{\ast \ast }=\frac{K(M-1)y_7{\lambda }_b^{\ast \ast }}{\pi \left({\lambda }_b^{\ast \ast }+y_8\right)}\end{array}$(10) where (11) $m_1=y_4{\phi }_2+y_3{\phi }_3$(11) Solving for the force of infection $\left({\lambda }_h^{\ast \ast }\right)$ with the help of  (10(10) $\begin{array}{rl}& S_n^{\ast \ast }=\frac{{\mu }_h{N}_h}{{\lambda }_h^{\ast \ast }+y_1},S_c^{\ast \ast }=\frac{{\mu }_h{N}_h\left(\gamma \delta m_1\rho {\lambda }_h^{\ast \ast }+y_2{y}_3{y}_4{y}_5{y}_6{\phi }_1\right)}{y_2{y}_4\left({\lambda }_h^{\ast \ast }+y_1\right)\left(y_3{y}_5{y}_6\left((1-\sigma ){\lambda }_h^{\ast \ast }+{\mu }_h\right)-\gamma \delta (1-\sigma )\rho {\lambda }_h^{\ast \ast }\right)}\\ & E_n^{\ast \ast }=\frac{{\lambda }_h^{\ast \ast }{S}_n^{\ast \ast }}{y_2},E_c^{\ast \ast }=\frac{(1-\sigma )y_2{S}_c{\lambda }_h^{\ast \ast }+{\phi }_2{\lambda }_h^{\ast \ast }{S}_n^{\ast \ast }}{y_2{y}_3},\\ & I_c^{\ast \ast }=\frac{\delta \left((1-\sigma )y_2{y}_4{S}_c^{\ast \ast }{\lambda }_h^{\ast \ast }+m_1{\lambda }_h^{\ast \ast }{S}_n^{\ast \ast }\right)}{y_2{y}_3{y}_4{y}_5},\\ & I_n^{\ast \ast }=\frac{\delta {\lambda }_h^{\ast \ast }{S}_n^{\ast \ast }}{y_2{y}_4},T^{\ast \ast }=\frac{\gamma \delta \left((1-\sigma )y_2{y}_4{S}_c^{\ast \ast }{\lambda }_h^{\ast \ast }+m_1{\lambda }_h^{\ast \ast }{S}_n^{\ast \ast }\right)}{y_2{y}_3{y}_4{y}_5{y}_6},L_b^{\ast \ast }=\frac{K{y}_7{y}_8(M-1)}{(1-ϵ)\pi \psi },\\ & S_b^{\ast \ast }=\frac{K{y}_7{y}_8(M-1)}{\pi \left({\lambda }_b^{\ast \ast }+y_8\right)},I_b^{\ast \ast }=\frac{K(M-1)y_7{\lambda }_b^{\ast \ast }}{\pi \left({\lambda }_b^{\ast \ast }+y_8\right)}\end{array}$(10) ) we obtain (12) ${\lambda }_h^{\ast \ast }\left(1-\frac{\delta {\theta }^{2}K(M-1)y_7{\text{β}}_b{\text{β}}_h{\lambda }_h^{\ast \ast }\left(d_1(1-\sigma )y_2{y}_4{S}_c^{\ast \ast }+d_2{S}_n^{\ast \ast }\right)}{\pi N_h\left(\delta \theta {\text{β}}_b{\lambda }_h^{\ast \ast }\left(d_1(1-\sigma )y_2{y}_4{S}_c^{\ast \ast }+d_2{S}_n^{\ast \ast }\right)+y_2{y}_3{y}_4{y}_5{y}_6{y}_8{N}_h\right)}\right)=0$(12) where ${\displaystyle d_1=\gamma {\nu }_2+{\nu }_1{y}_6,d_2=m_1(\gamma {\nu }_2+{\nu }_1{y}_6)+y_3{y}_5{y}_6}$ and $y_2,y_3,y_4,y_5,y_8$ have the same meaning as in  (4(4) $\begin{array}{rl}{y}_1& =({\phi }_1+{\mu }_h),y_2=(\delta +{\phi }_2+{\mu }_h),y_3=(\delta +{\mu }_h),y_4=({\phi }_3+{\mu }_h),\\ y_5& =(\gamma +{\mu }_h),y_6=(\rho +{\mu }_h),y_7=\left(\right(1-ϵ)\psi +\eta +{\mu }_l),y_8=(\alpha +{\mu }_b).\end{array}$(4) ).

From (12(12) ${\lambda }_h^{\ast \ast }\left(1-\frac{\delta {\theta }^{2}K(M-1)y_7{\text{β}}_b{\text{β}}_h{\lambda }_h^{\ast \ast }\left(d_1(1-\sigma )y_2{y}_4{S}_c^{\ast \ast }+d_2{S}_n^{\ast \ast }\right)}{\pi N_h\left(\delta \theta {\text{β}}_b{\lambda }_h^{\ast \ast }\left(d_1(1-\sigma )y_2{y}_4{S}_c^{\ast \ast }+d_2{S}_n^{\ast \ast }\right)+y_2{y}_3{y}_4{y}_5{y}_6{y}_8{N}_h\right)}\right)=0$(12) ) we have either ${\lambda }_h^{\ast \ast }=0$ or (13) $\left(1-\frac{\delta {\theta }^{2}K(M-1)y_7{\text{β}}_b{\text{β}}_h{\lambda }_h^{\ast \ast }\left(d_1(1-\sigma )y_2{y}_4{S}_c^{\ast \ast }+d_2{S}_n^{\ast \ast }\right)}{\pi N_h\left(\delta \theta {\text{β}}_b{\lambda }_h^{\ast \ast }\left(d_1(1-\sigma )y_2{y}_4{S}_c^{\ast \ast }+d_2{S}_n^{\ast \ast }\right)+y_2{y}_3{y}_4{y}_5{y}_6{y}_8{N}_h\right)}\right)=0$(13) ${\lambda }_h^{\ast \ast }=0$ represents the existence of disease-free equilibrium and (13(13) $\left(1-\frac{\delta {\theta }^{2}K(M-1)y_7{\text{β}}_b{\text{β}}_h{\lambda }_h^{\ast \ast }\left(d_1(1-\sigma )y_2{y}_4{S}_c^{\ast \ast }+d_2{S}_n^{\ast \ast }\right)}{\pi N_h\left(\delta \theta {\text{β}}_b{\lambda }_h^{\ast \ast }\left(d_1(1-\sigma )y_2{y}_4{S}_c^{\ast \ast }+d_2{S}_n^{\ast \ast }\right)+y_2{y}_3{y}_4{y}_5{y}_6{y}_8{N}_h\right)}\right)=0$(13) ) shows the existence of endemic equilibrium point. To investigate the nature of the endemic equilibrium point we substitute the values of $(S_n^{\ast \ast },S_c^{\ast \ast }$ and $S_b^{\ast \ast }$ in  (13(13) $\left(1-\frac{\delta {\theta }^{2}K(M-1)y_7{\text{β}}_b{\text{β}}_h{\lambda }_h^{\ast \ast }\left(d_1(1-\sigma )y_2{y}_4{S}_c^{\ast \ast }+d_2{S}_n^{\ast \ast }\right)}{\pi N_h\left(\delta \theta {\text{β}}_b{\lambda }_h^{\ast \ast }\left(d_1(1-\sigma )y_2{y}_4{S}_c^{\ast \ast }+d_2{S}_n^{\ast \ast }\right)+y_2{y}_3{y}_4{y}_5{y}_6{y}_8{N}_h\right)}\right)=0$(13) ) which gives the following polynomial (14) $g_2{\varpi }^2+g_1\varpi +g_0=0$(14) where $\begin{array}{rl}{g}_2& =\pi (1-\sigma )N_h\left(\gamma d_1{\delta }^2\theta m_1\rho {\text{β}}_b{\mu }_h+\left(y_3{y}_5{y}_6-\gamma \delta \rho \right)\left(\delta d_2\theta {\text{β}}_b{\mu }_h+y_2{y}_3{y}_4{y}_5{y}_6{y}_8\right)\right)\\ g_1& =\gamma {\delta }^2{d}_2{\theta }^{2}K(M-1)\rho (1-\sigma )y_7{\text{β}}_b{\text{β}}_h{\mu }_h+\pi (1-\sigma )y_1{y}_2{y}_3{y}_4{y}_5{y}_6{y}_8{N}_h\left(y_3{y}_5{y}_6-\gamma \delta \rho \right)\\ & +\pi y_3{y}_5{y}_6{\mu }_h{N}_h\left(\delta d_2\theta {\text{β}}_b{\mu }_h+y_2{y}_4\left(\delta d_1\theta (1-\sigma ){\phi }_1{\text{β}}_b+y_3{y}_5{y}_6{y}_8\right)\right)\\ g_0& =\pi {\mu }_h{N}_h{y}_1{y}_2{y}_3^2{y}_4{y}_5^2{y}_6^2{y}_8\left(1-R_{\mathrm{e}\mathrm{f}\mathrm{f}}\right)\left(1+R_{\mathrm{e}\mathrm{f}\mathrm{f}}\right)\end{array}$ From the Equation (14(14) $g_2{\varpi }^2+g_1\varpi +g_0=0$(14) ), it is clearly seen that the constant $g_0$ can be either positive or negative depending on the value of $R_{\mathrm{e}\mathrm{f}\mathrm{f}}$. If $R_{\mathrm{e}\mathrm{f}\mathrm{f}}<1$, then $g_0$ is positive. If $R_{\mathrm{e}\mathrm{f}\mathrm{f}}>1$, then $g_0$ is negative. Thus, we analyse the endemic equilibrium points of the model system (2.1) in two scenario: when $R_{\mathrm{e}\mathrm{f}\mathrm{f}}<1$ and when $R_{\mathrm{e}\mathrm{f}\mathrm{f}}>1$ with the consideration of discriminant of the quadratic equation (3.6) denoted by D. In this case if the solution of the quadratic equation is positive real root then the endemic equilibrium point exists. Now the solution of the quadratic equation is given by the formula ${\varpi }_1=-g_1+\sqrt{g_1^2-4g_2{g}_0},{\varpi }_2=-g_1-\sqrt{g_1^2-4g_2{g}_0}$ which lead into the following theorem.

Theorem 3.3

The model system (2.1) has

1. One endemic equilibrium if $R_{\mathrm{e}\mathrm{f}\mathrm{f}}>1,$ D>0 and $g_1>0$

2. One endemic equilibrium if $R_{\mathrm{e}\mathrm{f}\mathrm{f}}>1,$ D>0 and $g_1<0$

3. No endemic equilibrium if $R_{\mathrm{e}\mathrm{f}\mathrm{f}}<1$ and $g_1>0$

4. Two endemic equilibrium if $R_{\mathrm{e}\mathrm{f}\mathrm{f}}<1,g_1<0$ and $g_1>\sqrt{g_1^2-4g_2{g}_0}$

From Theorem 3 (iv) we see that the model system (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) has two endemic equilibrium point which leads into a phenomena of backward bifurcation.

3.4.1. Bifurcation analysis

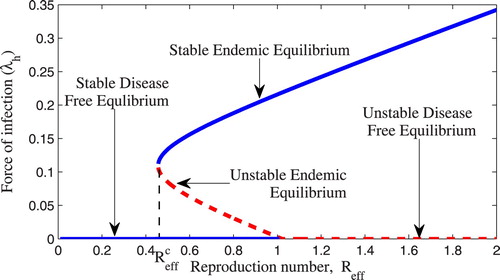
The backward bifurcation is a phenomena which shows co-existence of stable disease free and stable endemic equilibrium points when $R_{\mathrm{e}\mathrm{f}\mathrm{f}}<1$. In this situation $R_{eff}<1$ is not a sufficient condition for eliminating the disease. For eradication of the disease a new critical value $\left(R_{\mathrm{e}\mathrm{f}\mathrm{f}}^c\right)$ which is indicated at the turning point when backward bifurcation occurs is considered. In our case the model system (2.1) exhibit backward bifurcation when we increase the bitting rate and reduce the public health education as shown in Figure 2. That is when education campaign ${\phi }_1={\phi }_2={\phi }_3=0.02$ instead of ${\phi }_1={\phi }_2={\phi }_3=0.5$ in Table 3. This result shows that for eradication of onchocerciasis in the society, public health education campaign may be an important tool on reducing the bitting rate of black flies so as to reduce the effective reproduction number to be less than the critical value $(R_{\mathrm{e}\mathrm{f}\mathrm{f}}<R_{\mathrm{e}\mathrm{f}\mathrm{f}}^c<1).$

Figure 2. Backward bifurcation of the model system (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) drawn using parameter values in Table 3 except $\theta =2.6,{\phi }_1=0.02,{\phi }_2=0.02,{\phi }_3=0.02$.

3.5. Model validation

In this part, validity of the developed model system  (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) is assessed to see its suitability to be used for studying the dynamic of onchocerciasis in the presence of combined intervention strategies. This is done by fitting the model to real data with the help of literature values and find the goodness of fit. Maximum likelihood which is the method of maximizing the likelihood function of the summation of the square of the error is used in fitting the model system  (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) to the data. That is, $L\left(\vartheta \right)=\sum _i^n(y_i-y_i^{est}{)}^2$ where n is the number of observations, $y_i$ is the real data corresponding to $i^{th}$ observation and $y^{est}$ is the solution of the model system  (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) corresponding to a given parameter value. It is difficult to get the number of infected individuals because the disease is not tested (diagnosed) frequently like non-neglected diseases such as malaria. Therefore the collected secondary data used in model fitting in this study is the report of the number of treated individuals in some endemic African countries released by WHO under the Global Health Observatory Repository site available at www.who.int/gho/data/node.main.NTDONCHOCERCIASIS from 2005 to 2016 accessed 25/9/2017 11:30 am. As shown in Table 1 the real data are taken from six endemic countries.

Table 1. Reported number of individuals treated for onchocerciasis.

	Year
Country	2016	2015	2014	2013	2012	2011	2010	2009	2008	2007	2006	2005
Cameroon	8,161,467	7,572,216	7,203,643	6,176,064	550,0491	5,403,559	5,300,025	4,809,180	4,647,473	4,427,481	4,148,276	3,613,842
DRC	31,374,142	29,751,168	26,049,139	24,536,180	2,3126,855	22,403,957	20,290,244	17,704,257	9,534,666	9,343,606	8,310,318	4,876,791
Ethiopia	13,934,852	10,643,027	9,747,701	7,165,807	6,446,552	4,741,282	4,809,869	4,613,362	4,315,374	4,135,538	3,665,682	2,531,967
Ghana	4,331,666	3,416,583	3,372,058	3,495,861	3,466,716	1,776,626	1,491,516	544,959	1,784,353	No data	1,069,137	675,066
Nigeria	35,362,158	35,271,150	44,415,242	28,661,160	29,032,404	30,439,546	29,116,332	26,378,374	23,599,875	23,464,448	21,721,592	20,753,411
Tanzania	4,238,429	3,640,830	3,338,320	1,928,730	1,872,181	1,456,302	1,901,542	1,616,757	1,554,102	1,684,661	1,553,416	1,241,620

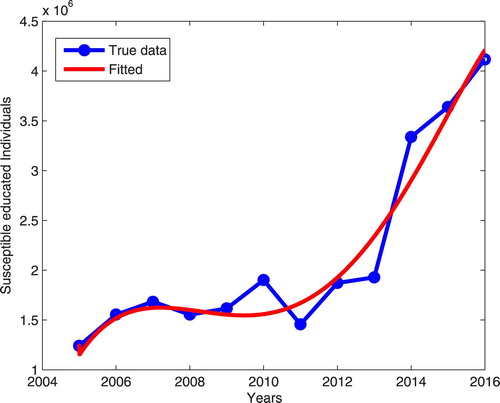
In this study the model system  (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(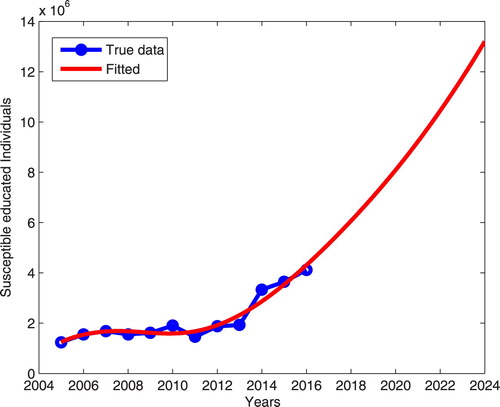3) ) is fitted to the real data from Tanzania as an example and it shows that the model system  (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) fits well to the data as shown in Figure 3. Figure 4 shows the prediction of the dynamics of susceptible compliant individual eight years after the last reported year (2016) of the real data in Tanzania. The prediction showed that there is an increase in the number of susceptible compliant individuals to approximately $13\ast {10}^6$ meaning that many individuals will be treated for onchocerciasis which may reduce the spread of the disease.

Figure 3. The dynamics of susceptible compliant individuals fitted to the real data of the number of individuals treated for Onchocerciasis.

Figure 4. The predicted dynamics of susceptible compliant individuals fitted to the real data of the number of individuals treated for Onchocerciasis in the presence of all intervention strategies.

3.6. Sensitivity analysis

In this section, we compute the sensitivity indices of all parameters in the effective reproduction number in order to know which parameter has great impact on either reducing or increasing the magnitude of the effective reproduction number so as to make decision on the best intervention required to control the disease. We use normalized sensitivity index of variable p as it is used by Shah and Gupta [29] which is defined as $p_q^r=\left(\mathrm{\partial }q/\mathrm{\partial }r\right)\times \left(r/q\right)$ where q is the effective reproduction number and r is the corresponding parameter. For instance, the sensitivity index of the biting rate θ is given by $\theta =\left(\mathrm{\partial }{R}_{\mathrm{e}\mathrm{f}\mathrm{f}}/\mathrm{\partial }\theta \right)\times \left(\theta /R_{\mathrm{e}\mathrm{f}\mathrm{f}}\right)=1$, ${\text{β}}_b=\left(\mathrm{\partial }{R}_{\mathrm{e}\mathrm{f}\mathrm{f}}/\mathrm{\partial }{\text{β}}_b\right)\times \left({\text{β}}_b/R_{\mathrm{e}\mathrm{f}\mathrm{f}}\right)=0.5000$, ${\text{β}}_h=\left(\mathrm{\partial }{R}_{\mathrm{e}\mathrm{f}\mathrm{f}}/\mathrm{\partial }{\text{β}}_h\right)\times \left({\text{β}}_h/R_{\mathrm{e}\mathrm{f}\mathrm{f}}\right)=0.5000$. The sensitivity indices of the rest parameters are shown in Table 2.

Table 2. Numerical values of sensitivity indices of $R_{\mathrm{e}\mathrm{f}\mathrm{f}}$.

Parameter	Sensitivity index	Parameter	Sensitivity index
θ	+1.0000	γ	−0.1109
${\mu }_b$	−0.8379	${\mu }_h$	−0.0559
ε	−0.5110	${\phi }_1$	−0.0144
${\text{β}}_h$	+0.5000	${\mu }_l$	−0.01290
${\text{β}}_b$	+0.5000	${\phi }_3$	−0.0108
${\nu }_2$	+0.3625	δ	+0.0087
α	−0.1775	${\phi }_2$	−0.0030
${\nu }_1$	+0.1258	η	−0.0026
σ	−0.1175

Table 3. Parameter values per year.

Parameter	Value	Source	Parameter	Value	Source
α	0.9	[21]	${\nu }_1$	0.3	assumed
${\text{β}}_b$	0.758	assumed	${\nu }_2$	0.2	assumed
${\text{β}}_h$	0.8354	assumed	π	600	assumed
γ	0.65	[32], [26]	ρ	0.0667–0.1	[20]
δ	0.5–1.3518	[14]	σ	0.3	assumed [17]
ε	0.4	assumed	${\phi }_1$	0.5	[17]
η	0.4	assumed	${\phi }_2$	0.5	[17]
θ	0.8	assumed	${\phi }_3$	0.5	[17]
${\mu }_b$	17.3809–26.0714	[14]	ψ	1.926	[24]
${\mu }_h$	0.01567	[8]	K	6000	[25]
${\mu }_l$	2	[24]

3.6.1. Interpretation of the sensitivity indices

As it is seen in Table 2, the sensitivity indices of $\theta ,{\text{β}}_h,{\text{β}}_b,\delta ,{\nu }_1$ and ${\nu }_2$ are positive while that of ${\mu }_b,ϵ,\gamma ,{\phi }_1,\sigma ,{\phi }_3,\alpha ,{\phi }_2,{\mu }_l,\eta$ are negative. The positive indices show that the parameter is direct proportional to the effective reproduction number. That is the increase (or decreases) of one of these parameters, increases (or decreases) the value of the effective reproduction number as a results increase (or decreases) the spread of the disease. The negative indices show that the parameter is inversely proportional to the effective reproduction number. That means the increase (or decreases) of one of these parameters, decreases (or increases) the value of the effective reproduction number consequently decrease (or increases) the spread of the disease. For instance the biting rate θ must be reduced by creating awareness to the people on how to protect themselves from black-flies so as to reduce the contact between susceptible human and infected black fies $\left({\text{β}}_h\right)$ as well as the contact between infected human and susceptible black flies $\left({\text{β}}_b\right)$.

4. Numerical results

The study of Hendy et al. [13] suggested that for the case of eliminating onchocerciasis, the ongoing intervention (ivermectin) must be combined with other intervention strategies. In this study we combine Ivermectin with public health education (to create awareness about the disease, how people can protect themselves using insect repellent and proper clothing when black flies are active, and how medication is provided), larviciding (to kill larvae reduce maturation to adult black flies) and trapping (collecting adult black flies using traps). For easy understanding the dynamic of onchocerciasis, numerical results of the model system (3(3) $\begin{array}{rl}\frac{d{S}_n}{dt}& ={\mu }_h{N}_h-({\lambda }_h+y_1)S_n,\\ \frac{d{S}_c}{dt}& ={\phi }_1{S}_n+\rho T-\left(\right(1-\sigma ){\lambda }_h+{\mu }_h)S_c,\\ \frac{d{E}_n}{dt}& ={\lambda }_h{S}_n-y_2{E}_n,\\ \frac{d{E}_c}{dt}& =(1-\sigma ){\lambda }_h{S}_c+{\phi }_2{E}_n-y_3{E}_c,\\ \frac{d{I}_n}{dt}& =\delta E_n-y_4{I}_n,\\ \frac{d{I}_c}{dt}& =\delta E_c+{\phi }_3{I}_n-y_5{I}_c,\\ \frac{dT}{dt}& =\gamma I_c-y_{6}T,\\ \frac{d{L}_b}{dt}& =\pi (S_b+I_b)\left(1-\frac{L_b}{K}\right)-y_7{L}_b,\\ \frac{d{S}_b}{dt}& =(1-ϵ)\psi L_b-{\lambda }_b{S}_b-y_8{S}_b,\\ \frac{d{I}_b}{dt}& ={\lambda }_b{S}_b-y_8{I}_b,\end{array}$(3) ) is carried out using Matlab ODE solver for the purpose of examining and comparing the different combination of strategies. In our simulation we used parameter values from literature and some are assumed according to the dynamics of the disease. For instance, following ivermectin treatment compliant human individuals have reduced ability of transmitting the disease therefore  nu_1 is assumed to be 0.3. According to Basanez et al. [3] the adult worms restart their reproduction slowly from three months onwards after a single dose of ivermectin and by one year the reproduced filarial load will only be about 20$\mathrm{\%}$ of their value before treatment. Since the drug is distributed to the whole population regardless of their infection status [3] and it is distributed after every 12 months the model assumes that the $20\mathrm{\%}$ filarial load will be cleared by the next ivermectin distribution round. Thus we further assumes that humans in treated compartment may contribute on the transmission of onchocerciasis with the reduced rate ${\nu }_2=0.2$. Also ${\text{β}}_h$ and ${\text{β}}_b$ are strictly range from 0 to 1 in this work. Throughout the simulation parameter values in Table 3 will be used unless stated and initial conditions of the state variables used are $S_n\left(0\right)=200,S_c\left(0\right)=120,E_n\left(0\right)=100,E_c\left(0\right)=100,I_n\left(0\right)=90,I_c\left(0\right)=30,T\left(0\right)=10,L_b\left(0\right)=5000,S_b\left(0\right)=3000,I_b\left(0\right)=120$.

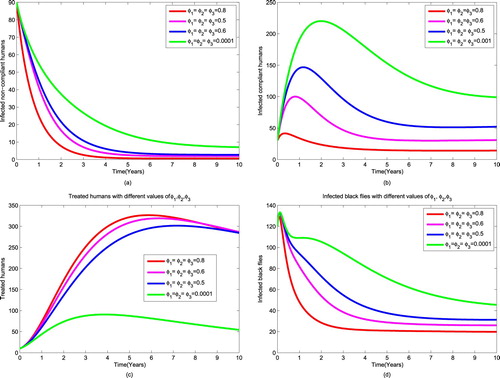
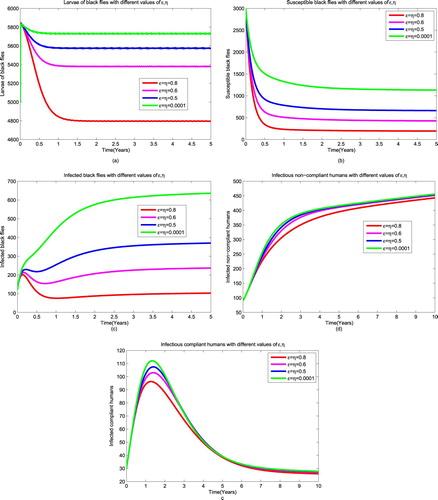
4.1. Strategy 1: ivermectin combined with public health education campaign

In this strategy we fix all parameters of larviciding and trapping to zero

$(ϵ=\eta =\alpha =0)$ and vary parameters associated with public health education from 0.0001 to 0.8 while ivermectin is in place. Figure 6 reveals that as we increase the rate of providing public health education to the society, the number of infectious non-compliant humans decreases almost to zero as in Figure 5(a). This might be due to the fact that the non-compliant humans become aware and move to compliant class. Since infectious humans have both microfilariae and adult worms, the number of compliant humans decrease because they are treated for microfilariae as shown in Figure 5(b). Although the number of infectious compliant humans decreases, the graph remains in endemic state (see Figure 5(b)). This is because some people are willing to be treated but they are ineligible (lactating mother one week after delivery, pregnant women). Also, public health education allows increment of the number of treated humans with adult worms as shown in Figure 5(c). The number of treated human humans decreases slowly because they host adult worms which will eventually die due to their life span (see Figure 5(c)). Furthermore, increasing awareness to the society reduce the number of infectious black flies to 19 (see Figure 5(d)). This may be caused by the fact that many people have been treated for microfilariae and the ineligible humans protect themselves to reduce contact with black flies but the protection is not $100\mathrm{\%}$. Generally, it is observed that the results of this strategy are significant when public health education implemented at a rate of $60\mathrm{\%}$ and above. Thus, this strategy can be used to reduce the spread of the disease.

Figure 5. Simulation results showing the effect of variation of public health education while ivermectin is in place on (a) Infectious non-compliant humans, (b) Infectious compliant humans (c) treated humans and (d) Infectious black flies.

Figure 6. Simulation results showing the effect of variation of larviciding while ivermectin is in place on (a)Larvae, (b) susceptible black flies, (c) infectious black flies, (d) infectious non-compliant humans and (e) infectious compliant humans.

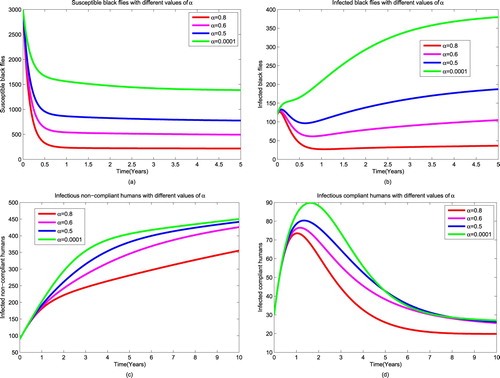
4.2. Strategy 2: ivermectin combined with larviciding

It is well known that larviciding is the process of applying larvicides safe for the environment in order to kill larvae stage of black flies. Since this process has a direct impact on controlling black flies, our explanation will start on vectors. To investigate the impact of this strategy, we set all parameters of public health education and trapping to zero, that is ${\phi }_1={\phi }_2={\phi }_3=\alpha =0$ and vary all parameters associated with larviciding from 0.0001 to 0.8. The results suggest that as we increase the efficacy of larviciding, there is a decrease of larvae population of black flies (see Figure 6(a)). As a results, we note a decrease in the number of susceptible black flies as shown in Figure 6(b). Moreover, the increase of the rate of implementing larviciding decreases the number of infectious black flies to 102, as well as the number of non-compliant and compliant humans as it is shown in Figure 6(c ,d,e), respectively, however these populations remain in endemic state. In this strategy we find that implementation of larviciding in high rate can reduce the spread of onchocerciasis if it will be combined with another intervention which will push the infectious individuals to zero.

4.3. Strategy 3: ivermectin combined with trapping technique

Again, to assess the impact of trapping while ivermectin is in place, we fix all parameters related to public health education and larviciding to zero, that is ${\phi }_1={\phi }_2={\phi }_3=ϵ=\eta =0$ then we vary parameters associated with trapping from 0.0001 to 0.8. The results showed that the increase of trapping vectors reduces the number of susceptible and infectious black flies to 36 as shown in Figure 7(a ,b), respectively. Also, the impact of trapping is seen in infectious human individuals that the increase of trapping decrease the number of infectious non-compliant and compliant human as it is shown in Figure 7(c ,d), respectively. Although the strategy decreases the number of infectious individuals, it does not bring them to zero. This result suggest that the strategy will reduces the transmission of onchocerciasis in the society if it will be combined with another intervention which will reduces the number of infectious individuals that is infectious black flies, non-compliant and compliant human to zero.

Figure 7. Simulation results showing the effect of variation of trapping while ivermectin is in place on (a) Susceptible black flies, (b) infectious black flies, (c) infectious non-compliant humans and (d) infectious compliant humans.

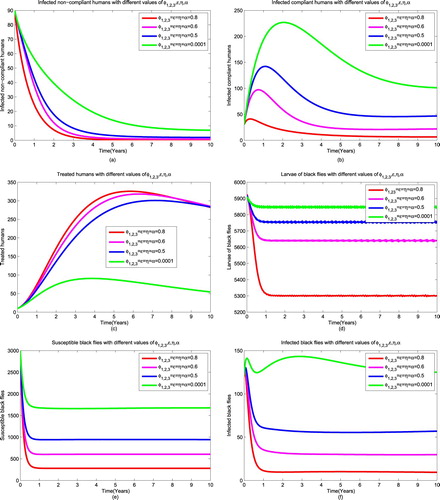
4.4. Strategy 4: ivermectin combined with public health education, larviciding and trapping

In this strategy we combine ivermectin together with public health education, larviciding and trapping. Increasing the rate of implementing the four interventions at the same time we find that the number of infectious non-compliant humans decreases to zero after about 4 years as it is shown in Figure 8(a). In Figure 8(b) we see that the number of compliant humans decreases as well but remains in endemic state because some compliant humans are treated for microfilariae and move to treated class while few of them are ineligible so they remain in compliant class. Moreover, the results of this strategy show that the number of treated humans with adult worms increases as shown in Figure 8(c). For black flies control, the strategy permit reduction of larvae, susceptible black flies as shown in Figure 8(d) respectively and also the number of infectious black flies decreases to 4 as shown in Figure 8(f). The combination of the four intervention strategies is the best strategy for reducing the spread of onchocerciasis since it leaves very few number of infectious black flies compared to the other three explained strategies above.

Figure 8. Simulations results showing the importance of combining ivermectin with public health education, larviciding and trapping.

5. Discussion and conclusion

A mathematical model of the transmission dynamics of onchocerciasis with combined intervention strategies is developed. The effective reproduction number of the model is determined. The stability of equilibrium point are proved. The model system (2.1) exhibit backward bifurcation which can be reduced into forward bifurcation by increasing awareness to the society. Furthermore, the model system is validated using real data of human individual treated for onchocerciasis and it fits well to these data. Sensitivity analysis was done and the results showed that the most sensitive parameter is the bitting rate $\left(\theta \right)$ followed by the probability that the contact between infectious back flies and susceptible human cause infection to susceptible human $\left({\text{β}}_h\right)$ and the probability that the contact between infectious human and susceptible black flies cause infection to susceptible black flies $\left({\text{β}}_b\right)$. Furthermore, numerical simulation was carried out and the results showed that the spread of onchocerciasis can be reduced if ivermectin will be implemented together with public health education, larviciding and trapping. The results is seen clearly if the add-on interventions are implemented at a rate of 60% and above. To accomplish this, public health education campaign must be conducted to the villages (where the disease is endemic) through radio, television, cinema, and brochures to create positive attitude to the people towards ivermectin so as to increase coverage and personal protection on humans. For the purpose of reducing maturation of larvae to adult black flies, a well planned larviciding program must be established to make sure that the process of killing large number of larvae is done effectively. Moreover, this results suggest that for the case of attaining the desired goal of eliminating onchocerciasis completely in endemic areas, together with strategy four (ivermectin, public health education, larviciding and trapping), there must be an alternative drug which will kill the adult worms in treated humans and which can be given to ineligible individuals so as to bring compliant and treated humans to disease-free equilibrium which may lead into pushing of infectious black flies to disease free as well.

The developed model can be extended by taking into account the inflow infected immigrant individuals and assess their impact on spreading onchocerciasis.

Acknowledgments

Authors are grateful for constructive comments from the anonymous reviewers.

Disclosure statement

No potential conflict of interest was reported by the authors.