Full article: Global stability of a delayed and diffusive virus model with nonlinear infection function

Formulae display: $MathJax Logo$ ?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.

Abstract

This paper studies a delayed viral infection model with diffusion and a general incidence rate. A discrete-time model was derived by applying nonstandard finite difference scheme. The positivity and boundedness of solutions are presented. We established the global stability of equilibria in terms of $R_{0}$ by applying Lyapunov method. The results showed that if $R_{0}$ is less than 1, then the infection-free equilibrium $E_{0}$ is globally asymptotically stable. If $R_{0}$ is greater than 1, then the infection equilibrium $E_{*}$ is globally asymptotically stable. Numerical experiments are carried out to illustrate the theoretical results.

Keywords:

1. Introduction

Mathematical models that describe within-host dynamics have been proposed and studied by constructing corresponding differential equations to get a better understanding of viral processes, particularly, their global dynamics behaviour has been investigated [Citation1, Citation2, Citation14, Citation17, Citation21, Citation28, Citation29, Citation32, Citation35–37]. For example, Wang and Zhou [Citation32] studied the following model: (1) $\{\begin{cases} \frac{d T}{d t} = s - d T (t) - (1 - ϵ) β T V, \\ \frac{d I}{d t} = (1 - α) (1 - ϵ) β T (t - τ_{1}) V (t - τ_{1}) - δ I, \\ \frac{d C}{d t} = α (1 - ϵ) β T (t - τ_{2}) V (t - τ_{2}) - μ C, \\ \frac{d V}{d t} = k_{1} δ I (t - τ_{3}) + k_{2} μ C (t - τ_{4}) - c V, \end{cases}$ (1) where T, I, C and V represent the concentrations of the uninfected cell, shorted-lived infected cells, chronically infected cells and free virus particles, respectively. s is the source term for uninfected cells. β represents the infection rate. ϵ is the efficacy of the therapy. $d, δ, μ$ and c are the mortality rates of uninfected cells, short infected cells, chronically infected cells and virus, respectively. The fractions α and $(1 - α)$ are the probabilities that, upon infection, an uninfected cell will become either chronically infected or short-lived infected. $k_{1} = N_{1} (1 - γ_{1})$ and $k_{2} = N_{2} (1 - γ_{2})$ where $N_{1}$ and $N_{2}$ are the average numbers of virions produced in the lifetime of short-lived and chronically infected cells, respectively. $γ_{1}$ and $γ_{2}$ are the efficacy of the therapy. $τ_{1}, τ_{2}, τ_{3}$ and $τ_{4}$ are the intracellular delays. The global dynamics of the model have been studied by constructing Lyapunov functionals. For more details, one can refer to [Citation32]. The key assumption in model (Equation1(1) $\{\begin{cases} \frac{d T}{d t} = s - d T (t) - (1 - ϵ) β T V, \\ \frac{d I}{d t} = (1 - α) (1 - ϵ) β T (t - τ_{1}) V (t - τ_{1}) - δ I, \\ \frac{d C}{d t} = α (1 - ϵ) β T (t - τ_{2}) V (t - τ_{2}) - μ C, \\ \frac{d V}{d t} = k_{1} δ I (t - τ_{3}) + k_{2} μ C (t - τ_{4}) - c V, \end{cases}$ (1) ) is that cells and viruses are well mixed, and the mobility of viruses was ignored. So, in order to study the influences of spatial structures of virus dynamics, Wang et al. [Citation30] studied the following model: (2) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - β T (x, t) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = β T (x, t - τ) V (x, t - τ) - δ I (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + p I (x, t) - c V (x, t), \end{cases}$ (2) where $T (x, t)$ , $I (x, t)$ and $V (x, t)$ represent the densities of uninfected cells, infected cells and free virus at position x and at time t, respectively. τ is the intracellular delay. D is the diffusion coefficient and Δ is the Laplacian operator.

The bilinear incidence rate $β T V$ used in models (Equation1(1) $\{\begin{cases} \frac{d T}{d t} = s - d T (t) - (1 - ϵ) β T V, \\ \frac{d I}{d t} = (1 - α) (1 - ϵ) β T (t - τ_{1}) V (t - τ_{1}) - δ I, \\ \frac{d C}{d t} = α (1 - ϵ) β T (t - τ_{2}) V (t - τ_{2}) - μ C, \\ \frac{d V}{d t} = k_{1} δ I (t - τ_{3}) + k_{2} μ C (t - τ_{4}) - c V, \end{cases}$ (1) ) and (Equation2(2) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - β T (x, t) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = β T (x, t - τ) V (x, t - τ) - δ I (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + p I (x, t) - c V (x, t), \end{cases}$ (2) ) is a simple description of the infection. Though the incidence rates $β T^{q} V$ , $\frac{β T V}{1 + a V}$ and $\frac{β T V}{1 + a T + b V + a b T V}$ are improved forms which are more commonly used [Citation22, Citation26, Citation31], the general incidence rates $f (T, V) V$ , $f (T, V)$ and $f (T, I, V) V$ can help us gain the unification theory by the omission of unessential details [Citation7, Citation8, Citation11, Citation13]. So, motivated by [Citation30, Citation32], we consider the following model with a general incidence rate which is similar to the one in [Citation7] (3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) $f (T, V) V$ is the general incidence rate and satisfies the following hypotheses: (4) $\begin{aligned} f (T, V) \geq 0, and f (T, V) = 0 if and only if T = 0; \\ there exists η > 0 such that f (T, V) V \leq η T for all T, V \geq 0; \\ \frac{\partial f (T, V)}{\partial T} > 0 for any fixed V \geq 0; \\ \frac{\partial f (T, V)}{\partial V} \leq 0 for any fixed T \geq 0; \\ \frac{\partial (f (T, V) V)}{\partial V} > 0 for any fixed T \geq 0. \end{aligned}$ (4) It is easy to check that a class of functions $f (T, V) V$ satisfying (Equation4(4) $\begin{aligned} f (T, V) \geq 0, and f (T, V) = 0 if and only if T = 0; \\ there exists η > 0 such that f (T, V) V \leq η T for all T, V \geq 0; \\ \frac{\partial f (T, V)}{\partial T} > 0 for any fixed V \geq 0; \\ \frac{\partial f (T, V)}{\partial V} \leq 0 for any fixed T \geq 0; \\ \frac{\partial (f (T, V) V)}{\partial V} > 0 for any fixed T \geq 0. \end{aligned}$ (4) ) includes some common used nonlinear incidence functions such as $f (T, V) V = \frac{β T V}{1 + b V}$ , $f (T, V) V = \frac{β T V}{1 + a T + b V}$ and $f (T, V) V = \frac{β T V}{1 + a T + b V + c T V}$ for $β, a, b, c > 0$ .

The initial conditions of model (Equation3(3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) ) are given as (5) $\begin{aligned} T (x, s) = & ϕ_{1} (x, s) \geq 0, I (x, s) = ϕ_{2} (x, s) \geq 0, C (x, s) = ϕ_{3} (x, s) \geq 0, \\ V (x, s) = & ϕ_{4} (x, s) \geq 0, (x, s) \in \bar{Ω} \times [- τ, 0], \end{aligned}$ (5) and we have considered model (Equation3(3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) ) with homogeneous Neumann boundary conditions (6) $\frac{\partial V}{\partial \vec{n}} = 0, t > 0, x \in \partial Ω,$ (6) where $τ = max {τ_{1}, τ_{2}, τ_{3}, τ_{4}}$ , Ω is a bounded interval in $R$ and $\frac{\partial}{\partial \vec{n}}$ denotes the outward normal derivative on $\partial Ω$ .

As we know, it is difficult or even impossible to find the exact analytical solutions for most nonlinear models, such as (Equation3(3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) ). In order to perform numerical simulations, we need to seek an efficient discrete method to discretize such nonlinear continuous models. However, some classical numerical discrete methods are unsuccessful in preserving the quantitative properties of corresponding continuous model. For example, for classical forward Euler's method, if the step size is selected small enough and the positivity conditions can be satisfied, then it can be shown that local asymptotic stability for an equilibrium is preserved while in some special cases numerical instability or Hopf bifurcation may appear. Thus how to design a feasible discrete scheme so that the same quantitative behaviours of solutions to the corresponding continuous models can be efficiently preserved is a challenging and interesting task. Recently, an interesting method which is called non-standard finite difference (NSFD) scheme has been proposed by Mickens [Citation18, Citation19]. NSFD has been applied to obtain discrete-time epidemic models [Citation4, Citation6, Citation9, Citation10, Citation20, Citation24, Citation25, Citation34] and references therein. Hence, motivated by the work of [Citation18, Citation19], we apply the NSFD scheme on model (Equation3(3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) ), then we obtain (7) $\{\begin{cases} \frac{T_{n + 1}^{m} - T_{n}^{m}}{Δ t} = s - d T_{n + 1}^{m} - (1 - ϵ) f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}, \\ \frac{I_{n + 1}^{m} - I_{n}^{m}}{Δ t} = (1 - α) (1 - ϵ) f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m} - δ I_{n + 1}^{m}, \\ \frac{C_{n + 1}^{m} - C_{n}^{m}}{Δ t} = α (1 - ϵ) f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m} - μ C_{n + 1}^{m}, \\ \frac{V_{n + 1}^{m} - V_{n}^{m}}{Δ t} = D \frac{V_{n + 1}^{m + 1} - 2 V_{n + 1}^{m} + V_{n + 1}^{m - 1}}{(Δ x)^{2}} + k_{1} δ I_{n - m_{3} + 1}^{m} + k_{2} μ C_{n - m_{4} + 1}^{m} - c V_{n + 1}^{m} . \end{cases}$ (7) Set $x \in Ω = [a, b]$ be a bounded interval in $R$ . Let $Δ t > 0$ be the time step size and $Δ x = \frac{b - a}{N}$ be the space step size with N being a positive integer. Assume that there exist four integers $m_{i} \in N$ (i=1,2,3,4) with $τ_{i} = m_{i} Δ t$ . Denote the mesh grid point as ${(x_{m}, t_{n}), m = 0, 1, 2, \dots, N, n \in N}$ with $x_{m} = a + m Δ x$ and $t_{n} = n Δ t$ . $(T_{n}^{m}, I_{n}^{m}, C_{n}^{m}, V_{n}^{m})$ are the approximations of solution $(T (x_{m}, t_{n}), I (x_{m}, t_{n}), C (x_{m}, t_{n}), V (x_{m}, t_{n}))$ at the discrete-time points. For simplicity, let $U_{n} = (U_{n}^{0}, U_{n}^{1}, \dots, U_{n}^{N})^{T}$ be the approximation solutions at the time $t_{n}$ , where $U \in {T, I, C, V}$ and the notation $(\cdot)^{T}$ denotes the transposition of a vector. The initial conditions of model (Equation7(7) $\{\begin{cases} \frac{T_{n + 1}^{m} - T_{n}^{m}}{Δ t} = s - d T_{n + 1}^{m} - (1 - ϵ) f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}, \\ \frac{I_{n + 1}^{m} - I_{n}^{m}}{Δ t} = (1 - α) (1 - ϵ) f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m} - δ I_{n + 1}^{m}, \\ \frac{C_{n + 1}^{m} - C_{n}^{m}}{Δ t} = α (1 - ϵ) f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m} - μ C_{n + 1}^{m}, \\ \frac{V_{n + 1}^{m} - V_{n}^{m}}{Δ t} = D \frac{V_{n + 1}^{m + 1} - 2 V_{n + 1}^{m} + V_{n + 1}^{m - 1}}{(Δ x)^{2}} + k_{1} δ I_{n - m_{3} + 1}^{m} + k_{2} μ C_{n - m_{4} + 1}^{m} - c V_{n + 1}^{m} . \end{cases}$ (7) ) are (8) $\begin{aligned} T_{s}^{m} = ϕ_{1} (x_{m}, t_{s}) \geq 0, I_{s}^{m} = ϕ_{2} (x_{m}, t_{s}) \geq 0, C_{s}^{m} = ϕ_{3} (x_{m}, t_{s}) \geq 0, \\ V_{s}^{m} = ϕ_{4} (x_{m}, t_{s}) \geq 0, for all s = - l, - l + 1, \dots, 0, l = max_{1 \leq i \leq 4} {m_{i}}, \end{aligned}$ (8) and the discrete boundary conditions are $V_{n}^{- 1} = V_{n}^{0}, V_{n}^{N + 1} = V_{n}^{N}, f o r n \in N .$ The main purpose of this paper is to demonstrate the discretized model (Equation7(7) $\{\begin{cases} \frac{T_{n + 1}^{m} - T_{n}^{m}}{Δ t} = s - d T_{n + 1}^{m} - (1 - ϵ) f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}, \\ \frac{I_{n + 1}^{m} - I_{n}^{m}}{Δ t} = (1 - α) (1 - ϵ) f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m} - δ I_{n + 1}^{m}, \\ \frac{C_{n + 1}^{m} - C_{n}^{m}}{Δ t} = α (1 - ϵ) f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m} - μ C_{n + 1}^{m}, \\ \frac{V_{n + 1}^{m} - V_{n}^{m}}{Δ t} = D \frac{V_{n + 1}^{m + 1} - 2 V_{n + 1}^{m} + V_{n + 1}^{m - 1}}{(Δ x)^{2}} + k_{1} δ I_{n - m_{3} + 1}^{m} + k_{2} μ C_{n - m_{4} + 1}^{m} - c V_{n + 1}^{m} . \end{cases}$ (7) ) derived by applying NSFD scheme can efficiently preserves the global dynamical properties to the original model (Equation3(3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) ). The rest of this paper is organized as follows. In Section 2, we study the dynamical behaviour of the continuous model (Equation3(3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) ). In Section 3, we investigate the global dynamics of discrete model (Equation7(7) $\{\begin{cases} \frac{T_{n + 1}^{m} - T_{n}^{m}}{Δ t} = s - d T_{n + 1}^{m} - (1 - ϵ) f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}, \\ \frac{I_{n + 1}^{m} - I_{n}^{m}}{Δ t} = (1 - α) (1 - ϵ) f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m} - δ I_{n + 1}^{m}, \\ \frac{C_{n + 1}^{m} - C_{n}^{m}}{Δ t} = α (1 - ϵ) f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m} - μ C_{n + 1}^{m}, \\ \frac{V_{n + 1}^{m} - V_{n}^{m}}{Δ t} = D \frac{V_{n + 1}^{m + 1} - 2 V_{n + 1}^{m} + V_{n + 1}^{m - 1}}{(Δ x)^{2}} + k_{1} δ I_{n - m_{3} + 1}^{m} + k_{2} μ C_{n - m_{4} + 1}^{m} - c V_{n + 1}^{m} . \end{cases}$ (7) ). An example, along with numerical simulations is presented in Section 4 to validate the theoretical results. A brief conclusion ends the paper.

2. Dynamical analysis of model (3)

2.1. Preliminaries

Let $X = C (\bar{Ω}, R^{4})$ be the space of continuous functions from the topological space $\bar{Ω}$ into the space $R^{4}$ . Denote $C = C ([- τ, 0], X)$ be the Banach space of continuous functions from $[- τ, 0]$ into $X$ with the usual supremum normal, and $C_{+} = C ([- τ, 0], X_{+})$ . When convenient, we identify an element $ϕ \in C$ as a function from $\bar{Ω} \times [- τ, 0]$ into $R^{4}$ defined by $ϕ (x, s) = ϕ (s) (x)$ . We adopt the notation that for $σ > 0$ , a function $u (\cdot) : [- τ, σ) \to X$ induces functions $u_{t} \in C$ for $t \in [0, σ)$ , defined by $u_{t} (θ) = u (t + θ)$ for $θ \in [- τ, 0]$ . Let $D = (0, 0, 0, D)^{T}$ . It follows from [Citation3] that the $X$ -realization of $D Δ$ generates an analytic semi-group $T (t)$ on $X$ .

Theorem 2.1

For any given initial data $ϕ \in C$ satisfying the condition (Equation5(5) $\begin{aligned} T (x, s) = & ϕ_{1} (x, s) \geq 0, I (x, s) = ϕ_{2} (x, s) \geq 0, C (x, s) = ϕ_{3} (x, s) \geq 0, \\ V (x, s) = & ϕ_{4} (x, s) \geq 0, (x, s) \in \bar{Ω} \times [- τ, 0], \end{aligned}$ (5) ), there exists a unique solution of problem (Equation3(3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) )–(Equation6(6) $\frac{\partial V}{\partial \vec{n}} = 0, t > 0, x \in \partial Ω,$ (6) ) defined on $[0, + \infty)$ and this solution remains non-negative and bounded for all $t \geq 0$ .

Proof.

For any $φ = (φ_{1}, φ_{2}, φ_{3}, φ_{4})^{T} \in C_{+}$ we define $F = (F_{1}, F_{2}, F_{3}, F_{4}) : C_{+} \to X$ as follows. For any $x \in \bar{Ω}$ , $\{\begin{cases} F_{1} (φ) (x) = s - d φ_{1} (x, 0) - (1 - ϵ) f (φ_{1} (x, 0), φ_{4} (x, 0)) φ_{4} (x, 0), \\ F_{2} (φ) (x) = (1 - α) (1 - ϵ) f (φ_{1} (x, - τ_{1}), φ_{4} (x, - τ_{1})) φ_{4} (x, - τ_{1}) - δ φ_{2} (x, 0), \\ F_{3} (φ) (x) = α (1 - ϵ) f (φ_{1} (x, - τ_{2}), φ_{4} (x, - τ_{2})) φ_{4} (x, - τ_{2}) - c φ_{3} (x, 0), \\ F_{4} (φ) (x) = k_{1} δ φ_{2} (x, - τ_{3}) + k_{2} μ φ_{3} (x, - τ_{4}) - c φ_{4} (x, 0) . \end{cases}$ We now reformulate (Equation3(3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) )–(Equation6(6) $\frac{\partial V}{\partial \vec{n}} = 0, t > 0, x \in \partial Ω,$ (6) ) as the abstract functional differential equation (9) $\{\begin{cases} \frac{d Φ}{d t} = A Φ + F (Φ_{t}), t > 0, Φ_{t} \in C \\ Φ_{0} = φ \in C_{+}, \end{cases}$ (9) where $Φ = (T, I, C, V)^{T}$ and $A Φ = (0, 0, 0, D Δ V)^{T}$ . It is clear that F is locally Lipschitz in $X$ . It follows from [Citation5, Citation15, Citation16, Citation27, Citation33] that system (Equation9(9) $\{\begin{cases} \frac{d Φ}{d t} = A Φ + F (Φ_{t}), t > 0, Φ_{t} \in C \\ Φ_{0} = φ \in C_{+}, \end{cases}$ (9) ) admits a unique local solution on $t \in [0, T_{max})$ , where $T_{max}$ is the maximal existence time for the solution of system (Equation9(9) $\{\begin{cases} \frac{d Φ}{d t} = A Φ + F (Φ_{t}), t > 0, Φ_{t} \in C \\ Φ_{0} = φ \in C_{+}, \end{cases}$ (9) ).

In order to demonstrate the boundedness of solutions. Define $U (x, t) = T (x, t) + I (x, t + τ_{1}) + C (x, t + τ_{2})$ and $d_{0} = min {d, δ, μ}$ , it then follows from model (Equation3(3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) ) that $\begin{aligned} \frac{\partial U (x, t)}{\partial t} & = s - d T (x, t) - δ I (x, t + τ_{1}) - μ C (x, t + τ_{2}) \\ \leq s - d_{0} U (x, t) . \end{aligned}$ Then we have $U (x, t) \leq max \{\frac{s}{d_{0}}, max_{x \in \bar{Ω}} \{φ_{1} (x, 0) + φ_{2} (x, - τ_{1}) + φ_{3} (x, - τ_{2})\}\} := η_{1},$ implying T, I and C are bounded.

From model (Equation3(3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) )–(Equation6(6) $\frac{\partial V}{\partial \vec{n}} = 0, t > 0, x \in \partial Ω,$ (6) ), we deduce that V satisfies (10) $\{\begin{aligned} \frac{\partial V}{\partial t} - D Δ V \leq k_{1} δ η_{1} + k_{2} μ η_{1} - c V, \\ \frac{\partial V}{\partial \vec{n}} = 0, \\ V (x, 0) = ϕ_{4} (x, 0) \geq 0. \end{aligned}$ (10) Let $\tilde{V} (t)$ be a solution to the ordinary differential equation $\{\begin{aligned} \frac{d \tilde{V}}{d t} = k_{1} δ η_{1} + k_{2} μ η_{1} - c \tilde{V}, \\ \tilde{V} (0) = max_{x \in \bar{Ω}} ϕ_{4} (x, 0) . \end{aligned}$ Then we get $\tilde{V} (t) \leq max {\frac{(k_{1} δ + k_{2} μ) η_{1}}{c}, max_{x \in \bar{Ω}} ϕ_{4} (x, 0)}$ , $\forall t \in [0, T_{m a x})$ . Thus $V (x, t) \leq \tilde{V} (t)$ follows from the comparison principle [Citation23]. Therefore, $V (x, t) \leq max \{\frac{(k_{1} δ + k_{2} μ) η_{1}}{c}, max_{x \in \bar{Ω}} ϕ_{4} (x, 0)\} := η_{2}, \forall (x, t) \in \bar{Ω} \times [0, T_{max}) .$ Based on the above analysis, we have demonstrated that $T (x, t)$ , $I (x, t)$ , $C (x, t)$ and $V (x, t)$ are bounded in $\bar{Ω} \times [0, T_{max})$ . It then follows from the standard theory for semilinear parabolic systems [Citation12] that $T_{m a x} = + \infty$ .

Let $[0, M]_{C} := {φ \in C : 0 \leq φ (s, x) \leq M, \forall s \in [- τ, 0], x \in \bar{Ω}}$ with $0 = (0, 0, 0, 0)$ and $M = (\frac{s}{d_{0}}, \frac{s η (1 - α) (1 - ϵ)}{d_{0} δ}, \frac{s η α (1 - ϵ)}{d_{0} μ}, \frac{s η (1 - ϵ) (k_{1} (1 - α) + k_{2} α)}{d_{0} c})$ . For any $φ = (φ_{1}, φ_{2}, φ_{3}, φ_{4}) \in [0, M]_{C}$ and any $ρ \geq 0$ , we obtain $\begin{aligned} φ (x, 0) + ρ F (φ) (x) \\ = (\begin{matrix} φ_{1} (x, 0) + ρ (s - d φ_{1} (x, 0) - (1 - ϵ) f (φ_{1} (x, 0), φ_{4} (x, 0)) φ_{4} (x, 0)) \\ φ_{2} (x, 0) + ρ (1 - α) (1 - ϵ) f (φ_{1} (x, - τ_{1}), φ_{4} (x, - τ_{1})) φ_{4} (x, - τ_{1}) - ρ δ φ_{2} (x, 0) \\ φ_{3} (x, 0) + ρ α (1 - ϵ) f (φ_{1} (x, - τ_{2}), φ_{4} (x, - τ_{2})) φ_{4} (x, - τ_{2}) - ρ c φ_{3} (x, 0) \\ φ_{4} (x, 0) + ρ k_{1} δ φ_{2} (x, - τ_{3}) + ρ k_{2} μ φ_{3} (x, - τ_{4}) - ρ c φ_{4} (x, 0) \end{matrix}) . \end{aligned}$ Recall from (Equation4(4) $\begin{aligned} f (T, V) \geq 0, and f (T, V) = 0 if and only if T = 0; \\ there exists η > 0 such that f (T, V) V \leq η T for all T, V \geq 0; \\ \frac{\partial f (T, V)}{\partial T} > 0 for any fixed V \geq 0; \\ \frac{\partial f (T, V)}{\partial V} \leq 0 for any fixed T \geq 0; \\ \frac{\partial (f (T, V) V)}{\partial V} > 0 for any fixed T \geq 0. \end{aligned}$ (4) ) that $f (T, V) V \leq η T$ for all $T, V \geq 0$ . Therefore, for any $0 \leq ρ \leq min {\frac{1}{(1 - ϵ) η + d}, \frac{1}{δ}, \frac{1}{μ}, \frac{1}{c}}$ , we have $φ (x, 0) + ρ F (φ) (x) \geq (\begin{matrix} (1 - ρ (d + (1 - ϵ) η)) φ_{1} (x, 0) \\ (1 - ρ δ) φ_{2} (x, 0) \\ (1 - ρ μ) φ_{3} (x, 0) \\ (1 - ρ c) φ_{4} (x, 0) \end{matrix}) \geq (\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \end{matrix}) = 0$ and $\begin{aligned} φ (x, 0) + ρ F (φ) (x) \\ \leq (\begin{matrix} φ_{1} (x, 0) + ρ (s - d φ_{1} (x, 0)) \\ ρ (1 - α) (1 - ϵ) η φ_{1} (x, - τ_{1}) + (1 - ρ δ) φ_{2} (x, 0) \\ ρ α (1 - ϵ) η φ_{1} (x, - τ_{2}) + (1 - ρ μ) φ_{3} (x, 0) \\ ρ k_{1} δ φ_{2} (x, - τ_{3}) + ρ k_{2} μ φ_{3} (x, - τ_{4}) + (1 - ρ c) φ_{4} (x, 0) \end{matrix}) \\ \leq (\begin{matrix} \frac{s}{d} \\ \frac{s η (1 - α) (1 - ϵ)}{d δ} \\ \frac{s η α (1 - ϵ)}{d μ} \\ \frac{s η (1 - ϵ) (k_{1} (1 - α) + k_{2} α)}{d c} \end{matrix}) = M . \end{aligned}$ Thus we can demonstrate that for small enough ρ, $φ (0) + ρ F (φ) \in [0, M]_{C},$ which implies that $lim_{ρ \to 0^{+}} \frac{1}{ρ} d i s t (φ (0) + ρ F (φ), [0, M]_{C}) = 0, \forall φ \in C .$ We are now prepared to refer to key results from the literature. Denote $K = [0, M]_{C}$ , $S (t, s) = T (t - s)$ and $B (t, φ) = F (φ)$ , it then follows from [Citation15] that (Equation3(3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) )–(Equation6(6) $\frac{\partial V}{\partial \vec{n}} = 0, t > 0, x \in \partial Ω,$ (6) ) has a unique mild solution $Φ (t, φ) \in [0, M]_{C}$ for $t \in [0, \infty)$ . Furthermore, since the semigroup $T (t)$ is analytic [Citation3]. Thus it follows from [Citation33] that the mild solution is classic for $t \geq τ$ . This completes the proof.

The dynamical outcomes of model (Equation3(3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) ) will be determined by the basic reproduction number $R_{0}$ , which is given by $R_{0} = \frac{(1 - ϵ) (k_{1} (1 - α) + k_{2} α) f (T_{0}, 0)}{c}, with T_{0} = \frac{s}{d} .$ It is clear that model (Equation3(3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) ) always has an infection-free equilibrium $E_{0} = (T_{0}, 0, 0, 0)$ and any positive equilibrium, denoted by $E_{*} = (T_{*}, I_{*}, C_{*}, V_{*})$ , must satisfy (11) $\{\begin{aligned} s = d T_{*} + (1 - ϵ) f (T_{*}, V_{*}) V_{*}, \\ (1 - α) (1 - ϵ) f (T_{*}, V_{*}) V_{*} = δ I_{*}, \\ α (1 - ϵ) f (T_{*}, V_{*}) V_{*} = μ C_{*}, \\ k_{1} δ I_{*} + k_{2} μ C_{*} = c V_{*} . \end{aligned}$ (11) Simple calculation shows that $\begin{aligned} I_{*} & = \frac{(1 - α) c V_{*}}{δ (k_{1} (1 - α) + k_{2} α)}, C_{*} = \frac{α c V_{*}}{μ (k_{1} (1 - α) + k_{2} α)}, \\ V_{*} & = \frac{(s - d T_{*}) (k_{1} (1 - α) + k_{2} α)}{c}, \end{aligned}$ and $T_{*}$ satisfies $H (T_{*}) := (1 - ϵ) f (T_{*}, \frac{(s - d T_{*}) (k_{1} (1 - α) + k_{2} α)}{c}) - \frac{c}{k_{1} (1 - α) + k_{2} α} = 0.$ It is easy to show that $H (0) = - \frac{c}{k_{1} (1 - α) + k_{2} α} < 0, H (T_{0}) = \frac{c (R_{0} - 1)}{k_{1} (1 - α) + k_{2} α} .$ According to (Equation4(4) $\begin{aligned} f (T, V) \geq 0, and f (T, V) = 0 if and only if T = 0; \\ there exists η > 0 such that f (T, V) V \leq η T for all T, V \geq 0; \\ \frac{\partial f (T, V)}{\partial T} > 0 for any fixed V \geq 0; \\ \frac{\partial f (T, V)}{\partial V} \leq 0 for any fixed T \geq 0; \\ \frac{\partial (f (T, V) V)}{\partial V} > 0 for any fixed T \geq 0. \end{aligned}$ (4) ), calculating shows $H^{'} (T) > 0$ . Thus there exists a unique $T_{1} \in (0, T_{0})$ such that $H (T_{1}) = 0$ if and only if $R_{0} > 1$ . So, a unique infection equilibrium $E_{*}$ exists when $R_{0} > 1$ .

Theorem 2.2

If $R_{0} \leq 1$ , then the only equilibrium is the infection-free equilibrium $E_{0} = (T_{0}, 0, 0, 0)$ . If $R_{0} > 1$ , then there exists a unique infection equilibrium $E_{*} = (T_{*}, I_{*}, C_{*}, V_{*})$ .

2.2. Stabilities of equilibria

Theorem 2.3

If $R_{0} \leq 1$ , then the infection-free equilibrium $E_{0}$ of model (Equation3(3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) ) is globally asymptotically stable.

Proof.

Define a Lyapunov functional $\begin{aligned} L_{1} & = \int_{Ω} {(k_{1} (1 - α) + k_{2} α) (T - T_{0} - \int_{T_{0}}^{T} \frac{f (T_{0}, 0)}{f (s, 0)} d s) + k_{1} I (x, t) + k_{2} C (x, t) \\ + V (x, t) + k_{1} (1 - α) (1 - ϵ) \int_{t - τ_{1}}^{t} f (T (x, s), V (x, s)) V (x, s) d s \\ + k_{2} α (1 - ϵ) \int_{t - τ_{2}}^{t} f (T (x, s), V (x, s)) V (x, s) d s \\ + k_{1} δ \int_{t - τ_{3}}^{t} I (x, s) d s + k_{2} μ \int_{t - τ_{4}}^{t} C (x, s) d s} d x . \end{aligned}$ For convenience, we let $u = u (x, t)$ and $u_{τ_{i}} = u (x, t - τ_{i})$ ( i = 1, 2, 3, 4) for any $u \in {T, I, C, V}$ . Calculating the time derivative of $L_{1}$ along a solution of model (Equation3(3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) ), we obtain $\begin{aligned} \frac{d L_{1}}{d t} & = \int_{Ω} {(k_{1} (1 - α) + k_{2} α) (1 - \frac{f (T_{0}, 0)}{f (T, 0)}) (d T_{0} - d T - (1 - ϵ) f (T, V) V) \\ + k_{1} ((1 - α) (1 - ϵ) f (T_{τ_{1}}, V_{τ_{1}}) V_{τ_{1}} - δ I) + k_{2} (α (1 - ϵ) f (T_{τ_{2}}, V_{τ_{2}}) V_{τ_{2}} - μ C) \\ + D Δ V + k_{1} δ I_{τ_{3}} + k_{2} μ C_{τ_{4}} - c V \\ + k_{1} (1 - α) (1 - ϵ) (f (T, V) V - f (T_{τ_{1}}, V_{τ_{1}}) V_{τ_{1}}) \\ + k_{2} α (1 - ϵ) (f (T, V) V - f (T_{τ_{2}}, V_{τ_{2}}) V_{τ_{2}}) + k_{1} δ (I - I_{τ_{3}}) + k_{2} μ (C - C_{τ_{4}})} d x \\ = \int_{Ω} {(k_{1} (1 - α) + k_{2} α) (1 - \frac{T}{T_{0}}) (1 - \frac{f (T_{0}, 0)}{f (T, 0)}) \\ + (R_{0} \frac{f (T, V)}{f (T, 0)} - 1) c V} d x + D \int_{Ω} Δ V d x . \end{aligned}$ Recall that $\int_{Ω} Δ V d x = 0$ and (Equation4(4) $\begin{aligned} f (T, V) \geq 0, and f (T, V) = 0 if and only if T = 0; \\ there exists η > 0 such that f (T, V) V \leq η T for all T, V \geq 0; \\ \frac{\partial f (T, V)}{\partial T} > 0 for any fixed V \geq 0; \\ \frac{\partial f (T, V)}{\partial V} \leq 0 for any fixed T \geq 0; \\ \frac{\partial (f (T, V) V)}{\partial V} > 0 for any fixed T \geq 0. \end{aligned}$ (4) ), we obtain $\frac{d L_{1}}{d t} \leq \int_{Ω} {(k_{1} (1 - α) + k_{2} α) (1 - \frac{T}{T_{0}}) (1 - \frac{f (T_{0}, 0)}{f (T, 0)}) + (R_{0} - 1) c V} d x .$ Recall the condition (Equation4(4) $\begin{aligned} f (T, V) \geq 0, and f (T, V) = 0 if and only if T = 0; \\ there exists η > 0 such that f (T, V) V \leq η T for all T, V \geq 0; \\ \frac{\partial f (T, V)}{\partial T} > 0 for any fixed V \geq 0; \\ \frac{\partial f (T, V)}{\partial V} \leq 0 for any fixed T \geq 0; \\ \frac{\partial (f (T, V) V)}{\partial V} > 0 for any fixed T \geq 0. \end{aligned}$ (4) ), it is easy to show that $\frac{d L_{1}}{d t} \leq 0$ whenever $R_{0} \leq 1$ . Moreover, it can be shown that the largest invariant set ${\frac{d L_{1}}{d t} = 0}$ is the singleton ${E_{0}}$ . By LaSalle's Invariance Principle, the infection-free equilibrium $E_{0}$ of model (Equation3(3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) ) is globally asymptotically stable when $R_{0} \leq 1$ . This completes the proof.

Theorem 2.4

If $R_{0} > 1$ , then the infection equilibrium $E_{*}$ is globally asymptotically stable.

Proof.

Constructing a Lyapunov functional $L_{2}$ as follows: $\begin{aligned} L_{2} & = \int_{Ω} {(k_{1} (1 - α) + k_{2} α) (T - T_{*} - \int_{T_{1}}^{T} \frac{f (T_{*}, V_{*})}{f (s, V_{*})} d s) + k_{1} (I - I_{*} - I_{*} \ln \frac{I}{I_{*}}) \\ + k_{2} (C - C_{*} - C_{*} \ln \frac{C}{C_{*}}) + (V - V_{*} - V_{*} \ln \frac{V}{V_{*}}) \\ + k_{1} (1 - α) (1 - ϵ) f (T_{*}, V_{*}) V_{*} \int_{t - τ_{1}}^{t} h (\frac{f (T (x, s), V (x, s)) V (x, s)}{f (T_{*}, V_{*}) V_{*}}) d s \\ + k_{2} α (1 - ϵ) f (T_{*}, V_{*}) V_{*} \int_{t - τ_{2}}^{t} h (\frac{f (T (x, s), V (x, s))}{f (T_{*}, V_{*}) V_{*}}) d s \\ + k_{1} δ I_{*} \int_{t - τ_{3}}^{t} h (\frac{I (x, s)}{I_{*}}) d s + k_{2} μ \int_{t - τ_{4}}^{t} h (\frac{C (x, s)}{C_{*}}) d s} d x, \end{aligned}$ where $h (x) = x - 1 - \ln x \geq 0$ for all x>0 and with a global minimum $h (1) = 0$ . In the calculation that follows we will use the equilibrium equations $\begin{aligned} s = (1 - ϵ) f (T_{*}, V_{*}) V_{*} + d T_{*}, (1 - α) (1 - ϵ) f (T_{*}, V_{*}) V_{*} = δ I_{*}, \\ α (1 - ϵ) f (T_{*}, V_{*}) V_{*} = μ C_{*}, k_{1} δ I_{*} + k_{2} μ C_{*} = c V_{*}, \end{aligned}$ and note that $\int_{Ω} Δ V (x, t) d x = 0$ , and $\int_{Ω} \frac{△ V (x, t)}{V (x, t)} d x = \int_{Ω} \frac{∥ \nabla V (x, t) ∥^{2}}{V^{2} (x, t)} d x$ . Then, calculating the time derivative of $L_{2}$ along a solution of model (Equation3(3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) ), we obtain $\begin{aligned} \frac{d L_{2}}{d t} & = \int_{Ω} {d T_{*} (k_{1} (1 - α) + k_{2} α) (1 - \frac{T}{T_{*}}) (1 - \frac{f (T_{*}, V_{*})}{f (T, V_{*})}) + (k_{1} (1 - α) + k_{2} α) \\ \times (1 - ϵ) (\frac{f (T_{*}, V_{*})}{f (T, V_{*})}) (f (T_{*}, V_{*}) V_{*} - f (T, V) V) \\ + k_{1} (1 - α) (1 - ϵ) f (T_{*}, V_{*}) V_{*} \\ \times (1 - \frac{I}{I_{*}}) (\frac{f (T_{τ_{1}}, V_{τ_{1}}) V_{τ_{1}}}{f (T_{*}, V_{*}) V_{*}} - \frac{I}{I_{*}}) + k_{2} α (1 - ϵ) f (T_{*}, V_{*}) V_{*} (1 - \frac{C_{*}}{C}) \\ \times (\frac{f (T, V) V}{f (T_{*}, V_{*}) V_{*}} - \frac{C}{C_{*}}) \\ + (1 - \frac{V_{*}}{V}) [k_{1} δ I_{*} (\frac{I_{τ_{3}}}{I_{*}} - \frac{V}{V_{*}}) + k_{2} μ C_{*} (\frac{C_{τ_{4}}}{C_{*}} - \frac{V}{V_{*}})] \\ + k_{1} δ I_{*} (\frac{f (T, V) V}{f (T_{*}, V_{*}) V_{*}} - \ln \frac{f (T, V) V}{f (T_{*}, V_{*}) V_{*}} - \frac{f (T_{τ_{1}}, V_{τ_{1}}) V_{τ_{1}}}{f (T_{*}, V_{*}) V_{*}} - \ln \frac{f (T_{τ_{1}}, V_{τ_{1}}) V_{τ_{1}}}{f (T_{*}, V_{*})}) \\ + k_{2} μ C_{*} (\frac{f (T, V) V}{f (T_{*}, V_{*}) V_{*}} - \ln \frac{f (T, V) V}{f (T_{*}, V_{*}) V_{*}} - \frac{f (T_{τ_{2}}, V_{τ_{2}}) V_{τ_{2}}}{f (T_{*}, V_{*}) V_{*}} + \ln \frac{f (T_{τ_{2}}, V_{τ_{2}}) V_{τ_{2}}}{f (T_{*}, V_{*})}) \\ + k_{1} δ I_{*} (\frac{I}{I_{*}} - \ln \frac{I}{I_{*}} - \frac{I_{τ_{3}}}{I_{*}} + \ln \frac{I_{τ_{3}}}{I_{*}}) + k_{2} μ C_{*} (\frac{C}{C_{*}} - \ln \frac{C}{C_{*}} - \frac{C_{τ_{3}}}{C_{*}} + \ln \frac{C_{τ_{3}}}{C_{*}}) \\ + D (1 - \frac{V_{*}}{V}) Δ V} d x \end{aligned}$ $\begin{aligned} = \int_{Ω} {d T_{*} (k_{1} (1 - α) + k_{2} α) (1 - \frac{T}{T_{*}}) (1 - \frac{f (T_{*}, V_{*})}{f (T, V_{*})}) - k_{1} δ I_{*} [h (\frac{f (T_{*}, V_{*})}{f (T, V_{*})}) \\ + h (\frac{f (T_{τ_{1}}, V_{τ_{1}}) V_{τ_{1}} I_{*}}{f (T_{*}, V_{*}) V_{*} I}) + h (\frac{I_{τ_{3}} V_{*}}{I_{*} V}) - \frac{f (T, V) V}{f (T, V_{*}) V_{*}} + \frac{V}{V_{*}} - \ln \frac{f (T, V_{*})}{f (T, V)}] \\ - k_{2} μ C_{*} [h (\frac{f (T_{*}, V_{*})}{f (T, V_{*})}) + h (\frac{f (T_{τ_{2}}, V_{τ_{2}}) V_{τ_{2}} C_{*}}{f (T_{*}, V_{*}) V_{*} C}) + h (\frac{C_{τ_{4}} V_{*}}{C_{*} V}) - \frac{f (T, V) V}{f (T, V_{*}) V_{*}} \\ + \frac{V}{V_{*}} - \ln \frac{f (T, V_{*})}{f (T, V)}]} d x - D V_{*} \int_{Ω} \frac{∥ \nabla V (x, t) ∥^{2}}{V^{2} (x, t)} d x . \\ = \int_{Ω} {d T_{*} (k_{1} (1 - α) + k_{2} α) (1 - \frac{T}{T_{*}}) (1 - \frac{f (T_{1}, V_{1})}{f (T, V_{1})}) \\ - k_{1} δ I_{*} [h (\frac{f (T_{*}, V_{*})}{f (T, V_{*})}) + h (\frac{f (T_{τ_{1}}, V_{τ_{1}}) V_{τ_{1}} I_{*}}{f (T_{*}, V_{*}) V_{*} I}) + h (\frac{I_{τ_{3}} V_{*}}{I_{*} V}) + h (\frac{f (T, V_{*})}{f (T, V)}) \\ + \frac{V}{V_{*}} (1 - \frac{f (T, V)}{f (T, V_{*})}) (1 - \frac{f (T, V_{*}) V_{*}}{f (T, V) V})] - k_{2} μ C_{*} [h (\frac{f (T_{*}, V_{*})}{f (T, V_{*})}) \\ + h (\frac{f (T_{τ_{2}}, V_{τ_{2}}) V_{τ_{2}} C_{*}}{f (T_{*}, V_{*}) V_{*} C}) + h (\frac{C_{τ_{4}} V_{*}}{C_{*} V}) + h (\frac{f (T, V_{*})}{f (T, V)}) \\ + \frac{V}{V_{*}} (1 - \frac{f (T, V)}{f (T, V_{*})}) (1 - \frac{f (T, V_{*}) V_{*}}{f (T, V) V})]} d x - D V_{*} \int_{Ω} \frac{∥ \nabla V (x, t) ∥^{2}}{V^{2} (x, t)} d x . \end{aligned}$ Recall the conditions (Equation4(4) $\begin{aligned} f (T, V) \geq 0, and f (T, V) = 0 if and only if T = 0; \\ there exists η > 0 such that f (T, V) V \leq η T for all T, V \geq 0; \\ \frac{\partial f (T, V)}{\partial T} > 0 for any fixed V \geq 0; \\ \frac{\partial f (T, V)}{\partial V} \leq 0 for any fixed T \geq 0; \\ \frac{\partial (f (T, V) V)}{\partial V} > 0 for any fixed T \geq 0. \end{aligned}$ (4) ), we then obtain that $\frac{d L_{2}}{d t} \leq 0$ whenever $R_{0} > 1$ . Moreover, it can be shown that the largest invariant set ${\frac{d L_{2}}{d t} = 0}$ is the singleton ${E_{*}}$ . By LaSalle's Invariance Principle, the infection equilibrium $E_{*}$ of model (Equation3(3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) ) is globally asymptotically stable when $R_{0} > 1$ . This completes the proof.

3. Dynamical analysis of model (7)

3.1. Preliminary results

In this section, we dedicate to the investigation of the discrete model (Equation7(7) $\{\begin{cases} \frac{T_{n + 1}^{m} - T_{n}^{m}}{Δ t} = s - d T_{n + 1}^{m} - (1 - ϵ) f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}, \\ \frac{I_{n + 1}^{m} - I_{n}^{m}}{Δ t} = (1 - α) (1 - ϵ) f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m} - δ I_{n + 1}^{m}, \\ \frac{C_{n + 1}^{m} - C_{n}^{m}}{Δ t} = α (1 - ϵ) f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m} - μ C_{n + 1}^{m}, \\ \frac{V_{n + 1}^{m} - V_{n}^{m}}{Δ t} = D \frac{V_{n + 1}^{m + 1} - 2 V_{n + 1}^{m} + V_{n + 1}^{m - 1}}{(Δ x)^{2}} + k_{1} δ I_{n - m_{3} + 1}^{m} + k_{2} μ C_{n - m_{4} + 1}^{m} - c V_{n + 1}^{m} . \end{cases}$ (7) ). It is easy to see that the discrete model (Equation7(7) $\{\begin{cases} \frac{T_{n + 1}^{m} - T_{n}^{m}}{Δ t} = s - d T_{n + 1}^{m} - (1 - ϵ) f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}, \\ \frac{I_{n + 1}^{m} - I_{n}^{m}}{Δ t} = (1 - α) (1 - ϵ) f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m} - δ I_{n + 1}^{m}, \\ \frac{C_{n + 1}^{m} - C_{n}^{m}}{Δ t} = α (1 - ϵ) f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m} - μ C_{n + 1}^{m}, \\ \frac{V_{n + 1}^{m} - V_{n}^{m}}{Δ t} = D \frac{V_{n + 1}^{m + 1} - 2 V_{n + 1}^{m} + V_{n + 1}^{m - 1}}{(Δ x)^{2}} + k_{1} δ I_{n - m_{3} + 1}^{m} + k_{2} μ C_{n - m_{4} + 1}^{m} - c V_{n + 1}^{m} . \end{cases}$ (7) ) has the same equilibria as model (Equation3(3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) ): the infection-free equilibrium $E_{0} = (T_{0}, 0, 0, 0)$ and the infection equilibrium $E_{*} = (T_{*}, I_{*}, C_{*}, V_{*})$ . In the following, we first show that the solution of model (Equation7(7) $\{\begin{cases} \frac{T_{n + 1}^{m} - T_{n}^{m}}{Δ t} = s - d T_{n + 1}^{m} - (1 - ϵ) f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}, \\ \frac{I_{n + 1}^{m} - I_{n}^{m}}{Δ t} = (1 - α) (1 - ϵ) f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m} - δ I_{n + 1}^{m}, \\ \frac{C_{n + 1}^{m} - C_{n}^{m}}{Δ t} = α (1 - ϵ) f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m} - μ C_{n + 1}^{m}, \\ \frac{V_{n + 1}^{m} - V_{n}^{m}}{Δ t} = D \frac{V_{n + 1}^{m + 1} - 2 V_{n + 1}^{m} + V_{n + 1}^{m - 1}}{(Δ x)^{2}} + k_{1} δ I_{n - m_{3} + 1}^{m} + k_{2} μ C_{n - m_{4} + 1}^{m} - c V_{n + 1}^{m} . \end{cases}$ (7) ) is non-negative and bounded. To this end, rewriting the discrete model (Equation7(7) $\{\begin{cases} \frac{T_{n + 1}^{m} - T_{n}^{m}}{Δ t} = s - d T_{n + 1}^{m} - (1 - ϵ) f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}, \\ \frac{I_{n + 1}^{m} - I_{n}^{m}}{Δ t} = (1 - α) (1 - ϵ) f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m} - δ I_{n + 1}^{m}, \\ \frac{C_{n + 1}^{m} - C_{n}^{m}}{Δ t} = α (1 - ϵ) f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m} - μ C_{n + 1}^{m}, \\ \frac{V_{n + 1}^{m} - V_{n}^{m}}{Δ t} = D \frac{V_{n + 1}^{m + 1} - 2 V_{n + 1}^{m} + V_{n + 1}^{m - 1}}{(Δ x)^{2}} + k_{1} δ I_{n - m_{3} + 1}^{m} + k_{2} μ C_{n - m_{4} + 1}^{m} - c V_{n + 1}^{m} . \end{cases}$ (7) ) yields (12) $\{\begin{cases} T_{n + 1}^{m} = T_{n}^{m} + Δ t [s - d T_{n + 1}^{m} - (1 - ϵ) f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}], \\ I_{n + 1}^{m} = \frac{I_{n}^{m} + Δ t (1 - α) (1 - ϵ) f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m}}{1 + δ Δ t}, \\ C_{n + 1}^{m} = \frac{C_{n}^{m} + Δ t α (1 - ϵ) f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m}}{1 + μ Δ t}, \\ A V_{n + 1} = V_{n} + Δ t k_{1} δ I_{n + 1} + Δ t k_{2} μ C_{n + 1}, \end{cases}$ (12) where matrix A of dimension $(N + 1) \times (N + 1)$ is given by $(\begin{matrix} c_{1} & c_{2} & 0 & \dots & 0 & 0 & 0 \\ c_{2} & c_{3} & c_{2} & \dots & 0 & 0 & 0 \\ 0 & c_{2} & c_{3} & \dots & 0 & 0 & 0 \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ & ⋮ & ⋮ \\ 0 & 0 & 0 & \dots & c_{3} & c_{2} & 0 \\ 0 & 0 & 0 & \dots & c_{2} & c_{3} & c_{2} \\ 0 & 0 & 0 & \dots & 0 & c_{2} & c_{1} \end{matrix})$ with $c_{1} = 1 + c Δ t + D Δ t / (Δ x)^{2}$ , $c_{2} = - D Δ t / (Δ x)^{2}$ and $c_{3} = 1 + c Δ t + 2 D Δ t / (Δ x)^{2}$ . It is easy to show that A is a strictly diagonally dominant matrix. Hence, A is non-singular. We then obtain that $V_{n + 1} = A^{- 1} (V_{n} + Δ t k_{1} δ I_{n + 1}^{m} + Δ t k_{2} μ C_{n + 1}^{m}) .$

Theorem 3.1

For any $Δ t > 0$ and $Δ x > 0$ , the solutions of the discrete model (Equation7(7) $\{\begin{cases} \frac{T_{n + 1}^{m} - T_{n}^{m}}{Δ t} = s - d T_{n + 1}^{m} - (1 - ϵ) f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}, \\ \frac{I_{n + 1}^{m} - I_{n}^{m}}{Δ t} = (1 - α) (1 - ϵ) f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m} - δ I_{n + 1}^{m}, \\ \frac{C_{n + 1}^{m} - C_{n}^{m}}{Δ t} = α (1 - ϵ) f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m} - μ C_{n + 1}^{m}, \\ \frac{V_{n + 1}^{m} - V_{n}^{m}}{Δ t} = D \frac{V_{n + 1}^{m + 1} - 2 V_{n + 1}^{m} + V_{n + 1}^{m - 1}}{(Δ x)^{2}} + k_{1} δ I_{n - m_{3} + 1}^{m} + k_{2} μ C_{n - m_{4} + 1}^{m} - c V_{n + 1}^{m} . \end{cases}$ (7) ) remain nonnegative and bounded for all $n \in N$ .

Proof.

We can claim that $T_{n} > 0$ for all $n \in N$ . In fact, assuming the contrary and letting $n_{1} > 0$ be the first time such that $T_{n_{1}} \leq 0$ and $T_{n} > 0$ , $I_{n} > 0$ , $C_{n} > 0$ , $V_{n} > 0$ for all $n < n_{1}$ . Since, $T_{n_{1} - 1}^{m} = T_{n_{1}}^{m} - Δ t [s - d T_{n_{1}}^{m} - (1 - ϵ) f (T_{n_{1}}^{m}, V_{n_{1} - 1}^{m}) V_{n_{1} - 1}^{m}] .$ Note that the conditions of (Equation4(4) $\begin{aligned} f (T, V) \geq 0, and f (T, V) = 0 if and only if T = 0; \\ there exists η > 0 such that f (T, V) V \leq η T for all T, V \geq 0; \\ \frac{\partial f (T, V)}{\partial T} > 0 for any fixed V \geq 0; \\ \frac{\partial f (T, V)}{\partial V} \leq 0 for any fixed T \geq 0; \\ \frac{\partial (f (T, V) V)}{\partial V} > 0 for any fixed T \geq 0. \end{aligned}$ (4) ), we then obtain $T_{n_{1} - 1}^{m} \leq 0$ , which contradicts our assumption and so $T_{n} > 0$ for all $n \in N$ . Moreover, it is easy to prove that the sequences ${I_{n}}$ , ${C_{n}}$ and ${V_{n}}$ are non-negative by using mathematical induction.

Next, we establish the boundedness of solutions. To this end, we define a sequence ${G_{n}}$ as follows: $G_{n}^{m} = T_{n}^{m} + I_{n + m_{1}}^{m} + C_{n + m_{2}}^{m} .$ Then, we have $G_{n + 1}^{m} - G_{n}^{m} \leq Δ t (s - ξ G_{n + 1}^{m}),$ where $ξ = min {d, δ, μ}$ . Thus we obtain $G_{n + 1}^{m} \leq \frac{1}{1 + ξ Δ t} G_{n}^{m} + \frac{s Δ t}{1 + ξ Δ t} .$ By using induction, we easily obtain $G_{n}^{m} \leq {(\frac{1}{1 + Δ t ξ})}^{n} G_{0}^{m} + \frac{s}{ξ} [1 - {(\frac{1}{1 + Δ t ξ})}^{n}] .$ Thus $lim_{n \to \infty} sup G_{n}^{m} \leq \frac{s}{ξ}, f o r a l l m \in {0, 1, \dots, N},$ which implies that ${G_{n}}$ is bounded. Therefore, ${T_{n}}$ , ${I_{n}}$ and ${C_{n}}$ are bounded.

By the last equation of model (Equation7(7) $\{\begin{cases} \frac{T_{n + 1}^{m} - T_{n}^{m}}{Δ t} = s - d T_{n + 1}^{m} - (1 - ϵ) f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}, \\ \frac{I_{n + 1}^{m} - I_{n}^{m}}{Δ t} = (1 - α) (1 - ϵ) f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m} - δ I_{n + 1}^{m}, \\ \frac{C_{n + 1}^{m} - C_{n}^{m}}{Δ t} = α (1 - ϵ) f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m} - μ C_{n + 1}^{m}, \\ \frac{V_{n + 1}^{m} - V_{n}^{m}}{Δ t} = D \frac{V_{n + 1}^{m + 1} - 2 V_{n + 1}^{m} + V_{n + 1}^{m - 1}}{(Δ x)^{2}} + k_{1} δ I_{n - m_{3} + 1}^{m} + k_{2} μ C_{n - m_{4} + 1}^{m} - c V_{n + 1}^{m} . \end{cases}$ (7) ) that $\sum_{m = 0}^{N} V_{n + 1}^{m} = \frac{1}{1 + c Δ t} [\sum_{m = 0}^{N} V_{n}^{m} + Δ t (\sum_{m = 0}^{N} k_{1} δ I_{n + 1 - m_{3}}^{m} + \sum_{m = 0}^{N} k_{2} μ C_{n + 1 - m_{4}}^{m})] .$ Note that ${I_{n}}$ and ${C_{n}}$ are bounded, there exists two positive constant $ρ_{1}, ρ_{2}$ such that $I_{n}^{m} \leq ρ_{1}$ , $C_{n}^{m} \leq ρ_{2}$ for $m \in {0, 1, \dots, N}$ . Thus we have $\sum_{m = 0}^{N} V_{n + 1}^{m} \leq \frac{1}{1 + c Δ t} (\sum_{m = 0}^{N} V_{n}^{m} + Δ t (N + 1) (k_{1} δ ρ_{1} + k_{2} μ ρ_{2})) .$ By induction, we have $\begin{aligned} \sum_{m = 0}^{N} V_{n}^{m} & \leq \frac{1}{(1 + c Δ t)^{n}} \sum_{m = 0}^{N} V_{0}^{m} + \frac{(k_{1} δ ρ_{1} + k_{2} μ ρ_{2}) (N + 1)}{c} (1 - \frac{1}{(1 + c Δ t)^{n}}) \\ \leq \sum_{m = 0}^{N} V_{0}^{m} + \frac{(k_{1} δ ρ_{1} + k_{2} μ ρ_{2}) (N + 1)}{c}, \end{aligned}$ implying ${V_{n}}$ is bounded. This completes the proof.

3.2. Global stability

Theorem 3.2

For any $Δ t > 0$ , $Δ x > 0$ , if $R_{0} \leq 1$ , then the infection-free equilibrium $E_{0}$ of system (Equation7(7) $\{\begin{cases} \frac{T_{n + 1}^{m} - T_{n}^{m}}{Δ t} = s - d T_{n + 1}^{m} - (1 - ϵ) f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}, \\ \frac{I_{n + 1}^{m} - I_{n}^{m}}{Δ t} = (1 - α) (1 - ϵ) f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m} - δ I_{n + 1}^{m}, \\ \frac{C_{n + 1}^{m} - C_{n}^{m}}{Δ t} = α (1 - ϵ) f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m} - μ C_{n + 1}^{m}, \\ \frac{V_{n + 1}^{m} - V_{n}^{m}}{Δ t} = D \frac{V_{n + 1}^{m + 1} - 2 V_{n + 1}^{m} + V_{n + 1}^{m - 1}}{(Δ x)^{2}} + k_{1} δ I_{n - m_{3} + 1}^{m} + k_{2} μ C_{n - m_{4} + 1}^{m} - c V_{n + 1}^{m} . \end{cases}$ (7) ) is globally asymptotically stable.

Proof.

Consider the following discrete Lyapunov functional: $\begin{aligned} G_{n} & = \sum_{m = 0}^{N} {\frac{1}{Δ t} [(k_{1} (1 - α) + k_{2} α) (T_{n}^{m} - T_{0} - \int_{T_{0}}^{T_{n}^{m}} \frac{f (T_{0}, 0)}{f (s, 0)} d s) + k_{1} I_{n}^{m} + k_{2} C_{n}^{m} \\ + (1 + c Δ t) V_{n}^{m}] + k_{1} (1 - α) (1 - ϵ) \sum_{j = n - m_{1}}^{n - 1} f (T_{j + 1}, V_{j}^{m}) V_{j}^{m} \\ + k_{2} α (1 - ϵ) \sum_{j = n - m_{2}}^{n - 1} f (T_{j + 1}, V_{j}^{m}) V_{j}^{m} + k_{1} δ \sum_{j = n - m_{3}}^{n - 1} I_{j + 1}^{m} + k_{2} μ \sum_{j = n - m_{4}}^{n - 1} C_{j + 1}^{m}} . \end{aligned}$ Then we have $\begin{aligned} G_{n + 1} - G_{n} \\ = \sum_{m = 0}^{N} {\frac{1}{Δ t} [(k_{1} (1 - α) + k_{2} α) (T_{n + 1}^{m} - T_{n}^{m} - \int_{T_{n}^{m}}^{T_{n + 1}^{m}} \frac{f (T_{0}, 0)}{f (s, 0)} d s) \\ + k_{1} δ (I_{n + 1}^{m} - I_{n}^{m}) + k_{2} μ (C_{n + 1}^{m} - C_{n}^{m}) + (1 + c Δ t) (V_{n + 1}^{m} - V_{n}^{m})] \\ + k_{1} (1 - α) (1 - ϵ) (\sum_{j = n + 1 - m_{1}}^{n} f (T_{j + 1}^{m}, V_{j}^{m}) V_{j}^{m} - \sum_{j = n - m_{1}}^{n - 1} f (T_{j + 1}^{m}, V_{j}^{m}) V_{j}^{m}) \\ + k_{2} α (1 - ϵ) (\sum_{j = n + 1 - m_{2}}^{n} f (T_{j + 1}^{m}, V_{j}^{m}) V_{j}^{m} - \sum_{j = n - m_{2}}^{n - 1} f (T_{j + 1}^{m}, V_{j}^{m}) V_{j}^{m}) \\ + k_{1} δ (\sum_{j = n + 1 - m_{3}}^{n} I_{j + 1}^{m} - \sum_{j = n - m_{3}}^{n - 1} I_{j + 1}^{m}) + k_{2} μ (\sum_{j = n + 1 - m_{4}}^{n} C_{j + 1}^{m} - \sum_{j = n - m_{4}}^{n - 1} C_{j + 1}^{m})} \\ \leq \sum_{m = 0}^{N} {(k_{1} (1 - α) + k_{2} α) (1 - \frac{f (T_{0}, 0)}{f (T_{n + 1}^{m}, 0)}) (s - d T_{n + 1}^{m} - (1 - ϵ) f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}) \\ + k_{1} ((1 - α) (1 - ϵ) f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m} - δ I_{n + 1}^{m}) \\ + k_{2} (α (1 - ϵ) f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m} - μ C_{n + 1}^{m}) + D \frac{V_{n + 1}^{m + 1} - 2 V_{n + 1}^{m} + V_{n + 1}^{m - 1}}{(Δ x)^{2}} \\ + k_{1} δ I_{n + 1 - m_{3}}^{m} + k_{2} μ C_{n + 1 - m_{4}}^{m} - c V_{n + 1}^{m} + c (V_{n + 1}^{m} - V_{n}^{m}) \\ + k_{1} (1 - α) (1 - ϵ) (f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m} - f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m}) \\ + k_{2} α (1 - ϵ) (f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m} - f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m}) \\ + k_{1} δ (I_{n + 1}^{m} - I_{n + 1 - m_{3}}^{m}) + k_{2} μ (C_{n + 1}^{m} - C_{n + 1 - m_{4}}^{m})} \\ = \sum_{m = 0}^{N} {d T_{0} (k_{1} (1 - α) + k_{2} α) (1 - \frac{T_{n + 1}^{m}}{T_{0}}) (1 - \frac{f (T_{0}, 0)}{f (T_{n + 1}^{m}, 0)}) \\ + c V_{n}^{m} (\frac{(1 - ϵ) (k_{1} (1 - α) + k_{2} α) f (T_{0}, 0)}{c} \frac{f (T_{n + 1}^{m}, V_{n}^{m})}{f (T_{n + 1}^{m}, 0)} - 1)} \\ \leq \sum_{m = 0}^{N} {d T_{0} (k_{1} (1 - α) + k_{2} α) (1 - \frac{T_{n + 1}^{m}}{T_{0}}) (1 - \frac{f (T_{0}, 0)}{f (T_{n + 1}^{m}, 0)}) + c V_{n}^{m} (R_{0} - 1)} . \end{aligned}$ The last inequality is followed by the condition (Equation4(4) $\begin{aligned} f (T, V) \geq 0, and f (T, V) = 0 if and only if T = 0; \\ there exists η > 0 such that f (T, V) V \leq η T for all T, V \geq 0; \\ \frac{\partial f (T, V)}{\partial T} > 0 for any fixed V \geq 0; \\ \frac{\partial f (T, V)}{\partial V} \leq 0 for any fixed T \geq 0; \\ \frac{\partial (f (T, V) V)}{\partial V} > 0 for any fixed T \geq 0. \end{aligned}$ (4) ). Thus if $R_{0} \leq 1$ , then we have $G_{n + 1} - G_{n} \leq 0,$ for all $n \in N$ , which implies that $G_{n}$ is a monotone decreasing sequence. Since $G_{n} \geq 0$ , there is a limit $lim_{n \to \infty} G_{n} \geq 0$ which implies that $lim_{n \to \infty} (G_{n + 1} - G_{n}) = 0$ , from which we get $lim_{n \to \infty} T_{n}^{m} = T_{0}$ and $lim_{n \to \infty} V_{n}^{m} (R_{0} - 1) = 0$ . We discuss two cases: (i) if $R_{0} < 1$ , from model (Equation7(7) $\{\begin{cases} \frac{T_{n + 1}^{m} - T_{n}^{m}}{Δ t} = s - d T_{n + 1}^{m} - (1 - ϵ) f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}, \\ \frac{I_{n + 1}^{m} - I_{n}^{m}}{Δ t} = (1 - α) (1 - ϵ) f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m} - δ I_{n + 1}^{m}, \\ \frac{C_{n + 1}^{m} - C_{n}^{m}}{Δ t} = α (1 - ϵ) f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m} - μ C_{n + 1}^{m}, \\ \frac{V_{n + 1}^{m} - V_{n}^{m}}{Δ t} = D \frac{V_{n + 1}^{m + 1} - 2 V_{n + 1}^{m} + V_{n + 1}^{m - 1}}{(Δ x)^{2}} + k_{1} δ I_{n - m_{3} + 1}^{m} + k_{2} μ C_{n - m_{4} + 1}^{m} - c V_{n + 1}^{m} . \end{cases}$ (7) ), we obtain $lim_{n \to \infty} I_{n}^{m} = 0$ , $lim_{n \to \infty} C_{n}^{m} = 0$ , for all $m \in {0, 1, \dots, N}$ ; (ii) if $R_{0} = 1$ , by $lim_{n \to \infty} T_{n}^{m} = T_{0}$ and from model (Equation7(7) $\{\begin{cases} \frac{T_{n + 1}^{m} - T_{n}^{m}}{Δ t} = s - d T_{n + 1}^{m} - (1 - ϵ) f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}, \\ \frac{I_{n + 1}^{m} - I_{n}^{m}}{Δ t} = (1 - α) (1 - ϵ) f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m} - δ I_{n + 1}^{m}, \\ \frac{C_{n + 1}^{m} - C_{n}^{m}}{Δ t} = α (1 - ϵ) f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m} - μ C_{n + 1}^{m}, \\ \frac{V_{n + 1}^{m} - V_{n}^{m}}{Δ t} = D \frac{V_{n + 1}^{m + 1} - 2 V_{n + 1}^{m} + V_{n + 1}^{m - 1}}{(Δ x)^{2}} + k_{1} δ I_{n - m_{3} + 1}^{m} + k_{2} μ C_{n - m_{4} + 1}^{m} - c V_{n + 1}^{m} . \end{cases}$ (7) ), we have $lim_{n \to \infty} I_{n}^{m} = 0$ , $lim_{n \to \infty} C_{n}^{m} = 0$ , $lim_{n \to \infty} V_{n}^{m} = 0$ . Thus concluding the above discussion implies that $E_{0}$ is globally asymptotically stable. This completes the proof.

Theorem 3.3

For any $Δ t > 0$ and $Δ x > 0$ , if $R_{0} > 1$ , then the infection equilibrium $E_{*}$ of model (Equation3(3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) ) is globally asymptotically stable.

Proof.

Define $\begin{aligned} {\tilde{G}}_{n} & = \sum_{m = 0}^{N} {\frac{1}{Δ t} [(k_{1} (1 - α) + k_{2} α) (T_{n}^{m} - T_{*} - \int_{T_{*}}^{T_{n}^{m}} \frac{f (T_{*}, V_{*})}{f (s, V_{*})} d s) \\ + k_{1} I_{*} h (\frac{I_{n}^{m}}{I_{*}}) + k_{2} C_{*} h (\frac{C_{n}^{m}}{C_{*}}) + (1 + c Δ t) h (\frac{V_{n}^{m}}{V_{*}})] \\ + \sum_{j = n - m_{1}}^{n - 1} k_{1} (1 - α) (1 - ϵ) f (T_{*}, V_{*}) V_{*} h (\frac{f (T_{j + 1}^{m}, V_{j}^{m}) V_{j}^{m}}{f (T_{*}, V_{*}) V_{*}}) \\ + \sum_{j = n - m_{2}}^{n - 1} k_{2} α (1 - ϵ) f (T_{*}, V_{*}) V_{*} h (\frac{f (T_{j + 1}^{m}, V_{j}^{m}) V_{j}^{m}}{f (T_{*}, V_{*}) V_{*}}) \\ + k_{1} δ I_{*} \sum_{j = n - m_{3}}^{n - 1} h (\frac{I_{j + 1}^{m}}{I_{*}}) + k_{2} μ C_{*} \sum_{j = n - m_{4}}^{n - 1} h (\frac{C_{j + 1}^{m}}{C_{*}})}, \end{aligned}$ where $h (x) = x - 1 - \ln x \geq 0$ for all x>0. Obviously, $φ (x)$ has a global minimum at x = 1 and $h (1) = 0$ .

Recall that model (Equation12(12) $\{\begin{cases} T_{n + 1}^{m} = T_{n}^{m} + Δ t [s - d T_{n + 1}^{m} - (1 - ϵ) f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}], \\ I_{n + 1}^{m} = \frac{I_{n}^{m} + Δ t (1 - α) (1 - ϵ) f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m}}{1 + δ Δ t}, \\ C_{n + 1}^{m} = \frac{C_{n}^{m} + Δ t α (1 - ϵ) f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m}}{1 + μ Δ t}, \\ A V_{n + 1} = V_{n} + Δ t k_{1} δ I_{n + 1} + Δ t k_{2} μ C_{n + 1}, \end{cases}$ (12) ) and the infection equilibrium conditions (Equation11(11) $\{\begin{aligned} s = d T_{*} + (1 - ϵ) f (T_{*}, V_{*}) V_{*}, \\ (1 - α) (1 - ϵ) f (T_{*}, V_{*}) V_{*} = δ I_{*}, \\ α (1 - ϵ) f (T_{*}, V_{*}) V_{*} = μ C_{*}, \\ k_{1} δ I_{*} + k_{2} μ C_{*} = c V_{*} . \end{aligned}$ (11) ), we then have the difference of ${\tilde{U}}_{n}$ satisfies $\begin{aligned} {\tilde{G}}_{n + 1} - {\tilde{G}}_{n} \\ = \sum_{m = 0}^{n} {\frac{1}{Δ t} [(k_{1} (1 - α) + k_{2} α) (T_{n + 1}^{m} - T_{n}^{m} - \int_{T_{n}^{m}}^{T_{n + 1}^{m}} \frac{T_{*}, V_{*}}{f (s, V_{*})} d s) \\ + k_{1} (I_{n + 1}^{m} - I_{n}^{m} + I_{*} \ln \frac{I_{n}^{m}}{I_{n + 1}^{m}}) + k_{2} (C_{n + 1}^{m} - C_{n}^{m} + C_{*} \ln \frac{C_{n}^{m}}{C_{n + 1}^{m}}) \\ + (1 + c Δ t) (V_{n + 1}^{m} - V_{n}^{m} + V_{*} \ln \frac{V_{n}^{m}}{V_{n + 1}^{m}})] + k_{1} (1 - α) (1 - ϵ) f (T_{*}, V_{*}) V_{*} \\ \times (\sum_{j = n + 1 - m_{1}}^{n} φ (\frac{f (T_{j + 1}^{m}, V_{j}^{m}) V_{j}^{m}}{f (T_{*}, V_{*}) V_{*}}) - \sum_{j = n - m_{1}}^{n - 1} h (\frac{f (T_{j + 1}^{m}, V_{j}^{m}) V_{j}^{m}}{f (T_{*}, V_{*}) V_{*}})) \\ + k_{2} α (1 - ϵ) f (T_{*}, V_{*}) V_{*} \sum_{j = n + 1 - m_{2}}^{n} h (\frac{f (T_{j + 1}^{m}, V_{j}^{m}) V_{j}^{m}}{f (T_{*}, V_{*}) V_{*}}) \\ + k_{2} α (1 - ϵ) f (T_{*}, V_{*}) V_{*} \sum_{j = n - m_{2}}^{n - 1} h (\frac{f (T_{j + 1}^{m}, V_{j}^{m}) V_{j}^{m}}{f (T_{*}, V_{*}) V_{*}}) \\ + k_{1} δ I_{*} (\sum_{j = n + 1 - m_{3}}^{n} h (\frac{I_{j + 1}^{m}}{I_{*}}) - \sum_{j = n - m_{3}}^{n - 1} h (\frac{I_{j + 1}^{m}}{I_{*}})) \\ + k_{2} μ C_{*} (\sum_{j = n + 1 - m_{4}}^{n} h (\frac{C_{j + 1}^{m}}{C_{*}}) - \sum_{j = n - m_{4}}^{n - 1} h (\frac{C_{j + 1}^{m}}{C_{*}}))} \\ \leq \sum_{m = 0}^{N} {\frac{1}{Δ t} [(k_{1} (1 - α) + k_{2} α) (1 - \frac{f (T_{*}, V_{*})}{f (T_{n + 1}^{m}, V_{*})}) (T_{n + 1}^{m} - T_{n}^{m}) \\ + k_{1} (1 - \frac{I_{*}}{I_{n + 1}^{m}}) (I_{n + 1}^{m} - I_{n}^{m}) + k_{2} (1 - \frac{C_{*}}{C_{n + 1}^{m}}) (C_{n + 1}^{m} - C_{n}^{m}) \\ + (1 - \frac{V_{*}}{V_{n + 1}^{m}}) (V_{n + 1}^{m} - V_{n}^{m}) + c Δ t (V_{n + 1}^{m} - V_{n}^{m} + V_{*} \ln \frac{V_{n}^{m}}{V_{n + 1}^{m}})] \end{aligned}$ $\begin{aligned} + k_{1} (1 - α) (1 - ϵ) [h (\frac{f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}}{f (T_{*}, V_{*}) V_{*}}) - h (\frac{f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m}}{f (T_{*}, V_{*}) V_{*}})] \\ + k_{2} α (1 - ϵ) [h (\frac{f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}}{f (T_{*}, V_{*}) V_{*}}) - h (\frac{f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m}}{f (T_{*}, V_{*}) V_{*}})] \\ + k_{1} δ I_{*} [h (\frac{I_{n + 1}^{m}}{I_{*}}) - h (\frac{I_{n + 1 - m_{3}}^{m}}{I_{*}})] + k_{2} μ C_{*} [h (\frac{C_{n + 1}^{m}}{C_{*}}) - h (\frac{C_{n + 1 - m_{3}}^{m}}{C_{*}})]} \\ = \sum_{m = 0}^{N} {(k_{1} (1 - α) + k_{2} α) (1 - \frac{f (T_{*}, V_{*})}{f (T_{n + 1}^{m}, V_{*})}) \\ \times (s - d T_{n + 1}^{m} - (1 - ϵ) f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}) \\ + k_{1} (1 - \frac{I_{*}}{I_{n + 1}^{m}}) ((1 - α) (1 - ϵ) f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) - δ I_{n + 1}^{m}) \\ + k_{2} (1 - \frac{C_{*}}{C_{n + 1}^{m}}) (α (1 - ϵ) f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) - μ C_{n + 1}^{m}) + (1 - \frac{V_{*}}{V_{n + 1}^{m}}) \\ \times (D \frac{V_{n + 1}^{m + 1} - 2 V_{n + 1}^{m} + V_{n + 1}^{m - 1}}{(Δ x)^{2}} + k_{1} δ I_{n + 1 - m_{3}}^{m} + k_{2} μ C_{n + 1 - m_{4}}^{m} - c V_{n + 1}^{m}) \\ + k_{1} (1 - α) (1 - ϵ) [h (\frac{f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}}{f (T_{*}, V_{*}) V_{*}}) - h (\frac{f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m}}{f (T_{*}, V_{*}) V_{*}})] \\ + k_{2} α (1 - ϵ) [h (\frac{f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}}{f (T_{*}, V_{*}) V_{*}}) - h (\frac{f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m}}{f (T_{*}, V_{*}) V_{*}})] \\ + k_{1} δ I_{*} [h (\frac{I_{n + 1}^{m}}{I_{*}}) - h (\frac{I_{n + 1 - m_{3}}^{m}}{I_{*}})] + k_{2} μ C_{*} [h (\frac{C_{n + 1}^{m}}{C_{*}}) - h (\frac{C_{n + 1 - m_{3}}^{m}}{C_{*}})] \end{aligned}$ $\begin{aligned} + c (V_{n + 1}^{m} - V_{n}^{m} + V_{*} \ln \frac{V_{n}^{m}}{V_{n + 1}^{m}})} \\ = \sum_{m = 0}^{N} {d T_{*} (k_{1} (1 - α) + k_{2} α) (1 - \frac{T_{n + 1}^{m}}{T_{*}}) (1 - \frac{f (T_{*}, V_{*})}{f (T_{n} + 1^{m}, V_{*})}) \\ + k_{1} (1 - α) (1 - ϵ) f (T_{*}, V_{*}) V_{*} [(1 - \frac{f (T_{*}, V_{*})}{f (T_{n} + 1^{m}, V_{*})}) (1 - \frac{f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}}{f (T_{*}, V_{*}) V_{*}}) \\ + (1 - \frac{I_{*}}{I_{n + 1}^{m}}) (\frac{f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m}}{f (T_{*}, V_{*}) V_{*}} - \frac{I_{n + 1}^{m}}{I_{*}}) \\ + (1 - \frac{V_{*}}{V_{n + 1}^{m}}) (\frac{I_{n + 1 - m_{3}}^{m}}{I_{*}} - \frac{V_{n + 1}^{m}}{V_{*}}) + (\frac{V_{n + 1}^{m}}{V_{*}} - \frac{V_{n}^{m}}{V_{*}} + \ln \frac{V_{n}^{m}}{V_{n + 1}^{m}}) \\ + h (\frac{f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}}{f (T_{*}, V_{*}) V_{*}}) - h (\frac{f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m}}{f (T_{*}, V_{*}) V_{*}}) \\ + h (\frac{I_{n + 1}^{m}}{I_{*}}) - h (\frac{I_{n + 1 - m_{3}}^{m}}{I_{*}})] + k_{2} α (1 - ϵ) f (T_{*}, V_{*}) V_{*} [(1 - \frac{f (T_{*}, V_{*})}{f (T_{n} + 1^{m}, V_{*})}) \\ \times (1 - \frac{f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}}{f (T_{*}, V_{*}) V_{*}}) + (1 - \frac{C_{*}}{C_{n + 1}^{m}}) (\frac{f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m}}{f (T_{*}, V_{*}) V_{*}} - \frac{C_{n + 1}^{m}}{C_{*}}) \\ + (1 - \frac{V_{*}}{V_{n + 1}^{m}}) (\frac{C_{n + 1 - m_{4}}^{m}}{C_{*}} - \frac{V_{n + 1}^{m}}{V_{*}}) + (\frac{V_{n + 1}^{m}}{V_{*}} - \frac{V_{n}^{m}}{V_{*}} + \ln \frac{V_{n}^{m}}{V_{n + 1}^{m}}) \\ + h (\frac{f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}}{f (T_{*}, V_{*}) V_{*}}) - h (\frac{f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m}}{f (T_{*}, V_{*}) V_{*}}) \\ + h (\frac{C_{n + 1}^{m}}{C_{*}}) - h (\frac{C_{n + 1 - m_{4}}^{m}}{C_{*}})]} - \frac{D V_{*}}{(Δ x)^{2}} \sum_{m = 0}^{N - 1} \frac{{(V_{n + 1}^{m + 1} - V_{n + 1}^{m})}^{2}}{V_{n + 1}^{m + 1} V_{n + 1}^{m}} \\ = \sum_{m = 0}^{N} {d T_{*} (k_{1} (1 - α) + k_{2} α) (1 - \frac{T_{n + 1}^{m}}{T_{*}}) (1 - \frac{f (T_{*}, V_{*})}{f (T_{n + 1}^{m}, V_{*})}) \end{aligned}$ $\begin{aligned} + k_{1} (1 - α) (1 - ϵ) f (T_{*}, V_{*}) V_{*} [3 - \frac{f (T_{*}, V_{*})}{f (T_{n + 1}^{m}, V_{*})} - \frac{I_{*} f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m}}{I_{n + 1}^{m} f (T_{*}, V_{*}) V_{*}} \\ - \frac{V_{*} I_{n + 1 - m_{3}}^{m}}{V_{n + 1}^{m} I_{*}} + \frac{f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}}{f (T_{n + 1}^{m}, V_{*}) V_{*}} - \frac{V_{n}^{m}}{V_{*}} + \ln \frac{V_{n}^{m}}{V_{n + 1}^{m}} + \ln \frac{f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m})}{f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}} \\ + \ln \frac{I_{n + 1 - m_{3}}^{m}}{I_{n + 1}^{m}}] + k_{2} α (1 - ϵ) f (T_{*}, V_{*}) V_{*} [3 - \frac{f (T_{*}, V_{*})}{f (T_{n + 1}^{m}, V_{*})} - \frac{V_{*} C_{n + 1 - m_{4}}^{m}}{V_{n + 1}^{m} C_{*}} \\ - \frac{C_{*} f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m}}{C_{n + 1}^{m} f (T_{*}, V_{*}) V_{*}} + \frac{f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}}{f (T_{n + 1}^{m}, V_{*}) V_{*}} - \frac{V_{n}^{m}}{V_{*}} + \ln \frac{V_{n}^{m}}{V_{n + 1}^{m}} \\ + \ln \frac{f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m})}{f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}} + \ln \frac{C_{n + 1 - m_{4}}^{m}}{C_{n + 1}^{m}}]} - \frac{D V_{*}}{(Δ x)^{2}} \sum_{m = 0}^{N - 1} \frac{{(V_{n + 1}^{m + 1} - V_{n + 1}^{m})}^{2}}{V_{n + 1}^{m + 1} V_{n + 1}^{m}} \\ = \sum_{m = 0}^{N} {d T_{*} (k_{1} (1 - α) + k_{2} α) (1 - \frac{T_{n + 1}^{m}}{T_{*}}) (1 - \frac{f (T_{*}, V_{*})}{f (T_{n + 1}^{m}, V_{*})}) \\ + k_{1} (1 - α) (1 - ϵ) f (T_{*}, V_{*}) V_{*} [- h (\frac{f (T_{*}, V_{*})}{f (T_{n + 1}^{m}, V_{*})}) - h (\frac{V_{*} I_{n + 1 - m_{3}}^{m}}{V_{n + 1}^{m} I_{*}}) \\ - h (\frac{I_{*} f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m}}{I_{n + 1}^{m} f (T_{*}, V_{*}) V_{*}}) + \frac{f (T_{n + 1}^{m}, V_{*}) V_{n}^{m}}{f (T_{n + 1}^{m}, V_{*}) V_{*}} - \frac{V_{n}^{m}}{V_{*}} \\ + \ln \frac{f (T_{n + 1}^{m}, V_{*})}{f (T_{n + 1}^{m}, V_{n}^{m})}] + k_{2} α (1 - ϵ) f (T_{*}, V_{*}) V_{*} [- h (\frac{f (T_{*}, V_{*})}{f (T_{n + 1}^{m}, V_{*})}) \\ - h (\frac{V_{*} C_{n + 1 - m_{4}}^{m}}{V_{n + 1}^{m} C_{*}}) - h (\frac{C_{*} f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m}}{C_{n + 1}^{m} f (T_{*}, V_{*}) V_{*}}) + \frac{f (T_{n + 1}^{m}, V_{*}) V_{n}^{m}}{f (T_{n + 1}^{m}, V_{*}) V_{*}} \\ - \frac{V_{n}^{m}}{V_{*}} + \ln \frac{f (T_{n + 1}^{m}, V_{*})}{f (T_{n + 1}^{m}, V_{n}^{m})}]} - \frac{D V_{*}}{(Δ x)^{2}} \sum_{m = 0}^{N - 1} \frac{{(V_{n + 1}^{m + 1} - V_{n + 1}^{m})}^{2}}{V_{n + 1}^{m + 1} V_{n + 1}^{m}} \end{aligned}$ $\begin{aligned} = \sum_{m = 0}^{N} {d T_{*} (k_{1} (1 - α) + k_{2} α) (1 - \frac{T_{n + 1}^{m}}{T_{*}}) (1 - \frac{f (T_{*}, V_{*})}{f (T_{n + 1}^{m}, V_{*})}) \\ + k_{1} (1 - α) (1 - ϵ) f (T_{*}, V_{*}) V_{*} [- h (\frac{f (T_{*}, V_{*})}{f (T_{n + 1}^{m}, V_{*})}) - h (\frac{V_{*} I_{n + 1 - m_{3}}^{m}}{V_{n + 1}^{m} I_{*}}) \\ - h (\frac{I_{*} f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m}}{I_{n + 1}^{m} f (T_{*}, V_{*}) V_{*}}) - h (\frac{f (T_{n + 1}^{m}, V_{*})}{f (T_{n + 1}^{m}, V_{n}^{m})}) \\ + \frac{V_{n}^{m}}{V_{*}} (1 - \frac{f (T_{n + 1}^{m}, V_{n}^{m})}{f (T_{n + 1}^{m}, V_{*})}) (\frac{f (T_{n + 1}^{m}, V_{*}) V_{*}}{f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}} - 1)] \\ + k_{2} α (1 - ϵ) f (T_{*}, V_{*}) V_{*} [- h (\frac{f (T_{*}, V_{*})}{f (T_{n + 1}^{m}, V_{*})}) - h (\frac{V_{*} C_{n + 1 - m_{4}}^{m}}{V_{n + 1}^{m} C_{*}}) \\ - h (\frac{C_{*} f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m}}{C_{n + 1}^{m} f (T_{*}, V_{*}) V_{*}}) - h (\frac{f (T_{n + 1}^{m}, V_{*})}{f (T_{n + 1}^{m}, V_{n}^{m})}) \\ + \frac{V_{n}^{m}}{V_{*}} (1 - \frac{f (T_{n + 1}^{m}, V_{n}^{m})}{f (T_{n + 1}^{m}, V_{*})}) (\frac{f (T_{n + 1}^{m}, V_{*}) V_{*}}{f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}} - 1)]} \\ - \frac{D V_{*}}{(Δ x)^{2}} \sum_{m = 0}^{N - 1} \frac{{(V_{n + 1}^{m + 1} - V_{n + 1}^{m})}^{2}}{V_{n + 1}^{m + 1} V_{n + 1}^{m}} . \end{aligned}$ It follows from the condition (Equation4(4) $\begin{aligned} f (T, V) \geq 0, and f (T, V) = 0 if and only if T = 0; \\ there exists η > 0 such that f (T, V) V \leq η T for all T, V \geq 0; \\ \frac{\partial f (T, V)}{\partial T} > 0 for any fixed V \geq 0; \\ \frac{\partial f (T, V)}{\partial V} \leq 0 for any fixed T \geq 0; \\ \frac{\partial (f (T, V) V)}{\partial V} > 0 for any fixed T \geq 0. \end{aligned}$ (4) ) that $(1 - \frac{f (T_{n + 1}^{m}, V_{n}^{m})}{f (T_{n + 1}^{m}, V_{*})}) (\frac{f (T_{n + 1}^{m}, V_{*}) V_{*}}{f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}} - 1) \leq 0$ . Recall that $φ (x) \geq 0$ for all x>0, we then obtain ${\tilde{G}}_{n + 1} - {\tilde{G}}_{n} \leq 0$ , for all $n \in N$ . This implies that ${\tilde{G}}_{n}$ is monotone decreasing sequence. Since ${\tilde{G}}_{n} > 0$ , there is a limit $lim_{n \to \infty} {\tilde{G}}_{n} \geq 0$ . Hence, $lim_{n \to \infty} ({\tilde{G}}_{n + 1} - {\tilde{G}}_{n}) = 0$ . Furthermore, from model (Equation7(7) $\{\begin{cases} \frac{T_{n + 1}^{m} - T_{n}^{m}}{Δ t} = s - d T_{n + 1}^{m} - (1 - ϵ) f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}, \\ \frac{I_{n + 1}^{m} - I_{n}^{m}}{Δ t} = (1 - α) (1 - ϵ) f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m} - δ I_{n + 1}^{m}, \\ \frac{C_{n + 1}^{m} - C_{n}^{m}}{Δ t} = α (1 - ϵ) f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m} - μ C_{n + 1}^{m}, \\ \frac{V_{n + 1}^{m} - V_{n}^{m}}{Δ t} = D \frac{V_{n + 1}^{m + 1} - 2 V_{n + 1}^{m} + V_{n + 1}^{m - 1}}{(Δ x)^{2}} + k_{1} δ I_{n - m_{3} + 1}^{m} + k_{2} μ C_{n - m_{4} + 1}^{m} - c V_{n + 1}^{m} . \end{cases}$ (7) ), it can be shown that $lim_{n \to \infty} T_{n}^{m} = T_{*}$ , $lim_{n \to \infty} I_{n}^{m} = I_{*}$ , $lim_{n \to \infty} C_{n}^{m} = C_{*}$ , $lim_{n \to \infty} V_{n}^{m} = V_{*}$ , for all $m \in {0, 1, \dots, N}$ , which implies that $E_{*}$ of model (Equation7(7) $\{\begin{cases} \frac{T_{n + 1}^{m} - T_{n}^{m}}{Δ t} = s - d T_{n + 1}^{m} - (1 - ϵ) f (T_{n + 1}^{m}, V_{n}^{m}) V_{n}^{m}, \\ \frac{I_{n + 1}^{m} - I_{n}^{m}}{Δ t} = (1 - α) (1 - ϵ) f (T_{n + 1 - m_{1}}^{m}, V_{n - m_{1}}^{m}) V_{n - m_{1}}^{m} - δ I_{n + 1}^{m}, \\ \frac{C_{n + 1}^{m} - C_{n}^{m}}{Δ t} = α (1 - ϵ) f (T_{n + 1 - m_{2}}^{m}, V_{n - m_{2}}^{m}) V_{n - m_{2}}^{m} - μ C_{n + 1}^{m}, \\ \frac{V_{n + 1}^{m} - V_{n}^{m}}{Δ t} = D \frac{V_{n + 1}^{m + 1} - 2 V_{n + 1}^{m} + V_{n + 1}^{m - 1}}{(Δ x)^{2}} + k_{1} δ I_{n - m_{3} + 1}^{m} + k_{2} μ C_{n - m_{4} + 1}^{m} - c V_{n + 1}^{m} . \end{cases}$ (7) ) is globally asymptotically stable. This completes the proof.

4. Numerical simulations

In this section, we perform numerical simulation to validate the main theoretical results obtained in previous sections. To this end, we reduce model (Equation3(3) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) f (T (x, t), V (x, t)) V (x, t), \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) f (T (x, t - τ_{1}), V (x, t - τ_{1})) V (x, t - τ_{1}) - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) f (T (x, t - τ_{2}), V (x, t - τ_{2})) V (x, t - τ_{2}) - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t) . \end{cases}$ (3) ) to the one with $f (T, V) = \frac{β T V}{1 + a V}$ , then the model reads as (13) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) \frac{β T V}{1 + a V}, \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) \frac{β T (x, t - τ_{1}) V (x, t - τ_{1})}{1 + a V (x, t - τ_{1})} - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) \frac{β T (x, t - τ_{2}) V (x, t - τ_{2})}{1 + a V (x, t - τ_{2})} - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t), \end{cases}$ (13) with the homogeneous Neumann boundary conditions $\frac{\partial V}{\partial x} = 0, t > 0, x \in \partial Ω$ and initial conditions $\begin{aligned} T (x, s) & = ϕ_{1} (x, s) \geq 0, I (x, s) = ϕ_{2} (x, s) \geq 0, C (x, s) = ϕ_{3} (x, s) \geq 0, \\ V (x, s) & = ϕ_{3} (x, s) \geq 0, (x, s) \in \bar{Ω} \times [- τ, 0], τ = max {τ_{1}, τ_{2}, τ_{3}, τ_{4}} . \end{aligned}$ The corresponding discrete model to (Equation13(13) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) \frac{β T V}{1 + a V}, \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) \frac{β T (x, t - τ_{1}) V (x, t - τ_{1})}{1 + a V (x, t - τ_{1})} - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) \frac{β T (x, t - τ_{2}) V (x, t - τ_{2})}{1 + a V (x, t - τ_{2})} - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t), \end{cases}$ (13) ) is given by (14) $\{\begin{cases} \frac{T_{n + 1}^{m} - T_{n}^{m}}{Δ t} = s - d T_{n + 1}^{m} - (1 - ϵ) \frac{β T_{n + 1}^{m} V_{n}^{m}}{1 + a V_{n}^{m}}, \\ \frac{I_{n + 1}^{m} - I_{n}^{m}}{Δ t} = (1 - α) (1 - ϵ) \frac{β T_{n + 1 - m_{1}}^{m} V_{n - m_{1}}^{m}}{1 + a V_{n - m_{1}}^{m}} - δ I_{n + 1}^{m}, \\ \frac{C_{n + 1}^{m} - C_{n}^{m}}{Δ t} = α (1 - ϵ) \frac{β T_{n + 1 - m_{2}}^{m} V_{n - m_{2}}^{m}}{1 + a V_{n - m_{2}}^{m}} - μ C_{n + 1}^{m}, \\ \frac{V_{n + 1}^{m} - V_{n}^{m}}{Δ t} = D \frac{V_{n + 1}^{m + 1} - 2 V_{n + 1}^{m} + V_{n + 1}^{m - 1}}{(Δ x)^{2}} + k_{1} δ I_{n - m_{3} + 1}^{m} + k_{2} μ C_{n - m_{4} + 1}^{m} - c V_{n + 1}^{m}, \end{cases}$ (14) with the discrete boundary condition $V_{n}^{- 1} = V_{n}^{0}, V_{n}^{N} = V_{n}^{N + 1}, f o r n \in N$ and the discrete initial conditions $\begin{aligned} T_{s}^{m} = ϕ_{1} (x_{m}, t_{s}) \geq 0, I_{s}^{m} = ϕ_{2} (x_{m}, t_{s}) \geq 0, C_{s}^{m} = ϕ_{3} (x_{m}, t_{s}) \geq 0, \\ V_{s}^{m} = ϕ_{4} (x_{m}, t_{s}) \geq 0, for all s = - l, - l + 1, \dots, 0, l = max_{1 \leq i \leq 4} {m_{i}} . \end{aligned}$ Let $Ω = [0, 20]$ , D = 0.05, $Δ t = 0.1$ and $Δ x = 1$ . For convenience, we set a = 0.00001, $τ_{1} = 3.5$ , $τ_{2} = 2.5$ , $τ_{3} = 1.5$ and $τ_{4} = 5$ in the following simulations. Some of the parameter values for these simulations are selected from [Citation32]. The numerical implementation of (Equation13(13) $\{\begin{cases} \frac{\partial T (x, t)}{\partial t} = s - d T (x, t) - (1 - ϵ) \frac{β T V}{1 + a V}, \\ \frac{\partial I (x, t)}{\partial t} = (1 - α) (1 - ϵ) \frac{β T (x, t - τ_{1}) V (x, t - τ_{1})}{1 + a V (x, t - τ_{1})} - δ I (x, t), \\ \frac{\partial C (x, t)}{\partial t} = α (1 - ϵ) \frac{β T (x, t - τ_{2}) V (x, t - τ_{2})}{1 + a V (x, t - τ_{2})} - μ C (x, t), \\ \frac{\partial V (x, t)}{\partial t} = D Δ V (x, t) + k_{1} δ I (x, t - τ_{3}) + k_{2} μ C (x, t - τ_{4}) - c V (x, t), \end{cases}$ (13) ) is carried out using the NSFD scheme described in (Equation14(14) $\{\begin{cases} \frac{T_{n + 1}^{m} - T_{n}^{m}}{Δ t} = s - d T_{n + 1}^{m} - (1 - ϵ) \frac{β T_{n + 1}^{m} V_{n}^{m}}{1 + a V_{n}^{m}}, \\ \frac{I_{n + 1}^{m} - I_{n}^{m}}{Δ t} = (1 - α) (1 - ϵ) \frac{β T_{n + 1 - m_{1}}^{m} V_{n - m_{1}}^{m}}{1 + a V_{n - m_{1}}^{m}} - δ I_{n + 1}^{m}, \\ \frac{C_{n + 1}^{m} - C_{n}^{m}}{Δ t} = α (1 - ϵ) \frac{β T_{n + 1 - m_{2}}^{m} V_{n - m_{2}}^{m}}{1 + a V_{n - m_{2}}^{m}} - μ C_{n + 1}^{m}, \\ \frac{V_{n + 1}^{m} - V_{n}^{m}}{Δ t} = D \frac{V_{n + 1}^{m + 1} - 2 V_{n + 1}^{m} + V_{n + 1}^{m - 1}}{(Δ x)^{2}} + k_{1} δ I_{n - m_{3} + 1}^{m} + k_{2} μ C_{n - m_{4} + 1}^{m} - c V_{n + 1}^{m}, \end{cases}$ (14) ). We first select the parameter values: s = 1000, $β = 8 \times 10^{- 7}$ , d = 0.01, $α = 0.195$ , $ϵ = 0.5$ , a = 0.5, $δ = 0.7$ , $μ = 0.07$ , $k_{1} = 100$ , $k_{2} = 4.11$ , c = 13. By a simple calculation, we have $R_{0} = 0.2502 < 1$ . 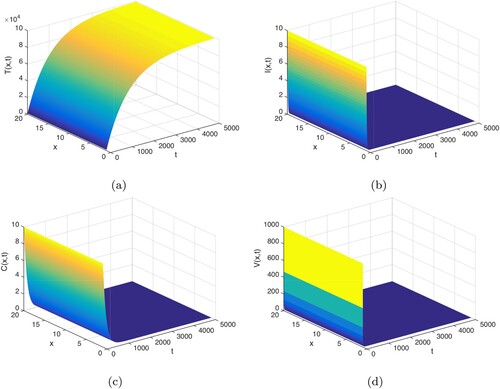Hence, in this case, the infection-free equilibrium $E_{0} = (10^{5}, 0, 0, 0)$ is globally asymptotically stable, which means that the virus is cleared and the infection dies out. Figure validates the above analysis.

Figure 1. $R_{0} < 1$ , the infection-free equilibrium $E_{0}$ is globally asymptotically stable.

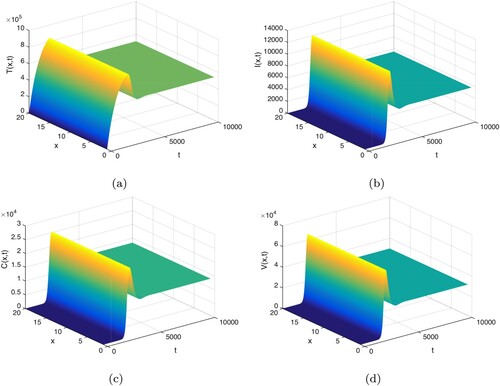
Next, we select $s = 10^{4}$ and keep the other parameters are the same with Figure . In this case, we have $R_{0} = 2.5016 > 1$ and the unique infection equilibrium $E_{*} = (5.1980 \times 10^{5}, 5.5223 \times 10^{3}, 1.3377 \times 10^{4}, 3.0032 \times 10^{4})$ is globally asymptotically stable, which means that the virus persists in the host and the infection becomes chronic. Figure confirms this observation.

Figure 2. $R_{0} > 1$ , the infection equilibrium $E_{*}$ is globally asymptotically stable.

5. Conclusion

In this paper, we have formulated a delayed and diffusive viral infection model incorporating shorted-lived and chronically infected cells and general nonlinear incidence function. Then, by applying NSFD scheme, we presented an efficient numerical method for the corresponding continuous model. Theoretically, we have shown that the stability conditions for the equilibria are identical in case of both the continuous and discrete models. Specifically, if $R_{0} \leq 1$ , then the infection-free equilibrium $E_{0}$ is globally asymptotically stable; if $R_{0} > 1$ , then the infection equilibrium $E_{*}$ is globally asymptotically stable. The results show that the NSFD scheme has the advantage that the positivity, boundedness and global properties of solutions for original continuous model are efficiently preserved.

As far as we know, there are few delayed and diffusive virus models considering both the shorted-lived and chronically infected cells, and no theoretical analysis has been made on this kind of models. Here, our main contribution is to construct suitable Lyapunov functional for both the continuous-time and discrete-time virus models, and present a general method to analyse this kind of models. Based on the above obtained results, one can extend this method to more complicated models.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by National Natural Science Foundation of China (11701445,11971379, 11801439,11701451,11702214), by Natural Science Basic Research Plan in Shaanxi Province of China (2020JQ-831), Scientific Research Program Funded by Shaanxi Provincial Education Department (20JK0642), by Young Talent fund of University Association for Science and Technology in Shaanxi, China (20180504).

References

Z. Bai and Y. Zhou, Dynamics of a viral infection model with delayed CTL response and immune circadian rhythm, Chaos Solitons Fract. 45(9–10) (2012), pp. 1133–1139.
Web of Science ®Google Scholar
L. Cai and X. Li, Stability and Hopf bifurcation in a delayed model for HIV infection of CD4 +T cells, Chaos Solitons Fract. 42(1) (2009), pp. 1–11.
Web of Science ®Google Scholar
D. Daners and P.K. Medina, Pitman Research Notes in Math. Ser., Vol. 279, Abstract Evolution Equations, Periodic Problems and Applications, 1992.
Google Scholar
D. Ding, W. Qin, and X. Ding, Lyapunov functions and global stability for a discretized multigroup SIR epidemic model, Discrete Contin. Dyn. Syst. B 20 (2015), pp. 1971–1981.
Web of Science ®Google Scholar
W.E. Fitzgibbon, Semilinear functional differential equations in Banach space, J. Differ. Equ. 29 (1978), pp. 1–14.
Web of Science ®Google Scholar
Y. Geng, J. Xu, and J. Hou, Discretization and dynamic consistency of a delayed and diffusive viral infection model, Appl. Math. Comput. 316 (2018), pp. 282–295.
Web of Science ®Google Scholar
K. Hattaf, A.A. Lashari, Y. Louartassi, and N. Yousfi, A delayed SIR epidemic model with general incidence rate, Electron. J. Qual. Theor. 3 (2013), pp. 1–9.
Google Scholar
K. Hattaf and N. Yousfi, Global properties of a discrete viral infection model with general incidence rate, Math. Methods Appl. Sci. 39(5) pp. 998–1004.
Web of Science ®Google Scholar
K. Hattaf and N. Yousfi, Global properties of a discrete viral infection model with general incidence rate, Math. Methods Appl. Sci. 39 (2016), pp. 998–1004.
Web of Science ®Google Scholar
K. Hattaf and N. Yousfi, A numerical method for delayed partial differential equations describing infectious diseases, Comput. Math. Appl. 72 (2016), pp. 2741–2750.
Web of Science ®Google Scholar
K. Hattaf, N. Yousfi, and A. Tridane, Mathematical analysis of a virus dynamics model with general incidence rate and cure rate, Nonlinear Anal. Real World Appl. 13 (2012), pp. 1866–1872.
Web of Science ®Google Scholar
D. Henry, Gerometric Theory of Semilinear Parabolic Equations, Lecture Notes in Mathematics, Vol. 840, Springer-Verlag, Berlin, New York, 1993.
Google Scholar
G. Huang, Y. Takeuchi, and W.B. Ma, Lyapunov functionals for delay differential equations model of viral infections, SIAM J. Appl. Math. 70 (2010), pp. 2693–2708.
Web of Science ®Google Scholar
M.Y. Li and H. Shu, Impact of intracellular delays and target-cell dynamics on in vivo viral infections, SIAM J. Appl. Math. 70 (2010), pp. 2434–2448.
Web of Science ®Google Scholar
R.H. Martin and H.L. Smith, Abstract functional differential equations and reaction-diffusion systems, Trans. Amer. Math. Soc. 321 (1990), pp. 1–44.
Web of Science ®Google Scholar
R.H. Martin and H.L. Smith, Reaction-diffusion systems with time delays: monotonicity, invariance, comparison and convergence, J. Reine. Angew. Math. 413 (1991), pp. 1–35.
Web of Science ®Google Scholar
C.C. McCluskey and Y. Yang, Global stability of a diffusive virus dynamics model with general incidence function and time delay, Nonlinear Anal. Real World Appl. 25 (2015), pp. 64–78.
Web of Science ®Google Scholar
R.E. Mickens, Nonstandard Finite Difference Models of Differential Equations, World Scientific, Singapore, 1994.
Google Scholar
R.E. Mickens, Dynamics consistency: a fundamental principle for constructing nonstandard finite difference scheme for differential equation, J. Diff. Equ. Appl. 9 (2003), pp. 1037–1051.
Google Scholar
Y. Muroya, Y. Bellen, Y. Enatsu, and Y. Nakata, Global stability for a discrete epidemic model for disease with immunity and latency spreading in a heterogeneous host population, Nonlinear Anal. Real World Appl. 13 (2013), pp. 258–274.
Web of Science ®Google Scholar
Y. Nakata, Global dynamics of a cell mediated immunity in viral infection models with distributed delays, J. Math. Anal. Appl. 375 (2011), pp. 14–27.
Web of Science ®Google Scholar
M.A. Obaid and A.M. Elaiw, Stability of virus infection models with antibodies and chronically infected cells, Abstract Appl. Anal. 2014 (2014), pp.1–12. Article ID 650371
Google Scholar
M.H. Protter and H.F. Weinberger, Maximum Principles in Differential Equations, Prentice Hall, Englewood Cliffs, 1967.
Google Scholar
W. Qin, L. Wang, and X. Ding, A non-standard finite difference method for a hepatitis B virus infection model with spatial diffusion, J. Differ. Equ. Appl. 20 (2014), pp. 1641–1651.
Web of Science ®Google Scholar
P. Shi and L. Dong, Dynamical behaviors of a discrete HIV-1 virus model with bilinear infective rate, Math. Methods Appl. Sci. 37 (2014), pp. 2271–2280.
Web of Science ®Google Scholar
X.Y. Song and U. Neumann Avidan, Global stability and periodic solution of the viral dynamics, J. Math. Anal. Appl. 329 (2007), pp. 281–297.
Web of Science ®Google Scholar
C.C. Travis and G.F. Webb, Existence and stability for partial functional differential equations, Trans. Amer. Math. Soc. 200 (1974), pp. 395–418.
Web of Science ®Google Scholar
T. Wang, Z. Hu, F. Liao, and W. Ma, Global stability analysis for delayed virus infection model with general incidence rate and humoral immunity, Math. Comput. Simul. 89 (2013), pp. 13–22.
Web of Science ®Google Scholar
F. Wang, Y. Huang, and X. Zou, Global dynamics of a PDE in-host viral model, Appl. Anal. 93 (2014), pp. 2312–2329.
Web of Science ®Google Scholar
K. Wang, W. Wang, and S. Song, Dynamics of an HBV model with diffusion and delay, J. Theor. Biol. 253(1) (2008), pp. 36–44.
PubMed Web of Science ®Google Scholar
Z.P. Wang and R. Xu, Stability and Hopf bifurcation in a viral infection model with nonlinear incidence rate and delayed immune response, Commun. Nonlinear. Sci. 17 (2012), pp. 964–978.
Web of Science ®Google Scholar
S. Wang and Y. Zhou, Global dynamics of an in-host HIV-1 infection model with the long-lived infected cells and four intracellular delays, Int. J. Biomath. 5 (06)(2012), pp. 1250058.
Google Scholar
J. Wu, Theory and Applications of Partial Functional Differential Equations, Springer, New York, 1996.
Google Scholar
J. Xu, Y. Geng, and J Hou, A non-standard finite difference scheme for a delayed and diffusive viral infection model with general nonlinear incidence rate, Comput. Math. Appl. 74(8) (2017), pp. 1782–1798.
Web of Science ®Google Scholar
J. Xu and Y. Zhou, Bifurcation analysis of HIV-1 infection model with cell-to-cell transmission and immune response delay, Math. Biosci. Eng. 13 (2016), pp. 343–367.
PubMed Web of Science ®Google Scholar
J. Xu, Y. Zhou, Y. Li, and Y. Yang, Global dynamics of a intracellular infection model with delays and humoral immunity, Math. Methods. Appl. Sci. 39 (2016), pp. 5427–5435.
Web of Science ®Google Scholar
Y. Yang, J. Zhou, X. Ma, and T. Zhang, Nonstandard finite difference scheme for a diffusive within-host virus dynamics model with both virus-to-cell and cell-to-cell transmissions, Comput. Math. Appl. 72 (2016), pp. 1013–1020.
Web of Science ®Google Scholar

Global stability of a delayed and diffusive virus model with nonlinear infection function

Abstract

1. Introduction

2. Dynamical analysis of model (3)

2.1. Preliminaries

2.2. Stabilities of equilibria

3. Dynamical analysis of model (7)

3.1. Preliminary results

3.2. Global stability

4. Numerical simulations

5. Conclusion

Disclosure statement

References

Information for

Open access

Opportunities

Help and information

Global stability of a delayed and diffusive virus model with nonlinear infection function

Abstract

1. Introduction

2. Dynamical analysis of model (3)

2.1. Preliminaries

2.2. Stabilities of equilibria

3. Dynamical analysis of model (7)

3.1. Preliminary results

3.2. Global stability

4. Numerical simulations

5. Conclusion

Disclosure statement

Additional information

Funding

References

Related research

To cite this article:

Download citation

Your download is now in progress and you may close this window

Login or register to access this feature

Information for

Open access

Opportunities

Help and information

Keep up to date