On the reproduction number in epidemics

Abstract

This note provides an elementary derivation of the basic reproduction number and the effective reproduction number from the discrete Kermack–McKendrick epidemic model. The derived formulae match those derived from the continuous version of the model; however, the derivation from discrete model is a bit more intuitive. The MATLAB functions for its calculation are given. A real case example is considered and the results are compared with those obtained by the R0 and the EpiEstim software packages.

KEYWORDS:

• Basic reproduction number
• effective reproduction number
• Kermack–McKendrick epidemic model

Introduction

In addition to the incidence and prevalence [1,2], the reproductive number is one of the most useful epidemiologic metrics for monitoring and controlling the development of an epidemic [3–9]. While the incidence and prevalence tell us something about the size of the epidemic, the reproduction number informs us of its spread rate.

There are two kinds of reproduction numbers: the basic reproduction number, $R_0$, and the effective (or time-varying) reproduction number, $R$. $R_0$ is defined only at the beginning of an outbreak and ‘represents the number of secondary cases that one case can produce if introduced to a susceptible population’ [10]. $R$ is defined over the entire period of an epidemic and represents ‘the average number of secondary infectious produced by typical infective during the entire period of infectiousness’ [11]. Neither $R_0$ nor$R$ is a natural constant, because their value depends on the epidemic model used. For various models used for analyzing properties and for calculation of $R_0$, see [12–24]. For properties and calculation of R, see [25–30]. For critical consideration of $R_0$, see [31] and references therein.

We first review the formulas for calculating $R_0$ and $R$ based on the continuous Kermack and McKendrick epidemic model [32,33]. Heesterbeek and Dietz [14] used the following form of the model (1) $I\left(t\right)=S\left(t\right)\underset{0}{\overset{\mathrm{\infty }}{\int }}A\left(\tau \right)I\left(t-\tau \right)d\tau ,$(1) where $I\left(t\right)$ is the incidence rate, $S\left(t\right)$ is the density of susceptibles in the population, $A\left(\tau \right)$ is excepted infectivity of a person with infection age $\tau$. They define (2) $R_0\equiv S_0\underset{0}{\overset{\mathrm{\infty }}{\int }}A\left(\tau \right)d\tau$(2) and derived the following expressions (3) $1=S_0\underset{0}{\overset{\mathrm{\infty }}{\int }}A\left(\tau \right)e^{-r\tau }d\tau$(3) where $S_0$ is the initial density of the susceptible population and $r$ is the natural growth rate. From these expressions, Wallinga and Lipsitch [34], by introducing generation time distribution (4) $w\left(t\right)\equiv \frac{A\left(t\right)}{{\int }_0^{\mathrm{\infty }}A\left(\tau \right)d\tau },$(4) deduce a formula for calculation of $R_0$, which has the form (5) $\frac{1}{R_0}=\underset{0}{\overset{\mathrm{\infty }}{\int }}w\left(\tau \right)e^{-r\tau }d\tau .$(5)

For practical calculation, they offer a discrete version of this formula implemented in the R₀ package [35].

It seems that Fraser [26] was the first who deduce a general formula for calculation of $R$ from the Kermack and McKendrick model. He starts with a generalization of Equation (1) in the form of a continuous renewal equation (6) $I\left(t\right)=\underset{0}{\overset{\mathrm{\infty }}{\int }}\text{β}\left(t,\tau \right)I\left(t-\tau \right)d\tau ,$(6) where $\text{β}\left(t,\tau \right)$ is the transmissibility. He defines the case reproduction number $R_c\left(t\right)$ as ‘the average number of people someone infected at time t can expect to infect’, thus (7) $R_c\equiv \underset{0}{\overset{\mathrm{\infty }}{\int }}\text{β}\left(t+\tau ,\tau \right)d\tau ,$(7) and the instantaneous reproduction number $R\left(t\right)$ as ‘the average number of people someone infected at time t could expect to infect should conditions remain unchanged’, expressed by the formula, (8) $R\equiv \underset{0}{\overset{\mathrm{\infty }}{\int }}\text{β}\left(t,\tau \right)d\tau .$(8)

Assuming that $\text{β}\left(t,\tau \right)$ can be factorized as (9) $\text{β}\left(t,\tau \right)=R\left(t\right)w\left(\tau \right),$(9) he deduces (10) $R\left(t\right)=\frac{I\left(t\right)}{{\int }_0^{\mathrm{\infty }}I\left(t-\tau \right)w\left(\tau \right)d\tau },$(10) and from this formula, a discrete version of the formula for calculation of $R$ and $R_c$. The method was implemented in the EpiEstim package [36,37].

We will follow the above ideas, but, unlike the authors mentioned, we will derive formulas for calculating the reproduction number from the discrete form of the Kermack–McKendrick epidemic model. In particular, this derivation does not need the factorization assumption Equation (9), and the derivation of the formula (4) for generation time is a bit more intuitive. For other discrete models, see [38] and references therein.

Kermack–McKendrick epidemic model

Let $I_{n,k}$ denote the number of infectious peoples at calendar time n and infection-age k. Let $I_{n,0}$ be the number of peoples who became infected at the calendar time n. We call them nth generation. The transition process of the epidemic for the nth generation is as follows $I_{n,0}\to I_{n+1,1}\to \cdots \to I_{n+k,k}\to \cdots ,$and the whole epidemic process may be schematically represented in this way [32,33]: $\begin{array}{cc}& t\to \\ \begin{array}{c}\tau \\ \downarrow \end{array}& \begin{array}{ccccccc}k/n& \text{|}& 0& 1& 2& 3& \cdots \\ 0& \text{|}& I_{0,0}& I_{1,0}& I_{2,0}& I_{3,0}& \cdots \\ 1& \text{|}& & I_{1,1}& I_{2,1}& I_{3,1}& \searrow \\ 2& \text{|}& & & I_{2,2}& I_{3,2}& \searrow \\ 3& \text{|}& & & & I_{3,3}& \searrow \\ ⋮& \text{|}& & & & & \searrow \end{array}\end{array}$

Here, t is calendar time and $\tau$ is the infection age.

Two hypotheses govern the epidemic process. The first one is that a decline in the number of infected in nth generation depends only on age. Thus, we have (11) $I_{n,k}-I_{n-1,k-1}=-{\psi }_{k-1}{I}_{n-1,k-1},$(11) where $0\le {\psi }_{k-1}\le 1$ is the removal rate. From this, it follows that (12) $I_{n,k}=B_k{I}_{n-k,0}.$(12)

A non-dimensional parameter $B_k\equiv \prod _{j=1}^k\left(1-{\psi }_{k-j}\right)$ can be interpreted as the probability that an individual of age k is still infectious [3,19].

Before stating the second hypothesis, we decompose $I_{n,0}$ to local $\left(I_{n,0}^{local}\right)$ and imported $\left(I_{n,0}^{imported}\right)$ cases [37]: (13) $I_{n,0}=I_{n,0}^{local}+I_{n,0}^{imported}.$(13)

The second hypothesis assumes that $I_{n,0}$ is proportional to the number of contacts each generation has with all susceptible left in time interval n [32]: (14) $I_{n,0}^{local}=S_n\sum _{k=1}^n{\varphi }_k{I}_{n,k}\left(n=1,2,\dots \right),$(14) where ${\varphi }_k$ is the infective rate at age $k$ and $S_n$ is the number of susceptible individuals at the time interval $n$. Using Equations (12), (13) and (14), we obtain (15) $I_{n,0}=S_n\sum _{k=1}^n{A}_k{I}_{n-k,0}+I_{n,0}^{imported}\left(n=1,2,\dots \right),$(15) where $A_k\equiv {\varphi }_k{B}_k$ is the infectivity at age $k$ [19,39]; i.e. the number of new infectives in unit time per ineffective contact. Note that the Equation (15) assumes that ‘an individual is not infective at the moment of infection’ [32], so, starting at the 0th generation, we assume (16) $I_{0,0}^{}=\kappa I_0+I_{0,0}^{imported},$(16) where $\kappa \ge 0$ is a constant and $I_0$ the number of infected individuals initially. Equations (16) and (15) represent the discrete Kermack–McKendrick epidemic model that we will use to derive the formulas for calculating $R_0$ and $R$.

Basic reproduction number

To derive the formula for calculation of $R_0$, we start with the epidemic process for 0th generation: $I_{0,0}\Rightarrow I_{1,1}\to I_{2,2}\to \cdots .$

Thus, the number of infectious individuals of 0th generation at each time interval is, by Equation (12), $I_{0,0}\Rightarrow B_1{I}_{0,0}\to B_2{I}_{0,0}\to \cdots .$and the new infected individuals produced by these infectives are, by Equation (15), (17) $I_{0,0}\Rightarrow S_1{A}_1{I}_{0,0}\to S_2{A}_2{I}_{0,0}\to \cdots .$(17)

The total number of secondary infections produced by 0th generation is thus (18) $C_0=I_{0,0}\sum _{k=1}^{\mathrm{\infty }}{S}_k{A}_k.$(18)

If (19) $S_0=S_1=\cdots ,$(19) i.e. the susceptible population remains the same (which would literally mean that the newly infected individual is immediately removed and replaced by a new susceptible, but practically that the population is large), and we set $I_0=1$ and $I_{0,0}^{imported}=0$ in Equation (16), then $I_{0,0}=\kappa$, and thus, by definition[14], (20) $R_0\equiv \kappa S_0\sum _{k=1}^{\mathrm{\infty }}{A}_k.$(20)

This is a discrete form of Equation (2).

Note. We could set $I_0=0$ and $I_{0,0}^{imported}=1$, but we want to keep $\kappa$ in the expression in order to use an empirical law for I, which depends on the initial condition $I_0$.

The sequence of infected individuals produced by one infective in a completely susceptible population is thus, by Equation (17), (21) $1\Rightarrow \kappa S_0{A}_1\to \kappa S_0{A}_2\to \cdots .$(21)

Dividing each term of this sequence by Equation (20), we obtain the sequence of the fractions of infected produced by one infected case: (22) $w_1,w_2,\cdots ,$(22) where (23) $w_k\equiv \frac{A_k}{\sum _{j=1}^{\mathrm{\infty }}{A}_j}\text{and}\sum _{k=1}^{\mathrm{\infty }}{w}_k=1.$(23)

Thus, $w_k$ can be interpreted as the probability that an infective individuals, produces a new case at age k. Equation (23) is a discrete form of Equation (4), and thus, by definition, the generation-time distribution. For more on generation time, see [40–42]. From Equations (20) and (23), we can express infectivity at age k as (24) $A_k=\frac{R_0}{\kappa S_0}{w}_k$(24)

Substituting Equation (24) for $A_k$ into Equation (15), and taking $I_{n,0}^{imported}=0$ and $S_0=S_1=\cdots$, we obtain (25) $R_0=\frac{\kappa I_{n,0}^{}}{\sum _{k=1}^n{w}_k{I}_{n-k,0}}.$(25)

This formula cannot be used directly for calculation of $R_0$ from observed incidences because these are assumed to be produced only by the 0th generation in a wholly susceptible population. Thus, to obtain the formula for computing of $R_0$ from Equation (25), we assume that infection is a continuous process that in its initial phase is governed by the exponential growth rate (26) $I\left(t\right)=I_0{e}^{rt},$(26) where $I_0$ and $r$ can be determined from observable data by regression analysis. Using Equation (26) and integrating it over a single time interval, we obtain (27) $I_{n,0}=\frac{1}{t_{n+1}-t_n}\underset{t_n}{\overset{t_{n+1}}{\int }}I\left(t\right)dt=I_0\underset{n}{\overset{n+1}{\int }}{e}^{rt}dt=\kappa I_0{e}^{rn},$(27) where (28) $\kappa =\frac{e^r-1}{r}.$(28)

Substituting Equation (27) for $I_{n,0}$ and Equation (28) for $\kappa$ into Equation (25), we obtain Wallinga–Lipsitch formula [34]: (29) $R_0=\frac{r}{\left(e^r-1\right)\sum _{k=1}^n{w}_k{e}^{-rk}}.$(29)

This is a discrete form of Equation (5). Note that calculation of $R_0$ by Equation (29) depends on n; however, practically $w_k=0$, for $k>K$, so we should take $n=K$. For more on the calculation of $R_0$ by Equation (29), see [35].

The effective reproduction number

By similar reasoning as in the previous section, we will derive the formula for calculation of the effective reproduction number R. For the nth generation, we have the following transition process $I_{n,0}\Rightarrow I_{n+1,1}\to I_{n+2,2}\to \cdots .$

Using Equation (12), the number of individuals who are still infective in the nth generation is $I_{n,0}\Rightarrow B_1{I}_{n,0}\to B_2{I}_{n,0}\to \cdots .$

The sequence of newly infected individuals generated by these infectives is $I_{n,0}\Rightarrow S_{n+1}{A}_1{I}_{n,0}\to S_{n+2}{A}_2{I}_{n,0}\to \cdots .$

The total number of secondary infections generated by the nth generation is therefore (30) $C_n=\sum _{k=1}^{\mathrm{\infty }}{S}_{n+k}{A}_k{I}_{n,0}.$(30)

We have two possibilities regarding $S_n$. The first is that, similar to the calculation of the $R_0$ for the 0th generation, where the population of the initial number of susceptibles does not change, we assume that the current population of the susceptibles does not change (31) $S_n=S_{n+1}=\cdots .$(31)

If we insert this and $I_{n,0}=1$ into Equation (30), then we can define the instantaneous reproduction number $R_n$ as (32) $R_n\equiv S_n\sum _{k=1}^{\mathrm{\infty }}{A}_k.$(32)

This is a discrete analogue of Equation (8). From Equation (15), we have (33) $S_n=\frac{I_{n,0}^{local}}{\sum _{k=1}^n{A}_k{I}_{n-k,0}}\left(n=1,2,\dots \right),$(33)

Extracting $A_k$ from Equation (23) and substituting Equation (33) into (32), we obtain the well-known Fraser formula [26]: (34) $R_n=\frac{I_{n,0}^{local}}{\sum _{k=1}^n{w}_k{I}_{n-k,0}}.$(34)

In particular, if $I_{n,0}=1$ (or any other constant) for all n, then $R_n\to 1$ as $n\to \mathrm{\infty }$. When $I_{n,0}^{local}=0$ for some n, then, for this n, we have $R_n=0$. If $w_k=1$ for $k=m$ and $w_k=0$ for all other k, i.e. an infected person is practically infectious for only one day, then $R_n=I_{n,0}/I_{n-m,0}$. This relation can be used for a quick but crude estimate of $R_n$.

Equation (34) is a discrete form of Equation (10). Substituting Equation (24) into (32), and taking $\kappa =1$, we obtain (35) $R_n=\frac{S_n}{S_0}{R}_0.$(35)

This is a well-known result for the SIR model [11]: the ratio of R and $R_0$ represents the fraction of susceptibles who are still in the population.

If we abandon condition (31) and put $I_{n,0}=1$ into Equation (30), then we can define the case reproduction number $R_{c,n}$ as (36) $R_{c,n}^{}\equiv \sum _{k=1}^{\mathrm{\infty }}{S}_{n+k}{A}_k.$(36)

Using Equation (33) for $S_n$ and substituting Equation (23) into (36), we obtain [26] (37) $R_{c,n}^{}=\sum _{k=1}^{\mathrm{\infty }}\frac{w_k{I}_{n+k,0}^{local}}{\sum _{j=1}^n{w}_j{I}_{n+k-j,0}}=\sum _{k=1}^{\mathrm{\infty }}{w}_k{R}_{n+k}.$(37)

We note that none of the formulas (29), (34) and (37), depend on the size of the initial susceptible population. Thus, they can thus be used to calculate the reproduction number from daily incidence reports once the distribution of generation time is known.

Examples

For practical calculation, we write a MATLAB programme using functions that are listed in the Appendix. These functions assume $w_k=0$, $k>K$ and $I_{n,0}=0$, $n>N$.

For a numerical example, we take data for Spanish influenza in Germany 1918–19 [43] and compare results of this calculation with results obtained by the R0 package [35] and the EpiEstim package [36].

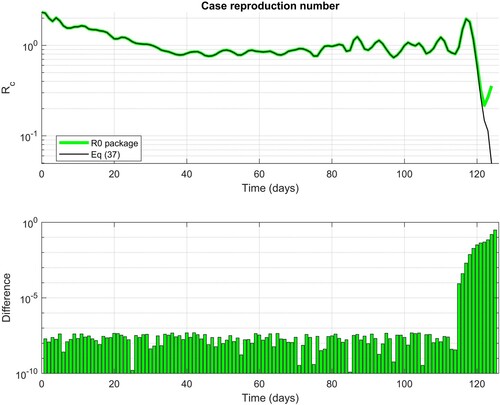
In Figure 1, we see that the calculation of $R_c$ by Equation (37) and those obtained by the R₀ package using the Wallinga–Teunis method [25] are practically identical; the absolute difference is less than ${10}^{-7}$. The difference is noticeable towards the end of data; i.e. on the length of the vector giving the generation time. Calculation of $R_c$ by formula (37) implicitly assumes that $R_{c,n}=0$; i.e. $I_{n,0}=0$ for $n>N$. In particular, this yields $R_{c,N}^{}=0$. The calculation of $R_c$ that includes only valid data is therefore limited to $n<N-K$.

Figure 1. Comparison of the case reproduction number calculated by Equation (37) and R0 package using the Wallinga–Teunis method.

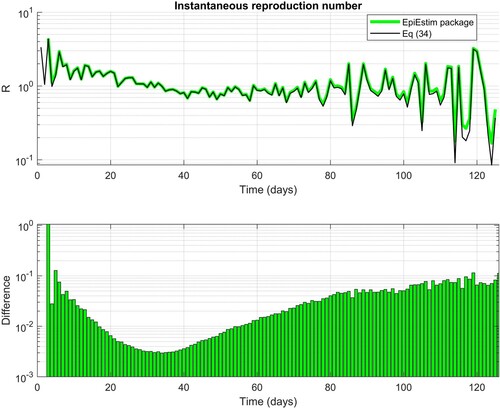
In Figure 2, we see that the absolute difference between the calculation of instantaneous reproduction number by Equation (34) and by function estimate_R from the EpiEstim package is in a range ${10}^{-2}$ to ${10}^{-1}$. The reason for the difference is that the function estimate_R implements a formula for calculating $R_t$, which, for statistical reasons, adds Gamma distribution parameters $a$ in the numerator and $1/b$ in the denominator of Equation (34) [36]. We note that this has a side effect: $R_t>0$, even if $I_t=0$; however, it prevents the possibility of an undefined 0/0 case.

Figure 2. Comparison of the instantaneous reproduction number calculated by Equation (34) and by the function estimate_R from EpiEstim package.

Conclusion

We have shown that the well-known formulae for calculating the various epidemic reproduction numbers can be derived from the classical discrete Kermack–McKendrick epidemic model. An advantage of the model is that it is more intuitive and some of the assumptions of the continuous model can be omitted. In particular, as already mentioned, the derivation does not require a factorization assumption on the epidemic's transmissibility.

The practical example shows that case reproduction number calculated by the formula (37) gives numerically almost the same result as the reproduction number determined by the algorithmically much more demanding Wallinga–Teunis method.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Appendix

MATLAB functions for calculation of the reproduction number.

function R0 = calcR0(w,r)

%CALCR0 Calculate basic reproduction number (Eq 29)

   R0 = r/((exp(r) - 1)*sum(w.*exp(-r*(1:length(w)))));

end

function R = calcR(w,I)

%CALCR Calculate instantaneous reproduction number (Eq 34)

   K = length(w);

   N = length(I);

   R = NaN(N,1);

   for n = 1:N

     s = 0;

  for k = 1:min(n,K)

    s = s + w(k)*I(n+1-k);

  end

  if s > 0

    R(n) = I(n)/s;

  end

 end

end

function [Rc,R] = calcRc(w,I)

%CALCRC Calculate case reproduction number (Eq 37)

   R = calcR(w,I);

   K = length(w);

   N = length(I);

   Rc = NaN(N,1);

   for n = 1:N

     s = 0;

     for k = 1:min(N-n+1,K)

       s = s + w(k)*R(n+k-1);

     end

     Rc(n) = s;

   end

end