Dynamics of an SIRWS model with waning of immunity and varying immune boosting period

Abstract

SIRS models capture transmission dynamics of infectious diseases for which immunity is not lifelong. Extending these models by a W compartment for individuals with waning immunity, the boosting of the immune system upon repeated exposure may be incorporated. Previous analyses assumed identical waning rates from R to W and from W to S. This implicitly assumes equal length for the period of full immunity and of waned immunity. We relax this restriction, and allow an asymmetric partitioning of the total immune period. Stability switches of the endemic equilibrium are investigated with a combination of analytic and numerical tools. Then, continuation methods are applied to track bifurcations along the equilibrium branch. We find rich dynamics: Hopf bifurcations, endemic double bubbles, and regions of bistability. Our results highlight that the length of the period in which waning immunity can be boosted is a crucial parameter significantly influencing long term epidemiological dynamics.

Keywords:

• Waning immunity
• immune boosting
• SIRWS system
• partitioning of immunity
• Hopf bifurcation

1. Introduction

The susceptible-infectious-recovered (SIR) approach has been widely applied in diverse forms to understand the transmission dynamics of communicable diseases. For many infections, immunity is not lifelong, and after some time, recovered individuals may become susceptible again. Prior to that, repeated exposure to the pathogen might boost the immune system, thus prolonging the length of immune period. A very general framework of waning-boosting dynamics has been introduced in [2]. Special cases of that are the SIRWS compartmental models, where W is the collection of individuals whose immunity is waning but can be boosted upon repeated exposure without experiencing the disease again.

SIRWS models formulated as systems of ordinary differential equations were studied in [5,7,10,12,13]. In these models, the immunity period is divided into two parts: upon recovery, previously infected individuals move to R, and from there they may transit to W as time elapses. If they are exposed again while being in W, their immunity can be boosted and they move back R. Otherwise, they eventually lose their immunity, become susceptible again an move back to S. The aforementioned studies model these two phases of the immune period by a symmetric partitioning, by assuming identical rates of transition from R to W and from W to S.

In contrast, our work removes this symmetry constraint, and we analyse how the different partitioning of the immune period into R and W, and varying boosting rates affect the dynamics of the model. First, the existence of equilibria and analytic conditions for their local stability are established. Then, using numerical tools and methods, we observe the emergence of complex phenomena through various bifurcations, such as endemic double bubbles, and multiple regions of bistability.

1.1. Modified SIRWS model

This section describes the SIRWS compartmental model in which the population is divided as follows. The individuals susceptible to infection are placed in S, those currently infectious in I, and those recovered from infection are divided into two compartments based on their immunity level. The fully immune are found in R and those with waned immunity are in W. Figure 1 depicts the flow diagram of our model governed by the system of ordinary differential equations (1a) $\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}& =-\text{β}IS+\omega \kappa W+\mu (1-S),\end{array}$(1a) (1b) $\begin{array}{rl}\frac{\mathrm{d}I}{\mathrm{d}t}& =\text{β}IS-\gamma I-\mu I,\end{array}$(1b) (1c) $\begin{array}{rl}\frac{\mathrm{d}R}{\mathrm{d}t}& =\gamma I-\alpha \kappa R+\nu \text{β}IW-\mu R,\end{array}$(1c) (1d) $\begin{array}{rl}\frac{\mathrm{d}W}{\mathrm{d}t}& =\alpha \kappa R-\omega \kappa W-\nu \text{β}IW-\mu W,\end{array}$(1d) where β, γ, and μ are referred to as the infection rate, recovery rate, and birth and death rate, respectively.

Figure 1. Flow diagram of the SIRWS system (1a(1a) $\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}& =-\text{β}IS+\omega \kappa W+\mu (1-S),\end{array}$(1a) ).

Recovered individuals may lose immunity by the chain of transitions $R\to W\to S$. The average duration of immune protection, that is the average time required to complete both of these transitions is ${\kappa }^{-1}$ and, hence, κ is the immunity waning rate. Members of W are still immune to infection and are subject to immune boosting upon re-exposure. The frequency of that re-exposure is modulated by the boosting force ν. In our analysis, hosts going through boosting are not infectious, such as in [2,5,10,12], as opposed to [18].

The population is normalized to 1 that is $N\left(t\right)=S\left(t\right)+I\left(t\right)+R\left(t\right)+W\left(t\right)=1$ for all $t\ge 0$. Vital dynamics is modelled with the rate μ for birth and death, and disease-induced fatality is not considered.

In former SIRWS model studies, e.g. [5,7,10,12,13], the immune waning rates are the same for individuals who move from the recovered compartment to the waning compartment and for those who transition onward to the susceptible compartment. In contrast, we consider an asymmetric partition of the immunity period by introducing the parameters $\alpha >1$ and $\omega >1$ setting the average time spent in R and W to $(\alpha \kappa {)}^{-1}$ and $(\omega \kappa {)}^{-1}$, respectively. Hence, (2) $\frac{1}{\alpha \kappa }+\frac{1}{\omega \kappa }=\frac{1}{\kappa }\text{that is}\omega =\frac{\alpha }{\alpha -1}.$(2) Note that the special case $\alpha =\omega =2$, representing the symmetric partition of immunity period, is what was considered in the aforementioned studies.

By considering various limiting scenarios of boosting for (1a(1a) $\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}& =-\text{β}IS+\omega \kappa W+\mu (1-S),\end{array}$(1a) ), it is apparent that the system exhibits SIRS-like dynamics as $\nu \to 0^{+}$ and SIR-like dynamics as $\nu \to \mathrm{\infty }$. In addition, we observe SIR-like dynamics as $\alpha \to 1^{+}$   ($\omega \to \mathrm{\infty }$) and SIS-like dynamics as $\alpha \to \mathrm{\infty }$   ($\omega \to 1^{+}$).

2. Equilibria and stability

This section first investigates system (1a(1a) $\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}& =-\text{β}IS+\omega \kappa W+\mu (1-S),\end{array}$(1a) ) in order to establish the formulae for the equilibria of our SIRWS model. Then, we analyse the transcritical bifurcation where these equilibria exchange stability in Section 2.1. Finally, we derive the Routh–Hurwitz stability criterion in Section 2.2.

We begin by utilizing the relation $W\left(t\right)=1-S\left(t\right)-I\left(t\right)-R\left(t\right),$to obtain the reduced system (3a) $\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}& =-\text{β}IS+\omega \kappa (1-S-I-R)+\mu (1-S),\end{array}$(3a) (3b) $\begin{array}{rl}\frac{\mathrm{d}I}{\mathrm{d}t}& =\text{β}IS-\gamma I-\mu I,\end{array}$(3b) (3c) $\begin{array}{rl}\frac{\mathrm{d}R}{\mathrm{d}t}& =\gamma I-\alpha \kappa R+\nu \text{β}I(1-S-I-R)-\mu R.\end{array}$(3c) Note that the region relevant for our epidemiological setting $\left(S\right(t),I(t),R(t\left)\right)\in \mathcal{D}:=\left\{\right(s,i,r)\in {\mathbb{R}}_{\ge 0}^3|0\le s+i+r\le 1\}$is forward invariant.

Now, let us turn our attention to equilibria of (3a(3a) $\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}& =-\text{β}IS+\omega \kappa (1-S-I-R)+\mu (1-S),\end{array}$(3a) ) and seek solutions of the steady state equations (4a) $\begin{array}{rl}& -\text{β}{I}^{\ast }{S}^{\ast }+\omega \kappa (1-S^{\ast }-I^{\ast }-R^{\ast })+\mu (1-S^{\ast })=0,\end{array}$(4a) (4b) $\begin{array}{rl}& \text{β}{I}^{\ast }{S}^{\ast }-\gamma I^{\ast }-\mu I^{\ast }=0,\end{array}$(4b) (4c) $\begin{array}{rl}& \gamma I^{\ast }-\alpha \kappa R^{\ast }+\nu \text{β}{I}^{\ast }(1-S^{\ast }-I^{\ast }-R^{\ast })-\mu R^{\ast }=0.\end{array}$(4c)

From (4b(4b) $\begin{array}{rl}& \text{β}{I}^{\ast }{S}^{\ast }-\gamma I^{\ast }-\mu I^{\ast }=0,\end{array}$(4b) ), we obtain that either $I^{\ast }=0$ or $S^{\ast }=\frac{\gamma +\mu }{\text{β}}$. In the first case, $R^{\ast }=0$ follows from (4c(4c) $\begin{array}{rl}& \gamma I^{\ast }-\alpha \kappa R^{\ast }+\nu \text{β}{I}^{\ast }(1-S^{\ast }-I^{\ast }-R^{\ast })-\mu R^{\ast }=0.\end{array}$(4c) ) and, finally, $S^{\ast }=1$ from (4a(4a) $\begin{array}{rl}& -\text{β}{I}^{\ast }{S}^{\ast }+\omega \kappa (1-S^{\ast }-I^{\ast }-R^{\ast })+\mu (1-S^{\ast })=0,\end{array}$(4a) ). Hence we obtain ${\xi }_0=(1,0,0),$the disease-free equilibrium (DFE) of (3a(3a) $\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}& =-\text{β}IS+\omega \kappa (1-S-I-R)+\mu (1-S),\end{array}$(3a) ). In the latter case when (5) $S^{\ast }=\frac{\gamma +\mu }{\text{β}},$(5) Equation (4a(4a) $\begin{array}{rl}& -\text{β}{I}^{\ast }{S}^{\ast }+\omega \kappa (1-S^{\ast }-I^{\ast }-R^{\ast })+\mu (1-S^{\ast })=0,\end{array}$(4a) ) yields $I^{\ast }=\frac{(\mu +\omega \kappa )(1-S^{\ast })-\omega \kappa R^{\ast }}{\text{β}{S}^{\ast }+\omega \kappa }=\frac{c_0{c}_1}{\text{β}}-\frac{\omega \kappa }{\gamma +\mu +\omega \kappa }{R}^{\ast },$with $\begin{array}{rl}{c}_0& =\frac{1}{\gamma +\mu +\omega \kappa }\cdot (1+\frac{\omega \kappa }{\mu })\text{and}\\ c_1& =\mu (\text{β}-(\gamma +\mu \left)\right).\end{array}$Then, using the formulae for $S^{\ast }$ and $I^{\ast }$, (4c(4c) $\begin{array}{rl}& \gamma I^{\ast }-\alpha \kappa R^{\ast }+\nu \text{β}{I}^{\ast }(1-S^{\ast }-I^{\ast }-R^{\ast })-\mu R^{\ast }=0.\end{array}$(4c) ) results in a quadratic equation for $R^{\ast }$. It is straightforward to verify that the leading term coefficient is positive, hence, the graph of it is an open up parabola with the y-intercept $\frac{\gamma c_0{c}_1}{\text{β}}(1+\frac{\nu c_0{c}_1}{\mu +\omega \kappa }).$Moreover, as shown in Appendix A.1, the solutions can be expressed as (6) ${R^{\ast }}_{\pm }=\frac{\gamma +\mu +\omega \kappa }{2\text{β}\omega \kappa }[(2c_0-\frac{1}{\gamma +\mu })c_1+\frac{1}{\nu (\gamma +\mu )}(c_2\mp \sqrt{(c_1\nu +c_2{)}^2+c_3\nu })],$(6) using $c_2,c_3$ given by $\begin{array}{rl}{c}_2& =(\gamma +\mu )(\alpha \kappa +\omega \kappa )+\mu (\gamma +\mu )+\alpha \omega {\kappa }^2\text{and}\\ c_3& =4\gamma (\text{β}-(\gamma +\mu \left)\right)\alpha \omega {\kappa }^2.\end{array}$Finally, substituting (6(6) ${R^{\ast }}_{\pm }=\frac{\gamma +\mu +\omega \kappa }{2\text{β}\omega \kappa }[(2c_0-\frac{1}{\gamma +\mu })c_1+\frac{1}{\nu (\gamma +\mu )}(c_2\mp \sqrt{(c_1\nu +c_2{)}^2+c_3\nu })],$(6) ) into the formula for $I^{\ast }$ results in (7) ${I^{\ast }}_{\pm }=\frac{\pm \sqrt{(c_1\nu +c_2{)}^2+c_3\nu }+(c_1\nu -c_2)}{2\text{β}\nu (\gamma +\mu )}.$(7) Hence, we obtained the two remaining equilibria of (3a(3a) $\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}& =-\text{β}IS+\omega \kappa (1-S-I-R)+\mu (1-S),\end{array}$(3a) ), namely the endemic equilibrium (EE) $\begin{array}{rl}{\xi }_{+}& =(S^{\ast },{I^{\ast }}_{+},{R^{\ast }}_{+}),\\ & \text{and}\\ {\xi }_{-}& =(S^{\ast },{I^{\ast }}_{-},{R^{\ast }}_{-}).\end{array}$

Clearly, ${I^{\ast }}_{-}\le 0$ whenever the square root is real as the inequality is readily satisfied for $\text{β}<\gamma +\mu$ (then $c_1,c_3<0$) and directly follows from (8) $\sqrt{(c_1\nu +c_2{)}^2+c_3\nu }\ge |c_1\nu -c_2|\iff 4c_1{c}_2+c_3\ge 0,$(8) when $\text{β}\ge \gamma +\mu$ (then $c_1,c_3\ge 0$). Moreover, the condition $\text{β}\ge \gamma +\mu$ is sufficient (but not necessary) for ${I^{\ast }}_{\pm }\in \mathbb{R}$. Obviously, in the epidemiological setting of this manuscript, solely ${\xi }_{+}$ may be admissible.

Another important implication of (8(8) $\sqrt{(c_1\nu +c_2{)}^2+c_3\nu }\ge |c_1\nu -c_2|\iff 4c_1{c}_2+c_3\ge 0,$(8) ) is that ${I^{\ast }}_{+}>0\iff \text{β}>\gamma +\mu \text{and}{I^{\ast }}_{+}=0\text{for}\text{β}=\gamma +\mu .$Observe that, in the case of equality, ${\xi }_0={\xi }_{+}$ holds. Furthermore, again for $\text{β}\ge \gamma +\mu$, the parabola for $R^{\ast }$ has a positive y-intercept, thus, both solutions are either positive or negative. Moreover, we have ${R^{\ast }}_{-}>0$ as $2c_0-\frac{1}{\gamma +\mu }>0$ is satisfied and $c_1\ge 0$. These imply the positivity of the other root that is ${R^{\ast }}_{+}>0$.

Now, summing (4a(4a) $\begin{array}{rl}& -\text{β}{I}^{\ast }{S}^{\ast }+\omega \kappa (1-S^{\ast }-I^{\ast }-R^{\ast })+\mu (1-S^{\ast })=0,\end{array}$(4a) ), (4b(4b) $\begin{array}{rl}& \text{β}{I}^{\ast }{S}^{\ast }-\gamma I^{\ast }-\mu I^{\ast }=0,\end{array}$(4b) ), and (4c(4c) $\begin{array}{rl}& \gamma I^{\ast }-\alpha \kappa R^{\ast }+\nu \text{β}{I}^{\ast }(1-S^{\ast }-I^{\ast }-R^{\ast })-\mu R^{\ast }=0.\end{array}$(4c) ) results in $(\omega \kappa +\mu +\nu \text{β}{I}^{\ast })(1-S^{\ast }-I^{\ast }-R^{\ast })-\alpha \kappa R^{\ast }=0,$hence, $S^{\ast }+I^{\ast }+R^{\ast }\le 1$ must hold for non-negative $S^{\ast },I^{\ast },R^{\ast }$ implying ${\xi }_{+}\in \mathcal{D}\iff \text{β}\ge \gamma +\mu$.

Finally, note that the basic reproduction number, see e.g. [2], of the system (3a(3a) $\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}& =-\text{β}IS+\omega \kappa (1-S-I-R)+\mu (1-S),\end{array}$(3a) )– and of (1a(1a) $\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}& =-\text{β}IS+\omega \kappa W+\mu (1-S),\end{array}$(1a) )– is ${\mathcal{R}}_0=\frac{\text{β}}{\gamma +\mu },$thus, we may rewrite the condition $\text{β}\ge \gamma +\mu$ as ${\mathcal{R}}_0\ge 1$.

Before continuing the analysis, let us summarize our findings so far.

• There is a unique DFE ${\xi }_0\in \mathcal{D}$, which exists for all parameter values in the system.

• If $R_0\le 1$, then there is no other equilibrium in $\mathcal{D}$.

• If $R_0>1$, then there is a unique, positive EE ${\xi }_{+}\in \mathcal{D}$.

2.1. Transcritical bifurcation at ${\mathcal{R}}_0=1$

For the stability analysis of the disease-free equilibrium ${\xi }_0$, consider the Jacobian matrix for our SIRWS system (3a(3a) $\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}& =-\text{β}IS+\omega \kappa (1-S-I-R)+\mu (1-S),\end{array}$(3a) ) (9) $J=\left[\begin{array}{ccc}-(\omega \kappa +\mu +\text{β}I)& -\text{β}S-\omega \kappa & -\omega \kappa \\ \text{β}I& -(\gamma +\mu -\text{β}S)& 0\\ -\nu \text{β}I& \gamma -2\nu \text{β}I+\nu \text{β}(1-S-R)& -(\alpha \kappa +\mu +\nu \text{β}I)\end{array}\right]$(9) and evaluate at the DFE ${\xi }_0$ $J{|}_{{\xi }_0}=\left[\begin{array}{ccc}-(\omega \kappa +\mu )& -\text{β}-\omega \kappa & -\omega \kappa \\ 0& -(\gamma +\mu -\text{β})& 0\\ 0& \gamma & -(\alpha \kappa +\mu )\end{array}\right].$Then, the corresponding eigenvalues are ${\lambda }_1=\text{β}-(\gamma +\mu ),{\lambda }_2=-(\mu +\alpha \kappa ),\text{and}{\lambda }_3=-(\mu +\omega \kappa ).$The two eigenvalues ${\lambda }_2,{\lambda }_3$ are negative and ${\lambda }_1<0$ iff $\text{β}<\gamma +\mu$. Hence, the DFE is locally asymptotically stable when ${\mathcal{R}}_0<1$ and unstable for ${\mathcal{R}}_0>1$.

The following Theorem describes the bifurcation associated with this stability change at ${\mathcal{R}}_0=1$ that is also demonstrated in Figure 2. The proof relies on Theorem 4.1 of [4] based on centre manifold theory [3,20]. For the sake of completeness, the relevant version of the original theorem is included in Appendix A.2.

Figure 2. Transcritical bifurcation of forward type and the appearance of the LAS endemic equilibrium ${\xi }_{+}$ at ${\mathcal{R}}_0=1$.

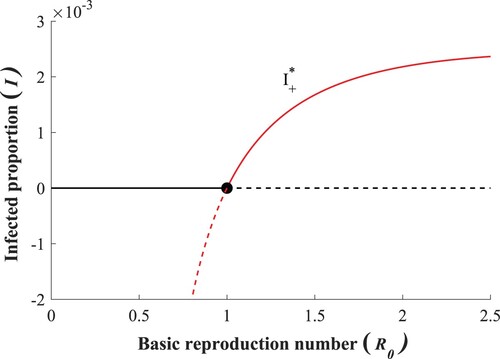
Theorem 2.1

A transcritical bifurcation of forward-type occurs at ${\mathcal{R}}_0=1$.

Proof.

Fix all parameters but β that will serve as the bifurcation parameter with ${\text{β}}^{\ast }=\gamma +\mu$ corresponding to the critical case ${\mathcal{R}}_0=1$.

We show that the conditions of Theorem A.1 are satisfied for the system $\dot{\mathbf{x}}=f(\mathbf{x},b)$, where $f=(f_1,f_2,f_3)\equiv (f_S,f_I,f_R)$is obtained by applying the substitutions $\text{β}\to b+{\text{β}}^{\ast }$ and $(S,I,R)\to (x_S,x_I,x_R)+{\xi }_0$ to Equations (3a(3a) $\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}& =-\text{β}IS+\omega \kappa (1-S-I-R)+\mu (1-S),\end{array}$(3a) ), (3b(3b) $\begin{array}{rl}\frac{\mathrm{d}I}{\mathrm{d}t}& =\text{β}IS-\gamma I-\mu I,\end{array}$(3b) ), and (3c(3c) $\begin{array}{rl}\frac{\mathrm{d}R}{\mathrm{d}t}& =\gamma I-\alpha \kappa R+\nu \text{β}I(1-S-I-R)-\mu R.\end{array}$(3c) ), with $\mathbf{x}=(x_1,x_2,x_3)\equiv (x_S,x_I,x_R).$

The matrix $A=D_{\mathbf{x}}f(\mathbf{0},0)$ ($=J|{\xi }_0$ with $\text{β}={\text{β}}^{\ast }$) has one simple zero eigenvalue and two eigenvalues with negative real part ${\lambda }_1=0,{\lambda }_2=-(\mu +\alpha \kappa ),{\lambda }_3=-(\mu +\omega \kappa ).$Now, let us calculate $\begin{array}{rl}{Z}_1& =\sum _{k,i,j=1}^3{v}_k{w}_i{w}_j\frac{{\mathrm{\partial }}^2{f}_k}{\mathrm{\partial }{x}_i\mathrm{\partial }{x}_j}(\mathbf{0},0)\text{and}\\ Z_2& =\sum _{k,i=1}^3{v}_k{w}_i\frac{{\mathrm{\partial }}^2{f}_k}{\mathrm{\partial }{x}_i\mathrm{\partial }b}(\mathbf{0},0),\end{array}$where w, v are the right and left eigenvectors of A corresponding to the zero eigenvalue.

Note that we may fix $w_2=1$ as Aw = 0 is underdetermined. Then, $\begin{array}{rl}{w}_1& =-[1+\frac{\alpha \kappa \gamma }{(\omega \kappa +\mu )(\alpha \kappa +\mu )}+\frac{\gamma }{\alpha \kappa +\mu }]\text{and}\\ w_3& =\frac{\gamma }{\alpha \kappa +\mu }\end{array}$follow. Analogously, we find a left eigenvector $v=(0,1,0)$.

As $v_1=v_3=0$, the sums get reduced to the terms containing $f_2\equiv f_I=(b+{\text{β}}^{\ast })x_I(x_S+1)-(\gamma +\mu )x_I.$Clearly, the nonzero second order partial derivatives of $f_I$ at $(\mathbf{0},0)$ are $\frac{{\mathrm{\partial }}^2{f}_I}{\mathrm{\partial }{x}_I\mathrm{\partial }b}(\mathbf{0},0)=1\text{and}\frac{{\mathrm{\partial }}^2{f}_I}{\mathrm{\partial }{x}_I\mathrm{\partial }{x}_S}(\mathbf{0},0)={\text{β}}^{\ast }=\gamma +\mu .$Hence, $\begin{array}{rl}{Z}_1& =2v_2{w}_1{w}_2\frac{{\mathrm{\partial }}^2{f}_I}{\mathrm{\partial }{x}_I\mathrm{\partial }{x}_S}(\mathbf{0},0)\\ & =-2[1+\frac{\alpha \kappa \gamma }{(\omega \kappa +\mu )(\alpha \kappa +\mu )}+\frac{\gamma }{\alpha \kappa +\mu }](\gamma +\mu )\text{and}\\ Z_2& =v_2{w}_2\frac{{\mathrm{\partial }}^2{f}_I}{\mathrm{\partial }{x}_I\mathrm{\partial }b}(\mathbf{0},0)=1.\end{array}$As $Z_1<0$ and $Z_2>0$ for all parameters, we can apply Theorem A.1 noting that even though $w_1<0$, as the first component of ${\xi }_0=(1,0,0)$ is positive, $w_1\ge 0$ is not required actually.

Translating the statement of the aforementioned Theorem to our original system (3a(3a) $\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}& =-\text{β}IS+\omega \kappa (1-S-I-R)+\mu (1-S),\end{array}$(3a) ), we obtain that when ${\mathcal{R}}_0$ increases through 1, a transcritical bifurcation of forward type occurs with ${\xi }_0$ losing and ${\xi }_{+}$ gaining local asymptotic stability (LAS), respectively.

2.2. The Routh–Hurwitz criterion for ${\xi }_{+}$

This section analyses the stability of the endemic equilibrium ${\xi }_{+}$ for fixed $\text{β},\gamma ,\kappa$, and μ, given that ${\mathcal{R}}_0>1$ holds.

Local asymptotic stability (LAS) is characterized by all eigenvalues of the Jacobian (9(9) $J=\left[\begin{array}{ccc}-(\omega \kappa +\mu +\text{β}I)& -\text{β}S-\omega \kappa & -\omega \kappa \\ \text{β}I& -(\gamma +\mu -\text{β}S)& 0\\ -\nu \text{β}I& \gamma -2\nu \text{β}I+\nu \text{β}(1-S-R)& -(\alpha \kappa +\mu +\nu \text{β}I)\end{array}\right]$(9) ) at ${\xi }_{+}$ having negative real part. Therefore, we consider the matrix $J{|}_{{\xi }_{+}}=\left[\begin{array}{ccc}-(\omega \kappa +\mu +\text{β}{I^{\ast }}_{+})& -(\gamma +\mu +\omega \kappa )& -\omega \kappa \\ \text{β}{I^{\ast }}_{+}& 0& 0\\ -\nu \text{β}{I^{\ast }}_{+}& \gamma -2\nu \text{β}{I^{\ast }}_{+}+\nu \text{β}(1-S^{\ast }-{R^{\ast }}_{+})& -(\alpha \kappa +\mu +\nu \text{β}{I^{\ast }}_{+})\end{array}\right]$and, in turn, its characteristic polynomial $a_0{\lambda }^3+a_1{\lambda }^2+a_2\lambda +a_3=0,$with (10) $\begin{array}{rl}{a}_0& =1,\\ a_1& =\text{β}{I^{\ast }}_{+}(1+\nu )+(\alpha \kappa +\omega \kappa +2\mu ),\\ a_2& =\text{β}{I^{\ast }}_{+}\left[\right(\alpha \kappa +\omega \kappa +2\mu )+\gamma +\text{β}\nu {I^{\ast }}_{+}+\mu \nu ]+(\omega \kappa +\mu )(\alpha \kappa +\mu ),\\ a_3& =\text{β}{I^{\ast }}_{+}\left[\right(\omega \kappa +\mu \left)\right(\alpha \kappa +\mu )+(\gamma +\mu )\text{β}\nu {I^{\ast }}_{+}+\gamma (\alpha \kappa +\omega \kappa +\mu )\\ & +\omega \kappa \text{β}\nu (1-S^{\ast }-{I^{\ast }}_{+}-{R^{\ast }}_{+})],\end{array}$(10) and $S^{\ast },{I^{\ast }}_{+},{R^{\ast }}_{+}$ as given in (5(5) $S^{\ast }=\frac{\gamma +\mu }{\text{β}},$(5) ), (6(6) ${R^{\ast }}_{\pm }=\frac{\gamma +\mu +\omega \kappa }{2\text{β}\omega \kappa }[(2c_0-\frac{1}{\gamma +\mu })c_1+\frac{1}{\nu (\gamma +\mu )}(c_2\mp \sqrt{(c_1\nu +c_2{)}^2+c_3\nu })],$(6) ), and (7(7) ${I^{\ast }}_{\pm }=\frac{\pm \sqrt{(c_1\nu +c_2{)}^2+c_3\nu }+(c_1\nu -c_2)}{2\text{β}\nu (\gamma +\mu )}.$(7) ).

Utilizing the Routh–Hurwitz (RH) criterion [15,16] yields that ${\xi }_{+}$ is LAS iff the following inequalities are satisfied $\begin{array}{rl}{a}_i& >0,\text{for}i=0,1,2,3,\text{and}\\ a_1{a}_2& >a_3.\end{array}$As the positivity of $a_0,\dots ,a_3$ is trivial, we are led to analyse the sign changes of the function (11) $y_{\nu }\left(\alpha \right)=a_1{a}_2-a_3,$(11) for $\alpha >1$ and $\nu >0$.

2.2.1. Transformation of $y_{\nu }\left(\alpha \right)$

The formulae in (7(7) ${I^{\ast }}_{\pm }=\frac{\pm \sqrt{(c_1\nu +c_2{)}^2+c_3\nu }+(c_1\nu -c_2)}{2\text{β}\nu (\gamma +\mu )}.$(7) ) and (10(10) $\begin{array}{rl}{a}_0& =1,\\ a_1& =\text{β}{I^{\ast }}_{+}(1+\nu )+(\alpha \kappa +\omega \kappa +2\mu ),\\ a_2& =\text{β}{I^{\ast }}_{+}\left[\right(\alpha \kappa +\omega \kappa +2\mu )+\gamma +\text{β}\nu {I^{\ast }}_{+}+\mu \nu ]+(\omega \kappa +\mu )(\alpha \kappa +\mu ),\\ a_3& =\text{β}{I^{\ast }}_{+}\left[\right(\omega \kappa +\mu \left)\right(\alpha \kappa +\mu )+(\gamma +\mu )\text{β}\nu {I^{\ast }}_{+}+\gamma (\alpha \kappa +\omega \kappa +\mu )\\ & +\omega \kappa \text{β}\nu (1-S^{\ast }-{I^{\ast }}_{+}-{R^{\ast }}_{+})],\end{array}$(10) ) appear to be (mostly) symmetric with respect to α and ω. Recall that these two parameters are closely related as $\alpha +\omega =\alpha \omega =\frac{{\alpha }^2}{\alpha -1}$directly follows from (2(2) $\frac{1}{\alpha \kappa }+\frac{1}{\omega \kappa }=\frac{1}{\kappa }\text{that is}\omega =\frac{\alpha }{\alpha -1}.$(2) ). These considerations suggest to introduce the substitution (12) $\eta =\kappa (\alpha +\omega )=\kappa \left(\alpha \omega \right)=\kappa \frac{{\alpha }^2}{\alpha -1},$(12) with $\eta \in [4\kappa ,\mathrm{\infty })$ and the $\alpha =\omega =2$ case corresponding to $\eta =4\kappa$. Nevertheless, in order to apply (12(12) $\eta =\kappa (\alpha +\omega )=\kappa \left(\alpha \omega \right)=\kappa \frac{{\alpha }^2}{\alpha -1},$(12) ), we need to establish that $a_3$ in (10(10) $\begin{array}{rl}{a}_0& =1,\\ a_1& =\text{β}{I^{\ast }}_{+}(1+\nu )+(\alpha \kappa +\omega \kappa +2\mu ),\\ a_2& =\text{β}{I^{\ast }}_{+}\left[\right(\alpha \kappa +\omega \kappa +2\mu )+\gamma +\text{β}\nu {I^{\ast }}_{+}+\mu \nu ]+(\omega \kappa +\mu )(\alpha \kappa +\mu ),\\ a_3& =\text{β}{I^{\ast }}_{+}\left[\right(\omega \kappa +\mu \left)\right(\alpha \kappa +\mu )+(\gamma +\mu )\text{β}\nu {I^{\ast }}_{+}+\gamma (\alpha \kappa +\omega \kappa +\mu )\\ & +\omega \kappa \text{β}\nu (1-S^{\ast }-{I^{\ast }}_{+}-{R^{\ast }}_{+})],\end{array}$(10) ) may be considered as a function of η. This holds due to the equality $\omega \kappa \text{β}\nu (1-S^{\ast }-{I^{\ast }}_{+}-{R^{\ast }}_{+})=\text{β}\nu (\gamma +\mu ){I^{\ast }}_{+}-c_1\nu ,$see Appendix A.3 for details.

Then, one obtains that $y_{\nu }\left(\alpha \right)\equiv y_{\nu }\left(\eta \right)={\hat{a}}_1{\hat{a}}_2-{\hat{a}}_3,$with $\begin{array}{rl}{\hat{a}}_1& =\hat{I}(1+\nu )+(\eta +2\mu ),\\ {\hat{a}}_2& =\hat{I}\left[\right(\eta +\mu )+(\gamma +\mu )+\mu \nu +\nu \hat{I}]+\mu (\eta +\mu )+\kappa \eta ,\\ {\hat{a}}_3& =\hat{I}\left[2\nu \hat{I}\right(\gamma +\mu )-\nu \mu (\text{β}-(\gamma +\mu ))+(\gamma +\mu \left)\right(\mu +\eta )+\kappa \eta ],\end{array}$where $\hat{I}=\text{β}{I^{\ast }}_{+}$.

Substitution (12(12) $\eta =\kappa (\alpha +\omega )=\kappa \left(\alpha \omega \right)=\kappa \frac{{\alpha }^2}{\alpha -1},$(12) ) reveals an important feature of $y_{\nu }\left(\alpha \right)$, namely, there is a bijection $(1,2)\ni \alpha \mapsto {\alpha }^{\prime }\in (2,\mathrm{\infty })$ such that $y_{\nu }\left(\alpha \right)=y_{\nu }\left({\alpha }^{\prime }\right)$. In particular, local extrema at $\alpha \ne 2$ appear in pairs.

Furthermore, using the chain rule, we obtain that $\frac{\mathrm{\partial }{y}_{\nu }}{\mathrm{\partial }\alpha }=\frac{\mathrm{\partial }{y}_{\nu }}{\mathrm{\partial }\eta }\cdot \frac{\mathrm{d}\eta }{\mathrm{d}\alpha }=\frac{\mathrm{\partial }{y}_{\nu }}{\mathrm{\partial }\eta }\cdot \frac{\kappa \alpha (\alpha -2)}{(\alpha -1{)}^2}.$Clearly, $\alpha =2$ (that is $\eta =4\kappa$) is a critical point of $y_{\nu }$ for all immune boosting parameters ν. By Lemma A.2, either all derivatives of $y_{\nu }$ are zero at $\alpha =2$ or the first non-vanishing derivative is of even order. As $y_{\nu }$ is analytic and not identically zero for any ${\mathcal{R}}_0>1$, the former is not possible, hence, $\alpha =2$ is a local extremum for all boosting rates ν.

3. Numerical analysis

This section summarizes the results of our numerical stability and bifurcation analysis of system (3a(3a) $\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}& =-\text{β}IS+\omega \kappa (1-S-I-R)+\mu (1-S),\end{array}$(3a) ) with respect to varying waning and boosting dynamics. In the remaining part of the manuscript, all other parameters are considered to be fixed following [10] to model pertussis as (13) $\begin{array}{rl}& \gamma =17,\\ & \kappa =1/10,\\ & \mu =1/80,\\ & \text{β}=260,\end{array}$(13) corresponding to an average infectious period of 21 days, average life expectancy of 80 years and a basic reproduction number ${\mathcal{R}}_0=15.28$.

First, Section 3.1 discusses how the local stability of ${\xi }_{+}$ changes given (13(13) $\begin{array}{rl}& \gamma =17,\\ & \kappa =1/10,\\ & \mu =1/80,\\ & \text{β}=260,\end{array}$(13) ) with varying α and ν. Then, Section 3.2 analyses these stability changes and the corresponding bifurcations. In addition, using numerical continuation methods, we observe the bistable regions in the $(\alpha ,\nu )$-plane.

3.1. Analysis of the Routh–Hurwitz criterion for ${\xi }_{+}$

Before carrying out any numerical computations, let us analyse the asymptotic behaviour of (11(11) $y_{\nu }\left(\alpha \right)=a_1{a}_2-a_3,$(11) ) as $\nu \to 0^{+}$, $\nu \to \mathrm{\infty }$, $\alpha \to 1^{+}$, and $\alpha \to \mathrm{\infty }$. The results, shown in Table 1, are valid for all parametrizations of (3a(3a) $\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}& =-\text{β}IS+\omega \kappa (1-S-I-R)+\mu (1-S),\end{array}$(3a) ) and do not rely on (13(13) $\begin{array}{rl}& \gamma =17,\\ & \kappa =1/10,\\ & \mu =1/80,\\ & \text{β}=260,\end{array}$(13) ).

Table 1. Limits of ${I^{\ast }}_{+}$, ${R^{\ast }}_{+}$, and the sign of $y_{\nu }\left(\alpha \right)$.

lim	${I^{\ast }}_{+}$	${R^{\ast }}_{+}$	$y_{\nu }\left(\alpha \right)$
$\nu \to 0^{+}$	${\displaystyle \frac{4c_1{c}_2+c_3}{4\text{β}{c}_2(\gamma +\mu )}}$	${\displaystyle \frac{\gamma (\text{β}-(\gamma +\mu \left)\right)(\mu +\omega \kappa )}{\text{β}{c}_2}}$	$>0$
$\nu \to \mathrm{\infty }$	${\displaystyle \frac{c_1}{\text{β}(\gamma +\mu )}}$	${\displaystyle \frac{c_1\gamma }{\text{β}\mu (\gamma +\mu )}}$	$>0$
$\alpha \to 1^{+}$	${\displaystyle \frac{(\kappa +\mu )(\text{β}-(\gamma +\mu \left)\right)}{\text{β}(\gamma +\mu +\kappa )}}$	${\displaystyle \frac{\gamma (\text{β}-(\gamma +\mu \left)\right)}{\text{β}(\gamma +\mu +\kappa )}}$	$>0$
$\alpha \to \mathrm{\infty }$	${\displaystyle \frac{(\kappa +\mu )(\text{β}-(\gamma +\mu \left)\right)}{\text{β}(\gamma +\mu +\kappa )}}$	0	$>0$

* The details of the computations are to be found in Appendix A.4.

As a consequence of these limits, there exists a compact region K in the $(\alpha ,\nu )$-plane such that the endemic equilibrium ${\xi }_{+}$ is LAS for $(\alpha ,\nu )\in (1,\mathrm{\infty })\times (0,\mathrm{\infty })\setminus K$.

3.1.1. Double bubbles of instability

Section 3.1 has readily established that it is sufficient to consider a compact subset in the $(\alpha ,\nu )$-plane for the stability analysis of ${\xi }_{+}$. Based on our experiments, we have restricted our attention to $(\alpha ,\nu )\in [1.01,18]\times [0.01,18]$ and obtained the heatmap in Figure 3 when studying the positivity of $y_{\nu }\left(\alpha \right)$.

Figure 3. Heatmap of the Routh–Hurwitz criterion $y_{\nu }\left(\alpha \right)$ capped at $[-1,1]$ with highlighted zero contour. Figure 3(b) zooms in on the region close to $\alpha =1$.

It is apparent that, for an interval of α values, $y_{\nu }\left(\alpha \right)$ is initially positive for small ν, then, as the boosting rate increases the RH criterion becomes negative for an interval of ν values, after which, it turns positive again. Now, let us look at the heatmap from the other direction. Note that for most interesting boosting rates ν, a similar stability switch may be observed over an α-interval. However, the dynamics is clearly more involved close to boosting rates around 14 as Figure 3 suggests the presence of multiple stability switches.

It is straightforward to localize such phenomena by finding local extrema of $y_{\nu }\left(\alpha \right)$ (as a function of α) whose value is zero. Hence, we looked for intersections of the curves $y_{\nu }\left(\alpha \right)=0\text{and}\frac{\mathrm{\partial }}{\mathrm{\partial }\alpha }{y}_{\nu }\left(\alpha \right)\equiv y_{\nu }^{\prime }\left(\alpha \right)=0$as shown in Figure 4 together with the positivity analysis of the derivative. Our findings confirm the presence of multiple switches close to $\nu \approx 13.7$, moreover, they highlight the existence of similar dynamics close to $\nu \approx 2.06362$ as well. Note that Figure 3 gives no hint of the latter.

Figure 4. Heatmap of $y_{\nu }^{\prime }\left(\alpha \right)$ capped at $[-1,1]$ with highlighted zero contours of $y_{\nu }\left(\alpha \right)$ and $y_{\nu }^{\prime }\left(\alpha \right)$. Figure 4(b) zooms in on the region close to $\alpha =1$.

Recall from Section 2.2.1 that local extrema of $y_{\nu }\left(\alpha \right)$ – other than $\alpha =2$ – appear in pairs. Hence, zooming in on these two regions, shown in Figure 5, reveals double bubbles of instability for certain boosting rates.

Figure 5. Zoomed-in heatmaps of the Routh–Hurwitz criterion $y_{\nu }\left(\alpha \right)$ with highlighted zero contour over regions of interest in the $(\alpha ,\nu )$-plane. Critical points $p_i=({\alpha }_i^{\ast },{\nu }_i^{\ast })$ on the contour are marked. (a) $\nu \approx 2.06362$. (b) $\nu \approx 13.7$.

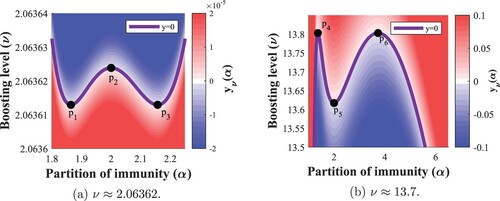
Note that the width of the ν-range where this phenomenon occurs in Figure 5(a) is less than $2\cdot {10}^{-5}$, thus, it should come as no surprise that it was not observable based on the original heatmap in Figure 3. The coordinates of the highlighted critical points are given in Table A1.

3.2. Numerical bifurcation analysis

In the following, we present numerical analysis of one parameter $\left(\alpha \right)$ and two parameter $(\alpha ,\nu )$ bifurcations of the endemic equilibria branch carried out using MatCont [6]. For a background on bifurcation analysis we refer to [9,19].

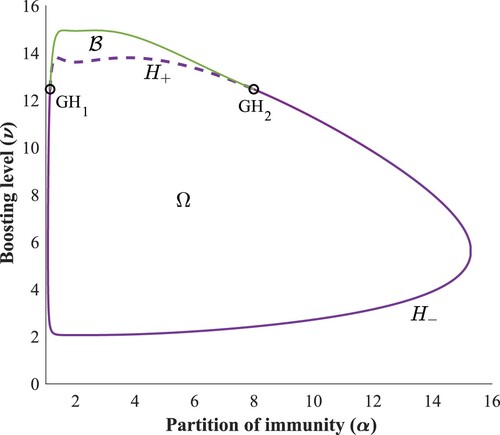
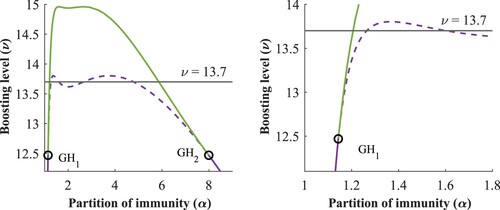
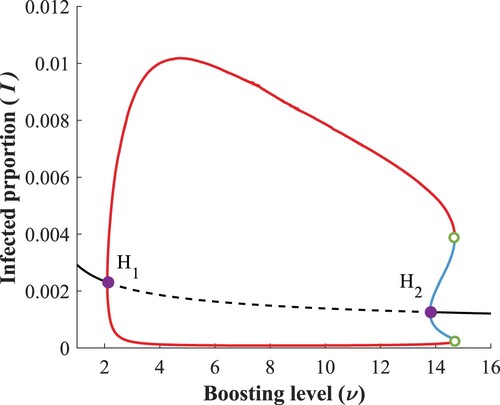
Motivated by the results of Section 3.1, in particular the region depicted in Figure 3(a), we computed the two parameter $(\alpha ,\nu )$ bifurcation diagram of system (3a(3a) $\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}& =-\text{β}IS+\omega \kappa (1-S-I-R)+\mu (1-S),\end{array}$(3a) ), see Figure 6. To fully understand the bifurcation diagram, let us denote by Ω the open domain enclosed by the purple coloured Hopf curve, which is continuous when supercritical (called $H_{-}$) and dashed when subcritical (called $H_{+}$). A stable limit cycle bifurcates from the equilibrium if we cross $H_{-}$ from outside to inside Ω, while an unstable cycle appears if we cross $H_{+}$ in the opposite direction.

Figure 6. Two-parameter $(\alpha ,\nu )$ bifurcation diagram.

It is apparent that for larger boosting rates (ν between 12 – 15), the local stability analysis of ${\xi }_{+}$ is not sufficient to capture all interesting dynamics.

The two new critical points identified are ${\mathrm{G}\mathrm{H}}_1=({\alpha }_{{\mathrm{G}\mathrm{H}}_1}^{\ast },{\nu }_{{\mathrm{G}\mathrm{H}}_1}^{\ast })$ and ${\mathrm{G}\mathrm{H}}_2=({\alpha }_{{\mathrm{G}\mathrm{H}}_2}^{\ast },{\nu }_{{\mathrm{G}\mathrm{H}}_2}^{\ast }\equiv {\nu }_{{\mathrm{G}\mathrm{H}}_1}^{\ast })$. The approximate coordinates of these generalized Hopf points are listed in Table A2 and they mark the parameter values where the Hopf bifurcation changes from supercritical to subcritical. The branch of the limit points of periodic cycles appears in green, which together with the dashed purple curve $H_{+}$ enclose a bistability region $\mathcal{B}$, where there exists a stable periodic solution alongside the LAS endemic equilibrium.

Let us now examine the bifurcation diagram in more detail over regions, characterized by various levels of boosting rate ν, where the dynamics is similar.

In all bifurcation plots that follow, the endemic equilibria branch (particularly the I component) is marked with black curve, solid when LAS and dashed when unstable. Red and blue curves represent branches of stable and unstable limit cycles, respectively, and Hopf bifurcation points are marked with purple dots.

3.2.0.1 Region: $0\le \nu <{\nu }_1^{\ast }\equiv {\nu }_3^{\ast }$

The system has a stable point attractor for all $\alpha >1$.

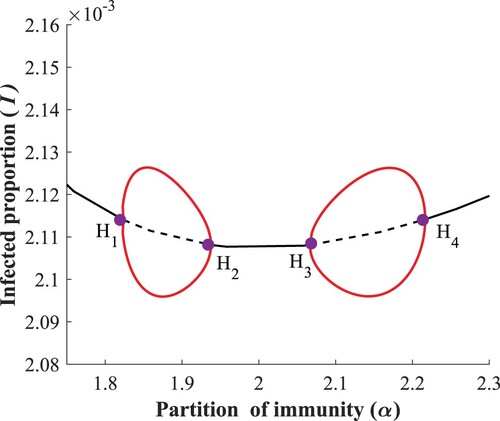
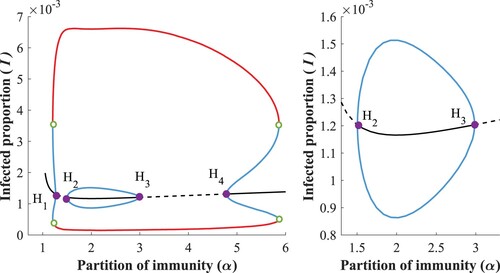
3.2.0.2 Region: ${\nu }_1^{\ast }\equiv {\nu }_3^{\ast }<\nu <{\nu }_2^{\ast }$

There are four supercritical Hopf bifurcation points on the endemic equilibria branch, see Figure 7 for a typical setting. Continuation of (the I-component of) limit cycles with respect to α starting from two Hopf bifurcation points, ${\mathrm{H}}_1$ and ${\mathrm{H}}_2$, forms an endemic bubble (the two branches of stable limit cycles coincide), see [14] for the origin of this concept. The same happens for the ${\mathrm{H}}_3,{\mathrm{H}}_4$ pair.

Figure 7. Bifurcation diagram w.r.t. α, when $\nu =2.06362$.

Recall that these double bubbles of instability (endemic bubbles) were readily observed in Figure 5(a). Such double bubbles have been conjectured in a delay differential model for waning and boosting [1]. For an overview of similar phenomena, the reader is referred to [8,11,17].

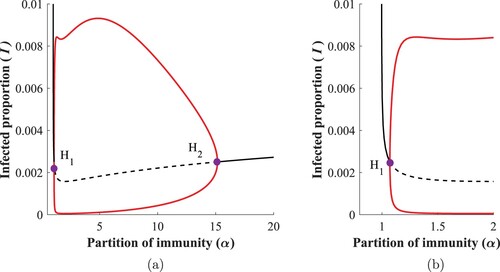
3.2.0.3 Region: ${\nu }_2^{\ast }<\nu <{\nu }_{{\mathrm{G}\mathrm{H}}_1}^{\ast }\equiv {\nu }_{{\mathrm{G}\mathrm{H}}_2}^{\ast }$

As the boosting rate increases, the middle supercritical Hopf points ${\mathrm{H}}_2$ and ${\mathrm{H}}_3$ (observed in the previous region) get closer to each other, finally collide and we obtain a single endemic bubble, Figure 8.

Figure 8. (a) Bifurcation diagram w.r.t. α, when $\nu =5.8$; (b) Zoom of (a) close to the vertical line $\alpha =1$.

3.2.0.4 Region: ${\nu }_{{\mathrm{G}\mathrm{H}}_1}^{\ast }\equiv {\nu }_{{\mathrm{G}\mathrm{H}}_2}^{\ast }<\nu <{\nu }_5^{\ast }$

As ν continues to grow in the two-parameter plane in Figure 6, two generalized Hopf points, ${\mathrm{G}\mathrm{H}}_1$ and ${\mathrm{G}\mathrm{H}}_2$, appear. They separate branches of sub- and supercritical Hopf bifurcations in the parameter plain. The stable limit cycles survive when we enter region $\mathcal{B}$. Crossing the subcritical Hopf boundary $H_{+}$ creates an extra unstable cycle inside the first one, while the equilibrium regains its stability. Two cycles of opposite stability exist inside the bistable region $\mathcal{B}$ and disappear at the green curve.

When we pass the generalized Hopf points and fix a ν in this region, then Figure 9 shows a typical bifurcation w.r.t. α. Observe here the two small α-parameter ranges of bistability where the EE and the larger amplitude periodic solution are both stable. The points marked with green circle are limit points of periodic orbits. The stable and unstable cycles collide and disappear on the green curve in Figure 6, corresponding to a fold bifurcation of cycles.

Figure 9. Bifurcation diagram w.r.t α, with $\nu =13.5$ (left) and zoom into the bistable region around $H_1$ (right).

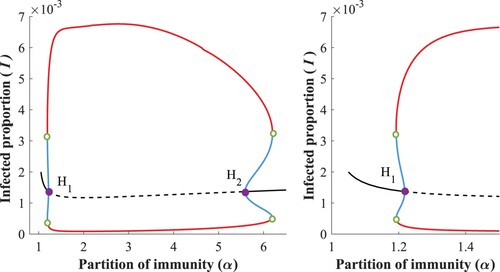
3.2.0.5 Region: ${\nu }_5^{\ast }<\nu <{\nu }_4^{\ast }\equiv {\nu }_6^{\ast }$

As we increase the boosting value, the dynamics is changing, as observed on the shape of the subcritical Hopf curve $H_{+}$ in Figure 10 and the heat map in Figure 5(b).

Figure 10. Two-parameter $(\alpha ,\nu )$ bifurcation diagram, bistability region.

In Figure 11, the bifurcation diagram confirms the existence of four subcritical Hopf bifurcation points. Here a small bubble appears inside the region of stable oscillations, which leads to an additional bistable region compared to the previous case.

Figure 11. Bifurcation diagram w.r.t α, with $\nu =13.7$ (left) and zoomed into the bubble (right).

When we increase the boosting in this region, i.e. still intersecting the subcritical Hopf curve, the Hopf points ${\mathrm{H}}_1$ and ${\mathrm{H}}_2$ as well as ${\mathrm{H}}_3$ and ${\mathrm{H}}_4$ move closer to each other, resulting in larger bistability regions, see also the heatmap Figure 5(b).

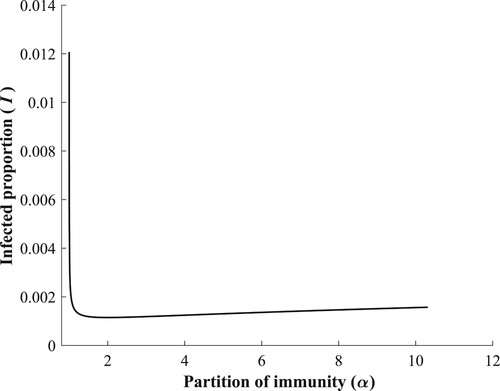
3.2.0.6 Region: ${\nu }_4^{\ast }\equiv {\nu }_6^{\ast }<\nu$

As we enter this region we leave $H_{+}$ and do not intersect any Hopf branches, hence, the continuation method utilized so far leaves us with a single stable equilibrium, Figure 12.

Figure 12. There are no bifurcations of equilibria when $\nu =14.5$.

There is however, a range of ν values in this region that belong to $\mathcal{B}$, as observed in Figure 6. For a better demonstration of the shape of the limit cycle branch, see Figure 13. The coordinates of the critical points can be found in Table A1.

Figure 13. Branch of the limit points of periodic solutions.

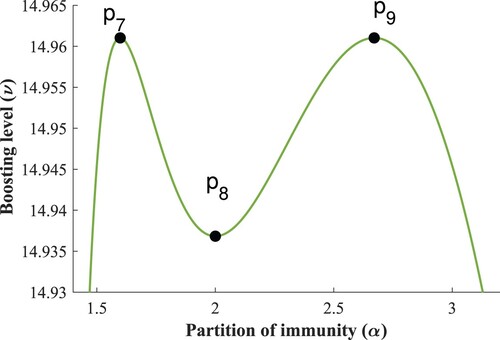
Considering the heatmaps in Figure 5, it was natural to investigate regions in the two parameter plane $(\alpha ,\nu )$ where ν is constant and look at bifurcations with respect to α. To capture the extension of the bistability region in the ν direction we can investigate the dynamics for α fixed and consider the boosting rate ν as the bifurcation parameter. For a typical setting see Figure 14.

Figure 14. Bifurcation diagram w.r.t. ν, when $\alpha =4$.

4. Conclusions

We generalized previous compartmental SIRWS models of waning and boosting of immunity by allowing different expected durations for individuals being in the fully immune compartment R and being in the waning immunity compartment W, from where their immunity can still be restored upon re-exposure. We proposed an asymmetric division of the immunity period in the SIRWS model to these two phases, characterized by a newly introduced bifurcation parameter. Other parameters were chosen to mimic pertussis. We observed and established a new symmetry in these divisions around the critical case of equal partitioning when analysing the stability criterion of the endemic equilibrium. This, combined with numerical bifurcation methods, enabled us to characterize the model dynamics for a relevant range of parameter values. We composed global bifurcation diagrams, and found complex and rich dynamics where stability switches, Hopf bifurcations, folds of periodic branches appeared, forming interesting structures in the parameter space. We found double endemic bubbles as well as regions of bistability. Note that in our model (similarly to most previous waning-boosting models [5,18]), the interesting dynamics occurs in the case $\nu >1$, which corresponds to the assumption that the probability of a partially immune person getting boosted is larger than that of a susceptible person contracting the infection.

This study confirmed that simple looking SIRWS ODE models can have very intricate dynamics. Our analysis highlighted that the division of the immunity period into maximally immune and boostable phases is a key parameter, which significantly determines the dynamics of the system. As a consequence, future epidemiological studies should attempt to estimate this quantity to have a better description of the influence of waning-boosting mechanisms on epidemic outcomes.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This research was completed in the National Laboratory for Health Security [RRF-2.3.1-21-2022-00006]. Additionally, the work was supported by the Ministry of Innovation and Technology of Hungary from the National Research, Development and Innovation Fund [project no. TKP2021-NVA-09]. In addition, F.B. and G.R. were supported by NKFIH [grant numbers FK 138924, KKP 129877]. M.P. was also supported by the Hungarian Scientific Research Fund [grant numbers K129322 and SNN125119]; F.B. was also supported by UNKP-21-5 and the Bolyai scholarship of the Hungarian Academy of Sciences.

Appendices

A.1. Derivation of the formula for ${R^{\ast }}_{\pm }$

We now derive the formula for ${R^{\ast }}_{\pm }$ used in Section 2. As we have seen, substituting the formulae for $S^{\ast }$ and $I^{\ast }$ into (4c(4c) $\begin{array}{rl}& \gamma I^{\ast }-\alpha \kappa R^{\ast }+\nu \text{β}{I}^{\ast }(1-S^{\ast }-I^{\ast }-R^{\ast })-\mu R^{\ast }=0.\end{array}$(4c) ), we obtain the quadratic equation $A(R^{\ast }{)}^2+B{R}^{\ast }+C=0,$with coefficients $\begin{array}{rl}A& =\frac{\omega \kappa \nu \text{β}(\gamma +\mu )}{(\gamma +\mu +\omega \kappa {)}^2},\\ B& =\frac{\omega \kappa \nu (\gamma +\mu +c_0{c}_1)-\left[\right(\gamma +\mu \left)\right(\mu +\alpha \kappa +\omega \kappa +\nu c_0{c}_1)+\omega \kappa (\alpha \kappa +\text{β}\nu \left)\right]}{\gamma +\mu +\omega \kappa },\\ C& =\frac{c_0{c}_1}{\text{β}}[\text{β}\nu +\gamma -\gamma \nu -\mu \nu -c_0{c}_1\nu ].\end{array}$The y-intercept C may be simplified as $\begin{array}{rl}C& =\frac{c_0{c}_1}{\text{β}}(\text{β}\nu +\gamma -\gamma \nu -\mu \nu -c_0{c}_1\nu ),\\ & =c_0{c}_1\nu +\frac{c_0{c}_1\gamma }{\text{β}}-\frac{c_0{c}_1\nu }{\text{β}}(\gamma +\mu +c_0{c}_1),\\ & =c_0{c}_1\nu +\frac{c_0{c}_1\gamma }{\text{β}}-\frac{c_0{c}_1\nu }{\text{β}}(\text{β}-\frac{c_0{c}_1\gamma }{\omega \kappa +\mu }-c_0{c}_1+c_0{c}_1),\\ & =\frac{c_0{c}_1\gamma }{\text{β}}+\frac{c_0^2{c}_1^2\gamma \nu }{\text{β}(\omega \kappa +\mu )},\\ & =\frac{c_0{c}_1\gamma }{\text{β}}(1+\frac{c_0{c}_1\nu }{\omega \kappa +\mu }).\end{array}$Then, the solution formula gives (A1) $R_{\pm }^{\ast }=\frac{-B}{2A}\mp \frac{\sqrt{B^2-4AC}}{2A}.$(A1) We split (A1(A1) $R_{\pm }^{\ast }=\frac{-B}{2A}\mp \frac{\sqrt{B^2-4AC}}{2A}.$(A1) ) into two parts and evaluate them separately. $\begin{array}{rl}\frac{-B}{2A}& =\frac{\gamma +\mu +\omega \kappa }{2\omega \kappa \nu \text{β}(\gamma +\mu )}\left(\right(\gamma +\mu \left)\right(\mu +\alpha \kappa +\omega \kappa +\nu c_0{c}_1)+\omega \kappa (\alpha \kappa +\text{β}\nu )-\omega \kappa \nu (\gamma +\mu +c_0{c}_1\left)\right)\\ & =\frac{\gamma +\mu +\omega \kappa }{2\omega \kappa \nu \text{β}(\gamma +\mu )}\\ & \times \left(\right(\gamma +\mu \left)\right(\alpha \kappa +\omega \kappa +\mu )+(\gamma +\mu )\nu c_0{c}_1+\omega \alpha {\kappa }^2+\omega \kappa \text{β}\nu -\omega \kappa \nu (\text{β}-\frac{\gamma c_0{c}_1}{\omega \kappa +\mu }))\\ & =\frac{\gamma +\mu +\omega \kappa }{2\omega \kappa \text{β}}(\frac{(\gamma +\mu )(\alpha \kappa +\omega \kappa +\mu )+\omega \alpha {\kappa }^2}{\nu (\gamma +\mu )}+\frac{(\gamma +\mu )\nu c_0{c}_1}{\nu (\gamma +\mu )}+\frac{\omega \kappa \nu \gamma c_0{c}_1}{\nu (\gamma +\mu )(\omega \kappa +\mu )})\\ & =\frac{\gamma +\mu +\omega \kappa }{2\omega \kappa \text{β}}(\frac{c_2}{\nu (\gamma +\mu )}+c_0{c}_1+\frac{\omega \kappa \gamma c_0{c}_1}{(\omega \kappa +\mu )(\gamma +\mu )})\\ & =\frac{\gamma +\mu +\omega \kappa }{2\omega \kappa \text{β}}(\frac{c_2}{\nu (\gamma +\mu )}+c_0{c}_1+\frac{\omega \kappa \gamma (\text{β}-\gamma -\mu )}{(\omega \kappa +\mu +\gamma )(\gamma +\mu )})\\ & =\frac{\gamma +\mu +\omega \kappa }{2\omega \kappa \text{β}}(\frac{c_2}{\nu (\gamma +\mu )}+c_0{c}_1+c_0{c}_1-\frac{c_1}{\gamma +\mu })\\ & =\frac{\gamma +\mu +\omega \kappa }{2\omega \kappa \text{β}}(\frac{c_2}{\nu (\gamma +\mu )}+2c_0{c}_1-\frac{c_1}{\gamma +\mu }).\end{array}$Then, the other term in (A1(A1) $R_{\pm }^{\ast }=\frac{-B}{2A}\mp \frac{\sqrt{B^2-4AC}}{2A}.$(A1) ) is $\begin{array}{rl}& \mp \frac{\sqrt{B^2-4AC}}{2A}\\ & =\mp \frac{(\gamma +\mu +\omega \kappa {)}^2}{2\omega \kappa \nu \text{β}(\gamma +\mu )}\\ & \times \sqrt{\frac{\left(\mu \right(\text{β}-\gamma -\mu ){)}^2}{(\gamma +\mu +\omega \kappa {)}^2}{\nu }^2+\frac{T_0}{(\gamma +\mu +\omega \kappa {)}^2}\nu +\frac{\left(\right(\gamma +\mu \left)\right(\alpha \kappa +\omega \kappa +\mu )+\alpha \omega {\kappa }^2{)}^2}{(\gamma +\mu +\omega \kappa {)}^2}},\end{array}$with $\begin{array}{rl}{T}_0& =2(\text{β}-(\gamma +\mu \left)\right)(\gamma {\mu }^2+{\mu }^3+\omega \kappa {\mu }^2+\alpha \kappa {\mu }^2+\alpha \gamma \kappa \mu +\omega \gamma \kappa \mu +2\alpha \omega \gamma {\kappa }^2+\alpha \omega \mu {\kappa }^2)\\ & =4\gamma \alpha \omega {\kappa }^2(\text{β}-(\gamma +\mu \left)\right)+2\mu (\text{β}-(\gamma +\mu \left)\right)\left[\right(\gamma +\mu \left)\right(\omega \kappa +\alpha \kappa +\mu )+\alpha \omega {\kappa }^2]\\ & =c_3+2c_1{c}_2.\end{array}$Hence, $\begin{array}{rl}& \mp \frac{\sqrt{B^2-4AC}}{2A}\\ & =\mp \frac{(\gamma +\mu +\omega \kappa {)}^2}{2\omega \kappa \nu \text{β}(\gamma +\mu )}\sqrt{\frac{c_1^2}{(\gamma +\mu +\omega \kappa {)}^2}{\nu }^2+\frac{(2c_1{c}_2+c_3)}{(\gamma +\mu +\omega \kappa {)}^2}\nu +\frac{c_2^2}{(\gamma +\mu +\omega \kappa {)}^2}}\\ & =\mp \frac{\gamma +\mu +\omega \kappa }{2\omega \kappa \nu \text{β}(\gamma +\mu )}\sqrt{c_1^2{\nu }^2+c_2^2+2\nu c_1{c}_2+c_3\nu }\\ & =\mp \frac{\gamma +\mu +\omega \kappa }{2\omega \kappa \nu \text{β}(\gamma +\mu )}\sqrt{(c_1\nu +c_2{)}^2+c_3\nu }.\end{array}$Recombining the two terms yields the formula $R_{\pm }^{\ast }=\frac{\gamma +\mu +\omega \kappa }{2\text{β}\omega \kappa }[(2c_0-\frac{1}{\gamma +\mu })c_1+\frac{1}{\nu (\gamma +\mu )}(c_2\mp \sqrt{(c_1\nu +c_2{)}^2+c_3\nu })].$

A.2. Transcritical bifurcation of forward type

For the sake of completeness, we include a slightly adjusted version of Theorem 4.1. from Castillo–Chavez and Song [4].

Theorem A.1

Let $f\in C^2({\mathbb{R}}^n\times \mathbb{R},{\mathbb{R}}^n)$ and consider the system of ordinary differential equations $\frac{\mathrm{d}x}{\mathrm{d}t}=f(\mathbf{x},b),$with b as a parameter. Assume that $\mathbf{0}$ is an equilibrium point, i.e. $f(\mathbf{0},b)=0$ for all $b\in \mathbb{R}$. In addition, assume the following:

(i)	The linearization of the system at $(\mathbf{0},0)$ $A:=D_{\mathbf{x}}f(\mathbf{0},0)={\left(\frac{\mathrm{\partial }{f}_i}{\mathrm{\partial }{\mathbf{x}}_j}\right(\mathbf{0},0\left)\right)}_{i,j=1}^n$has zero as a simple eigenvalue and all other eigenvalues of A have negative real parts.
(ii)	The matrix A has a non-negative right eigenvector w and a left eigenvector v corresponding to the zero eigenvalue.

Let $f_k$ be the k-th component of f and define $\begin{array}{rl}{Z}_1& =\sum _{k,i,j=1}^n{v}_k{w}_i{w}_j\frac{{\mathrm{\partial }}^2{f}_k}{\mathrm{\partial }{\mathbf{x}}_i\mathrm{\partial }{\mathbf{x}}_j}(\mathbf{0},0)\text{and}\\ Z_2& =\sum _{k,i=1}^n{v}_k{w}_i\frac{{\mathrm{\partial }}^2{f}_k}{\mathrm{\partial }{\mathbf{x}}_i\mathrm{\partial }b}(\mathbf{0},0).\end{array}$If $Z_1<0$ and $Z_2>0$, then as b changes from negative to positive, the equilibrium $\mathbf{0}$ changes its stability from stable to unstable. At the same time, a negative unstable equilibrium becomes positive and locally asymptotically stable. Hence, a forward bifurcation occurs at b = 0.

A.3. Transformation of $y_{\nu }\left(\alpha \right)$

The alternative, simpler form of $\omega \kappa \text{β}\nu (1-S^{\ast }-{I^{\ast }}_{+}-{R^{\ast }}_{+})$, used in Section 2.2.1, is obtained as follows. $\begin{array}{rl}& \omega \kappa \text{β}\nu (1-S^{\ast }-{I^{\ast }}_{+}-{R^{\ast }}_{+})\\ & \omega \kappa \text{β}\nu (1-\frac{\gamma +\mu }{\text{β}})-\omega \kappa \text{β}\nu \frac{\sqrt{(c_1\nu +c_2{)}^2+c_3\nu }+(c_1\nu -c_2)}{2\text{β}\nu (\gamma +\mu )}\\ & -\omega \kappa \text{β}\nu \frac{\gamma +\mu +\omega \kappa }{2\text{β}\omega \kappa }[(2c_0-\frac{1}{\gamma +\mu })c_1+\frac{1}{\nu (\gamma +\mu )}(c_2-\sqrt{(c_1\nu +c_2{)}^2+c_3\nu })]\\ & =\omega \kappa \nu \frac{c_1}{\mu }+\frac{\omega \kappa }{2}\frac{c_2-\sqrt{(c_1\nu +c_2{)}^2+c_3\nu }}{\gamma +\mu }-\frac{\omega \kappa }{2}\frac{c_1\nu }{\gamma +\mu }-\frac{\nu }{2}(\gamma +\mu +\omega \kappa )2c_{0}c1\\ & -\frac{\nu (\gamma +\mu )}{2}[-\frac{1}{\gamma +\mu }{c}_1+\frac{1}{\nu (\gamma +\mu )}(c_2-\sqrt{(c_1\nu +c_2{)}^2+c_3\nu })]\\ & +\frac{\nu \cdot \omega \kappa }{2}\frac{c_1}{\gamma +\mu }-\frac{\omega \kappa }{2}\frac{c_2-\sqrt{(c_1\nu +c_2{)}^2+c_3\nu }}{\gamma +\mu }\\ & =\omega \kappa \nu \frac{c_1}{\mu }-\frac{\nu }{2}(\gamma +\mu +\omega \kappa )2c_{0}c1+\frac{\nu }{2}{c}_1-\frac{1}{2}(c_2-\sqrt{(c_1\nu +c_2{)}^2+c_3\nu })\\ & =\omega \kappa \nu \frac{c_1}{\mu }-\nu (1+\frac{\omega \kappa }{\mu })c1+\frac{\nu }{2}{c}_1-\frac{1}{2}(c_2-\sqrt{(c_1\nu +c_2{)}^2+c_3\nu })\\ & =\frac{\sqrt{(c_1\nu +c_2{)}^2+c_3\nu }-(c_1\nu +c_2)}{2}=\text{β}\nu (\gamma +\mu ){I^{\ast }}_{+}-c_1\nu .\end{array}$We now present two Lemmas on derivatives of function compositions. The first is a version of the classical result by Faà di Bruno generalizing the chain rule.

Lemma A.1

Faà di Bruno

Let $f:I\to U$ and $g:U\to V$ be analytic functions, where $I,U,V\subseteq R$ are connected subsets. Consider the Taylor expansions $f\left(t\right)=\sum _{k=0}^{\mathrm{\infty }}{\left(f\right)}_k(t-t_0{)}^k$ centred at $t_0\in I$ with $t\in I$ and $g\left(x\right)=\sum _{k=0}^{\mathrm{\infty }}{\left(g\right)}_k(x-x_0{)}^k$ centred at $x_0=f\left(t_0\right)$ for $x\in U$. Then, the composite function $(g\circ f)$ attains the Taylor expansion $(g\circ f)\left(t\right)=\sum _{k=0}^{\mathrm{\infty }}{(g\circ f)}_k(t-t_0{)}^k$ centred at $t_0$ with the coefficients $\begin{array}{rl}{(g\circ f)}_0& ={\left(g\right)}_0\text{and}\\ {(g\circ f)}_k& =\sum _{\begin{array}{c}{b}_1+2b_2+\dots +k{b}_k=k\\ m:=b_1+b_2+\dots +b_k\end{array}}\frac{m!}{b_1!b_2!\dots b_k!}{\left(g\right)}_m\prod _{i=1}^k({\left(f\right)}_i{)}^{b_i},\end{array}$where $k\ge 1$ and $b_1,\dots ,b_k$ are nonnegative integers.

Using the results of Lemma A.1 and assuming that the inner function has a vanishing first derivative and the outer function has a cascade of vanishing derivatives, the following Lemma establishes a similar property for the composite function.

Lemma A.2

Assume that f and g are as in Lemma A.1 and that ${\left(f\right)}_1=0$. Then,

(a)	${(g\circ f)}_2=0$ ⇔ ${\left(g\right)}_1=0$,
(b)	if ${\left(g\right)}_i=0$ for $i=1,\dots ,k-1$, then ${(g\circ f)}_{2k}=0$ ⇔ ${\left(g\right)}_k=0$,
(c)	if ${\left(g\right)}_i=0$ for $i=1,\dots ,k$, then ${(g\circ f)}_{2k+1}=0$.

Proof.

The claims directly follow from Lemma A.1 by noting that in the formula of ${(g\circ f)}_k$, for terms with $m>k/2$, the inequality $b_1>0$ must hold, hence, any such term must evaluate to zero.

A.4. Asymptotic behaviour of equilibria

The analytic computations of the behaviour of the equilibria of SIRWS system for large and small boosting (ν) $\begin{array}{rl}& \underset{\nu \to 0^{+}}{lim}{I^{\ast }}_{+}=\frac{(\alpha \kappa +\mu )(\gamma +\mu +\omega \kappa )c_1{c}_0}{\text{β}{c}_2},\underset{\nu \to \mathrm{\infty }}{lim}{I^{\ast }}_{+}=\frac{\left|c_1\right|+c_1}{2\text{β}(\gamma +\mu )},\\ & \underset{\nu \to 0}{lim}{R^{\ast }}_{+}=\frac{\gamma +\mu +\omega \kappa }{2\text{β}\omega \kappa }[(2c_0-\frac{1}{\gamma +\mu })c_1-\frac{2c_1{c}_2+c_3}{2c_2(\gamma +\mu )}],\\ & \underset{\nu \to \mathrm{\infty }}{lim}{R^{\ast }}_{+}=\frac{\gamma +\mu +\omega \kappa }{2\text{β}\omega \kappa }[(2c_0-\frac{1}{\gamma +\mu })c_1-\frac{\left|c_1\right|}{(\gamma +\mu )}].\end{array}$Here, we consider the behaviour of the equilibria as $\alpha \to 1^{+}$ and $\alpha \to \mathrm{\infty }$ $\underset{\alpha \to \mathrm{\infty }}{lim}{I^{\ast }}_{+}=\frac{1}{\text{β}(\gamma +\mu )}[c_1+\frac{\gamma \kappa (\text{β}-(\gamma +\mu \left)\right)}{\gamma +\mu +\kappa }],$As a remark, the limit as $\alpha \to \mathrm{\infty }$ and as $\alpha \to 1^{+}$ are the same. $\underset{\alpha \to \mathrm{\infty }}{lim}{R^{\ast }}_{+}=0,$and lastly, $\underset{\alpha \to 1^{+}}{lim}{R^{\ast }}_{+}=\frac{1}{\text{β}(\gamma +\mu )}[\frac{c_1\gamma }{\mu }+\frac{\gamma \kappa (\text{β}-(\gamma +\mu \left)\right)}{\gamma +\mu +\kappa }].$

A.5. Numerical values of marked bifurcation points

Table A1. Critical points on the contour $y_{\nu }\left(\alpha \right)=0$ as marked in Figure 5 and critical points on the limit cycles branch as marked in Figure 13.

	α	ν
$p_1=({\alpha }_1^{\ast },{\nu }_1^{\ast })$	1.864273655292	2.063612920385
$p_2=({\alpha }_2^{\ast },{\nu }_2^{\ast })$	2.0	2.063623848262
$p_3=({\alpha }_3^{\ast },{\nu }_3^{\ast })$	2.157040937065	${\nu }_1^{\ast }$
$p_4=({\alpha }_4^{\ast },{\nu }_4^{\ast })$	1.366092512212	13.80272643151
$p_5=({\alpha }_5^{\ast },{\nu }_5^{\ast })$	2.0	13.61692960743
$p_6=({\alpha }_6^{\ast },{\nu }_6^{\ast })$	3.731549995264	${\nu }_4^{\ast }$
$p_7=({\alpha }_7^{\ast },{\nu }_7^{\ast })$	1.5987662507	14.9610290034
$p_8=({\alpha }_8^{\ast },{\nu }_8^{\ast })$	2	14.936830813
$p_9=({\alpha }_9^{\ast },{\nu }_9^{\ast })$	2.670631735	${\nu }_7^{\ast }$

Table A2. Critical GH points as marked in Figure 6.

	α	ν
${\mathrm{G}\mathrm{H}}_1=({\alpha }_{{\mathrm{G}\mathrm{H}}_1}^{\ast },{\nu }_{{\mathrm{G}\mathrm{H}}_1}^{\ast })$	1.1430260422	12.469198884
${\mathrm{G}\mathrm{H}}_2=({\alpha }_{{\mathrm{G}\mathrm{H}}_2}^{\ast },{\nu }_{{\mathrm{G}\mathrm{H}}_2}^{\ast })$	7.9917337529	12.469198884