Mapping urban building stocks for vulnerability assessment – preliminary results

Abstract

This paper discusses a methodology to collect building inventory data by combining image processing techniques, field work or tools such as Google Street View and applying statistical inferences. Following the methodology outlined in Marinescu (2002), a family of Gabor filters are first constructed, which are then applied to an optical high-resolution image. The output from the processed image is segmented using Self-Organising Maps. This paper examines the relationship between the segmented areas in the image and the building type distribution within each segmented area, by deriving the distribution from field data. The relationship between the average number of buildings in these cells against the number of grid cells allocated to each segmentation cluster is also investigated. Finally, using these results, the overall building inventory distribution for the whole of the case study site of Pylos is presented.

Keywords:

• building inventory data collection
• remote sensing
• high-resolution optical satellite images
• Gabor filters
• Self-Organising Maps
• field data

1. Introduction

Building inventory data, a key component for natural catastrophe loss modelling, are often difficult to obtain. If they are available, the level of detail included as well as the quality of the data varies from country to country. The key parameters required for catastrophe modelling are: structure type, building height, area, age and use type. The geographical scale at which the hazard to be modelled occurs will also have an effect on the level of aggregation as well as the detail required for the building inventory data to be fed into the model, although in the recent years better quality data is increasingly being required for all hazards (Dr. Gunasekera, personal communication, 17 August 2010).

The objective of this study is to propose a building inventory data collection method that applies image processing techniques on high-resolution optical satellite images or aerial images with spatial resolution of 1 m or less. The spatial resolution of the images as well as the geographical coverage of these images implies that the analysis proposed here is done optimally at the urban scale, i.e. towns and cities. For data collection at a larger geographical scale, i.e. national or regional scale, a separate methodology will be required.

Building inventory collection methods have traditionally relied on the availability of census data. Particularly in the insurance sector, data on building inventory are of importance to run loss models for various hazards. However, the attributes that are included in the available building inventory dataset or the scale at which the data are aggregated do not always suit the scale of analysis required, resulting in the use of inappropriate data for the scale of analysis. It is particularly important for re-insurers to be able to compare the risk in various regions across the globe in a standardised way. For these reasons, the capability to capture building inventory data in a standardised way is highly sought.

Various research groups have been investigating ways to improve building inventory data collection at various scales using remotely sensed data. At the individual building level, techniques ranging from the use of Light Detection and Ranging (LiDAR) data (e.g. Brenner 2005) to sophisticated photogrammetric methods that reconstruct the 3D geometric shape of the buildings from a single high-resolution optical satellite images (Sarabandi et al. 2008) have been demonstrated, although these methods only extend to extracting the physical geometric models of the buildings and do not allow for the other attributes required for loss modelling to be captured. Sarabandi et al. (2008) recognising that identifying the structure type and the occupancy type information for buildings are more difficult than extracting the geometric shape of buildings using remote sensing, investigates the use of statistical inference using models. Data obtained from the tax assessor's office and information on attributes of the buildings captured using optical imagery were used to construct these models, the response variable being the structure type or occupancy type for a building. The baseline model only uses information on the height and average area for a building, which are the only two variables that can be captured with reasonable accuracy using 3D models of buildings. As more explanatory variables were added to the model (e.g. configuration, roof type, etc.), the prediction rate improved. However, the model requires existing building inventory data, which may not be available in many cases.

This paper consists of three parts: the focus of the first part of the study is on unsupervised image segmentation techniques to segment the image according to the morphology seen in the image. The segmentation methodology follows Marinescu (2002) that uses the Gabor wavelet filter and Self-Organising Maps (SOM). Marinescu demonstrated in his work using a 1 m spatial resolution aerial photograph of London and overlaying a grid that there is a relationship between the morphology seen in the grid cells labelled as belonging to the same cluster segmented using the SOM and the actual building types on the ground, and that the image can be used as a means to estimate the building type distribution across the urban built-up area using this principle. Here the same methodology has been tested on a much smaller urban area, i.e. the town of Pylos in Greece where a building-by-building survey result was available as validation data. The segmentation technique applied in Marinescu's work assumed homogenous building types within one grid cell/cluster, wh ereas in Pylos where the built-up area shows more variation in terms of the buildings contained in one grid cell, this is not necessarily the case. Instead, a different assumption was made which is that the clusters of grid cells created using the SOM (i.e. areas where the analysis of the image suggests having similar morphology) will contain similar building type distributions.

The second part of this study will use the unsupervised segmentation results to see how the buildings, in terms of structure types, correspond to these clusters derived using the image. Finally, in the final section, using the building type distribution for each cluster derived in the previous step, building inventory data will be produced for Pylos, adopting the proposed methodology which will be compared to the field survey data. The paper will conclude by expressing the need for more building inventory data so that more case studies can be carried out to test the various assumptions employed in this study. The analysis of more ground data can also help uncover the typical number of building types that can be expected to be found in one urban area. This information will assist in identifying the number of clusters to be used in the segmentation process using SOM.

2. Methodology

2.1. Feature extraction with Gabor filters

The methodology outlined in Marinescu (2002), which was adopted for this study, starts by overlaying a grid that covers the urban area in the image. In this study, a high-resolution panchromatic satellite image (Quickbird – 60 cm spatial resolution) was obtained for the Greek town of Pylos (Figure 1).1 Here, following Marinescu, a minimum grid cell size of 128×128 pixels has been adopted. Thus far, cell sizes of 128×128 and 192×192 pixels, corresponding to 76.8 and 115.2 m on the ground, have been tested. Larger cell sizes will be tested in the next phase of the study. Each grid cell is processed using a family of Gabor wavelet filters, to quantify the response of the image to the frequencies and directionality each filter is designed for.

Figure 1.  Greek town of Pylos, as seen in the 0.6 m spatial resolution optical satellite panchromatic Quickbird image. Digital Globe ©, 2008.

Urban built-up areas exhibit ‘patterns’ in optical images that are caused by the variation of the brightness values in the image. The frequency at which the brightness changes corresponds to the location of the edge of the objects in the image, e.g. boundaries of a building. Gabor wavelet filters are used in this study to quantify these frequencies seen in the image. Buildings with similar geometric characteristics can be expected to exhibit similar frequency patterns, which are then assumed to have similar structural attributes. The same can be expected from objects other than buildings such as roads (e.g. width, orientation and shape of the road layouts). A more detailed description of Gabor filters can be found in Marinescu (2002).

Through the case study of a small section of London, Marinescu identified that the use of 12 filters, namely a combination of three wavelengths and four directions that each correspond to frequencies of 4, 8 and 16 m and orientations of 0°, 45°, 90°, 135°, produces the optimal results. The same combinations of frequencies and orientations have been used for this study. Figure 2 shows an example of a Gabor filters generated and applied to the image for this study.

Figure 2.  Example of a Gabor filter applied to the panchromatic image of Pylos, Greece. Wavelength: 16 m; orientation: 45°.

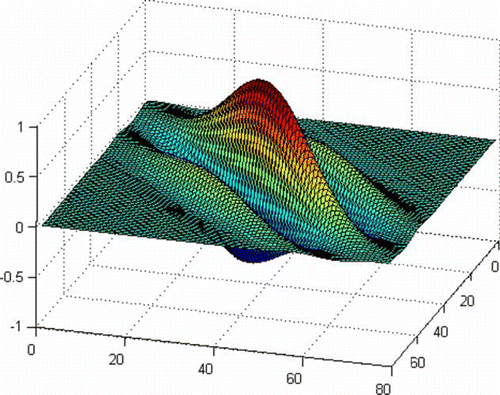
The 12 Gabor filters are each applied to the individual grid cells in the image. The filters are moved pixel-by-pixel, whereby the central pixel value will be replaced with the response value from the filter. In simple terms, the response to the filter will be higher in places where the frequency and directionality of change in brightness in the image correspond to that of the filter applied. Once a filter has been passed through all pixels in the grid cell, the new values for each cell are binned using a 10-bin histogram. Since 12 filters are applied to the image, the final output becomes a 120-dimension vector that is generated for each cell.

2.2. Unsupervised segmentation using Self-Organising Maps (SOM)

Once the 120-dimension vector has been obtained for each cell in the image, this data are subjected to unsupervised segmentation using SOM to uncover the clusters based on the morphology in the urban image. SOM maps high-dimensional data onto low-dimensional (or 2D) planes, preserving the most prominent patterns in the dataset (Guo et al. 2005). It is also a visualisation tool for exploratory analysis of high-dimensional datasets. For SOM in this study, SOMVIS, a freeware written in Java by Guo et al. (2005) has been used. Kohonen (2001) provides a detailed mathematical exploration of SOM. Guo et al. (2005) provides a summary of the history of the development of SOM.

The process starts by randomly creating nodes within the n dimensional data space (in this case 120 dimensions). The number of nodes to be used is predefined by the user and should be n×n. Some distance metric is used to quantify the distances between the actual data points, and the artificially created nodes and data points are assigned to the best matching node. The neighbouring nodes are then adjusted according to a predefined updating law, by altering the neighbouring nodes by a small amount so that the similarity between them increases (Kohonen 2001). The process is iterated until the nodes stabilise. Some clustering examples are shown in Figure 3. For all subsequent analysis, the results from the segmentation carried out using only the cells that contain buildings and cell size of 192×192 pixels and nine SOM nodes have been used.

Figure 3.  Example of SOM nodes. The size of the colour-coded circles corresponds to the number of cells that have been assigned to that node. Left: SOM with nine nodes; right: SOM with 49 nodes.

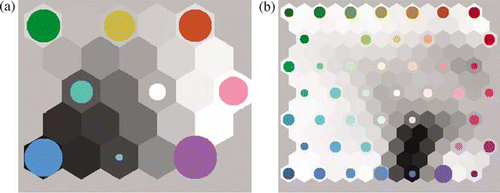
To test the assumption made for this study, i.e. that the grid cells with similar responses to the Gabor filters contain similar building type distributions, firstly the 120-dimensional dataset produced in the previous step was segmented into clusters in the data space using SOM. In this instance, Euclidean distance was used to measure the multivariate similarities between the cells, however, other measures such as Chi-square distance are known to perform well (Puzicha et al. 1997, Marinescu 2002).

2.3. Summary of the field survey data for Pylos

The field data for Pylos were collected by Antonios Pomonis and Maria Gaspari over 2 weeks in the summer of 2008 for the project SEAHELLARC,2 where the risk from future earthquakes and tsunami was assessed for the urban areas along the west coast of Greece. The data consist of a spreadsheet that records the structure type, number of storeys, use type and age (where possible) at a building-by-building level. The main structure types seen in Pylos are reinforced concrete (RC) and unreinforced masonry (URM), with some buildings where the ground floor is RC and first floor is URM which will be called class mixed. A few timber frame buildings also exist but have been ignored in this study.

To make the assessment simpler for this study, the class mixed was combined with RC, since the response of the structure to an earthquake would be more similar to that of RC. In terms of the number of storeys, of the total number of buildings (843) included in the dataset, approximately 76% are either one or two storeys, 22% (192) are three storeys and 1% (9) are four storeys high. Since the variation in the building height is minimal, no distinction will be made between the various building heights. Of the 843 buildings, the buildings to the south located in the outskirts of Pylos have been excluded from this study.

2.4. The relationship between the number of cells assigned to one cluster and the number of buildings found in these cells

In the final methodology, the building inventory data collection method will apply a uniform building (structure) type distribution to each of the cells belonging to one cluster. However, since the cells do not contain the same number of buildings, it is necessary to have an estimate of the total number of buildings, or the percentage of the number of buildings in one cluster, so that the building type distribution representing one cluster can be weighted in the final estimate.

3. Results

3.1. Sensitivity analysis of the unsupervised segmentation

The 12 Gabor filters were applied to the panchromatic image of Pylos using grid cell sizes of 128×128 and 192×192 pixels. The resulting vectors were clustered using SOM. The differences in the segmentation results when including/excluding the grid cells without any buildings, as well as the change that occurs when altering the number of SOM nodes has been tested for both pixel sizes. The Quickbird image that the filter was applied to has a 0.6 m spatial resolution, meaning 128 pixels equals to 76.8 m and 192 pixels equals to 115.2 m on the ground. Figure 4 shows some results.

Figure 4.  Segmentation results. Each cell is coloured according to the allocated cluster ID, and there is no correlation between the cells with the same colours across the different results. The numbers in the grid cells are the cluster IDs allocated to each cell.

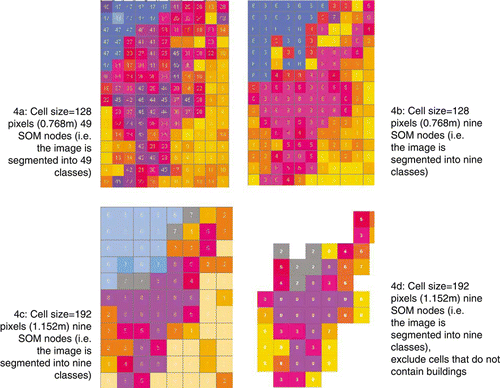
Overall results seen in Figure 4 show that the methodology is capable of differentiating the urban area from other land cover types, regardless of the parameters chosen for the segmentation. Naturally, the segmentation carried out using 49 nodes (and 128 pixels) shows more variation within the built-up area, compared to when nine nodes are used. With the nine nodes, the main built-up area is labelled as one cluster, with the fringes showing slight variations. The effect of the use of these different clusters should be considered in the context of estimating the final building inventory distribution for the whole town of Pylos. Although the focus of this study is to investigate the use of different parameters on the clustering results, a methodology to produce an estimate of the building inventory using the proposed segmentation methods is described in the final section of this paper. Figure 5 shows some of the cells that have been labelled as belonging to the same cluster.

Figure 5.  Samples of cells that have been allocated to the same cluster.

3.2. Comparison between the image clusters and the building type distribution

To see if there is a correlation between the clusters generated using the segmentation method and the building types contained in each of the grid cells, the building (structure) type distribution for each grid cell was extracted and compared within each cluster. The extraction of the building type distribution was possible due to the availability of the field survey data. Figure 6 shows the bar charts of the distributions seen in each of the clusters for the results obtained using the parameters: 192 pixels, nine SOM nodes and excluding the cells that do not contain buildings. The bar charts for the cells are grouped according to the cluster they belong to.

Figure 6.  Example of the structure type distribution extracted from the field data for the cells that have been assigned to the same class. From the top, in clockwise order: distribution of buildings in cluster ID 0, 6 and 3, using the results from the grid cell size of 192×192 pixels and nine SOM nodes, excluding the cells that do not contain any buildings. The numbers on the x-axis show the unique cell ID given to each cell in the image.

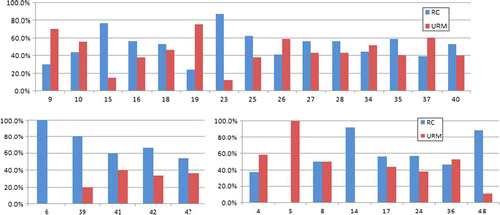
A general trend in each of the clusters can be observed. For instance in Cluster 3, there are more RC buildings than URM, whereas in Cluster 0, there tend to be more URM buildings than RC buildings. It must be remembered here that the number of buildings contained in each cell is not the same and this must be taken into account when estimating the total building inventory. In the next section, with a view to developing a streamlined methodology to estimate the building inventory for Pylos where field data is not available, the relationship between the number of buildings in each cell for each segmentation cluster and the number of cells allocated to each cluster will be investigated.

4. Estimating the building type distribution for Pylos using the unsupervised segmentation technique

If building inventory data for Pylos were to be derived without relying on field data, how can this be achieved using the unsupervised segmentation described in this paper? One possible methodology is described here. The starting point will be the unsupervised segmentation using the Gabor filter and SOM. Thus far, comparison between the segmentation result and the field building inventory data suggests that using cell sizes of 192×192 pixels and a SOM with nine nodes produce the optimal results. After the unsupervised segmentation is carried out, the cell that is closest to the SOM node will be used as the cell that contains the ‘average’ building type distribution for that SOM cluster. The building type distribution for this average can be derived relatively easily when field data are available. However, if it is not, then field survey or tools such as Street View could be utilised. Street View will enable the data on the building types in the ‘average’ cell to be collected through visual inspection of the facade of the buildings.

For the Pylos data, there is a positive correlation between the number of cells assigned to the same cluster and the average number of buildings in each cluster. Figure 7 shows the linear relationship derived using the field data and the clusters created using the segmentation method. Using this relationship, building numbers have been allocated to each cluster. Table 1 shows the new proportion of the building numbers allocated to each segmentation cluster derived using the relationship.

Figure 7.  The strong linear relationship observed between the average number of buildings in the cells assigned to the same cluster and the number of cells assigned to one cluster.

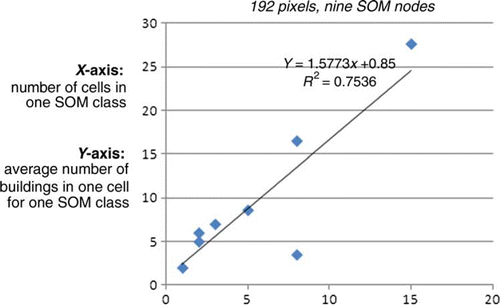
Table 1. The proportion of buildings assigned to each class after applying the linear relationship to the clusters according to the number of cells. Cluster ID 1 does not contain any buildings and therefore has been omitted.

Cluster ID	Total number of buildings extracted from field data	Total number of buildings estimated in each class
0	375	368
2	10	8
3	136	108
4	12	8
5	2	2
6	45	44
7	21	17
8	32	108
Total	633	662

Using the estimated building numbers for each SOM cluster ID derived in Section 4, and also using the building type distribution of the ‘average’ cell for each SOM cluster identified using the segmentation technique, the structure type distribution for the whole of Pylos has been estimated. The results are shown in Table 2.

Table 2. Proportion of building types estimated using the segmentation method, compared against the field data.

	Field data		Estimated from image
Cluster ID	RC	URM	RC	URM
0	206	204	89	279
2	7	3	5	3
3	73	56	62	41
4	7	5	5	3
5	0	2	0	2
6	30	12	24	16
7	12	9	6	10
8	18	10	0	108
Sub-total	353	301	191	462
	54.0%	46.0%	29.2%	70.8%

5. Discussion

When considering using the unsupervised segmentation methodology proposed in this study to estimate the building inventory data distribution for a town the size of Pylos, the number of grid cells where field survey or the equivalent needs to be done should be kept to a minimum to optimise the efficiency of the methodology. The trade-off will be between the accuracy achievable and the economy of using as few cells as possible as the template ‘average’ cells that represents one cluster where ground data are to be collected. In this sense, the use of the minimum number of SOM clusters, i.e. nine, would obviously be the most economical option.

The segmentation results, regardless of the parameters used, show that the urban area in this study is clearly distinguishable using the Gabor filter and the SOM. The number of SOM clusters used to segment the image clearly has an effect on the number of urban morphology clusters that are created within the urban area(Figure 4). Upon visual inspection of the urban area in the image of Pylos, there are at least two clusters, i.e. the area in the west half of the town where the buildings have relatively generous plots and are built among a road network with a regular grid layout and the east half of the image where the buildings are more densely built and an irregular road network. These two areas are only distinguished when using 25 SOM clusters to segment the image with grid cell sizes of 192 pixels. The question becomes whether it is worthwhile using 25 clusters to segment a town the size of Pylos. It may be possible to aggregate some of the clusters, depending on some distance metric. In terms of the ground data, a t-test has been carried out to see if there is a statistical significance in the difference in the proportion of the RC buildings from one cluster to another. At the 95% confidence level, the difference is not significant, hence in this case, it may not make sense to treat the clusters as having different building distributions, based on the ground data. Table 2 shows that the final estimated building inventory data for the whole of Pylos do not tally with the ground validation data. However, in light of the results of the t-test on the ground data, an alternate methodology that considers the entire urban area as one cluster may be sought.

As for the distance metric currently used for the SOM, Chi-square distance should be tested against the results derived using Euclidean distance in the current methodology. More combinations of grid cell sizes and SOM cluster need to be tested, as well as considering other measures (e.g. vegetation, historical development of the areas within the urban area) that may help aid the segmentation process. A knowledge-based classification methodology that allows the representation of urban areas that combine these various aspects may be appropriate.

6. Conclusions and further work

A method to estimate the ratio of structure types in an urban area at an urban scale using remotely sensed data is proposed based on unsupervised segmentation techniques by combining Gabor Filters and SOM. The unsupervised segmentation allows the urban area to be classified into a predefined number of clusters when segmenting the data using SOM; however, it may be possible to aggregate some of the clusters when estimating the overall building inventory. The estimation method of the structure type distribution produced for Pylos requires further refinement, taking into account further the complexity of a built-up area. A more probabilistic approach may be required.

In terms of other methodologies, the performance of supervised segmentation, where templates are selected manually and distance measures employed to assign a grid cell to a cluster should be tested and compared against these results to assess the suitability of such a method.

6.1. On the importance of validation and the collection of reference data

From a methodological point of view, more building inventory data are urgently needed so that more case studies can be carried out to investigate the characteristics of building type distributions within urban areas of various sizes, particularly in terms of the number of clusters. How large does an urban area need to be to contain more than one cluster? The answer will only become clear if validation data are available. This information will also assist in identifying the optimal number of clusters to be used in the segmentation process using SOM, as well as the number of buildings that needs to be surveyed on the ground to produce the overall building stock data for vulnerability assessment.

Data collection on the ground is a time-consuming and expensive activity. To maximise the outputs from such exercise, parameters to be collected should be pre-determined and agreed. An agreement on a set of standardised parameters to be collected to assess vulnerabilities from each hazard would be valuable for future data collection exercises.

In the context of global initiatives such as the Global Earthquake Model (GEM), exposure mapping will be a key to understanding the risk to areas around the world from earthquakes in a standardised way. When trying to collect data on exposure (buildings) at a global scale, collecting data on the ground is simply not feasible. Adopting remote sensing techniques such as the methodology presented in this study will be an attractive alternative, even at a national scale, provided that access to data is possible and the computing power to process the images are available. However, if methods such as the one presented in this paper are to be adopted in which inference are a core component, then having validation data to calibrate the methodology becomes key to its success.

Notes on contributors

Keiko Saito is a Geographic Information Systems (GIS) and Remote Sensing specialist. Her area of interest is in the application of GIS and remote sensing to quantify and visualise the risk from natural disasters on the built environment. Dr Saito is a Willis Research Network Fellow, focusing on the use of remote sensing to improve collection of exposure data. Other experiences include volcanic risk assessment, monitoring and evaluating recovery after natural disasters using remotely sensed data and tsunami survivor surveys among others. She also has an established track record in post-event field surveys. She is currently the Deputy Director at the Cambridge University Centre for Risk in the Built Environment (CURBE) based at the Department of Architecture, University of Cambridge.

Robin Spence is Emeritus Professor of Architectural Engineering and Director of Cambridge University Centre for Risk in the Built Environment (CURBE) at the Department of Architecture, University of Cambridge with more than 30 years of experience in earthquake engineering. His principal research and consultancy interests are disaster risk assessment and disaster mitigation. He has directed numerous research and consultancy contracts and he is the author of several books and more than 150 technical papers in these areas. Projects on risk assessment have ranged from earthquake, floods and windstorm to subsidence. Research projects on disaster mitigation have been funded by EU, EPSRC (UK), as well as the private (re)insurance sector. He was President of the European Association for Earthquake Engineering between 2002 and 2006.

Acknowledgements

The authors would like to thank Willis Research Network for providing the funding to carry out this study and their continuing support. We would also like to thank Antonios Pomonis and Maria Gaspari from the SEAHELLARC project, who kindly provided access to the Quickbird satellite image of Pylos used in this study as well as access to ground validation data collected through their field surveys for SEAHELLARC.

Notes

1. The Quickbird image of Pylos was obtained courtesy of the EU funded (FP6) project, SEAHELLARC.

2. SEismic and tsunami risk assessment and mitigation scenarios in the western HELLenic ARC. Available from: http://www.seahellarc.gr/[Accessed 8 July 2010].