Improving a Penman–Monteith evapotranspiration model by incorporating soil moisture control on soil evaporation in semiarid areas

Abstract

Penman–Monteith (PM) theory has been successfully applied to calculate land surface evapotranspiration (ET) for regional and global scales. However, soil surface resistance, related to soil moisture, is always difficult to determine over a large region, especially in arid or semiarid areas. In this study, we developed an ET estimation algorithm by incorporating soil moisture control, a soil moisture index (SMI) derived from the surface temperature and vegetation index space. We denoted this ET algorithm as the PM-SMI. The PM-SMI algorithm was compared with several other algorithms that calculated soil evaporation using relative humidity, and validated with Bowen ratio measurements at seven sites in the Southern Great Plain (SGP) that were covered by grassland and cropland with low vegetation cover, as well as at three eddy covariance sites from AmeriFlux covered by forest with high vegetation cover. The results show that in comparison with the other methods examined, the PM-SMI algorithm significantly improved the daily ET estimates at SGP sites with a root mean square error (RMSE) of 0.91 mm/d, bias of 0.33 mm/d, and R² of 0.77. For three forest sites, the PM-SMI ET estimates are closer to the ET measurements during the non-growing season when compared with the other three algorithms. At all the 10 validation sites, the PM-SMI algorithm performed the best. PM-SMI 8-day ET estimates were also compared with MODIS 8-day ET products (MOD16A2), and the latter showed negligible bias at SGP sites. In contrast, most of the PM-SMI 8-day ET estimates are around the 1:1 line.

Keywords:

• ET
• Penman–Monteith
• soil moisture
• MODIS

1. Introduction

Evapotranspiration (ET), which includes soil evaporation and vegetation transpiration, is a major component of the global water cycle, and plays a central role in climate and meteorology, plant community dynamics, and carbon and nutrient biogeochemistry (Vörösmarty, Federer, and Schloss 1998). ET returns 60% of the precipitation to the atmosphere (Oki and Kanae 2006) and imposes an important constraint on the water supply. In addition, more than half of the absorbed solar energy is utilized for ET (Trenberth, Fasullo, and Kiehl 2009). Accordingly, accurate estimation of ET is extremely valuable for better irrigation management, especially in semiarid areas.

Remote sensing has been recognized as the most feasible means to provide a spatial distribution of land surface ET, as it can be used to estimate the land surface parameters required for estimation of ET, such as Normalized Difference Vegetation Index (NDVI), Leaf Area Index (LAI), albedo, and land surface temperature (T_s). Remote sensing-based methods can be divided into four types: (1) empirical statistical methods (Bella, Rebella, and Paruelo 2000; Carlson, Capehart, and Gillies 1995; Wang and Liang 2008); (2) residual methods based on the residual of surface energy balance through thermal infrared data (Anderson et al. 1997; Bastiaanssen et al. 1998; Norman, Kustas, and Humes 1995; Su 2002); (3) triangle/trapezoid methods linked with vegetation index and T_s (Jiang and Islam 1999; Jiang and Islam 2001; Moran et al. 1994; Stisen et al. 2008; Tang, Li, and Tang 2010; Wang, Li, and Cribb 2006; Zhang et al. 2005); and (4) Penman–Monteith or Priestley–Taylor methods (Cleugh et al. 2007; Fisher, Tu, and Baldocchi 2008; Leuning et al. 2008; Mu et al. 2007a; Yuan et al. 2010; Zhang et al. 2010).

The empirical methods relate ET to vegetation parameters and key environmental control factors. These methods are naturally empirical, but their applications in other areas are limited because these methods do not provide an explicit formula to follow (Lu and Zhuang 2010). Some methods have proposed a universal empirical method that is suitable for different land cover (Wang and Liang 2008; Wang et al. 2010). However, experiments show that the composition of tree species strongly influence ET. Land cover dependent coefficients may be a better choice than a universal formulation (Wang and Dickinson 2012).

For the residual method, surface temperature (T_s), air temperature (T_a), and aerodynamic resistance (r_a) are first critically used to calculate sensible heat flux. Land surface temperature retrieved from thermal infrared data is strongly affected by clouds, resulting in discontinuous valid data with an error of about 1 K (Wan et al. 2002). Air temperature may have an unacceptable error depending on the elevation and number of distributed stations, if the ground-station measured values are interpolated spatially (Hamann and Wang 2005; Stahl et al. 2006). The difference between aerodynamic temperature and surface temperature results in the introduction of KB-1, which is a function of the structural characteristics of the vegetation, level of water stress, and climatic conditions (Lhomme et al. 1997), and is difficult to estimate precisely, especially on a regional or global scale. In addition, remote sensing can only directly capture instantaneous information, which may not meet the requirements of all applications (Li et al. 2009). The residual method may not be suitable for the estimation of period-averaged ET because of the difficulties in using 8- or 16-day composites of once-daily measurements of radiative surface temperature (Cleugh et al. 2007).

Although triangle/trapezoid methods are simple, and require only T_s and the vegetation index, they have the following potential limitations: (1) determination of the dry and wet edges requires a certain degree of subjectivity; (2) a large number of pixels over a flat area with a wide range of soil wetness and fractional vegetation cover (F_v) are required to ensure that dry and wet limits exist in the triangle/trapezoid space (Sun et al. 2012). Zhang et al. (2005, 2008) determined the true dry edge based on an energy balance equation to overcome the limitations mentioned above. However, the estimated ET is still an instantaneous value.

The main challenge in the practical application of the Penman–Monteith or Priestley–Taylor equation is to determinate the surface resistance, which is related to LAI, soil moisture status, leaf physiological attributes, and soil attributes. Based on some definitions and assumptions, Kelliher et al. (1995) derived an expression for surface resistance that considered the effects of soil and canopy. Leuning et al. (2008) introduced a factor in the surface resistance model that indicates the ratio of the actual ET to the potential ET. Cleugh et al. (2007) adopted the Penman–Monteith equation to estimate the 16-day ET based on a canopy resistance sub-model driven by MODIS-derived vegetation data and daily surface meteorological inputs including incoming solar radiation, surface air temperature, and vapor pressure deficit (VPD). Mu et al. (2007a) further modified the model developed by Cleugh et al. to estimate the global ET, and its partitioning into soil evaporation and vegetation transpiration. In their soil evaporation sub-model, soil resistance is controlled by air relative humidity, assuming that it reflects soil moisture status (Fisher, Tu, and Baldocchi 2008). Based on the model described by Mu et al. (2007a), Zhang et al. (2010) developed a model to estimate ET using remotely sensed NDVI data. Yuan et al. (2010) modified Mu et al.'s (2007a) model by adding the constraint of air temperature to stomatal conductance and calculating the vegetation cover fraction using LAI instead of EVI. Vinukollu et al. (2011) pointed out that Mu et al.'s (2007a) model underestimated ET for grassland, cropland, and woody savanna. Mu et al. (2011) improved Mu et al.'s (2007a) model by adding a nighttime ET component and wet soil surface component to enhance the ET estimates.

Soil resistance is largely controlled by soil moisture. However, directly monitoring large-scale soil moisture is always a challenge for remote sensing. Passive microwave sensors, such as TRMM and AMSR-E, have 1–1.5 passes per day but a coarse spatial resolution (25 km) that can only be used to estimate global or large-area soil moisture. Conversely, active microwave sensors (SAR: Synthetic Aperture Radar) have higher spatial resolution (10–30 m), but low repeat intervals (once in 16–25 days). Optical–thermal infrared sensors, such as MODIS and AVHRR/NOAA, have moderate resolution (250 m to 1 km) and one or two overpasses per day, which is suitable for regional- or large-scale applications. In addition, the triangle/trapezoid method formed by land surface temperature and vegetation index data is considered as a simple and suitable method to monitor soil moisture, and has been applied by many researchers (Gao et al. 2011; Mallick, Bhattacharya, and Patel 2009; Sandholt, Rasmussen, and Andersen 2002; Wang et al. 2004). However, this method has the same disadvantages as the triangle ET method. To reduce the uncertainties associated with the determination of the dry edge, Zhang et al. (2008) developed the theoretical dry edge based on the energy balance equation. Then, Sun et al. (2012) showed that the theoretical dry edge could monitor soil moisture better than the traditional dry edge, which is fitted by scatterplots.

Mu et al. (2007b) have pointed out that the use of VPD alone is not enough to indicate the effects of the environmental water stress on plant growth for the arid and semiarid areas. For the similar reason, the VPD alone should not be enough to represent the water stress on ET especially in the arid and semiarid regions. In this study, we incorporated a soil moisture index (SMI), extracted from T_s–F_v space, into the Penman–Monteith equation to estimate ET over semiarid areas, which is abbreviated as the PM-SMI method. We then compared this method with those developed by Mu et al. (2007a), Mu et al. (2011), and Yuan et al. (2010), which are abbreviated as PM-Mu2007, PM-Yuan, and PM-Mu2011 below, in which soil evaporation is controlled by relative humidity.

2. ET algorithms

Soil evaporation in PM-Mu2007, PM-Mu2011, and PM-Yuan is limited by relative humidity, assuming that VPD (saturation vapor pressure deficit) can be used as an indicator of environmental water stress (Fisher, Tu, and Baldocchi 2008; Granger and Gray 1989). The PM-SMI algorithm is revised from PM-Mu2007, and we used SMI instead of the relative humidity, as soil moisture control.

2.1. PM-Mu2007 algorithm

Net radiation (R_n) is linearly partitioned between the canopy and the soil surface using F_v,

(1)

where R_nc and R_ns are the total net incoming radiation (R_n) partitioned to the canopy and soil, respectively. F_v is estimated as follows:

(2)

where NDVI_min and NDVI_max are the signals from bare soil and dense green vegetation, which are set as seasonally and geographically invariant constants of 0.05 and 0.95, respectively (Zhang et al. 2009). The total latent heat flux is the sum of vegetation transpiration and soil evaporation:

(3)

where λE is the latent heat flux, λE_c is the vegetation transpiration (W/m²), and λE_s is the soil evaporation (W/m²). Finally, ET (mm) is calculated as:

(4)

where λ (2.43×10⁶ J/kg) is the latent heat of vaporization.

2.1.1. Vegetation transpiration

Vegetation transpiration is calculated as:

(5)

where Δ (Pa/K) is the slope of the curve relating saturated water vapor pressure to temperature, ρ(kg/m³) is the air density, C_p (J/kg/K) is the specific heat capacity of air, γ (Pa/K) is the psychrometric constant, VPD (Pa) is the saturation vapor pressure deficit (VPD=e_sat – e₀, where e_sat is the saturation vapor pressure, e₀ is the actual vapor pressure), r_a (s/m) is the aerodynamic resistance, and r_c (s/m) is the canopy resistance, which is the reciprocal of canopy conductance g_c (g_c=1/r_c). LAI is used as a scalar to convert the stomatal conductance (g_s) calculated at the leaf level to a canopy conductance, and g_s is estimated as described by Mu et al. (2007a), assuming that it is mainly affected by VPD and air temperature:

(6)

where m(T_min) is a temperature stress factor, m(VPD) is a water/moisture stress factor, C_L is the mean potential stomatal conductance per unit leaf area, and m(VPD) and m(T_min) are calculated as Mu et al. (2007a):

(7)

(8)

where VPD_open and T_{min_open} are the biome-specific critical value of VPD and minimum air temperature (T_min) at which the canopy stomata are completely open, respectively; VPD_close and T_{min_close} are the biome-specific critical value of VPD and T_min at which canopy stomata are completely closed, respectively. The values of C_L, VPD_open, VPD_close, T_{min_open}, and T_{min_close} are listed in a Biome Properties Look-Up Table (Mu et al. 2007a). Aerodynamic resistance is calculated as follows:

(9)

(10)

where r_r (s/m) is the resistance to radiative heat transfer and r_h (s/m) is the resistance to convective heat transfer and assumed to be equal to the boundary layer resistance (Thornton 1998), which is set as 107 s/m (Mu et al. 2007a).

2.1.2. Soil evaporation

Relative humidity is used as a constraint for potential soil evaporation to calculate actual soil evaporation:

(11)

The total aerodynamic resistance to vapor transport (r_tot) is the sum of surface resistance (r_s) and the aerodynamic resistance, which is the same value as r_h (107 m/s) (Mu et al. 2007a; Thornton 1998).

2.2. PM-SMI algorithm

In the PM-SMI algorithm, vegetation transpiration is calculated the same way as PM-Mu2007. Soil evaporation is estimated by incorporating soil moisture control as follows:

(12)

where G is the soil heat flux and r_s (s/m) is the soil resistance, which is estimated from the surface soil water content (assumed to be representative of the 0–5 cm layer) with an exponential equation (Kustas, Zhan, and Schmugge 1998; Sellers, Heiser, and Hall 1992),

(13)

where W is the actual surface soil water content, W_s is the water content at saturation, which is a function of the soil texture, a and b are the experimentally derived parameters, adopted as 8.4 and 5.9, respectively, here (Kustas, Zhan, and Schmugge 1998). In addition, W/W_s could also be substituted by a relative soil moisture index (SMI) in Equation (13), expressed as Equation (14):

(14)

T_s–F_v triangle is adopted widely to estimate soil moisture. However, the dry edge observed in the remote sensing data is characterized by lower temperatures compared with the theoretical dry edge, and thus, the observed dry edge determined by scatter plots is usually lower than the theoretical dry edge (Stisen et al. 2008). In this study, SMI is calculated from an improved T_s–F_v triangle space (Sun et al. 2012), in which the dry edge is determined by the energy balance equation. Sun et al. (2012) demonstrated that the new dry edge set a standard for different days and that the drought index calculated from the improved T_s–F_v space could monitor soil moisture conditions better than the traditional T_s–F_v space could. The details could be found in Appendix 1. Soil heat flux (G) is calculated as:

(15)

where k is the ratio between G and R_n for bare soil. Halliwell and Rouse (1987) reported a daily k value of 0.16– 0.18 at Churchill, Manitoba, while Rouse (1984) found a daily k value of 0.16– 0.24 in Hudson Bay. Therefore, we set the daily k value as 0.18 (Jacobsen 1999).

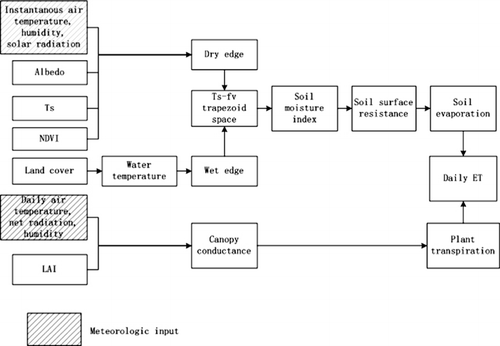
Figure 1 shows the logic behind the PM-SMI ET algorithm for estimating daily ET.

Figure 1. Flowchart of the PM-SMI ET algorithm for calculating daily ET.

2.3. PM-Mu2011 algorithm

Mu et al. (2011) added two items to improve ET estimation, evaporation from the wet canopy surface (λE_wet) and nighttime ET. The total λE is expressed as:

(16)

The estimation of r_c, r_a, and r_tot are also revised. The details are provided in Mu et al. (2011).

2.4. PM-Yuan algorithm

PM-Yuan adopted the same equations as PM-Mu2007, except for m(T_min), which follows the equation detailed by Fisher, Tu, and Baldocchi (2008):

(17)

where T_opt (°C) is the optimum air temperature for photosynthesis, which is set as 25°C (Yuan et al. 2010). In this algorithm, biome property parameters such as C_L, VPD_open, VPD_close, and T_opt are invariant across the various land cover types.

3. Data

To compare the performance of ET algorithms applied to different vegetation cover conditions, we used two data-sets. One data-set included seven sites in the Southern Great Plain (SGP) collected from 2004. The SGP is located in the middle of the USA, and primarily covered by grassland and cropland with low vegetation cover. The other data-set included three sites of the AmeriFlux network sampled in 2005. These sites are located in eastern USA, and primarily covered by forest with high vegetation cover.

3.1. SGP

The SGP site was the first field measurement site established by the Atmospheric Radiation Measurement Program. More than 30 instrument clusters have been placed around the SGP site, at the Central Facility and at Boundary, Extended, and Intermediate Facilities. The locations for the instruments were selected so that the measurements reflect conditions over the typical distribution of land uses within the site. The SGP covers most of Oklahoma and the southern part of Kansas, which is a heterogeneous land cover area characterized by mixed farming, interrupted forest, and tall and short grass. Major soil types are silt loam, loamy sand, and loam. The region produces much of the nation's grain and fiber, including more than 60% of the wheat and 36% of the cotton. Water supplied as irrigation in the region amounts to billions of cubic meters (2×10¹⁰ m³ in 1990) annually and is governed by the determination of ET in the region. An area including seven study sites (Table 1), was selected in this study, and the Energy Balance Bowen Ratio (EBBR) system was placed to obtain ET measurements.

Table 1. Location, soil type and land cover of study sites.

Site	Lat	Lon	Land cover
E7_Elk_Falls	37.383 N	96.18 W	Grass
E8_Coldwater	37.333 N	99.309 W	Grass
E9_Ashton	37.133 N	97.266 W	Grass
E13_Lamont	36.605 N	97.485 W	Crop
E15_Ringwood	36.431 N	98.284 W	Grass
E20_Meeker	35.564 N	96.988 W	Grass
E27_Earlsboro	35.269 N	96.740 W	Grass
Duke Forest Hardwoods	35.974 N	79.100 W	Mixed forest
North Carolina Loblolly Pine	35.803 N	76.668 W	Mixed forest
Walker Branch	35.959 N	84.287 W	Deciduous broad-leaf forest

EBBR produces 30-minute estimates of the vertical fluxes of sensible and latent heat at the local surface. Flux estimates are calculated from the observations of net radiation, soil surface heat flux, and the vertical gradients of temperature and relative humidity. Meteorological data collected by the EBBR are used to calculate the bulk aerodynamic fluxes, which are used in the Bulk Aerodynamic Technique EBBR value-added product to replace sunrise and sunset spikes in the flux data. A unique aspect of the system is the automatic exchange mechanism which helps to reduce errors from instrument offset drift.

λE is estimated as a function of the Bowen ratio β:

(18)

where β is estimated from the vertical gradients of temperature (ΔT_a) and specific humidity (Δe₀).

3.2. AmeriFlux sites

An area in the eastern USA including three flux towers, Duke Forest Hardwoods, North Carolina Loblolly Pine, and Walker Branch, were selected. Detailed information regarding these sites is listed in Table 1.

The ET at the AmeriFlux sites was measured by the eddy covariance (EC) method (http://public.ornl.gov/ameriflux/data-get.cfm). The eddy covariance method is accepted as the best method for direct measurement of heat fluxes and is widely used in global measurement experiments (Baldocchi et al. 2001). Unfortunately, it suffers from an energy imbalance problem, defining the energy closure ratio (ECR) as:

(19)

where λE_ec and H_ec are the original latent heat flux (λE) and sensible heat flux (H) measured by the eddy covariance method. The ECR of the three sites used in this study is listed in Table 3. Wilson et al. (2002) argued that ECR is about 0.8 for the global FluxNet measurements, which results in a substantial underestimation of λE and H. However, ECR should be equal to unity according to the energy balance law. Although several reasons are proposed to explain the energy imbalance issue, the mechanism for this imbalance remains unclear (Gao 2005; Wilson et al. 2002; Yang et al. 2004). We applied the correction method, assuming that Bowen ratio is correctly measured, proposed by Twine et al. (2000) to obtain the corrected λE measurements for validation:

(20)

3.3. Remote sensing data

Four MODIS products, including the 16-day vegetation indices at 1-km resolution (MOD13A2), daily T_s products at 1-km resolution (MOD11A1), 8-day albedo products at 1-km resolution (MCD43B3), and 8-day ET products (MOD16A2) at 1-km resolution were used. These data were acquired through the EOS data gateway (https://wist.echo.nasa.gov), except for the MOD16A2 which were downloaded from frp://ftp.ntsg.umt.edu. Two algorithms were used to retrieve T_s from the MODIS thermal and middle infrared spectral regions: the generalized split window algorithm (Wan and Dozier 1996) and the MODIS day/night land surface temperature algorithm (Wan and Li 1997). The accuracy of the MODIS T_s product is better than 1 K (Wan et al. 2002; Wan et al. 2004). The 16-day NDVI extracted from MOD13A2 was time series smoothed by the locally adjusted cubic spline capping (LACC) method (Chen, Feng, and Chen 2006), which can produce flexible and mathematically smooth capping curves and fit rapid seasonal changes, for the purpose of identifying the atmosphere-contaminated data points and their replacements through temporal interpolation. The data were then linear interpolated to give the daily value. The albedo product consists of black sky and white sky albedo. To derive the overall surface albedo, we followed the method described by Su et al. (2007) by averaging the above two estimates. The MOD16 ET data-sets were estimated using the ET algorithm described by Mu et al. (2011). The MOD16 ET algorithm uses NASA's MERRA GMAO (GEOS-5) daily meteorological reanalysis data, collection 4 MOD12Q1, collection 5 MCD43B2/B3 and MOD15A2 as input. The 8-day ET is the sum of ET during these 8-day time periods. All these products described above were converted to UTM projection using the Modis Reprojection Tool.

Two study regions were selected for this study. One is in the middle of the USA, containing seven SGP sites. The selected window size for the remote sensing image was 562×526 km, extended in longitude from 95.3°W to 99.5°W and in latitude from 34.5°N to 38.5°N, which is the spatial subset from tile H10V05 of 2004 and covered most of the SGP. Another is in eastern USA, containing three AmeriFlux sites, for which the selected window size of the remote sensing image was 884×592 km. This area extended in longitude from 75.1°W to 85.4°W and in latitude from 34.5°N to 39.8°N, which is the spatial subset from tile H11V05 of 2005.

3.4. Methodology

In this study, although SMI distribution could be estimated based on T_s–F_v space, we use in situ meteorological data such as T_a, RH, and R_n. Therefore, only in situ ET is estimated using measured meteorological data and 3×3 1-km pixels of remote sensing data surrounding each site. Below is the description of each step.

1. Deriving the dry edge using instantaneous value of air temperature, vapor pressure (e₀), solar radiation (S₀), T_s, albedo, and NDVI;

2. Calculating the SMI distribution based on the improved T_s–F_v space and extracting 3×3 pixels value of SMI, NDVI, and LAI images surrounding each study site;

3. Estimating daily ET using in situ daily value of air temperature, relative humidity (RH), R_n, and each pixel value of SMI, NDVI, and LAI;

4. The PM-SMI ET average over the 3×3 pixels was validated with tower ET observations;

5. Compared to the other three ET algorithms with the same input measurement data.

4. Results and discussion

Table 2 shows the mean NDVI, mean LAI, max NDVI, max LAI, and mean soil water content for each site. The vegetation cover is low for SGP sites, which were covered by grassland and cropland. There is a mix of good density improved pasture in site E7; therefore, the value of NDVI and LAI in this site is relatively high (max NDVI=0.75, max LAI=3.1). The vegetation cover is high for the three forest sites. The soil type of E8 and E15 is sandy; therefore, the mean soil water content is lower than 0.15 m³/m³.

Table 2. The mean NDVI, mean LAI, max NDVI, max LAI and mean soil water content for each site. The mean and max values of NDVI and LAI were obtained from the MODIS NDVI and LAI products. The mean soil water content was obtained from surface soil moisture measurements taken at 5 cm. The data from SGP sites was collected from 2004 and the data from AmeriFlux sites was collected from 2005.

Site	Mean NDVI	Mean LAI	Max NDVI	Max LAI	Mean soil water content (m^3/m^3)
E7	0.54	1.4	0.75	3.1	0.37
E8	0.45	0.8	0.52	1.5	0.14
E9	0.49	0.6	0.62	1.1	0.32
E13	0.53	0.9	0.67	2.1	0.32
E15	0.48	0.64	0.60	1.0	0.11
E20	0.55	1.2	0.73	2.6	0.32
E27	0.56	1.1	0.74	2.3	0.18
Duke FH	0.67	2.42	0.85	5.9	0.33
North CLP	0.63	2.27	0.86	6.3	0.33
Walker B	0.68	2.44	0.88	6	0.2

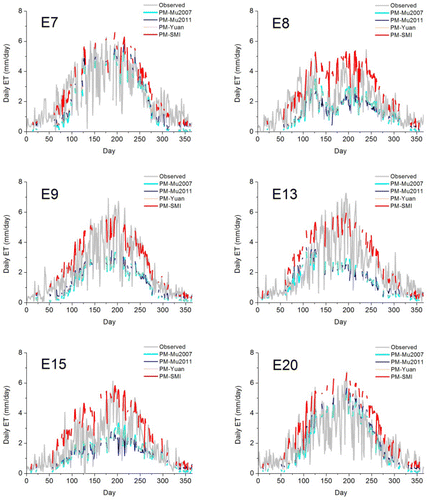
Since T_s is affected by clouds, the results of the PM-SMI algorithm were only available for less than half of the year. As shown in Table 3, the PM-SMI algorithm significantly enhanced the ET estimates for all of the SGP sites, which were covered by grassland and cropland, while the other three ET algorithms had relatively large errors. For example, at site E9, the root mean square error (RMSE) of PM-Mu2007, PM-Mu2011, PM-Yuan, and PM-SMI is 1.69, 1.64, 1.67, and 0.39 mm, respectively, while the bias is –1.49, –1.34, –1.45, and –0.03 mm, respectively, and the R² is 0.94, 0.87, 0.95, and 0.95, respectively. Although the R² values of the PM-SMI ET estimates are close to those of the PM-Mu2007 and PM-Yuan ET estimates, the RMSE and bias were greatly reduced, indicating that PM-SMI ET estimates capture the magnitude of ET measurements better than the other three algorithms. For all the seven SGP sites, the RMSE and bias of PM-Mu2011 (1.37 mm and –0.93 mm) are lower than that of PM-Mu2007 (1.4 mm and –1.06 mm). However, the R² of PM-Mu2011 (0.64) is lower than the PM-Mu2007 (0.69). The RMSE, bias, and R² of PM-Yuan fall between those of PM-2007 and PM-2011. Although PM-Mu2011 improved the ET estimates when compared with PM-Mu2007 at grasslands and croplands as reported by Mu et al. (2011), results of this study indicate that PM-Mu2011 still underestimates ET.

Table 3. Available days, root mean square error (RMSE: mm/day), absolute bias (bias: mm/day), and square of correlation coefficient (R²) of four ET algorithms for each site. (1) PM-Mu2007; (2) PM-Mu2011; (3) PM-Yuan; and (4) PM-SMI.

Site	ECR	Available days	RMSE1	RMSE2	RMSE3	RMSE4	Bias1	Bias2	Bias3	Bias4	R^21	R^22	R^23	R^24
E7	–	148	1.30	1.08	1.22	0.74	−1.01	−0.71	−0.95	−0.05	0.79	0.81	0.81	0.86
E8	–	161	1.48	1.49	1.44	1.05	−1.14	−1.20	−1.11	0.43	0.44	0.55	0.46	0.58
E9	–	162	1.69	1.64	1.67	0.39	−1.49	−1.34	−1.45	−0.03	0.94	0.87	0.95	0.95
E13	–	153	1.89	1.95	1.88	0.97	−1.35	−1.23	−1.29	0.18	0.60	0.40	0.54	0.75
E15	–	161	1.38	1.49	1.39	0.98	−1.05	−1.07	−1.04	0.57	0.73	0.69	0.74	0.76
E20	–	149	1.02	0.87	0.96	0.83	−0.76	−0.46	−0.71	0.34	0.82	0.81	0.84	0.85
E27	–	127	1.22	1.01	1.18	0.90	−0.91	−0.67	−0.85	0.26	0.83	0.86	0.84	0.81
SGP	–		1.40	1.37	1.37	0.91	−1.06	−0.93	−1.02	0.33	0.69	0.64	0.69	0.77
Duke FH	0.81	180	0.56	0.93	0.53	0.58	−0.05	−0.43	−0.02	0.09	0.93	0.84	0.93	0.91
North CLP	0.70	158	0.88	1.46	0.86	0.68	−0.67	−0.89	−0.66	−0.38	0.91	0.72	0.91	0.89
Walker B	0.64	98	1.31	0.82	1.30	1.42	0.76	0.37	0.78	0.98	0.74	0.80	0.73	0.68
Forest	–		0.99	1.20	0.97	0.96	−0.12	−0.45	−0.10	0.15	0.75	0.69	0.75	0.74
All	–		1.31	1.33	1.28	0.88	−0.82	−0.80	−0.78	0.24	0.66	0.64	0.66	0.78

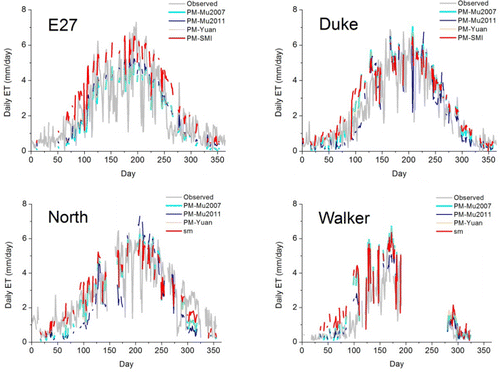
Among the forest sites, in Duke Forest Hardwoods (Mixed forest), North Carolina Loblolly Pine (Mixed forest) and Walker Branch (Deciduous Broad-leaf forest), there were no large differences among ET estimates of PM-Mu2007, PM-Yuan, and PM-SMI. Although PM-Mu2011 showed the lowest RMSE and bias and the highest R² in Walker Branch, PM-Mu2011 showed the lowest correlation and highest RMSE and bias across all the three forest sites.

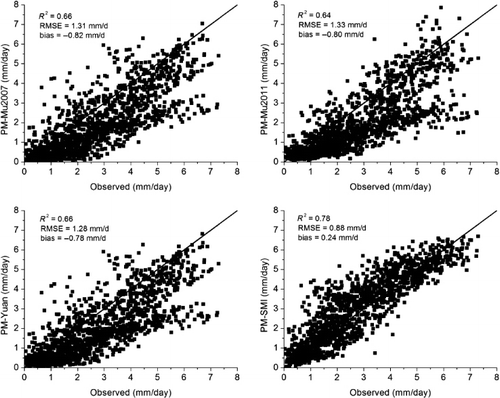
Across all 10 sites, the PM-SMI algorithm also had the best performance, with an RMSE of 0.88 mm, bias of 0.24 mm and R² of 0.78. PM-Yuan ET estimates had a slightly lower RMSE and bias (1.28 mm, –0.78 mm), and higher R² (0.66) than PM-Mu2007 (1.31 mm, –0.82 mm and 0.66) and PM-Mu2011 (1.33 mm, –0.8 mm and 0.64). PM-Mu2011 had a lower bias than PM-Mu2007, but the RMSE was higher and the R² was lower. Mu et al. (2011) also indicated that PM-Mu2011 had a reduced bias relative to PM-Mu2007, although it had a slightly increased RMSE and decreased R².

Figure 2 shows the scatterplots between the observed and the estimated ET with four algorithms. PM-Mu2007, PM-Mu2011, and PM-Yuan significantly underestimate ET and PM-SMI performs the best among the four ET algorithms. Figure 3 shows comparisons of the ET measurements and the ET estimates with four algorithms. The PM-SMI ET estimates match well across the annual variation for all SGP sites. PM-Mu2007, PM-Mu2011, and PM-Yuan algorithms obviously underestimated ET across SGP sites, where soil evaporation plays a dominant role. However, for E7, E20, and E27, which have relatively good vegetation condition (Table 2), these three algorithms' ET estimates are closer to the ET measurements, with a lower bias (Table 3). No significant difference was observed among the four algorithms' ET estimates for the three forest sites during the growing season. However, the PM-SMI ET estimates are closer to the ET measurements in the non-growing season when compared with the other three algorithms.

Figure 2. Scatterplots between observed ET and estimated ET.

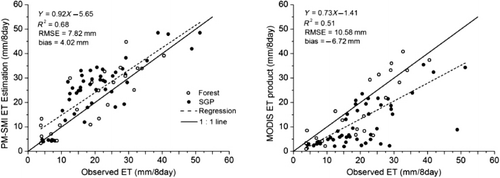
Figure 3. The ET measurements (gray line) and ET estimates with PM-Mu2007 (cyan line), PM-Mu2011 (blue line), PM-Yuan (yellow line), and PM-SMI algorithms (red line) for 10 sites.

Figure 4 shows comparisons of the 8-day ET measurements with the PM-SMI 8-day ET estimates and MODIS 8-day ET product. For the PM-SMI ET estimates, it was difficult to obtain continuous daily ET owing to the lack of continuous T_s. Therefore, the valid PM-SMI 8-day ET was combined for every 8-day period, during which there are more than six valid daily ET values. The MODIS 8-day ET was extracted directly from the MOD16A2 product. As shown in Figure 4, the MODIS 8-day ET was significantly lower than the ET measurements for the SGP sites, with R², RMSE, and bias values of 0.51, 10.58 mm, and –6.72 mm, respectively. In contrast, most of the PM-SMI 8-day ET estimates were around the 1:1 line. However, the PM-SMI 8-day ET estimates were slightly larger than the ET measurements, with a bias of 4.02 mm. The PM-SMI daily ET was estimated based on clear day conditions with no clouds, resulting in larger ET values when compared to those obtained for cloudy days. Therefore, it is reasonable that the PM-SMI 8-day ET estimates combined from the cloudless daily ET were slightly larger than the measurements. The R² and RMSE of the PM-SMI 8-day ET estimates were 0.68 and 7.82 mm, respectively.

Figure 4. Comparisons of 8-day ET measurements to PM-SMI 8-day ET estimates and the MODIS 8-day ET product.

However, relatively large differences between PM-SMI ET estimates and ET measurements still exist for a few sites, including E8, E13, E15, and Walker Branch. These discrepancies may be explained by the following:

1. Estimation error of soil heat flux. Surface available energy used in the Penman–Monteith equation is estimated from net radiation minus soil heat flux. However, soil heat flux, which is correlated with soil properties, soil moisture, and vegetation condition, has high spatial variability. The ratio between G and R_n over bare soil ranges from 0.20 to 0.50 depending on the soil moisture (Idso, Aase, and Jackson 1975), and from 0.05 to 0.30 depending on the vegetation cover (Clothier et al. 1986; Kustas and Daughtry 1990). Therefore, it is a challenge to estimate soil heat flux. In our study, relative bias of G ranged from –30% to 30%, which may result in some uncertainties associated with the ET estimates.

2. Algorithm limitations. Biophysical parameters (C_L, VPD_close, and VPD_open) used in this study are the same as those used in the PM-Mu 2011 algorithm. However, Mu et al. (2007a), Mu et al. (2011), Yuan et al. (2010), and Zhang et al. (2010), all have recalibrated the biophysical parameters of Penman–Monteith ET algorithms based on their studies. The parameters such as a and b, which are used to compute soil resistance (r_s) from SMI, are also the same as those used by Kustas, Zhan, and Schmugge (1998). However, these values are a function of soil texture, which is heterogeneous in our study region, and consists of silt loam, sandy loam, clay loam, and loamy sand. Unfortunately, ground measurement sites for different biome types or soil textures are not sufficient for analysis. Therefore, it is not possible to refit these parameters.

3. SMI. The SMI incorporated in the PM-SMI algorithm is estimated based on improved T_s–F_v trapezoid space (Sun et al. 2012). The assumption of monitoring soil moisture based on T_s–F_v space is that meteorological parameters and land surface attributes are homogeneous (Friedl and Davis 1994; Lambin and Ehrlich 1995; Zhang et al. 2008). However, Sun et al. (2012) showed that sites with sandy soil, such as E8 and E15, could result in an evident difference in heat property and relationships between T_s and soil moisture when compared to other soil types, which was likely a major cause of large errors at E8 and E15.

4. Inaccuracy of ET measurements. Surface energy flux data from the SGP sites measured by Bowen ratio do not have energy balance non-closure problem. However, data from three forest sites, measured by the eddy covariance flux towers, have lack of energy balance closure. Although latent heat flux was corrected using the method of Twine et al. (2000), correcting error and reducing uncertainty in the ET measurements is still uncertain due to the closure error (Shuttleworth 2007). The large errors at the Walker Branch site may result from a low energy balance ratio, which is about 50% on most days.

5. Validation. We found that some research used one pixel containing the study site to validate (Yuan et al., 2010), some research used 3×3 pixels to validate (Mu et al. 2007a), and some research used footprint model to validate (Jia et al. 2012). To reduce the effect of heterogeneity of land surface, we used 3×3 pixels surrounding the study sites to validate the results. Actually, this is a simplified method while the area of these pixels could mostly represent the source area of flux measurements. The source area is always varying with the observation height, wind velocity and direction, atmospheric stability, and the roughness length of land surface. For the EC and EBBR measurements, which used in this study, the source area of them might either located in only one MODIS pixel or covered some parts of two to four pixels, with different relative contribution within the source area.

5. Conclusions

Penman–Monteith equation is a classical method used to calculate ET. However, surface resistance, which is related to soil moisture, is always difficult to obtain. In this study, we developed an ET algorithm by incorporating the SMI derived from an improved T_s–F_v space. The PM-Mu2007algorithm has been successfully applied on the global scale (Mu et al. 2007a; Mu et al. 2009), and was recently adjusted by Yuan et al. (2010) and Zhang et al. (2009). Mu et al. (2011) pointed out that PM-Mu2007 underestimates ET for cropland, grassland, and woody savanna, which was also confirmed by other studies (Vinukollu et al. 2011). Mu et al. (2011) improved this ET algorithm and enhanced the ET estimates most for woody savannas, grasslands, and croplands. Soil evaporation in these ET algorithms was controlled by VPD. However, the VPD alone is not enough to represent the water stress on ET especially in the arid and semiarid regions (Mu et al. 2007b). Generally in the arid and semiarid areas, the vegetation cover fraction is low, the plant transpiration is low as well, and hence the soil evaporation is the largest part of the ET components.

In this study, we tried to improve Mu et al.'s 2007 ET algorithm by incorporating the SMI to account for the soil moisture constraint on soil evaporation to develop the PM-SMI ET algorithm. ET estimates derived from PM-SMI algorithm were compared with PM-Mu2007, PM-Mu2011, and PM-Yuan algorithm and validated by seven SGP sites that were covered by cropland and grassland with low vegetation cover, as well as three AmeriFlux sites covered by forest with high vegetation cover. The results showed that the PM-SMI algorithm significantly improved daily ET estimates at SGP sites with an RMSE of 0.91 mm, bias of 0.33 mm, and R² of 0.77. PM-Mu2011 reduced the RMSE and bias of ET estimates when compared with PM-Mu2007, but still underestimated ET. For the three forest sites, no large difference was observed among the ET estimates produced by these four algorithms during the growing season. However, the PM-SMI ET estimates are closer to the ET measurements in the non-growing season when compared with the other three algorithms. For all 10 validation sites, PM-SMI also had the best performance, followed by PM-Yuan.

PM-SMI 8-day ET estimates were also compared with MODIS 8-day ET product (MOD16A2). MODIS 8-day ET was significantly lower than the ET measurements for the SGP sites, with R², RMSE, and bias values of 0.51, 10.58 mm, and –6.72 mm, respectively. In contrast, most PM-SMI 8-day ET estimates were around the 1:1 line, with R ², RMSE, and bias values of 0.68, 7.82 mm, and 4.02 mm, respectively.

ET distribution is necessary in many applications, and the method proposed in this manuscript would be a meaningful attempt to get the ET maps. Unfortunately, the input meteorological data, such as net radiation (R_n) was only collected from study sites. We could not get a good product of R_n distribution of the study area. We will try to make some analysis about the ET distribution in the future. The application of PM-SMI is limited by land surface temperature, which is used to obtain the SMI, since surface temperature is largely affected by clouds and it is difficult to capture consistent and valid data. Passive microwave sensors, such as AMSR-E, which have all-weather surface sensing capability, have been used to retrieve soil water content (Bindlish et al. 2003; Njoku et al. 2003). However, the application of this technique is limited by its coarse spatial resolution (25 km). In the future, we plan to downscale the soil moisture product derived from AMSR-E to fine scales matching MODIS 1 km resolution.

Acknowledgements

This work was funded by the High-Tech Research and Development Program of China (No. 2009AA122100) and the National Science and Technology Ministry (2012BAH29B02). We thank Dr Tongren Xu for providing the measurement data. SGP data of the Atmospheric Radiation Measurement (ARM) Project of the US Department of Energy is downloaded from http://www.arm.gov/. Eddy covariance flux tower sites are part of the AmeriFlux. We gratefully acknowledge the efforts of researchers at these sites. Research at the Duke Forest Hardwoods, North Carolina Loblolly Pine and Walker Branch sites was led by Ram Oren, Asko Noormets and Tilden Meyers.

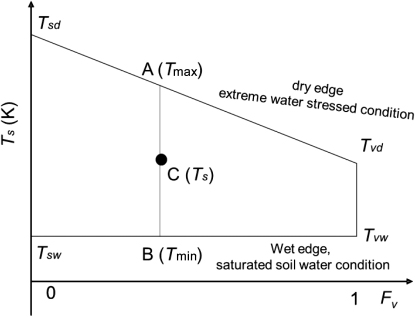
Appendix A: Calculation of relative soil moisture based on T_s−F_v space.

Relative soil moisture index (SMI) is calculated as Equation (A1) and determined from T_s−F_v space as shown in Figure A1. In this T_s−F_v space, the dry edge is determined based on the energy balance equation (Zhang et al. 2008). Sun et al. (2012) showed that the new dry edge could monitor soil moisture better than the traditional dry edge, which is fitted by scatterplots.

(A1)

The dry edge was determined from energy balance formula:

(A2)

For the extreme dry condition, there is no LE, so Equation (A2) could be expressed as:

(A3)

The sensible heat flux H is estimated as:

(A4)

Net radiation R_n can be expressed as:

(A5)

where S₀ is the solar radiation reaching the earth's surface, α is albedo, σ is Stefan–Boltzmann constant,. ε_a is the atmospheric emissivity under clear skies, calculated as follows (Brutsaert 1975):

(A6)

ε_s is the emissivity of land surface, estimated by (Zhang et al. 2008):

(A7)

where ε_v and ε_ss are emissivity for vegetation (0.97) and soil (0.95), respectively. Instantaneous G at midday can be calculated as follows (Su 2002):

(A8)

where Γ_v and Γ_s are the ratios between G and R_n for bare soil and fully covered vegetation surface, respectively. The value of Γ_s is taken as 0.315 (Kustas and Daughtry 1990), while 0.05 for Γ_v (Monteith 1973). For dry bare soil, the vegetation cover F_v=0, taking Equations (A4), (A5), and (A8) into Equation (A3), surface temperature is derived as follows:

(A9)

where the subscript sd denotes dry bare soil. For full-cover vegetation with no available water, the vegetation cover F_v=1, taking Equations (A4), (A5), and (A8) into Equation (A3), surface temperature is given by:

(A10)

where the subscript vd denotes true dry full cover vegetation. T_sd or T_vd can be iteratively computed if the α_sd, α_vd, T_sda, T_vda, r_sda, r_vda, e₀, and S₀ are acquired.

Figure A1. T_s−F_v trapezoid space. The upper solid line is the dry edge, estimated from the energy balance formula, representing extreme water stressed conditions. The lower solid line is the wet edge, representing saturated soil water conditions.

We adopt an empirical method proposed by Zaksek and Schroedter-Homscheidt (2009) to estimate instantaneous T_a:

where z_v is the solar zenith angle, a_v is the solar azimuth angle, α is the albedo, s_a is the solar incidence angle, s is the slope, and Δh is the difference between the station elevation and the mean elevation within a 20 km vicinity. Assuming that the theoretically driest atmospheric conditions is close to the observed driest conditions, the pixel with the greatest air temperature around the upper-left corner in the trapezoid represents the driest bare soil, and the pixel with the greatest air temperature around the upper-right corner in the trapezoid represents the driest full-cover vegetation. The temperatures of these two pixels are represented as T_sda and T_vda.

For α_sd and α_vd, we select the maximum albedo from the bare soil and full cover vegetation, corresponding to soil and vegetation dry conditions, respectively.

Assuming that there is not much variation for S₀ on a regional scale (Mueller et al. 2004) for a clear sky, the averaged value of measured S₀ is adopted as the input. The location of the theoretical dry edge is not sensitive to e_a (Sun et al. 2012); thus, the averaged value of e_a is also adopted as the input.