ABSTRACT
While impressive direct geolocation accuracies better than 5.0 m CE90 (90% of circular error) can be achieved from the last DigitalGlobe’s Very High Resolution (VHR) satellites (i.e. GeoEye-1 and WorldView-1/2/3/4), it is insufficient for many precise geodetic applications. For these sensors, the best horizontal geopositioning accuracies (around 0.55 m CE90) can be attained by using third-order 3D rational functions with vendor’s rational polynomial coefficients data refined by a zero-order polynomial adjustment obtained from a small number of very accurate ground control points (GCPs). However, these high-quality GCPs are not always available. In this work, two different approaches for improving the initial direct geolocation accuracy of VHR satellite imagery are proposed. Both of them are based on the extraction of three-dimensional GCPs from freely available ancillary data at global coverage such as multi-temporal information of Google Earth and the Shuttle Radar Topography Mission 30 m digital elevation model. The application of these approaches on WorldView-2 and GeoEye-1 stereo pairs over two different study sites proved to improve the horizontal direct geolocation accuracy values around of 75%.
1. Introduction
Orthorectification of Very High Resolution (VHR) satellite imagery plays a crucial role in remote sensing applications such as mapping, land use/land cover classification, segmentation or just for adding georeferenced image data into Geographic Information Systems. In this way, users can produce their own highly accurate orthorectified images by using commercial off-the-shelf software and ancillary data such as digital elevation model (DEM) and ground control points (GCPs) through raw VHR optical satellite imagery (Toutin Citation2004; Fraser and Hanley Citation2005; Aguilar et al. Citation2008a; Åstrand et al. Citation2012; Aguilar, Saldaña, and Aguilar Citation2013). In the best conditions, geopositioning accuracies in terms of planimetric root mean square error (RMSE2D) to around 0.7 pixels are readily achievable at sensor orientation phase (i.e. excluding terrain effects) by using refined rational polynomial coefficients (RPCs) from a few highly accurate GCPs (Fraser and Ravanbakhsh Citation2009; Aguilar, Saldaña, and Aguilar Citation2013). Considering VHR satellite images with Ground Sample Distance (GSD) ranging from 0.4 m to 0.6 m GSD, the aforementioned 0.7 pixels would correspond to CE90 values between 0.42 m and 0.64 m.
The new breed of DigitalGlobe’s VHR satellites (i.e. GeoEye-1 (Geo1) and WorldView-1/2/3/4) are capable of capturing panchromatic imagery of the land surface with GSD even lower than 0.5 m and, more surprising, with an impressive horizontal geolocation accuracy without GCPs (direct sensor orientation excluding terrain effects) better than 5.0 m CE90 (DigitalGlobe Citation2014). In fact, an important improvement in direct sensor orientation has been reported for the new DigitalGlobe’s sensors. For instance, 19 m CE90 was achieved on 411 mono QuickBird images (Mulawa Citation2014), while much more accurate CE90 values of 4.5, 4.6, 3.6 and 4.4 m were attained involving 719 WorldView-1 single images, 718 WorldView-2 (WV2) images, 1796 WorldView-3 and 129 Geo1 images, respectively (Mulawa and Comp Citation2014). In the case of stereo pairs, the vertical accuracy specification for WorldView1/2/3/4 products (excluding terrain effects) turns out to be 5.0 m LE90 (90% of linear error) (DigitalGlobe Citation2014).
However, these impressive horizontal geolocation accuracies without GCPs are insufficient for many precise geodetic applications. In that sense, Google Earth (GE), the most popular virtual globe, is able to provide georeferenced images which can be potentially used as a source of GCPs anywhere in the world. For example, Chen and Chaapel (Citation2010) used GCPs extracted from GE to perform geometric corrections of WV2 pan-sharpened images. In the same way, Yousefzadeh and Mojaradi (Citation2012) applied GE-extracted GCPs to carry out the orthorectification procedure for IRS-p6 (RESOURCESAT-1) sensors with three different resolutions (5.8, 23.5 and 56 m for Liss-4, Liss-3 and AWiFs respectively). Frankl et al. (Citation2015) processed vertical and low oblique aerial photographs to obtain an ortho-mosaic by using 15 GCPs derived from GE. However, GE states that positional data provided are only approximations and, therefore, their accuracy is not officially documented. Because of that a few studies have been conducted to determine the positional accuracy of GE. Potere (Citation2008) reported a positional accuracy of 39.7 m RMSE2D from collecting Independent Check Points (ICPs) extracted from the Landsat GeoCover at a global scale. Yousefzadeh and Mojaradi (Citation2012) estimated a horizontal accuracy of 6.1 m RMSE2D by using ICPs extracted from 1:2000 scale maps of three towns in Iran. Benker, Langford, and Pavlis (Citation2011) calculated a positional accuracy of 2.64 m RMSE2D for the GE terrain model of the Big Bend region, Texas, USA. Paredes-Hernandez et al. (Citation2013) reported an accuracy of 5.0 m RMSE2D based on 466 ICPs extracted from a cadastral database located over a rural area in Tamaulipas, Mexico. Pulighe, Baiocchi, and Lupia (Citation2016) addressed the most recent assessment of the GE images horizontal accuracy over Rome (Italy) for the years 2007, 2011 and 2013, taking as reference 41 accurate Differential Global Positioning System (DGPS) points and 57 cadastral points. They reported accuracies ranging from 0.45 to 1.51 m RMSE2D. In a nutshell, GE positional accuracy is very variable depending on the site, the imagery source and the time of capture.
This work aims to improve the direct sensor orientation accuracy of DigitalGlobe’s VHR satellite imagery by using three-dimensional GCPs extracted from freely available ancillary data at global coverage such as multi-temporal information of GE (coordinates X and Y) and the Shuttle Radar Topography Mission (SRTM) 30 m DEM (coordinate Z). In this way, two different approaches for selecting freely available GCPs from GE are proposed. The positional accuracies are compared at sensor orientation and orthorectification phases through both accurate DGPS- and GE-derived GCPs. Although the proposed approaches were applied on two VHR satellite stereo pairs from WV2 and Geo1, they could be also used for single images.
2. Material and methods
2.1. Study sites
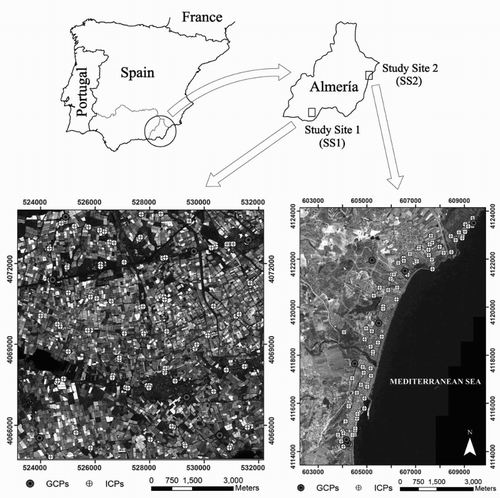
The two study areas () are located in the province of Almería (Southern Spain). The first one, Study Site 1 (SS1), comprises a rectangle area of about 8000 ha centred on the geographic coordinates 36.7824°N and 2.6867°W with reference to the World Geodetic System 1984 (WGS84). It is just at the core of the greatest concentration of greenhouses in the world, the so-called ‘Sea of Plastic’. The second study site (SS2) is centred on the WGS84 geographic coordinates 37.2109°N and 1.8027°W, comprising a coastal fringe of around 11 km long and 775 m wide. Both study areas present a smooth relief.
2.2. Datasets
2.2.1. WV2 stereo pair
A panchromatic (PAN) along track stereo pair from WV2 was acquired on 5 July 2015 () covering the study site SS1. It was collected in Ortho Ready Standard Level-2A (ORS2A) format, presenting both radiometric and geometric corrections. ORS2A format is georeferenced to a cartographic projection using a surface with constant height. It also counts on the corresponding RPC sensor camera model and metadata file. The delivered products were ordered with a dynamic range of 11 bits.
Table 1. Characteristics of panchromatic images from Geo1 and WV2 stereo pairs.
2.2.2. Geo1 stereo pair
The second stereo pair was collected on 27 August 2011 () over the study site SS2. It was a PAN GeoStereo product from Geo1 with a dynamic range of 11 bits. Geo1 GeoStereo images present both radiometric and geometric corrections very similar to those applied to WV2 ORS2A imagery.
2.2.3. DGPS ground points collection
The goal was to obtain a reliable measurement at the field of an important number of ground points (GPs) with accuracy better than a decimetre. The selected GPs were always located on well-defined features over the study areas (). It is important to note that GPs represent all the available points collected at the field and, after that, they can be used as GCPs (GPs used only to compute the sensor model) or ICPs (GPs exclusively applied in the accuracy assessment). For each study area, seven homogeneously distributed GPs were selected as GCPs () whereas the remaining GPs were used as ICPs. The GPs coordinates were obtained by DGPS through a total GPS Topcon HiPer PRO station working in real-time kinematic mode (RTK). The WGS84 UTM coordinates of 127 and 120 GPs were measured over the study sites SS1 and SS2 respectively. The Earth Gravitational Model of 2008 (EGM2008) was the geoid model applied to transform ellipsoidic heights to orthometric elevations, which were used in this work.
2.2.4. Extraction of GE GPs over the study sites
Using the Historical Imagery option recently included in GE, we could extract WGS84 UTM coordinates from six different VHR images in the SS1 and SS2 study sites (). Only 80 out of the 127 RTK-measured GPs in SS1 and 60 out of the 120 in SS2 could be properly marked in at least three historical images provided by GE. Regarding the original source of each GE image, it is important to point out that the proprietor of the rights of the image appeared in the GE screen. When the image vendor at a specific date was DigitalGlobe, the DigitalGlobe ImageFinder tool was used in order to know the characteristics of that image and what sensor took it. When the image vendor was not DigitalGlobe, then the source of this VHR image had to be an aerial orthoimage.
Table 2. GPs extracted from GE using the historical imagery option for each study site.
2.2.5. GE accuracy around the world
In order to compare the accuracy of the coordinates extracted from GE in our two study sites with other areas around the world, seven evenly distributed GPs were selected in four square areas with sides of 10 km (similar to our SS1 area and the Maussane test site used by Åstrand et al. (Citation2012)) located at different countries and even continents. This comparison was carried out by means of error ellipses computed by the standard deviational ellipse method (Wong and Lee Citation2005). This approach provides information on the precision of the different GPs’ positions and, in addition, the user can make visual comparisons of the relative precisions by looking at the shape of the ellipses, their sizes and the orientation of each ellipse.
The new areas selected () were located at Agadir (Morocco), Hebei Province (China), Bari (Italy) and Sinaloa State (Mexico). These areas were centred on the following WGS84 geographic coordinates: Agadir (30.1503°N, 9.4387°W), Hebei (36.6759°N, 114.7851°E), Bari (41.0119°N, 16.9617°E) and Sinaloa (24.8532°N, 107.6523°E). All these areas present a large number of agricultural greenhouses. At this point, it is important to highlight that this work is included in the frame of a research project aimed at greenhouse detection from satellite imagery.
Figure 2. GPs selected in each square area around the world with sides of 10 km: (a) Agadir (Morocco), WV2 image taken on 2 January 2016; (b) Hebei (China), WV2 image taken on 29 December 2014; (c) Bari (Italy), Aerial Orthoimage taken on 29 August 2015; (d) Sinaloa (Mexico), Geo1 image taken on 11 December 2014.Source: Google Earth, Google©.

2.3. Methodology for sensor orientation and orthorectification
Four different strategies (detailed below) based on the type of GCPs used were conducted in this work to perform the sensor orientation and, finally, to generate the orthoimages in a similar way to the one reported by Aguilar, Saldaña, and Aguilar (Citation2013).
2.3.1. DGPS strategy
This strategy is supported by seven high-accurate, three-dimensional GCPs measured by DGPS. The sensor model was based on the well-known rational functions using vendor-supplied RPCs and compensated in image space using a zero-order transformation (RPC0) where only a simple shift along X and Y axes is computed according to the accurate reference provided by the seven GCPs. A number of GCPs ranging from 4 to 7 were recommended for attaining the best results by using the RPC0 model (Åstrand et al. Citation2012; Aguilar, Saldaña, and Aguilar Citation2013). The software used in this work was OrthoEngine 2016 (PCI Geomatics, Richmond Hill, Ontario, Canada). It is based on the block adjustment method developed by Grodecki and Dial (Citation2003). It is important to keep in mind that, for each strategy tested, the row and column coordinates in the image of each GP (GCPs or ICPs) were only marked once to promote an appropriate comparison.
The accuracy at the sensor orientation phase of each stereo pair was carried out by statistics (Mean, standard deviation (SD), RMSE, CE90 and LE90) computed at 120 and 113 ICPs for the study sites SS1 and SS2, respectively. It is worth noting that, given such a high number of ICPs, the estimated error for RMSE calculation would be below 10% (Aguilar, Aguilar, and Agüera Citation2008b).
After the sensor orientation phase, a digital surface model (DSM) was extracted for each study site using OrthoEngine 2016. The selected setting parameters were 1 m resolution, hilly terrain and filling holes with a medium smoothing filter.
The final 0.5 m GSD PAN orthoimages in each study site were generated from the most near-nadir image and using the DSM extracted from each stereo pair. A sinusoidal resampling kernel (sin(x)/x with 16 × 16 windows) (Toutin Citation2004) was applied to original image cells. Only 69 and 49 ICPs placed on the bare ground were considered for the geometric accuracy assessment at this phase for the study sites SS1 and SS2, respectively.
At this point, it is important to underline that due to the smoothness of the investigated areas covered by agricultural greenhouses, the impact of the DSM accuracy over the generated orthoimages is quite small, especially if we use nadiral VHR images. In these conditions, it would be possible to replace the elevation data from a VHR satellite stereo pair, and use a single VHR satellite image together with a global DEM such as SRTM. It is known that SRTM can supply height information at an accuracy of few (2–4) metres in these smooth areas. However this would be not certainly the case in more mountainous morphologies or even in urban areas.
2.3.2. Direct geolocation strategy
Direct georeferencing orientations were performed through OrthoEngine by only using the supplied RPCs as sensor orientation (i.e. without ancillary GCPs). The DSMs were extracted from each stereo pair and the orthoimages were attained in the same aforementioned way. Geometric accuracies were computed from the residuals attained at the same ICPs used in the DGPS strategy for sensor orientation and orthorectification phases. It is important to note that the application of the direct geolocation strategy allows to obtain the three-dimensional WGS84 UTM coordinates for any GP by marking it on both images from the stereo pair. Again, if you are working with a single VHR satellite image, you would have to use a global DEM to extract the altimetric information required.
2.3.3. GE DigitalGlobe strategy
This strategy can be used when the VHR satellite image to orthorectify has been taken by a sensor with a very good absolute and relative direct geolocation (without ancillary GCPs). That is the case of the DigitalGlobe’s Geo1 or WorldView-1/2/3/4 sensors. Both ORS2A and Geo formats present an impressive absolute direct geolocation (better than 5.0 m CE90), with systematic residual errors which can be corrected by a simple shift in X and Y directions (Fraser and Ravanbakhsh Citation2009; Åstrand et al. Citation2012; Aguilar, Saldaña, and Aguilar Citation2013). The idea was to find the most accurate image source of GE for extracting seven GCPs through using the support of the direct geolocation supplied by the newest DigitalGlobe’s sensors. The detailed steps are the following:
The horizontal DigitalGlobe direct geolocation coordinates for each i GP (XDGi, YDGi) were computed. In this work, the most near-nadir single images were used to generate the horizontal direct coordinates only based on RPCs (i.e. a stereo pair is not necessary). It is important to note that DigitalGlobe’s ORS2A and GEO formats are both georeferenced to a cartographic projection using a surface with constant height. The number of GPs tested was ranging from 11 to 69 considering the two study sites and the 12 image sources from GE. The reader should bear in mind that we have six sets of GE coordinates for each study site.
The same horizontal coordinates of the GP (i) were also extracted from a single image source (j) provided by GE (XGEj,i, YGEj,i).
The simple 2D translation between DigitalGlobe and GE coordinates was computed. The shift along X (tx) and Y (ty) directions can be attained by Equation (1).
The computed shifts were used to translate the GE coordinates for each GP (i) to obtain, from the image source (j), the transformed GE coordinates (XTGEj,i, YTGEj,i) (Equation (2)).
The RMSE in X and Y directions (RMSEx and RMSEy) between DigitalGlobe and GE transformed coordinates could be computed (Equation (3)).
The planimetric RMSE (RMSE2D,j) was computed as an estimate of the accuracy provided by the horizontal coordinates extracted from the image source j of GE (Equation (4)).
The most accurate image source (j) provided by GE was identified from the lowest RMSE2D,j computed value. So, the original horizontal coordinates of the seven GCPs (the same for every strategy) were extracted from this GE image source.
Finally, as we are working with stereo pairs, the elevation coordinate for each GCP was taken from the DigitalGlobe direct geolocation (ZDGi). In the case of single DigitalGlobe VHR satellite images, the elevation could be attained from the global SRTM 30 m DEM.
(1)
(2)
(3)
(4)
Once the seven three-dimensional GCPs were attained, the sensor orientation was performed using RPC0. Then the DSMs were extracted from each stereo pair and, finally, the corresponding orthoimages were generated. Geometric accuracies were again computed on the same ICPs used in all strategies, for both sensor orientation and orthorectification phases. It is important to note that the true coordinates assigned to the ICPs were always those measured by DGPS.
2.3.4. GE General strategy
In this case, the seven GCPs were extracted from GE without previous direct geolocation. This strategy would be advisable to be applied on VHR satellite imagery with poor direct geolocation or with sensors presenting higher-order error sources (e.g. QuickBird) which need more complex transformation such as shift and drift model or full affine correction model (Fraser and Hanley Citation2005; Aguilar et al. Citation2008a; Tong, Liu, and Weng Citation2010). The goal was to compute the most accurate possible horizontal coordinates using all the image sources available in GE for the study area, attaining the elevation from the global SRTM 30 m DEM. So, in this case, the core of the strategy was just to use all the possible historical images to compute average values for the coordinates of the GCPs after having identified and excluded the possible outliers. The detailed approach is explained below:
The average values of X and Y for each i GP considering all the image sources (j) of GE (XGEAi, YGEAi) were computed (Equation (5)). Note that only points clearly visible in at least four multi-temporal GE image data were considered.
The standard deviation of the residuals computed in each GE image data were calculated for X and Y directions (SDxi, SDyi) (Equation (6)).
For any GP i, the X coordinate extracted from a GE image source (j) presenting an error with respect to the average higher than 1.25 × SDxi was considered as an outlier and so removed. The same was done for Y coordinates (Equation (7)). The SD parameter value of 1.25 was obtained by tuning a range of values (0.5, 0.75, 1.0, 1.25 and 1.5) in both study sites.
The average values of X and Y for each i GP considering all the GE image sources (j) and excluding the outliers were computed (Equation (8)) to obtain the final horizontal coordinates of the ith DP (XGPi, YGPi).
The corresponding elevations (i.e. Z coordinate) were computed for every GP by using the global SRTM 30 m DEM.
(5)
(6)
(7)
(8)
Once the same seven GCPs were attained, the RPC0 sensor model adjustment was performed. The orthoimages were obtained from using the previously extracted DSMs. The geometric accuracy assessment was performed as in the previous cases.
3. Results and discussion
3.1. GE accuracy
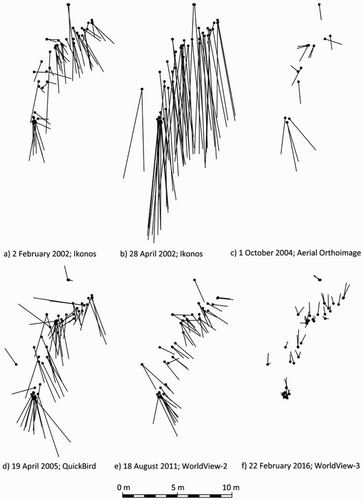
and show the horizontal GPs coordinates residuals (XGEj,i − XDGPSi, YGEj,i − YDGPSi) distribution in the study sites SS1 and SS2 for each GE image source (date). GE positional accuracy was extremely variable as it was already reported by Pulighe, Baiocchi, and Lupia (Citation2016). The RMSE2D values in SS1 were ranging from 10.25 m (QuickBird image depicted in (c)) to 0.57 m (Aerial Orthoimage in (d)). In the case of SS2, the best RMSE2D value of 0.82 m was attained from an image of WorldView-3 ((f)), while the worst value (9.74 m) was computed on an Ikonos image ((b)). Both best values of RMSE2D were located into the range reported by Pulighe, Baiocchi, and Lupia (Citation2016) for GE aerial orthoimages.
Figure 3. GE vs. DGPS coordinates. Ground coordinates residuals distribution in the study site SS1 for each date (GE image data).

Figure 4. GE vs DGPS coordinates. Ground coordinates residuals distribution in the study site SS2 for each date (GE image data).
Potere (Citation2008) noted that GE image data available in developed countries had significantly better georeferencing accuracy than in developing countries. In that sense, Chen and Chaapel (Citation2010) suggested that GE imagery may not be very accurate outside of North America.
depicts the standard deviational ellipses (i.e. a graphical representation of the horizontal variability for GE extracted GPs) computed for seven GCPs located at different sites covered with agricultural greenhouses around the world. The precision of the horizontal coordinates measured from different GE image data (dates) resulted to be the best in Bari (Italy), where five GE image datasets (three aerial orthoimages and two Geo1 images) containing all the seven GCPs were used. Mexico, with seven DigitalGlobe’s images (Geo1 and WV2) used by GE, turned out to be the second place in precision. The third place was for Morocco, which had the highest number of GE image datasets from DigitalGlobe (7 dates) and from SPOT (2 dates). Our study site SS2 took fourth place. The worst accuracies were computed on SS1 and China test sites, the last counting on five GE image datasets from WV2 and Geo1.
Figure 5. Comparison of GE horizontal accuracy using standard deviational ellipses computed on seven GCPs located at different sites around the world. The frame containing each area is a rectangle 10.5 km high and 9 km wide. Note that ellipses have been enlarged for visual purposes by applying a scale factor of 100 for every case (see graphical scale). The points extracted from GE are presented as grey crosses.

3.2. Sensor orientation
and depict the accuracy results at the sensor orientation stage attained from using the four aforementioned strategies on the study sites SS1 and SS2, respectively. Due to the fact that Geo1 Geo and WV2 ORS2A images present a very good relative accuracy, they only need a simple translation for their geometric correction (RPC0 sensor model). In this way, the four strategies applied different RPC-bias correction based on the same seven GCPs, but entering different coordinates. Because of that, it was noted that the uncertainty or random errors, measured as SD in object space, were exactly the same in all strategies for each study site. The last was due to the fact that the coordinates in the image space for each strategy were exactly the same for each GP (GCPs and ICPs). These values could be supposed as the best possible geopositioning accuracy results after applying the ideal bias correction. In that sense, the differences in accuracy between the four tested strategies are mainly due to systematic errors or bias, measured as Mean values.
Table 3. Accuracy values at sensor orientation computed on 120 ICPs over SS1 (WV2 stereo pair) for each strategy.
Table 4. Accuracy values at sensor orientation computed on 113 ICPs over SS2 (Geo1 stereo pair) for each strategy.
When using the most accurate GCPs (DGPS strategy), the horizontal biases (Mean2D) were around 0.10 and 0.22 m for the study sites SS1 and SS2, respectively, while the elevation biases kept lower than 0.14 m. The planimetric random errors (SD2D) were 0.39 and 0.34 m for SS1 and SS2, respectively, while the vertical SD (SDZ) took values of 0.36 m for SS1 and 0.64 m for SS2. These values were exactly the same as that in the rest of strategies. The RMSE2D value, a global accuracy measure for both systematic and random errors, was 0.40 m (0.8 pixels) for both study sites. RMSEZ values of 0.39 m (0.78 pixels) and 0.64 m (1.28 pixels) were attained for SS1 and SS2, respectively. These RMSE values lie within the range mentioned in literature. For example, Fraser and Ravanbakhsh (Citation2009) reported that geopositioning accuracy to around 0.5–0.7 pixels in planimetry and 0.7–1 pixel in height would be readily achievable from the 0.5 m GSD VHR satellite stereo pairs. In other work, Meguro and Fraser (Citation2010) reported planimetric and vertical accuracies of 0.8 and 1.50 pixels, respectively, by using a stereo pair of pan-sharpened Geo1 images and RPC0 sensor model.
In the case of Direct Geolocation strategy, the best direct planimetric geopositioning accuracy was achieved on SS1, although it performed the worst direct vertical geolocation. These accuracies represented our initial baseline situation without counting on ancillary GCPs.
Planimetric accuracy improvements of 57% (SS1) and 54% (SS2) in terms of CE90 values were attained by using GE General strategy considering all the GE image sources depicted in and . Even better results (71% for SS1 and 77% for SS2) were achieved through GE DigitalGlobe strategy. In the case of SS1, the aerial orthoimage taken on 15 August 2007 was selected as the best GE image source, presenting an error of 0.44 m RMSE2D in the 7 selected GCPs. In this case, an impressive sensor orientation accuracy of 0.78 m CE90 was obtained as compared to the reference planimetric accuracy of 0.61 m achieved from using DGPS GCPs. In the study site SS2, 1.20 m CE90 was achieved from using the 7 GCPs extracted from the GE image source taken on 22 February 2016, having an RMSE2D of 0.82 m.
The vertical accuracy values achieved by using the GE General strategy, based on the SRTM DEM with 30 m grid-sample distance and an absolute vertical height accuracy lesser than 16 m (LE90) (Rabus et al. Citation2003), turned out to be much more changeable. In this case, an improvement of 47% in LE90 accuracy was attained on SS1, while a decrease of 164% was observed on SS2. When using the GE DigitalGlobe strategy, the vertical accuracy values in both study sites showed slight improvements ranging from 5% to 11%.
3.3. Orthorectification
and show the horizontal accuracy results achieved at the orthorectification phase of the most near-nadir images on SS1 and SS2, respectively. The best RMSE2D values (reference values) attained through the DGPS strategy were 0.52 and 0.44 m for SS1 and SS2, respectively. It is noteworthy that the computed RMSE2D values were only increased to 0.58 m (SS1) and 0.90 m (SS2) when applying the GE DigitalGlobe strategy. More modest improvements of 42% and 52%, in terms of RMSE2D for SS1 and SS2, respectively, were obtained through the GE General strategy as compared to the Direct Geolocation one.
Table 5. Accuracy values of the orthorectified image computed at 69 ICPs over SS1 for each strategy.
Table 6. Accuracy values of the orthorectified image computed at 49 ICPs over SS2 for each strategy.
Aguilar, Saldaña, and Aguilar (Citation2013) reported accuracies (RMSE2D) ranging from 0.40 to 0.63 m on orthoimages derived from WV2 and Geo1 single images by using a very accurate LiDAR DEM and DGPS GCPs. RMSE2D values of 0.74, 1.11 and 1.07 m were attained by Åstrand et al. (Citation2012) from using a 0.6 m vertical accuracy DEM and working on WV2 ORS2A single images presenting off-nadir angles of 26.7°, 31.6° and 36°, respectively.
3.4. GE General and DigitalGlobe approaches
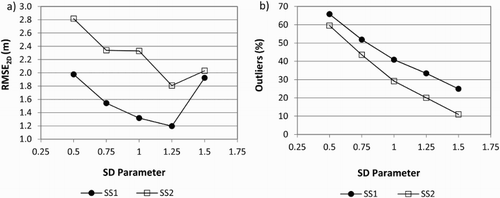
The GE General strategy proved not to be very reliable for extracting GCPs in both planimetry and elevation. Its major drawback was related to the search of a proper threshold to detect and remove outliers. In fact, (a) depicts the sensitivity analysis of the factor multiplying SD (SD parameter) on horizontal accuracy. Although the ideal SD parameter was set to 1.25 for both study sites, the reliability of the results should be contrasted in other study sites. For an SD parameter equal to 1.25, the detection of outliers was ranging from 20% to 33% for SS2 and SS1, respectively ((b)). As a further work, it would be interesting to test out other outlier detection methods. On the other hand, the use of a coarse global DEM such as SRTM 30 led to poor and changeable vertical accuracies, sometimes even worse than those obtained from direct geolocation.
Figure 6. Determination of the SD parameter for the GE General Strategy on SS1 and SS2: (a) Sensitivity analysis to estimate the influence of SD parameter on the horizontal accuracy (RMSE2D); (b) Percentage of detected outliers depending on each SD parameter.
The GE DigitalGlobe strategy is clearly the best option to extract GCPs from the GE database if the VHR satellite image to orthorectify is taken by Geo1 or WorldView-1/2/3/4 sensors. depicts the RMSE2D,j computed value for each GE image dataset and study site. The most accurate GE image source is pointed by the lowest RMSE2D,j. The reader can see that the RMSE2D,j results are very similar to the random errors (SD2D) computed from using the best GPs coordinates (DGPS coordinates). Moreover, the number of GPs needed to calculate the RMSE2D,j does not have to be very high. From only 11 GPs the results seem to be very robust.
Table 7. Selection of the most accurate date (image dataset) in the context of the GE DigitalGlobe strategy based on the computation of RMSE2D,j.
It is important to note that the difference between RMSE2D from DGPS coordinates and RMSE2D,j should somehow represent the systematic errors. Particularly interesting would be to use a VHR satellite stereo pair in order to calculate elevations from direct geolocation.
4. Conclusions
Many authors had already used GE to extract GPs coordinates; however and to the best knowledge of the authors, this study provides the first two approaches dealing with the extraction of the most accurate GCPs horizontal coordinates derived from the GE multi-temporal historical imagery database. These GCPs extracted from GE were used to compute the sensor orientation of VHR satellite stereo pairs, to extract the DSM, and finally to generate the orthoimage from the most near-nadir image. Both GE strategies were compared at sensor orientation and orthorectification stages to the best possible geometrically corrected products obtained from very accurate DGPS GCPs and, also, to the direct geolocation (i.e. without ancillary GCPs) strategy.
Horizontal accuracies of 0.52 and 0.44 m RMSE2D for the final orthoimages were achieved by using DGPS GCPs on the study sites SS1 and SS2, respectively. However, users can generate orthoimages with RMSE2D values lower than 2 m through the GE General strategy by using vertical coordinates from the global SRTM 30 DEM, although the results attained by this approach could not to be very reliable. Much more accurate orthoimages with RMSE2D better than 1 m can be attained through the GE DigitalGlobe Strategy. It is important to highlight that all the results depicted in this work were attained working on very smooth study areas covered by agricultural greenhouses, where GE had several good image sources.
Although the proposed approaches were applied on VHR satellite stereo pairs from WV2 and Geo1, they could be also used for single images, especially in smooth areas. To do this, the Z coordinate would have to be extracted from a global DEM (e.g. SRTM) for both strategies, and after that, the final orthorectification process could be carried out by using again this global DEM.
The GE-positional accuracy was extremely variable depending on the site, the imagery source and even time. The best image sources available in GE were aerial orthoimages and the last breed of DigitalGlobe’s VHR sensors (i.e. WV3, WV2 and Geo1). Notwithstanding some researchers have reported that GCPs from GE in developing countries could have poor accuracy, it has not been proved in this article. In fact, it was surprising to find that better precision could be attained in Agadir (Morocco) than in either of the two study areas tested in this work and located in Spain.
Although these findings are quite promising, they should be further contrasted through working on other study sites around the world.
Acknowledgements
We are grateful to Piotr Cichón and Malgorzata Betlej (AGH University of Science and Technology of Krakow (Poland)) for their important collaboration. It takes part of the general research lines promoted by the Agrifood Campus of International Excellence ceiA3. We also thank the journal’s anonymous reviewers for their valuable comments, which greatly improved our paper.
Disclosure statement
No potential conflict of interest was reported by the authors.
ORCID
Manuel A. Aguilar http://orcid.org/0000-0003-0404-9875
Fernando J. Aguilar http://orcid.org/0000-0002-5144-6411
Antonio Novelli http://orcid.org/0000-0002-5671-9220
Additional information
Funding
References
- Aguilar, M. A., F. Agüera, F. J. Aguilar, and F. Carvajal. 2008a. “Geometric Accuracy Assessment of the Orthorectification Process from Very High Resolution Satellite Imagery for Common Agricultural Policy Purposes.” International Journal of Remote Sensing 29 (24): 7181–7197. doi: 10.1080/01431160802238393
- Aguilar, M. A., F. J. Aguilar, and F. Agüera. 2008b. “Assessing Geometric Reliability of Corrected Images from Very High Resolution Satellites.” Photogrammetric Engineering & Remote Sensing 74 (12): 1551–1560. doi: 10.14358/PERS.74.12.1551
- Aguilar, M. A., M. M. Saldaña, and F. J. Aguilar. 2013. “Assessing Geometric Accuracy of the Orthorectification Process from GeoEye-1 and WorldView-2 Panchromatic Images.” International Journal of Applied Earth Observation and Geoinformation 21: 427–435. doi: 10.1016/j.jag.2012.06.004
- Åstrand, P. J., M. Bongiorni, M. Crespi, F. Fratarcangeli, J. N. Da Costa, F. Pieralice, and A. Walczynska. 2012. “The Potential of WorldView-2 for Ortho-image Production within the ‘Control with Remote Sensing Programme’ of the European Commission.” International Journal of Applied Earth Observation and Geoinformation 19: 335–347. doi: 10.1016/j.jag.2012.06.003
- Benker, S. C., R. P. Langford, and T. L. Pavlis. 2011. “Positional Accuracy of the Google Earth Terrain Model Derived from Stratigraphic Unconformities in the Big Bend Region, Texas, USA.” Geocarto International 26 (4): 291–301. doi: 10.1080/10106049.2011.568125
- Chen, P., and C. Chaapel. 2010. “Pan-sharpening and Geometric Correction WorldView-2 Satellite.” GeoInformatics 4: 30–33.
- DigitalGlobe. 2014. “Geolocation Accuracy of WorldView Products.” Accessed September 16. http://global.digitalglobe.com/sites/default/files/WorldView_Geolocation_Accuracy.pdf.
- Frankl, A., V. Seghers, C. Stal, P. de Mayer, G. Petrie, and J. Nyssen. 2015. “Using Image-based Modelling (SfM–MVS) to Produce a 1935 Ortho-mosaic of the Ethiopian Highlands.” International Journal of Digital Earth 8 (5): 421–430. doi: 10.1080/17538947.2014.942715
- Fraser, C. S., and H. B. Hanley. 2005. “Bias-compensated RPCs for Sensor Orientation of High-resolution Satellite Imagery.” Photogrammetric Engineering & Remote Sensing 71 (8): 909–915. doi: 10.14358/PERS.71.8.909
- Fraser, C. S., and M. Ravanbakhsh. 2009. “Georeferencing Accuracy of GeoEye-1 Imagery.” Photogrammetric Engineering & Remote Sensing 75 (6): 634–638.
- Grodecki, J., and G. Dial. 2003. “Block Adjustment of High-resolution Satellite Images Described by Rational Polynomials.” Photogrammetric Engineering & Remote Sensing 69 (1): 59–68. doi: 10.14358/PERS.69.1.59
- Meguro, Y., and C. S. Fraser. 2010. “Georeferencing Accuracy of GeoEye-1 Stereo Imagery: Experiences in a Japanese Test Field.” International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences 38 (8): 1069–1072.
- Mulawa, D. 2014. “Geolocation Accuracy Performance of the DigitalGlobe Constellation During 2013.” The joint agency commercial imagery evaluation (JACIE) workshop, Louisville, Kentucky USA, March 23–28, 2014.
- Mulawa, D., and C. Comp. 2014. “Geolocation Accuracy Performance of the DigitalGlobe Constellation During 2015.” The joint agency commercial imagery evaluation (JACIE) workshop, Fort Worth, Texas, USA, April 12–14, 2016.
- Paredes-Hernandez, C. U., W. E. Salinas-Castillo, F. Guevara-Cortina, and X. Martinez-Becerra. 2013. “Horizontal Positional Accuracy of Google Earth’s Imagery over Rural Areas: A Study Case in Tamaulipas, Mexico.” Boletim de Ciências Geodésicas 19: 588–601. doi: 10.1590/S1982-21702013000400005
- Potere, D. 2008. “Horizontal Positional Accuracy of Google Earth’s High-resolution Imagery Archive.” Sensors 8: 7973–7981. doi: 10.3390/s8127973
- Pulighe, G., V. Baiocchi, and F. Lupia. 2016. “Horizontal Accuracy Assessment of Very High Resolution Google Earth Images in the City of Rome, Italy.” International Journal of Digital Earth 9 (4): 342–362. doi: 10.1080/17538947.2015.1031716
- Rabus, B., M. Eineder, A. Roth, and R. Bamler. 2003. “The Shuttle Radar Topography Mission – A New Class of Digital Elevation Models Acquired by Spaceborne Radar.” ISPRS Journal of Photogrammetry and Remote Sensing 57 (4): 241–262. doi: 10.1016/S0924-2716(02)00124-7
- Tong, X., S. Liu, and Q. Weng. 2010. “Bias-corrected Rational Polynomial Coefficients for High Accuracy Geo-positioning of QuickBird Stereo Imagery.” ISPRS Journal of Photogrammetry and Remote Sensing 65: 218–226. doi: 10.1016/j.isprsjprs.2009.12.004
- Toutin, T. 2004. “Review Article: Geometric Processing of Remote Sensing Images: Models, Algorithms and Methods.” International Journal of Remote Sensing 25 (10): 1893–1924. doi: 10.1080/0143116031000101611
- Wong, D. W. S. and J. Lee. 2005. Statistical Analysis of Geographic Information with ArcView GIS and ArcGIS. Hoboken, NJ: John Wiley & Sons.
- Yousefzadeh, M., and B. Mojaradi. 2012. “Combined Rigorous-generic Direct Orthorectification Procedure for IRS-p6 Sensors.” ISPRS Journal of Photogrammetry and Remote Sensing 74: 122–132. doi: 10.1016/j.isprsjprs.2012.09.005