Region-based classification of PolSAR data using radial basis kernel functions with stochastic distances

ABSTRACT

Region-based classification of PolSAR data can be effectively performed by seeking for the assignment that minimizes a distance between prototypes and segments. Silva et al. [“Classification of segments in PolSAR imagery by minimum stochastic distances between wishart distributions.” IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 6 (3): 1263–1273] used stochastic distances between complex multivariate Wishart models which, differently from other measures, are computationally tractable. In this work we assess the robustness of such approach with respect to errors in the training stage, and propose an extension that alleviates such problems. We introduce robustness in the process by incorporating a combination of radial basis kernel functions and stochastic distances with Support Vector Machines (SVM). We consider several stochastic distances between Wishart: Bhatacharyya, Kullback-Leibler, Chi-Square, Rényi, and Hellinger. We perform two case studies with PolSAR images, both simulated and from actual sensors, and different classification scenarios to compare the performance of Minimum Distance and SVM classification frameworks. With this, we model the situation of imperfect training samples. We show that SVM with the proposed kernel functions achieves better performance with respect to Minimum Distance, at the expense of more computational resources and the need of parameter tuning. Code and data are provided for reproducibility.

KEYWORDS:

• PolSAR
• image classification
• stochastic distance
• minimum distance classifier
• SVM

1. Introduction

The availability of Polarimetric Synthetic Aperture Radar (PolSAR) sensors has increased as a consequence of the technological advances in Remote Sensing. Compared to conventional SAR sensors, PolSAR is able to acquire the amplitude, phase, and orientation of the electromagnetic waves reflected from targets in different transmission and reception polarizations. The use of these images is challenging, among other reasons, because of the data structure (complex matrices in each pixel), their properties (the Gaussian additive noise is not valid), and the signal-to-noise ratio (typically very low). Bearing these characteristics in mind, several specific methods have been developed for PolSAR image processing and classification.

PolSAR image classification has been intensively investigated. The notion that more information on the same area leads to better classification is intuitive. Lee, Grunes, and Kwok (1994) and Cloude and Pottier (1997) proposed two pioneer approaches for PolSAR data classification. While the former develops a pixel-based method based on the Maximum Likelihood Classifier under the Complex Multivariate Wishart distribution, the latter is an unsupervised classification through the eigenvalue analysis of coherency matrices.

Several PolSAR data classification approaches have been proposed since then. Frery, Correia, and Freitas (2007) used specific probability density functions for PolSAR intesity data in the classic Maximum Likelihood Classifier method. Ersahin, Cumming, and Ward (2010) based their approach for segmentation and classification of PolSAR data with on spectral graph partitioning. Du et al. (2014) used a Kernel Extreme Learning Machine with multiple polarimetric and spatial features. Tao et al. (2015) proposed a feature extraction method based on Independent Component Analysis and tensor decomposition. Recently, Hou et al. (2017) proposed a semi-supervised method able to learn even when the training data quality and quantity are both poor.

Silva et al. (2013) investigated the use of stochastic distances between Complex Multivariate Wishart distributions on a region-based approach. The performance of using the Kullback-Leibler, Bhattacharyya, Hellinger, Rényi, and Chi-Square stochastic distances was assessed, providing evidence that such leads to better results when compared to the Maximum Likelihood Classifier using the Complex Multivariate Wishart distribution for pixel-based PolSAR classification as proposed in Lee, Grunes, and Kwok (1994). Furthermore, the Kullback-Leibler, Bhattacharyya, and Rényi distances are more indicated than Hellinger and Chi-Square.

Adopting stochastic distance between Complex Multivariate Wishart models and a hypothesis test derived from this kind of measure, Negri, Silva, and Mendes (2016) presented a new version of K-Means algorithm for region-based classification of PolSAR data. Similarly, Negri et al. (2016) verified the use of Bhattacharyya distance with a Support Vector Machine (SVM) through kernel functions for region-based classification of SAR data. However, to the best of the authors' knowledge, there is still room for investigating other distances and specific distributions for PolSAR images.

This study aims at analyzing the use of a number of stochastic distances as inputs for an SVM with kernel functions for PolSAR region-based classification. Additionally, it presents comparisons with the Minimum Distance Classifier framework investigated by Silva et al. (2013). Such comparisons are conducted on PolSAR images, both simulated and from operational sensors, and different classification scenarios. Such scenarios include an analysis of the often encountered situation of using imperfect, i.e. contaminated, training samples.

The remainder of this article is organized as follows. Fundamental concepts regarding statistical PolSAR modeling, and the use of stochastic distances for region-based classification are presented in Section 2. In Section 3, these concepts are applied in two case studies. Conclusions are presented in Section 4.

2. Statistical region-based PolSAR classification

2.1. Statistical PolSAR modeling

The backscatter signal measured by a PolSAR sensor can be represented through the complex scattering vector ${\mathbf{z}}^{\mathrm{T}}\mathbf{=}\mathbf{\left(}{\mathbf{S}}_{\mathbf{h}\mathbf{h}}{\mathbf{S}}_{\mathbf{h}\mathbf{v}}{\mathbf{S}}_{\mathbf{v}\mathbf{h}}{\mathbf{S}}_{\mathbf{v}\mathbf{v}}\mathbf{\right)}$. Each component of $\mathbf{z}$ is a complex number that carries the amplitude and phase of a polarization combination. The polarizations are indicated by the subscripts in $\mathbf{z}$, where, for example, hv denotes the signal recorded with vertical polarization from a signal initially emitted with horizontal polarization. Considering the reciprocity of an atmospheric medium, which makes $S_{hv}$ similar to $S_{vh}$, the scattering vector is simplified to ${\mathbf{z}}^{\mathrm{T}}\mathbf{=}\mathbf{\left(}{\mathbf{S}}_{\mathbf{h}\mathbf{h}}{\mathbf{S}}_{\mathbf{h}\mathbf{v}}{\mathrm{\S }}_{\mathbf{v}\mathbf{v}}\mathbf{\right)}$ (Frery, Correia, and Freitas, 2007).

An N-looks covariance matrix is the average of N backscatter measurements in a neighborhood:(1) $\mathbf{Z}=\frac{1}{N}\sum _{\ell =1}^N{\mathbf{z}}_{\ell }{\mathbf{z}}_{\ell }^{\star T}=\left(\begin{array}{ccc}{Z}_{hh}& Z_{hhhv}& Z_{hhvv}\\ Z_{hhhv}^{\star }& Z_{hv}& Z_{hvvv}\\ Z_{hhvv}^{\star }& Z_{hvvv}^{\star }& Z_{vv}\end{array}\right),$(1) where ⋆ and T represent the conjugate and transposed operators, respectively. The diagonal elements of $\mathbf{Z}$ are nonnegative numbers that represent the intensity of the signal measured on a specific polarization.

Assuming that $\mathbf{z}$ follows a zero-mean Complex Gaussian distribution (cf. Goodman, 1963), it is possible to obtain the distribution of $\mathbf{Z}$, the scaled Complex Multivariate Wishart law, which is characterized by the following probability density function:(2) $f\left(\mathbf{Z};N,\mathbf{\Sigma }\right)=\frac{N^{3N}|\mathbf{Z}{|}^{N-3}\exp \{-N\mathrm{Tr}\left({\mathbf{\Sigma }}^{-1}\mathbf{Z}\right)\}}{|\mathbf{\Sigma }{|}^N{\mathrm{\Gamma }}_3\left(N\right)},$(2) where ${\mathrm{\Gamma }}_3\left(N\right)={\pi }^3\prod _{i=0}^2\mathrm{\Gamma }(N-i),N\ge 3$.

The parameters N and $\mathbf{\Sigma }$ are the number of looks and the target mean covariance matrix. The determinant, inversion and trace operators are denoted $|\cdot |$, $(\cdot {)}^{-1}$ and $Tr(\cdot )$, respectively.

The scaled Complex Multivariate Wishart model is valid in textureless areas. Target variability can be included by one or more additional parameters; the reader is referred to the work by Deng et al. (2017) for a comprehensive survey of models for PolSAR data.

2.2. Stochastic distances between Complex Multivariate Wishart distributions

A divergence is a measure of the difficulty of discriminating between two models. Csiszár (1967) proposed the φ divergence family, providing a formally organized framework to analytically obtain divergence measures between distributions. Salicru et al. (1994) proposed a more general class of divergences, the $h-\phi$ divergence, through the adoption of an additional function (h).

Consider the random variables X and Y defined on the same support $\mathcal{X}$ with distributions characterized by the densities $f_X(\mathbf{x}\mathbf{;}{\theta }_{\mathbf{1}}\mathbf{)}$ and $f_Y(\mathbf{x}\mathbf{;}{\theta }_{\mathbf{2}}\mathbf{)}$, respectively, where ${\theta }_1$ and ${\theta }_2$ are parameters. The $h-\phi$ divergence between X and Y is given by:(3) $d_{\phi }^h(X,Y)=h\left({\int }_{\mathbf{x}\in \mathcal{X}}\phi \left(\frac{f_X(\mathbf{x};{\theta }_1)}{f_Y(\mathbf{x};{\theta }_2)}\right)f_Y(\mathbf{x};{\theta }_2)\mathrm{d}\mathbf{x}\right),$(3) where $\phi :(0,\mathrm{\infty })\to [0,\mathrm{\infty })$ is a convex function and $h:(0,\mathrm{\infty })\to [0,\mathrm{\infty })$ is a strictly increasing function with $h\left(0\right)=0$ and $h^{\prime }\left(v\right)>0$ for all $v\in (0,\mathrm{\infty })$. Several well-known divergence measures can be obtained by choosing h and φ, but they are not necessarily symmetric.

The symmetrization $\mathrm{D}(X,Y)=\left(d_{\phi }^h\right(X,Y)+d_{\phi }^h(Y,X\left)\right)/2$ allows to obtain distances measures from any divergence $d_{\phi }^h$. This leads to the following properties:

1. Non-negativity: $\mathrm{D}(X,Y)\ge 0$;

2. Identity (of indiscernible): $\mathrm{D}(X,Y)=0\iff X=Y$;

3. Symmetry: $\mathrm{D}(X,Y)=\mathrm{D}(Y,X)$.

   Additionally, if a distance has the following property, then it is a metric:

4. Triangle inequality: $\mathrm{D}(X,Z)\le \mathrm{D}(X,Y)+\mathrm{D}(Y,Z)$,

where X, Y and Z have the same support $\mathcal{X}$. It is noteworthy that Bathacharrya, Kullback-Leibler, Rényi, Hellinger and Chi-Square distances are not metrics since the triangle inequality is not fulfilled.

Nascimento, Cintra, and Frery (2010) computed the Bathacharrya, Kullback-Leibler, Rényi (of order β), Hellinger, Jensen-Shannon, Arithmetic-Geometric, Triangular and Harmonic Mean stochastic distances between ${\mathcal{G}}^{\mathcal{0}}$ distributions. These distances were successfully used to evaluate contrast differences among regions in intensity Synthetic Aperture Radar (SAR) images.

Frery, Nascimento, and Cintra (2014) developed analytic expressions for the first four aforementioned stochastic distances between scaled Complex Multivariate Wishart distributions. Previously, the Chi-Square stochastic distance between Complex Multivariate Wishart distributions was presented in Frery, Nascimento, and Cintra (2011). These distances were used by Silva et al. (2013) in PolSAR imagery classification by a minimum distance criterion.

Let X and Y be two random variables modeled by scaled Complex Multivariate Wishart distributions $X\sim \mathcal{W}({\mathbf{\Sigma }}_{\mathbf{1}}\mathbf{,}\mathbf{N}\mathbf{)}$ and $Y\sim \mathcal{W}({\mathbf{\Sigma }}_{\mathbf{2}}\mathbf{,}\mathbf{N}\mathbf{)}$. The Bathacharrya, Kullback-Leibler, Rényi (order $0<\beta <1$) and Hellinger stochastic distances expressions between scaled Complex Multivariate Wishart distributions, according to Frery, Nascimento, and Cintra (2014), are given by:(4) $\begin{array}{cc}{\mathrm{D}}_{\mathrm{B}}(X,Y)& =N\left[\frac{\log |{\mathbf{\Sigma }}_1|+\log |{\mathbf{\Sigma }}_2|}{2}-\log \left|{\left(\frac{{\mathbf{\Sigma }}_1^{-1}+{\mathbf{\Sigma }}_2^{-1}}{2}\right)}^{-1}\right|\right],\end{array}$(4) (5) $\begin{array}{cc}{\mathrm{D}}_{\mathrm{K}}(X,Y)& =N\left[\frac{\mathrm{Tr}({\mathbf{\Sigma }}_1^{-1}{\mathbf{\Sigma }}_2+{\mathbf{\Sigma }}_2^{-1}{\mathbf{\Sigma }}_1)}{2}-3\right],\end{array}$(5) (6) $\begin{array}{c}{\mathrm{D}}_{\mathrm{R}}^{\beta }(X,Y)=\frac{\log 2}{1-\beta }+\frac{1}{\beta -1}\log \left\{{\left[|{\mathbf{\Sigma }}_1{|}^{-\beta }|{\mathbf{\Sigma }}_2{|}^{\beta -1}|{(\beta {\mathbf{\Sigma }}_1^{-1}+(1-\beta \left){\mathbf{\Sigma }}_2^{-1}\right)}^{-1}|\right]}^N\right.\\ +\left.{\left[|{\mathbf{\Sigma }}_1{|}^{\beta -1}|{\mathbf{\Sigma }}_2{|}^{-\beta }|{(\beta {\mathbf{\Sigma }}_2^{-1}+(1-\beta \left){\mathbf{\Sigma }}_1^{-1}\right)}^{-1}|\right]}^N\right\}\end{array}$(6) (7) $\begin{array}{cc}{\mathrm{D}}_{\mathrm{H}}(X,Y)& =1-{\left[\frac{\left|2{({\mathbf{\Sigma }}_1^{-1}+{\mathbf{\Sigma }}_2^{-1})}^{-1}\right|}{\sqrt{|{\mathbf{\Sigma }}_1||{\mathbf{\Sigma }}_2|}}\right]}^N,\end{array}$(7) (8) $\begin{array}{c}{\mathrm{D}}_{\mathrm{C}}(X,Y)={\left(\frac{|{\mathbf{\Sigma }}_1|}{|{\mathbf{\Sigma }}_2{|}^2}\mathrm{abs}\left(\left|{\left(2{\mathbf{\Sigma }}_2^{-1}-{\mathbf{\Sigma }}_1^{-1}\right)}^{-1}\right|\right)\right)}^N\\ +{\left(\frac{|{\mathbf{\Sigma }}_2|}{|{\mathbf{\Sigma }}_1{|}^2}\mathrm{abs}\left(\left|{\left(2{\mathbf{\Sigma }}_1^{-1}-{\mathbf{\Sigma }}_2^{-1}\right)}^{-1}\right|\right)\right)}^N-2,\end{array}$(8) where $\mathrm{abs}(\cdot )$ returns the modulus of a real number.

2.3. Region-based PolSAR image classification

Let $\mathcal{I}$ be an image defined on the grid $\mathcal{S}\subset {\mathbb{N}}^2$ whose pixels are elements of the attribute space $\mathcal{X}$. We use the notation $\mathcal{I}\left(s\right)=\mathbf{x}$ to represent that a pixel $s\in \mathcal{S}$ of $\mathcal{I}$ has attribute $\mathbf{x}\in \mathcal{X}$. The image support can be partitioned in $r\ge 1$ disjoint subsets ${\mathcal{R}}_i\subset \mathcal{S},i=1,\dots ,r$, such that ${\cup }_{i=1}^r{\mathcal{R}}_i=\mathcal{S}$.

A region-based classification process consists of associating a class ${\omega }_j$ from a set of c possible classes Ω to all the pixels that comprise the region ${\mathcal{R}}_i$. A supervised region-based decision rule is built trough information available from a set of labeled regions $\mathcal{D}=\left\{\right({\mathcal{R}}_k,{\omega }_j)\in \mathcal{S}\times \mathrm{\Omega }:k=1,\dots ,s;j=1,\dots ,c\}$. The notation $({\mathcal{R}}_k,{\omega }_j)$ indicates that ${\mathcal{R}}_k$ is assigned to the class ${\omega }_j$.

Silva et al. (2013) adopt the Minimum Distance Classifier framework using stochastic distances as a measure to compare the similarity between classes and unlabeled regions. We refer to this method as Minimum Stochastic Distance Classifier (MSDC). The pixel values in an unlabeled region are used to estimate a probability distribution. This region is then assigned to the closest class in distribution, according to an stochastic distance. The class distributions are modeled based on information from $\mathcal{D}$.

Formally, let ${\mathcal{R}}_i$ be an unlabeled region and let $\mathrm{D}({\hat{f}}_{{\mathcal{R}}_i},{\hat{f}}_{{\omega }_j})$ be a stochastic distance between distributions estimated from the attributes of the pixels in ${\mathcal{R}}_i$ and the class ${\omega }_j$. An assignment $({\mathcal{R}}_i,{\omega }_j)$ is made when the following rule is satisfied:(9) $({\mathcal{R}}_i,{\omega }_j)\iff j=\underset{j=1,\dots ,c}{\arg \min }\mathrm{D}({\hat{f}}_{{\mathcal{R}}_i},{\hat{f}}_{{\omega }_j}).$(9) In Equation (9(9) $({\mathcal{R}}_i,{\omega }_j)\iff j=\underset{j=1,\dots ,c}{\arg \min }\mathrm{D}({\hat{f}}_{{\mathcal{R}}_i},{\hat{f}}_{{\omega }_j}).$(9) ), ${\hat{f}}_{{\omega }_j}$ is estimated with all the pixels assigned to ${\omega }_j$ in $\mathcal{D}$.

Other methods can be adopted to perform region-based classification beyond the MSDC as, for instance, Support Vector Machines (SVMs). SVMs have received great attention because of their excellent generalization ability, their independence of data distribution and their robustness with respect to the Hughe's phenomenon (Bruzzone and Persello, 2009).

The use of kernel functions, $K:{\mathcal{X}}^2\to \mathbb{R}$, is a common strategy to improve SVM classification performance on nonlinearly separable patterns. Kernel functions also allow the application of SVMs in problems where patterns cannot be represented as vectors.

A kernel function $K:{\mathcal{X}}^2\to \mathbb{R}$ is symmetric and conforms to the Mercer theorem conditions (Theodoridis and Koutroumbas, 2008). However, as such verification may be not trivial there are alternative ways to develop such functions. For example, adopting the radial basis function model (Schölkopf and Smola, 2002):(10) $K({\mathbf{x}}_u,{\mathbf{x}}_v)=g\left(\tilde{m}\left({\mathbf{x}}_u,{\mathbf{x}}_v\right)\right),$(10) where $g:\mathbb{R}\to \mathbb{R}$ is a strictly positive real function and $\tilde{m}:{\mathcal{X}}^2\to \mathbb{R}$ is a metric.

Equation (10(10) $K({\mathbf{x}}_u,{\mathbf{x}}_v)=g\left(\tilde{m}\left({\mathbf{x}}_u,{\mathbf{x}}_v\right)\right),$(10) ) gives a hint to develop suitable kernel functions for PolSAR region-based image classification. A sensible choice for g is the negative exponential function, and m, as a measure of similarity between the input data, a metric based on stochastic distances between distributions. It is noteworthy that Equations (4(4) $\begin{array}{cc}{\mathrm{D}}_{\mathrm{B}}(X,Y)& =N\left[\frac{\log |{\mathbf{\Sigma }}_1|+\log |{\mathbf{\Sigma }}_2|}{2}-\log \left|{\left(\frac{{\mathbf{\Sigma }}_1^{-1}+{\mathbf{\Sigma }}_2^{-1}}{2}\right)}^{-1}\right|\right],\end{array}$(4) ) to (8(8) $\begin{array}{c}{\mathrm{D}}_{\mathrm{C}}(X,Y)={\left(\frac{|{\mathbf{\Sigma }}_1|}{|{\mathbf{\Sigma }}_2{|}^2}\mathrm{abs}\left(\left|{\left(2{\mathbf{\Sigma }}_2^{-1}-{\mathbf{\Sigma }}_1^{-1}\right)}^{-1}\right|\right)\right)}^N\\ +{\left(\frac{|{\mathbf{\Sigma }}_2|}{|{\mathbf{\Sigma }}_1{|}^2}\mathrm{abs}\left(\left|{\left(2{\mathbf{\Sigma }}_1^{-1}-{\mathbf{\Sigma }}_2^{-1}\right)}^{-1}\right|\right)\right)}^N-2,\end{array}$(8) ) will not produce valid kernel functions since they do not attain the triangle inequality.

However, if $\mathrm{D}$ is a stochastic distance with $\tau \in {\mathbb{R}}_{+}$ such that $\mathrm{D}({\mathcal{R}}_u,{\mathcal{R}}_v)\le \tau$ for $u,v=1,\dots ,r$, the following expression provides a metric:(11) $m({\mathcal{R}}_u,{\mathcal{R}}_v)=\left\{\begin{array}{cc}0& \mathrm{if}{\mathcal{R}}_u={\mathcal{R}}_v,\\ \mathrm{D}({\mathcal{R}}_u,{\mathcal{R}}_v)+\tau & \mathrm{if}{\mathcal{R}}_u\ne {\mathcal{R}}_v.\end{array}\right.$(11) The identity property of m stems from (11(11) $m({\mathcal{R}}_u,{\mathcal{R}}_v)=\left\{\begin{array}{cc}0& \mathrm{if}{\mathcal{R}}_u={\mathcal{R}}_v,\\ \mathrm{D}({\mathcal{R}}_u,{\mathcal{R}}_v)+\tau & \mathrm{if}{\mathcal{R}}_u\ne {\mathcal{R}}_v.\end{array}\right.$(11) ). Non-negativity and symmetry are inherited from $\mathrm{D}$, which is a distance, since adding a positive constant will not invalidate such proprieties. Finally, the triangle inequality is fulfilled since the following relations are satisfied:$\begin{array}{rl}& m({\mathcal{R}}_u,{\mathcal{R}}_v)+m({\mathcal{R}}_v,{\mathcal{R}}_w)\ge m({\mathcal{R}}_u,{\mathcal{R}}_w)\\ & \iff \mathrm{D}({\mathcal{R}}_u,{\mathcal{R}}_v)+\tau +\mathrm{D}({\mathcal{R}}_v,{\mathcal{R}}_w)+\tau \ge \mathrm{D}({\mathcal{R}}_u,{\mathcal{R}}_w)+\tau \\ & \iff \mathrm{D}({\mathcal{R}}_u,{\mathcal{R}}_v)+\mathrm{D}({\mathcal{R}}_v,{\mathcal{R}}_w)+\tau \ge \mathrm{D}({\mathcal{R}}_u,{\mathcal{R}}_w),\end{array}$once we have that $\mathrm{D}({\mathcal{R}}_u,{\mathcal{R}}_w)\le \tau$. 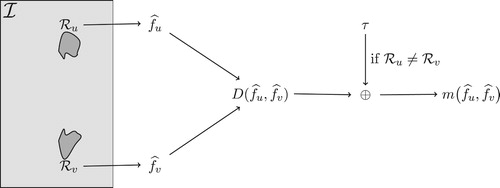The constant τ can be chosen as the largest distance measured by $\mathrm{D}$ in the classification problem. Figure 1 illustrates this procedure.

Figure 1. Schema of the construction of a kernel function K between regions ${\mathcal{R}}_{\mathcal{u}}$ and ${\mathcal{R}}_{\mathcal{v}}$.

We can thus define kernel functions for PolSAR region-based image classification using the model from Equation (10(10) $K({\mathbf{x}}_u,{\mathbf{x}}_v)=g\left(\tilde{m}\left({\mathbf{x}}_u,{\mathbf{x}}_v\right)\right),$(10) ), the expression from Equation (11(11) $m({\mathcal{R}}_u,{\mathcal{R}}_v)=\left\{\begin{array}{cc}0& \mathrm{if}{\mathcal{R}}_u={\mathcal{R}}_v,\\ \mathrm{D}({\mathcal{R}}_u,{\mathcal{R}}_v)+\tau & \mathrm{if}{\mathcal{R}}_u\ne {\mathcal{R}}_v.\end{array}\right.$(11) ) and considering the substitution of $\mathrm{D}$ by a stochastic distance given by Equations (4(4) $\begin{array}{cc}{\mathrm{D}}_{\mathrm{B}}(X,Y)& =N\left[\frac{\log |{\mathbf{\Sigma }}_1|+\log |{\mathbf{\Sigma }}_2|}{2}-\log \left|{\left(\frac{{\mathbf{\Sigma }}_1^{-1}+{\mathbf{\Sigma }}_2^{-1}}{2}\right)}^{-1}\right|\right],\end{array}$(4) ) to (8(8) $\begin{array}{c}{\mathrm{D}}_{\mathrm{C}}(X,Y)={\left(\frac{|{\mathbf{\Sigma }}_1|}{|{\mathbf{\Sigma }}_2{|}^2}\mathrm{abs}\left(\left|{\left(2{\mathbf{\Sigma }}_2^{-1}-{\mathbf{\Sigma }}_1^{-1}\right)}^{-1}\right|\right)\right)}^N\\ +{\left(\frac{|{\mathbf{\Sigma }}_2|}{|{\mathbf{\Sigma }}_1{|}^2}\mathrm{abs}\left(\left|{\left(2{\mathbf{\Sigma }}_1^{-1}-{\mathbf{\Sigma }}_2^{-1}\right)}^{-1}\right|\right)\right)}^N-2,\end{array}$(8) ):(12) $K({\mathcal{R}}_u,{\mathcal{R}}_v)={\mathrm{e}}^{-\gamma m\left({\mathcal{R}}_u,{\mathcal{R}}_v\right)},$(12) where $\gamma \in {\mathbb{R}}_{+}$ is a user-adjusted parameter. We denote the kernel functions obtained from the Bathacharrya, Kullback-Leiber, Hellinger, Rényi e Chi-Square distances as ${\mathrm{K}}_{\mathrm{B}}$, ${\mathrm{K}}_{\mathrm{K}}$, ${\mathrm{K}}_{\mathrm{H}}$, ${\mathrm{K}}_{\mathrm{R}}$ and${\mathrm{K}}_{\mathrm{C}}$, respectively.

We make clear that $K({\mathcal{R}}_{\mathcal{u}}\mathcal{,}{\mathcal{R}}_{\mathcal{v}}\mathcal{)}$ denotes a kernel function between estimates of distributions ${\hat{f}}_u$ and ${\hat{f}}_v$ computed with the observations in regions ${\mathcal{R}}_{\mathcal{u}}$ and ${\mathcal{R}}_{\mathcal{v}}$.

3. Experiments and results

In this section, we present studies of region-based image classification of actual and simulated PolSAR data using the stochastic distances presented in Section 2.2 by both MSDC (i.e. ${\mathrm{D}}_{\mathrm{B}}$, ${\mathrm{D}}_{\mathrm{K}}$, ${\mathrm{D}}_{\mathrm{H}}$, ${\mathrm{D}}_{\mathrm{R}}$ and ${\mathrm{D}}_{\mathrm{C}}$) and through the kernel functions, defined in Section 2.3 (i.e. ${\mathrm{K}}_{\mathrm{B}}$, ${\mathrm{K}}_{\mathrm{K}}$, ${\mathrm{K}}_{\mathrm{H}}$, ${\mathrm{K}}_{\mathrm{R}}$ and ${\mathrm{K}}_{\mathrm{C}}$).

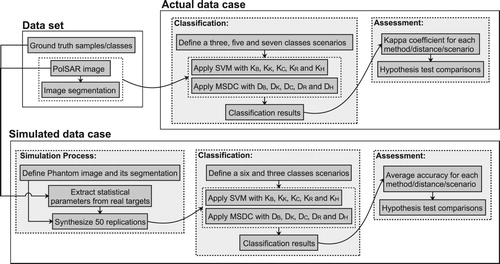
The first study (Section 3.1) consists of the classification of simulated images generated with basis on parameters estimated from targets in an actual image. The second case study (Section 3.2) focuses on the classification of the PolSAR image used to extract the parameters. The results are compared by accuracy measures and hypothesis tests.

The scenarios considered in both studies allow a robustness analysis. Specifically, the results from simulated data are assessed through the overall accuracy, while the actual data are verified with the kappa coefficient of agreement (Congalton and Green, 2009).

Figure 2 presents an overview of the experiment design, whereas the specifics are discussed in the following sections.

Figure 2. The experiment design overview.

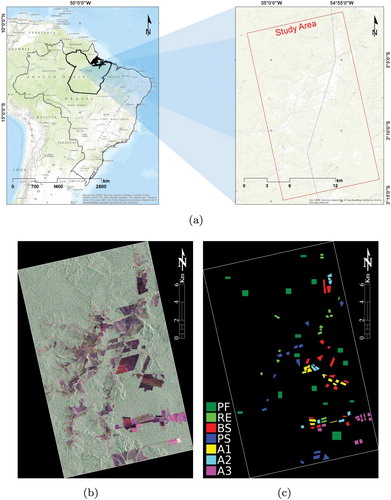
The actual PolSAR data belongs to an image acquired on 2009 March 13 by the ALOS-PALSAR sensor with approximately $20\mathrm{m}\times 20\mathrm{m}$ resolution after a $3\times 3$ multi-look process. This image, with center near to $3^{\circ }{8}^{\prime }{19}^{″}$ South and ${54}^{\circ }{55}^{\prime }{26}^{″}$ West, corresponds to a region near the Tapajós National Forest, State of Pará, Brazil.

A field work campaign conducted in September 2009 identified the following land use and land cover (LULC) types: Primary Forest (PF), Regeneration (RE), Pasture (PS), Bare Soil (BS), and three types of Agriculture (A1, A2 and A3). These agricultural classes differ on the crop type or growing stage. Figures 3(a), 3(b) and 3(c) present the study area location, a color composition of the ALOS-PALSAR image and the LULCs, respectively.

Figure 3. The study area, actual PolSAR image and the spatial distribution of the LULC samples used in the study. (a) Study area location, (b) ALOS-PALSAR image in RGB color composition (HH, HV, VV) and (c) LULC samples.

The experiments run on a computer with an Intel Core i7 processor, and 16 GB of RAM running the Debian Linux version 8.1 operating system. The platform was the IDL (Interactive Data Language) version 7.1 programming platform.

3.1. Classification of simulated data

3.1.1. Image simulation

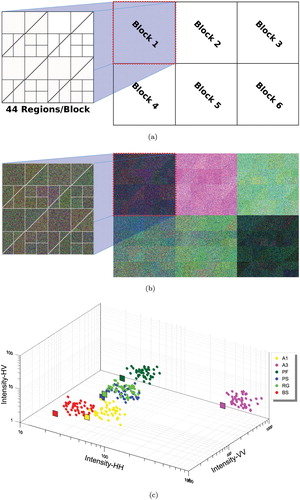
The process adopted for simulated images involves two primary steps. The first step consists of defining a ‘phantom image’ which is an idealized model for the spatial distribution of classes. The phantom is formed by six identical blocks of $512\times 512$ pixels. Each block represents a distinct class, which is partitioned into 44 segments of different dimension. Figure 4(a) illustrates the phantom image and the structure inside the blocks.

Figure 4. Simulated data. (a) Phantom - Blocks, (b) Simulation example and (c) Mean covariance matrices (squares), and 44 perturbed covariance matrices (circles) in semilogarithmic scale.

The second step consists of simulating pixels values. For this purpose, we adopted a procedure based on Goodman (1963). In order to obtain samples from the Wishart distribution with covariance matrix $\mathrm{\Sigma }$ and L looks, we obtain L independent deviates from scattering vectors following a Complex Multivariate Gaussian distribution with zero mean and covariance matrix Θ:(13) $\tilde{\mathbf{z}}=\left(z_1{z}_2{z}_3\right)+\left(z_4{z}_5{z}_6\right)\mathrm{i};\left(z_1{z}_2{z}_3{z}_4{z}_5{z}_6\right)\sim \mathcal{N}\left(\mathbf{0},\mathrm{\Theta }\right),$(13) where $\mathrm{i}$ represents the imaginary unit and the covariance matrix of the Gaussian law is$\mathrm{\Theta }=\left(\begin{array}{cc}\left[\mathrm{\Re }\left(\mathrm{\Sigma }\right)\right]& \left[-\mathrm{\Im }\left(\mathrm{\Sigma }\right)\right]\\ \left[\mathrm{\Im }\left(\mathrm{\Sigma }\right)\right]& \left[\mathrm{\Re }\left(\mathrm{\Sigma }\right)\right]\end{array}\right).$We then apply Equation (1(1) $\mathbf{Z}=\frac{1}{N}\sum _{\ell =1}^N{\mathbf{z}}_{\ell }{\mathbf{z}}_{\ell }^{\star T}=\left(\begin{array}{ccc}{Z}_{hh}& Z_{hhhv}& Z_{hhvv}\\ Z_{hhhv}^{\star }& Z_{hv}& Z_{hvvv}\\ Z_{hhvv}^{\star }& Z_{hvvv}^{\star }& Z_{vv}\end{array}\right),$(1) ) to obtain an observation. Each class is modeled by a covariance matrix $\mathrm{\Sigma }$ obtained by averaging observations from the corresponding LULC.

We introduce intra-class variability to describe ‘imperfect’ samples and, with this, model plausible errors in the training stage. Frery, Ferrero, and Bustos (2009) analyzed the effect of such errors in classification, and showed that incorporating context is a way of alleviating such problem.

Consider the (true, unobserved) covariance matrix Σ that describes a class. If it is estimated with perfect samples, i.e. with independent identically distributed observations from the hypothesized distribution, then its maximum likelihood estimate $\hat{\mathrm{\Sigma }}$ will be as close to Σ as the information in the sample permits. Errors in the training stage may lead to suboptimal estimates in terms of bias and variance. We model this situation by introducing random perturbations in $\hat{\mathrm{\Sigma }}$, as follows.

The user believes each class is characterized by Σ but, in fact, the data come from 44 slightly different models: ${\mathrm{\Sigma }}_1,\dots ,{\mathrm{\Sigma }}_{44}$. These models are built by adding random covariance matrices ${\mathrm{{\rm Y}}}_1,\dots ,{\mathrm{{\rm Y}}}_{44}$ to $\hat{\mathrm{\Sigma }}$, which is obtained estimating from actual data from a single class. Each perturbation covariance matrix is formed as${\mathrm{{\rm Y}}}_{\ell }={\left(S_{\ell ,hh}{S}_{\ell ,hv}{S}_{\ell ,vv}\right)}^{\mathrm{T}}{\left(S_{\ell ,hh}{S}_{\ell ,hv}{S}_{\ell ,vv}\right)}^{\star },1\le \ell \le 44,$where $S_{\ell ,ij}$ are independent uniform random variables on $\sqrt{\theta {\overline{I}}_{ij}\left(2\sqrt{L}\right)}\cdot (-1,1)$, where ${\overline{I}}_{ij}$ is the ij diagonal element of $\hat{\mathrm{\Sigma }}$, and $\theta >0$ controls the perturbation. With this, each mean intensity ${\overline{I}}_{ij}$ in ${\mathrm{\Sigma }}_{\ell }$ is a value in ${\overline{\hat{I}}}_{ij}\cdot [1,\theta {\sigma }_{ij}]$, where ${\overline{\hat{I}}}_{ij}$ is the (wrongly assumed for the whole block) mean intensity, and ${\sigma }_{ij}$ is the standard deviation of ${\hat{I}}_{ij}$.

Notice that the correct model for each class would be a mixture of 44 distributions, but the user will train each class with samples from 11 (typically slightly) different laws; cf. the colored squares in Figure 5(a). With this, we assess how the classification techniques perform in the practical situation of using less classes for describing a complex truth, and not collecting samples from all the underlying classes. Figure 4(c) shows, in logarithmic scale, the intensity of averaged covariance matrices as squares, and their respective 44 perturbed versions.

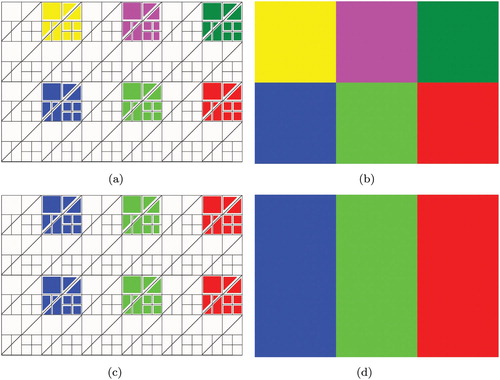
Figure 5. Simulated data. (a) Training samples – six classes case, (b) Ideal result for six classes, (c) Training samples – three classes case and (d) Ideal result for three classes.

As can be seen from Figure 4(c) we consider the following situations:

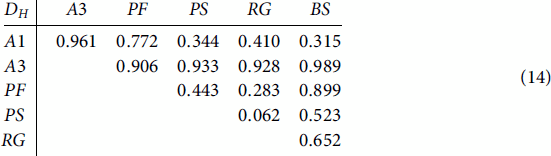
• Classes that do not overlap, e.g. A1 and A3, A1 and PF, A1 and RG, A3 and all others, PF and BS, PS and BS, RG and BS

• Classes with some overlap, e.g. A1 and PS, A1 and BS,

• Classes that overlap, e.g. PS and RG.

This is corroborated by (14) below, which shows the Hellinger distances between the classes.

Figure 4(b) presents a simulated image, where it is possible to identify the intra-class variability. The covariance matrices that plays the rule of $\hat{\mathrm{\Sigma }}$ in the simulation process, estimated from observed LULC samples shown in Figure 3(c), are presented as Appendix.

3.1.2. Classification and results

A set of fifty images were simulated independently following the procedure described in Section 3.1.1 Each image was then classified using the MSDC and SVM methods. MSDC used the stochastic distances between Complex Multivariate Wishart distributions by plugging Equations (4(4) $\begin{array}{cc}{\mathrm{D}}_{\mathrm{B}}(X,Y)& =N\left[\frac{\log |{\mathbf{\Sigma }}_1|+\log |{\mathbf{\Sigma }}_2|}{2}-\log \left|{\left(\frac{{\mathbf{\Sigma }}_1^{-1}+{\mathbf{\Sigma }}_2^{-1}}{2}\right)}^{-1}\right|\right],\end{array}$(4) ) to (8(8) $\begin{array}{c}{\mathrm{D}}_{\mathrm{C}}(X,Y)={\left(\frac{|{\mathbf{\Sigma }}_1|}{|{\mathbf{\Sigma }}_2{|}^2}\mathrm{abs}\left(\left|{\left(2{\mathbf{\Sigma }}_2^{-1}-{\mathbf{\Sigma }}_1^{-1}\right)}^{-1}\right|\right)\right)}^N\\ +{\left(\frac{|{\mathbf{\Sigma }}_2|}{|{\mathbf{\Sigma }}_1{|}^2}\mathrm{abs}\left(\left|{\left(2{\mathbf{\Sigma }}_1^{-1}-{\mathbf{\Sigma }}_2^{-1}\right)}^{-1}\right|\right)\right)}^N-2,\end{array}$(8) ) in (9(9) $({\mathcal{R}}_i,{\omega }_j)\iff j=\underset{j=1,\dots ,c}{\arg \min }\mathrm{D}({\hat{f}}_{{\mathcal{R}}_i},{\hat{f}}_{{\omega }_j}).$(9) ). SVM also employed these distances through the kernel functions in (11(11) $m({\mathcal{R}}_u,{\mathcal{R}}_v)=\left\{\begin{array}{cc}0& \mathrm{if}{\mathcal{R}}_u={\mathcal{R}}_v,\\ \mathrm{D}({\mathcal{R}}_u,{\mathcal{R}}_v)+\tau & \mathrm{if}{\mathcal{R}}_u\ne {\mathcal{R}}_v.\end{array}\right.$(11) ) and (12(12) $K({\mathcal{R}}_u,{\mathcal{R}}_v)={\mathrm{e}}^{-\gamma m\left({\mathcal{R}}_u,{\mathcal{R}}_v\right)},$(12) ).

Furthermore, although the simulated images have six well-defined blocks of targets (regions), such objects where classified in two scenarios (i.e. classes configurations). The first scenario considers each block as a single class, the second scenario considers the blocks 1 and 4; 2 and 5; and 3 and 6 as three distinct classes. The second scenarios describes situations where the user specifies less classes than those actually present in the image. According to this organization, Figures 5(a) and 5(b) present the training samples and the ideal results expected for the first scenario; similarly, Figures 5(c) and 5(d) refer to the second scenario.

Using preliminary tests, the order of the Rényi distance (β) was set to 0.9 for both SVM and MSDC methods. The SVM penalty and kernel parameter were adjusted for each image, considering a fixed parameter space, through an exhaustive search for the configuration which produces the most accurate results with respect to testing samples. In this study, penalty ranges in $\{1,10,100,1000,10000\}$ and the kernel flexibility γ in$\{0.05,0.1,0.15,\dots ,10.0\}$.

Two multiclass strategies were considered for SVM in order to assess relationships between strategies, scenarios, kernels and method performance: One-Against-All (OAA) and One-Against-One (OAO), denoted SVM-OAA and SVM-OAO respectively. Details about these strategies can be found in Webb and Copsey (2011).

We measured the accuracy of each classification result by the number of correctly classified regions, without taking into account training regions. Figure 6 represents the classification accuracy achieved by each method for different configurations (i.e. stochastic distances/kernel and multiclass strategy for SVM). Table 1 presents the p-values of a bilateral t-test to check the statistical equality between the accuracy values achieved by two distinct combinations of methods and distances. Further discussions about statistical equality are based on 95% of confidence.

Figure 6. The accuracy of classification results for the simulated data set. (a) Six classes classification and (b) Three classes classification.

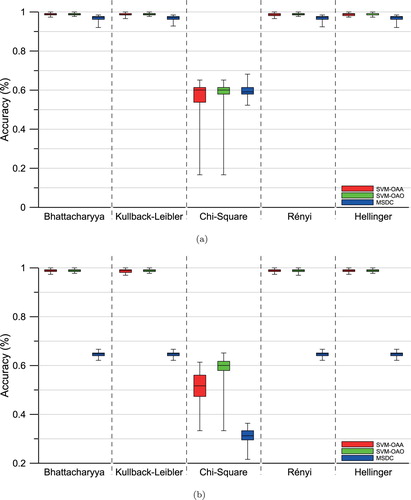
Table 1. Test statistic p-values for the t test that verifies that two classification techniques produce equivalent results. Values above (below) the diagonal correspond to the six (three, resp.) classes. Underlined values indicate equivalent coefficients at the 95% level.

		B			K			C			R			H
		SA	SO	MS	SA	SO	MS	SA	SO	MS	SA	SO	MS	SA	SO	MS
	SA	–	.808	.191	.929	.872	.186	.001	.000	.000	.927	.850	.189	.979	.850	.191
B	SO	.914	–	.147	.757	.936	.142	.001	.000	.000	.752	.957	.145	.797	.966	.147
	MS	.000	.000	–	.228	.162	.984	.002	.000	.000	.224	.156	.987	.203	.161	1.00
	SA	.861	.785	.000	–	.815	.224	.001	.000	.000	1.00	.795	.227	.000	.796	.228
K	SO	.978	.935	.000	.840	–	.157	.001	.000	.000	.811	.979	.160	.858	.973	.162
	MS	.000	.000	.996	.000	.000	–	.002	.000	.000	.220	.151	.997	.199	.156	.984
	SA	.000	.000	.064	.000	.000	.064	–	.881	.691	.001	.001	.002	.001	.001	.002
C	SO	.000	.000	.355	.000	.000	.335	.478	–	.785	.000	.000	.000	.000	.000	.000
	MS	.000	.000	.000	.000	.000	.000	.016	.001	–	.000	.000	.000	.000	.000	.000
	SA	.903	.822	.000	.955	.881	.000	.000	.000	.000	–	.790	.223	.949	.792	.224
R	SO	.986	.906	.000	.880	.996	.000	.000	.000	.000	.921	–	.154	.837	.993	.156
	MS	.000	.000	.996	.000	.000	1.00	.064	.355	.000	.000	.000	–	.202	.159	.987
	SA	.972	.889	.000	.000	.951	.000	.000	.000	.000	.933	.987	.000	–	.875	.203
H	SO	.949	.964	.000	.814	.971	.000	.000	.000	.000	.853	.938	.000	.886	–	.161
	MS	.000	.000	1.00	.000	.000	.996	.064	.335	.000	.000	.000	.996	.000	.000	–

In the following tables SA, SO and MS represent the SVM-OAA, SVM-OAO and MSDC methods, and B, K, C, R and H represent the Bhattacharyya, Kullback-Leibler, Chi-Square, Rényi and Hellinger stochastic distances in the kernel functions.

Focusing on the results of the first scenario (six classes), illustrated in Figure 6(a), we obtain high accuracy values regardless the method or distance adopted, except for the Chi-Square distance. Six hundred classifications were produced by three methods (SVM-OAA, SVM-OAO and MSDC), four distances (Bhattacharyya, Kullback-Leibler, Rényi and Hellinger, except Chi-Square) and fifty synthetic images. The minimum and maximum values observed over the 600 classifications were 92% and 100% respectively.

The Chi-Square distance does not only produce lower accuracy, but also higher variation in comparison to the other distances/methods. Numerical problems with the Chi-square distance have been reported by Frery, Nascimento, and Cintra (2011). Furthermore, the use of such distance in MSDC and SVM through (8(8) $\begin{array}{c}{\mathrm{D}}_{\mathrm{C}}(X,Y)={\left(\frac{|{\mathbf{\Sigma }}_1|}{|{\mathbf{\Sigma }}_2{|}^2}\mathrm{abs}\left(\left|{\left(2{\mathbf{\Sigma }}_2^{-1}-{\mathbf{\Sigma }}_1^{-1}\right)}^{-1}\right|\right)\right)}^N\\ +{\left(\frac{|{\mathbf{\Sigma }}_2|}{|{\mathbf{\Sigma }}_1{|}^2}\mathrm{abs}\left(\left|{\left(2{\mathbf{\Sigma }}_1^{-1}-{\mathbf{\Sigma }}_2^{-1}\right)}^{-1}\right|\right)\right)}^N-2,\end{array}$(8) ) provides statistically equal results.

SVM has better performance than MSDC in the second scenario. Usually, OAO multiclass strategy provides higher average accuracy compared to OAA, even though both strategies provide statistically equal results. Furthermore, we note that the methods are not influenced by the adopted distance, with exception of the Chi-Square distance, where the results are very similar. It is noteworthy that Batthacharyya, Rényi and Hellinger distances in SVM lead to accurate results and small deviations.

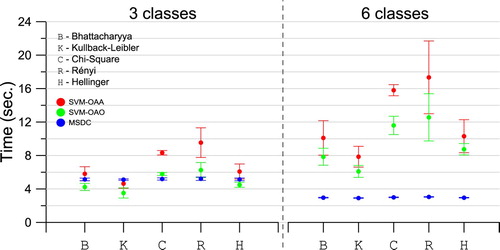
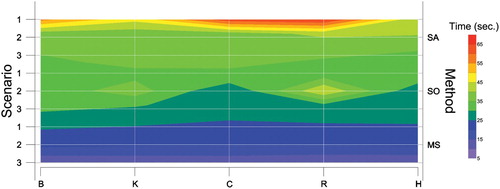
Figure 7 presents the computational time spent for training and performing the classification by each method. We observe that in the first scenario the MSDC method spends approximately 3 s, while SVM has a higher cost, specially when OAA strategy is adopted. The reason for this is the training stage, which although SVM with OAO strategy requires splitting the multiclass classification in fifteen binary problems, when OAA is adopted the SVM training needs to solve six large quadratic optimization problems (for details, see Theodoridis and Koutroumbas, 2008).

Figure 7. The computational of the analyzed methods in the expriment with synthetic data.

Additionally, we note that MSDC it is more expensive in the second scenario than in the first. Although the second scenario has fewer classes, the quantity of training regions is larger and, then, requires more time to estimate the parameters (i.e. the covariance matrix of each classes) of the probability distribution function that models the classes. With respect to SVM, in general it requires less time in comparison to the first scenario since there are less classes. OAA is still more expensive in the second scenario. Furthermore, the Kullback-Leibler kernel function requires the shortest average times SVM.

3.2. Classification of data from an actual sensor

This section presents classification results of the ALOS-PALSAR image shown in Figure 3(b). In analogy to Section 3.1.2, we discuss a variety of classification scenarios.

The first scenario uses all LULC classes identified in the study area; cf. Table 2. The union of the agriculture classes (i.e. A1, A2 and A3) defines the new class called Agricultural Areas (AA). A second scenario is created with the five classes AA, PF, PS, RG and BS. The last third scenario consists of three classes: Agricultural Areas, High Biomass (HB) and Low Biomass (LB). HB is obtained merging Primary Forest and Regeneration classes, LB comes from the union between Pasture and Bare Soil. We obtain the training and testing samples of AA, HB and LB classes by merging the sample polygons of the individual classes. These scenarios describe practical situations of users with different interests and knowledge of the area. The Appendix provides the sample covariance matrices from the six LULC classes.

Table 2. Summary of the land cover classes samples.

	Training		Testing
LULC Classes	Polygons	Pixels	Polygons	Pixels
Agruculture 1 (A1)	4	3669	8	7455
Agruculture 2 (A2)	4	2902	8	6731
Agruculture 3 (A3)	3	2332	8	7049
Primary Forest (PF)	3	5430	10	29306
Pasture (PS)	5	3334	10	12866
Regeneration (RE)	5	2570	10	7307
Bare Soil (BS)	5	5384	11	13352

Figures 8(a), 8(b) and 8(c) show the spatial distribution of training and testing samples of each scenario, while Table 2 presents a summary of the LULC samples. The spatial distribution of these samples is also shown in Figure 8(a), where training and test samples are shown in solid and empty polygons, respectively.

Figure 8. Spatial distribution of the samples on the different considered scenarios and the adopted segmentation. (a) Scenario 1, (b) Scenario 2, (c) Scenario 3 and (d) Segmentation.

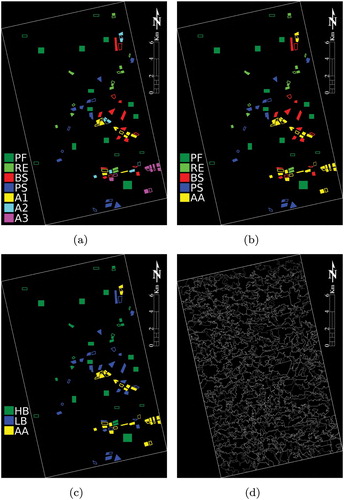
The region-based classification requires a segmentation. It was performed using the region-growing method available in the Geographic Information System SPRING (Camara et al., 1996, freely available at http://www.dpi.inpe.br/spring/english/), choosing the segmentation parameter by visual inspection. Figure 8(d) shows the segments contours.

We applied all possible combinations of methods, distances and multiclass strategies to the image and its segmentation. The SVM parameters were obtained following the same procedures and space searches described in Section 3.1.2. The data were spatially subsampled taking one every three pixels in both horizontal and vertical direction in order to reduce the spatial dependence. The accuracy was measured by the kappa agreement coefficient with respect to the test samples.

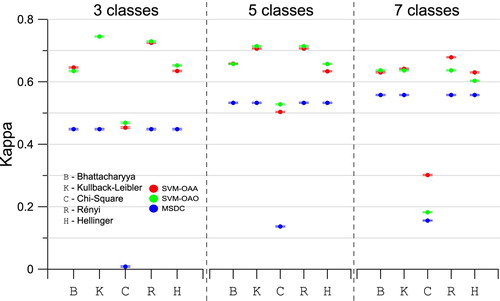
Figure 9 shows the kappa values along with their standard deviation. Additionally, Tables 3–5 present the p-values of a bilateral hypothesis test to check the statistical equality between kappa values achieved by two distinct combinations of methods and distances for each scenario. Further discussions about statistical equality are based on 95% of confidence.

Figure 9. Classification accuracy.

Table 3. p-values from hypothesis test for comparing methods and distances with seven classes. Underlined values indicate equivalent coefficients at the 95% level.

		B			K			C			R			H
		SA	SO	MS	SA	SO	MS	SA	SO	MS	SA	SO	MS	SA	SO	MS
B	SA	–	.014	.000	.000	.014	.000	.000	.000	.000	.000	.014	.000	1.00	.000	.000
	SO		–	.000	.052	1.00	.000	.000	.000	.000	.000	1.00	.000	.014	.000	.000
	MS			–	.000	.000	1.00	.000	.000	.000	.000	.000	1.00	.000	.000	1.00
K	SA				–	.052	.000	.000	.000	.000	.000	.052	.000	.000	.000	.000
	SO					–	.000	.000	.000	.000	.000	1.00	.000	.014	.000	.000
	MS						–	.000	.000	.000	.000	.000	1.00	.000	.000	1.00
C	SA							–	.000	.000	.000	.000	.000	.000	.000	.000
	SO								–	.000	.000	.000	.000	.000	.000	.000
	MS									–	.000	.000	.000	.000	.000	.000
R	SA										–	.000	.000	.000	.000	.000
	SO											–	.000	.014	.000	.000
	MS												–	.000	.000	1.00
H	SA													–	.000	.000
	SO														–	.000

Table 4. p-values from hypothesis for comparing methods and distances with five classes. Underlined values indicate equivalent coefficients at the 95% level.

		B			K			C			R			H
		SA	SO	MS	SA	SO	MS	SA	SO	MS	SA	SO	MS	SA	SO	MS
B	SA	–	.697	.000	.000	.000	.000	.000	.000	.000	.000	.000	.000	.000	.697	.000
	SO		–	.000	.000	.000	.000	.000	.000	.000	.000	.000	.000	.000	1.00	.000
	MS			–	.000	.000	1.00	.00	.100	.000	.000	.000	1.00	.000	.000	1.00
K	SA				–	.002	.000	.000	.000	.000	1.00	.002	.000	.000	.000	.000
	SO					–	.000	.000	.000	.000	.002	1.00	.000	.000	.000	.000
	MS						–	.000	.100	.000	.000	.000	1.00	.000	.000	1.00
C	SA							–	.000	.000	.000	.000	.000	.000	.000	.000
	SO								–	.000	.000	.000	.100	.000	.000	.100
	MS									–	.000	.000	.000	.000	.000	.000
R	SA										–	.002	.000	.000	.000	.000
	SO											–	.000	.000	.000	.000
	MS												–	.000	.000	1.00
H	SA													–	.500	.000
	SO														–	.000

Table 5. p-values from hypothesis tests for comparing methods and distances with three classes. Underlined values indicate equivalent coefficients at the 95% level.

		B			K			C			R			H
		SA	SO	MS	SA	SO	MS	SA	SO	MS	SA	SO	MS	SA	SO	MS
B	SA	–	.000	.000	.000	.000	.000	.000	.000	.000	.000	.000	.000	.000	.031	.000
	SO		–	.000	.000	.000	.000	.000	.000	.000	.000	.000	.000	.970	.000	.000
	MS			–	.000	.000	1.00	.154	.000	.000	.000	.000	1.00	.000	.000	1.00
K	SA				–	.069	.000	.000	.000	.000	.000	.000	.000	.000	.000	.000
	SO					–	.000	.000	.000	.000	.000	.000	.000	.000	.000	.000
	MS						–	.154	.000	.000	.000	.000	1.00	.000	.000	1.00
C	SA							–	.000	.000	.000	.000	.154	.000	.000	.154
	SO								–	.000	.000	.000	.000	.000	.000	.000
	MS									–	.000	.000	.000	.000	.000	.000
R	SA										–	.105	.000	.000	.000	.000
	SO											–	.000	.000	.000	.000
	MS												–	.000	.000	1.00
H	SA													–	.000	.000
	SO														–	.000

We observe that the Chi-Square distance produces low kappa values in both methods and with both multiclass strategies for SVM. This is due to the aforementioned numerical instabilities presented by this measure. While most of the considered distances ranged, in the experiments, from ${10}^{-1}$ to ${10}^2$, the Chi-Square had its values approximately in 0 to ${10}^6$.

Results provided by MSDC using the Bhatacharyya, Kullback-Leibler, Rényi and Hellinger are statistically the same.

Similarly to the results presented in Section 3.1.2, the choice of a multiclass strategy does not have strong influence on the performance of SVM. Except when the Batthacharyya distance is used, the increased in intra-class variability, which occurs when the number of classes decrease, suggests the use of OAO strategy in SVM. Observing the SVM performance as function of the stochastic distance integrated in its kernel, the Rényi distance has the highest accuracy in the first scenario. Regarding the second and third scenarios, SVM performs better when the kernel functions are enhanced with Kullback-Leibler and Rényi distances.

The influence of the scenario is noteworthy. As the number of classes decreases, leading to increasing intra-class variability, the performance of MSDC also decreases. Converseley, the classification accuracy of SVM tends to increase while the number of classes decrease.

In summary, SVM presented better performance with respect to MSDC. Kullback-Leibler and Rényi distances are the preferred choice for defining radial basis kernel functions for the region-based classification with SVM.

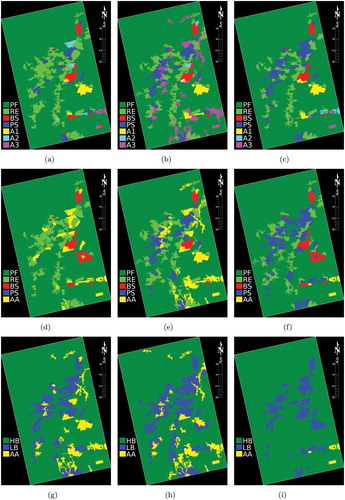
Figure 10 shows selected results. The first scenario, that considers seven classes, posses a difficult problem to both methods to discriminate the agricultural classes (i.e. A1, A2 and A3). With respect to the second scenario, while SVM with OAA strategy does not distinguish PS and MSDC often confuses AA with PS, the SVM with OAO strategy provides a better separation between such classes. In the last scenario MSDC was not apt to separating AA and LH classes, differently fom SVM. This last method, specially when using OAA strategy, provides a better classification of HB and LB areas; cf. the central region of the study area.

Figure 10. Actual data classification results. (a) SA/B – Scenario 1, (b) SO/K – Scenario 1, (c) MS/R – Scenario 1, (d) SA/H – Scenario 2, (e) SO/R – Scenario 2, (f) MS/K – Scenario 2, (g) SA/R – Scenario 3, (h) SO/K – Scenario 3 and (i) MS/H – Scenario 3.

Figure 11 presents the computational time spent by the methods in the experiments with actual data. It can be noted a gradual increase in the processing time when dealing with scenarios with more classes. As previously observed in the first case study, the use of OAA strategy by SVM implies more processing time compared to OAO. MSDC is the least computational intensive method. Furthermore, the time execution is relatively insensitive to choices of distances.

Figure 11. Computational time of the analyzed methods in the experiment with actual data.

4. Conclusions

The objective of this study was to verify the performance of SVM for region-based classification of PolSAR image in comparison to MSDC. For this purpose, we adopted radial basis functions derived from stochastic distances between Complex Multivariate Wishart distributions: Bhatacharyya, Kullback-Leibler, Chi-Square, Rényi and Hellinger. We used simulated images and data from an operational sensor, and proposed a number of scenarios which describe different situations of ability to discriminate classes. These scenarios depict actual situations users encounter in practice.

It was found that SVM it is more robust than MSDC in both simulated and actual data sets because, depending on the adopted multiclass strategy, SVM has equal or superior performance on simple scenarios (first scenarios of simulated and actual data sets – Figures 6(a) and 9) and superior in more complex scenarios (second scenario of simulated and second and third scenarios with actual data sets – Figures 6(b) and 9).

The main drawbacks of SVM are its computational cost and the need to tuning the penalty and the kernel parameter.

As previously verified by Silva et al. (2013), the Chi-Square distance is not indicated to perform classification through MSDC. Its numerical instabilities lead to relative poor performance.

Face to the exposed results, the SVM method presented a better performance compared to MSDC. With respect to radial basis kernel functions considered in this study for region-based classification with SVM, the preferred ones are Kullback-Leibler and Rényi distances. The use of distinct stochastic distances on MSDC does not lead to improved accuracy, so the choice should be based on computational execution time.

Underlying research materials

The underlying research materials for this article can be accessed at: https://github.com/rogerionegri/SVM-PolSAR.

Disclosure statement

There is no conflict of interest involving this research.

ORCID

Rogério G. Negri http://orcid.org/0000-0002-4808-2362

Alejandro C. Frery http://orcid.org/0000-0002-8002-5341

Wagner B. Silva http://orcid.org/0000-0002-5686-5105

Tatiana S. G. Mendes http://orcid.org/0000-0002-0421-5311

Luciano V. Dutra http://orcid.org/0000-0002-7757-039X

Additional information

Funding

The authors thank Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) (Grant 2014/14830-8), UNESP/PROPe (Grant 2016/1389), Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) and Fundação de Amparo à Pesquisa do Estado de Alagoas (Fapeal) for funding this research.