Topological relations between spherical spatial regions with holes

ABSTRACT

There is growing interest in globally modelling the entire planet. Although topological relations between spherical simple regions and topological relations between regions with holes in the plane have been investigated, few studies have focused on the topological relations between spherical spatial regions with holes. The 16-intersection model (16IM) is proposed to describe the topological relations between spatial regions with holes. A total of 25 negative conditions are proposed to eliminate the impossible topological relations between spherical spatial regions with holes. The results show that (1) 3 disjoint relations, 3 meet relations, 66 overlap relations, 7 cover relations, 3 contain relations, 1 equal relation, 7 coveredBy relations, 3 inside relations, 1 attach relation, 52 entwined relations, and 28 embrace relations can be distinguished by the 16IM and that (2) the formalisms of attach, entwined, and embrace relations between the spherical spatial regions without holes based on the 9IM and that between the spherical spatial regions with holes based on the simplified 16IM are different, whereas the formalisms of other types of relations between spherical spatial regions without holes based on the 9IM and that between the spherical spatial regions with holes based on a simplified 16IM are the same.

KEYWORDS:

• Topological relations
• spatial region with holes
• 16-intersection model (16IM)
• spatial analysis

1. Introduction

Since Digital Earth was proposed, the related technologies of capturing, storing, processing and displaying geographical information have made considerable progress (Gore 1998; Vilchesblázquez et al. 2014). Many geographical phenomena occur on a global scale, such as global climate change (Kadiyala et al. 2015), and global land cover (Chen et al. 2017). Although the Digital Earth platform has the ability to store, retrieve and visualize global data (Goodchild and Woodgate 2012; Hernandez 2017), advanced analysis (e.g. spatial analysis on the sphere (Nicholas 2013), spatial simulation (Chen and Lin 2018; Mekni 2018)) should be further performed. The analysis of spatial relations is one foundation for the advanced analysis. The spatial relation is commonly grouped into topological relations, direction relations, and metric relations (Worboys 1992; Sharma 1996). Among these spatial relations, topology is considered to be first-class information (Egenhofer and Mark 1995). The topological relations are effective for spatial querying and human decision-making (Dube 2017). With the attention of the global-scale geographical phenomena, topological relations between the global-scale spatial entities should also attract more attention.

Many geographical objects and phenomena are presented as surface distributions, such as lakes, forests, and cities. The spatial region in the two-dimensional space, three-dimensional space and spherical space are different. The region in the two-dimensional space is a plane (Open Geospatial Consortium 1999) and the region in the three-dimensional space is normally a free surface (Zlatanova 2000a; Lee and Kwan 2005; Open Geospatial Consortium 2012), whereas, the region in the spherical space is a surface that is strictly attached to the surface of the sphere (Otoo and Zhu 1993; Gold and Mostafavi 2000). The two-dimensional space, three-dimensional space and spheric space are also different. The two-dimensional space (Egenhofer and Herring 1991; Schneider and Behr 2006; Long and Li 2013; Shen, Chen, and Liu 2018) and three-dimensional space (Egenhofer 1995; Zlatanova 2000b; Kurata 2009) are usually defined as infinite space, whereas the spherical space (Egenhofer 2005) is usually defined as finite space. Moreover, many geographical objects and phenomena have holes, such as lakes with islands and a state within a state. As a type of spatial region, a spatial region with holes has the characteristics of the separated boundaries and separated holes (Egenhofer, Clementini, and Di Felice 1994). Topological relations between spatial regions with holes are more complex than topological relations between simple spatial regions.

The formalization of topological relations has been investigated. Although the 4-intersection model (4IM) (Egenhofer and Franzosa 1991), the 9-intersection model (9IM) (Egenhofer and Herring 1991), and their extended models (Egenhofer, Clementini, and Di Felice 1994; Chen et al. 2001; Kurata 2008; Shen, Zhou, and Chen 2017) can represent topological relations, most studies focus on simple spatial objects. A relation matrix is proposed to model the topological relations between regions with holes (Egenhofer, Clementini, and Di Felice 1994). The relation matrix is a detail model, whereas this model is highly complex. The topological relations between complex spatial objects based on the 9IM were explored (Schneider and Behr 2006), whereas the holes were not considered in the 9IM. Worboys and Bofakos (1993) and Hazarika and Hazarika (2012) also discussed the topological relations between regions with holes in the plane. However, research on the topological relations among spherical spatial regions with holes has not been explored.

Although considerable research has been performed to study topological relations for many spatial objects embedded in various spaces based on different topological relationship models, further work is required to consider how many and what types of topological relations between spherical spatial regions with holes can be realized. Unlike the two-dimensional planar spatial region and three-dimensional free-form surface, the spherical region is a surface that is strictly attached to the surface of the sphere. The global geographical phenomena are widely represented as spherical regions. Therefore, the topological relations between the global geographical phenomena should be explored. Because the holes should be considered and spherical regions with holes are embedded in a finite space for the topological relations between spherical spatial regions with holes, topological relations between spherical spatial regions with holes are different from the previous studies. Therefore, the aim of this research is to study the topological relations between spherical spatial regions with holes. To study the topological relations between spherical spatial regions with holes, two aspects are considered: (1) topological relation models for spherical spatial regions with holes, and (2) all the topological relations between spherical spatial regions with holes based on the proposed topological relation models.

The remainder of this paper is outlined as follows. Section 2 introduces the proposed topological relation model for spherical spatial regions with holes. Section 3 describes the possible topological relations between spherical spatial regions with holes. Section 4 discusses the topological relations between spatial regions without holes and the topological relations between spatial regions with holes. Section 5 provides an example of topological relations between spherical spatial regions with holes. Section 6 presents the study’s conclusions and discusses future work.

2. Sixteen-intersection model

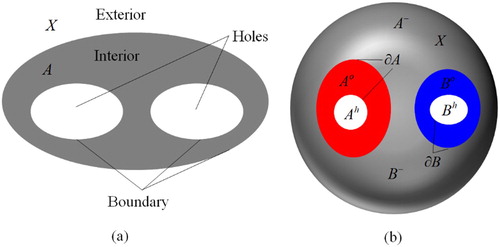
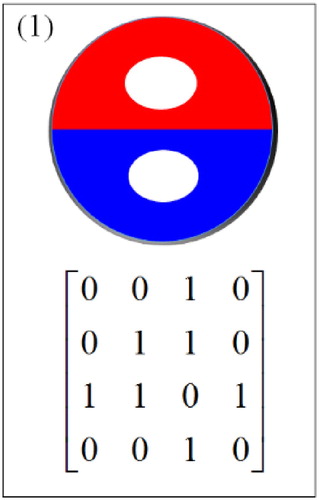
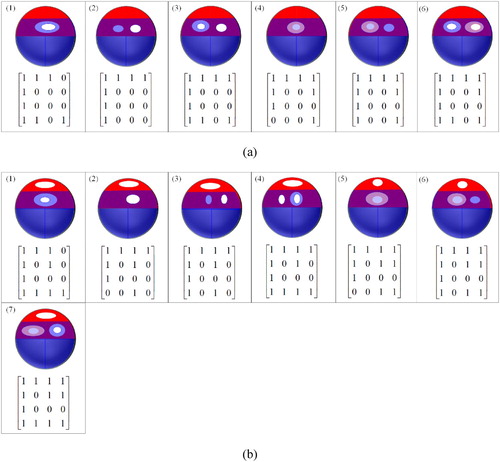
A spatial region without holes is usually defined as a connected interior, a connected boundary and a connected exterior. Unlike spatial region without holes, a spatial region with holes is defined as a connected interior, several separated boundaries, a connected exterior, and several separated holes. Therefore, a spatial region with holes can be divided into four parts: interior, boundary, exterior and holes (Figure 1(a)).

Figure 1. Interior, boundary, exterior and holes of spatial region with holes.

Since spatial region with holes has the characteristics of connected interior, separated boundaries and separated holes, for any spatial region with holes A need meets the following properties: (1) the holes of A cannot touch the boundary or the exterior of A, (2) the interior of A is connected, (3) there is no intersection between any two holes of A, and (4) there is no intersection between any two boundaries of A.

Let spatial object A as a spatial region with holes and spatial object B as a spatial region with holes be the subsets of space X (Figure 1(b)). The colour of spatial object A is red and the colour of spatial object B is blue in Figure 1(b) and the following figures. The 16-intersection model (16IM) between A and B describes a topological relation with a 4 × 4 matrix and is represented by the following formula:(1) $R_{16IM}(A,B)=\left[\begin{array}{cccc}{A}^o\cap B^o& A^o\cap \mathrm{\partial }B& A^o\cap B^{-}& A^o\cap B^h\\ \mathrm{\partial }A\cap B^o& \mathrm{\partial }A\cap \mathrm{\partial }B& \mathrm{\partial }A\cap B^{-}& \mathrm{\partial }A\cap B^h\\ A^{-}\cap B^o& A^{-}\cap \mathrm{\partial }B& A^{-}\cap B^{-}& A^{-}\cap B^h\\ A^h\cap B^o& A^h\cap \mathrm{\partial }B& A^h\cap B^{-}& A^h\cap B^h\end{array}\right]$(1) where A’s interior, boundary, exterior and holes are denoted by $A^o$, $\mathrm{\partial }A$, $A^{-}$ and $A^h$, while B’s interior, boundary, exterior and holes are denoted by $B^o$, $\mathrm{\partial }B$, $B^{-}$ and $B^h$. The value of the intersection in Formula (1) can be drawn from {0, 1}, where 0 means that the intersection is empty, and 1 represents that the intersection is non-empty. By considering the values empty and non-empty, 65,536 (65,536 = 2¹⁶) binary topological relations can be distinguished. The question ‘What topological relations between spherical spatial regions with holes can occur in reality within the 16IM?’ will be discussed in Section 3.

3. Topological relations between spherical spatial regions with holes based on the 16IM

Egenhofer (2005) concluded that 11 topological relations between two spherical simple regions based on the 9IM can be realized. These 11 topological relations are disjoint, meet, overlap, cover, contain, equal, coveredBy, inside, attach, entwined, and embrace. The mentioned 11 topological relations are further divided based on the 16IM. To list all of the possible topological relations, two steps are taken. First, all the topological relations based on the 16IM are assumed to be possible. Next, negative conditions are proposed to exclude the non-existing topological relations, and the topological relations that can be realized in the spherical space are given. All the negative conditions for the topological relations between spherical spatial regions with holes based on the 16IM are reasonable. The rationality of these negative conditions is based on the definition of the spatial regions with holes, the features of the 16IM, and the characteristics of spherical space. In the following formulas, $\overline{A}$ that is the closure of A is the union of the $A^o$ and $\mathrm{\partial }A$, $\overline{B}$ that is the closure of B is the union of the $B^o$ and $\mathrm{\partial }B$, and X is the whole spherical space, respectively. In the following formulas, ‘*’ means that the value of the intersection can take an arbitrary value (0 or 1), or ‘*’ means that the value of the intersection is irrelevant. In the following figures, the colour of the hole is black if A’s holes and B’s holes coincide.

3.1. Disjoint relation

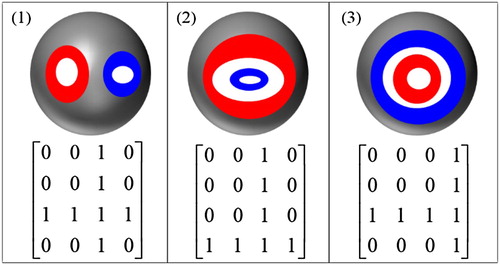
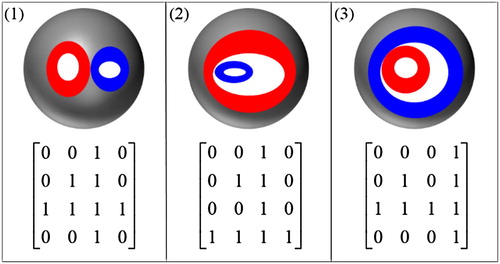
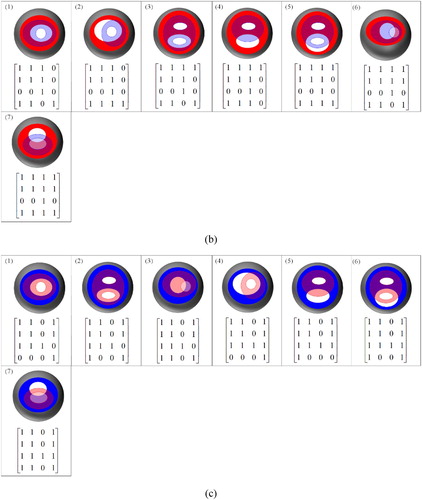
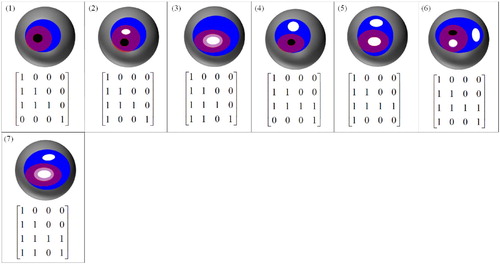
A disjoint relation means that a spatial object A is spatially disjoint with another spatial object B. If the intersection between A’s closure and B’s closure is an empty set, then the topological relation between A and B is disjoint (Formula (2)). There are two situations for the disjoint relation. The first situation is that one spatial object is located in the exterior of another spatial object (Figure 2(1)). The second situation is that one spatial object is located in the holes of another spatial object (Figure 2(2–3)). Therefore, there are three disjoint relations that can be realized based on the 16IM (Figure 2).(2) $A.Disjoint\left(B\right)\Rightarrow \overline{A}\cap \overline{B}=\phi$(2)

Figure 2. Disjoint relations between two spatial regions with holes based on the 16IM.

3.2. Meet relation

A meet relation means that a spatial object A spatially touches another spatial object B. If the intersection between A’s interior and B’s interior is an empty set, the intersection between A’s closure and B’s closure is a non-empty set, and the intersection between A’s exterior and B’s exterior is a non-empty set, then the topological relation between A and B is a meet (Formula (3)). Similar to the disjoint relation, there are two situations for the meet relation. The first situation is that one spatial object’s interior is located in the exterior of another spatial object (Figure 3(1)). The second situation is that one spatial object’s interior is located in the holes of another spatial object (Figure 3(2–3)). Therefore, there are three meet relations that can be realized based on the 16IM (Figure 3).(3) $A.Meet\left(B\right)\Rightarrow (A^o\cap B^o=\phi )\wedge (\overline{A}\cap \overline{B}\ne \phi )\wedge (A^{-}\cap B^{-}\ne \phi )$(3)

Figure 3. Meet relations between two spatial regions with holes based on the 16IM.

3.3. Overlap relation

An overlap relation means that a spatial object A spatially overlaps another spatial object B. If the intersection between A’s interior and B’s interior is a non-empty set, the intersection between A’s closure and B’s closure is not equal to A’s closure or B’s closure, and the intersection between A’s exterior and B’s exterior is a non-empty set, then the topological relation between A and B is overlap (Formula (4)).(4) $A.Overlap\left(B\right)\Rightarrow (A^o\cap B^o\ne \phi )\wedge (\overline{A}\cap \overline{B}\ne \overline{A})\wedge (\overline{A}\cap \overline{B}\ne \overline{B})\wedge (A^{-}\cap B^{-}\ne \phi )$(4)

There are three situations for the overlap relation if holes are not considered (Formula (5)). The first situation is that A’s interior, boundary and exterior intersect with B’s interior, boundary and exterior. The second situation is that A’s exterior does not intersect with B’s interior and boundary. The third situation is that B’s exterior does not intersect with A’s interior and boundary. To further categorize the overlap topological relations, negative conditions are proposed to eliminate the impossible relations.(5) $R_{16IM}(A,B)=\left[\begin{array}{cccc}1& 1& 1& \ast \\ 1& 1& 1& \ast \\ 1& 1& 1& \ast \\ \ast & \ast & \ast & \ast \end{array}\right]\vee \left[\begin{array}{cccc}1& 1& 1& \ast \\ 1& 1& 1& \ast \\ 0& 0& 1& \ast \\ \ast & \ast & \ast & \ast \end{array}\right]\vee \left[\begin{array}{cccc}1& 1& 0& \ast \\ 1& 1& 0& \ast \\ 1& 1& 1& \ast \\ \ast & \ast & \ast & \ast \end{array}\right]$(5)

Condition 3.1:

For the first situation of the overlap relation, A’s holes at least intersect with one part of B’s interior, boundary, exterior and holes. Likewise, B’s holes at least intersect with one part of A’s interior, boundary, exterior and holes.(6) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ 0& 0& 0& 0\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\end{array}\right]$(6)

Proof 1:

Because $B^o\cup \mathrm{\partial }B\cup B^{-}\cup B^h=X$ and $A^h\subset X$, A’s holes at least intersect with one part of B’s interior, boundary, exterior and holes. ▪

Condition 3.2:

For the first situation of the overlap relation, if A’s holes intersect with B’s boundary, then A’s holes must intersect with B’s interior. Likewise, if B’s holes intersect with A’s boundary, then B’s holes must intersect with A’s interior.(7) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ 0& 1& \ast & \ast \end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \end{array}\right]$(7)

Proof 2:

If a set $x$ belongs to A’s holes and $x$ belongs to B’s boundary, then the neighbourhood of $x$ must be the subset of A’s holes, and the neighbourhood of $x$ must be the subset of $B^o\cup \mathrm{\partial }B\cup B^{-}$ or $B^o\cup \mathrm{\partial }B\cup B^h$. Therefore, A’s holes must intersect with B’s interior. ▪

Condition 3.3:

For the first situation of the overlap relation, if A’s holes intersect with B’s interior and boundary, then A’s holes at least intersect with one part of B’s exterior and holes. Likewise, if B’s holes intersect with A’s interior and boundary, then B’s holes at least intersect with one part of A’s exterior and holes.(8) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ 1& 1& 0& 0\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 1\\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\end{array}\right]$(8)

Proof 3:

If a set $x$ belongs to A’s holes and $x$ belongs to B’s interior and boundary, then the neighbourhood of $x$ must be the subset of A’s holes, and the neighbourhood of $x$ must be the subset of $B^o\cup \mathrm{\partial }B\cup B^{-}$ or $B^o\cup \mathrm{\partial }B\cup B^h$. Therefore, A’s holes at least intersect with one part of B’s exterior and holes. ▪

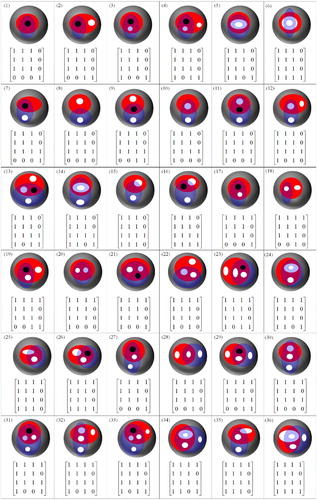
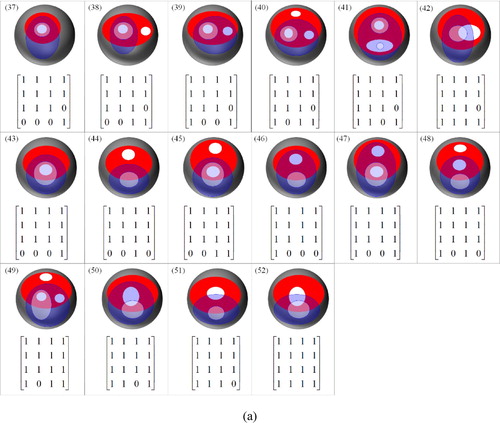
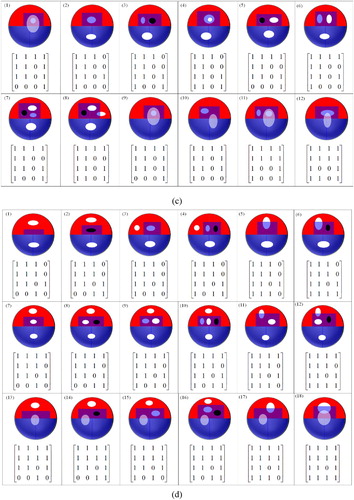
Based on the conditions 3.1–3.3, a total of 52 topological relations have been obtained, and the formalism of the 16IM and corresponding illustration are drawn (Figure 4(a)).

Figure 4. Overlap relations between two spatial regions with holes based on the 16IM.

short-legendFigure 4.

short-legendFigure 4.

Condition 3.4:

For the second situation of the overlap relation, A’s holes must intersect with B’s interior and boundary.(9) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ 0& \ast & \ast & \ast \end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & 0& \ast & \ast \end{array}\right]$(9)

Proof 4:

Because A’s exterior does not intersect with B’s interior, B’s interior and boundary can only intersect with A’s holes. ▪

Condition 3.5:

For the second situation of the overlap relation, if A’s holes intersect with B’s interior and boundary, then A’s holes at least intersect with one part of B’s exterior and holes. Likewise, condition 3.5 can be proven according to proof 3.(10) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ 1& 1& 0& 0\end{array}\right]$(10)

Condition 3.6:

For the second situation of the overlap relation, if B’s holes intersect with A’s boundary, then B’s holes must intersect with A’s interior and holes. Likewise, condition 3.6 can be proven according to proof 2.(11) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & 0\end{array}\right]$(11)

Condition 3.7:

For the second situation of the overlap relation, it is impossible for the intersection between B’s holes and A’s exterior.(12) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & \ast \end{array}\right]$(12)

Proof 5:

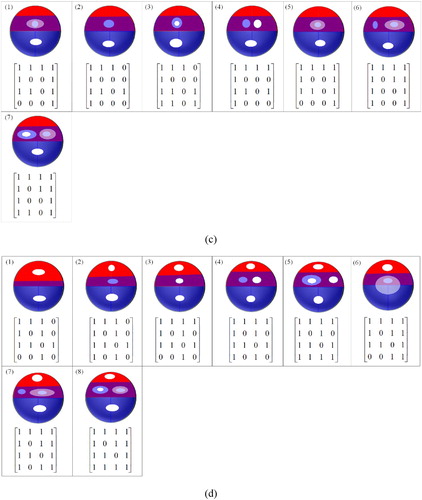
Because A’s exterior does not intersect with B’s interior, B’s holes must be inside A’s external boundary. Therefore, it is impossible for the intersection between B’s holes and A’s exterior. Condition 3.1 also holds true for the second situation of the overlap relation. Based on the conditions 3.1, and 3.4–3.7, a total of seven topological relations have been obtained, and the formalism of the 16IM and corresponding illustration are drawn (Figure 4(b)). ▪

Condition 3.8:

For the third situation of the overlap relation, B’s holes must intersect with A’s interior and boundary. Likewise, condition 3.8 can be proven according to proof 4.(13) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \end{array}\right]$(13)

Condition 3.9:

For the third situation of the overlap relation, if B’s holes intersect with A’s interior and boundary, then B’s holes at least intersect with one part of A’s exterior and holes. Likewise, condition 3.9 can be proven according to proof 3.(14) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & 1\\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\end{array}\right]$(14)

Condition 3.10:

For the third situation of the overlap relation, if A’s holes intersect with B’s boundary, then A’s holes must intersect with B’s interior and holes. Likewise, condition 3.10 can be proven according to proof 2.(15) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ 0& 1& \ast & \ast \end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & 1& \ast & 0\end{array}\right]$(15)

Condition 3.11:

For the third situation of the overlap relation, it is impossible to have the intersection between A’s holes and B’s exterior. Likewise, condition 3.11 can be proven according to proof 5.(16) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & 1& \ast \end{array}\right]$(16)

Condition 3.1

also holds true for the third situation of the overlap relation. Based on the conditions 3.1, and 3.8–3.11, a total of seven topological relations have been obtained, and the formalism of the 16IM and corresponding illustration are drawn (Figure 4(c)).

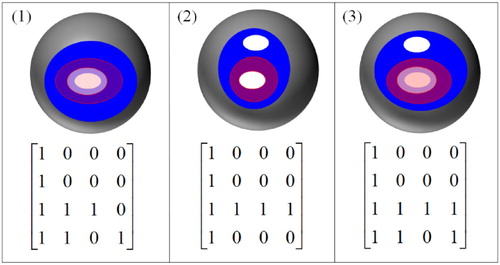
3.4. Cover relation

A cover relation means that a spatial object A spatially covers another spatial object B. If the intersection between A’s closure and B’s closure is equal to B’s closure, the intersection of A’s exterior and B’s interior is an empty set, the intersection of A’s exterior and B’s boundary is an empty set, and the intersection of A’s boundary and B’s boundary is a non-empty set, then the topological relation between A and B is a cover (Formula (17)).(17) $A.Cover\left(B\right)\Rightarrow (\overline{A}\cap \overline{B}=\overline{B})\wedge (A^{-}\cap B^o=\phi )\wedge (A^{-}\cap \mathrm{\partial }B=\phi )\wedge (\mathrm{\partial }A\cap \mathrm{\partial }B\ne \phi )$(17)

According to Formula (17), there is only one situation for the cover relation if holes are not considered (Formula (18)). To further categorize the cover topological relations, negative conditions are proposed to eliminate the impossible relations.(18) $R_{16IM}(A,B)=\left[\begin{array}{cccc}1& 1& 1& \ast \\ 0& 1& 1& \ast \\ 0& 0& 1& \ast \\ \ast & \ast & \ast & \ast \end{array}\right]$(18)

Condition 3.12:

For the cover relation, if the intersection between B’s holes and A’s boundary is a non-empty set, then the intersection between B’s holes and A’s interior and holes are a non-empty set.(19) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & 0\end{array}\right]$(19)

Proof 6:

For the cover relation, the intersection between A’s closure and B’s closure is equal to B’s closure. If B’s holes intersect with A’s boundary, then B’s holes may contain at least a complete or incomplete internal boundary of A. If B’s holes contain an incomplete internal boundary of A, then the intersection between A’s closure and B’s closure is not equal to B’s closure. Therefore, B’s holes must contain at least a complete internal boundary of A, and that means that B’s holes contain at least one hole of A. Therefore, the intersection between B’s holes and A’s interior and holes are a non-empty set. ▪

Condition 3.13:

For the cover relation, it is impossible to have the intersection between A’s holes and B’s interior.(20) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ 1& \ast & \ast & \ast \end{array}\right]$(20)

Proof 7:

If A’s holes intersect with B’s interior, then one part of B belongs to the A’s holes and$\overline{A}\cap \overline{B}\ne \overline{B}$ must be true. Therefore, the intersection between A’s holes and B’s interior are a non-empty set. ▪

Condition 3.14:

For the cover relation, it is impossible to have the intersection between A’s holes and B’s boundary. Likewise, condition 3.14 can be proven according to proof 7.(21) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & 1& \ast & \ast \end{array}\right]$(21)

Conditions 3.1 and 3.7 also hold true for the cover relation. Based on conditions 3.1, 3.7, and 3.12–3.14, a total of seven topological relations have been obtained, and the formalism of the 16IM and corresponding illustration are drawn (Figure 5).

Figure 5. Cover relations between two spatial regions with holes based on the 16IM.

3.5. Contain relation

A contain relation means that a spatial object A spatially contains another spatial object B. If the intersection between A’s closure and B’s closure is equal to B’s closure, the intersection between A’s interior and B’s interior is a non-empty set, and the intersection between A’s boundary and B’s boundary is an empty set, then the topological relation between A and B is a contain (Formula (22)).(22) $A.Contain\left(B\right)\Rightarrow (\overline{A}\cap \overline{B}=\overline{B})\wedge (A^o\cap B^o\ne \phi )\wedge (\mathrm{\partial }A\cap \mathrm{\partial }B=\phi )$(22)

According to Formula (22), there is only one situation for the contain relation if the holes are not considered (Formula (23)).(23) $R_{16IM}(A,B)=\left[\begin{array}{cccc}1& 1& 1& \ast \\ 0& 0& 1& \ast \\ 0& 0& 1& \ast \\ \ast & \ast & \ast & \ast \end{array}\right]$(23)

Condition 3.15:

For the contain relation, if the intersection between A’s holes and B’s holes are a non-empty set, and the intersections between A’s holes and B’s interior, boundary and exterior are an empty set, then the intersection between B’s holes and A’s boundary must be a non-empty set.(24) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & \ast \\ 0& 0& 0& 1\end{array}\right]$(24)

Proof 8:

If the intersection between A’s holes and B’s holes are a non-empty set, and the intersections between A’s holes and B’s interior, boundary and exterior are an empty set, then A’s holes must be inside of B’s holes. In this case, the intersection between B’s holes and A’s boundary must be a non-empty set. ▪

Condition 3.16:

For the contain relation, it is impossible that the intersection between A’s holes and B’s exterior and holes are a non-empty set, the intersection between A’s holes and B’s interior and boundary are an empty set, and the intersection between B’s holes and A’s boundary are an empty set. Likewise, this condition can be proven according to proof 8.(25) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & \ast \\ 0& 0& 1& 1\end{array}\right]$(25)

Conditions 3.1, 3.7, 3.12, 3.13, and 3.14 hold true for the contain relation. Based on conditions 3.1, 3.7, and 3.12–3.16, a total of three topological relations have been obtained, and the formalism of the 16IM and corresponding illustration are drawn (Figure 6).

3.6. Equal relation

An equal relation means that a spatial object A is spatially equal to another spatial object B. If the intersection between A’s interior and B’s interior is a non-empty set, the intersection between A’s exterior and B’s interior is an empty set, the intersection between A’s interior and B’s exterior is an empty set, the intersection between A’s exterior and B’s boundary is an empty set, and the intersection between A’s boundary and B’s exterior is an empty set, then the topological relation between A and B is equal (Formula (26)). There is an equal relation that can be realized based on the 16IM (Figure 7).(26) $\begin{array}{rl}& A.Equal\left(B\right)\Rightarrow (A^o\cap B^o\ne \phi )\wedge (A^{-}\cap B^o=\phi )\wedge (A^o\cap B^{-}=\phi )\wedge (A^{-}\cap \mathrm{\partial }B=\phi )\\ & \wedge (\mathrm{\partial }A\cap B^{-}=\phi )\end{array}$(26)

Figure 6. Contain relations between two spatial regions with holes based on the 16IM.

Figure 7. Equal relation between two spatial regions with holes based on the 16IM.

3.7. CoveredBy relation

A coveredBy relation means that a spatial object A is spatially covered by another spatial object B. CoveredBy and cover topological relations are mutually inverse relations. The matrices of the negative conditions of the coveredBy topological relation and that of the cover topological relation are transposed matrices. If the intersection between A’s closure and B’s closure is equal to A’s closure, the intersection between A’s interior and B’s exterior is an empty set, the intersection between A’s boundary and B’s exterior is an empty set, and the intersection of A’s boundary and B’s boundary is a non-empty set, then the topological relation between A and B is a coveredBy (Formula (27)).(27) $A.CoveredBy\left(B\right)\Rightarrow (\overline{A}\cap \overline{B}=\overline{A})\wedge (A^o\cap B^{-}=\phi )\wedge (\mathrm{\partial }A\cap B^{-})=\phi )\wedge (\mathrm{\partial }A\cap \mathrm{\partial }B)\ne \phi )$(27)

According to Formula (27), there is only one situation for the coveredBy relation if holes are not considered (Formula (28)). To further categorize the coveredBy topological relations, negative conditions are proposed to eliminate the impossible relations.(28) $R_{16IM}(A,B)=\left[\begin{array}{cccc}1& 0& 0& \ast \\ 1& 1& 0& \ast \\ 1& 1& 1& \ast \\ \ast & \ast & \ast & \ast \end{array}\right]$(28)

Condition 3.17:

For the coveredBy relation, if the intersection between A’s holes and B’s boundary is a non-empty set, then the intersection between A’s holes and B’s interior and holes are a non-empty set.(29) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ 0& 1& \ast & \ast \end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & 1& \ast & 0\end{array}\right]$(29)

Condition 3.18:

For the coveredBy relation, it is impossible to have the intersection between B’s holes and A’s interior. Likewise, condition 3.18 can be proven according to proof 7.(30) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & 1\\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \end{array}\right]$(30)

Condition 3.19:

For the coveredBy relation, it is impossible to have the intersection between B’s holes and A’s boundary. Likewise, condition 3.19 can be proven according to proof 7.(31) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \end{array}\right]$(31)

Conditions 3.1 and 3.11 also hold true for the coveredBy relation. Based on conditions 3.1, 3.11, and 3.17–3.19, a total of seven topological relations have been obtained, and the formalism of the 16IM and corresponding illustration are drawn (Figure 8).

3.8. Inside relation

An inside relation means that a spatial object A is spatially inside another spatial object B. Inside and contain topological relations are mutually inverse relations. The matrices of the negative conditions of the inside topological relation and that of the contain topological relation are transposed matrices. If the intersection between A’s closure and B’s closure is equal to A’s closure, the intersection between A’s interior and B’s interior is a non-empty set, and the intersection between A’s boundary and B’s boundary is an empty set, then the topological relation between A and B is inside (Formula (32)).(32) $A.Inside\left(B\right)\Rightarrow (\overline{A}\cap \overline{B}=\overline{A})\wedge (A^o\cap B^o\ne \phi )\wedge (\mathrm{\partial }A\cap \mathrm{\partial }B=\phi )$(32)

Figure 8. CoveredBy relations between two spatial regions with holes based on the 16IM.

According to Formula (32), there is only one situation for the inside relation if holes are not considered (Formula (33)).(33) $R_{16IM}(A,B)=\left[\begin{array}{cccc}1& 0& 0& \ast \\ 1& 0& 0& \ast \\ 1& 1& 1& \ast \\ \ast & \ast & \ast & \ast \end{array}\right]$(33)

Condition 3.20:

For the inside relation, if the intersection between B’s holes and A’s holes is a non-empty set, and the intersections between B’s holes and A’s interior, boundary and exterior is an empty set, then the intersection between A’s holes and B’s boundary must be a non-empty set. Likewise, this condition can be proven according to proof 8.(34) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ \ast & 0& \ast & 1\end{array}\right]$(34)

Condition 3.21:

For the inside relation, it is impossible that the intersection between B’s holes and A’s exterior and holes is a non-empty set, the intersection between B’s holes and A’s interior and boundary is an empty set, and the intersection between A’s holes and B’s boundary is an empty set. Likewise, this condition can be proven according to proof 8.(35) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ \ast & 0& \ast & 1\end{array}\right]$(35)

Conditions 3.1, 3.11, 3.17, 3.18, and 3.19 also hold true for the inside relation. Based on conditions 3.1, 3.11, and 3.17–3.21, a total of three topological relations have been obtained, and the formalism of the 16IM and corresponding illustration are drawn (Figure 9).

Figure 9. Inside relations between two spatial regions with holes based on the 16IM.

3.9. Attach relation

An attach relation means that a spatial object A spatially attaches another spatial object B. If the intersection between A’s interior and B’s interior is an empty set, the intersection between A’s closure and B’s closure is a non-empty set, and the intersection between A’s exterior and B’s exterior is an empty set, then the topological relation between A and B is an attach (Formula (36)). There is an attach relation that can be realized based on the 16IM (Figure 10).(36) $A.Attach\left(B\right)\Rightarrow (A^o\cap B^o=\phi )\wedge (\overline{A}\cap \overline{B}\ne \phi )\wedge (A^{-}\cap B^{-}=\phi )$(36)

Figure 10. Attach relation between two spatial regions with holes based on the 16IM.

3.10. Entwined relation

An entwined relation means that a spatial object A spatially entwines another spatial object B. If the intersection between A’s interior and B’s interior is a non-empty set, the intersection between A’s closure and B’s closure is not equal to A’s closure or B’s closure, the intersection between A’s boundary and B’s boundary is a non-empty set, the intersection of one spatial object’s boundary and another spatial object’s interior is a non-empty set, and the intersection between A’s exterior and B’s exterior is a non-empty set, then the topological relation between A and B is entwined (Formula (37)).(37) $\begin{array}{rl}& A.Entwined\left(B\right)\Rightarrow (A^o\cap B^o\ne \phi )\wedge (\overline{A}\cap \overline{B}\ne \overline{A})\wedge (\overline{A}\cap \overline{B}\ne \overline{B})\wedge (\mathrm{\partial }A\cap \mathrm{\partial }B\ne \phi )\\ & \wedge (\mathrm{\partial }A\cap B^o\ne \phi )\wedge (\mathrm{\partial }B\cap A^o\ne \phi )\wedge (A^{-}\cap B^{-}=\phi )\end{array}$(37)

There are four situations for the entwined relation if holes are not considered (Formula (38)). The first situation is that A’s exterior does not intersect with B’s boundary and exterior and B’s exterior does not intersect with A’s boundary. The second situation is that A’s exterior does not intersect with B’s boundary and exterior. The third situation is that B’s exterior intersects with A’s boundary and exterior. The fourth situation is that A’s exterior intersects with B’s exterior. To further categorize the entwined topological relations, negative conditions are proposed to eliminate the impossible relations.(38) $R_{16IM}(A,B)=\left[\begin{array}{cccc}1& 1& 1& \ast \\ 1& 1& 0& \ast \\ 1& 0& 0& \ast \\ \ast & \ast & \ast & \ast \end{array}\right]\vee \left[\begin{array}{cccc}1& 1& 1& \ast \\ 1& 1& 1& \ast \\ 1& 0& 0& \ast \\ \ast & \ast & \ast & \ast \end{array}\right]\vee \left[\begin{array}{cccc}1& 1& 1& \ast \\ 1& 1& 0& \ast \\ 1& 1& 0& \ast \\ \ast & \ast & \ast & \ast \end{array}\right]\vee \left[\begin{array}{cccc}1& 1& 1& \ast \\ 1& 1& 1& \ast \\ 1& 1& 0& \ast \\ \ast & \ast & \ast & \ast \end{array}\right]$(38)

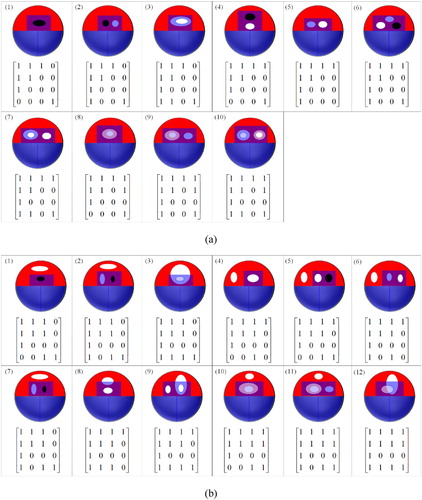
Conditions 3.1, 3.2, 3.5, 3.7, 3.9, and 3.11 hold true for the first situation of the entwined relation. Based on conditions 3.1, 3.2, 3.5, 3.7, 3.9, and 3.11, a total of 10 topological relations have been obtained, and the formalism of the 16IM and corresponding illustration are drawn ( Figure 11(a)).

Figure 11. Entwined relation between two spatial regions with holes based on the 16IM.

short-legendFigure 11.

Condition 3.22:

For the second situation of the entwined relation, the intersection between A’s holes and B’s exterior is not null.(39) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & 0& \ast \end{array}\right]$(39)

Proof 9:

Because A’s boundary intersects with B’s exterior and A’s exterior does not intersect with B’s exterior, A’s holes must intersect with B’s exterior. ▪

Conditions 3.1, 3.2, 3.5, 3.7, and 3.9 also hold true for the second situation of the entwined relation. Based on conditions 3.1, 3.2, 3.5, 3.7, 3.9, and 3.22, a total of 12 topological relations have been obtained, and the formalism of the 16IM and corresponding illustration are drawn (Figure 11(b)).

Condition 3.23:

For the third situation of the entwined relation, the intersection between A’s exterior and B’s holes is not null. Likewise, condition 3.23 can be proven according to proof 9.(40) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & \ast \end{array}\right]$(40)

Conditions 3.1, 3.2, 3.5, 3.9, and 3.11 also hold true for the third situation of the entwined relation. Based on conditions 3.1, 3.2, 3.5, 3.9, 3.11, and 3.23, a total of 12 topological relations have been obtained, and the formalism of the 16IM and corresponding illustration are drawn (Figure 11(c)).

Conditions 3.1, 3.2, 3.5, 3.9, 3.22, and 3.23 also hold true for the fourth situation of the entwined relation. Based on conditions 3.1, 3.2, 3.5, 3.9, 3.22, and 3.23, a total of 18 topological relations have been obtained, and the formalism of the 16IM and corresponding illustration are drawn (Figure 11(d)).

3.11. Embrace relation

An embrace relation means that a spatial object A spatially embraces another spatial object B. If the intersection between A’s interior and B’s interior is a non-empty set, the intersection between A’s closure and B’s closure is not equal to A’s closure or B’s closure, the intersection between A’s boundary and B’s boundary is an empty set, the intersection of one spatial object’s boundary and other spatial object’s interior is a non-empty set, and the intersection between A’s exterior and B’s exterior is a non-empty set, then the topological relation between A and B is embraced (Formula (41)).(41) $\begin{array}{rl}& A.Entwined\left(B\right)\Rightarrow (A^o\cap B^o\ne \phi )\wedge (\overline{A}\cap \overline{B}\ne \overline{A})\wedge (\overline{A}\cap \overline{B}\ne \overline{B})\wedge (\mathrm{\partial }A\cap \mathrm{\partial }B=\phi )\\ & \wedge (\mathrm{\partial }A\cap B^o\ne \phi )\wedge (\mathrm{\partial }B\cap A^o\ne \phi )\wedge (A^{-}\cap B^{-}=\phi )\end{array}$(41)

Similar to the Entwined relation, there are four situations for the Entwined relation if holes are not considered (Formula (42)). The first situation is that A’s exterior does not intersect with B’s boundary and exterior and B’s exterior does not intersect with A’s boundary. The second situation is that A’s exterior does not intersect with B’s boundary and exterior. The third situation is that B’s exterior intersects with A’s boundary and exterior. The fourth situation is that A’s exterior intersects with B’s exterior. To further categorize the Entwined topological relations, negative conditions are proposed to eliminate the impossible relations.(42) $R_{16IM}(A,B)=\left[\begin{array}{cccc}1& 1& 1& \ast \\ 1& 0& 0& \ast \\ 1& 0& 0& \ast \\ \ast & \ast & \ast & \ast \end{array}\right]\vee \left[\begin{array}{cccc}1& 1& 1& \ast \\ 1& 0& 1& \ast \\ 1& 0& 0& \ast \\ \ast & \ast & \ast & \ast \end{array}\right]\vee \left[\begin{array}{cccc}1& 1& 1& \ast \\ 1& 0& 0& \ast \\ 1& 1& 0& \ast \\ \ast & \ast & \ast & \ast \end{array}\right]\vee \left[\begin{array}{cccc}1& 1& 1& \ast \\ 1& 0& 1& \ast \\ 1& 1& 0& \ast \\ \ast & \ast & \ast & \ast \end{array}\right]$(42)

Condition 3.24:

For the embrace relation, the hole of one spatial object must contain the hole of another spatial object if the intersection of A’s holes and B’s holes is not an empty set.(43) $\begin{array}{rl}& R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ 0& 0& 0& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ 0& 0& 1& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ 0& 1& 0& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ 0& 1& 1& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ 1& 0& 0& 1\end{array}\right]\\ & \vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ 1& 0& 1& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ 0& 0& 0& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ 0& 0& 1& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ 0& 1& 0& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ 0& 1& 1& 1\end{array}\right]\\ & \vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ 1& 0& 0& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ 1& 0& 1& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & 0\\ 0& 0& 0& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & 0\\ 0& 0& 1& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & 0\\ 0& 1& 0& 1\end{array}\right]\\ & \vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & 0\\ 0& 1& 1& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & 0\\ 1& 0& 0& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & 0\\ 1& 0& 1& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & 1\\ 0& 0& 0& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & 1\\ 0& 0& 1& 1\end{array}\right]\\ & \vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & 1\\ 0& 1& 0& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & 1\\ 0& 1& 1& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & 1\\ 1& 0& 0& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & 1\\ 1& 0& 1& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 1\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ 0& 0& 0& 1\end{array}\right]\\ & \vee \left[\begin{array}{cccc}\ast & \ast & \ast & 1\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ 0& 0& 1& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 1\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ 0& 1& 0& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 1\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ 0& 1& 1& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 1\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ 1& 0& 0& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 1\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 0\\ 1& 0& 1& 1\end{array}\right]\\ & \vee \left[\begin{array}{cccc}\ast & \ast & \ast & 1\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ 0& 0& 0& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 1\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ 0& 0& 1& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 1\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ 0& 1& 0& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 1\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ 0& 1& 1& 1\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & 1\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ 1& 0& 0& 1\end{array}\right]\\ & \vee \left[\begin{array}{cccc}\ast & \ast & \ast & 1\\ \ast & \ast & \ast & 0\\ \ast & \ast & \ast & 1\\ 1& 0& 1& 1\end{array}\right]& \end{array}$(43)

Proof 10:

Since the intersection of A’s boundary and B’s boundary is an empty set, and the intersection of A’s holes and B’s holes is not an empty set, the hole of one spatial object must contains the hole of the other spatial object. ▪

Condition 3.25:

For the embrace relation, the hole of one spatial object does not intersect with the boundary of another spatial object if the intersection of A’s holes and B’s holes is an empty set. (44) $R_{16IM}(A,B)\ne \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & 1& \ast & 0\end{array}\right]\vee \left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & 1\\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & 0\end{array}\right]$(44)

Proof 11:

If the hole of one spatial object intersects with the boundary of another spatial object, then the intersection between the two boundaries must be a non-empty set. Since A’s boundary and B’s boundary is an empty set, A’s holes do not intersect with B’s boundary and B’s holes do not intersect with A’s boundary. ▪

Conditions 3.1, 3.2, 3.5, 3.7, 3.9, 3.11, 3.24, and 3.25 hold true for the first situation of the embrace relation. Based on these conditions, a total of six topological relations have been obtained, and the formalism of the 16IM and corresponding illustrations are drawn ( Figure 12(a)).

Figure 12. Embrace relation between two spatial regions with holes based on the 16IM.

short-legendFigure 12.

Conditions 3.1, 3.2, 3.5, 3.7, 3.9, 3.22, 3.24, and 3.25 hold true for the second situation of the embrace relation. Based on these conditions, a total of seven topological relations have been obtained, and the formalism of the 16IM and corresponding illustrations are drawn (Figure 12(b)).

Conditions 3.1, 3.2, 3.5, 3.9, 3.11, 3.23, 3.24, and 3.25 hold true for the third situation of the embrace relation. Based on these conditions, a total of seven topological relations have been obtained, and the formalism of the 16IM and corresponding illustrations are drawn (Figure 12(c)).

Conditions 3.1, 3.2, 3.5, 3.9, 3.22, 3.23, 3.24 and 3.25 hold true for the fourth situation of the embrace relation. Based on these conditions, a total of eight topological relations have been obtained, and the formalism of the 16IM and corresponding illustrations are drawn (Figure 12(d)).

4. Discussion

4.1. The comparison of topological relations between spherical spatial regions without holes and topological relations between spherical spatial regions with holes

The topological relations between spherical spatial regions without holes within the framework of the 9IM have been discussed (Egenhofer 2005). The topological relations between spherical spatial regions with holes within the framework of the 16IM are explored in the research. It is very necessary to compare the topological relations between spherical spatial regions without holes and the topological relations between spherical spatial regions with holes. A spatial object is divided into interior, boundary, exterior, and holes in the 16IM; however, a spatial object is divided into interior, boundary, and exterior in the 9IM. Since holes are considered to a separate part, the 16IM is a refinement of the 9IM. If the holes are attributed to the exterior in the 16IM (Formula (45)), then the simplified 16IM can be obtained. In Formula (45), the elements in the same rectangle are merged into one element. If the value of one element in the rectangle is equal to 1, then the value of the merged element is equal to 1; otherwise, the value of the merged element is equal to 0 (Formula (46)). Table 1 lists the comparison results of the topological relations between spherical spatial regions without holes based on the 9IM and the topological relations between spherical spatial regions with holes based on the simplified 16IM.(45) $R_{16IM}(A,B)=\left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \end{array}\right]$(45) (46) $E(e_1,\dots ,e_i,\dots ,e_n)=\left\{\begin{array}{c}1(e_1=1,\dots ,or{e}_i=1,\dots ,or{e}_n=1)\\ 0(e_1=0,\dots ,and{e}_i=0,\dots ,and{e}_n=0)\end{array}\right.$(46)

Table 1. Comparison results of the topological relations between spherical spatial regions without holes based on the 9IM and the topological relations between spherical spatial regions with holes based on the simplified 16IM.

Topological relations	9IM (Egenhofer, 2005)	Simplified 16IM
Disjoint relation	$\left[\begin{array}{ccc}0& 0& 1\\ 0& 0& 1\\ 1& 1& 1\end{array}\right]$	$\left[\begin{array}{ccc}0& 0& 1\\ 0& 0& 1\\ 1& 1& 1\end{array}\right]$
Meet relation	$\left[\begin{array}{ccc}0& 0& 1\\ 0& 1& 1\\ 1& 1& 1\end{array}\right]$	$\left[\begin{array}{ccc}0& 0& 1\\ 0& 1& 1\\ 1& 1& 1\end{array}\right]$
Overlap relation	$\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]$	$\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]$
Cover relation	$\left[\begin{array}{ccc}1& 1& 1\\ 0& 1& 1\\ 0& 0& 1\end{array}\right]$	$\left[\begin{array}{ccc}1& 1& 1\\ 0& 1& 1\\ 0& 0& 1\end{array}\right]$
Contain relation	$\left[\begin{array}{ccc}1& 1& 1\\ 0& 0& 1\\ 0& 0& 1\end{array}\right]$	$\left[\begin{array}{ccc}1& 1& 1\\ 0& 0& 1\\ 0& 0& 1\end{array}\right]$
Equal relation	$\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$	$\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$
CoveredBy relation	$\left[\begin{array}{ccc}1& 0& 0\\ 1& 1& 0\\ 1& 1& 1\end{array}\right]$	$\left[\begin{array}{ccc}1& 0& 0\\ 1& 1& 0\\ 1& 1& 1\end{array}\right]$
Inside relation	$\left[\begin{array}{ccc}1& 0& 0\\ 1& 0& 0\\ 1& 1& 1\end{array}\right]$	$\left[\begin{array}{ccc}1& 0& 0\\ 1& 0& 0\\ 1& 1& 1\end{array}\right]$
Attach relation	$\left[\begin{array}{ccc}0& 0& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right]$	$\left[\begin{array}{ccc}0& 0& 1\\ 0& 1& 1\\ 1& 1& 1\end{array}\right]$
Entwined relation	$\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 0\\ 1& 0& 0\end{array}\right]$	$\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 0\\ 1& 0& 1\end{array}\right],\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 0& 1\end{array}\right],\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 0\\ 1& 1& 1\end{array}\right],\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]$
Embrace relation	$\left[\begin{array}{ccc}1& 1& 1\\ 1& 0& 0\\ 1& 0& 0\end{array}\right]$	$\left[\begin{array}{ccc}1& 1& 1\\ 1& 0& 0\\ 1& 1& 1\end{array}\right],\left[\begin{array}{ccc}1& 1& 1\\ 1& 0& 1\\ 1& 0& 1\end{array}\right],\left[\begin{array}{ccc}1& 1& 1\\ 1& 0& 0\\ 1& 0& 0\end{array}\right],\left[\begin{array}{ccc}1& 1& 1\\ 1& 0& 1\\ 1& 1& 1\end{array}\right]$

The following conclusions can be concluded from Table 1. The formalisms of the disjoint, meet, overlap, cover, contain, equal, coveredBy, and inside topological relations are the same based on the 9IM and simplified 16IM. However, the formalisms of the attach, entwined, and embrace topological relations are different based on the 9IM and simplified 16IM. For the attach relation, since there are separate boundaries and separated exterior of the spatial region with holes in the simplified 16IM and the non-empty set of the intersection between two closures, the intersection between A’s boundary and B’s exterior, the intersection between B’s boundary and A’s exterior, and the intersection between A’s exterior and B’s exterior must be a non-empty set. For the entwined and embrace relations, since there are separate boundaries and separated exterior of the spatial region with holes in the simplified 16IM and the non-empty set of the intersection between two closures, the above–mentioned two topological relations have multiple formalisms.

4.2. The calculation of topological relations between spherical spatial regions with holes

For the calculation of topological relations between spherical spatial regions with holes, algorithms have been defined and implemented. Geometry engine open source (GEOS) which is a C++ implementation of the functions and predicates defined in the OpenGIS ‘Simple Features for SQL’ specification is referred to for defining algorithms. The union of two simple spatial regions can be calculated based on GEOS. The intersections between two boundaries of simple spatial regions can be calculated based on GEOS. By determining whether a point is inside a polygon based on GEOS, the relative position relation of a point and a polygon can be determined. In other words, whether a point in the interior, boundary, exterior, or holes of a region can be determined. For spatial region with holes A_1-n and spatial region with holes B_1-n, A₁ and B₁ are the simple regions surrounded by outer boundaries, and A_i and B_i $(i\ge 2andi\le n)$ are the simple regions surrounded by inner boundaries. Following steps are the algorithms of the topological relations calculation.

1. The union of A₁ and B₁ is calculated based on GEOS. If the region surrounded by outer boundary of the union is equal to the surface of the sphere, the intersection between A’s exterior and B’s exterior is equal to 0 and the topological relation is one of the attach, entwined, and embrace. Otherwise, the intersection between A’s exterior and B’s exterior is equal to 1 and the topological relation is one of the disjoint, meet, overlap, cover, contain, equal, coveredBy, and inside.

2. The intersections of the boundary of A_i$(i\ge 1andi\le n)$ and the boundary of B_j $(j\ge 1andj\le n)$ are calculated based on GEOS. The boundaries are separated at the intersection to form a number of edges.

3. The 16-intersections of A and B are calculated. After determining the relative position relation of points on edges and spatial regions, and the relative position relation of points on edges’ neighborhood and spatial regions, the 16-intersections of A and B are obtained.

5. Instance of topological relations between spherical spatial regions with holes

There are many spatial regions with holes in the geospatial world. In this experiment, the distribution of two lakes and the distribution of precipitation are taken as examples (Figure 13). Lake Tai (LT) and Lake Hongze (LH) are the third and fourth largest freshwater lakes in China, respectively. There are many islands in the lakes. The precipitation (P) was below 10 mm from 14:00 on 17 May 2018 to 14:00 on 18 May 2018 in China. Both the geometries of the two lakes and the precipitation have holes. To analyse the topological relations between the spherical spatial regions with holes, the above-mentioned spatial objects were uploaded to Google Earth.

Figure 13. Distribution of two lakes and precipitation. (a) The globe view of the two lakes and precipitation. (b) The partial view of the two lakes and precipitation.

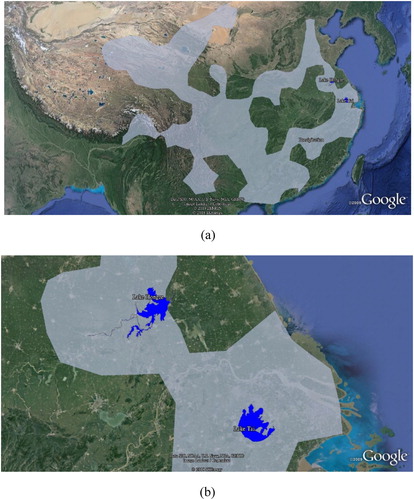
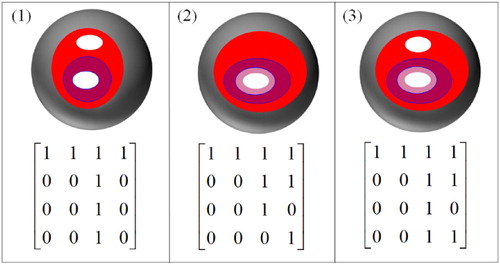
Based on the 16IM, the formalism of the 16IM among the spatial objects in Figure 13 are given (Formulas (47)–(51)). The topological relation between LT and LH and the topological relation between LH and LT are the same disjoint relation. The topological relation between LT and the P is one of an inside relation. The topological relation between LH and the P and the topological relation between the P and LH are an overlap relation, whereas the formalism of the 16IM are different. The topological relation between the P and LT is one of a contain relation.(47) $R_{16IM}(LT,LH)=R_{16IM}(LH,LT)=\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 1& 0\\ 1& 1& 1& 1\\ 0& 0& 1& 0\end{array}\right]$(47) (48) $R_{16IM}(LT,P)=\left[\begin{array}{cccc}1& 0& 0& 0\\ 1& 0& 0& 0\\ 1& 1& 1& 1\\ 1& 0& 0& 0\end{array}\right]$(48) (49) $R_{16IM}(LH,P)=\left[\begin{array}{cccc}1& 1& 1& 0\\ 1& 1& 1& 0\\ 1& 1& 1& 1\\ 1& 0& 0& 0\end{array}\right]$(49) (50) $R_{16IM}(P,LT)=\left[\begin{array}{cccc}1& 1& 1& 1\\ 0& 0& 1& 0\\ 0& 0& 1& 0\\ 0& 0& 1& 0\end{array}\right]$(50) (51) $R_{16IM}(P,LH)=\left[\begin{array}{cccc}1& 1& 1& 1\\ 1& 1& 1& 0\\ 1& 1& 1& 0\\ 0& 0& 1& 0\end{array}\right]$(51)

We make the following conclusions according to the above experiment. Although both Formulas (49) and (51) are the overlap relations, their formalisms are different. Since the holes are identified in the 16IM, the 16IM can be regarded as the refinement of the 9IM. The topological relations between two objects A and B are relative. The formalism of the topological relation between A and B can be transposed by the formalism of the topological relation between B and A.

6. Conclusions

In this research, the topological relations between spherical spatial regions with holes are analysed. (1) There are a total of 25 negative conditions that are proposed to eliminate the impossible topological relations between spherical spatial objects with holes. (2) There are 3 disjoint relations, 3 meet relations, 66 overlap relations, 7 cover relations, 3 contain relations, 1 equal relation, 7 coveredBy relations, 3 inside relations, 1 attach relation, 52 entwined relations, and 28 embrace relations that have been distinguished by the 16IM. (3) The comparisons of the topological relations between spatial regions without holes and the topological relations between spatial regions with holes have been discussed. (4) The formalisms of disjoint, meet, overlap, cover, contain, equal, coveredBy, and inside relations between the spatial regions without holes based on the 9IM and that between the spatial regions with holes based on simplified 16IM are the same, whereas the formalisms of attach, entwined, and embrace relations between spatial regions without holes based on the 9IM and that are between spatial regions with holes based on the simplified 16IM are different.

Although the 16IM is suitable for the representation of topological relations between spatial regions with holes, the 16IM is more complex than the 9IM. Moreover, the topological relations between other spherical spatial objects, such as bodies or bodies with holes, were not considered. Furthermore, the topological relations in other spaces, such as three-dimensional space, should be considered in the future. Although an instance of the topological relations between spherical spatial regions with holes has been given, the further application of topological relations between spatial regions with holes should be studied. Although algorithms for the calculation of topological relations between spherical spatial regions with holes have been proposed, a lot of in-depth research work is needed for real world applications. Qualitative reasoning is an important research field, standard transitive inference rules about point sets (Egenhofer 1994) can be introduced to study the qualitative reasoning of topological relations between spherical spatial regions in the future. There is no doubt that the topological relations between spherical spatial objects will promote advanced analysis in special tools, such as Digital Earth (Guo et al 2017) and Virtual Geographic Environments (Lin et al. 2013; Lin, Chen, Lu 2013).

Acknowledgements

We would like to thank the editors and anonymous referees for their constructive comments.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

Min Chen http://orcid.org/0000-0001-8922-8789

Additional information

Funding

This research was supported by the National Basic Research Program of China (973 Program) [No. 2015CB954103], and Priority Academic Program Development of Jiangsu Higher Education Institutions [No. 164320H116].