Mathematics Mediational Means and Learner Centredness: Insights from ‘traditional’ Malawian Secondary School Geometry Lessons

Abstract

We re-examine a Malawian teacher’s lessons which, using the framework of mathematic problem-solving developed by Polya, the typology of levels of task demand from Stein and colleagues and Malawi’s description of learner-centred education (LCE), were described as teacher-centred and evaluated as ‘not good’. We studied seven video-recorded circle geometry lessons taught by the teacher and analysed these first using an LCE framework and then the Mathematics Discourse in Instruction (MDI) framework, adapted to suit the analysis of geometry lessons. The LCE analysis revealed that while the lessons were undoubtedly teacher-centred, they were not at the extreme end of an LCE continuum. Analysis using an adapted MDI framework showed that the teacher’s use of mediational means opened opportunities to learn mathematics. We argue that LCE frameworks are useful in mathematics education research as they do not dichotomise teaching practices, but they are insufficient. They can obscure opportunities made available to learn mathematics. Frameworks that illuminate such opportunities are needed to fully describe mathematics teaching practices. Furthermore, we identified links between the elements of LCE exhibited and the mathematical mediational means in use. These suggest that supporting teachers to strengthen their mathematical mediational means in use could enable movement towards more learner-centered teaching.

Keywords:

• LCE framework
• MDI framework
• geometric proof development
• Malawi

Introduction

Learner-centred education (LCE) is highly regarded as an effective means to achieving Sustainable Development Goal 4 of promoting inclusive and equitable quality education for all and promoting lifelong learning. In Malawi, teachers continue to be urged to move from ‘chalk and talk’ to more inquiry-based student-centred learning (Ministry of Education Science Technology (MoEST), 2013; Mtika & Gates, 2010). To achieve this shift, the Malawi curriculum emphasises the use of learner-centred teaching and learning approaches and that a ‘good lesson’ is a lesson where students are actively involved in exploring and constructing knowledge (MoEST, 2013). In this context, teaching is dichotomised as either teacher-centred and associated with a ‘not good lesson’ and low learner achievement, or learner-centred and associated with a ‘good lesson’ and high learner achievement.

This dichotomy informed an earlier study by Mwadzaangati (2017) where she explored mathematical knowledge for teaching geometric proof development in schools with high learner achievement in mathematics. The expectation was to observe and learn from ‘good mathematics lessons’. The study used mathematics education frameworks for problem solving (Polya, 1945) and levels of task demand (Stein et al., 1996), leading to descriptions of lessons as ‘good’ or ‘learner-centred’ where the teacher involved learners in exploratory pedagogic strategies using a high cognitive level geometric proof development tasks. Other lessons were regarded as ‘not good’ because learners were not involved in exploratory pedagogic strategies and used low cognitive demand tasks (Mwadzaangati, 2017, 2019). Although Polya’s (1945) and Stein et al.’s (1996) frameworks are not explicitly LCE, they resonated with the conception of LCE in Malawi, i.e. with emphasis on involving learners in exploring mathematics using high cognitive demand tasks to elicit high cognitive level thinking. A question remained: why were the teachers who taught ‘not good’ or ‘teacher-centred’ lessons also regarded as performing best in their schools? In addition, why were their students also high performing in national examinations? We argue that while the mathematics education frameworks used achieved the earlier study’s purposes of exploring knowledge for teaching geometric proof development, they did not adequately describe the quality of mathematics opportunities made available during instruction. We therefore ask what might become visible if we re-analyse some ‘not good’ geometry lessons using different lenses. As Charalambous and Praetorius (2018) have shown, different analytical frameworks might capture aspects of mathematics and pedagogy that were beyond the focus in the earlier study.

We have combined Guthrie’s (2011, 2018) framework that posits ‘five classroom teaching styles in a continuum from more to less teacher-centred’ (2018, p. 1), with the Mathematics Discourse in Instruction (MDI) framework that illuminates mathematical mediational means in use in instruction, to study a particular teacher’s geometry lessons previously categorised as ‘not good’. We analyse the mathematical quality of the lessons and the teacher’s pedagogical practices to locate the teacher in both Guthrie’ continuum (we refer to this from here on as a LCE continuum) and the MDI, and to further explore the relationship (if any) between the extent of LCE exhibited by the teacher and the mathematics mediational means in use. We contend that with a mathematical eye, and a more nuanced view of LCE as a continuum, we can strengthen our description of mathematics teaching and thus be better placed to offer appropriate Professional Development to diverse teachers to support them to move towards offering both LCE lessons and high-quality mathematics. We pursue the following research questions:

(1)	Where on the LCE continuum does the teacher’s instruction lie?
(2)	What mathematics mediational means are in use in his teaching?
(3)	How do the elements of LCE learning styles exhibited relate to the mathematics mediational means in use and so opportunities to learn?

Review of Learner-centred Education

Learner-centred education is rooted in socio-constructivist theories that view learners as active constructors of knowledge and learner achievement as a function of inquiry-based learning strategies (Lattimer, 2015; Mtika & Gates, 2010). Despite a consensus that LCE correlates positively with learner achievement, there is no universal agreement on the definition of LCE (Mtika & Gates, 2010). Nevertheless, the common features across different conceptions are that LCE emphasises social interaction of learners and reflects each student’s active learning and personal progress (Lattimer, 2015; Schweisfurth, 2013). We align our study with Schweisfurth’s (2015) view that learning is ‘situated within broad cultural norms, within a community and individual context, and based on interactions between teachers and learners’ (p. 262). Hence LCE is not an absolute contrast to teacher-centred education, but rather a continuum from less learner-centred pedagogical practices at one end to more learner-centred pedagogical practices at the other (Guthrie, 2011, 2018). As an indicator of quality education, the LCE concept has been invoked in many developing countries in their commitment to Sustainable Development Goal 4 (Schweisfurth, 2015). However, in its broadly conceived form, LCE has not only been differently interpreted across country contexts, but also resisted (Hoadley, 2018). Hoadley (2018) bemoans that despite the widespread resistance to LCE pedagogies in developing countries, no efforts have been made to identify productive pedagogic practices in these contexts, and further that ‘what is to be learnt (subject knowledge) is notably absent in the vast body of literature around curriculum and pedagogy in developing country contexts’ (p. 24).

Literature shows that research has also shifted from viewing LCE as a dichotomy of teacher-centered and learner-centered practice to a continuum that ranges from less to more learner-centred practice. Lattimer’s (2015) study that we discuss further below points to Guthrie’s (2011) framework of teaching styles as shown in Figure 1 as forming the basis for re-conceptualising LCE as a continuum. Later, Guthrie (2018) himself explicitly describes the five styles as a continuum from more to less teacher-centred and ranging from authoritarian to democratic teaching practice.

Figure 1. Classroom teaching styles model (Guthrie, 2011, p. 205).

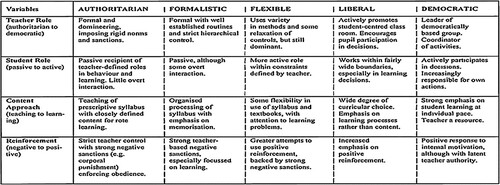
Guthrie (2011) uses four variables to characterise each teaching style: teacher role, student role, content approach and reinforcement. The authoritarian teacher is very formal and domineering, requiring obedience to organisational norms and a passive student role. He equates this teaching style with teacher-centred practice because the underlying epistemology is knowledge transmission rather than knowledge construction. On the other hand, the democratic teaching is underpinned by a constructivist epistemology, promoting progressive learning by involving learners in knowledge construction, and equated to learner-centered practice. Guthrie (2018) acknowledged research that regarded the flexible style as more LCE practice, but argued for it to be placed amongst authoritarian and formalistic styles as all are underpinned by a view of knowledge transmission. Liberal and democratic styles, in contrast, are considered learner-centred practices as they involve learners in knowledge construction. Notwithstanding the value of Guthrie’s epistemological partitioning, we regard a teacher who exhibits elements of a flexible style as being closer to learner-centred practice than the one with a formalist style. We suggest that the differences in the degrees of teacher/learner involvement in three learning styles regarded as teacher-centred are helpful in locating where the teacher is coming from and moving to.

Schweisfurth (2015) agrees with Guthrie (2011) that LCE is not an absolute pedagogical practice but a continuum and builds on the LCE literature by suggesting seven minimum standards for LCE. Both Guthrie’s (2011) and Schweisfurth’s (2013) models have been used to examine the degree of LCE in mathematics lessons. Lattimer (2015), for example, contrasted two Kenyan teachers who both used traditional instruction, but whose teaching differed substantively. She found that a Form I mathematics teacher’s lesson on measurement with tasks involving calculating the areas of a triangle and the area of space between two rectangles was ‘formalistic’ in Guthrie’s (2011) terms and met only one of Schweisfurth’s (2013) LCE standards. In contrast, a Form II mathematics teacher’s lesson on calculating the distance travelled by a car over a given time and the time taken to travel a given distance, was ‘flexible’ in Guthrie’s (2011) terms and met all Schweisfurth’s (2013) LCE standards. Lattimer’s study provoked us to ask: while the instruction of John (pseudonym for the teacher in focus in this paper) was also traditional, where on the LCE continuum would his kind of instruction lie? We only used Guthrie’s (2011) styles of teaching to locate the teacher on the continuum as we found Schweisfurth’s (2013) LCE minimum standards open to multiple interpretations and problematic to operationalise.

Returning to Lattimer’s (2015) study and her analysis of lessons in terms of LCE pedagogical practices, the content or mathematics made available to learn was backgrounded. Briefly, in the first formalistic class, students completed six different area calculation tasks. In contrast, the second flexible and more learner-centered class completed two very similar problems easily solved using the formulae for relative speed. How, if at all, does this factor into opportunities for learning mathematics in the lessons? As Charalambous and Praetorius (2018) argue, pedagogical theories are about general instructional strategies but do not provide specific insights into the teaching of a particular subject just as content-specific frameworks provide insights into the teaching of a particular subject but can obscure insights into general pedagogical issues. We agree: there is no framework that has the capacity to capture instruction in its entirety—different content-specific analytical tools ‘illuminate certain instructional aspects but leave others less visible’ (Charalambous & Praetorius, 2018, p. 335). Therefore, our aim in this paper is to add to the growing insights into the complexity of LCE by asking: what else could we learn by further analysing John’s lessons using a mathematics specific framework developed in the South African context—the Mathematics Discourse in Instruction (MDI) framework (Adler & Ronda, 2015). The MDI is useful not only as it emerged in an educational context similar to that of Malawi, but because it is neutral with regard to pedagogic norms with emphasis on describing mathematics opportunities made available to learn in a lesson.

The Theoretical Grounding of Mathematical Discourse in Instruction Framework

MDI is a conceptual framework for describing the quality of mathematics teaching (see Adler & Ronda, 2015). Briefly here, MDI is constructed from key tenets of socio-cultural theory in the Vygotskian (1978) sense, and thus an orientation to mathematics as ‘scientific’ knowledge, and teaching/learning as mediation towards increasingly general and sophisticated ideas in the discipline. The starting point in MDI is that teaching, and thus learning, is always about something, and bringing that into focus—its mediation—is the teacher’s work. This ‘something’, using Marton et al.’s (2004) language, is the object of learning, consisting of the mathematical ‘object’ and the capability associated with it that the teacher aims to focus on in the lesson. While in practical terms, it aligns with a lesson goal, in socio-cultural terms it points to that which needs to be mediated and thus the goal-directed activity of the teacher. In the MDI framework presented in Figure 2, the key generative mechanisms for this work of teaching are exemplification, explanatory talk and learner participation. What sits between (i.e. mediates) the object (of learning) and the subject (the learner) are four key symbolic mediational means in mathematics classroom instruction—examples, tasks, word use and justifications. These work together with learner participation to exemplify and elaborate the object of learning, and so open (or close) opportunities to learn.

Figure 2. Mathematics Discourse in Instruction Framework adapted from Adler and Ronda (2015, p. 239).

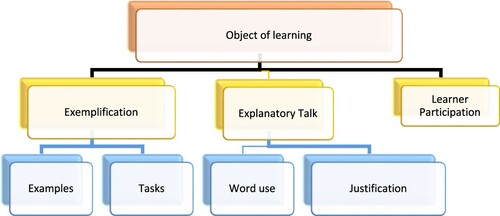
To this end, MDI co-ordinates aspects of variation theory (e.g. Marton et al., 2004) into its overall socio-cultural framing to enable analysis of what changes (variance) amidst what remains the same (invariance) across an example set in a lesson, and through this, possibilities to generalise about an object of learning (Watson & Mason, 2006). Explanatory talk draws from research on language practices to include the words we use and how we use them to name and justify mathematical concepts and processes. Word use and justification afford or constrain understanding and generalising about the object of learning, which in this paper is the development of a geometric proof.

The Teaching and Learning of Geometric Proof Development

Geometry is a key aspect of high school mathematics because it enhances the development of spatial reasoning, visualisation skills, deductive reasoning and proving (Chinnappan et al., 2012). Research has shown, however, that within the domain of geometry, proof development is very difficult for students to learn and for teachers to teach (Chinnappan et al., 2012). One of the challenges for students is the way they perceive diagrams—what is exemplified in MDI’s terms—and consequently their interpretations of the geometric properties encoded into diagrams (Fujita & Jones, 2007). The challenge for many teachers is the content knowledge of Euclidean Geometry and pedagogical content knowledge needed for effective geometry teaching (Abdullah & Zakaria, 2013). In MDI terms this would extend beyond what is exemplified, i.e. how diagrams are selected and used, to explanatory talk (Adler & Ronda, 2015). As Abdulla and Zakaria (2013) explain, the dominant approach in many classrooms encourages students to memorise and reproduce proofs. Students are not given an opportunity to investigate, observe, discover and express geometry theorems: proofs are presented as ready-made ideas to be accepted without question (Abdullah & Zakaria, 2013). This kind of geometric instructional practice aligns with authoritarian teaching practices on the LCE continuum with limited opportunities for meaning construction through learners’ activity and their use of mathematical language (learner word use and justification in MDI). These studies suggest that teachers could benefit from professional development that supports them to shift towards teaching approaches that promote learners’ activity through inquiry-based tasks and the use of mathematical language.

Design and Methodology

Description of the Teacher

John was in his thirteenth year of teaching secondary mathematics. He had a first-degree qualification for teaching mathematics and was teaching at a conventional secondary school in Malawi. These are public secondary schools, mainly consisting of students with high performance in Grade 8 national examinations. John was teaching circle geometry in a Grade 11 class of 65 learners. He was regarded as one of the best teachers in the school because his students performed very well in mathematics in national examinations. However, in her previous study, Mwadzaangati (2017) categorised John’s lessons as ‘not good’ because they were teacher-centred and did not engage learners in exploring circle geometry theorems using cognitively activating and/or problem-solving tasks (Polya, 1945; Stein et al., 1996).

LCE and MDI Analysis

We began the analysis by watching the video-recorded lessons and reading original lesson transcripts several times. We revised some of the original transcripts by adding information that was visible in the video data but not in the transcripts, like chalkboard work and specifying how the teacher responded to learners’ answers. Our aim was to make visible LCE practices and MDI mediational means in use by the teacher during the lessons. For LCE, we used Guthrie’s (2011) categories of learning styles to determine where John lies on the continuum. For MDI, following Adler and Ronda (2015), we divided the lessons into episodes, as unit of analysis, by identifying a change in mathematical object in focus (e.g. from recalling properties to defining mathematical objects). We analysed the examples and tasks in each episode, as well as mathematical word use and justifications. Working with principles of variation suggested by Watson and Mason (2006), we examined the variation in the example set of cyclic quadrilaterals across the lesson. These were largely represented as diagrams, and we zoomed in on three key dimensions of variation visible across the example set: diagram orientation, diagram complexity and whether and how contrast was used. As the orientation of a cyclic quadrilateral is related to the position of its vertices, there is a wide range of possible orientations. Following Huang and Leung (2017) we distinguished standard oriented diagrams (SO), i.e. prototypical diagrams drawn in their familiar or usual/upright position, from non-standard oriented (NSO) diagrams, i.e. non-prototypical diagrams drawn in unfamiliar/unusual/non-upright positions. In terms of diagram complexity, we distinguished between a basic diagram (BD), i.e. where no reconfiguration is required for the task at hand, such as one cyclic quadrilateral in a circle, and a complex diagram (CD), i.e. where there are overlapping diagrams and a reconfiguration was needed, for example when the cyclic quadrilateral that needed to be in focus had to be isolated or marked out from another quadrilateral.

With respect to tasks, Adler and Ronda (2015) distinguish known operation/procedure, application and problem-solving tasks. In his geometry lesson, John included a range of tasks that we have distinguished in a similar way, adding in further distinctions as follows: recalling known geometric properties/definitions (DK), applying known geometric properties (AK), defining new geometric properties (DN), applying a new property to do simple calculations using only that property (ANS), applying new properties to do complex calculations, and so use of more than one property (ANC) and proving using reasons (PR). As in Adler and Ronda (2015), for naming and word use, we analysed whether words used by the teacher and/or learners were colloquial (NM), such as the use of everyday language and/or ambiguous pronouns, and/or read as a string of symbols or names only (Ms), and/or if the mathematical words were used appropriately (Ma). We further added a code for determining if the mathematical words were used partially or in pseudomathematical ways (Mp), e.g. cancel. We coded justifications as partially general (GP) when the generalisation or justification for a geometric statement was not complete and general full (GF) for complete justification as in the original MDI framework. We introduced new codes for describing whether the teacher legitimated a learner’s answer through revoicing (LR), or wrote the learner’s response on the chalkboard (LW), or said yes/no/or good (L). On learner participation, we used the original MDI codes to describe whether learners only answered yes or no questions (Y/N), or what or how questions in phrases or sentences (P/S), or why questions (D). We introduced new codes to describe if learners answered the questions in chorus form (C) or individually (I).

Findings

Describing the Lessons

The dataset examined comprised seven lessons. From these, we identified a routine practice across John’s teaching. He began each lesson with a recap of prior knowledge by asking learners to recall relevant geometric properties, and then solving at least one related problem. He then introduced the theorem to be learnt in the current lesson by verbalising it orally, illustrating it in a diagram on the board and asking learners to define some mathematical objects that built the theorem. He then developed the proof of the theorem, and while he asked learners leading questions, he mostly carried out each step himself. Lastly, he applied the theorem by working on at least one example with the learners, and then giving them either classwork or homework exercises. We have selected coded episodes 2 and 4 (see Tables 2 and 3) from the fourth lesson on ‘The interior opposite angles of a cyclic quadrilateral are supplementary’ as these are illustrative of our deeper analysis of John’s lessons using Guthrie’s LCE continuum and the MDI frameworks.

Analysis of John’s Lessons using LCE Framework

Applying Guthrie’s (2011) LCE categories of learning styles to John’s lessons, we see that learners are not only passive, they answer John’s questions as shown in both episodes 2 and 4. Although there is strict teacher control of all lessons as shown in episode 4 (81, 84), he does not reinforce negative sanctions (see lines 23, 31 and 34). Hence, he is not completely formalist but lies between being formalist and flexible. He is formalistic in teacher roles with respect to the approach to content: he has a routine way of developing the proofs that requires memorisation. As shown in episode 4, he has hierarchical control of the lesson as he decides what to prove (81, 86 and 90), the diagram and the names of the angles to be used for developing the proof and the construction to be made (81). He also decides statements to be used for developing the proof (82–107). In contrast, he is more flexible with student roles: he does not only lecture but also invites learners to answer questions as indicated in both episodes. He also uses positive reinforcements including saying ‘yes’ (e.g. 25, 35 and 84), and he re-voices learners’ responses in a respectful manner in both episodes.

Analysis of the Lessons Using MDI Framework

Analysis of the lessons using the MDI framework revealed that John made available several mathematics mediational means while constraining others. In each lesson, he made available accumulating tasks and example sets. As shown in Table 1, across lesson 4, he varied both the orientation and complexity of the cyclic quadrilateral used and used a counter example.

Table 1. Tasks and examples used by John in lesson 4

Regarding variation of examples, as shown in Table 1, we coded diagrams in episodes 2 and 3 as well as the first two diagrams in episode 5 as BD because they contain one quadrilateral in each circle, and do not require any reconfiguration to do their related tasks. We coded the diagram in episode 1 as CD because it requires reconfiguring or isolating the set of angles at the centre and at the circumference for applying the theorem. We coded diagrams for writing the proof in episode 4 as CD because they also required reconfiguring the quadrilateral to be used for the proof since two quadrilaterals (BOCD and BACD) overlap. In episodes 2–5, there were no diagrams whose quadrilaterals are entirely upright, but some quadrilaterals are prototypical because they are drawn in familiar/usual way, e.g. diagrams in episodes 2 and 3 unlike those in episode 4. As such, we coded diagrams in episodes 2 and 3 as SO and those in 4 as NSO. In episode 2 John used contrast to illustrate what was and what was not included in the class of cyclic quadrilaterals (33). Tables 2 and 3 present the coding in part of episodes 2 and 4 respectively.

Table 2. Part of lesson episode 2 (italic purple is learner-centred education analysis and other codes are Mathematics Discourse in Instruction)

Table 3.   Part of lesson episode 4

As Tables 1–3 show, John made available to learners several recall, defining, application and proof tasks. Episode 1 and Table 1 include tasks of defining known geometric objects, such as the circle and quadrilateral (19 and 26), and defining new geometric objects, like a cyclic quadrilateral (28). Since the definitions of a circle and a quadrilateral were already known by the learners, we coded these tasks as DK. As Table 1 shows, the tasks of defining a cyclic quadrilateral in episode 2 and explaining the meaning of the theorem interior opposite angles of a cyclic quadrilateral are supplementary in episode 3 were coded DN because these objects were part of new learning. In episode 4, John offered a proof development task, coded PR, although he carried out the task himself. In episode 5 shown in Table 1, the worked example was a simple application numerical task (ANS) that required application of single property of interior opposite angles of cyclic quadrilateral are supplementary to find measures of angles x and y. He also offered complex numerical application tasks requiring application of more than one theorem/property to calculate measures of angles. For example, in the second exercise example, the task of calculating measures of angles t and x requires application of the theorems angle subtended by the arc at the centre of the circle is two times the angle subtended by the arc at the circumference of the circle and the interior opposite angles of a cyclic quadrilateral are supplementary.

Regarding learner participation, Table 1 shows that John invited individual (I) learners to answer questions (P/S) in tasks of defining known geometric objects such as circle and quadrilateral (19 and 26), and in defining new geometric objects like cyclic quadrilateral (28). The defining of the mathematical objects was done logically, beginning with defining mathematical objects embedded in other mathematical objects. For example, ‘circle’ and ‘quadrilateral’ were defined first because they build the concept of a ‘cyclic quadrilateral’. Using Guthrie’s LCE continuum, John legitimated learner’s responses through saying yes or no (Y/N) and thus with positive reinforcement, revoicing learners’ definitions in a respectful manner (LR), regarded as establishing mutual respect (25, 28), and then writing (LW) the definitions on the chalkboard. When learners could not give a complete definition of a cyclic quadrilateral (Mp), he used a counter example by drawing diagrams with varied positions of vertices of quadrilateral (31). This enabled learners to move from a partial definition of a cyclic quadrilateral (30) to defining a cyclic quadrilateral completely (Ma) using its features (34) and to justify why the first quadrilateral is not cyclic (GF).

In episode 4, which is about developing the proof, John began by asking learners to mention the steps to be followed when writing a proof. The learners mentioned the steps as (1) identifying the given information, (2) identifying the statement to be proved, (3) identifying the construction to be made, and (4) writing the proof. He then drew a diagram of a cyclic quadrilateral and used it for illustrating how to develop the proof and proceeded with the writing of the proving statements. Thus, in the task of developing a proof (PR) in episode 4, we see that students are given opportunities to use mathematical language through answering individually (I) what questions (P/S) and why (D) questions to complete and to justify (D) the statements (82–93). In Guthrie’s continuum, this implies that learners are not completely learning passively, but they are given opportunities to learn actively through answering questions. The asking of questions also means that John does not only lecture (33, 81), but he varies teaching methods. Some of the statements and justifications given by the learners are mathematical (Ma) and he revoices them and legitimates them in the same mathematical language verbally (LR), by writing on chalkboard (LW) or by saying yes or no (Y/N). In Guthrie’s LCE continuum this means that John establishes mutual respect with the learners and uses positive reinforcements. Some statements given by the learners are partially mathematical (Mp) and he revoices them and legitimates them in the same partial mathematical language (85–86, 91–92).

We also notice in episode 4 that John did not provide some mathematics mediational opportunities to learn. Firstly, he does not involve learners in an empirical exploration that would enable learners to discover the relationship about the opposite angles of the cyclic quadrilateral. Secondly, he provides a cyclic quadrilateral in which the construction of joining B and C to the centre O is already done. Consequently, the learners have no opportunities to explore the construction that would enable proof. Thirdly, he does not give the learners opportunities to explore ways of developing the proof as he suggests the statements and properties to use. Although he involves learners in completing the geometric statements for the proof and justifying the statements, his way of questioning shows that he decides the proving statements; what can you say about angle BOC (82). He also decides how to connect the statements logically (102–106); as such, the learners do not have opportunities to explore the proof and decide the statements to be used and how these statements could be connected, hence there are no opportunities for developing learners’ geometric reasoning and deductive reasoning. While we acknowledge that it is very difficult for learners to develop a geometric proof from scratch on their own, we argue that this does not imply that the teacher should not challenge the learners to explore ways of developing the proof.

Discussion of the Findings

When we compare John with the two Kenyan teachers referred to in the review on learner-centred education section using Guthrie’s (2011) LCE continuum, we find some similarities and differences. John was like the first Kenyan teacher who exhibited a formalist teaching style in terms of the teacher role as he was in total control of the lessons, doing most of the thinking, particularly on proof tasks (Lattimer, 2015). John however offered more than the first Kenyan teacher in several ways. He did not ask questions that promoted chorus answers but required individual answers, hence promoting some active participation of the learners like the second Kenyan teacher. He built on learners’ prior knowledge and enhanced mutual respect through revoicing learners’ answers and saying ‘yes’. This implies that he exhibits some flexibility, like the second Kenyan teacher (Lattimer, 2015). He, however, was not completely flexible because he did not involve learners into exploring mathematics, with teaching that leads to memorisation (Guthrie, 2011), supporting Mwadzaangati’s (2017; 2019) findings that led her to categorise John’s lessons as ‘not good’ through the lack of exploratory activities and involvement of learners in critical thinking tasks.

Concerning the mathematical mediational means made available, there was variation in the examples and tasks for enhancing understanding of the mathematical objects and movement towards generality (Adler & Ronda, 2015; Watson & Mason, 2006). The use of standard (prototypical) diagrams familiar to learners, in this case quadrilaterals for defining mathematical objects and introducing a theorem, is a recommended basis for understanding non-standard (non-prototypical) diagrams (Huang & Leung, 2017). John offered clear explanations in defining mathematical objects and explaining what constitutes a proof and its application. Definitions play an important role in geometry in identifying mathematical objects and assigning properties to mathematical objects (Fujita & Jones, 2007). He also gave individual learners opportunities to use mathematical language through explaining geometric properties and providing their justifications as expected in mathematics classrooms (Adler & Ronda, 2015). We noticed that in some instances, both the teacher’s and the learners’ talk did not lead to full mathematical explanations and that some definitions were partial. Although we coded these as partially mathematical, we however regard these as school mathematics used for operational purposes (Adler & Ronda, 2015). The use of school mathematics is common in geometry because definitions are hierarchical. Making provision for complete definitions of geometry concepts is thus not always possible (Fujita & Jones, 2007). The findings also show that some mathematical opportunities were constrained in John’s lessons. He engaged learners in numerical application tasks but not proof tasks, and thus did not offer opportunities that could enhance learners’ proof development skills. The task that he used for teaching proof development could demand some degree of cognitive effort in how to apply different theorems and properties (Stein et al., 1996). However, since John did most of the thinking this was reduced to low-level thinking by the learners, as also found by Mwadzaangati (2019).

Across the seven lessons, we noted links between the learners’ roles and the mathematical mediational means the teacher made available to learn. He invited learners to define mathematical objects and express justifications—thus learners took active roles in the lesson in terms of LCE. He legitimated the learners’ responses and used them to develop full mathematical definitions and statements—thus establishing mutual respect and providing positive reinforcements. We therefore claim that in these lessons, a partial LCE approach was manifested in class through the teacher’s clear and full mathematical definitions that and explanations, together with the use of varied examples and the involvement of learners in answering a range of mathematical questions. From this analysis we can suggest that stimulating John’s teaching practice to include (1) varied tasks and task demand, (2) varied diagrams in terms of both orientation and complexity and (3) questions posed that do not only direct learners to recall the property or give simple answers but also to think mathematically, could set him, and other similar teachers, on the road towards the democratic side of the LCE continuum.

Conclusion

In this paper, we contribute to the debate on LCE and quality teaching and learning using Guthrie’s (2011) LCE continuum and MDI frameworks to examine the quality of mathematics mediational means made available in a Malawian teacher’s geometry lessons which were initially pedagogically labelled as teacher-centred and ‘not good’. We have shown that this Malawian teacher is on the move from formalist to flexible instruction, with possibilities for moving towards democratic and more learner-centred practice (Guthrie, 2018). Using the MDI framework, we showed that he made available several mathematics mediational means, although he constrained others. We agree with the authors who argue that the literature on LCE in developing countries tends to polarise the practice by only focusing on the two ends of the continuum but not the process in between. We further argue that LCE pedagogical approaches obscure opportunities to notice the mathematical mediational means made available or constrained in a lesson. We therefore suggest the co-ordination of frameworks that illuminate both mathematical content and LCE aspects if we are to describe the teachers’ practices more adequately—and through this be better positioned to support their movement along an LCE continuum. We also point to links between aspects of the LCE continuum of the teacher and the quality of mathematics mediational means made available. We suggest professional development that supports teachers to make available key mathematics mediational means and that further research is needed on the relationship between the quality of mathematics made available to learn and LCE practices.

Acknowledgement

This paper is based on postdoctoral fellowship work in the Wits Maths Connect Project at University of the Witwatersrand and in collaboration with the Faculty of Education at University of Malawi. Any opinion, conclusion or recommendation expressed in this material is that of the authors.

Disclosure Statement

No potential conflict of interest was reported by the authors.